2021届高三数学精准培优专练 外接球(文) 教师版
2021届高三数学精准培优专练 圆锥曲线综合(理) 教师版

b a
x,
∴点 F2 到渐近线的距离 d
bc a2 b2
b ,即
PF2
b,
∴ OP
OF2 2 PF2 2
c2
b2
a , cos PF2O
b c
,
∵ PF1 6 OP ,∴ PF1 6a ,
在三角形 F1PF2 中,
由余弦定理可得 PF1 2 PF2 2 F1F2 2 2 PF2 F1F2 cos PF2O ,
y 轴交于
OP
点 M , BM 与 PP 的交点 N 恰为线段 PP 的中点,则椭圆 C 的离心率为( )
A. 3 2
B. 2 2
C. 2 3
【答案】D
【解析】设 P(x0, y0 ) ,则 P(x0,0) ,
OP OP
(1, 0) ,
由题意 OP
OP
c ,得
P
的横坐标为 c ,
OP
D. 1 3
MF
MF
对点增分集训
一、选择题
1.已知双曲线
x2 a2
y2 b2
1(a,b
0)
的渐近线被圆 (x 2)2
y2
4
截得的弦长等于 2
3 ,则双曲线两条渐近
线相夹所成的锐角为( )
A. π 6
B. π 3
C. π 2
D. 2π 3
【答案】B
【解析】过圆心 A(2, 0) 作渐近线 y b x 的垂线, a
2021 届高三精准培优专练
培优点 圆锥曲线综合
一、圆锥曲线综合
例
1:已知 O 为坐标原点,
A
,
B
分别是椭圆
C
:
x2 a2
2023年高考数学考法专练——外接球与内切球

2023年高考数学考法专练——外接球与内切球考法一、 墙角模型例1、长方体1111ABCD A B C D -的8个顶点在同一球面上,且12,3,1AB AD AA ===,则球面面积为( )A .83π B .43π C .4π D .8π例2、已知正三棱锥S -ABC 的三条侧棱两两垂直,2,则此三棱锥的外接球的表面积为( )A .πB .3πC .6πD .9π例32的正四面体的外接球体积为___________.跟踪练习1、长方体1111ABCD A B C D -的长、宽、高分别为2,2,1,其顶点都在球O 的球面上,则球O 的表面积为______.2、在三棱锥P ABC -中,已知PA ,PB ,PC 两两垂直,且1PA =,2PB =,3PC =,则三棱锥P ABC -的外接球的表面积为3、已知正四棱柱(底面为正方形且侧棱与底面垂直的棱柱)的底面边长为3,侧棱长为4,则其外接球的表面积为4、在四面体S ABC -中,SA ⊥平面ABC ,三内角B ,A ,C 成等差数列,2SA AC ==,1AB =,则该四面体的外接球的表面积为5、如图,在ABC 中,3AB AC ==1cos 3BAC ∠=-,D 是棱BC 的中点,以AD 为折痕把ACD △折叠,使点C 到达点C '的位置,则当三棱锥C ABD '-体积最大时,其外接球的表面积为6、在三棱锥P ABC -中,点A 在平面PBC 中的投影是PBC 的垂心,若ABC 是等腰直角三角形且1AB AC ==,3PC =,则三棱锥P ABC -的外接球表面积为7、已知三棱锥S ABC -的三条侧棱,,SA SB SC 两两互相垂直且13,5AC AB ==的表面积为14π,则BC =______________.8、三棱锥P ABC -中,PA ⊥平面ABC ,直线PB 与平面ABC 所成角的大小为30,AB =60ACB ∠=︒,则三棱锥P ABC -的外接球的表面积为________.9、已知三棱锥A BCD -的所有顶点都在球O 的球面上,且AB ⊥平面BCD ,AB =4AC AD ==,CD =O 的表面积为___________.10、已知长方体1111ABCD A B C D -的体积为1AA =,则当长方体1111ABCD A B C D -的表面积最小时,该长方体外接球的体积为__________.考法二、汉堡模型例1、《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC -为鳖臑,PA ⊥平面ABC ,2PA AB ==,4AC =,三棱锥P ABC -的四个顶点都在球O 的球面上,则球O 的表面积为( )A .12πB .20πC .24πD .32π例2、已知三棱锥A BCD -的所有顶点都在球O 的球面上,且AB ⊥平面BCD ,2AB =,CD =,AC AD ==O 的表面积为( )AB .2πC .3πD .6π例3、已知边长为3的正ABC 的顶点和点D 都在球O 的球面上.若6AD =,且AD ⊥平面ABC ,则球O 的表面积为( )A .B .48πC .24πD .12π跟踪练习1、已知各顶点都在同一球面上的正四棱柱的底面边长为a ,高为h ,球的体积为,则这个正四棱柱的侧面积的最大值为( )A .B .C .D .2、(多选)在四面体ABCD 中,AB AC ⊥,AC CD ⊥,直线AB ,CD 所成的角为60°,AB CD ==,4AC =,则四面体ABCD 的外接球表面积为( )A .π3B .52πC .80πD .208π3、已知四棱锥P ABCD -的五个顶点都在球О的球面上,PA ⊥平面ABCD ,底面ABCD 是高为12的等腰梯形,//AD BC ,1AD PA ==,2BC =,则球О的表面积为( )A .10πB .4πC .5πD .6π 4、在四棱锥P ABCD -中,已知PA ⊥底面,,ABCD AB BC AD CD ⊥⊥,且120,2BAD PA AB AD ∠=︒===,则该四棱锥外接球的体积为( )A .B .203πCD .5、设直三棱柱111ABC A B C -1AB AC AA ==,120BAC ∠=︒,则此直三棱柱的高是______ .6、已知正三棱柱的高与底面边长均为2,则该正三棱柱内半径最大的球与其外接球的表面积之比为( )A .17B .7C .37D .77、已知三棱锥P ABC ﹣的四个顶点都在球O 的表面上,PA ⊥平面ABC ,AB BC ⊥且8PA =,6AC =,则球O 的表面积为( )A .10πB .25πC .50πD .100π8、三棱锥P ABC -中,PA ⊥平面ABC ,30ABC ∠=︒,APC ∆的面积为3,则三棱锥P ABC -的外接球体积的最小值为( )A B C . D .9、已知四棱锥P ABCD -的顶点都在球O 的球面上,PA ⊥底面ABCD ,1AB AD ==,2BC CD ==,若球O 的表面积为9π,则四棱锥P ABCD -的体积为( )A .4B .43C .D .3考点三 斗笠模型例1、在三棱锥P ABC -中,PA PB PC ===AB AC BC ===,则三棱锥P ABC -外接球的表面积是( )A .9πB .15π2C .4πD .25π4例2、某圆锥的侧面展开后,是一个圆心角为23π的扇形,则该圆锥的体积与它的外接球的体积之比为( ) A .243256 B .128243 C .128729 D .256729例3、设圆锥的顶点为A ,BC 为圆锥底面圆O 的直径,点P 为圆O 上的一点(异于B 、C ),若BC =三棱锥A PBC -的外接球表面积为64π,则圆锥的体积为___________.跟踪练习1、已知圆锥的顶点和底面圆周都在球O 面上,圆锥的侧面展开图的圆心角为23π,面积为3π,则球O 的表面积等于( )A .818πB .812πC .1218πD .1212π 2、已知一个圆锥的底面半径为2,高为3,其体积大小等于某球的表面积大小,则此球的体积是( )A .BC .4πD .43π 3、正三棱锥P -ABC 底面边长为2,M 为AB 的中点,且PM ⊥PC ,则三棱锥P -ABC 外接球的体积为( )A .323πB .6πCD .34、已知在高为2的正四棱锥P ABCD -中,2AB =,则正四棱锥P ABCD -外接球的体积为( )A .4πB .92πC .274πD .83π 5、已知一个圆锥的底面面积为3π,侧面展开图是半圆,则其外接球的表面积等于___________. 考点四、垂面模型例1、在三棱锥P ABC -中,PAC △是等边三角形,平面PAC ⊥平面,ABC AB AC ==60CAB ∠=,则三棱锥P ABC -的外接球体积为( )A .43πBC .323πD .3例2、如图所示,在三棱锥A BCD -中,平面ACD ⊥平面BCD ,ACD △是以CD 为斜边的等腰直角三角形,AB BC ⊥,24AC CB ==,则该三棱锥的外接球的表面积为( )A .32πB .40πC .40103D .6423例3、已知三棱锥P ABC -的每个顶点都在球O 的球面上,平面ABC ⊥平面PBC ,AC BC ⊥,6AC =,8AB =,214PC PB ==,则三棱锥P ABC -外接球的表面积为( )A .503πB .533πC .100πD .32π跟踪练习1、在三棱锥D ABC -中,平面ABC ⊥平面ABD ,AB AD ⊥,4AB AD ==,6ACB π∠=,若三棱锥D ABC -的四个顶点都在同一个球面上,则该球的表面积为___________.2、在四面体ABCD 中,BCD △是边长为2的等边三角形,ABD △是以BD 为斜边的等腰直角三角形,平面ABD ⊥平面A BC ,则四面体ABCD 的外接球的表面积为__________.3、在四面体ABCD 中,已知平面ABD ⊥平面ABC ,且4AB AD DB AC CB =====,其外接球表面积为 ( )A .403πB .803πC .16πD .20π4、在三棱锥P ABC -中,平面PAB ⊥平面,23,90ABC PA PB AB BAC ===∠=︒,4AC =,则三棱锥P ABC -的外接球的表面积为( )A .20πB .643πC .32πD .80π5、已知三棱锥A BCD -中,平面ABD ⊥平面BCD ,若1AD DB BC CD ====,120ADB ∠=︒,则该三棱锥的外接球的表面积为( )A .7π3B .10π3C .20π3D .13π3考点五 矩形模型例1、若矩形ABCD 的面积是4,沿对角线AC 将矩形ABCD 折成一个大小是60°的二面角B -AC -D ,则四面体ABCD 的外接球的体积最小值为( )A .8πB .823C 6πD 1717例2、在三棱锥S ABC -中,2SAC SBC π∠=∠=,23ACB π∠=,1AC BC ==.若三棱锥S ABC -的体积为1,则该三棱锥外接球的表面积为( )A .13πB .373πC .49πD .52π例3、已知三棱锥,3,1,4,22A BCD AB AD BC BD -====A BCD -的体积最大时,则外接球的表面积为___________.跟踪练习1、四面体ABCD 中,90ABC BCD ∠=∠=︒,2AB BC CD ===,23AD =表面积为__________.2、在矩形ABCD 中23AB =2AD =,沿对角线BD 进行翻折,则三棱锥C ABD -外接球的表面积为( )A .4πB .6πC .12πD .16π3、将长、宽分别为4和3的长方形ABCD 沿对角线AC 折成直二面角,得到四面体A BCD -,则四面体A BCD -的外接球的表面积为( )A .25πB .50πC .5πD .10π4、中国古代数学家刘徽所注释的《九章算术》中,称四个面均为直角三角形的四面体为“鳖臑”.如图所示的鳖臑ABCD 中,AB ⊥面BCD ,CD BC ⊥,若1CD =,5AC =且顶点,,,A B C D 均在球O 上,则球O 的表面积为______. 考法六 、 怀表模型例1、已知S ,A ,B ,C 四点都在某个球表面上,ABC 与SBC 都是边长为1的正三角形,二面角A BC S --的大小为23π,则该球的表面积为( ) A .43π B .73π C .3π D .133π 例2、如图,菱形ABCD 的边长为6,3BAD π∠=,将其沿着对角线BD 折叠至直二面角A BD C --,连接AC ,得到四面体ABCD ,则此四面体的外接球的表面积为例3、已知菱形ABCD 的边长为4,对角线4BD =,将ABD △沿着BD 折叠,使得二面角A BD C --为120︒,则三棱锥A BCD -的外接球的表面积为___________.跟踪练习1、已知边长为ABCD 中,60A ∠=,现沿对角线BD 折起,使得二面角A BD C --为120︒,此时点A 、B 、C 、D 在同一个球面上,则该球的表面积为( ).A .20πB .28πC .32πD .36π2、在边长为3的菱形ABCD 中,BD =ABCD 沿其对角线AC 折成直二面角B AC D --,若,,,A B C D 四点均在某球面上,则该球的表面积为___________.考法七、 其他模型外接球例1、已知四棱锥P ABCD -中,ABD △是边长为2BC CD ==,60BPD ∠=,二面角P BD C --的余弦值为13-,当四棱锥的体积最大时,该四棱锥的外接球的体积为( )A .8πB .C .D .12π例2、已知三棱锥A BCD -中,===AB BD DA DC =,BC =A BD C --的大小为135︒,则三棱锥A BCD -外接球的表面积为( )A .64πB .52πC .40πD .32π例3、在四面体ABCD 中,2==AC BD ,AD BC ==AB CD ==___________.跟踪练习1、在三棱锥S ABC -中,90SBA SCA ∠=∠=︒,底面ABC 是等边三角形,三棱锥S ABC -则三棱锥S ABC -的外接球表面积的最小值是( )A .12πB .24πC .6πD .10π2、已知球O 的半径为R ,A ,B ,C 三点在球O 的球面上,球心O 到平面ABC 的距离为12R ,3AB AC ==,120BAC ∠=︒,则球O 的表面积为( )A .48πB .16πC .64πD .36π3、已知四面体ABCD 中,60BAD ∠=︒,90BCD ∠=︒,2AB AD ==,H 是BD 的中点,CH BD ⊥,120AHC ∠=︒,则四面体的外接球的表面积为( )A .275πB .3215πC .94πD .529π4、在棱长为8的正方体1111ABCD A B C D -中,P 为棱1DD 上一点,且P 到11C D 的距离与到AC 的距离相等,则四面体P ACD -的外接球的表面积为( )A .128πB .132πC .133πD .164π5、球O 的两个相互垂直的截面圆1O 与2O 的公共弦AB 的长度为2,若1O AB △是直角三角形,2O AB △是等边三角形,则球O 的表面积为( )A .9πB .12πC .16πD .20π6、如图是一个由6个正方形和8个正三角形围成的十四面体,其所有顶点都在球O 的球面上,若十四面体的棱长为1,则球O 的表面积为( )A .2πB .4πC .6πD .8π7、已知三棱锥P ABC -的四个顶点都在半径为R 的球面上,且3BAC π∠=,2BC =,若三棱锥P ABC-体积的最大值为32R ,则该球的表面积为( ) A .649π B .329π C .6427π D .169π 8、等边ABC 的边长为2,点D 为AC 的中点,将ABD △沿BD 折起到A BD ',使得23A DC π'∠=,若该三棱锥的所有顶点都在同一个球面上,则该球的表面积为______.考法八、 内切球例1、如图,在四棱锥P ABCD -中,O 是正方形ABCD 的中心,PO ⊥底面ABCD ,5PA =2AB =,则四棱锥P ABCD -内切球的体积为( )A 3πB 43πC 113πD 1253π 例2、已知球O 是棱长为24的正四面体ABCD 的内切球,球1O 与球O 外切且与正四面体的三个侧面都相切,则球1O 的表面积为( )A .24πB .12πC .8πD .6π例3、已知直三棱柱111ABC A B C -的底面ABC 为等边三角形,若该棱柱存在外接球与内切球,则其外接球与内切球表面积之比为( )A .25:1B . 1C .5:1D 1跟踪练习1、设球O 内切于正三棱柱111ABC A B C -,则球O 的体积与正三棱柱111ABC A B C -的体积的比值为________.2、已知球1O 是棱长为2的正方体1111ABCD A B C D -的内切球,球2O (在正方体1111ABCD A B C D -内部)与平面ABCD ,平面11ABB A 和平面11ADD A 都相切,并且与球1O 相切,则球1O 与球2O 的半径之比为___________.4、已知正三棱锥 P ABC -的底面边长为2,,PAB PBC 分别切于点,M N ,则MN 的长度为___________.5、《九章算术》中将四个面都为直角三角形的三棱锥称之为鳖臑,若三棱锥P ABC -为鳖臑, PA ⊥平面ABC ,4PA BC ,3AB =,AB BC ⊥,若三棱锥P ABC -有一个内切球O ,则球O 的体积为( ) A .92π B .94π C .916π D .9π6、阿基米德是古希腊伟大的数学家、物理学家、天文学家,是静态力学和流体静力学的奠基人,和高斯、牛顿并列为世界三大数学家,他在不知道球体积公式的情况下得出了圆柱容球定理,即圆柱内切球(与圆柱的两底面及侧面都相切的球)的体积等于圆柱体积的三分之二.那么,圆柱内切球的表面积与该圆柱表面积的比为( )A .12B .13C .23D .347、已知在三梭锥A BCD -中,2AB CD ==,3AD AC BC BD ====,则该三棱锥内切球的体积为( )A B C D。
2021高三数学(理)精准培优专项训练《16利用空间向量求夹角》教师版
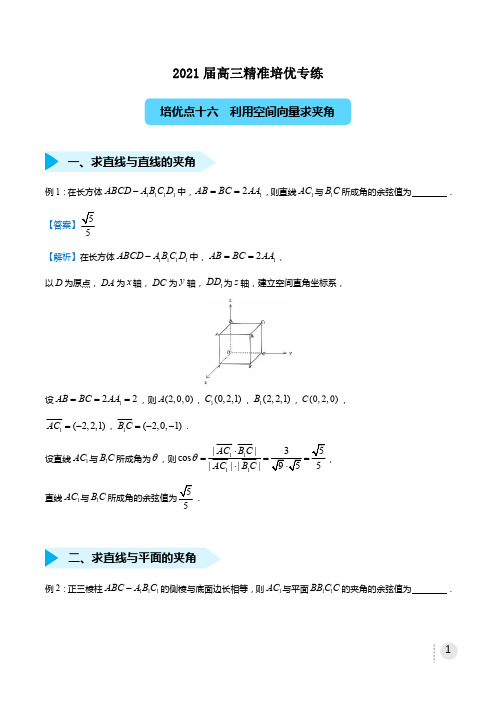
1
C.
2
3
D.
4
【答案】A
【解析】根据题意画出图形如下图所示:
∵平面 ABD 平面 BCD ,平面 ABD 平面 BCD BD , BD DC , ∴ DC 平面 ABD . 以过点 D 且与平面 BCD 垂直的直线为 z 轴建立空间直角坐标系 D xyz ,
3
则 D(0, 0, 0) , B(2, 0, 0) , C (0, 2, 0) , A(1, 0, 3) ,∴ DB (2, 0, 0) , AC (1, 2, 3) ,
,即
1 2 3 2
x x
2z 2y
0 0
,
取 x 4 ,得 n (4, 3, 1) ,
4
设直线 AC1 与平面 EFG 所成角为 ,
则直线
AC1 与平面 EFG 所成角的正弦值为 sin
cos
n, AC1
4 78 39
.
3.如图所示,正方体 ABCD A1B1C1D1 的棱 AB ,A1D1 的中点分别为 E ,F ,则直线 EF 与平面 AA1D1D
∴ cos DB, AC
DB AC
2
2
,
| DB | | AC | 2 2 2 4
∴异面直线 AC 与 BD 所成角的余弦值为 2 . 4
2.正方体 ABCD A1B1C1D1 的棱上(除去棱 AD )到直线 A1B 与 CC1 的距离相等的点有 3 个,记这 3 个 点分别为 E , F , G ,则直线 AC1 与平面 EFG 所成角的正弦值为( )
设 AB BC 2AA1 2 ,则 A(2, 0, 0) , C1(0, 2,1) , B1(2, 2,1) , C (0, 2, 0) ,
2023年高考数学---外接球与内接球问题真题练习(含答案解析)

2023年高考数学---外接球与内接球问题真题练习(含答案解析)1.(2022·全国·高考真题(文))已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( ) A .13B .12CD【答案】C【解析】[方法一]:【最优解】基本不等式设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r , 设四边形ABCD 对角线夹角为α,则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅⋅=(当且仅当四边形ABCD 为正方形时等号成立)即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r 又设四棱锥的高为h ,则22r h 1+=,2123O ABCDV r h −=⋅⋅=当且仅当222r h =即h .故选:C[方法二]:统一变量+基本不等式由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为a ,底面所在圆的半径为r ,则r =,所以该四棱锥的高h13V a = (当且仅当22142a a =−,即243a =时,等号成立)所以该四棱锥的体积最大时,其高h =. 故选:C .[方法三]:利用导数求最值由题意可知,当四棱锥为正四棱锥时,其体积最大,设底面边长为a ,底面所在圆的半径为r ,则2r a =,所以该四棱锥的高h 13V a =2(02)a t t =<<,V =设()322t t f t =−,则()2322t f t t −'=,403t <<,()0f t '>,单调递增, 423t <<,()0f t '<,单调递减,所以当43t =时,V 最大,此时h故选:C.【整体点评】方法一:思维严谨,利用基本不等式求最值,模型熟悉,是该题的最优解; 方法二:消元,实现变量统一,再利用基本不等式求最值;方法三:消元,实现变量统一,利用导数求最值,是最值问题的常用解法,操作简便,是通性通法.2.(2021·全国·高考真题(理))已知A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC −的体积为( )A B C D 【答案】A【解析】,1AC BC AC BC ⊥==,ABC ∴为等腰直角三角形,AB ∴=则ABC ,又球的半径为1, 设O 到平面ABC 的距离为d ,则d =所以11111332O ABC ABCV Sd −=⋅=⨯⨯⨯故选:A.3.(2022·全国·高考真题)已知正三棱台的高为1,上、下底面边长分别为都在同一球面上,则该球的表面积为( ) A .100π B .128πC .144πD .192π【答案】A【解析】设正三棱台上下底面所在圆面的半径12,r r ,所以123432,260sin 60r r =,即123,4r r ==,设球心到上下底面的距离分别为12,d d ,球的半径为R ,所以1d 2d =121d d −=或121d d +=,1=1,解得225R =符合题意,所以球的表面积为24π100πS R ==. 故选:A .4.(2022·全国·高考真题)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤ )A .8118,4⎡⎤⎢⎥⎣⎦B .2781,44⎡⎤⎢⎥⎣⎦C .2764,43⎡⎤⎢⎥⎣⎦D .[18,27]【答案】C【解析】∵球的体积为36π,所以球的半径3R =,[方法一]:导数法设正四棱锥的底面边长为2a ,高为h , 则2222l a h =+,22232(3)a h =+−, 所以26h l =,2222a l h =−所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯−⨯− ⎪⎝⎭,所以5233112449696l l V l l ⎛⎫⎛⎫−'=−= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l <≤0V '<,所以当l =V 取最大值,最大值为643,又3l =时,274V =,l =814V =, 所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,.故选:C.[方法二]:基本不等式法由方法一故所以()()()3221224211646122(333333h h h V a h h h h h h h ⎡⎤−++==−=−⨯⨯=⎢⎥⎣⎦…当且仅当4h =取到),当32h =时,得a =,则22min 11327;3324V a h ==⨯=当l =39322h =+=,a =正四棱锥体积221119816433243V a h ==⨯=<,故该正四棱锥体积的取值范围是2764[,].435.(2020·全国·高考真题(理))已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC 的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为( ) A .64π B .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r ππ=∴=,ABC 为等边三角形,由正弦定理可得2sin60AB r =︒=,1OO AB ∴==1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥==,∴球O 的表面积2464S R ππ==.故选:A6.(2020·全国·高考真题(理))已知△ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )AB .32C .1D 【答案】C 【解析】设球O 的半径为R ,则2416R ππ=,解得:2R =. 设ABC 外接圆半径为r ,边长为a ,ABC212a ∴=,解得:3a =,2233r ∴=∴球心O 到平面ABC 的距离1d ==.故选:C.。
(新高考专用)2021届高三一轮复习精准培优专练2 函数的图像与性质 教师版

C. ( 1 ,1] 2
D.[ 1 ,1] 2
【解析】∵ g(x) lg(2x 2 x) 0 ,∴ 0 2x2 x 1,∴ 1 x 0 或 1 x 1,
2
2
∴ A [ 1 , 0) (1 ,1] ,
2
2
∵ x [2, 1] ,∴ 2x2 x [1,10] , 0 g(x) 1,故 B [0,1] , 2
D. f (2) f ( 5) f (3) 2
【解析】∵ f (x 1) f (x 1) ,则函数 f (x) 的周期T 2 ,
当
x [1,1]
时,
f
(x)
x(1
e
2 x
) 1
x
ex ex
1 1
,
则
f
(
x)
x
e e
x x
1 1
x
1 1
ex ex
x
e e
x x
1 1
f
(x) ,则函数
f (x) 为偶函数,
2
2
9.已知定义在 R 上的函数 f (x) 满足 f (x) f (2 x) ,其图象经过点 (2,0) ,且对任意 x1 ,
x2 (1, ) ,且 x1 x2 ,(x1 x2)[ f (x1) f (x2)] 0 恒成立,则不等式 (x 1) f (x) 0 的
6
解集为( )
A. (,1]
0
,故排除
B,只有
A
符合.
6.已知函数
f
(x)
x2
2x,
x0 ,若 |
f (x) | ax ,则实数 a 的取值范围是(
)
ln(x 1), x 0
A. (,0]
【原创】(新高考)2021届高三精准培优专练1 基本不等式及应用 解析

答案:(1) ;(2) .
(1) ,
,
综上,得 .
即若 个单位的固体碱只投放一次,
则能够维持有效抑制作用的时间为 .
(2)当 时, 单调递增;
④由于 ,所以 ,有基本不等式得 ,所以④正确,
综上所述,正确不等式的序号是①④,故选A.
2.下列不等式一定成立的是()
A. B. C. D.
答案:D
当 都为负数时,A、C选项不正确;
当 为正数时,B选项不正确;
根据基本不等式,有 ,故选D.
3.设 , ,则 的大小关系是()
A. B. C. D.不确定
而此时 ,所以 ,
当且仅当 时取等号,
所以 的最小值是 ,故选B.
8.若 ,使得 成立,则实数 的最大值为()
A. B. C. D.
答案:C
可得 ,当且仅当 ,即 时等号成立,
若 ,使得 成立,则 , ,
故选C.
9.若关于 的方程 有解,则实数 的取值范围是()
A. B.
C. D.
答案:D
由 ,得 ,
所以 ,(当且仅当 取等号)
所以 的取值范围为 .
22.由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱, 个单位的固体碱在水中逐步溶化,水中的碱浓度 与时间 的关系,可近似地表示为 ,只有当河流中碱的浓度不低于 时,才能对污染产生有效的抑制作用.
(1)如果只投放 个单位的固体碱,则能够维持有效抑制作用的时间有多长?
14.正数 , 满足 ,则 的取值范围是________.
2021届高三数学精准培优专练 线性规划(文) 学生版
2021届高三精准培优专练例1:设变量x ,y 满足约束条件2030230x x y x y +≥⎧⎪-+≥⎨⎪+-≤⎩,则目标函数6z x y =+的最大值为 .例2:若,x y 满足约束条件22220x y y x x +≥⎧⎪-≤⎨⎪-≤⎩,则2yx +的取值范围为( )A .1[,1]2B .1(,][1,)2-∞-+∞C .[0,1]D .1[,1]2例3:已知x ,y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩,若z ax y =+的最大值为4,则a =( )A .3B .2C .2-D .3-例4:某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg ,乙材料1kg ,用5个工时;生产一件产品B 需要甲材料0.5kg ,乙材料0.3kg ,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元.该企业现有甲材料150kg ,乙培优点 线性规划一、求线性目标的最值二、求非线性目标的最值三、线性规划的含参问题四、线性规划的实际应用材料90kg ,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为元.一、选择题1.已知,x y 满足10304x y x y y -+≤⎧⎪+-≥⎨⎪≤⎩,若对任意,x y 都有2x y a +≤成立,则a 的取值范围是( )A .(2,)+∞B .[2,)+∞C .[4,)+∞D .[10,)+∞2.已知变量x ,y 满足的不等式组02010x x y kx y ≥⎧⎪-≤⎨⎪-+≥⎩表示的平面区域是一个直角三角形,则实数k =( )A .12-B .12C .0D .0或12-3.若实数x 、y 满足1x y ≤≤,则222x y x ++的最小值为( )A .12B .12-C .22D .212- 4.设x ,y 满足约束条件01030y x y x y ≥⎧⎪-+≥⎨⎪+-≤⎩,则3z x y =-的最大值为( )A .1B .3C .5D .65.如果点(,)P x y 在平面区域22021020x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩上,则22(1)x y ++的最大值和最小值分别是( )A .3,5B .9,95C .9,2D .3,2对点增分集训6.设变量x ,y 满足约束条件22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩,则1y x s x -=+的取值范围是( )A .1[0,]2B .1[,0]2-C .1[,1]2-D .[0,1]7.设变量,x y 满足约束条件202011x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩,则目标函数4z x y =-+的最大值为( )A .2B .3C .5D .68.已知实数,x y 满足约束条件121x y x y y a +≥-⎧⎪-≤⎨⎪≤⎩,若目标函数3z x y =-的最大值为2,则a 的值为( )A .1-B .12C .1D .29.已知实数,x y 满足26002x y x y x -+≥⎧⎪+≥⎨⎪≤⎩,若目标函数z mx y =-+的最大值为210m -+,最小值为22m --,则实数m 的取值范围是( ) A .[2,1]-B .[1,3]-C .[1,2]-D .[2,3]10.已知x ,y 满足约束条件20531203x y x y y --≤⎧⎪--≥⎨⎪≤⎩,当目标函数z ax by =+(0a >,0b >)在该约束条件下取得最小值1时,则123a b+的最小值为( ) A.4+B.4C.3+D.311.某化肥厂生产甲、乙两种混合肥料,需要A ,B ,C 三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.现有A 种原料200吨,B 种原料360吨,C 种原料300吨,在此基础上生产甲乙两种肥料的最大利润为( )万元. A .108B .112C .116D .12012.设实数x ,y 满足约束条件202502x y x y y --≤⎧⎪+-≥⎨⎪≤⎩,则22x y u xy +=的取值范围是( )A .10[2,]3B .5[,2]3C .5[1,]3D .2[,1]3二、填空题13.已知实数x ,y 满足22222x y x y x y +≥⎧⎪-≤⎨⎪+≤⎩,若(0)z x my m =->的最大值为4,则(0)z x my m =->的最小值为 .14.已知变量x ,y 满足240260x y x x y -+≤⎧⎪≥⎨⎪+-≤⎩,则13y z x +=-的取值范围是 .15.某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨消耗一级子棉2吨、二级子棉1吨,生产乙种棉纱1吨消耗一级子棉1吨、二级子棉2吨,每吨甲种、乙种棉纱的利润分别是900元和600元,工厂在生产中要求消耗一级子棉不超过300吨、二级子棉不超过270吨,且甲种棉纱的产量不能超过乙种棉纱的产量60吨.在此条件下,生产甲、乙两种棉纱可以获得的最大利润为 元.16.太极图被称为“中华第一图”.从孔庙大成殿梁祝,到楼观台、三茅宫、白外五观的标记物;从道袍、 卦摊、中医、气功、武术到南韩国、新加坡空军机徽……太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分的区域可用不等式组()()222222401111x y x x y x y ⎧+≤⎪⎪≤+-≤⎨⎪++≥⎪⎩或来表示,设(,)x y 是阴影部分中任意一点,则2z x y =+的最大值为 .例1:【答案】18【解析】由约束条件2030230xx yx y+≥⎧⎪-+≥⎨⎪+-≤⎩,作出可行域如图,(0,3)A,化目标函数6z x y=+为66x zy=-+,由图可知,当直线66x zy=-+过A时,直线在y轴上的截距最大,z有最大值为18.例2:【答案】A【解析】作出约束条件22220x yy xx+≥⎧⎪-≤⎨⎪-≤⎩所表示的的可行域如图:2yx+表示区域内的点与点(2,0)-连线的斜率,联立方程组222xx y=⎧⎨+=⎩,可解得(2,2)B-,同理可得(2,4)A,当直线经过点B时,斜率取最小值:21222-=-+;培优点九线性规划答案当直线经过点A 时,斜率取最大值4122=+,则2yx +的取值范围是1[,1]2-,故选A .例3:【答案】B【解析】作出不等式组对应的平面区域如图:(阴影部分).则(2,0)A ,(1,1)B ,若z ax y =+过A 时取得最大值为4,则24a =,解得2a =,此时,目标函数为2z x y =+,即2y x z =-+,平移直线2y x z =-+,当直线经过(2,0)A 时,截距最大,此时z 最大为4,满足条件, 若z ax y =+过B 时取得最大值为4,则14a +=,解得3a =, 此时,目标函数为3z x y =+,即3y x z =-+,平移直线3y x z =-+,当直线经过(2,0)A 时,截距最大,此时z 最大为6,不满足条件,故2a =,故选B . 例4:【答案】216000【解析】设生产产品A 、产品B 分别为x 、y 件,利润之和为z 元,那么 1.50.51500.3905360000x y x y x y x y +≤⎧⎪+≤⎪⎪+≤⎨⎪≥⎪≥⎪⎩,①目标函数2100900z x y =+,二元一次不等式组①等价于33001039005360000x y x y x y x y +≤⎧⎪+≤⎪⎪+≤⎨⎪≥⎪≥⎪⎩,②作出二元一次不等式组②表示的平面区域(如图),即可行域.将2100900z x y =+变形,得73900z y x =-+,平移直线73y x =-, 当直线73900zy x =-+经过点M 时,z 取得最大值, 解方程组10390053600x y x y +=⎧⎨+=⎩,得M 的坐标(60,100),所以当60x =,100y =时,max 210060900100216000z =⨯+⨯=元.一、选择题 1.【答案】D【解析】令2z x y =+,画出10304x y x y y -+≤⎧⎪+-≥⎨⎪≤⎩表示的可行域,由可行域知,目标函数过点A 时取最大值,由104x y y -+=⎧⎨=⎩,可得3x =,4y =,可得(3,4)A 时,z 的最大值为10.∴要使2x y a +≤恒成立,只需使目标函数的最大值小于等于a 即可, ∴a 的取值范围为10a ≥.故选D . 2.【答案】D【解析】由约束条件02010x x y kx y ≥⎧⎪-≤⎨⎪-+≥⎩作出可行域如图,直线10kx y -+=过定点(0,1)B ,∵不等式组02010x x y kx y ≥⎧⎪-≤⎨⎪-+≥⎩表示的平面区域是一个直角三角形,∴当0k =时,平面区域为直角三角形OBC 及其内部区域;当12k =-时,平面区域为直角三角形OAB 及其内部区域.∴k 的值应为0或12-,故选D .3.【答案】B【解析】x ,y 满足1x y ≤≤,表示的可行域如图,22222(1)1x y x x y++=++-它的几何意义是可行域内的点与点(1,0)-的距离的平方减去1.显然点(1,0)-到直线0x y+==,∴222min1(2)(122x y x++=-=-.故选B.4.【答案】C【解析】由1030yx yx y≥⎧⎪-+≥⎨⎪+-≤⎩根据题意画出对应的平面区域如图,ABC△区域为满足不等式组的所有点的集合,设3m x y=-,1133y x m=-.当直线1133y x m=-过点(1,2)B时,m取最小值,且min165m=-=-;当直线1133y x m=-过点(3,0)A时,m取最大值,且max303m=-=;∴[5,3]m∈-,则max5z=,故选C.5.【答案】B【解析】如图,先作出点(,)P x y所在的平面区域:22(1)x y ++表示动点P 到定点(0,1)Q -距离的平方,当点P 在(1,0)-时,22PQ =,而点Q 到直线210x y -+=的距离的平方为925<, ∴22(1)x y ++的最小值为95; 当点P 在(0,2)时,离Q 最远,29PQ =,∴22(1)x y ++的最大值为9.故选B .6.【答案】C【解析】令y x n -=,1x m +=,则1x m =-,1y m n =+-,代入22022010x y x y x y --≤⎧⎪-+≥⎨⎪+-≥⎩,得30230230m n m n m n --≤⎧⎪+-≤⎨⎪+-≥⎩,作出可行域如图,1y x s x -=+化为ns m=. 分别联立方程组30230m n m n --=⎧⎨+-=⎩,230230m n m n +-=⎧⎨+-=⎩,解得(2,1)A -,(1,1)C .∴ns m=的范围为1[,1]2-.故选C .7.【答案】C【解析】已知不等式组表示的平面区域如图中的阴影部分,目标函数的几何意义是直线4y x z =+在y 轴上的截距,由图可知目标函数在点A 处取得最大值.由201x y x -+=⎧⎨=-⎩,点(1,1)A -,所以max 4(1)15z =-⨯-+=,故选C . 8.【答案】C【解析】由已知条件作出可行域如图所示,其中(1,)A a a --,1(,)2a B a +,(0,1)C -, 目标函数3z x y =-可化为3y x z =-, 当直线过点B 时z 最大,所以3(1)22a a +-=,解得1a =,故选C .9.【答案】C【解析】画出可行域如下图所示,依题意可知,目标函数在点(2,10)A 取得最大值,在点(2,2)B -取得最小值. 由图可知,当0m ≥时,[0,2]m ∈;当0m <时,[1,0)m ∈-, ∴实数m 的取值范围是[1,2]-,故选C . 10.【答案】C【解析】如下图,画出可行域,目标函数的斜率为0ak b=-<, ∴当目标函数过点(3,1)A 时函数取得最小值,即31a b +=,那么12126()(3)333333b a a b a b a b a b +=++=++≥+=+ 等号成立的条件为63b aa b=.故选C . 11.【答案】B【解析】设x ,y 表示生产甲、乙两种肥料的车皮数,利润为z 万元.由已知x ,y 满足452008536031030000x y x y x y x y +≤⎧⎪+≤⎪⎪+≤⎨⎪≥⎪≥⎪⎩,该二元一次不等式组所表示的区域为图中的阴影部分.目标函数23z x y =+是斜率为23-,随z 变化的一束平行直线,3z为直线在y 轴上的截距, 当3z取最大值时,z 的值最大.又因为x ,y 满足约束条件,所以由图可知,当直线23z x y =+经过可行域中的点M 时, 截距3z 的值最大,即z 的值最大,解方程组45200310300x y x y +=⎧⎨+=⎩,得点M 的坐标为(20,24)M ,∴max 220324112z =⨯+⨯=,故选B . 12.【答案】A【解析】作出不等式组所表示的平面区域如图:则0x >,0y >,22x y y xu xy x y+==+, 设yt x=,则1u t t =+,由图象可知直线y tx =经过点(1,2)A 时,斜率t 取得最大值2;经过点(3,1)B 时,斜率t 取得最小值13.∴123t ≤≤. 211u t '=-,当0u '≥时,[1,2]t ∈;当0u '≤时,1[,1]3t ∈, ∴1u t t=+在1[,1]3上单调递减,在[1,2]上单调递增,可得110[2,]3u t t=+∈.故选A .二、填空题 13.【答案】6-【解析】作出可行域如图,目标函数化简得:1zy x m m=-, ∵0m >,故只可能在,A B 处取最大值. 联立220220x y x y +-=⎧⎨--=⎩,解得(2,2)B --,联立22020x y x y +-=⎧⎨+-=⎩,解得(0,2)C ,联立20220x y x y +-=⎧⎨--=⎩,解得(2,0)A ,若目标函数(0)z x my m =->过点A 时,2z =不符合题意, ∴过B 时取得最大值,此时422m =-+,解得3m =,3z x y =-过点C 时,min 6z =-.14.【答案】[13,4]--【解析】由变量x,y满足240260x yxx y-+≤⎧⎪≥⎨⎪+-≤⎩,作出可行域如图:由2402x yx-+=⎧⎨=⎩,解得(2,3)A;由24060x yx y-+=⎧⎨+-=⎩,解得810(,)33B,13yzx +=-的几何意义为可行域内动点与定点(3,1)D-连线的斜率.∵31423DAk+==--,101313833DBk+==--,∴13yzx+=-的取值范围是[13,4]--.15.【答案】147000【解析】设生产甲、乙两种棉纱分别为x吨、y吨,利润总额为z元,则有23002270600,0x yx yx yx y+≤⎧⎪+≤⎪⎨-≤⎪⎪≥≥⎩,目标函数为900600z x y=+.作出不等式组所表示的可行域,把900600z x y =+变形为32600z y x =-+,其中600z 是这条直线在y 轴上的截距, 当直线900600z x y =+经过可行域上A 点时,截距600z最大,即z 最大.解方程组23002270x y x y +=⎧⎨+=⎩,得A 的坐标为110x =,80y =,∴max 900600147000z x y =+=. 16.【答案】1+【解析】如图,作出直线:20l x y +=,当直线l 往上平移至与阴影部分的圆22(1)1x y +-=的边界相切时,z 最大,此时圆心(0,1)到直线2x y z +=的距离等于半径1,1=,解得1z =+。
2021届高三数学精准培优专练 平行垂直的证明(文) 学生版
12021届高三精准培优专练培优点平行垂直的证明
一、平行的证明例1:如图,在四棱锥PABCD中,底面ABCD是平行四边形,点E在PC上,3PCPE,3PD.
(1)证明:CD∥平面ABE;(2)若M是BC中点,点N在PD上,MN∥平面ABE,求线段PN的长.2
二、垂直的证明例2:如图,在直三棱柱111ABCABC中,1BCBB,12BACBCAABC,点E是1AB与1
AB
的交点,点D在线段AC上,1BC∥平面1
ABD
.
(1)求证:1
BDAC
;
(2)求证:1AB平面1
ABC
.
对点增分集训一、选择题1.设,表示两个不同平面,m表示一条直线,下列命题正确的是()3
A.若m∥,∥,则m∥B.若m∥,m∥,则∥
C.若m,,则m∥D.若m,m,则∥
2.如图,三棱柱111ABCABC中,侧棱1AA底面111ABC,底面三角形111
ABC是正三角形,E是BC中
点,则下列叙述正确的是()
A.1CC与1
BE是异面直线
B.AC平面11
ABBA
C.AE,11BC为异面直线,且11
AEBC
D.11AC∥平面1
ABE
3.已知正方体1111ABCDABCD中,E,F,G分别是1BB,1DD,11
AB的中点,则下列说法错误的
是()A.1BD∥平面11AFCB.CE∥平面11
AFC
C.CE∥平面11AFCD.AE∥平面11
AFC
4.如图,在正四面体PABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论不成立的是()
A.BC∥平面PDFB.DF平面PAE4
C.平面PDF平面PAED.平面PDE平面ABC5.若平面∥平面,点A,C,B,D,则ACBD∥的充要条件是()A.ABCD∥B.ADCBC.AB与CD相交D.直线AB与直线CD共面6.如图,在四棱锥PABCD中,PAB△与PBC△都是正三角形,平面PAB平面PBC,ACBD,则下列结论不一定成立的是()
2021届高三数学精准培优专练 三视图与体积表面积(文) 学生版
①四个侧面都是直角三角形;
②最长的侧棱长为 2 6 ;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为 24π .
4
其中正确的个数是( )
A. 0
B.1
C. 2
D. 3
11.某工人现欲用车床将一正方体铁块进行加工处理,加工后成品的三视图如图所示.网格纸上小正方形
3.【答案】A 【解析】由三视图得凿去部分是圆柱与半球的组合体,
其中圆柱的高为 5 ,底面圆的半径为 3 ,半球的半径为 3 , 所以组合体的体积为 π 32 5 1 4 π 33 63π ,故选 A.
23
4.【答案】C
【解析】由三视图可知,该几何体是高为 4 的四棱锥,如图所示,记为 P ABCD .
为( )
A. 8 3π
B. 8 4π
C. 8 5π
7.某几何体的三视图如图所示,则这个几何体的体积是(
D. 8 6π
)
A.13
B.14
C.15
8.某装饰品的三视图如图所示,则该装饰品的表面积为(
D.16
)
3
A.16 π
B.16 ( 5 1)π C.16 ( 5 1)π D. 20 ( 5 1)π
A. 3 3
B. 3 2
C. 9
D. 6
二、填空题
13.已知某几何体的三视图如图所示(侧视图中曲线为四分之一圆弧),则该几何体的体积为
.
5
14.如图是某几何体的三视图,图中方格的单位长度为1,则该几何体的表面积为
.
15.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为
高三优质精准培优专练数学(理)(学生版)(2021年整理)
高三优质精准培优专练数学(理)(学生版)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高三优质精准培优专练数学(理)(学生版)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高三优质精准培优专练数学(理)(学生版)(word版可编辑修改)的全部内容。
数学(理)培优点一函数的图象与性质01 培优点二函数零点06 培优点三含导函数的抽象函数的构造10 培优点四恒成立问题14 培优点五导数的应用18 培优点六三角函数23 培优点七解三角形29 培优点八平面向量33 培优点九线性规划36 培优点十等差、等比数列40培优点十一数列求通项公式43 培优点十二数列求和47 培优点十三三视图与体积、表面积51 培优点十四外接球56 培优点十五平行垂直关系的证明59 培优点十六利用空间向量求夹角67 培优点十七圆锥曲线的几何性质76 培优点十八离心率81 培优点十九圆锥曲线综合86 培优点二十几何概型932019届高三精准培优专练1.单调性的判断例1:(1)函数()212log (4)f x x -=的单调递增区间是( )A .(0,)+∞B .(0),-∞C .(2,)+∞D .(),2-∞-(2)223y x x +-+=的单调递增区间为________.2.利用单调性求最值例2:函数y x =________. 3.利用单调性比较大小、解抽象函数不等式例3:(1)已知函数()f x 的图象向左平移1个单位后关于y 轴对称,当211x x >>时,()()2121()0f x f x x x -⋅-⎡⎤⎣⎦<恒成立,设12a f ⎛⎫=- ⎪⎝⎭,()2b f =,()3c f =,则a ,b ,c 的大小关系为 ( ) A .c a b >>B .c b a >>C .a c b >>D .b a c >>(2)定义在R 上的奇函数()y f x =在(0,)+∞上递增,且102f ⎛⎫= ⎪⎝⎭,则满足19log 0f x ⎛⎫> ⎪⎝⎭的x 的集合为________________. 4.奇偶性例4:已知偶函数()f x 在区间[0,)+∞上单调递增,则满足1(21)3f x f ⎛⎫-< ⎪⎝⎭的x 的取值范围是( )A .12,33⎛⎫ ⎪⎝⎭B .12,33⎡⎫⎪⎢⎣⎭C .12,23⎛⎫⎪⎝⎭D .12,23⎡⎫⎪⎢⎣⎭5.轴对称例5:已知定义域为R 的函数()y f x =在[]0,7上只有1和3两个零点,且()2y f x =+与()7y f x =+ 都是偶函数,则函数()y f x =在[]0,2013上的零点个数为( )培优点一 函数的图象与性质A .404B .804C .806D .4026.中心对称例6:函数()f x 的定义域为R ,若()1f x +与()1f x -都是奇函数,则( ) A .()f x 是偶函数 B .()f x 是奇函数 C .()()2f x f x =+ D .()3f x +是奇函数7.周期性的应用例7:已知()f x 是定义在R 上的偶函数,()g x 是定义在R 上的奇函数,且()()1g x f x =-, 则()()20172019f f +的值为( ) A .1-B .1C .0D .无法计算一、选择题 1.若函数()2f x x a=+的单调递增区间是[)3,+∞,则a 的值为( )A .2-B .2C .6-D .62.已知函数()2log 1y ax =-在()1,2上是增函数,则实数a 的取值范围是( ) A .(]0,1B .[]1,2C .[1,)+∞D .[2,)+∞3.设函数()()()ln 1ln 1f x x x =-+-,则()f x 是( ) A .奇函数,且在(0,1)内是增函数 B .奇函数,且在(0,1)内是减函数 C .偶函数,且在(0,1)内是增函数 D .偶函数,且在(0,1)内是减函数4.已知函数()y f x =的图象关于1x =对称,且在(1,)+∞上单调递增,设12a f ⎛⎫=- ⎪⎝⎭,()2b f =, ()3c f =,则a ,b ,c 的大小关系为( )A .c b a <<B .b a c <<C .b c a <<D .a b c <<5.已知()f x 是奇函数,()g x 是偶函数,且()2(11)f g -+=,())114(f g -=+,则()1g 等于( )A .4B .3C .2D .1对点增分集训36.函数1()cos (0)f x x x x x x ⎛⎫=--π≤≤π≠ ⎪⎝⎭且的图象可能为( )7.奇函数()f x 的定义域为R ,若()1f x +为偶函数,且()12f =,则()()45f f +的值为( ) A .2B .1C .1-D .2-8.函数()f x 的图象向右平移1个单位,所得图象与曲线e x y =关于y 轴对称,则()f x 的解析式为( )A .()1e xf x +=B .()1e xf x -=C .()1e xf x -+=D .()1e xf x --=9.使2)og (l 1x x <+-成立的x 的取值范围是( ) A .()1,0-B .[)1,0-C .()2,0-D .[)2,0-10.已知偶函数()f x 对于任意R x ∈都有()()1f x f x +=-,且()f x 在区间[]0,1上是单调递增的,则()65f -.,1()f -,()0f 的大小关系是( ) A .()0 6.5()()1f f f <-<- B .()6.5()()01f f f -<<- C .()()(60)1.5f f f -<-<D .()10()( 6.5)f f f -<<-11.对任意的实数x 都有()()()221f x f x f -=+,若(1)y f x =-的图象关于1x =对称,且()02f =, 则()()20152016f f +=( ) A .0B .2C .3D .412.已知函数()e 1x f x =-,()243g x x x =-+-,若存在()()f a g b =,则实数b 的取值范围为( ) A .[0,3]B .(1,3)C .22,22⎡-+⎣D .()22,22+二、填空题13.设函数()100010x x x f x >⎧⎪==⎨⎪-<⎩,()21()g x x f x -=,则函数()g x 的递减区间是_______.14.若函数()R ()f x x ∈是周期为4的奇函数,且在[0,2]上的解析式为()()101sin 12x x x xx f x ⎧-≤≤⎪=⎨π<≤⎪⎩,则294146f f ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭________.15.设函数()||f x x a =+,()1g x x =-,对于任意的R x ∈,不等式()()f x g x ≥恒成立,则实数a 的取值范围是________.16.设定义在R 上的函数()f x 同时满足以下条件:①()0()f x f x +-=;②()()2f x f x =+;③当01x ≤≤时,()21x f x =-,则()1351(2)222f f f f f ⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭________.三、解答题17.已知函数()ln(2)a f x x x=+-,其中a 是大于0的常数. (1)求函数()f x 的定义域;(2)当4()1,a ∈时,求函数()f x 在[2,)+∞上的最小值; (3)若对任意,[)2x ∈+∞恒有()0f x >,试确定a 的取值范围.18.设()f x 是定义域为R 的周期函数,最小正周期为2,且()1()1f x f x =+-,当10x -≤≤时,()f x x =-.(1)判定()f x 的奇偶性;(2)试求出函数()f x 在区间[]1,2-上的表达式.1.零点的判断与证明例1:已知定义在()1,+∞上的函数()ln 2f x x x =--,培优点二 函数零点求证:()f x 存在唯一的零点,且零点属于()3,4.2.零点的个数问题例2:已知函数()f x 满足()()3f x f x =,当[)1,3x ∈,()ln f x x =,若在区间[)1,9内, 函数()()g x f x ax =-有三个不同零点,则实数a 的取值范围是( ) A .ln 31,3e ⎛⎫⎪⎝⎭ B .ln 31,93e ⎛⎫⎪⎝⎭ C .ln 31,92e ⎛⎫⎪⎝⎭ D .ln 3ln 3,93⎛⎫⎪⎝⎭3.零点的性质例3:已知定义在R 上的函数()f x 满足:()[)[)2220,121,0x x f x xx ⎧+∈⎪=⎨-∈-⎪⎩,且()()2f x f x +=,()252x g x x +=+,则方程()()f x g x =在区间[]5,1-上的所有实根之和为( ) A .5-B .6-C .7-D .8-4.复合函数的零点例4:已知函数()243f x x x =-+,若方程()()20f x bf x c ++=⎡⎤⎣⎦恰有七个不相同的实根,则实数b 的取值范围是( ) A .()2,0-B .()2,1--C .()0,1D .()0,2一、选择题1.设()ln 2f x x x +-=,则函数()f x 的零点所在的区间为( )对点增分集训高三优质精准培优专练数学(理)(学生版)(word 版可编辑修改) A .()0,1B .()1,2C .()2,3D .()3,42.已知a 是函数()12log 2x x f x =-的零点,若00x a <<,则()0f x 的值满足( )A .()00f x =B .()00f x >C .()00f x <D .()0f x 的符号不确定3.函数2()2f x x a x=--的一个零点在区间()1,2内,则实数a 的取值范围是( ) A .()1,3B .()1,2C .()0,3D .()0,24.若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a -----+-=+的两个零点分别位于区间( ) A .(),a b 和(),b c 内 B .(,)a -∞和(),a b 内 C .(),b c 和(),c +∞内D .(,)a -∞和(),c +∞内5.设函数()f x 是定义在R 上的奇函数,当0x >时,()e 3x f x x =+-,则()f x 的零点个数为( ) A .1B .2C .3D .46.函数()2201ln 0x x x xx f x ⎧+-≤=⎨-+>⎩的零点个数为( )A .3B .2C .7D .07.已知函数()101x x xf x ≤⎧⎪=⎨>⎪⎩,则使方程()x f x m +=有解的实数m 的取值范围是( )A .()1,2B .(],2-∞-C .()(),12,-∞+∞D .(][),12,-∞+∞8.若函数()312f x ax a +-=在区间()1,1-内存在一个零点,则a 的取值范围是( )A .1,5⎛⎫+∞ ⎪⎝⎭B .()1,1,5⎛⎫-∞-+∞ ⎪⎝⎭C .11,5⎛⎫- ⎪⎝⎭D .(),1-∞-9.已知函数()00ex x x f x ≤⎧=⎨>⎩,则使函数()()g x f x x m =+-有零点的实数m 的取值范围是( )A .[)0,1B .(1),-∞C .(](),12,-∞+∞D .(](),01,-∞+∞10.已知()f x 是奇函数且是R 上的单调函数,若函数221()()y f x f x λ++=-只有一个零点,则实8数λ的值是( ) A .14B .18C .78-D .38-11.已知当[]0,1x ∈时,函数21()y mx =-的图象与y x m =+的图象有且只有一个交点,则正实数m 的取值范围是( ) A .(0,1][23,+)∞ B .(]0,13[),+∞ C .(0,2][23,+)∞D .(0,2][3,+)∞12.已知函数()y f x =和()y g x =在[]2,2-的图像如下,给出下列四个命题: (1)方程()0f g x =⎡⎤⎣⎦有且只有6个根 (2)方程()0g f x =⎡⎤⎣⎦有且只有3个根 (3)方程()0f f x =⎡⎤⎣⎦有且只有5个根 (4)方程()0g g x =⎡⎤⎣⎦有且只有4个根则正确命题的个数是( ) A .1B .2C .3D .4二、填空题13.函数()052log ||x f x x -=-.的零点个数为________.14.设函数31y x =与2212x y -⎛⎫= ⎪⎝⎭的图象的交点为00(,)x y ,若0,1()x n n ∈+,n ∈N ,则0x 所在的区间是______.15.函数()22026ln 0f x x x x x x ⎧-≤=⎨-+>⎩的零点个数是________.16.已知函数()23||f x x x =+,R x ∈,若方程()1|0|f x a x --=恰有4个互异的实数根,则实数a 的取值范围是________________. 三、解答题17.关于x 的二次方程21()10x m x ++-=在区间[]0,2上有解,求实数m 的取值范围.18.设函数()1()10f x x x=->.(1)作出函数()f x 的图象;(2)当0a b <<且()()f a f b =时,求11a b+的值;(3)若方程()f x m =有两个不相等的正根,求m 的取值范围.1.对于()()'0f x a a >≠,可构造()()h x f x ax =-例1:函数()f x 的定义域为R ,()12f -=,对任意R x ∈,()2f x '>,则()24f x x >+的解集为( ) A .()1,1-B .()1-+∞,C .()1-∞-,D .()-∞+∞,培优点三 含导函数的抽象函数的构造2.对于()()'0xf x f x +>,构造()()h x xf x =;对于()()'0xf x f x ->,构造()()f x h x x=例2:已知函数()y f x =的图象关于y 轴对称,且当(),0x ∈-∞,()()0f x xf x '+<成立,()0.20.222a f =,()log 3log 3b f ππ=,()33log 9log 9c f =,则a ,b ,c 的大小关系是( )A .a b c >>B .a c b >>C .c b a >>D .b a c >>3.对于'()()0f x f x +>,构造()()e x h x f x =;对于'()()f x f x >或'()()0f x f x ->,构造()()ex f x h x =例3:已知()f x 为R 上的可导函数,且R x ∀∈,均有()()f x f x '>,则有( ) A .2016e (2016)(0)f f -<,2016(2016)e (0)f f > B .2016e (2016)(0)f f -<,2016(2016)e (0)f f < C .2016e (2016)(0)f f ->,2016(2016)e (0)f f > D .2016e (2016)(0)f f ->,2016(2016)e (0)f f < 4.()f x 与sin x ,cos x 构造例4:已知函数()y f x =对任意的,22x ππ⎛⎫∈- ⎪⎝⎭满足()()cos sin 0f x x f x x '+>,则( )A .()04f π⎛⎫> ⎪⎝⎭B .()03f f π⎛⎫<2- ⎪⎝⎭C34f ππ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭ D34f ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭一、选择题1.若函数()y f x =在R 上可导且满足不等式()()0xf x f x '+>恒成立,对任意正数a 、b ,若a b <, 则必有( )对点增分集训A .()()af b bf a <B .()()bf a af b <C .()()af a bf b <D .()()bf b af a <2.已知函数()()R f x x ∈满足()11f =,且()12f x '<,则()122x f x <+的解集为( ) A .}{11x x |-<<B .}{1x x |<-C .}{11x x x |<->或D .}{1x x |>3.已知函数()f x 的定义域为R ,()f x '为()f x 的导函数,且()()()10f x x f x '+->,则( ) A .()10f =B .()0f x <C .()0f x >D .()()10x f x -<4.设函数()f x '是函数()()R f x x ∈的导函数,已知()()f x f x '<,且()()4f x f x ''=-,()40f =,()21f =则使得()2e 0x f x -<成立的x 的取值范围是( )A .()2-+∞,B .()0+∞,C .()1+∞,D .()4+∞,5.已知函数()1y f x =-的图象关于点()1,0对称,函数()y f x =对于任意的()0,πx ∈满足()()sin cos f x x f x x >'(其中()f x '是函数()f x 的导函数),则下列不等式成立的是( )A .ππ36f ⎛⎫⎛⎫-> ⎪ ⎪⎝⎭⎝⎭B 3ππ42f ⎛⎫⎛⎫<-- ⎪ ⎪⎝⎭⎝⎭C ππ223f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D 5π3π64f ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭6.定义在R 上的函数()f x 的导函数为()f x ',若对任意实数x ,有()()f x f x >',且()2018f x +为奇函数,则不等式()2018e 0x f x +<的解集为( ) A .(),0-∞B .()0,+∞C .1e ,⎛⎫-∞ ⎪⎝⎭D .1e,⎛⎫+∞ ⎪⎝⎭7.已知函数()2f x +是偶函数,且当2x >时满足()()()2xf x f x f x ''>+,则( ) A .()()214f f <B .()3232f f ⎛⎫> ⎪⎝⎭C .()5042f f ⎛⎫< ⎪⎝⎭D .()()13f f <8.已知定义域为R 的奇函数()y f x =的导函数为()y f x =',当0x ≠时,()()0f x f x x+'>, 若1133a f ⎛⎫= ⎪⎝⎭,()33b f =--,11ln ln 33c f ⎛⎫= ⎪⎝⎭,则a ,b ,c 的大小关系正确的是( )A .a b c <<B .b c a <<C .a c b <<D .c a b <<9.已知定义在R 上的函数()f x 的导函数为()f x ',()()222e x f x f x --=(e 为自然对数的底数), 且当1x ≠时,()()()10x f x f x -->⎡⎤⎣⎦',则( ) A .()()10f f <B .()()2e 0f f >C .()()33e 0f f >D .()()44e 0f f <10.定义在R 上的函数()f x 的导函数为()'f x ,()00f =若对任意R x ∈,都有()()'1f x f x >+,则使得()e 1f x x +<成立的x 的取值范围为( ) A .(),1∞-B .(),0∞-C .()1,+∞-D .0,+∞()11.已知函数()f x 是定义在区间()0,+∞上的可导函数,满足()0f x >且()()'0f x f x +<(()'f x 为函数的导函数),若01a b <<<且1ab =,则下列不等式一定成立的是( ) A .()()()1f a a f b >+ B .()()()1f b a f a >- C .()()af a bf b >D .()()af b bf a >12.定义在R 上的奇函数()y f x =满足()30f =,且当0x >时,不等式()()'f x xf x >-恒成立,则函数()()lg 1g x xf x x =++的零点的个数为( ) A .1 B .2 C .3 D .4二、填空题13.设()f x 是R 上的可导函数,且'()()f x f x ≥-,(0)1f =,21(2)ef =.则(1)f 的值为________.14.已知,22x ⎛⎫∈- ⎪⎝π⎭π,()1y f x =-为奇函数,()()'tan 0f x f x x +>,则不等式()cos f x x >的解集为_________.15.已知定义在实数集R 的函数()f x 满足()27f =,且()f x 导函数()3f x '<,则不等式()ln 3ln 1f x x >+的解集为__________.16.已知函数()f x 是定义在()(),00,-∞+∞上的奇函数,且()10f =.若0x <时,()()'0xf x f x ->, 则不等式()0f x >的解集为__________.1.参变分离法例1:已知函数()ln af x x x=-,若()2f x x <在()1,+∞上恒成立,则a 的取值范围是_________. 2.数形结合法例2:若不等式()log sin 20,1a x x a a >>≠对于任意的π0,4x ⎛⎤∈ ⎥⎝⎦都成立,则实数a 的取值范围是___________. 3.最值分析法培优点四 恒成立问题例3:已知函数()()ln 10f x a x a =+>,在区间()1,e 上,()f x x >恒成立,求a 的取值范围___________.一、选择题1.已知函数()()2ln 1,03,x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩,若()()20f x m x -+≥,则实数m 的取值范围是( ) A .(],1-∞B .[]2,1-C .[]0,3D .[)3,+∞2.已知函数()3224f x x x x =--+,当[]3,3x ∈-时,()214f x m m ≥-恒成立,则实数m 的取值范围是( ) A .()3,11-B .()3,11C .[]3,11D .[]2,73.若函数()2ln 2f x x ax =+-在区间1,22⎛⎫⎪⎝⎭内单调递增,则实数a 的取值范围是( ) A .(],2-∞- B .()2,-+∞C .12,8⎛⎫-- ⎪⎝⎭D .1,8⎡⎫-+∞⎪⎢⎣⎭ 4.已知对任意21,e e x ⎡⎤∈⎢⎥⎣⎦不等式2e xax >恒成立(其中e 2.71828=,是自然对数的底数),则实数a的取值范围是( )A .e 0,2⎛⎫⎪⎝⎭B .()0,eC .(),2e -∞-D .24,e ⎛⎫-∞ ⎪⎝⎭5.已知函数()2e x f x x =,当[]1,1x ∈-时,不等式()f x m <恒成立,则实数m 的取值范围是( )A .1,e⎡⎫+∞⎪⎢⎣⎭B .1,e⎛⎫+∞ ⎪⎝⎭C .[)e,+∞D .()e,+∞6.当[]2,1x ∈-时,不等式32430ax x x -++≥恒成立,则实数a 的取值范围是( ) A .[]5,3--B .96,8⎡⎤--⎢⎥⎣⎦C .[]6,2--D .[]4,3--7.函数()2e 1xf x x=-+,若存在(]00,2x ∈使得()00m f x ->成立,则实数m 的范围是( ) 对点增分集训A .21e 5,⎛⎫-+∞ ⎪⎝⎭B .()1,-+∞C .()1,+∞D .1e,2⎛⎫-+∞ ⎪⎝⎭8.设函数()ln f x x ax =+,若存在()00,x ∈+∞,使()00f x >,则a 的取值范围是( )A .1,1e ⎛⎫- ⎪⎝⎭B .1,e ⎛⎫-∞ ⎪⎝⎭C .()1,-+∞D .1,e⎛⎫-+∞ ⎪⎝⎭9.若对于任意实数0x ≥,函数()e x f x ax =+恒大于零,则实数a 的取值范围是( ) A .(),e -∞B .(],e -∞-C .[)e,+∞D .()e,-+∞10.已知函数()()()3f x a x a x a =-++,()22x g x =-,若对任意x ∈R ,总有()0f x <或()0g x <成立,则实数a 的取值范围是( ) A .(),4-∞-B .()4,0-C .[)4,0-D .()4,-+∞11.已知函数()e xf x ax x=-,()0,x ∈+∞,当21x x >时,不等式()()12210f x f x x x -<恒成立,则实数a 的取值范围为( ) A .(],e -∞B .(),e -∞C .e ,2⎛⎫-∞ ⎪⎝⎭D .e ,2⎛⎤-∞ ⎥⎝⎦12.设函数()()e 31x f x x ax a =--+,其中1a <,若有且只有一个整数0x 使得()00f x ≤,则a 的取值范围是( )A .23,e 4⎛⎫⎪⎝⎭ B .23,e 4⎡⎫⎪⎢⎣⎭C .2,1e⎛⎫⎪⎝⎭D .2,1e ⎡⎫⎪⎢⎣⎭二、填空题13.设函数()f x x a =+,()1g x x =-,对于任意的x ∈R ,不等式()()f x g x ≥恒成立,则实数a 的取值范围是__________.14.函数()ln 1f x x x ax =-+,其中a ∈R ,若对任意正数x 都有()0f x ≥,则实数a 的取值范围为____________.15.已知函数()21ln 22f x x ax x =--,若函数()f x 在1,22⎡⎤⎢⎥⎣⎦上单调递增,则实数a 的取值范围是__________.16.已知关于x 的不等式21log 02m mx x ⎛⎫+> ⎪⎝⎭-在[]1,2上恒成立,则实数m 的取值范围为___________. 三、解答题17.设函数()()()2ln 1f x x a x x =++-,其中a ∈R , (1)讨论函数()f x 极值点的个数,并说明理由; (2)若0x ∀>,()0f x ≥成立,求a 的取值范围.18.设函数()2e mx f x x mx =+-,(1)证明:()f x 在(),0-∞单调递减,在()0,+∞单调递增;(2)若对于任意1x ,[]21,1x ∈-,都有()()12e 1f x f x -≤-,求m 的取值范围.培优点五导数的应用1.利用导数判断单调性例1:求函数()()32=+--的单调区间333e xf x x x x-2.函数的极值例2:求函数()e x f x x -=的极值.3.利用导数判断函数的最值例3:已知函数()()ln m f x x m x=-∈R 在区间[]1,e 上取得最小值4,则m =___________.一、单选题1.函数()ln f x x x =-的单调递减区间为( ) A .() 0,1 B .() 0,+∞ C .() 1,+∞D .()() ,01,-∞+∞2.若1x =是函数()ln f x ax x =+的极值点,则( ) A .()f x 有极大值1-B .()f x 有极小值1-对点增分集训C .()f x 有极大值0D .()f x 有极小值03.已知函数()3f x x ax =--在(],1-∞-上单调递减,且()2ag x x x=-在区间(]1,2上既有最大值,又有最小值,则实数a 的取值范围是( ) A .2a >-B .3a ≥-C .32a -≤<-D .32a -≤≤-4.函数321y x x mx =+++是R 上的单调函数....,则m 的范围是( ) A .1,3⎛⎫+∞ ⎪⎝⎭B .1,3⎛⎫-∞ ⎪⎝⎭C .1,3⎡⎫+∞⎪⎢⎣⎭D .1,3⎛⎤-∞ ⎥⎝⎦5.遇见你的那一刻,我的心电图就如函数1ln sin 1x y x x -⎛⎫=+⎪+⎝⎭的图象大致为( ) A .B .C .D .6.函数()321213f x x ax x =+-+在()1,2x ∈内存在极值点,则( ) A .1122a -<<B .1122a -≤≤ C .12a <-或12a >D .12a ≤-或12a ≥7.已知()22f x ax x a =++,x ∈R ,若函数()()()322g x x a x f x =---在区间()1,3-上单调递减,则实数a 的取值范围是( )A .1a <-或3a >B .1a ≤-或3a ≥C .9a <-或3a >D .9a ≤-或3a ≥8.函数()y f x =在定义域3,32⎡⎤-⎢⎥⎣⎦内可导,其图像如图所示.记()y f x =的导函数为()y f x =',则不等式()0f x '≤的解集为( )A .[]1,12,33⎡⎤-⎢⎥⎣⎦B .1481,,233⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦C .[)31,1,222⎡⎤-⎢⎥⎣⎦D .31144,,,323233⎡⎤⎡⎤⎡⎤--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦9.设函数()()1ln 03f x x x x =->,则()y f x =( )A .在区间1,1e⎛⎫ ⎪⎝⎭,()1,e 内均有零点B .在区间1,1e⎛⎫ ⎪⎝⎭,()1,e 内均无零点 C .在区间1,1e⎛⎫⎪⎝⎭内有零点,在区间()1,e 内无零点D .在区间1,1e⎛⎫⎪⎝⎭内无零点,在区间()1,e 内有零点10.若函数()()323321f x x ax a x =++++既有极大值又有极小值,则实数a 的取值范围为( ) A .12a -<<B .12a -≤≤C .1a ≤-或2a ≥D .1a <-或2a >11.已知函数()3223f x x ax bx c =+++的两个极值点分别在()1,0-与()0,1内,则2a b -的取值范围是( )A .33,22⎛⎫- ⎪⎝⎭ B .3,12⎛⎫- ⎪⎝⎭ C .13,22⎛⎫- ⎪⎝⎭ D .31,2⎛⎫⎪⎝⎭12.设函数()y f x =在区间(),a b 上的导函数为()f x ',()f x '在区间(),a b 上的导函数为()f x '',若在区间(),a b 上()0f x ''>,则称函数()f x 在区间(),a b 上为“凹函数”,已知()5421122012f x x mx x =--在区间()1,3上为“凹函数”,则实数m 的取值范围为( ) A .31,9⎛⎫-∞ ⎪⎝⎭B .31,59⎡⎤⎢⎥⎣⎦C .(],5-∞D .(],3-∞-二、填空题13.函数()3222f x x x =-在区间[]1,2-上的最大值是___________.14.若函数()32334f x x ax x a =-+-在(),1-∞-,()2,+∞上都是单调增函数,则实数a 的取值集合是______.15.函数()()2ln 1f x x a x a =--∈R 在[]1,2内不存在极值点,则a 的取值范围是___________. 16.已知函数()e ln x f x a x =+, ①当1a =时,()f x 有最大值;②对于任意的0a >,函数()f x 是()0,+∞上的增函数; ③对于任意的0a <,函数()f x 一定存在最小值; ④对于任意的0a >,都有()0f x >.其中正确结论的序号是_________.(写出所有正确结论的序号) 三、解答题17.已知函数()()ln f x x ax a =-∈R(1)讨论函数()f x 在()0,+∞上的单调性; (2)证明:2e e ln 0x x ->恒成立.18.已知函数()()2e ,x f x a x bx a b =+-∈R ,其导函数为()'y f x =.(1)当2b =时,若函数()'y f x =在R 上有且只有一个零点,求实数a 的取值范围; (2)设0a ≠,点()(),,P m n m n ∈R 是曲线()y f x =上的一个定点,是否存在实数()00x x m ≠使得()()000'2x m f x n f x m +⎛⎫-=- ⎪⎝⎭成立?并证明你的结论.1.求三角函数值 例1:已知π3π044βα<<<<,π3cos 45α⎛⎫-= ⎪⎝⎭,3π5sin 413β⎛⎫+=⎪⎝⎭,求()sin αβ+的值.2.三角函数的值域与最值例2:已知函数()πππcos 22sin sin 344f x x x x ⎛⎫⎛⎫⎛⎫=-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,(1)求函数()f x 的最小正周期和图像的对称轴方程; (2)求函数()f x 在区间ππ,122⎡⎤-⎢⎥⎣⎦的值域.3.三角函数的性质例3:函数()2cos2f x x x +( )A .在ππ,36⎛⎫--⎪⎝⎭上单调递减 B .在ππ,63⎛⎫⎪⎝⎭上单调递增培优点六 三角函数C .在π,06⎛⎫- ⎪⎝⎭上单调递减D .在π0,6⎛⎫⎪⎝⎭上单调递增一、单选题1.若π1sin 63α⎛⎫-= ⎪⎝⎭,则2πcos 23α⎛⎫+⎪⎝⎭的值为( ) A .13-B .79-C .13D .792.函数()π2sin 26f x x ⎛⎫=-+ ⎪⎝⎭的一个单调递增区间是( )A .ππ,63⎡⎤-⎢⎥⎣⎦B .π5π,36⎡⎤⎢⎥⎣⎦C .ππ,36⎡⎤-⎢⎥⎣⎦D .π2π,63⎡⎤⎢⎥⎣⎦3.已知1tan 4tan θθ+=,则2πcos 4θ⎛⎫+= ⎪⎝⎭( )A .15B .14C .13D .124.关于函数()()π3sin 213f x x x ⎛⎫=-+∈ ⎪⎝⎭R ,下列命题正确的是( )A .由()()121f x f x ==可得12x x -是π的整数倍B .()y f x =的表达式可改写成()π3cos 216f x x ⎛⎫=++ ⎪⎝⎭C .()y f x =的图象关于点3π,14⎛⎫⎪⎝⎭对称D .()y f x =的图象关于直线π12x =-对称 5.函数()2πππcos 2sin sin 555f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭的最大值是( ) 对点增分集训高三优质精准培优专练数学(理)(学生版)(word 版可编辑修改)A .1B .πsin 5C .π2sin 5D .56.函数()()sin 0y x ωϕω=+>的部分图象如图所示,则ω,ϕ的值分别可以是( )A .1,π3B .1,2π3-C .2,2π3D .2,π3-7.已知函数()()πsin 0,2f x x ωϕωϕ⎛⎫=+>≤ ⎪⎝⎭,π4x =-和π4x =分别是函数()f x 取得零点和最小值点横坐标,且()f x 在ππ,1224⎛⎫- ⎪⎝⎭单调,则ω的最大值是( ) A .3B .5C .7D .98.已知函数()cos sin f x x x =⋅,给出下列四个说法:2014π33f ⎛⎫= ⎪⎝⎭①②函数()f x 的周期为π; ()f x ③在区间ππ,44⎡⎤-⎢⎥⎣⎦上单调递增;()f x ④的图象关于点π,02⎛⎫- ⎪⎝⎭中心对称其中正确说法的序号是( ) A .②③B .①③C .①④D .①③④9.已知0ω>,函数()πsin 4f x x ω⎛⎫=+ ⎪⎝⎭在π,π2⎛⎫⎪⎝⎭上单调递减,则ω的取值范围是( )A .10,2⎛⎤⎥⎝⎦B .(]0,2C .15,24⎡⎤⎢⎥⎣⎦D .13,24⎡⎤⎢⎥⎣⎦10.同时具有性质:①()f x 最小正周期是π;②()f x 图象关于直线π3x =对称;③()f x 在ππ,63⎡⎤-⎢⎥⎣⎦上是增函数的一个函数是( )A .πsin 23xy ⎛⎫=+ ⎪⎝⎭B .πsin 26y x ⎛⎫=- ⎪⎝⎭C .πcos 23y x ⎛⎫=+ ⎪⎝⎭D .πsin 23y x ⎛⎫=+ ⎪⎝⎭11.关于函数()1π2sin 26f x x ⎛⎫=+ ⎪⎝⎭的图像或性质的说法中,正确的个数为( )①函数()f x 的图像关于直线8π3x =对称; ②将函数()f x 的图像向右平移π3个单位所得图像的函数为1π2sin 23y x ⎛⎫=+ ⎪⎝⎭;③函数()f x 在区间π5π,33⎛⎫- ⎪⎝⎭上单调递增;④若()f x a =,则1πcos 233a x ⎛⎫-= ⎪⎝⎭.A .1B .2C .3D .412.函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>≤ ⎪⎝⎭的图象关于直线π3x =对称,它的最小正周期为π,则函数()f x 图象的一个对称中心是( ) A .π,012⎛⎫-⎪⎝⎭B .π,13⎛⎫ ⎪⎝⎭ C .5π,012⎛⎫⎪⎝⎭D .π,012⎛⎫⎪⎝⎭二、填空题13.函数πcos 24y x ⎛⎫=+ ⎪⎝⎭的单调递减区间是_________.14.已知()0,πα∈,且3cos 5α=,则πtan 4α⎛⎫-= ⎪⎝⎭_________________.15.函数()sin 2f x x x =在π0,2x ⎛⎫∈ ⎪⎝⎭的值域为_________.16.关于()()π4sin 2,3f x x x ⎛⎫+∈ ⎪⎝⎭R =,有下列命题①由()()120f x f x ==可得12x x -是π的整数倍;②()y f x =的表达式可改写成π4cos 26y x ⎛⎫=- ⎪⎝⎭;③()y f x =图象关于π,06⎛⎫- ⎪⎝⎭对称;④()y f x =图象关于π6x =-对称.其中正确命题的序号为________(将你认为正确的都填上). 三、解答题17.已知()π2sin 2cos26f x x a x ⎛⎫=++ ⎪⎝⎭()a ∈R ,其图象在π3x =取得最大值.(1)求函数()f x 的解析式;(2)当π0,3α⎛⎫∈ ⎪⎝⎭,且()65f α=,求sin2α值.18.已知函数()()2πsin sin 02f x x x x ωωωω⎛⎫=++> ⎪⎝⎭的最小正周期为π. (1)求ω的值;(2)求函数()f x 在区间2π0,3⎡⎤⎢⎥⎣⎦上的取值范围.1.解三角形中的要素例1:ABC △的内角A ,B ,C 所对的边分别为a ,b ,c ,若c b =,60B =,则C =_____.2.恒等式背景例2:已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边, 且有cos sin 0a C C b c --=.培优点七 解三角形(1)求A ;(2)若2a =,且ABC △b ,c .一、单选题1.在ABC △中,1a =,6A π∠=,4B π∠=,则c =( ) ABCD2.在ABC △中,三边长7AB =,5BC =,6AC =,则AB BC ⋅等于( ) A .19B .19-C .18D .18-3.在ABC △中,角A ,B ,C 所对应的边分别是a ,b ,c ,若2cos c a B =,则三角形一定是( ) A .等腰直角三角形B .直角三角形C .等腰三角形D .等边三角形4.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若3C π=,c 3b a =,则ABC △的面积为( ) ABCD对点增分集训5.在ABC △中,内角A ,B ,C 的对边分别为a ,b ,c ,若22a b bc -=,sin C B =,则A =( )A .30︒B .60︒C .120︒D .150︒6.设ABC △的三个内角A ,B ,C 所对的边分别为a ,b ,c ,如果()()3a b c b c a bc +++-=,且a =那么ABC △外接圆的半径为( ) A .1BC .2D .47.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且222b c a bc +=+,若2sin sin sin B C A ⋅=,则ABC △的形状是( ) A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形8.ABC △的内角A ,B ,C 的对边分别是a ,b ,c 且满足cos cos a B b A c -=,则ABC △是( ) A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形9.在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知ABC △的面积为,2b c -=,1cos 4A =-,则a 的值为( )A .8B .16C .32D .6410.在ABC △中,a ,b ,c 分别为角A ,B ,C 所对的边.若()sin cos 0b a C C +-=, 则A =( ) A .4πB .3πC .34π D .23π 11.在ABC △中,内角A ,B ,C 的对边分别是a ,b ,c ,若cos cos cos a b cA B C==,则ABC △是( ) A .直角三角形B .钝角三角形C .等腰直角三角形D .等边三角形12.在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =c =tan 21tan A cB b+=, 则C ∠=( ) A .6π B .4πC .4π或34π D .3π二、填空题13.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,c =2216b a -=,则角C 的最大值为_____;14.已知ABC △的三边a ,b ,c 成等比数列,a ,b ,c 所对的角分别为A ,B ,C ,则sin cos B B +的取值范围是_________.15.在ABC △中三个内角A ∠,B ∠,C ∠,所对的边分别是a ,b ,c ,若()2sin cos 2sin cos b C A A C +=-,且23a =,则ABC △面积的最大值是________16.在锐角ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且A ,B ,C 成等差数列,3b =,则ABC △面积的取值范围是__________. 三、解答题17.己知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,且3cos 2sin a A C+=.(1)求角A 的大小;(2)若5b c +=,且ABC △的面积为3,求a 的值.18.如图,在ABC △中,点D 在BC 边上,60ADC ∠=︒,27AB =,4BD =..(1)求ABD △的面积.(2)若120BAC ∠=,求AC 的长.1.代数法例1:已知向量a ,b 满足=3a ,b ()⊥+a a b ,则b 在a 方向上的投影为( ) A .3 B .3-C .D 2.几何法例2:设a ,b 是两个非零向量,且2==+=a b a b ,则=-a b _______. 3.建立直角坐标系例3:在边长为1的正三角形ABC 中,设2BC BD =,3CA CE =,则AD BE ⋅=__________.培优点八 平面向量B CADE一、单选题1.已知向量a,b满足1=a,2=b,且向量a,b的夹角为4π,若λ-a b与b垂直,则实数λ的值为( )A.12-B.12C.24-D.242.已知向量a,b满足1=a,2=b,7+=a b,则⋅=a b()A.1 B.2C.3D.23.如图,平行四边形ABCD中,2AB=,1AD=,60A∠=,点M在AB边上,且13AM AB=,则DM DB⋅=()A.1-B.1 C.3-D.34.如图,在ABC△中,BE是边AC的中线,O是BE边的中点,若AB=a,AC=b,则AO=( )对点增分集训高三优质精准培优专练数学(理)(学生版)(word 版可编辑修改) A .1122+a bB .1124+a bC .1142+a bD .1144+a b5.在梯形ABCD 中,AB CD ∥,1CD =,2AB BC ==,120BCD ∠=,动点P 和Q 分别在线段BC 和CD 上,且BP BC λ=,18DQ DC λ=,则AP BQ ⋅的最大值为( ) A .2-B .32- C .34D .986.已知ABC △中,2AB =,4AC =,60BAC ∠=︒,P 为线段AC 上任意一点,则PB PC ⋅的范围是( )A .[]14,B .[]04,C .944⎡⎤-⎢⎥⎣⎦,D .[]24-,7.已知非零向量a ,b ,满足=a 且()()320+⋅-=a b a b ,则a 与b 的夹角为( ) A .4πB .2πC .34π D .π8.在Rt ABC △中斜边BC a =,以A 为中点的线段2PQ a =,则BP CQ ⋅的最大值为( ) A .2-B .0C .2D .9.设向量a ,b ,c ,满足1==a b ,12⋅=-a b ,6,0--=a b c c ,则c 的最大值等于( )A .1 BC D .210.已知a 与b 为单位向量,且⊥a b ,向量c 满足2--=c a b ,则c 的取值范围为( )A .1,1⎡+⎣B .2⎡-+⎣C .D .3⎡-+⎣11.平行四边形ABCD 中,AC ,BD 在AB 上投影的数量分别为3,1-,则BD 在BC 上的投影的取值范围是( ) A .()1,-+∞B .()1,3-C .()0,+∞D .()0,312.如图,在等腰直角三角形ABC 中,AB AC ==D ,E 是线段BC 上的点,且13DE BC =,则AD AE ⋅的取值范围是( )A .84,93⎡⎤⎢⎥⎣⎦B .48,33⎡⎤⎢⎥⎣⎦C .88,93⎡⎤⎢⎥⎣⎦D .4,3⎡⎫+∞⎪⎢⎣⎭二、填空题13.已知向量()1,2=a ,()2,2=-b ,()1,λ=c ,若()2+∥c a b ,则λ=________. 14.若向量a ,b 满足1=a ,2=b ()⊥+a a b ,则a 与b 的夹角为__________.15.已知正方形ABCD 的边长为2,E 是CD 上的一个动点,则求AE BD ⋅的最大值为________.16.在ABC △中,90C ∠=︒,30B ∠=︒,2AC =,P 为线段AB 上一点,则PB PC +的取值范围为____.1.简单的线性规划问题应注意取点是否取得到例1:已知实数x ,y 满足24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩,则32z x y =-的最小值是( )A .4B .5C .6D .72.目标函数为二次式例2:若变量x ,y 满足120x x y x y ≤⎧⎪≥⎨⎪++≥⎩,则22z x y =+的最大值为( )培优点九 线性规划AB.7C.9D.10 3.目标函数为分式例3:设变量x,y满足约束条件22022010x yx yx y--≤⎧⎪-+≥⎨⎪+-≥⎩,则11ysx+=+的取值范围是()A.31,2⎡⎤⎢⎥⎣⎦B.1,12⎡⎤⎢⎥⎣⎦C.[]1,2D.1,22⎡⎤⎢⎥⎣⎦4.面积问题例4:若不等式组3434xx yx y≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线4y kx=+分成面积相等的两部分,则k的值为( )A.73B.37C.173-D.317-一、单选题1.若实数x,y满足10xyx y≥⎧⎪≥⎨⎪+-≤⎩,则z x y=-的最大值为( )A.2B.1 C.0 D.1-2.已知实数x,y满足线性约束条件3023004x yx yx+-≤⎧⎪--≤⎨⎪≤≤⎩,则其表示的平面区域的面积为()A.94B.274C.9D.2723.已知实数x,y满足122022x yx yx y-≤⎧⎪-+≥⎨⎪+≥⎩,若z x ay=-只在点()43,处取得最大值,则a的取值范围是( )对点增分集训高三优质精准培优专练数学(理)(学生版)(word 版可编辑修改)A .()1-∞-,B .()2-+∞,C .()1-∞,D .12⎛⎫+∞ ⎪⎝⎭,4.已知实数x ,y 满足约束条件222020x x y x y ≤⎧⎪-+≥⎨⎪++≥⎩,则5x z y -=的取值范围为( ) A .2433⎡⎤-⎢⎥⎣⎦,B .4233⎡⎤-⎢⎥⎣⎦,C .3324⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭,,D .3342⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭,,5.若实数x ,y 满足约束条件22390x y x y x +≤⎧⎪-≤⎨⎪≥⎩,则22z x y =+的最大值是( )A B .4 C .9 D .106.已知点()12A ,,若动点()P x y ,的坐标满足02x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则AP 的最小值为( )AB.1 C D7.x ,y 满足约束条件20220220x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩,若z y ax =-取得最大值的最优解不唯一,则实数a 的值为( ) A .12或1-B .2或12C .2或1D .2或1-8.若x ,y 满足不等式组40240 4x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩,则215y x ≤+成立的概率为( )A .1556B .1116C .58D .389.若x ,y 满足不等式组20510080x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩,则32z x y =-+的最小值为( )A .7B .6C .265D .4高三优质精准培优专练数学(理)(学生版)(word 版可编辑修改)10.已知平面直角坐标系xOy 上的区域D由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩给定.若()M x y ,为D 上动点,点A的坐标为).则z OM OA =⋅的最大值为( )A.B. C .4 D .311.若不等式组20510080x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩所表示的平面区域内存在点()00x y ,,使0020x ay ++≤成立,则实数a 的取值范围是( )A .[)1,-+∞B .(],1-∞-C .(],1-∞D .[)1,+∞12.已知圆()()22:1C x a y b -+-=,平面区域60:400x y x y y +-≤⎧⎪Ω-+≥⎨⎪≥⎩,若圆心C ∈Ω,且圆C 与x 轴相切,则圆心(),C a b 与点()2,8连线斜率的取值范围是( ) A .77,,35⎛⎤⎡⎫-∞-+∞ ⎪⎥⎢⎝⎦⎣⎭B .77,,35⎛⎤⎛⎫-∞-+∞ ⎪⎥⎝⎦⎝⎭C .77,35⎛⎫- ⎪⎝⎭D .77,35⎡⎤-⎢⎥⎣⎦二、填空题13.设x ,y 满足10302x y x y x +-≥⎧⎪-+≥⎨⎪≤⎩,则21z x y =++的最大值为____________. 14.若变量x ,y 满足约束条件210220x x y x y ≤⎧⎪-+≤⎨⎪+-≥⎩,则22z x y =+的最小值为_________.15.已知实数x ,y 满足110x y x y x -≤⎧⎪+≤⎨⎪≥⎩,则22x y x ++的最小值为______.16.某公司计划明年用不超过6千万元的资金投资于本地养鱼场和远洋捕捞队.经过对本地养鱼场年利润率的调研,其结果是:年利润亏损10%的概率为02.,年利润获利30%的概率为0.4,年利润获利50%的概率为0.4,对远洋捕捞队的调研结果是:年利润获利为60%的概率为0.7,持平的概率为0.2,年利润亏损20%的可能性为0.1.为确保本地的鲜鱼供应,市政府要求该公司对远洋捕捞队的投资不得高于本地养鱼场的投资的2倍.根据调研数据,该公司如何分配投资金额,明年两个项目的利润之和最大值为_________千万.1.等差数列的性质例1:已知数列{}n a ,{}n b 为等差数列,若117a b +=,3321a b +=,则55a b +=_______. 2.等比数列的性质例2:已知数列{}n a 为等比数列,若4610a a +=,则()713392a a a a a ++的值为( ) A .10B .20C .100D .2003.等差、等比综合培优点十 等差、等比数列例3:设{}n a 是等差数列,{}n b 为等比数列,其公比1q ≠,且()01,2,3,,i b i n >=,若11a b =,1111a b =, 则有( ) A .66a b =B .66a b >C .66a b <D .66a b >或66a b <一、单选题1.我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,中间三尺重几何."意思是:“现有一根金锤,长5尺,头部1尺,重4斤,尾部1尺,重2斤,且从头到尾,每一尺的重量构成等差数列,问中间三尺共重多少斤.”( ) A .6斤B .7斤C .8斤D .9斤2.设n S 为等差数列{}n a 的前n 项和,若540S =,9126S =,则7S =( ) A .66B .68C .77D .843.已知等比数列{}n a 的前n 项和为n S ,且满足122n n S λ+=+,则λ的值为( ) A .4B .2C .2-D .4-4.已知等差数列{}n a 的前n 项和为n S ,5714a a +=,则11S =( ) A .140B .70C .154D .775.已知数列{}n a 是公比为q 的等比数列,且1a ,3a ,2a 成等差数列,则公比q 的值为( )A .12-B .2-C .1或12-D .1-或126.公比不为1的等比数列{}n a 的前n 项和为n S ,且12a -,212a -,3a 成等差数列,若11a =,则4S =( ) A .5-B .0C .5D .77.等比数列{}n a 的各项均为正数,且564718a a a a +=,则3132310log log log a a a +++=( )对点增分集训。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12021届高三精准培优专练培优点外接球
一、构造正方体与长方体的外接球问题例1:已知直三棱柱111
ABCABC
的6个顶点都在球O的球面上,若3AB,4AC,ABAC,
112AA,则球O的半径为()
A.3172B.210C.132D.310【答案】C【解析】∵ABAC,∴直三棱柱111
ABCABC
的底面ABC为直角三角形,
把直三棱柱111
ABCABC
补成长方体,
则长方体的体对角线就是球O的直径,即球O的半径为222341213
22
.
二、与正棱锥有关的外接球问题例2:一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()
A.334B.33C.34D.312
【答案】C【解析】∵正三棱锥的四个顶点都在半径为1的球面上,且底面的三个顶点在该球的大圆上,∴球心是底面三角形的中心,
∵球的半径为1,∴底面三角形的边长为3,即该正三棱锥的体积为2133(3)1
344
.2
三、其他柱体、锥体的外接球问题例3:已知,AB是球O的球面上的两点,90AOB,C为该球面上的动点,若三棱锥OABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【答案】C
【解析】设球O的半径为R,则212AOBSR△,当OC平面AOB时,三棱锥OABC的体积最大,此时21136
32VRR
,解得6R,
所以球O的表面积为24π6144πS
.
对点增分集训一、选择题1.一个四棱柱的底面是正方形,侧棱与底面垂直,其长度为4,棱柱的体积为16,棱柱的各项点在一个球面上,则这个球的表面积是()A.16πB.20πC.24πD.32π【答案】C【解析】正四棱柱的高为4,体积为16,则底面面积为4,即底面正方形的边长为2,正四棱柱的对角线长即球的直径为26,即球的半径为6,球的表面积为24π.2.一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则几何体的外接球的表面积为()3
A.3πB.43πC.12πD.123π【答案】A【解析】把原来的几何体补成以DA,DC,DP为长、宽、高的长方体,原几何体四棱锥与长方体是同一个外接球,
22221113Rl
,
3
2R,2
3
=4π4π3π
4SR
球.
3.直三棱柱111ABCABC中,ABBC,12ABBCAA,则该三棱柱的外接球的表面积为()A.4πB.8πC.12πD.32π3
【答案】C
【解析】∵在直三棱柱111ABCABC中,ABBC,12ABBCAA
,
∴AB,BC,1
AA
为棱构造一个正方体,
则外接球的半径222222
3
2R
,故表面积为2
4π12πSR
.
4.点A,B,C,D在同一个球的球面上,3ABBCAC,若四面体ABCD体积的最大值为3,则这个球的表面积为()A.169π16B.289π16C.25π16D.8π【答案】B【解析】设ABC△的中心为E,过点E作平面ABC的垂线l,
则有题意可知,点D在直线l上,ABC△的面积为1333sin603
24S
.
由体积的最大值可得11333
334SDEDE
,则4DE.
由题意易知,外接球的球心在DE上,设球心为点O,半径ODOBR.
ABC△的外接圆半径满足2sinar
A,即
32
sin60r
,∴1rBE.4
在OBERt△中,222OEBEOB,即222(4)1RR,解得178R.
据此可得这个球的表面积为22892894π4ππ
6416SR
.
5.一个正四面体的所有棱长都为2,四个顶点在同一个球面上,则此球的表面积为()A.3πB.4πC.33πD.6π【答案】A【解析】如图,将四面体补成正方体,则正方体的棱长是1,正方体的体对角线长为3,
即此球的半径32R,故球的表面积
24π3πSR
.
6.已知三棱锥PABC的四个顶点都在同一个球面上,底面ABC△满足6BABC,90B,若该三棱锥体积最大值为3,则其外接球的表面积为()A.21πB.32π3C.16π3D.16π【答案】D【解析】因为ABC△为等腰三角形,所以AC为截面圆的直径,22=23ACABAC
,5
即该三棱锥的外接球的球心O在截面ABC中的射影为AC的中点D,当P,O,D三点共线且P,O位于截面同一侧时,三棱锥的体积最大,此时三棱锥的高为PD,所以1166=3
32PD
,解得=3PD,
设外接球的半径为R,则3ODR,OCR,在OCDRt△中,13
2CDAC
,由勾股定理得
222(3)(3)RR
,解得2R,
所以外接球的表面积为24π216πS
.
7.已知四面体ABCD中,6ABAD,4AC,213CD,AB平面ACD,则四面体ABCD外接球的表面积为()A.36πB.88πC.92πD.128π【答案】B【解析】在ACD△中,由6AD,4AC,213CD,可得222ADACCD
,则ACAD,
又AB平面ACD,故222246688222R
,
则24π(22)88πV
.
8.已知A,B是球O的球面上两点,60AOB,C为该球面上的动点,若三棱锥OABC体积的最大值为183,则球O的体积为()A.81πB.128πC.144πD.288π【答案】D
【解析】由题意可知221111(sin60)(sin60)1833232COABVRhRR,6R,34=π288π3VR球.6
9.已知A,B,C,D是同一个球面上的四个点,其中ABC△是正三角形,AD平面ABC,26ADAB,则该球的表面积为()
A.16πB.24πC.323πD.48π【答案】C【解析】把A,B,C,D扩展为三棱锥,上下地面中心连线的中点与A的距离为球的半径,26ADAB,
3OE,ABC△是正三角形,所以2221()332AEABAB,223(3)23AO.
所以球的体积为34π(23)323π
3.
10.已知三棱锥PABC的所有顶点都在球O的球面上,PAAB,PAAC,60BAC,2PA,2AB,3AC,则球O的表面积为()
A.40π3B.30π3C.20π3D.10π
3
【答案】A
【解析】设ABC△外接圆半径为r,三棱锥外接球半径为R,∵2AB,3AC,60BAC,
∴22212cos60492237
2BCABACABAC
,即7BC,
∴2212sin603BCr,解得213r,
∵PAAB,PAAC,∴PA平面ABC,7
则将三棱锥补成三棱柱可得,2222110()1
293
PARr,
即球O的表面积为21040π4π4π
33SR
.
11.如图,在四面体PABC中,4PAPBPC,点O是点P在平面ABC上的投影,且2tan
2APO
.则四面体PABC的外接球的体积为()
A.86πB.24πC.323πD.48π【答案】A【解析】∵在四面体PABC中,4PAPBPC,
点O是点P在平面ABC上的投影,且2tan
2APO
.
∴3sin3APO,6cos3APO,∴433AO,463PO.
由题意知四面体PABC的外接球的球心O在线段PO上,∴222OOAOAO
,∴2224643()()33RR,解得6R.
∴四面体PABC的外接球的体积为86π.
