分离定律算法
分离定律和自由组合定律适用的范围

分离定律和自由组合定律1. 介绍在数学和逻辑学中,分离定律和自由组合定律是两个基本的运算规则。
它们在逻辑推理、集合论、布尔代数等领域中具有广泛的应用。
2. 分离定律分离定律是一种逻辑推理的规则,也被称为分配律或分解律。
它可以帮助我们将一个复合命题分解成两个或多个简单命题的逻辑连接。
分离定律的一般形式为:对于任意命题P、Q和R,有以下等价式成立:•P ∧ (Q ∨ R) ≡ (P ∧ Q) ∨ (P ∧ R)•P ∨ (Q ∧ R) ≡ (P ∨ Q) ∧ (P ∨ R)其中,∧表示逻辑与(and)运算,∨表示逻辑或(or)运算。
分离定律的应用可以简化复杂的逻辑表达式,提高推理的效率。
例如,假设我们有一个命题P表示“今天是星期一”,命题Q表示“明天是星期二”,命题R表示“后天是星期三”。
那么,P ∧ (Q ∨ R)可以解读为“今天是星期一,并且明天是星期二或者后天是星期三”。
根据分离定律,我们可以将其分解成两个命题:“今天是星期一,并且明天是星期二”或者“今天是星期一,并且后天是星期三”。
3. 自由组合定律自由组合定律是一种集合论中的运算规则,它允许我们对多个集合进行交、并、差等运算,并且可以按照任意的顺序进行组合。
自由组合定律的一般形式为:对于任意集合A、B和C,有以下等价式成立:• A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)• A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)• A (B ∪ C) = (A B) ∩ (A C)• A (B ∩ C) = (A B) ∪ (A C)其中,∩表示集合的交运算,∪表示集合的并运算,。
自由组合定律的应用可以帮助我们更好地理解集合之间的关系,并且简化集合运算的过程。
例如,假设集合A表示“所有男性”,集合B表示“所有成年人”,集合C表示“所有大学生”。
那么,A ∩ (B ∪ C)可以解读为“既是男性,又是成年人或者大学生”。
自由组合定律分离定律

自由组合定律分离定律
自由组合定律:在逻辑学中,自由组合定律是指一个命题公式中的变量可以被任意组合而不改变其实质,即变量可以自由组合。
例如,命题公式(p ∨q) ∧(q ∨r)中,变量q可以自由组合,所以可以将它改写为(p ∨r) ∧(r ∨s)。
分离定律:在集合论中,分离定律是指一个集合中所有满足某个条件的元素可以组成一个子集。
例如,假设集合A={1,2,3,4,5},我们可以通过分离定律将其中所有偶数组成一个新的集合B={2,4}。
这个定律是集合论中最基本的公理之一,被广泛应用于各种数学领域。
分离定律中概率计算怎么讲
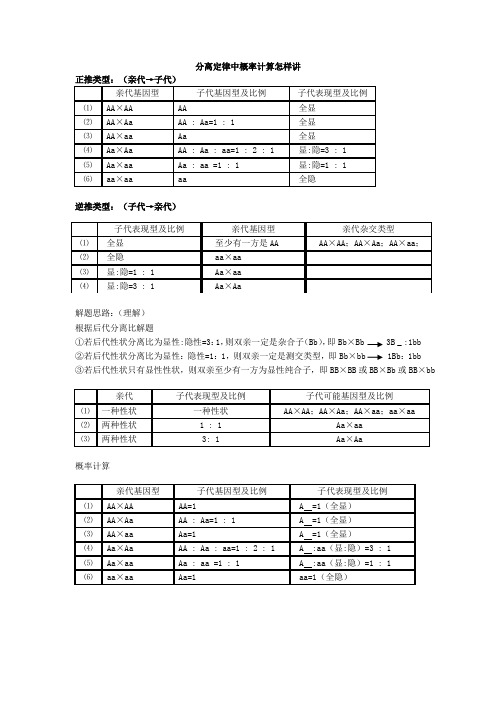
分离定律中概率计算怎样讲正推类型:(亲代→子代)亲代基因型子代基因型及比例子代表现型及比例⑴AA×AA AA 全显⑵AA×Aa AA : Aa=1 : 1 全显⑶AA×aa Aa 全显⑷Aa×Aa AA : Aa : aa=1 : 2 : 1 显:隐=3 : 1⑸Aa×aa Aa : aa =1 : 1 显:隐=1 : 1⑹aa×aa aa 全隐逆推类型:(子代→亲代)子代表现型及比例亲代基因型亲代杂交类型⑴全显至少有一方是AA AA×AA;AA×Aa;AA×aa;⑵全隐aa×aa⑶显:隐=1 : 1 Aa×aa⑷显:隐=3 : 1 Aa×Aa解题思路:(理解)根据后代分离比解题①若后代性状分离比为显性:隐性=3:1,则双亲一定是杂合子(Bb),即Bb×Bb 3B _ :1bb②若后代性状分离比为显性:隐性=1:1,则双亲一定是测交类型,即Bb×bb 1Bb:1bb③若后代性状只有显性性状,则双亲至少有一方为显性纯合子,即BB×BB或BB×Bb或BB×bb亲代子代表现型及比例子代可能基因型及比例⑴一种性状一种性状AA×AA;AA×Aa;AA×aa;aa×aa⑵两种性状 1 : 1 Aa×aa⑶两种性状3: 1 Aa×Aa概率计算亲代基因型子代基因型及比例子代表现型及比例⑴AA×AA AA=1 A =1(全显)⑵AA×Aa AA : Aa=1 : 1 A =1(全显)⑶AA×aa Aa=1 A =1(全显)⑷Aa×Aa AA : Aa : aa=1 : 2 : 1 A :aa(显:隐)=3 : 1⑸Aa×aa Aa : aa =1 : 1 A :aa(显:隐)=1 : 1⑹aa×aa Aa=1 aa=1(全隐)正常情况下,子代基因型AA×Aa→1/2AA+1/2AaAa×Aa→1/4AA+1/2Aa+1/4aaAa×aa→1/2Aa+1/2aa子代表现型AA×Aa→AAa×Aa→3/4A +1/4aaAa×aa→1/2A +1/2aa其中在Aa×Aa→3/4A +1/4aa或1/4AA+1/2Aa+1/4aa中,AA : Aa : aa=1 : 2 : 1若子代已经为显性,那么,AA : Aa =1 : 2AA占显性的1/3,Aa占2/3即1/3AA+2/3Aa例1下图是某家族性遗传病的系谱图(假设该病受一对遗传因子控制,A是显性.a是隐性),请回答下面的问题。
分离定律的应用及解题方法课件

28
6、小麦抗锈病对易染锈病为显性。现有甲、 乙两种抗锈病的小麦,其中一种为纯种,若要鉴 别和保留纯合的抗锈病小麦,下列最简便易行
的方法是( D )
A.甲与乙杂交 B.甲与乙杂交得F1,再自交
C.甲、乙分别和隐性类型测交 D.甲、乙分别自交
分离定律的应用及解题方法
ቤተ መጻሕፍቲ ባይዱ
29
7、用黄色公鼠a分别与黑色母鼠b和c交配,
B.F2中有的表现父本的性状, 有的表现母本的性状
C.子一代只表现某一亲本的性状
D.F2有时出现父本的性状, 有时出现母本的性状
分离定律的应用及解题方法
25
2、大豆的白花和紫花为一对相对性状。下列四
组杂交实验中,能判定性状显隐性关系的是( B )
①紫花×紫花→紫花
②紫花×紫花→301紫花+110白花
D.1/6
分离定律的应用及解题方法
12
【例题】
5、一对夫妇均正常,且他们的双亲也都正常,但双亲都
有一白化病的兄弟,求他们婚后生白化病孩子的概率
是多少?
1/9
①这对夫妇的基因型及概率均为1/3AA,2/3Aa
②只有这对夫妇的基因型全为Aa才能出现白化病患
者
.Aa×Aa
↓
1/4aa
故他们婚后生白化病孩的概率是(2/3)*(2/3)*(1/4)=1/9
8/9
分离定律的应用及解题方法
18
六、杂合子连续自交的概率问题分析
杂合子Aa连续自交,第n代的比例分析
隐性 显性性 隐性性
杂合 纯合 显性纯
Fn
纯合 状个体 状个体 子 子 合子
子
所占 1 1- 12-
比例 2n
分离定律卡方检验公式

分离定律卡方检验公式一、卡方检验简介卡方检验(Chi-square test)是一种用于检验两个分类变量之间是否存在关联关系的统计方法。
它是由英国统计学家卡尔·皮尔逊(Karl Pearson)发明的,基于卡方分布理论,适用于观察频数的数据分析。
二、卡方检验的应用场景卡方检验广泛应用于生物学、医学、社会科学等领域,主要应用于以下场景:1.研究两个分类变量之间的相互依赖关系;2.检验列联表中的期望频数与实际频数是否存在显著差异;3.评估调查问卷或实验设计的有效性。
三、卡方检验的步骤1.建立原假设(H0):假设两个分类变量之间不存在关联关系;2.收集数据,构建列联表(contingency table);3.计算观测频数、期望频数和卡方统计量;4.计算卡方分布的P值;5.与显著性水平(通常为0.05)进行比较,判断结果是否显著。
四、卡方检验公式及计算过程卡方检验的公式为:χ= Σ [ (Oij - Eij) / Eij ]其中,Oij表示观测频数,Eij表示期望频数。
计算过程如下:1.根据列联表中的数据,计算期望频数;2.计算每个单元格的卡方值;3.求和所有单元格的卡方值,得到总的卡方统计量。
五、分离定律与卡方检验分离定律是遗传学中的一个基本原理,指两个基因座的等位基因在生殖细胞中分离,独立地遗传给后代。
卡方检验可以用于检验分离定律是否符合实际观察数据。
六、实例分析以一个遗传学研究为例,研究者收集了甲、乙两个品种的植物杂交数据,构建了一个2×2列联表。
通过卡方检验,可以检验甲、乙品种的性状是否符合孟德尔的分离定律。
七、注意事项1.确保研究变量为分类变量,且具有两分类;2.样本容量足够大,以降低抽样误差;3.正确计算期望频数,避免计算错误;4.结合实际研究背景,选择合适的显著性水平。
【总结】卡方检验是一种有效的关联性分析方法,通过对分类变量之间的观测频数进行统计分析,可以评估变量之间的关联程度。
分离定律的解题方法

◆ 陆 平
( 吉 林 省 梨 树 县 郭 家 店 高 级 中学 校 )
【 关键词】显 隐
搭架
基因
概率
分 离定律
分离定律的解题思路如下 ( 设 等 位 基 因 为 A、 a ): 判 显 隐 一 搭 架 子 是 :1 / 4( A A) +1 / 2( A a )= 3 / 4 。
( 1 )由亲代推 断予代 的基 因型与表 现型 ( 正推法 )
亲本组合
AA×AA AA×Aa AA×a a Aa XAa Aa ×a a
予代基因型及 比例
AA AA a a =l : 2 : l Aa : a a =l : l
根 据 分 离 定律 , 亲本 的 一 对 基 因 一 定 分 别 传 给 不 同 的 子 代 : 子 代 的 产生的概 率,用相 关的两种配子 的概 率相乘 。 上例 中杂合 的双亲产生 A
一
对 基 因 也 一 定 分 别 来 自两 位双 亲 。 所 以 若 子 代 只 要 有 隐 性 表 型 ,则 亲 配 子 和 a配 子 的 概 率 各 为 1 / 2, 生 白 化 病 的 孩 子 的 概 率 为 1 / 2 X1 / 2=
1 / 4。
本 一 定 至 少含 有 一 个 a 。
2 . 表 型 比法
( 3 )棋 盘 法 。 对 于 包 含 多 种 性状 的 问题 此 法 较 为直 观 ,不 易 出错 。 如 人类 白化 病 遗 传 中 ,一 对 夫 妇 的 基 因 型 都 是 A a ,利 用 棋 盘 法 他 们 孩 子 的 基 因 型及 表 现 型 是 :
、
判显隐 ( 判 定相 对 性状 中 的 显 隐 性 )
高中生物分离定律概率计算技巧

高中生物分离定律概率计算技巧《高中生物分离定律概率计算技巧》嗨,大家好!我是一个对生物特别感兴趣的小学生,今天我想和大家聊聊高中生物里的分离定律概率计算技巧。
你可能会想,哎呀,高中生物,这对小学生来说是不是太难了呀?其实呀,只要我能懂一点,那大家肯定也能懂呢!咱们先来说说啥是分离定律。
就好像有一堆彩色的小球,有红的有蓝的,放在一个大盒子里。
这些小球呢,就好比是生物里的基因。
比如说,有一种植物,它的花有红色和白色两种颜色,这红色和白色的基因就像那些不同颜色的小球一样。
一个基因呢,是从爸爸那里来的,另一个是从妈妈那里来的。
这就像从盒子里拿两个小球一样。
那概率计算是咋回事呢?就像我们玩猜小球颜色的游戏。
假如说,红色基因是显性的,用A表示,白色基因是隐性的,用a表示。
那当爸爸和妈妈都是Aa的时候,他们生出的孩子是红色花(AA或者Aa)的概率是多少呢?这就需要我们来计算啦。
我们可以画个小表格,就像我们做数学乘法表一样。
爸爸可以给出A或者a,妈妈也可以给出A或者a。
那组合起来就有四种情况啦:AA、Aa、aA、aa。
这里面AA、Aa、aA都是红色花,只有aa是白色花。
那红色花的概率就是3/4,白色花的概率就是1/4。
这就好像我们猜小球颜色,有3次可能是红色,1次可能是白色。
再比如说,要是爸爸是AA,妈妈是Aa呢?那爸爸只能给出A,妈妈可以给出A 或者a。
组合起来就是AA和Aa两种情况,而且都是红色花,那生出红色花孩子的概率就是100%啦。
这就像盒子里大部分都是红色小球,那我们随便拿,大概率拿到的都是红色小球呢。
还有一种情况,要是爸爸是Aa,妈妈是aa呢?爸爸可以给出A或者a,妈妈只能给出a。
组合起来就是Aa和aa,那生出红色花(Aa)的概率就是1/2,白色花(aa)的概率也是1/2。
这就好像盒子里红色小球和白色小球数量差不多,那我们拿到红色或者白色小球的可能性就差不多一样大。
我们在计算的时候,一定要把各种可能的情况都想清楚。
自由组合定律与分离定律

自由组合定律与分离定律
自由组合定律和分离定律是逻辑分析中常用的两个定律。
自由组合定律(Commutative Law of Logic)是指在逻辑运算中,两个命题进行逻辑运算的结果不受它们在运算中的位置影响。
例如,对于两个命题P和Q,其合取运算(逻辑与,表示为 P ∧ Q)满足自由组合定律,即 P ∧ Q = Q ∧ P。
同样地,析取运算(逻辑或,表示为 P ∨ Q)也满足自由组合定律,即 P ∨ Q = Q ∨ P。
分离定律(Distributive Law of Logic)是指在逻辑运算中,一个逻辑运算可以分解为两个不同的逻辑运算的组合。
例如,对于三个命题P、Q和R,合取运算与析取运算之间满足分离定律,即 P ∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R)。
同样地,析取运算与合取运算之间也满足分离定律,即 P ∨ (Q ∧ R) = (P ∨Q) ∧ (P ∨ R)。
这两个定律在逻辑推理、代数运算和集合运算等领域都有广泛的应用,并且对于理解和分析复杂的命题和命题间的关系非常有帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分离定律算法
分离定律算法是一种用于简化布尔代数表达式的算法。
它是化简布尔代数表达式的一种重要方法,可用于简化逻辑电路设计中的门电路等。
本文将介绍分离定律算法的原理、步骤和例子。
1. 原理
分离定律算法是建立在布尔代数中的两个基本定律上的。
这两个基本定律是:
(1)交换律:AB=BA,A+B=B+A
(2)结合律:A+(B+C)=(A+B)+C,A(BC)=(AB)C
利用这两个基本定律,就可以得到分离定律:
(3)分配律:A(B+C)=AB+AC,(A+B)(C+D)=AC+AD+BC+BD
分离定律的基本思路是,将一个代数式根据分配律展开,并去掉其中的公因子,从而化简表达式。
2. 步骤
分离定律算法的具体步骤如下:
(1)读入布尔代数表达式。
(2)根据分配律,将该表达式展开。
(3)去掉每一项中的公因子。
(4)将去掉公因子的项合并,得到化简后的表达式。
3. 例子
假设有一个布尔代数表达式为:(A+B)(A+C)
按照分离定律算法的步骤,可以将其展开:
(A+B)(A+C)=A(A+C)+B(A+C)
然后去掉公因子,得到:
A(A+C)+B(A+C)=A+AC+AB+BC
最后合并项,化简得到:
A+B+C(其中,AB+BC可以用化简公式继续化简。
)
这样就得到了原表达式的简化形式。
总之,分离定律算法是布尔代数中一种重要的化简方法,能够简化逻辑电路设计中的门电路等。
通过应用分离定律算法,不仅可以减少逻辑电路中电路元件的数量,提高电路设计的可靠性和稳定性,还能够降低电路成本,提高生产效率。
因此,学习和掌握分离定律算法对于电子电路工程师来说是十分必要的。
