高中数学立体几何外接球问题专题02 正四面体模型
正四面体外接球半径和高的关系

正四面体外接球半径和高的关系
正四面体是一个特殊的三维几何形体,它有四个面,每个面都
是一个等边三角形。
外接球是指可以完全包围这个四面体的球,而
外接球的半径和四面体的高之间存在着一定的关系。
首先,让我们来看一下正四面体的性质。
正四面体的高是从其
中一个顶点到对立面(底面)的垂直距离,也就是说,从顶点垂直
向底面作垂线,垂线的长度就是正四面体的高。
外接球的半径和正四面体的高之间的关系可以通过以下步骤来
推导。
首先,我们知道正四面体的高可以通过它的边长来表示。
设
正四面体的边长为 a,那么它的高可以表示为(a√6)/3。
接下来,我们来求外接球的半径。
设外接球的半径为 R。
根据
正四面体的性质,外接球的半径 R 和正四面体的边长 a 之间存在
着以下关系,R = (a√6)/4。
因此,我们可以得出正四面体外接球半径和高的关系为,外接
球的半径 R 等于正四面体的高乘以√6再除以4,即R = (h√6)/4,其中 h 表示正四面体的高。
综上所述,正四面体外接球的半径和高之间的关系可以用公式R = (h√6)/4 来表示,其中 R 表示外接球的半径,h 表示正四面体的高。
这个公式可以帮助我们在已知正四面体高的情况下求得外接球的半径,或者在已知外接球半径的情况下求得正四面体的高。
正四面体外接球和内切球的半径的九种求法

正四面体外接球和内切球的半径的九种求法【作者简介】张秀洲(1987.06),江苏滨海人,毕业于湖南师范大学,中学数学一级教师,省先进工作者,州、县优秀班主任,州先进个人,县优秀教师,县优秀教育工作者,县教师培训师团队成员,县“国培计划”(A307)指导教师,吉首大学“国培计划”(B101)指导老师。
2016年被花垣县人民政府授予“高考优秀教师”荣誉称号,2013年、2019年被花垣县人民政府记“三等功”。
如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球。
如果一个球与多面体的各面都相切,且此球在多面体的内部,则称这个球为此多面体的内切球。
有关多面体外接球与内切球的问题,是立体几何的一个重点,也是高考考查的一个热点。
研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用。
本文重点研究正四面体外接球和内切球的半径的求法:正四面体是特殊的正三棱锥,所有的棱长都相等,四个面是全等的等边三角形,有外接球、内切球,且球心重合.分析:如图1,因为正四面体ABCD的外接球的球心O到点B,C,D的距离相等,所以O在平面BCD内的射影O1到点B,C,D的距离也相等.又因为在正四面体ABCD中△BCD是正三角形,所以O1是△BCD的中心,进而在正四面体ABCD中,有AO1⊥平面BCD,所以球心O在高线AO1上;同理:球心O也在其它面的高线上.图1又正四面体ABCD中各面上的高都相等,所以,由OA=OB=OC=OD,得:点O到正四面体各面的距离相等,所以点O也是正四面体ABCD的内切球的球心.这样,正四面体的内切球的球心与外接球的球心重合.已知正四面体ABCD棱长为a,设外接球半径为R,内切球半径为r,球心为O ,则正四面体的高h即34R h =即14r h =.外接球半径是内切球半径的3倍.下面从不同角度、用不同方法进行探求:方法一:(勾股定理)如图2,因为在正四面体ABCD 中,△BCD 是正三角形,O 1是其中心,所以O 1D. 因为OO 1⊥平面BCD ,O 1D ⊂平面BCD , 所以OO 1⊥O 1D .所以,在Rt △OO 1D 中,由勾股定理,得22211OD OO O D =+,即222R R ⎫⎫=-+⎪⎪⎪⎪⎝⎭⎝⎭.解得R =,所以r R =-.. 知识联系:正三角形的内切圆的圆心与外接圆的圆心重合,半径之比为1:2;正四面体的内切球的球心与外接球的球心重合,半径之比1:3.方法二:(三角正切倍角公式)如图3,因为在正四面体ABCD 中,△BCD 是正三角形,O 1是其中心,所以OO 1⊥平面BCD ,O 1D,高1h AO =. 1,,2.OA OD ADO DAO DOO θθ=∴∠=∠=∠= 在1Rt ADO ∆中,11tan DO AO θ===2222tan 2tan 21tan 1θθθ∴===--⎝⎭在1Rt ODO ∆中,113tan 2DO OO r θ====r ∴=,R h r =-==. 图2图3. 方法三:(平行线法)如图4,连接DO 并延长交平面ABC 于点G ,则G 为△ABC 的中心.连结DO 1并延长交BC 于中点E ,则A ,G ,E 三点共线,113EO EGED EA==; 再连接1GO ,则1GO ∥AD ,从而有1113O O O G EG AO AD EA ===,所以134AO AO =,1114OO AO ==.. 方法四:(分割体积法)如图5,记正四面体ABCD 的体积为V ,每个面的面积为S ,高为h ,内切球球心为O ,连结OA ,OB ,OC ,OD ,则O ABC O BCD O ACD O ABD V V V V V ----=+++,所以11433Sh Sr =⋅,从而13,.44r h R h ====. 【方法拓展延伸】1.多面体的体积为V ,表面积为S ,利用体积分割法,可得其内切球的半径为3Vr S=; 2.高为h ,各面面积均为S 的棱锥内的任意一点到各面的距离之和为定值h .方法五:(补形法)以正四面体的各棱为正方体的面对角线,将其补形为正方体.由于过不共面的四点有且只有一个球,所以正四面体的外接球也是正方体的外接球.设正方体的棱长为x,则2R =且a ,所以R =,从而13r R =.. 【方法拓展延伸】1.若三棱锥的三条侧棱两两垂直,则其外接球也是以这三条侧棱为同一顶点出发的三条棱的长方体的外接球,若设其三条侧棱长分别为,,,a b c 则易得外接球的半径为R =. 2.若点P 到两两垂直的三个面的距离分别为,,,a b c 点O 为它们的公共点,则图4图5图6PO =22212a b c ++. 3.若点P 到两两垂直且共点于O 的三条直线m ,n ,l 的距离分别为x ,y ,z ,则PO =2222()2x y z ++.方法六:(相交弦定理)设外接球球心为O ,半径为R ,过A 点作球的直径,交底面BCD ∆于1O ,则1O 为BCD ∆的外心,求得1163,,33AO a DO a == 由相交弦定理得2663(2).333a R a a ⎛⎫⋅-= ⎪ ⎪⎝⎭解得64R a =. 666633412r a R a a a ∴=-=-= 故所求的外接球的半径和内切球的半径分别为64a 和612a . 方法七:(坐标法)如图6, 建立如图所示的空间直角坐标系, 则6333(0,0,),(0,,0),(,,0),(,,0)332626a a A a B a C a D a -- 设球心O 的坐标为(,,)x y z ,则由OA OB OC OD R ====,得2222OA OB OC OD ===,即22222222222263()()333()()263()()26x y z a x y a z ax y a z ax y a z ++-=+++=-+-+=++-+解得60,.12x y z a ===所以66,.124r z a R a ∴=== 故所求的外接球的半径和内切球的半径分别为64a 和612a . 方法八:(相似法)(侧棱、高相似)如图7, 作111 , AO BCD O O BCD 平面于点则点是的中心,⊥∆高163h AO a ==,设O 为球心,则1.O AO ∈设M 是AB 的中点,连结OM ,OB ,BO 1,AO BO OM AB =∴⊥190AMO AO B ∴∠=∠=,又1MAO O AB ∠=∠,AMO ∴∆∽1AO B ∆, 1AM AO AO AB ∴=,即2,63aRa a = 6666,.43412R a r h R a a a ∴==-=-=方法九:(相似法)(斜高、高相似)如图8, 作111 , AO BCD O O BCD 平面于点则点是的中心,⊥∆高163h AO a ==,设O 为球心,则1.O AO ∈设E 为BC 中点,连结AE ,EO 1,作ON AE ⊥于N 点,则N 是ABC ∆中心,N 是AE 的三等分点, ON ABC ON r 平面,是内切圆半径,⊥且Rt ANO ∆∽1Rt AEO ∆1AN AO AO AE ∴=, 即336332aR a a =,6666,.43412R a r h R a a a ∴==-=-= 以上从不同角度针对正四面体的外接球半径、内切球半径作了讨论,从而从不同方面对思维作了训练,不仅对正四面体的外接球半径、内切球半径有了透彻的认识,同时对解题能力的提高是有帮助的.。
3.4基本几何体之正四面体

基本几何体之正四面体设正四面体的棱长为a ,如下图1、侧面中线AM a =2、高线AH =3、外接球半径R =4、内切球半径12r a =5、对棱距离(BC 与AD 两异面直线的距离)2EF a =其中E 、F 为相应中点,EF 既垂直于BC 又垂直于AD6、AC 垂直BD 、AB 垂直CD 、AD 垂直BC (实际所有正三棱锥都有这个结论,正四面体是特殊的正三棱锥)注1:外接球与内切球半径的求法首先在正四面体中,外接球与内切球的球心是合一的,而且必须在高线AH 上,设球心为O ,外接球半径为R ,内切球半径为r ,而且H 必是一个切点。
如下图所示则有222r R AH R r BH ⎧+==⎪⎨⎪+=⎩又H 还是BCD的重心,有2233BH BM ===因此解222r R a R r ⎧+=⎪⎪⎨⎫⎪+=⎪⎪⎪⎝⎭⎩,即可求得R 与r注2:对棱间距的求法将正四面体放在正方体中讨论(以后会经常这样子做)。
只要在正方体中取不相邻的四个顶点就构成了正四面体。
如下:显然EF等于正方体的棱长,即2a例1 (05年北京)在正四面体P —ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,下面四个结论中不成立的是(C )解析:如下图,做出PO为该四面体的高线,O必在AE上。
A:BC//DF可以得到BC//面PDF,对B:PO DFDF PAEAE DF⊥⎫⇒⊥⎬⊥⎭面,也对C:PO显然不在面PDF中,因此面PDF垂直面ABC不可能D:PO在面PAE内,因此面PAE与面ABC垂直要解此题,必须对正四面体的性质十分熟练。
如O必落在AE上,且O必不在DF上。
因为必有O为ABC的重心。
2=3AO AE,而EF为中位线,所以O必不在EF上。
立体几何的外接球问题

立体几何中的外接球问题概 述①长方形的外接圆圆心为对角线的中点,222a b R +=(,a b 为长方形的长、宽)。
长方体的外接球球心为体对角线的中点,222(,,2a b c R a b c ++=为长方体的长、宽、高)。
②三角形的外接圆圆心是底边的中垂线的交点,外接圆半径可由,余弦定理求得2sin a r A=;等边三角形的外心是高的三等分点(靠底边);直角三角形的外心是斜边中点。
③三棱锥或其它几何体,其外接球球心一定在过面的外心且与该面垂直的垂线上。
④过球心的截面截得的圆是大圆。
⑤勾股定理、正弦定理、余弦定理、射影定理、面积法、体积法等平面几何性质灵活应用。
1.圆柱、直棱柱、一侧棱垂直底面的棱锥设底面外接圆半径为r ,高为h ,则外接球半径224h R r =+'Rt OAO ∆。
2、圆锥、各侧棱都相等的棱锥(包括正三棱锥、正四棱锥)设底面外接圆半径为r ,高为H ,则外接球半径222H r R H +=,截面图中1Rt OAO ∆勾股定理解得。
()222222H r R H R r R H+=-+⇒=。
3、等腰四面体补成长、宽、高分别为,,x y z 的长方体,则2222222222222222x y b a b c x z c x y z z y a ⎧+=⎪+++=⇒++=⎨⎪+=⎩外接球半径222222222x y z a b c R ++++==。
注:(1)棱长为a 的正四面体外接球半径2226422a a a aR ++==; (2)从某顶点出发,三棱长为,,a b c 的直角三棱锥外接球半径2222a b c R ++=。
补体法:(1)正四面体;(2)等腰四面体;(3)直角三棱锥或其他。
4、有两个面互相垂直的三棱锥设两垂直面的交线长为l ,两垂直面的外接圆半径分别为12,r r 则外接球半径2222212124l R r d r r =+=+-。
cc b baa r 2O O 2O 1C A5、任意三棱锥已知两面外接圆半径分别为12,r r ,两面外心到交线的距离分别为12,d d ,两面的交线长为l ,已知或可求二面角α,2222111222,44l l O E d r O E d r ==-==-,221212122cos O O d d d d α=+-221212122cos sin sin d d d d O O OE ααα+-==,222222121222cos 4sin 4d d d d l l R OE αα+-=+=+。
正四面体的性质及应用
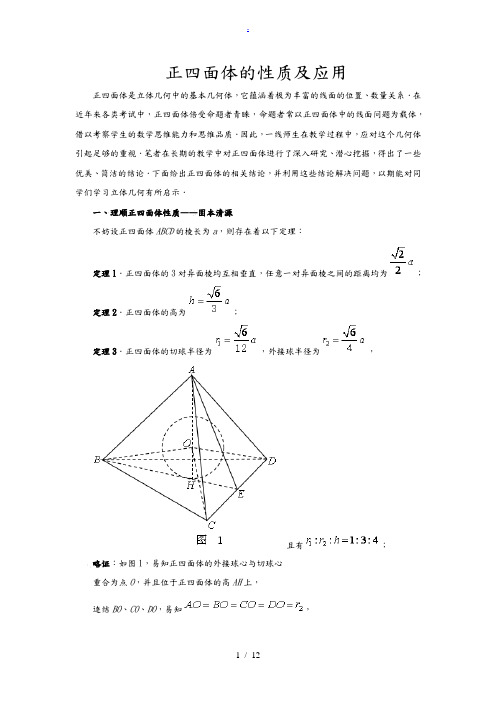
正四面体的性质及应用正四面体是立体几何中的基本几何体,它蕴涵着极为丰富的线面的位置、数量关系.在近年来各类考试中,正四面体倍受命题者青睐,命题者常以正四面体中的线面问题为载体,借以考察学生的数学思维能力和思维品质.因此,一线师生在教学过程中,应对这个几何体引起足够的重视.笔者在长期的教学中对正四面体进行了深入研究、潜心挖掘,得出了一些优美、简洁的结论.下面给出正四面体的相关结论,并利用这些结论解决问题,以期能对同学们学习立体几何有所启示.一、理顺正四面体性质——固本清源不妨设正四面体ABCD的棱长为a,则存在着以下定理:定理1.正四面体的3对异面棱均互相垂直,任意一对异面棱之间的距离均为;定理2.正四面体的高为;定理3.正四面体的切球半径为,外接球半径为,且有;略证:如图1,易知正四面体的外接球心与切球心重合为点O,并且位于正四面体的高AH上,连结BO、CO、DO,易知,且,从而AO、BO、CO、DO两两所确定的平面将正四面体分割成四个形状相同的正三棱锥:,,且每一个小正三棱锥的高都是切球的半径,于是有,即,亦即有,所以,.故定理4.正四面体的全面积为,体积为;定理5.正四面体底面任一点O到三个侧面的距离的之和;正四面体任意一点到四个侧面的距离之和(仿定理3利用体积分割法易证).定理6.正四面体的侧棱与其底面所成的线面角大小为;定理7.正四面体相邻侧面所成的二面角的大小为;略证:设相邻两个侧面所成的角为,由于四个侧面的面积均相等,所以由射影面积公式知.定理8.设正四面体的侧棱与底面所成的角为,相邻两个侧面所成的二面角记为,则有略证:如图1所示,易知,,由H为的中心,易知,从而.定理9.正四面体的外接球的球心与切球的球心O重合且为正四面体的中心;中心与各个顶点的四条连线中两两夹角相等,其大小为,此角即为化学中甲烷分子结构式中的键位角.略证:如图1,在三角形AOB中,,,由余弦定理可求得,于是.同理可得.定理10.正四面体接于一正方体,且它们共同接于同一个球,球的直径等于正方体的对角线.二、运用正四面体性质——化繁为易1.巧算空间距离例1.一个球与正四面体的6条棱都相切,若正四面体的棱长为a,则求此球的体积.分析一:由定理10知,将正四面体嵌于正方体的部,然后再利用正四面体的棱与球相切,则该半径与正方体的切半径相等进行求解.解法一.如图2所示,将正四面体补成正方体,易知与正四面体的各棱相切的球即为正方体的切球.∵正四面体的棱长为a,∴正方体的棱长为.∴正方体的切球半径.∴.分析二:根据正四面体的对称性,结合定理1可知,该球的球心应位于正四面体的中心,其直径即为正四面体相对棱之间的距离.解法二.∵正四面体的棱长为a,∴由定理1可知,相对棱间的距离为.即该球的半径为.∴.例2.在棱长为2的正四面体木块ABCD的棱AB上有一点P(),过P点要锯出与棱AB垂直的截面,当锯到某个位置时因故停止,这时量得在面ABD上锯痕,在面ABC上的锯缝,求锯缝MN的值.解:如图3,取AB的中点E,连结CE,DE,则为正四面体相邻两面的二面角的平面角,由条件知∠MPN也是正四体相邻两面的二面角的平面角,即∠NPM=∠CED,由定理7可知,于是,在中,由余弦定理得,∴2.妙求空间角例3.设P为空间一点,PA、PB、PC、PD是四条射线,若PA、PB、PC、PD两两所成的角相等,则这些角的余弦值为.解:如图4,构造正四面体ABCD,设P为四面体的中心,则PA、PB、PC、PD两两所成的角相等,设,由正四面体的性质,可知余弦值为例4.如图5,在正四面体ABCD中,E、F分别为棱AD、BC的中点,连结AF、CE.⑴求异面直线直线AF和CE所成的角;⑵求CE与面BCD所成的角.解:⑴连结FD,在平面AFD,过点E作EG∥AF交DF于点G.则是异面直线AF与CE所成的角(或其补角).设正四面体ABCD的棱长为a,可得,,.由余弦定理可求得.故异面直线AF与CE所成的角为.⑵由已知易知平面AFD⊥平面BCD,在平面AFD,过点E作EH⊥FD于点H,连结CH,则∠ECH为CE与平面BCD所成的角.∵EH为正四面体高的一半,由正四面体性质的定理2知.∴.∴CE与底面BCD所成的角为.例5.如图6,正四面体ABCD的四个顶点在同一个球面上,CC1和DD1是该球的直径,求面ABC与面AC1D1所成角的正弦值.解:由正四面体性质定理10知正四面体接于一球,该正方体也接于此球,且正方体的对角线为此球的直径,如图所示,即CC1、DD1为该球的直径.连结C1D1,交AB于点M,连结MC.∵MC⊥AB,MD1⊥AB,∴∠CMD1为平面ABC与平面AC1D1所成的角.设正方体棱长为a,在中,.∴平面ABC与平面ACD所成的角的正弦值为.归纳反思:正四面体是立体几何中一个重要的数学问题载体,在平时的学习过程中若能有意识地研究它、利用它,就能较好地培养我们数学思维的“方向感”和思路的“归属感”,有助于促进自己数学思维空间的拓展、数学品质的提升.1.在正四面体P ABC-中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是②.①//BC面PDF;②面PDF⊥面ABC;③DF⊥面PAE;④面PAE⊥面ABC.2.正四面体ABCD中,AB与平面ACD所成角的余弦值为3.3.如图,正四面体ABCD的棱长为2,点E,F分别为棱AD,BC的中点,则EF BA的值为()A.4B.4-C.2-D.24.以下说法 ①三个数20.3a =,2log 0.3b =,0.32c =之间的大小关系是b a c <<;②已知:指数函数()(0,1)x f x a a a =>≠过点(2,4),则log 41a y =;③已知正四面体的边长为2cm ,则其外接球的体积为33cm π; ④已知函数()y f x =的值域是[1,3],则()(1)F x f x =-的值域是[0,2];⑤已知直线//m 平面α,直线n 在α,则m 与n 平行.其中正确的序号是①③.5.在正四面体A BCD -中,M 为AB 的中点,则直线CM 与AD 所成角的余弦值为()A .12B .2C .3D .23选:C .6.在正四面体ABCD 中,E 、F 分别为棱AD 、BC 的中点,连接AF 、CE ,则异面直线AF 和CE 所成角的正弦值为()A .13B .23C .24D .5 选:D .【点评】本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.本题易错点在于要看清是求异面直线AF 和CE 所成角的正弦值,而不是余弦值,不要错选答7.如图所示,在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +的最小值为7,则该正四面体的外接球的体积是()A 6πB .6πC 36D .32π 选:A .8.棱长为1的正四面体ABCD 中,E 为棱AB 上一点(不含A ,B 两点),点E 到平面ACD 和平面BCD 的距离分别为a ,b ,则11a b +的最小值为6 【考点】7F :基本不等式及其应用【专题】31:数形结合;35:转化思想;5F :空间位置关系与距离;5T :不等式【分析】设点O 是正三角形ACD 的中心,连接OB ,作EF AO ⊥,垂足为点F .AO 交CD 于点M ,则点M 为CD 的中点.设(01)AE AB λλ=<<.23AO AM =,3AM ,22BO AB AO =-.由//EF BO ,可得6EF BO a λ===.同理可得:6)b EN λ=-.代入利用基本不等式的性质即可得出. 【解答】解:如图所示,设点O 是正三角形ACD 的中心,连接OB ,作EF AO ⊥,垂足为点F .AO 交CD 于点M ,则点M 为CD 的中点.设(01)AE AB λλ=<<.223333AO AM ===, 226BO AB AO ∴=- //EF BO ,6EF BO a λ∴===. 同理可得:6)b EN λ==-.∴21111161()11(1)()2a b λλλλλλ+=+=⨯=+---当且仅当12λ=时取等号.故答案为:9.已知M 是正四面体ABCD 棱AB 的中点,N 是棱CD 上异于端点C ,D 的任一点,则下列结论中,正确的个数有()(1)MN AB ⊥;(2)若N 为中点,则MN 与AD 所成角为45︒;(3)平面CDM ⊥平面ABN ;(4)存在点N ,使得过MN 的平面与AC 垂直.A .1个B .2个C .3个D .4个【考点】LM :异面直线及其所成的角;LO :空间中直线与直线之间的位置关系;LW :直线与平面垂直;LY :平面与平面垂直【专题】14:证明题【分析】连接CM 、DM ,可证明出AB ⊥平面CDM ,从而MN AB ⊥,得(1)正确;取AC 中点E ,连接EM 、EN ,利用三角形中位线定理证明出EN 、NM 所成的直角或锐角,就是异面直线MN 、AD 所成的角,再通过余弦定理,可以求出MN 与AD 所成角为45︒,故(2)正确;根据(1)的正确结论:MN AB ⊥,结合平面与平面垂直的判定定理,得到(3)正确;对于(4),若存在点N ,使得过MN 的平面与AC 垂直,说明存在N 的一个位置,使MN AC ⊥.因此证明出“不论N 在线段CD 上的何处,都不可能有MN AC ⊥”,从而说明不存在点N ,使得过MN 的平面与AC 垂直.【解答】解:(1)连接CM 、DM正ABC ∆中,M 为AB 的中点CM AB ∴⊥同理DM AB ⊥,结合MC M D M =AB ∴⊥平面CDM ,而MN ⊆平面CDMMN AB ∴⊥,故(1)是正确的;(2)取AC 中点E ,连接EM 、ENADC ∆中,E 、N 分别是AC 、CD 的中点//EN AD ∴,12EN AD =. EN ∴、NM 所成的直角或锐角,就是异面直线MN 、AD 所成的角设正四面体棱长为2a ,在MCD ∆中,2CM DM a === 则Rt MNC ∆中122CN a a =⨯=∴MN = 在MNE ∆中,122ME EN a a ==⨯=∴222cos 2EN MN EM ENM EN MN +-∠==⨯⨯ 45ENM ∴∠=︒,即异面直线MN 、AD 所成的角是45︒,故(2)正确;(3)由(1)的证明知:AB ⊥平面CDMAB ⊂平面ABN∴平面ABN ⊥平面CDM ,故(3)正确;(4)若有MN AC ⊥,根据(1)的结论MN AB ⊥,因为AB 、AC 相交于A 点,所以MN ⊥平面ABCMCD ∆中,CM MD ==,2CD a =2221cos 023CM MD CD CMD CM MD +-∴∠==> 可得CMD ∠是锐角,说明点N 在线段CD 上从C 到D 运动过程中, CMN ∠的最大值是锐角,不可能是直角,因为CM ⊂平面ABC ,CM 与NM 不能垂直,以上结论与MN ⊥平面ABC 矛盾,故不论N 在线段CD 上的何处,都不可能有MN AC ⊥.因此不存在点N ,使得过MN 的平面与AC 垂直.综上所述,正确的命题为(1)(2)(3)故选:C .10.棱长为a 的正四面体中,给出下列命题:①正四面体的体积为324a V =;②正四面体的表面积为2S ;③切球与外接球的表面积的比为1:9;④正四面体的任意一点到四个面的距离之和均为定值.上述命题中真命题的序号为②③④.【考点】LE :棱柱、棱锥、棱台的侧面积和表面积;LF :棱柱、棱锥、棱台的体积【专题】31:数形结合;35:转化思想;49:综合法;5F :空间位置关系与距离【分析】①正四面体的高h ==,体积为213V =,计算即可判断出正误;②正四面体的表面积为24S a =,即可判断出正误;③分别设切球与外接球的半径为r ,R ,则23143r ⨯,解得r ;R +=,解得R ,即可判断出正误; ④正四面体的任意一点到四个面的距离之和为H,则221133H ⨯=【解答】解:①正四面体的高h =,体积为3231324a V ==≠,因此不正确;②正四面体的表面积为224S a =,正确;③分别设切球与外接球的半径为r ,R ,则2314312r ⨯=,解得r =;R +=,解得R . :1:3r R ∴=,因此表面积的比为1:9,正确;④正四面体的任意一点到四个面的距离之和为H ,则221133H ⨯=化简可得:H =,即为正四面体的高,均为定值,正确.上述命题中真命题的序号为②③④.。
正四面体外接球公式

正四面体外接球公式为了推导正四面体外接球的半径公式,首先我们需要先了解一些正四面体的性质。
一、正四面体的性质:1.正四面体的面积公式:一个正四面体的面积可以通过以下公式计算:A=√3*a²,其中a是正四面体的一个边长。
2.正四面体的高公式:一个正四面体的高可以通过以下公式计算:h=(√6/3)*a,其中a是正四面体的一个边长。
3.正四面体的体积公式:一个正四面体的体积可以通过以下公式计算:V=(√2/12)*a³,其中a是正四面体的一个边长。
4.正四面体的垂直高公式:一个正四面体的垂直高可以通过以下公式计算:H=(√6/4)*a,其中a是正四面体的一个边长。
二、正四面体外接球的性质:1.正四面体外接球的半径R,可以通过以下公式计算:R=(√6/4)*a,其中a是正四面体的一个边长。
这是一个重要的结论,可以称之为正四面体外接球半径公式。
推导过程:我们首先使用勾股定理来证明正四面体外接球半径公式。
我们知道正四面体的高是等边三角形高线段的1/3,所以正四面体的高为(√6/3)*a。
又根据正四面体外接球的性质,球的半径,也就是外接球的半径R,正好是正四面体垂直高的2/3倍。
所以我们有:R=(2/3)*(h)。
我们可以把h代入R的公式中,得到:R=(2/3)*((√6/3)*a)=(√6/9)*a。
然而,这个结果与我们之前提到的正四面体外接球半径公式不相符。
所以我们需要检查我们之前提到的正四面体外接球半径公式有没有错误。
我们可以使用三角函数来验证正确性。
正四面体的一个面上的顶角是60度,所以它的两个邻边与外接球的半径之间的夹角也是60度。
根据正余弦定理:cos(60) = a / (2R)。
根据余弦函数的性质:cos(60) = 1/2所以我们可以得到:1/2=a/(2R)即:R=(1/2)*a这可以证明我们的正四面体外接球半径公式是正确的。
综上所述,正四面体外接球半径公式为:R=(1/2)*a或R=(√6/4)*a。
高考数学一轮复习第六章专题六几何体的外接球与内切球问题课件

)
A.4 3π
B.8π
C.12π
D.20π
解析:在底面△ABC 中,由正弦定理得底面△ABC 外接圆的
半径为
r=2sin B∠CBAC=2sin2
3π= 4
2.
直三棱柱 ABC-A1B1C1 的外接球的半径 R= ( 2)2+12= 3,
r2+A2A12=
则直三棱柱 ABC-A1B1C1 的外接球的体积为43πR3=4 3π.
当
λ=12时,cos〈E→B,E→G〉=2
3
2 .
∴cos〈E→B,E→G〉的最大值为2
3
2 .
∵A→C=(-1,1,0),A→F=(0,1,1), ∴E→B·A→C=E→B·A→F=0. ∴EB⊥AC,EB⊥AF. ∵AC∩AF=A,∴EB⊥平面 AFC. ∵E→B·E→G>0,∴cos〈E→B,E→G〉即为 EG 与平面 AFC 所成角
如图 6-7 所示,把四面体 S-ABC 补全为长方体 ABCD-SPMN, 其中 SA,AB,BC 为长方体中首尾相连且两两相互垂直的三条棱, 点 H 为 PM 中点.
图 6-7
∵GH∥AP,∴G,H 两点到平面 AEF 的距离相等.
设点 H 到平面 AEF 的距离为 d.
∵△APF 是边长为 2 2的等边三角形,
[例 1]已知一个圆锥底面半径为 1,母线长为 3,则该圆锥内
切球的表面积为( )
A.π
B.32π
C.2π
D.3π
解析:依题意,作出圆锥与球的轴截面,如图
6-1 所示.设球的半径为 r,易知轴截面三角形边 AB
上的高为 2 2,因为△SOD∽△SBE,所以SSOB=OBED,
即2 32-r=1r,解得 r= 22.所以圆锥内切球的表面
立体几何专题:外接球与内切球

立体几何专题:外接球与内切球一、什么是外接球与内切球1. 一个几何体的顶点都在其外接球球面上,所以球心到各顶点的距离都相等。
2. 一个几何体的内切球球面与几何体各面都相切,所以球心到各面的距离都相等。
二、棱柱的外接球1.2.基本方法:3. 四棱柱4. 三棱柱〔劄w 全国ii 文4)休祝为*的正方体的顶点那在同一球向上.則该球的義面积为()例2. £2013天津文1的已知一亍正方体的所有顶点都在一牛球面上.若球的体积为:厂则正方体播&为 _______例3.〔刼慚山东理科 正方体的内切球与其外接球的体积比为t }A . 1:^3 R. 1:3 C. l :W5 D. 1^例4.(2010课标卷文理刀设怅方徉的长宽高分别为九 W 其顶点都在一于球面卜’則该球的表面积为例生(2UI-I ft 西理引已知底两边KA t 侧械怪骨屈的正四揍柱的各顶点均在同一平球面上,则谨球的体积为(例7. (2010新课标理10)设三棱柱的侧棱垂直于底面、所有棱的长都为",顶点都在一个球 面上.则该球的表面积为() T 7 . 1 ] , rA .B . ■ ^ra'C . - - w ~D . 5JT (I ?3 3 捌H. (2OB 辽宁文理10}已知三棱柱ABC-A^C\的6个顶点都在球(7的球面上.若AB = 3, AC = 4. AB 丄MC"為=1N 则球O 的半径为( )C.8HD.4xaVnB * 2VlO例氏一个言棧柱的三视图如图所示,其中骼视图是一个顶角为I酣的毒膳二角形,则该直三A.20TT梭柱的外接球表面和为(三、棱锥的外接球1.正四面体与正三棱锥2•正四面体外接球3补体例1乩已知四面休P-顽中,PA - 4, AC= 2^7 = HC - 2^5 PA丄平面PUC,則四面体尸-磁的外接球的体积为(】例11・(2U16福州一蟆}已知点在同一个球面上,朋丄平面BCD.BC丄匸力若AB^(J,AC=2JU,J ID=K,则gC两点间的球面距蔑是___________________例12. (2C16衡水中学二檯}已知三^D-ABC的四个顶点都在球◎的表面上*若AB ^3t AC % AB丄AC, DR丄T iffinffC f DB T 2'则球O 的半怪为___________例G三棱锥A-BCD, AB丄Z?G AD丄CD^ffC丄CD, AB =迈、BC = CD = \"则此三棱锥外接球的体积为___________________例M在四面体ABCD中.已知AH = CD = 5t AC^BD = 5.AD=BC = ^^l四面体外接球的表面积为__________________例15.《九章算数》中,将底面为长方形且有一条侧梭与底直垂直的四梭链称之为阳马,将四个面都为直角三角也的四面体称之为罄購,已知直三樓柱ABC - AAQ t^iBC = ~ t AB = \BC= 4..4J, = 5^3将盲三楼柱沿櫻和面对角线分割成一个阳马和一个则矍購的体积与其外接球的体积分别为()B. 20阴罟直C, D* 20点翠前例某几何体的三观图如图所示,正视圈为等腰二角形,俯观图为等腰梯形,则该几何体的外接球的表面积是 _____________四、内切球1•有内切球的几何体2.半径例24. (2014湖南理6】一块石材的几何体三视图如图所示.将该石材切削、打眛 加工成 球,则能得到的最大球的半牲等于{丨D,4蛀9・Q k — . 占• V 6*B -K v g A K £ H ?:«区£、-老65拴<-—驱K o aa 呱— J 黑lil ffi 川風務JE 赢M .f i。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题02 正四面体模型一、解题技巧归纳总结1.正四面体如图,设正四面体ABCD 的的棱长为a ,显然正四面体和正方体有相同的外接球.正方体外接球半径为R ==,即正四面体外接球半径为R =.二、典型例题例1.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是( ).A .2B .2C D例2.正四面体的棱长为1,则其外接球的表面积为 .三、配套练习1.棱长为1的正四面体的外接球的半径为( )A B C .1 D 2.棱长为a 的正四面体的外接球和内切球的体积比是( )A .9:1B .4:1C .27:1D .8:13.如图所示,在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +则该正四面体的外接球的体积是( )A B .6π C D .32π4.表面积为( )A .B .12πC .8πD .5.一个正四面体的棱长为2,则这个正四面体的外接球的表面积为( )A .6πB .8πCD .11π6.相互垂直的两个平面分别截球面得两个圆.,则两圆的公共弦长是( )A .34BC .1D .127.如图所示,正四面体ABCD 中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +则该正四面体的外接球表面积是( )A .12πB .32πC .8πD .24π8.已知正四面体的棱长为4,则此四面体的外接球的表面积是( )A .24πB .18πC .12πD .6π9.一个棱长为6的正四面体内部有一个任意旋转的正方体,当正方体的棱长取得最大值时,正方体的外接球的表面积是( )A .4πB .6πC .12πD .24π10.如图,在棱长为1的正四面体ABCD 中,G 为BCD ∆的重心,M 是线段AG 的中点,则三棱锥M BCD -的外接球的表面积为( )A.πB.32πC.64πD.68π11.正四面体(四个面均为正三角形的四面体)的外接球和内切球上各有一个动点P、Q,若线段PQ长度的最大值为463,则这个四面体的棱长为.12.已知正四面体ABCD的棱长为1,M为棱CD的中点,则二面角M AB D--的余弦值为;平面MAB 截此正四面体的外接球所得截面的面积为.13.已知某正四面体的内切球体积是1,则该正四面体的外接球的体积是.14.一个正四面体的展开图是边长为22的正三角形,则该四面体的外接球的表面积为.15.如图所示,正四面体ABCD中,E是棱AD的中点,P是棱AC上一动点,BP PE+的最小值为14,则该正四面体的外接球的体积是.答案例1.棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是( ).A B C D【解析】如图球的截面图就是正四面体中的∆ABD ,已知正四面体棱长为2,所以=AD =1AC ,所以=CD故选:C .例2.正四面体的棱长为1,则其外接球的表面积为 .【解析】解析:依题意,正四面体的外接球半径R =,其表面积为23=42S R ππ=,故答案为32π. 三、配套练习1.棱长为1的正四面体的外接球的半径为( )A B C .1 D 【解析】已知正四面体A BCD -的棱长为1,过B 作BE CD ⊥,交CD 于E , A 作AF ⊥平面BCD ,交BE 于F ,连结AE ,设球心为O ,则O 在AF 上,连结BO ,BE AE ===23BF BE ==13EF BE ==,AF , 设球半径为R ,则BO AO R ==,222)R R ∴=+-,解得R =故选:A .2.棱长为a 的正四面体的外接球和内切球的体积比是( )A .9:1B .4:1C .27:1D .8:1【解析】把棱长为a 的正四面体镶嵌在棱长为x 的正方体内,∴外接球和内切球的球心重合,为正方体的中心O ,∴=2211)63x h =⨯,h =,h ==∴3:1=, ∴正四面体的外球和内切球的体积比是27:1,故选:C .3.如图所示,在正四面体A BCD -中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +则该正四面体的外接球的体积是( )A B .6π C D .32π 【解析】将侧面ABC ∆和ACD ∆展成平面图形,如图所示:设正四面体的棱长为a则BP PE +的最小值为1cos1202BE a a 2a ∴=. 在正四面体A BCD -的边长为2,外接球的半径R ==外接球的体积343V R π==. 故选:A .4.表面积为( )A .B .12πC .8πD .【解析】表面积为将正四面体补成一个正方体,则正方体的棱长为2,正方体的对角线长为,正四面体的外接球的直径为正方体的对角线长,∴外接球的表面积的值为24(3)12ππ=.故选:B .5.一个正四面体的棱长为2,则这个正四面体的外接球的表面积为( )A .6πB .8πCD .11π【解析】正四面体的外接球的直径为正方体的对角线长,∴外接球的表面积的值为264()62ππ=. 故选:A .6.相互垂直的两个平面分别截球面得两个圆.,则两圆的公共弦长是( )A .34BC .1D .12【解析】正四面体扩展为正方体,它们的外接球是同一个球,正方体的对角线长就是球的直径,正方体的棱长为:1所以球的半径为:R =, 设相互垂直两圆的圆心分别为1O 、2O ,球心为O ,公共弦为AB ,其中点为E ,则12OO EO 为矩形,于是对角线12O O OE =,而OE =, 12AE ∴=,则1AB =; 故选:C .7.如图所示,正四面体ABCD 中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +则该正四面体的外接球表面积是( )A .12πB .32πC .8πD .24π【解析】将三角形ABC 与三角形ACD 展成平面,BP PE +的最小值,即为BE 两点之间连线的距离,则BE =设2AB a =,则120BAD ∠=︒,由余弦定理221414222a a a a+--=,解得a =则正四面体棱长为 所以,设外接球半径为R ,则6223R == 则表面积244312S R πππ===.故选:A .8.已知正四面体的棱长为4,则此四面体的外接球的表面积是( )A .24πB .18πC .12πD .6π【解析】将正四面体补成一个正方体,则正方体的棱长为∴外接球的表面积的值为24(6)24ππ=.故选:A .9.一个棱长为6的正四面体内部有一个任意旋转的正方体,当正方体的棱长取得最大值时,正方体的外接球的表面积是( )A .4πB .6πC .12πD .24π【解析】正方体可以在正四面体纸盒内任意转动,∴正方体在正四面体的内切球中,∴正方体棱长最大时,正方体的对角线是内切球的直径,点O 为内切球的圆心,连接PO 并延长交底面ABC 与点D ,点D 是底面三角形ABC 的中心,PD ∴⊥底面ABC ,OD ∴为内切球的半径,连接BO ,则BO OP =,在Rt BDP ∆中,263BD ==PD在Rt BDO ∆中,2222222()OD BD OB BD OP BD OP OD =+=+=+-,代入数据得OD =,令正方体棱长为a ,则23a =a∴此时正方体的外接球半径:r =. ∴当正方体的棱长取得最大值时,正方体的外接球的表面积是:22446S r πππ==⨯=. 故选:B .10.如图,在棱长为1的正四面体ABCD 中,G 为BCD ∆的重心,M 是线段AG 的中点,则三棱锥M BCD -的外接球的表面积为( )A .πB .32πCD 【解析】连接BG ,四面体ABCD 中,由G 为BCD ∆的重心,可得AG ⊥面BCD ,M 是线段AG 的中点,BG =AG =M 为线段AG 的中点,MG ∴=设三棱锥M BCD -外接球的半径为R ,则2R =22)(R +,R ∴=, ∴三棱锥M BCD -外接球的表面积为2342R ππ=. 故选:B .11.正四面体(四个面均为正三角形的四面体)的外接球和内切球上各有一个动点P 、Q ,若线段PQ 长度,则这个四面体的棱长为 4 . 【解析】设这个四面体的棱长为a ,则它的外接球与内切球的球心重合,且半径R =外,r =内,+= 4a ∴=. 故答案为:4.12.已知正四面体ABCD 的棱长为1,M 为棱CD 的中点,则二面角M AB D --的余弦值为 ;平面MAB 截此正四面体的外接球所得截面的面积为 .【解析】如图,M 为棱CD 的中点,AM CD ∴⊥,BM CD ⊥,又AM BM M =,CD ∴⊥平面AMB ,则AM B ∠为二面角A CD B --的平面角,由对称性,可知二面角C AB D --的平面角等于AM B ∠. 由正四面体ABCD 的棱长为1,可得AM BM ==,则1cos()2AMB ∠== 平面AMB 平分二面角C AB D --,∴二面角M AB D --的余弦值1cos()2AMB =∠= 设BCD ∆的外心为G ,连接AG,求得23BG BM ==AG ==, 设正四面体ABCD 的外接球的半径为R,则222)R R -+=,解得R = 平面MAB 过正四面体ABCD 的外接球的球心,∴平面MAB截此正四面体的外接球所得截面的面积为238ππ⨯=.38π. 13.已知某正四面体的内切球体积是1,则该正四面体的外接球的体积是 27 . 【解析】正四面体的外接球和内切球的半径之比为3:1,∴正四面体的外接球和内切球的体积比是27:1,正四面体的内切球体积是1,∴该正四面体的外接球的体积是27.故答案为:27.14.一个正四面体的展开图是边长为的正三角形,则该四面体的外接球的表面积为 3π .【解析】如图,一个正四面体的展开图是边长为∴G ,则23AG AD ==,正四面体的高PG ==. 再设正四面体外接球的球心为O ,连接OA ,则222)R R =+-,解得R =.∴该四面体的外接球的表面积为243ππ⨯=. 故答案为:3π.15.如图所示,正四面体ABCD 中,E 是棱AD 的中点,P 是棱AC 上一动点,BP PE +则该正四面体的外接球的体积是 .【解析】将侧面ABC ∆和ACD ∆展成平面图形,如图所示: 设正四面体的棱长为a ,则BP PE +的最小值为2cos1202a BE a ︒=a ∴=在棱锥A BCD -中,设底面三角形BCD 的中心为M ,外接球的球心为O ,F 为BC 的中点,则DF ==23DM DF ∴==AM ==.设外接球的半径OA OD r ==,则OM r =-,在Rt OMD ∆中,由勾股定理可得:222)r r =-+,解得:r =.∴外接球的体积为343r π=.故答案为:.。
