北师大版高中数学必修4§1.7.3正切函数的诱导公式导学案
高中数学 7.3 正切函数的诱导公式多媒体教学优质课件 北师大版必修4

0~2π的 角的三角 函数 (sānjiǎh ánshù)
π±α
锐角 (ruìj iǎo) 的三 角函 数
第六页,共14页。
由此可知,我们可以利用(lìyòng)诱导公式,将任意 角的三角函数问题转化为锐角的三角函数问题.
第七页,共14页。
例 1.若 tanα= 2 ,借助三角函数定义求角α的正弦函数值和余弦函数值. 3
第十三页,共14页。
重要的不是(bù shi)知识的数量,而是知识的
质量,有些人知道很多很多,但却不知道最有
用的东西。
——列夫•托尔斯泰
第十四页,共14页。
7.3 正切函数的诱导(yòudǎo)公 式
第一页,共14页。
1.会推导正切函数的诱导公式. 熟练掌握正切函数的诱导公式,并能根据公式解决(jiějué)化简、
求值等问题.
第二页,共14页。
同学们已经知道,在正、余弦函数中,我们(wǒ men)是先学 诱导公式,再学图像与性质的. 在学正切函数时,我们(wǒ men) 为什么要先学图像与性质,再学诱导公式呢?
为_____5___3_____.
2. 已知 tanx>0,则 x 的取值范围为__(_k___,_k______2__)_.
2
3. 已知 tanx=1,则 sinx 的值为______2__________.
第十一页,共14页。
4. 求值: 1 tan( 37 ) 2 tan( 43 ) .
6
6
解:∵tanα= 2 >0,∴α是第一象限或第三象限的角 3
(1)如果α是第一象限的角,则由 tanα= 2 可知,角α终边上必有一点 P(3,2). 3
所以 x=3,y=2. ∵r=|OP|= 13 ∴sinα= y = 2 13 , cosα= x = 3 13 .
高中数学北师大版必修4学案:1.7 正切函数 Word版含解析

§7 正切函数 7.1 正切函数的定义 7.2 正切函数的图像与性质 7.3 正切函数的诱导公式1.理解任意角的正切函数的定义.2.能画出y =tan x ⎝ ⎛⎭⎪⎫x ∈R ,x ≠π2+k π,k ∈Z 的图像.(重点)3.理解正切函数的定义域、值域、周期性、奇偶性,及其在区间⎝ ⎛⎭⎪⎫-π2,π2内的单调性.(重点)4.正切函数诱导公式的推导及应用.(难点)[基础·初探]教材整理1 正切函数的定义、图像及性质阅读教材P 36~P 38“动手实践”以上部分,完成下列问题. 1.正切函数的定义在直角坐标系中,如果角α满足:α∈R ,α≠π2+k π(k ∈Z ),且角α的终边与单位圆交于点P (a ,b ),那么比值ba 叫作角α的正切函数,记作y =tan α,其中α∈R ,α≠π2+k π(k ∈Z ).2.正切线如图1-7-1所示,线段AT 为角α的正切线.图1-7-13.正切函数的图像与性质判断(正确的打“√”,错误的打“×”) (1)正切函数y =tan x 的定义域为R .( ) (2)正切函数y =tan x 的最小正周期为π.( ) (3)正切函数y =tan x 是奇函数.( )(4)正切函数y =tan x 的图像关于x 轴对称.( ) 【解析】 (1)y =tan x的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪x ≠π2+k π,k ∈Z. (2)y =tan x 的周期为k π(k ∈Z ),最小正周期为π. (3)因为y =tan x的定义域⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ≠π2+k π,k ∈Z关于原点对称,且tan(-x )=-tan x ,故为奇函数.(4)由图知,正切函数图像既不关于x 轴对称,也不关于y 轴对称.【答案】 (1)× (2)√ (3)√ (4)× 教材整理2 正切函数的诱导公式阅读教材P 38~P 39例1以上部分,完成下列问题. 正切函数的诱导公式判断(正确的打“√”,错误的打“×”) (1)tan ⎝ ⎛⎭⎪⎫3π2-α=cot α.( )(2)正切函数的诱导公式中的角为任意角.( ) (3)tan(k π-α)=-tan α.( )【解析】 (1)tan ⎝ ⎛⎭⎪⎫3π2-α=tan ⎝ ⎛⎭⎪⎫π+π2-α=tan ⎝ ⎛⎭⎪⎫π2-α=cot α,所以(1)正确. (2)无论角α是哪个象限的角,诱导公式都适合,故(2)正确. (3)tan(k π-α)=-tan α,故(3)正确. 【答案】 (1)√ (2)√ (3)√[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1:_________________________________________________________ 解惑:___________________________________________________________ 疑问2:_________________________________________________________解惑:___________________________________________________________ 疑问3:_________________________________________________________ 解惑:___________________________________________________________[小组合作型]如图P ,Q是单位圆上的两点,O 是坐标原点,∠AOP =π6,∠AOQ =α,α∈[0,π).图1-7-2(1)若已知角θ的终边与OP 所在的射线关于x 轴对称,求tan θ; (2)若已知Q ⎝ ⎛⎭⎪⎫35,45,试求tan α.【精彩点拨】求出角的终边与单位圆的交点后,利用正切函数的定义求解. 【自主解答】 (1)∵角θ的终边与OP 所在的射线关于x 轴对称,且P ⎝ ⎛⎭⎪⎫32,12, 故θ的终边与单位圆交于P ′⎝ ⎛⎭⎪⎫32,-12,则tan θ=-1232=-33. (2)∵∠AOQ =α且Q ⎝ ⎛⎭⎪⎫35,45,∴tan α=4535=43.1.解决本题的关键是熟记正切函数的定义,即tan α=ba .2.已知角终边上的一点M (a ,b )(a ≠0),求该角的正切函数值,或者已知角α的正切值,求角α终边上一点的坐标,都应紧扣正切函数的定义求解,在解题过程中,应注意分子、分母的位置.3.tan α=sin αcos α知其中两个,可求另一个.[再练一题]1.角α的终边经过点P (-b,4)且cos α=-35,求tan α的值.【导学号:66470022】【解】 由题意知cos α=-b b 2+42=-35,∴b =±3.又cos α=-35<0,∴P 在第二象限,∴b =3. ∴tan α=-43.(1)化简:sin (π+α)·cos (π-α)·tan ⎝ ⎭⎪-2-αtan ⎝ ⎛⎭⎪⎫π2+α·cos ⎝ ⎛⎭⎪⎫3π2+α;(2)求值:tan 3π4-tan 2π31+tan ⎝ ⎛⎭⎪⎫-4π3·tan ⎝ ⎛⎭⎪⎫-π4.【精彩点拨】 解答本题可依据先用周期性或关于-α的诱导公式,把角绝对值“化小”,再利用恰当的公式化简.【自主解答】 (1)原式= (-sin α)·(-cos α)·tan ⎝ ⎛⎭⎪⎫π2-α(-cot α)·sin α=sin αcos α·cot α(-cot α)·sin α=-cos α.(2)原式=tan ⎝ ⎛⎭⎪⎫2π-π4-tan ⎝ ⎛⎭⎪⎫π-π31+tan ⎝ ⎛⎭⎪⎫π+π3tan π4=-tan π4+tan π31+tan π3=3-13+1=2- 3.在使用诱导公式化简时,一定要记准诱导公式中名称变还是不变以及准确判断角所在象限.一般地,我们将α看作锐角(实质上是任意角),那么π-α,π+α,2π-α,π2+α,π2-α分别是第二、三、四、二、一象限的角.[再练一题]2.(1)化简:tan (540°-α)tan (α-270°)tan (α+180°)tan (α-180°)tan (810°+α)tan (-α-360°);(2)若a =cos (α+π)sin 2(3π+α)tan (4π+α)tan (π+α)cos 3(-α-π),求a 2+a +1的值. 【解】 (1)tan (540°-α)tan (α-270°)tan (α+180°)tan (α-180°)tan (810°+α)tan (-α-360°)=tan (-α)tan (α-90°)tan αtan αtan (90°+α)tan (-α)=(-tan α)(-cot α)tan αtan α(-cot α)(-tan α) =tan α·cot α·tan αtan α·cot α·tan α=1.(2)a =cos (α+π)sin 2(3π+α)tan (4π+α)tan (π+α)cos 3(-α-π)=(-cos α)sin 2αtan α·tan α(-cos 3α)=-cos α·sin 2αsin αcos α·sin αcos α·(-cos 3α)=-cos 3αsin 2αsin 2α(-cos 3α)=1, ∴a 2+a +1=1+1+1=3.利用正切函数的图像作出y =|tan x |的图像,并写出使y =3的x 的集合.【精彩点拨】 先化成分段函数,再借助正切函数的图像作图. 【自主解答】 ∵当x ∈⎝ ⎛⎦⎥⎤k π-π2,k π时,y =tan x ≤0,当x ∈⎝ ⎛⎭⎪⎫k π,k π+π2时,y =tan x >0, ∴y =|tan x |=⎩⎪⎨⎪⎧-tan x ,x ∈⎝ ⎛⎦⎥⎤k π-π2,k πk ∈Z ,tan x ,x ∈⎝ ⎛⎭⎪⎫k π,k π+π2,k ∈Z .如图所示.使y =3的x的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k π±π3,k ∈Z.1.三点两线画图法“三点”是指⎝ ⎛⎭⎪⎫-π4,-1,(0,0),⎝ ⎛⎭⎪⎫π4,1;“两线”是指x =-π2和x =π2.在三点、两线确定的情况下,类似于五点法作图,可大致画出正切函数在⎝ ⎛⎭⎪⎫-π2,π2上的简图,然后向右、向左扩展即可得到正切曲线.2.如果由y =f (x )的图像得到y =f (|x |)及y =|f (x )|的图像,可利用图像中的对称变换法完成;即只需作出y =f (x )(x ≥0)的图像,令其关于y 轴对称便可以得到y =f (|x |)(x ≤0)的图像;同理只要作出y =f (x )的图像,令图像“上不动下翻上”便可得到y =|f (x )|的图像.3.利用函数的图像可直观地研究函数的性质,如判断奇偶性、周期性、解三角不等式等.[再练一题]3.求下列函数的定义域. (1)y =11+tan x;(2)y =tan x +lg(1-tan x ). 【解】 (1)由⎩⎪⎨⎪⎧1+tan x ≠0,x ≠k π+π2(k ∈Z ),得⎩⎪⎨⎪⎧x ≠k π-π4(k ∈Z ),x ≠k π+π2(k ∈Z ),∴函数的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π+π2且x ≠k π-π4,k ∈Z . (2)要使函数y =tan x +lg(1-tan x )有意义.则⎩⎨⎧tan x ≥0,1-tan x >0⇒0≤tan x <1.由正切函数的图像可得k π≤x <k π+π4,k ∈Z .∴原函数的定义域为⎩⎨⎧⎭⎬⎫x |k π≤x <k π+π4,k ∈Z .[探究共研型]探究1 【提示】 不是,正切函数的定义域是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≠k π+π2,k ∈Z.正切曲线在每一个开区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )上是增加的,但在整个定义域上不是增加的.探究2 函数y =tan x 的周期是多少?y =|tan x |的周期呢? 【提示】 y =tan x 的周期是π,y =|tan x |的周期也是π.探究3 函数y =tan x 的图像有什么特征?【提示】 正切曲线是被互相平行的直线x =k π+π2(k ∈Z )所隔开的无穷支曲线组成的,是间断的,无对称轴,只有对称中心.已知f (x )=-a tan x (a ≠0). (1)判断f (x )在x ∈⎣⎢⎡⎦⎥⎤-π3,π3上的奇偶性;(2)求f (x )的最小正周期; (3)求f (x )的单调区间;(4)若a >0,求f (x )在⎣⎢⎡⎭⎪⎫π4,π2上的值域.【精彩点拨】 通过f (-x )与f (x )的关系判断奇偶性,求单调区间时注意a 的符号.【自主解答】 (1)∵f (x )=-a tan x (a ≠0),x ∈⎣⎢⎡⎦⎥⎤-π3,π3,∴f (-x )=-a tan(-x )=a tan x =-f (x ). 又定义域⎣⎢⎡⎦⎥⎤-π3,π3关于原点对称,∴f (x )为奇函数. (2)f (x )的最小正周期为π.(3)∵y =tan x 在⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )上单调递增, ∴当a >0时,f (x )在⎝ ⎛⎭⎪⎫k π-π2,k π+π2上单调递减,当a <0时,f (x )在⎝ ⎛⎭⎪⎫k π-π2,k π+π2上单调递增.(4)当a >0时,f (x )在⎣⎢⎡⎭⎪⎫π4,π2上单调递减,故x =π4时,f (x )max =-a ,无最小值. ∴f (x )的值域为(-∞,-a ].1.由函数的性质(如周期性、有界性、对称性)可指导我们画出函数的图像. 2.由函数的图像又可以直观地总结函数的性质.函数的主要性质包括定义域、值域、周期性、奇偶性和单调性.[再练一题]4.画出函数y =tan |x |的图像,并根据图像判断其单调区间、奇偶性. 【解】 由y =tan |x |得,y =⎩⎪⎨⎪⎧tan x ,x ≥0且x ≠π2+k π(k ∈Z ),-tan x ,x <0且x ≠π2+k π(k ∈Z ).根据y =tan x 的图像,作出y =tan |x |的图像如图所示:由图像可知,函数y =tan |x |是偶函数.单调增区间为:⎣⎢⎡⎭⎪⎫0,π2,⎝ ⎛⎭⎪⎫π2+k π,3π2+k π(k =0,1,2,3,…); 单调减区间为:⎝ ⎛⎦⎥⎤-π2,0,⎝ ⎛⎭⎪⎫-3π2+k π,-π2+k π(k =0,-1,-2,-3,…).[构建·体系]1.tan 5π6的值为( )A .3B .- 3 C.33 D .-33【解析】 tan 5π6=tan ⎝ ⎛⎭⎪⎫π-π6=-tan π6=-33. 【答案】 D2.函数y =tan ⎝ ⎛⎭⎪⎫x +π4的定义域是( ) A .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≠-π4 B .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≠π4 C.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≠k π-π4,k ∈Z D .⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x ≠k π+π4,k ∈Z 【解析】 由题意得x +π4≠k π+π2,k ∈Z ,所以x ≠k π+π4,k ∈Z .【答案】 D3.已知角α的终边上一点P (-2,1),则tan α=________.【解析】 由正切函数的定义知tan α=1-2=-12. 【答案】 -124.函数y =tan x ,x ∈⎣⎢⎡⎦⎥⎤0,π4的值域是________.【导学号:66470023】【解析】 函数y =tan x 在⎣⎢⎡⎦⎥⎤0,π4上是增加的,所以y max =tan π4=1,y min =tan 0=0.【答案】 [0,1]5.求以下各式的值.(1)7cos 270°+3sin 270°+tan 765°;(2)tan 225°+tan 750°tan (-30°)-tan (-45°). 【解】 (1)原式=7cos(180°+90°)+3sin(180°+90°)+tan(2×360°+45°)=-7cos 90°-3sin 90°+tan 45°=0-3×1+1=-2.(2)原式=tan (180°+45°)+tan (2×360°+30°)-tan 30°+tan 45° =tan 45°+tan 30°tan 45°-tan 30°=1+331-33=2+ 3.我还有这些不足:(1)______________________________________________________________(2)______________________________________________________________ 我的课下提升方案:(1)______________________________________________________________(2)______________________________________________________________。
高中数学 第一章 三角函数 1.7.3 正切函数的诱导公式练习 北师大版必修4

7.3 正切函数的诱导公式3.已知tan(π+α)+=2,则tan(π-α)=()A.2B.-2C.1D.-1解析:由已知可得tan α+=2,解得tan α=1.于是tan(π-α)=-tan α=-1.答案:D4.已知a=tan 1,b=tan 2,c=tan 3,则a,b,c的大小关系是()A.a>b>cB.a>c>bC.b>c>aD.c>b>a解析:b=tan 2=tan(2-π),c=tan 3=tan(3-π),又-<2-π<3-π<1<,且y=tan x在上是增加的,则有tan(2-π)<tan(3-π)<tan 1,即b<c<a.答案:B5.给出下列各函数值,其中符号为负的是()A.sin(-1 000°)B.cos(-2 200°)C.tan(-10)D.解析:sin(-1 000°)=sin(-3×360°+80°)=sin 80°>0;cos(-2 200°)=cos 2 200°=cos(6×360°+40°)=cos 40°>0;tan(-10)=-tan 10<0;sin>0,cos π=-1<0,tan=tan<0,故>0.答案:C6.tan=.解析:tan=-tan=-tan=-tan=tan.答案:7.已知tan(π-x)=,则tan(x-3π)=.解析:由tan(π-x)=知,tan x=-,故tan(x-3π)=-tan(3π-x)=tan x=-.答案:-84+log9=.解析:∵sin=sin=sin,tan=-tan=tan,∴log4+log9=log4+log9=lo=-=-.答案:-9.求下列各式的值:(1)cos+tan;(2)sin 810°+tan 765°+tan 1 125°+cos 360°.解:(1)cos+tan=cos+tan=cos+tan+1=.(2)原式=sin(2×360°+90°)+tan(2×360°+45°)+tan(3×360°+45°)+cos(0°+360°)=sin 90°+tan 45°+tan 45°+cos 0°=4.10.设tan=a,求的值.解:∵tan=tan=tan=a,∴原式==.11:当k=2或3时,.证明:当k=2时,左边==右边.当k=3时,左边==右边.故当k=2或3时,原等式成立.。
2020-2021学年北师大版数学必修4课件:1.7.3 正切函数的诱导公式

(2)正切函数的诱导公式中的角为任意角.
(3)tan(kπ-α)=-tan α.
()
()
2.tan 5 的值为
6
()
A. 3
B.- 3
C. 3
3
【解析】选D.tan
5 6
=tan
( )=-tan
6
6
D.- 3
3
=- 3 .
3
3.(教材二次开发:例题改编)已知角α终边上有一点P(5n,4n)(n≠0),则
6
6
A.- 3
B.0
C. 2 3
3
3
D.- 2 3
3
2.若f(x)=tan x,则f(600°)的值为 ( )
A. 3
B. 3
C. 3
D. 3
3
3
3.求以下各式的值:(1)7cos 270°+3sin 270°+tan 765°.
(2) tan 225 tan 750 .
tan(30) tan(45)
2
2.已知函数f(x)=sin x ,g(x)=tan(π-x),则 ( )
2
A.f(x)与g(x)都是奇函数
B.f(x)与g(x)都是偶函数
C.f(x)是奇函数,g(x)是偶函数
D.f(x)是偶函数,g(x)是奇函数
3.(教材二次开发:例题改编)已知P(2,-3)是α终边上一点,则tan(2π+α)等
5
5
+tan 2
5
-
tan 2 -tan =0.
5
5
答案:0
5.已知角α的终边经过点P(4,-3).
(1)求sin α,cos α,tan α的值.
北师大版高中数学必修4教案备课正切函数的诱导公式
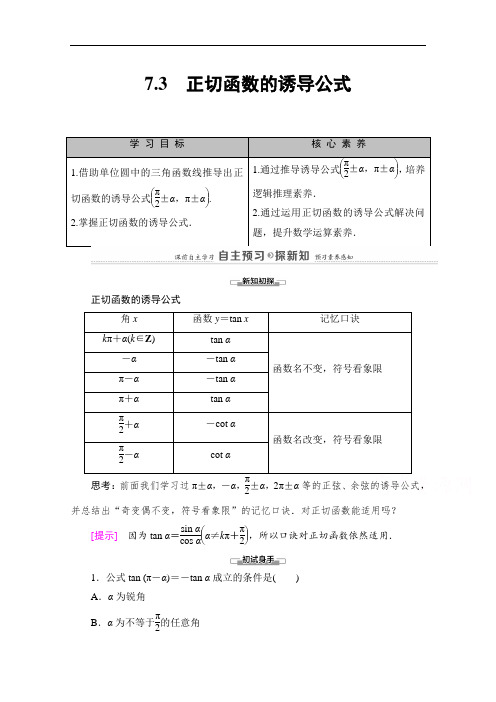
7.3 正切函数的诱导公式学 习 目 标核 心 素 养1.借助单位圆中的三角函数线推导出正切函数的诱导公式⎝ ⎛⎭⎪⎫π2±α,π±α.2.掌握正切函数的诱导公式.1.通过推导诱导公式⎝ ⎛⎭⎪⎫π2±α,π±α,培养逻辑推理素养.2.通过运用正切函数的诱导公式解决问题,提升数学运算素养.正切函数的诱导公式角x 函数y =tan x记忆口诀k π+α(k ∈Z )tan α 函数名不变,符号看象限-α -tan α π-α -tan α π+α tan α π2+α -cot α函数名改变,符号看象限π2-αcot α思考:前面我们学习过π±α,-α,π2±α,2π±α等的正弦、余弦的诱导公式,并总结出“奇变偶不变,符号看象限”的记忆口诀.对正切函数能适用吗?[提示] 因为tan α=sin αcos α⎝ ⎛⎭⎪⎫α≠k π+π2,所以口诀对正切函数依然适用.1.公式tan (π-α)=-tan α成立的条件是( ) A .α为锐角B .α为不等于π2的任意角C .α为任意角D .α≠k π+π2(k ∈Z )D [由正切函数的定义可知α≠k π+π2(k ∈Z ).] 2.下列诱导公式中错误的是( ) A .tan (π-α)=-tan α B .cos ⎝ ⎛⎭⎪⎫π2+α=sin αC .sin (π+α)=-sin αD .cos (π-α)=-cos α [答案] B3.tan ⎝ ⎛⎭⎪⎫3π2+α等于( )A .-cot αB .cot αC .tan αD .-tan α[答案] A4.tan 5π6的值为( ) A . 3 B .- 3 C .33D .-33 D [tan 5π6=tan ⎝ ⎛⎭⎪⎫π-π6=-tan π6=-33.]三角函数间关系的应用【例1】 已知角α的顶点在原点,始边与x 轴的非负半轴重合,终边经过点P (3,y ),且tan α=-43.(1)求sin α+cos α的值;(2)求sin (π-α)+2cos (π+α)sin⎝⎛⎭⎪⎫3π2-α-cos ⎝⎛⎭⎪⎫3π2+α的值.[解](1)因为tan α=y3=-43,所以y=-4,则r=5.∴sin α=-45,cos α=35,则sin α+cos α=-15.(2)原式=sin α-2cos α-cos α-sin α=tan α-2-1-tan α=-43-2-1+43=-10313=-10.三角函数之间关系的应用利用三个三角函数之间的关系:tan α=sin αcos α进行弦切互化;正用可以做到切化弦,逆用可以做到弦化切.1.已知α为第二象限角,且tan α-1tan α=154,求sin ⎝⎛⎭⎪⎫π2+α-sin (π+α)sin ⎝⎛⎭⎪⎫π2-α-sin (π-α)的值.[解]由tan α-1tan α=154,得4tan2α-15tanα-4=0,得tan α=-14或tan α=4.又α为第二象限的角,所以tan α=-14.故sin ⎝⎛⎭⎪⎫π2+α-sin (π+α)sin ⎝⎛⎭⎪⎫π2-α-sin (π-α)=cos α+sin αcos α-sin α=1+tan α1-tan α=35.利用诱导公式求值【例2】 求下列各式的值: (1)tan ⎝ ⎛⎭⎪⎫-26π3;(2)tan 10°+tan 170°+sin 1 866°-sin (-606°). [思路探究] 利用诱导公式化为锐角三角函数,再求值. [解] (1)tan ⎝ ⎛⎭⎪⎫-26π3=-tan 26π3=-tan ⎝ ⎛⎭⎪⎫8π+2π3=-tan 2π3=tan π3= 3.(2)原式=tan 10°+tan (180°-10°)+sin 1 866°-sin (-606°)=tan 10°-tan 10°+sin (5×360°+66°)-sin [(-2)×360°+114°]=sin 66°-sin 66°=0.利用诱导公式求值一般为:把负角三角函数化为正角三角函数,再化为0~2π间的三角函数,最后转化为锐角三角函数求值.2.求下列三角函数的值: (1)tan 150°;(2)tan ⎝ ⎛⎭⎪⎫-19π6.[解](1)tan 150°=tan ()180°-30°=-tan 30°=-33.(2)tan ⎝ ⎛⎭⎪⎫-19π6=-tan 19π6=-tan ⎝ ⎛⎭⎪⎫3π+π6=-tan ⎝ ⎛⎭⎪⎫π+π6=-tan π6=-33.利用诱导公式化简与证明[探究问题]1.与正切函数有关的式子求值时应注意什么问题?[提示]求含有正切函数关系式的某个函数的定义域时,要注意正切函数值存在的条件.求值域时,不要忽视这个函数的定义域.2.利用正切函数的诱导公式解决给角求值的解题流程是怎样的?[提示]【例3】(1)化简:sin (π+α)·cos (π-α)·tan ⎝⎛⎭⎪⎫-3π2-αtan ⎝⎛⎭⎪⎫π2+α·cos ⎝⎛⎭⎪⎫3π2+α;(2)求值:tan7π4-tan2π31+tan ⎝⎛⎭⎪⎫-4π3·tan ⎝⎛⎭⎪⎫-π4.[思路探究]解答本题可依据先用周期性或关于-α的诱导公式,把角绝对值“化小”,再利用恰当的公式化简.[解](1)原式=(-sin α)·(-cos α)·tan⎝⎛⎭⎪⎫π2-α(-cot α)·sin α=sin αcos α·cot α(-cot α)·sin α=-cos α.(2)原式=tan ⎝⎛⎭⎪⎫2π-π4-tan ⎝⎛⎭⎪⎫π-π31+tan ⎝⎛⎭⎪⎫π+π3tanπ4=-tanπ4+tanπ31+tanπ3=3-13+1=2- 3.1.将例3(1)变为“已知tan (3π-α)=15,求sin (π+α)·tan (π-α)·tan ⎝⎛⎭⎪⎫-32π-αtan ⎝⎛⎭⎪⎫π2+α·cos ⎝⎛⎭⎪⎫32π+α的值”.[解]因为tan (3π-α)=tan (-α)=-tan α=15,所以tan α=-15.原式=-sin α(-tan α)·sin ⎝⎛⎭⎪⎫-32π-αcos ⎝⎛⎭⎪⎫-32π-αsin ⎝⎛⎭⎪⎫π2+αcos ⎝⎛⎭⎪⎫π2+α·sin α=-sin α·(-tan α)⎝⎛⎭⎪⎫--cos αsin αcos α-sin α·sin α=-tan α=15.2.将例3(2)变为“若a=cos (α+π)sin2(3π+α)tan(4π+α)tan (π+α)cos3(-α-π)”,试求a2+a+1的值.[解]a=cos(α+π)sin2(3π+α)tan(4π+α)tan (π+α)cos3(-α-π)=(-cosα)sin2αtanα·tan α(-cos3α)=-cosα·sin2αsin αcos α·sin αcos α·(-cos3α)=-cos3αsin2αsin2α(-cos3α)=1,∴a2+a+1=1+1+1=3.1.三角函数式化简的常用方法(1)依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的三角函数.(2)切化弦:一般需将表达式中的切函数转化为弦函数.2.三角恒等式的证明策略:在证明时一般从左边到右边,或从右边到左边,或左右归一,总之,应遵循化繁为简的原则.定义法,化弦法,拆项折角法,公式变形法.1.正切函数的诱导公式在记忆时可简单记为“奇变偶不变,符号看象限”,即k ·π2±α中,如果k 为奇数,则正切变余切,至于符号取决于角k ·π2±α所在的象限.2.在对三角式进行化简、求值、证明中,要遵循诱导公式先行的原则. 特别提醒:应用正切函数的诱导公式时,必须等式两边都有意义.1.判断(正确的打“√”,错误的打“×”) (1)tan ⎝ ⎛⎭⎪⎫3π2-α=cot α.( ) (2)对任意α∈R ,都有tan (-α)=-tan α. ( ) (3)tan (k π-α)=-tan α.( )[答案] (1)√ (2)× (3)√ 2.tan 300°+sin 450°的值为( ) A .1+3 B .1- 3 C .-1- 3 D .-1+3 B [tan 300°+sin 450°=tan (360°-60°)+sin (360°+90°) =-tan 60°+sin 90°=1- 3.] 3.若cot α=m ,则tan ⎝ ⎛⎭⎪⎫3π2-α=( )A .mB .-mC .1mD .-1mA [tan ⎝ ⎛⎭⎪⎫3π2-α=tan ⎣⎢⎡⎦⎥⎤π+⎝ ⎛⎭⎪⎫π2-α=tan ⎝ ⎛⎭⎪⎫π2-α=cot α=m .]4.已知角α的终边经过点P (4,-3). (1)求sin α,cos α,tan α的值; (2)求sin ⎝ ⎛⎭⎪⎫π2-αsin (π+α)·tan (π-α)cos (α+π)的值.[解] (1)因为r =42+(-3)2=5,所以sin α=y r =-35,cos α=x r =45,tan α=y x =-34.(2)sin ⎝ ⎛⎭⎪⎫π2-αsin (π+α)·tan (π-α)cos (α+π)=cos α-sin α·-tan α-cos α =-tan αsin α=--34-35=-54.。
高中数学北师大版必修四教学案第一章 §7 第2课时 正切函数的诱导公式 Word版含答案

第课时正切函数的诱导公式[核心必知]诱导公式+α()(π);α=-()(α)α-;=-π(α());-α=-π()()α=α;-+π()(α=;)α()=*-;α*()α=.[问题思考].以上公式中的角α是任意角吗?提示:是任意角,但α必须使公式两边的函数值有意义.即公式 ()~()中α≠+π,∈;(),()中α≠π,∈..以上公式符合正、余弦函数诱导公式的规律“奇变偶不变,符号看象限”吗?提示:符合.讲一讲.求下列各式的值();()°+°(-°)-(-°)).[尝试解答] () =-=-=-=-=-=-.()原式=°+°)=°+°,-°+°)==+.利用正切函数的诱导公式解决给角求值的解题流程如下:α),\((-α)=-α))练一练.计算:°.解:原式=- (°+°)=-(π+) °=°=×=.讲一讲.化简+.[尝试解答] 原式=+αα,(-α))=α)α)-ααα)=-=.利用诱导公式对三角函数关系式进行化简时要熟练诱导公式,化简的结果要力求简单,分母中一般不含三角函数,能求值的要求值.练一练. 化简:.解:原式=αα(°+α)(-α))=.讲一讲。
高中数学第一章三角函数1.7.3正切函数的诱导公式课件2北师大版必修4
第二十二页,共37页。
(3)应用三角函数关系(guān xì)的策略:“1”的代换,可以将“1”看作
“sin2α+cos2α”整体代入;弦切互化,正用tanα= 可以做到切 sin 化弦,逆用可以做到弦化切,其中切化弦是最常用的求值、化简c的os变换
方法.
第二十三页,共37页。
【补偿(bǔcháng)训练】已知tanθ=2,则
5 (3)因为(yīn wèi)cos(-120°)=cos 120°=-cos 60°=- , 所以f(α)=-cosα= . 1
2
第二十九页,共37页。
【方法(fāngfǎ)技巧】 1.三角函数式化简的常用方法(fāngfǎ) (1)依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的 三角函数. (2)切化弦:一般需将表达式中的切函数转化为弦函数.
第十一页,共37页。பைடு நூலகம்
【解析(jiě xī)】1.原式= 2.原式=sin 120°cos(360°-30°)-sin(720°-30°)cos(-720° +60°)+tan(720°-45°)+
第十二页,共37页。
【方法技巧】 1.用正切函数诱导公式解题(jiě tí)的一般步骤 与正弦、余弦函数的最小正周期为2π不同,正切函数的最小正周期为π,因此 其解题(jiě tí)的一般步骤为:
第二页,共37页。
(5)tan(π+α)= _____ta_n;α
(6)tan( +α)= _______-c;otα (7)tan( -α)= ______. cotα
第三页,共37页。
【即时小测】
1.思考下列问题
(1)诱导公式中的角α是锐角吗?
高中数学第一章三角函数1.7正切函数知识导航学案北师大版必修4
§7 正切函数知识梳理1.任意角的正切函数 (1)定义如图1-6-1所示,单位圆与角α的终边交于P 点.设P (a ,b ),则ab是角α的函数,称为正切函数,记为ab=tan α(α∈R ).通常用x,y 表示自变量和因变量,将正切函数表示为y=tanx. (2)正切线如图1-6-1所示,单位圆与x 轴的正半轴交于点A ,过点A 作x 轴的垂线AT ,交角α的终边或反向延长线于T ,则有向线段AT 叫做角α的正切线.当角α的终边在y 轴上时,角α的正切线不存在.图1-6-1(3)正切线所表示的正切值可如下确定:正切线的方向表示正切值的符号,同y 轴一致,向上为正,向下为负;正切线的长度是正切值的绝对值.(4)任意角的正切函数定义的推广图1-6-2如图1-6-2所示,设P(x,y)是α的终边上任意一点,则tan α=xy . 对于每一个确定的α,都分别有唯一确定的正切值与之对应,所以这个对应法则都是以角α为自变量的函数,叫做正切函数.正切函数值与点P 在角α终边上的位置无关,只依赖于角α的大小.2.任意角的正切值的符号(1)用图形表示:正切函数值在各象限的符号如图1-6-3所示.图1-6-33.正切函数的图像和性质(1)图像:如图1-6-4所示.图1-6-4知识导学1.复习初中学过的锐角的正切函数,本节是锐角正切函数的补充和延伸.2.任意角的正切值的符号记忆口诀:“一三正,二四负”.其含义是终边在第一、三象限的任意角正切值为正.3.三角函数值在各象限的符号的记忆方法:三角函数值在各象限的符号可用以下口诀记忆:“一全正,二正弦,三两切,四余弦”.其含义是在第一象限各三角函数值全为正,在第二象限只有正弦值为正,在第三象限只有正、余切值为正,在第四象限只有余弦值为正(这里说的三角函数值不指正割和余割函数).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*******“双主”高效课堂数学导学案
2015---2016学年度第二学期 姓名: 组名: 使用时间2016年 月 日
年 级 科 目 课 题 主 备 人 备 课 方 式 课 时 负责人(签字) 审核领导(签字) 序
号
SX11
高 一 数学 §1.7.3正切函数的诱导公式 1
学习目标:
1、知识与技能
(1)通过观察正切函数的图象,掌握数行结合思想;
(2)结合正切函数图象分析得到正切函数的诱导公式;
(3)通过数行结合,类比推理等思想,培养学生分析问题、解决问题的能力.
2、过程与方法
通过运用正、余弦的概念作比较,得出正切函数的概念,也可以仿照正、余弦公式推出正切函
数的诱导公式;通过单位圆用的正切线画出正切函数的图像,并从图像总结正切函数的性质.
3、情感态度与价值观
使学生对正切函数的概念有一定的体会,会用联系的观点看问题,建立数形结合的思想,激发
学生学习积极性;培养学生分析问题、解决问题的能力;让学生体验自身探索成功的喜悦感,培养
学生自信心;培养学生形成实事求是的科学态度和锲而不舍的钻研精神.
学习重点:正切函数的概念、诱导公式、图像与性质.
学习难点:熟练运用诱导公式和性质分析问题、解决问题.
基础达标:
1、 画出正切曲线图像:
2、总结正切函数的性质:
定义域:
值 域:
周期性:
奇偶性:
单调性:
对称性:
3、化简下列各式(诱导公式):
)tan(k )tan( )2tan(
)tan(
)2tan( )23tan(
)23tan( )2tan(
合作交流:
1、若43tan,借助三角函数的定义,求sin,cos.
2、 确定下列式子的符号:
(1)sin273tan125 (2)1tan (3)tan108cos305
3、化简下列各式:
(1))675tan()60tan(210tan315tan (2)psin+q2cos+k2tan
(3)mtan+n2cos-psin-q23cos-r2sin
思考探究:
1、对于诱导公式的推导,利用了什么方法?请举例推导其中一个.
2、利用诱导公式求任意角的三角函数值的步骤是什么?
达标检测:
1、tan 225°等于( )
A.3 B.33 C.1 D.-1
2、若tan 126°=m,则cot 36°等于( )
A.m B.-m C.±m D不能确定
3、10tan()3=
4、已知31)sin(,0<<3,
求:)23sin()25tan(
5、化简:
学习小结:
学后反思:
