三边测量法,分步定位法比较
大地测量学基础:第5章 大地测量基本技术与方法(1)

§5-1 建立国家平面大地控制网的基本原理 §5-2 建立国家高程控制网的基本原理 §5-3 建立工程测量控制网的基本原理 §5-4 大地测量仪器 §5-5 精密角度测量方法 §5-6 精密距离测量方法 §5-7 精密高差测量方法 备讲1—精密水准仪与水准尺的检验 备讲2—球气差系数和大气折光系数 备讲3—三角高程测量的精度 备讲4—垂线偏差对三角高程的影响
折角,折线上的转折点叫导线点(控制点)。 • 测定导线点平面坐标的工作叫导线测量。通过测量导线边长和转
折角,再根据起算点及附合点的已知数据,可求出所有导线点的 平面坐标。
β
D
• 导线的形式:附合导线、闭合导线、支导线和导线网。
• 导线网是由若干条附合导线或闭合导线构成的网状图形。 • 导线网包括:一个节点的导线网、两个以上节点的导线网和两个
A
a
az B
• VLBI测量长度的相对精度可达10-6。
• 该技术在研究地球极移、地球自转速率的短周期变化、地球固体 潮、大地板块运动的相对速率和方向中得到广泛的应用,在常规 大地测量中很少用。
3*、惯性测量系统(INS)
• 惯性测量是利用惯性力学基本原理,在相距较远的两点之间,对 装有惯性测量系统的运动载体(汽车或直升飞机)从一个已知点到另 一个待定点的加速度,分别沿三个正交的坐标轴方向对加速度分 量进行两次积分,从而求定其运动载体在三个坐标轴方向的坐标 增量,进而求出待定点的位置。
• 因此,在普遍应用全站仪和GPS定位技术的现代,城市控制测量 和工程控制测量基本上不采用三角网。
2. 导线测量法 • 导线:由设站点(控制点)连成的折线(若干条直线首尾相连)。 • 布设控制点时,使点与点之间单线相连形成链状折线,测量出边
基于RSSI的测距差分修正定位算法_任维政

基于 RSSI 的测距差分修正定位算法*
任维政 , 徐连明 , 邓中亮* , 王 川
(北京邮电大学电子工 程学院 , 北京 100876)
摘 要 :为了抑制 RSSI 误差对无线传感器节点自身定位精度的影响 , 以三边定位算法为基础 , 定义了个 体差异差 分系数 、距
离差分系数和距离差分定位方程 , 把离目标节点最近的 信标节点 作为参 考节点 对基于 RSSI 的 测距进 行差分 修正 , 并将差 分
分定位方程
di =d′i -ρie i0 i =1 , 2 , … , n
(8)
第7期
任维政 , 徐连明等 :基于 RSSI 的测距差分修正定位算法
1 249
其中 , di 为目标节点到第 i 个信标节点的修正距离 ,
参考节点测量距离误差 e0i =d′0i -d0i , n 为参与定
位的信标节点个数 。
-d
2 i
x2i
-x2k
+y
2 j
-y2k
+d2k
-d
2 j
(2)
1 .2 无线电传播路径损耗模型分析
由于传感器节点自身具备通信能力 , 通信控制
芯片通常会提 供测量 RSSI 的方法 , 在信标 节点广
播自身坐标的 同时可完成 RSSI 的测量 , 故 而是一
种低功率 、低代价的测距技术 。 其误差主要来源于
PL(d)=P L(d0)+10klg
d d0
+X σ
(4)
其中 , P L(d)为经过距离 d 后的路径损耗 , dB ;Xσ为
平均值为 0 的高斯分布随机变数 , 其标准差范围为 4
~ 10 。式中 k 的范围在 2 至 5 之间 。取 d =1 m , 代入 式(3), 可得到 Lo ss , 即P L(d0)的值 。这样根据上式
0-无线传感器网络节点定位算法的研究综述

式 ( 3 ) 用线性方程组表示为: AX = b, 其中: (x 1 - x n ) ( y 1 - yn ) A = 2# ( x n- 1 - x n )
2 1 2 n 2 1
;X = ( y n- 1 - yn )
2 2 2
x ; y
x - x + y - y n + dn - d 1 b= x
[ 7] [ 8]
随着微机电系统 ( M EMS )、 无线通信和数字电子 技术的发展 , 无线传感器网络 ( W SN ) 在军事应用、 目 标追踪、 环境监测、 医疗保健、 空间探索等领域都得到 广泛的应用 。节点位置信息是无线传感器网络应 [ 3] 用的基础, 节点定位 技术在无线传感器网络中具有 重要的地位。 [ 4] GPS 是目前应用最广的定位服务, 但受到成本、 功耗、 扩展性等问题的限制 , 甚至在某些场合可能根本 无法实现。目前, 主要解决方法是利用少量已知节点, 通 过节点定位算法, 以获得节点的信息。因此, 要采用一定 的定位机制与算法来实现 W SN 的节点定位。从 1992年 [ 5 6] AT&T 实验室开发出室内定位系统 Activ e Badge 至今,
∃ 14∃
机
电
工
程
第 26 卷
射功率 , 在接收节点测量接收功率 , 计算传播损耗, 使 用理论或经验的信号传播模型将传播损耗转 化为距 离 , 该技术主要使用 RF 信号。该方法功耗低、 价廉。 但由于环境的影响, 其建模比较麻烦。通常有可能产 生 ! 50% 的测距误差。 TDOA( ti m e difference on arriv al)。在节点上安装 超声波收发器和 RF 收发器。测距时, 在发射端两种收 发器同时发射信号, 利用声波与电磁波在空气中传播速 度的差异 , 把时间转化为距离。该技术的测距精度比 RSSI高, 但也会受非视距 ( NLOS)问题对超声波信号的 传播影响。 AOA ( ang le of arriv al) 。以 两个或更多基 站发射 信号的到达角度来估计节点的位置。该测量技术将距 离的测量转化为角度的测量。 AOA 技 术也受外界环 境影响 , 而且需要额外硬件 , 可能无法满足传感器对硬 件尺寸和功耗的要求。 TOA( ti m e of arr iv al) 。通过测量信号传播时间来 测量距离, 需要节点间时间同步。因 W S N 节点的硬件 尺寸、 价格和功耗限制 , 其实际场合使用的较少。
《大地测量学基础》试卷(A)含答案
《大地测量学基础》试卷(A)一、解释下列术语(每个2分,共10分)大地水准面球面角超底点纬度高程异常水准标尺零点差二、填空(1-15小题每空1分;16题4分,共36分)1、在地球自转中,地轴方向相对于空间的变化有______和_____。
2、时间的度量单位有______和______两种形式。
3、重力位是______和_____之和,重力位的公式表达式为_______。
4、椭球的形状和大小一般用_______来表示。
5、在大地控制网优化设计中把_____、______和_____作为三个主要质量控制标准。
6、测距精度表达式()m a b D=±+⨯中,的单位是______,表示的意义是_____;的单位是______,表示的意义是_____。
7、利用测段往返不符值计算的用来衡量水准测量外业观测的精度指标用_____来表示,其意义是______。
8、利用闭合环闭合差计算的用来衡量水准测量外业观测的精度指标用_____来表示,其意义是______。
9、某点在高斯投影3°带的坐标表示为XA=3347256m, YA=37476543m,则该点在6°带第19带的实际坐标为xA=___________________,yA=___________________。
10、精密水准测量中每个测段设置______个测站可消除水准标尺______零点差的影响。
11、点P从B=0°变化到B=90°时,其卯酉圈曲率半径从______变化到_____。
12、某点P的大地纬度B=30°,则该点法线与短轴的交点离开椭球中心的距离为_____。
13、高斯投影中,_____投影后长度不变,而投影后为直线的有_____,其它均为凹向_____的曲线。
14、大地线克莱劳方程决定了大地线在椭球面上的_______;在椭球面上某大地线所能达到的最大纬度为60°,则该大地线穿越赤道时的大地方位角表达式为_____(不用计算出数值)。
gps期末复习试题库及答案

一、填空1、RTK 数据链发送的是基准站载波相位观测量和坐标。
2、码相位测量测定的是测距码从卫星到接收机的传播时间。
3、采用后处理星历代替广播星历可减弱卫星星历误差影响。
4、双差模型可消除接收机钟差误差影响。
5、电离层影响,白天是晚上的 5 倍。
6、电离层影响,夏天是冬天的 4 倍。
7、电离层影响在一天中的中午最强。
8、对流层影响与温度、气压和湿度有关。
9、卫星信号由多条路径到达接收机而引起的误差叫多路径误差。
10、测站点远离水面,以避免多路径误差影响。
11、抑径板可减弱多路径误差影响。
12、抑径板是通过遮挡反射信号来减弱多路径误差的。
13、各接收机定向标志同时朝北,可消除相位中心偏影响。
14、点位误差随精度衰减因子的增大而增大。
15、精度衰减因子用英文缩写 DOP 表示。
16、HDOP 表示水平位置精度衰减因子。
17、PDOP 表示空间位置精度衰减因子。
18、精度衰减因子与卫星的空间分布有关。
19、两同步观测的测站上的单差相减叫双差。
20、实时伪距差分定位也叫 RTD 。
21、实时载波相位差分定位也叫 RTK 。
22、参考站向流动站发射差分信号。
23、差分定位有数据链相对定位没有。
24、97 规程规定的四等 GPS 基线的固定误差是 10mm 。
25 、97 规程规定的四等 GPS 基线的比例误差系数是10ppm 。
26、网中的三个已知点坐标可用来解算大地坐标转换的7 个参数。
27、由同步观测基线构成的闭合环叫同步环。
28、由非同步观测基线构成的闭合环叫异步环。
29、五台接收机同步观测的基线数为 10 。
30、五台接收机同步观测的独立基线数为 4 。
31、同步图形扩展方式有点连式、边连式和网连式。
32、相邻两个同步图形有 2 个公共点的连接收方式叫边连式。
33、GPS 网测量中所用接收机必须具有载波相位观测功能。
34、四等 GPS 网的重复设站数应不少于 1.6 。
35、97 规程规定,各等级 GPS 网观测时, PDOP 宜小于 6 。
GNSS原理及测试方案

GNSS原理及测试方案GNSS(全球导航卫星系统)是一种通过卫星信号提供地理定位和导航的技术,包括美国的GPS、俄罗斯的GLONASS、欧洲的Galileo和中国的北斗系统等。
GNSS的原理是基于卫星发射的微波信号,接收器通过测量卫星信号的时间差和多普勒效应,来计算出接收器的位置、速度和时间。
首先,GNSS接收器通过接收卫星发射的信号来确定接收器所处的位置。
每颗卫星都会向地球发送一个包含时间和卫星位置信息的信号。
GNSS接收器接收到至少4颗卫星的信号后,可以通过三边测量法来确定接收器的位置。
三边测量法是通过测量信号从卫星发射到接收器的时间差,来计算出接收器到卫星的距离。
通过多边测量法的组合,可以得到接收器的三维坐标。
其次,GNSS接收器利用多普勒效应来计算速度。
多普勒效应是当信号源和接收器之间相对运动时,会导致信号的频率发生变化。
GNSS接收器通过测量卫星信号的频率变化,可以计算出接收器的速度。
最后,GNSS接收器可以通过卫星信号的时间戳来同步接收器的本地时间。
每个卫星都使用精确的原子钟来进行时间计量。
接收器接收到多个卫星的时间信号后,可以通过插值的方法来计算出接收器的本地时间。
在测试GNSS性能时,通常需要考虑以下几个方面:1.精准性和准确性测试:测试GNSS接收器的定位精度和速度准确度。
这可以通过在已知位置上放置参考接收器,并比较其测量结果来实现。
2.接收性能测试:测试GNSS接收器在不同环境条件和信号干扰下的性能表现。
这可以通过在开放地区、城市、森林等不同场景中进行测试,观察接收器在复杂环境中的表现。
3.位置更新速度测试:测试GNSS接收器在移动状态下的位置更新速度。
这可以通过将接收器安装在车辆或无人机上,并观察接收器的定位速度和精度来实现。
4.功耗测试:测试接收器的功耗,以评估其在不同供电条件下的可持续使用时间。
5.单点位置测试:将接收器放置在一个固定位置上,观察其在不同时间段内的定位精度和稳定性。
Trilateration三边测量定位算法
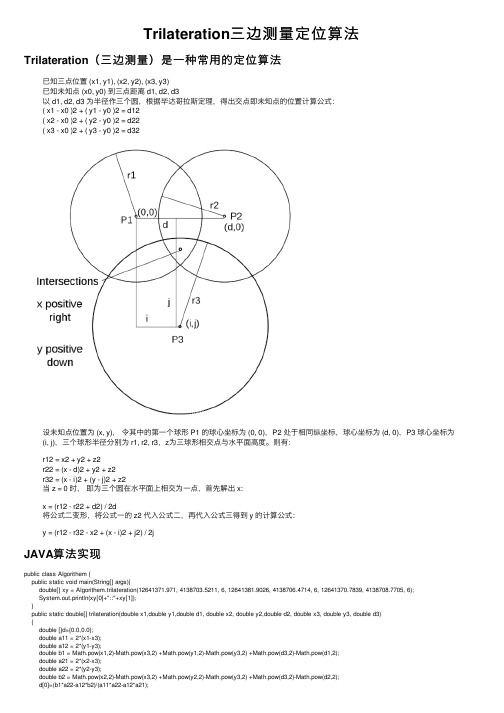
Trilateration三边测量定位算法Trilateration(三边测量)是⼀种常⽤的定位算法已知三点位置 (x1, y1), (x2, y2), (x3, y3)已知未知点 (x0, y0) 到三点距离 d1, d2, d3以 d1, d2, d3 为半径作三个圆,根据毕达哥拉斯定理,得出交点即未知点的位置计算公式:( x1 - x0 )2 + ( y1 - y0 )2 = d12( x2 - x0 )2 + ( y2 - y0 )2 = d22( x3 - x0 )2 + ( y3 - y0 )2 = d32设未知点位置为 (x, y),令其中的第⼀个球形 P1 的球⼼坐标为 (0, 0),P2 处于相同纵坐标,球⼼坐标为 (d, 0),P3 球⼼坐标为(i, j),三个球形半径分别为 r1, r2, r3,z为三球形相交点与⽔平⾯⾼度。
则有:r12 = x2 + y2 + z2r22 = (x - d)2 + y2 + z2r32 = (x - i)2 + (y - j)2 + z2当 z = 0 时,即为三个圆在⽔平⾯上相交为⼀点,⾸先解出 x:x = (r12 - r22 + d2) / 2d将公式⼆变形,将公式⼀的 z2 代⼊公式⼆,再代⼊公式三得到 y 的计算公式:y = (r12 - r32 - x2 + (x - i)2 + j2) / 2jJAVA算法实现public class Algorithem {public static void main(String[] args){double[] xy = Algorithem.trilateration(12641371.971, 4138703.5211, 6, 12641381.9026, 4138706.4714, 6, 12641370.7839, 4138708.7705, 6);System.out.println(xy[0]+"::"+xy[1]);}public static double[] trilateration(double x1,double y1,double d1, double x2, double y2,double d2, double x3, double y3, double d3){double []d={0.0,0.0};double a11 = 2*(x1-x3);double a12 = 2*(y1-y3);double b1 = Math.pow(x1,2)-Math.pow(x3,2) +Math.pow(y1,2)-Math.pow(y3,2) +Math.pow(d3,2)-Math.pow(d1,2);double a21 = 2*(x2-x3);double a22 = 2*(y2-y3);double b2 = Math.pow(x2,2)-Math.pow(x3,2) +Math.pow(y2,2)-Math.pow(y3,2) +Math.pow(d3,2)-Math.pow(d2,2);d[0]=(b1*a22-a12*b2)/(a11*a22-a12*a21);d[1]=(a11*b2-b1*a21)/(a11*a22-a12*a21);return d;}}D3.js实现定义三个圆的坐标及半径,计算出交点的坐标 (obj_x, obj_y).var x_0 = 150, y_0 = 150;var x_1 = x_0, y_1 = y_0, d = 150, x_2 = x_0 + d, x_3 = 225, y_3 = 315, r = 100;var i = x_3 - x_0, j = y_3 - y_0;var x = (Math.pow(r, 2) - Math.pow(r, 2) + Math.pow(d, 2)) / (2 * d) + x_0;var obj_x = x + x_0;var y = (Math.pow(r, 2) - Math.pow(r, 2) - Math.pow(x, 2) + Math.pow((x - i), 2)+ Math.pow(j, 2)) / (2 * j);var obj_y = y + y_0;绘出圆形及交点:svg.append("circle").attr("cx", x_1).attr("cy", y_1).attr("r", r).style("fill", "blue").style("opacity", 0.3);svg.append("circle").attr("cx", x_2).attr("cy", y_0).attr("r", r).style("fill", "red").style("opacity", 0.4);svg.append("circle").attr("cx", x_3).attr("cy", y_3).style("opacity", 0.5).attr("r", r).style("fill", "yellow");svg.append("circle").attr("cx", obj_x).attr("cy", obj_y).attr("r", 3).style("fill", "red");多于⽤实现定位算法,与之相同的也许还可以采⽤K-Means或Overlap聚类算法,后两者在地图标注上使⽤⽐较⼴。
三边测量法的MATLAB定位程序说明

% 1.参考节点A(xa,ya),B(xb,yb),C(xc,yc)% 2.定位节点D(locx,locy)到这三点的距离分别为da,db,dc%返回:% (locx,locy)为计算的定位节点D点的位置坐标%syms x y %f符号变量%--------------求解方程组------------------------------------f1='2*x*(xa-xc)+xc^2-xa^2+2*y*(ya-yc)+yc^2-ya^2=dc^2-da^2';f2='2*x*(xb-xc)+xc^2-xb^2+2*y*(yb-yc)+yc^2-yb^2=dc^2-db^2';[xx,yy]=solve(f1,f2,x,y); %解关于x,y的符号方程组,得到解的符号表示,并存入xx,yypx=eval_r(xx); %解的数值px(1),px(2)py=eval_r(yy); %解的数值py(1),py(2)locx=px;locy=py;%二、m函数find_three_p.m文件内容function [xa,ya,xb,yb,xc,yc]=find_three_p(x,y)%从N点中随机选出不同的三点% 输入:x,y是N点的坐标%输出:xa,ya,xb,yb,xc,yc% 为选出的任意三点的坐标len=length(x);% 取一点t=fix(len*rand(1,1))+1;ma=t;xa=x(t);ya=y(t);%取第二点while(1)t=fix(len*rand(1,1))+1;if(t~=ma)mb=t;xb=x(t);yb=y(t);break;endend%取第三点while(1)t=fix(len*rand(1,1))+1;if (t~=ma)&&(t~=mb) mc=t;xc=x(t);yc=y(t);break;endend%三、主文件locac3.m文件内容%*********locac3.m****************%---采用三边定位法对未知节点定位---------clear;len=1000; %参考节点数maxx=1000;%参考节点分布的最大横坐标maxy=1000;%参考节点分布的最大纵坐标%------参考点[cx,cy]-----------------cx=maxx*rand(1,len);cy=maxy*rand(1,len);plot(cx,cy,'k^');%参考节点图%--------未知节点(mx,my)-----------mlen=200; %未知点数mx=maxx*rand(1,mlen);my=maxy*rand(1,mlen);hold on;plot(mx,my,'go'); %盲节点图%---------定位估计----------------------wucha_p=0.00001; %定位误差for p=1:mlen %对每个未知盲节点[xa,ya,xb,yb,xc,yc]=find_three_p(cx,cy); %从参考点中任意选出三点 da=sqrt((mx(p)-xa)^2+(my(p)-ya)^2);db=sqrt((mx(p)-xb)^2+(my(p)-yb)^2);dc=sqrt((mx(p)-xc)^2+(my(p)-yc)^2);[locx(p),locy(p)]=triposition(xa,ya,da,xb,yb,db,xc,yc,dc); %计算定位坐标 plot(locx(p),locy(p),'r*');endlegend('参考节点','盲节点','定位节点','Location','SouthEast');title('三边测量法的定位');wdot=0;%统计定位正确的点数for p=1:mlendr(p)=sqrt((locx(p)-mx(p))^2+(locy(p)-my(p))^2);if dr(p)<wucha_pwdot=wdot+1;endenddisp('未知节点定位准确率:');wdot/mlen。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通信专业课程设计一太原科技大学课程设计(论文)设计(论文)题目:基于RSSI的三边测量法和分步定位法在ZigBee定位系统中的研究及比较姓名鲁骥学号 ************班级通信101501学院电子信息工程学院指导教师郑秀萍2013年 12 月 20 日太原科技大学课程设计(论文)任务书学院(直属系):电子信息工程学院时间: 2013年11月25日基于RSSI的三边测量法和分步定位法在ZigBee定位系统中的研究及比较摘要目前无线定位技术是Zigbee无线传感器网络研究的热点问题之一,随着定位需求与应用的增加,如何提高基于Zigbee技术的无线定位系统的定位精度是Zigbee无线传感器网络领域亟待解决的问题。
在三边测量法分析基础上,提出一种新型分步定位法。
通过利用待测移动节点最近的3个参考节点可快速计算出移动节点的坐标值,从而使定位算法更容易实现。
通过matlab 平台仿真,结果表明,分步定位法在不增加任何硬件成本的前提下可显著减小定位误差,提高定位精度。
与三边测量法相比,分步定位法可广泛应用于各种基于RSSI的定位场合。
关键词:ZigBee;RSSI( 接收信号强度指示);三边测量法;分步定位法目录摘要 (I)第1章绪论 (1)第2章基于RSSI算法的三边测量法和分步定位法 (2)2.1三边测量法和分步定位法概述 (2)2.2基于测距的RSSI算法 (2)2.2.1 RSSI算法原理 (2)2.2.2 RSSI算法原理的实现 (3)2.3基于RSSI的三边测量法和分步定位法 (3)2.3.1 基于RSSI的三边测量法 (3)2.3.2 基于RSSI的分步定位法 (4)第3章三边测量法和分步定位法仿真及分析比较 (6)3.1实验过程 (6)3.2实验结果分析 (8)3.3总结 (8)参考文献 (9)附录 (10)附录一:三边测量法仿真程序 (10)附录二:分步定位法仿真程序 (10)第1章绪论ZigBee 技术是短距离无线通信中的一种技术,人们已经利用它解决了许多实际的问题。
该技术具备很多优点和几个突出的优势:(1)低功耗。
ZigBee节点的电池工作时间可以维持半年到两年。
(2)低成本。
ZigBee技术不仅数据传输量小而且速率低,因此成本得到大幅度降低,另外ZigBee协议相对简单并且是免费的。
(3)高可靠性。
使用了CSMA/CA机制,避免数据发送时发生争用信道。
(4)低传输速率。
数据传输速率最大只有250kbit/s,最小是仅为lOkbit/s。
(5)大容量网络。
最多能够支持65000个节点。
(6)短时延性。
ZigBee设备搜索时延和通信时延都很短。
(7)安全性高。
提供AES(高级加密标准)-128加密算法,具备数据完整性认证功能。
以ZigBee无线传感为基础的无线传感网,在实际应用时经常需要对网络中存在的移动节点进行位置判断。
无线传感网不同于传统的无线定位系统,由于低功耗、低成本的要求,这种定位计算要求使用的网络通信开销尽可能小,对硬件设备的要求尽可能低。
因此需要一种针对ZigBee无线传感网络特点的定位算法来解决这个问题。
常用的基于ZigBee的定位算法分为:基于测距的定位算法和基于非测距的定位算法。
常用的基于测距的定位算法有:基于接收信号强度测量法(RSSI)、到达时间测量法(TOA)、到达时间差测量法(TDOA)和到达角度测量法(AOA)。
常用的基于非测距的定位算法有:质心算法、凸规划法、网络多跳路由算法(DV-hop)。
这两类算法各有优缺点:基于测距的定位算法精度较高,但是对硬件要求也高,功耗大,算法处理复杂,不适合大规模应用的 ZigBee 传感网络。
而基于非测距的定位算法较简单,实现成本低,相对而言功耗也低,非常适合大规模的应用的ZigBee无线传感网络,但是精度较低,对网络节点依赖度高。
其中,基于RSSI的三边测量法是定位技术的基本模块之一,三边测量法使得每个移动节点利用三个或三个以上的参考节点即可定位,但是定位精度不高。
分步定位算法只需要3个参考节点,定位精度比较好,但是在功耗和成本方面比较大,该算法避免了采用三边测量法可能无解的情况,使得其适应性更强。
本文研究了基于RSSI(Received Signal Strength Indication,接收的信号强度指示)的三边测量法和分步定位算法,并在MatLab平台对其进行研究及比较。
在相同条件下,分步定位算法可显著减小定位误差。
第2章基于RSSI算法的三边测量法和分步定位法2.1 三边测量法和分步定位法概述三边测量法是基于RSSI原理,选择三个或三个以上的参考节点,相互连接成若干个三角形,构成各种网(锁)状图形。
通过观测三角形的边长,再根据参考节点的坐标,起始边的边长和坐标方位角,经解算三角形和坐标方位角推算可得到三角形各边的边长和坐标方位角,进而有直角坐标正算公式计算移动节点的平面坐标。
分步定位算法是基于RSSI原理,通过利用待测移动节点最近的 3个参考节点可快速计算出移动节点的坐标值,从而使定位算法更容易实现实验结果表明,该方法在不增加任何硬件成本的前提下可显著提高定位精度并增强系统稳定性,同时降低环境噪声带来的测量误差与常规定位算法相比,该算法可广泛应用于各种基于距离的定位场合。
2.2基于测距的RSSI算法基于测距的定位技术需要测量参考节点到移动节点之间的距离,然后根据几何三边定位算法,两角一边定位算法计算移动节点坐标。
测量误差的大小将直接影响最后计算出的移动节点坐标。
基于非测距的定位技术在计算移动节点坐标时,不需要事先测量到参考节点的距离,而是通过移动节点与参考节点的网络拓扑关系来估算移动节点坐标。
这种方式由于少了距离测量这个步骤,对网络节点硬件要求大大降低。
但是由于是估算,定位精度一般不如基于测距的定位算法。
在节点定位中,涉及到两类重要的节点,即参考节点和移动节点。
它们的本质区别在于节点在加入网络之前能否知道自己的坐标位置,参考节点是知道的,而移动节点不知道,移动节点只能借助参考节点和网络中其它的参数来计算自己的坐标位置。
2.2.1 RSSI算法原理RSSI(Received Signal Strength Indication,接收的信号强度指示)是指网络中的移动节点通过测量来自静态的参考节点信号的信号强度来确定自身位置的一种算法。
由移动节点发送定位请求,RF通信范围内接收到定位请求的参考节点自动回应移动节点。
移动节点在能够接收到回应信号中选择三个信号强度最大的信号,提取信号强度并且根据强度判断出自己与系统中三个参考节点之间的距离。
移动节点的轨迹就是以参考节点为圆心,以两种节点之间的距离为半径的圆周上。
三个参考节点就可以确定三条动态轨迹,三条动态轨迹的交点就是移动节点。
该定位算法的基本原理如图2.1所示。
其中SN是参考(静态)节点,DN是移动(动态)节点,r是移动节点到对应参考节点的距离,移动节点的位置就是三个圆的交点。
图2.1 RSSI定位算法示意图2.2.2 RSSI算法原理的实现zigbee定位系统采用基于RSSI的技术,定位系统由协调器节点,参考节点和移动节点组成。
协调器节点用串口线与PC连接,负责将接收到的信息发送到PC处理。
移动节点从参考节点处接收数据包信号,获得参考节点位置坐标及相应的RSSI值并将其送入定位引擎,然后可以读出由定位引擎计算得到的自身位置。
由参考节点发送给移动节点的数据包至少包含参考节点的坐标参数(X,Y),而RSSI值可由接收节点计算获得。
RSSI的理论值可表示为:RSSI=−(10n∙lgd+A) (2−1)式2-1中,射频参数 A和n用于描述网络工作环境。
在全向模式下,射频参数A被定义为以 dBm(分贝毫瓦)为单位表示的距发射端 1m处接收到的信号强度绝对值。
如信号强度为-40dBm,那么参数n被定为40定位引擎的期望。
参数 A 为30.0~50.0,精度为0.5。
A的一个典型值为 40.0。
d 为节点之间的距离。
n的取值范围为15~25。
2.3基于RSSI的三边测量法和分步定位法2.3.1 基于RSSI的三边测量法三边测量法的原理如下图2.2所示,以三个节点A、B、C为圆心作圆,坐标分别为(X a,Y a),(X b,Y b),(X c,Y c),这三个圆周相交于一点D,交点D即为移动节点,A、B、C即为参考节点,A、B、C与交点D的距离分别为d a,d b,d c。
假设交点D的坐标为(X,Y)。
图2.2 三边测量法示意图{√(X−X a)2+(Y−Y a)2=d a√(X−X b)2+(Y−Y b)2=d b√(X−X c)2+(Y−Y c)2=d c(2−2)由式2-2可以得到交点D的坐标为:(XY)=(2(X a−X c) 2(Y a−Y c)2(X b−X c) 2(Y b−Y c))−1(X a2−X c2+Y a2−Y c2+d c2−d a2X a2−X c2+Y b2−Y c2+d c2−d b2) (2−3)三边测量法的缺陷是:由于各个节点的硬件和功耗不尽相同,所测出的距离不可能是理想值,从而导致上面的三个圆未必刚好交于一点,在实际中,肯定是相交于一个小区域,因此利用此方法计算出来的(X,Y)坐标值存在一定的误差。
这样就需要通过一定的算法来估计一个相对理想的位置,作为当前移动节点坐标的最优解。
2.3.2 基于RSSI的分步定位法分步定位法测量原理如图2.3所示:图2.3 分步定位法测量原理图分步定位法的步骤如下:1.分别以参考节点 A ,B 为圆心,以测得的参考节点与移动节点之间的距离RA ,RB为半径画圆,这两圆的位置可能出现以下3种情况: 两圆相离,没有交点;两圆相切,有一个交点; 两圆相交,有两个交点。
2.两圆相离时,则判定以参考节点A ,B 为圆心,定位出的移动节点O 的AB 相关位置OAB 在线段AB 上,且两线段长度|AOAB|:|OABB|=RA :RB ;当两圆相切时,则判定以参考节点A ,B 为圆心,定位出的移动节点 O 的AB 相关位置 OAB 就是该切点; 当两圆相交时,则根据参考节点C 的坐标和RC 作方向参考,可以确定出其中一个交点为相对合适的移动节点O 的AB 相关位置OAB 。
3.再分别以参考节点A ,C 为圆心,参考节点B ,C 为圆心,重复步骤1,2可分别确定出移动节点O 的AC 相关位置OAC ,以及移动节点O 的BC 相关位置OBC 。
4.理想状态下OAB ,OAC ,OBC 相交于一点,则该交点即为移动节点O 的实际位置坐标。
5.当OAB (X AB ,Y AB ),OAC (X AC ,Y AC ),OBC (X BC ,Y BC )不重合时,求出△OABOACOBC 的中心坐标作为移动节点O (X,Y )的实际位置坐标。
