宜宾市高新2010级一诊考试参考答案(理科)
2010年高考完整版-理综(化学_物理生物)试题及答案-(四川卷)

的体积分数 y(M)与反应条件的关系如图所示。其中:Z 表 示反应开始时 N 的物质的量与 M 的物质的量之比。 下列说 法正确的是 A.同温同压 Z 时,加入催化剂,平衡时 Q 的体积分数增加 B.同压同 Z 时,升高温度,平衡时 Q 的体积分数增加 C.同温同 Z 时,增加压强,平衡时 Q 的体积分数增加 D.同温同压时,增加 Z,平衡时 Q 的体积分数增加。 答案:B 解析:本题考查了平衡移动原理的应用。A 项加入催化剂只能改变反应速率,不会使平衡移 动。B 项由图像(1)知随着温度的升高 M 的体积分数降低,说明正反应吸热,所以温度升 高平衡正向移动,Q 的体积分数增加。C 项对比(1) (2)可以看出相同温度条件,压强增 大 M 的体积分数增大,所以正反应是体积缩小的反应,增大压强 Q 的体积分数减小。D 项 由 C 项可以判断 D 也不对。 二、选择题(本题共 4 小题。在每小题给出的四个选项中,有的只有一个选项正确,有的有 多个选项正确,全部选对的得 6 分,选对但不全的得 3 分,有选错的得 0 分。 ) 14.下列现象中不能说明分子间存在分子力的是 A.两铅块能被压合在一起 C.水不容易被压缩 【答案】D 【解析】 空气容易压缩是因为分子间距大, 而水不容易压缩是因为分子间距小轻微压缩都使 分子力表现为斥力。ABC 说明存在分子力。 15.下列说法正确的是 A.α 粒子大角度散射表明α 粒子很难进入原子内部 B. 氨原子跃迁发出的光从空气射入水时可能发生全反射 C. 裂变反应有质量亏损,质量数不守恒 D.γ 射线是一种波长很短的电磁波 【答案】 D 【解析】α 粒子的散射学习现象表明大多数 α 粒子不发 生偏转,说明穿过了原子,少数 α 粒子发生偏转,说明 B.钢绳不易被拉断 D.空气容易被压缩
[键入文字]
2019年12月7日四川省宜宾市高2020届高2017级一诊考试理科综合试题化学参考答案宜宾一诊

2019年12月7日四川省宜宾市高2020届高2017级一诊考试理科综合试题化学参考答案宜宾一诊诊一宾宜四川省宜宾市高2020届高2017级高三一诊化学参考答案题号78910111213答案C C B D D A B26.(14分)(1)第二周期IVA族(2分)(2)A(2分)(3)AD(2分)(4)2Mn2++5S2O82-+8H2O2MnO4-+10SO42-+16H+(2分)>(2分)(5)+3(2分)MnO·4ZnO·5Fe2O3(2分)27.(14分)(1)250mL容量瓶(1分)(2)冰水浴(2分)(3)防止因NaClO溶液过量,将生成的水合肼氧化,降低产率(2分)(4)B(1分)C(1分)(5)①酸式(1分)溶液由无色变蓝色且半分钟内颜色不再变化(2分)②N2H4·H2O+2I2=N2↑+4HI+H2O(2分)③50.0(2分)28.(15分)(1)-744kJ·mol-1(2分)低温(1分)(2)①0.01mol·L-1·min-1(2分)②5(2分)不(2分)③AC(2分)(3)①D(2分)②尚未达到催化剂工作温度(或尚未达到反应的温度)(2分)35.(15分)(1)增大接触面积,加快反应速率,提高浸取率(2分)(2)做还原剂,将MnO2和Fe3+还原(2分)SiO2(1分)(3)H2O2+2Fe2++4H+=2Fe3++2H2O、H2O2+SO2=2H ++SO42-(2分)(4)将Fe3+、Al3+完全沉淀,Mn2+不沉淀(2分)(5)防止NH4HCO3分解(2分)(NH4)2SO4(2分)(6)1.05(2分)。
四川省成都市高中2010届高三一诊(数学理)word版

3. 在等差数列 {an } 中, a1 + a2 = 3, a2 + a5 = 5 ,则公差为 d 的值为
久赢屋-高中学习网
C、3 D、4
A、1
B、2
4. 已知 α、β 、γ 是三个不同的平面,则下令命题正确的是 A、若 α ⊥ γ , β ⊥ γ , 则α // β B、若 β // α , γ // α , 则β // γ C、若 α、β 、γ 两两相交,则交线互相平行 D、若 α 与 β 、 γ 所成的锐二面角相等,则 β // γ
1 ,假定每次射击是否击中目标相互之间没有影响。 5
(I)若该射手用这 3 支已经试射校正过的枪各射击一次,求目标被击中的次数为奇数的 概率; (II)若该射手用这 4 支抢各射击一次,设目标被击中的次数为 ξ ,求随机变量 ξ 的分布 列和数学期望 Eξ 。
w. w . ^w .k . s.5* u . c.# o@m
w . w. ^w . k. s .5* u. c .#o@m
B、3957
C、3959
D、3961
久赢屋-高中学习网
第 II 卷
注意事项: 1. 用钢笔或圆珠笔直接答在试题卷中。 2. 答卷前将密封线内的项目填写清楚。 3. 本卷共 10 小题,共 90 分。 二、填空题:本大题共 4 小题,每小题 4 分,共 16 分。把答案填在题中横线上。 13. 已知 a ∈ ( 0, π ) , cos (π + a ) =
是 A、 ⎢ 0, ⎥ 8 C、 ⎢ −1, ⎥ 8
⎡ 1⎤ ⎣ ⎦ ⎡ ⎣ 1⎤ ⎦
B、 [ −1, 0) ∪ (0, ]
重庆市高2010级高三上期一诊考试题(数学理)
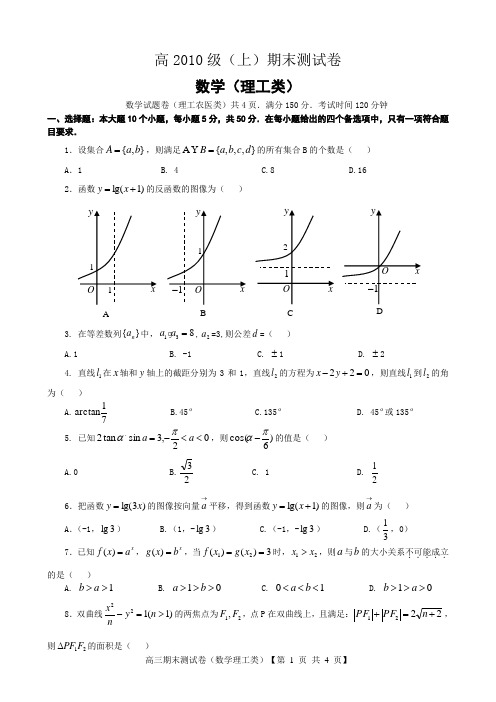
高2010级(上)期末测试卷数学(理工类)数学试题卷(理工农医类)共4页.满分150分.考试时间120分钟一、选择题:本大题10个小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项符合题目要求.1.设集合},{b a A =,则满足},,,{A d c b a B = 的所有集合B 的个数是( ) A . 1 B. 4 C.8 D.162.函数)1lg(+=x y 的反函数的图像为( )3. 在等差数列}{n a 中,138a a =,2a =3,则公差d =( )A.1B. -1C. ±1D. ±24. 直线1l 在x 轴和y 轴上的截距分别为3和1,直线2l 的方程为022=+-y x ,则直线1l 到2l 的角为( )A.71arctanB.45C.135D. 45 或135 5. 已知αtan 2.02,3sin <<-=a a π,则)6cos(πα-的值是( ) A.0 B.23C. 1D. 216.把函数)3lg(x y =的图像按向量→a 平移,得到函数)1lg(+=x y 的图像,则→a 为( ) A .(-1,3lg ) B.(1,-3lg ) C.(-1,-3lg ) D.(31,0) 7.已知xa x f =)(,xb x g =)(,当3)()(21==x g x f 时,21x x >,则a 与b 的大小关系不可能成立.....的是( )A. 1>>a bB. 01>>>b aC. 10<<<b a D. 01>>>a b8.双曲线)1(122>=-n y nx 的两焦点为21,F F ,点P 在双曲线上,且满足:2221+=+n F P F P ,ABCDA .1B .21C .2D .4 9.称→→→→-=b a b a d ),(为两个向量→a 、→b 间的“距离”.若向量→a 、→b 满足:①1=→b ;②→→≠b a ;③对任意的R t ∈,恒有),(),(→→→→≥b a d b t a d 则( )A .→→⊥b a B.)(→→→-⊥b a a C. )(→→→-⊥b a b D. )()(→→→→-⊥+b a b a10.关于x 的方程0)1(122=++++b xx a x x 有实数根,则22b a +的最小值是( ) A .52B .1C .54D .52二、填空题:(本大题共5个小题,共25分,把答案填写在答题卡相应位置上)11.抛物线022=+y x 的焦点坐标是________ ____. 12.不等式2log 12>+x 的解集是____ ________.13.已知正数x 、y 满足⎩⎨⎧≥+-≤-05302y x y x ,则x z )41(=.y)21(的最小值为__________.14.已知数列}{n a 满足,11,211221++-==-n na n n a a n n 则数列}{n a 的通项n a =__________ . 15 如图,一条螺旋线是用以下办法画成:ABC ∆是边长为1的正三角形,曲线32211,,A A A A CA 分别以A 、B 、C 为圆心,AC 、1BA 、2CA 为半径画弧,曲线321A A CA 称为螺旋线旋转一圈.然后又以A 为圆心3AA 为半径画弧,这样画到第n 圈,所得的螺旋线的长度n l =_____ _____.(用π表示即可)三、解答题:(本大题共6个小题,共75分)(各题解答必须写出必要的文字说明、演算步骤和推理过程).16.(本小题满分13分)已知向量)4,3(-=−→−OA ,)3,6(-=−→−OB ,)3,5(m m OC ---=−→−.(Ⅰ)若C B A ,,三点共线,求实数m 的值; (Ⅱ)若ABC ∠为锐角,求实数m 的取值范围.已知函数)0,0(cos sin cos 2)(2>>+=b a x x b x a x f ,)(x f 的最大值为a +1,最小值为21-. (Ⅰ)求)(x f 的最小正周期;(Ⅱ)求)(x f 的单调递增区间.18.(本小题满分13分) 已知数列}{n a 中,11=a ,113--⋅=n n n a a ).,2(*N n n ∈≥数列}{nb 的前n 项和))(9(log *3N n a S n n n ∈=. (Ⅰ)求数列}{n b 的通项公式;(Ⅱ)求数列{}n b 的前n 项和.19.(本小题满分12分) 已知ax xa x f ---=2log )(2是奇函数.(Ⅰ)求a 的值;(Ⅱ)若关于x 的方程x m x f --⋅=2)(1有实解,求m 的取值范围.已知点)1,1(A 是椭圆)0(12222>>=+b a b y a x 上一点,21,F F 是椭圆的两焦点,且满足421=+AF AF .(Ⅰ)求椭圆的两焦点坐标;(Ⅱ)设点B 是椭圆上任意一点,如果AB 最大时,求证A 、B 两点关于原点O 不对称; (Ⅲ)设点C 、D 是椭圆上两点,直线AC 、AD 的倾斜角互补,试判断直线CD 的斜率是否为定值?若是定值,求出定值;若不是定值,说明理由.21.(本小题满分12分)已知曲线C :1xy =过C 上一点(n n A x ,)n y 作一斜率21+-=n n x k 的直线交曲线C 于另一点11(n n A x ++,1)n y +,点列*()n A n N ∈的横坐标构成数列}{n x ,其中7111=x . (Ⅰ)求证:}3121{+-n x 是等比数列; (Ⅱ)求证:23123(1)(1)(1)x x x -+-+-+…*(1)1()n n x n N +-<∈.。
四川省成都市高中2010届高三一诊(数学理)word版

四川省成都市高中2010届高三一诊(数学理)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
第I 卷1至2页,第II 卷3至8页,考试结束后,将本试卷和答题卡一并交回。
全卷满分为150分,完成时间为120分钟。
第I 卷注意事项:1. 答第I 卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题看上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3. 本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A B 、互斥,那么 球的表面积公式24S R π=()()()P A B P A P B +=+其中R 表示球的半径如果事件A B 、相互独立,那么 球的体积公式243V R π=()()()P A B P A P B ⋅=⋅其中R 表示球的半径如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生在k 次的概率:()()1n kkk n n P k C P P -=⋅-()0,1,2k n =⋅⋅⋅一、选择题:1. 已知集合{}{}1,0,1,|12M N x x =-=-<<,则M N =A 、{}1,0,1-B 、{}0,1C 、{}1,0-D 、{}12. 设复数121,2z i z i =+=-在复平面内对应的点分别是12,,Z Z 则12,Z Z 两点间的距离为A 、4B 、C 、3D 3. 在等差数列{}n a 中,12253,5a a a a +=+=,则公差为d 的值为A 、1B 、2C 、3D 、44. 已知αβγ、、是三个不同的平面,则下令命题正确的是 A 、若,,//αγβγαβ⊥⊥则 B 、若//,//,//βαγαβγ则C 、若αβγ、、两两相交,则交线互相平行D 、若α与β、γ所成的锐二面角相等,则//βγ5. 将函数tan 23y x π⎛⎫=+⎪⎝⎭的图象按向量,112a π⎛⎫=⎪⎝⎭平移,则平移后所得图象的解析式为A 、tan 214y x π⎛⎫=+- ⎪⎝⎭B 、tan 216y x π⎛⎫=+- ⎪⎝⎭C 、tan 214y x π⎛⎫=++ ⎪⎝⎭D 、tan 216y x π⎛⎫=++ ⎪⎝⎭6. 在ABC ∆中,2,1,AB AC BD DC ===,则AD BD ⋅的值为A 、23-B 、23C 、34-D 、347. 若log a b 有意义,则“log 0a b <”是“()()110a b --<”的 A 、充分不必要条件 B 、必要不充分条件C 、充要条件D 、既不充分也不不要条件8. 设随机变量ξ服从正态分布2(2,2)N ,则()23P ξ<<可以被表示为A 、()11P ξ-<B 、()1212P ξ-<C 、()01P ξ<<D 、()112P ξ+< 9. 为预防和控制甲流感,某学校医务室欲将23支相同的温度计分发到高三年级10个班级中,要求分发到每个班级的温度计不少于2支,则不同的分发方方式共有 A 、120种 B 、175种 C 、220种 D 、820种 10.已知定义在R 上奇函数()f x 满足()()11f x f x +=-且()f x 在区间[]3,5上单调递增,则函数()f x 在区间[]1,3上的A 、最大值是()1f ,最小值是()3fB 、最大值是()3f ,最小值是()1fC 、最大值是()1f ,最小值是()2fD 、最大值是()2f ,最小值是()3f11. 已知关于x 的方程112042xxa ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭在区间[]1,0-上有实数根,则实数a 的取值范围是A 、10,8⎡⎤⎢⎥⎣⎦B 、1[1,0)(0,]8-C 、11,8⎡⎤-⎢⎥⎣⎦D 、[]1,0-12. 把正整数排列成三角形数阵(如图甲),然后擦去第偶数行中的奇数和第奇数行中的偶数,得到新的三角形数阵(如图乙),再把图乙中的数按从小到大的顺序排成一列,得到一个数列{}n a ,则2010a =A 、3955B 、3957C 、3959D 、3961第II 卷注意事项:1. 用钢笔或圆珠笔直接答在试题卷中。
四川省宜宾市2025届高三第一次诊断性测试物理试题(含答案)

四川省宜宾市2025届高三第一次诊断性测试物理试题(考试时间: 75分钟 ; 全卷满分 : 100分) 2024.11注意事项:1.答卷前,考生务必将自己的考号、姓名、班级填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将答题卡交回。
第Ⅰ卷(非选择题,共43分)一、单项选择题:本题共7小题,每小题4分,共28分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.中国空间站已于2022年全面建成,支持长期载人在轨飞行,进行空间科学研究和技术试验,是中国空间探索的重要里程碑。
若该空间站仅在地球引力作用下,绕地球沿椭圆轨道运动,则运动过程中不变的物理量是A.机械能B.动能C.加速度D.动量2.伽利略为了研究自由落体的规律,采用“冲淡”重力的方法,测量了铜球在较小倾角斜面上运动的位移和时间,发现位移与时间的平方成正比。
增大斜面倾角,该规律仍然成立。
于是,他外推到斜面倾角为90°时,就得到了自由落体运动的规律。
下列说法正确的是A. “冲淡”重力是指使铜球的重力变小了B.铜球位移与时间的平方成正比能说明铜球做匀加速直线运动C.伽利略对倾角为90°时的实验情况进行了相关数据的准确测量D.伽利略通过“斜面实验”来研究落体运动规律是为了便于测量速度3.如图甲是夏季常出现的日晕现象,日晕是太阳光通过卷层云时,受到冰晶的折射或反射形成的。
图乙为一束太阳光射到六角形冰晶上的光路图,a、b为其折射出的光线中的两种单色光,比较a、b两种单色光,下列说法正确的是A. b光比a光更容易发生明显衍射现象B.在冰晶中,a光的波速与b光的波速一样大C.通过同一装置发生双缝干涉,a光的相邻明条纹间距较大D. a、b两种光分别从水射入空气发生全反射时,a光的临界角比b光的小4.两玩具车在两条平行的车道上同向行驶,t=0时两车都在同一计时线处,它们在四次比赛中的2-t图像如图所示。
2021届宜宾一诊 理科数学试题(含答案)
合要求的.1.复数4i3i21-+的值为A.i 5251--B.i 5251+-C.i 5251- D.i 5251+2.命题“R x ∈∀,0522≥+-x x ”的否定是A.R x ∈∀,0522≤+-x x B.R x ∈∀,0522<+-x x C.R x ∈∃0,052020<+-x x D.R x ∈∃0,052020≤+-x x 3.已知集合{}0432<--=x x x A ,{}0>=x x B ,则=B A A.{}40<<x x B.{}01<<-x x C.{}41<<-x x D.{}4<x x 4.某团支部随机抽取甲乙两位同学连续9期“青年大学习”的成绩(单位:分),得到如图所示的成绩茎叶图,关于这9期的成绩,则下列说法正确的是A.甲成绩的平均数高于乙成绩的平均数B.乙成绩的极差为40C.甲乙两人成绩的众数相等D.甲成绩的中位数为325.符号><x 表示大于或等于x 的最小整数,在下图中输入的b a ,依次为0.3-和1.4,则输出的是一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符(考试时间:120分钟全卷满分:150分)理科数学2021届宜宾“一诊”A.0.3B.0.4C.0.6D.0.76.如图,ABC ∆是等边三角形,ADC ∆是等腰直角三角形,︒=∠90ADC ,线段BD AC ,交于点O ,设=BC a ,=BA b ,用a ,b 表示OD 为A.=OD b a 6363+B.=OD b a 3333+-C.=OD b a 6363+-D.=OD b a 3333+7.若51()a x x-展开式中所有项的系数和为1,则其展开式中x 的系数为A.2- B.10- C.16- D.80-8.函数()sin cos f x x x x =-+部分图象大致形状为AB C D9.已知52cos 3sin =-αα,则=+++)6cos()32sin(παπαA.54-B.52-C.0D.5210.《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半。
高中2010级绵阳一诊数学文科答案
绵阳市高2010级第一次诊断性考试数学(文)参考解答及评分标准一、选择题:本大题共12小题,每小题5分,共60分.BCCAD DABAC DB二、填空题:本大题共4小题,每小题4分,共16分.13.0 14.500 15.a =-1(答案不唯一)16.②⑤三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.17.解:由⎩⎨⎧≠->-123023x x ,解得32>x 且x ≠1,即A ={x |32>x 且x ≠1}, 由x-21≥1解得1≤x <2,即B ={x |1≤x <2}. ………………………………4分 (1)于是R A ={x |x ≤32或x =1},所以(R A )∩B ={1}. ……………………7分 (2)∵ A ∪B ={x |32>x },即C ={x |32>x }. 由|x -a |<4得a -4<x <a +4,即M ={x |a -4<x <a +4}.∵ M ∩C =∅,∴ a +4≤32,解得a ≤310-.…………………………………………………12分 18.解:(1)∵ A 班的5名学生的平均得分为(5+9+9+9+9)÷5=8, 方差4.2])89()89()89()88()58[(512222221=-+-+-+-+-=S ;B 班的5名学生的平均得分为(6+7+8+9+10)÷5=8, 方差2])108()98()88()78()68[(512222222=-+-+-+-+-=S .∴ S 12>S 22,∴ B 班的预防知识的问卷得分要稳定一些.…………………………………8分(2)共有1025=C 种抽取样本的方法, 其中样本6和7,6和8,8和10,9和10的平均数满足条件, 故所求的概率为52104=.………………………………………………………12分 19.解:(1)设{a n }的公差为d ,由题设有⎪⎪⎩⎪⎪⎨⎧=⨯⨯+=⨯⨯+.440219202012029101011d a d a ,解得a 1=3,d =2.……………………………………5分 a n =a 1+(n -1)d =3+(n -1)×2=2n +1,即{a n }的通项公式为a n =2n +1. ………………………………………………6分(2)由)2(2)123(+=++=n n n n S n ,得)2(11+=n n S n , ……………………8分 ∴ T n )2(1531421311+++⨯+⨯+⨯=n n )21151314121311(21+-++-+-+-=n n )2111211(21+-+-+=n n , =)2(21)1(2143+-+-n n . …………………………………………………12分 20.解:(1)令y =f (x )=a x +2-1,于是y +1=a x +2,∴ x +2=log a (y +1),即x =log a (y +1)-2,∴ )(1x f -=log a (x +1)-2(x >-1).………………………………………………3分(2)当0<a <1时,)(1x f -ma x =log a (0+1)-2=-2,)(1x f -min =log a (1+1)-2=log a 2-2,∴ -2-(2log a -2)=2,解得22=a 或22-=a (舍). 当a >1时,)(1x f -ma x =log a 2-2,)(1x f -min =-2,∴ 2)2()22(log =---a ,解得2=a 或2-=a (舍).∴ 综上所述,22=a 或2=a .……………………………………………7分 (3)由已知有log a 1-x a ≤log a (x +1)-2, 即1log -x a a ≤21log ax a +对任意的]2131[,∈a 恒成立. ∵ ]2131[,∈a , ∴ 21ax +≤1-x a .① 由21ax +>0且1-x a >0知x +1>0且x -1>0,即x >1, 于是①式可变形为x 2-1≤a 3, 即等价于不等式x 2≤a 3+1对任意的]2131[,∈a 恒成立.∵ u =a 3+1在]2131[,∈a 上是增函数,∴2728≤a 3+1≤89,于是x 2≤2728, 解得9212-≤x ≤9212. 结合x >1得1<x ≤9212. ∴ 满足条件的x 的取值范围为⎥⎥⎦⎤ ⎝⎛92121,.…………………………………12分 21.解:(1)∵ a =1时,x x b x x f -+=23231(), ∴ 1)(2-+='x b x x f . 由题知21是方程012=-+x b x 的根,代入解得23=b , 于是123)(2-+='x x x f . 由0)(>'x f 即01232>-+x x ,可解得x <-2,或x >21, ∴ f (x )的单调递增区间是(-∞,-2),(21,+∞).…………………………4分 (2)∵ 22)(a x b ax x f -+=', ∴ 由题知x 1,x 2是方程ax 2+b x -a 2=0的两个根.∴ ab x x -=+21,x 1x 2=-a , ∴ |x 1-x 2|=244)(221221=+=-+a a b x x x x . 整理得b =4a 2-4a 3.……………………………………………………………8分 ∵ b ≥0,∴ 0<a ≤1.则b 关于a 的函数g (a )=4a 2-4a 3(0<a ≤1).于是)32(4128)(2a a a a a g -=-=',∴ 当)320(,∈a 时,0)(>'a g ;当⎥⎦⎤ ⎝⎛∈132,a 时,.0)(<'a g ∴ g(a )在)320(,上是增函数,在⎥⎦⎤ ⎝⎛132,上是减函数. ∴ 2716)32()(max ==g a g ,0)1()(min ==g a g , ∴ 0≤b ≤2716. ………………………………………………………………12分22.解:(1)n =1时2)1(12+-=S a a 2)1(1+-=a a a 2=,∴ a a a a ==2212(常数). n ≥2时,由已知a n +1=(a -1)S n +2有a n =(a -1)S n -1+2,两式相减得a n +1-a n =(a -1)a n ,整理得a n +1=a ·a n ,即a a a nn =+1(常数) 即对n =1,2,3,…,2k -1均有a a a nn =+1(常数) 故{a n }是以a 1=2,a 为公比的等比数列.∴ a n =2a n -1.……………………………………………………………………5分(2))]2()2()2[(log 1)(log 11102212-⋅⋅⋅==n n n a a a na a a nb )2(log 112102-++++⋅=n n a n]2[log 12)1(2-⋅=n n n a n a n 2log 211-+=.……………………………………………………9分 (3)由已知1222-=k a ,得12112log 2111222--+=-+=-k n n b k n , 由02112123121123>---=---+=-k n k n b n 知21+>k n , ∴ 当n =1,2,…,k 时n n b b -=-23|23|, 当n =k +1,k +2,…,2k 时23|23|-=-n n b b , ∴ |23||23||23||23|21221-+-++-+--k k b b b b 23232323232322121-++-+-+-++-+-=++k k k k b b b b b b =]122)12([]122)10([+-+++--++-k k k k k k k k k =122-k k , ∴ 原不等式变为122-k k ≤4,解得324-≤k ≤324+, ∵ k ∈N *,且k ≥2,∴ k =2,3,4,5,6,7.……………………………………………………14分。
四川省宜宾市2025届高三第一次诊断性考试语文试题(有答案)
宜宾市高三第一次诊断性考试语文(考试时间150分钟;总分150分)注意事项:1.答卷前,考生务必将自己的姓名、班级、考号填写在答题卡上。
2.回答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
答非选择题时,将答案书写在答题卡相应位置上。
写在本试卷上无效。
3.考试结束后,将本试题卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读 I(本题共 5 小题,19 分)阅读下面的文字,完成1~5题。
材料一:然而,进化论仍然不是对生命的完整描述,这一点达尔文在1859年出版《物种起源》时就心知肚明。
因为进化论从一开始就并未试图解释:大自然怎么能实现如此大规模的生物多样性。
1904年,荷兰植物学家胡戈·德弗里斯(Hugo de Vries)曾在加州大学伯克利分校做过一系列有关达尔文著作的讲座。
结束时他用了一句口号作为结语:“自然选择可以解释适者的生存,但却不能解释适者的降临。
”必须先有生命形式出现,自然选择才可能从中筛选。
假设你是个雇主,想找个又能完成手头工作,又能与其他员工和谐相处的人,那么你尽可以左挑右选。
但是,如果压根就没有应聘者出现,你的招聘就只能收摊了。
那么,适应大自然生存的“应聘者”从何而来呢?这个领域的顶尖科学家们在谈到生物多样性时,频繁使用“偶然”“意外”或“不可预测”这样的字眼,其频繁程度仿佛已经解释了一切。
“偶然,纯粹的偶然”,是分子生物学先驱之一雅克·莫诺描述生命进化时用的字眼。
莫诺在他颇具影响力的《偶然性和必然性》一书中,根据久经考验的观察数据提出了一项宣言,即有机体 DNA 的偶然突变有助于变异在有机体中代代相传。
“所以必然得出的结论是,”他写道,“只有偶然性才是生物界中每一次革新和所有创造的源泉。
进化这座宏伟大厦的根基是绝对自由的,但又是盲目的纯粹偶然性:这一个现代生物学的中心概念,已不再是一种只是可能或甚至是可想象的假设了。
宜宾市普通高中2017级一诊考理科数学试题(含答案)
宜宾市高2017级高三第一次诊断测试理科数学注意事项:1. 答卷前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将答题卡交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合要求的。
1.已知集合{1,2,3,4,5,6}U =,{1,3,4}A =,则U A =ðA .{5,6}B .{1,2,3,4}C .{2,5,6}D .{2,3,4,5,6}2.若复数1(2)i m m ++-(i 是虚数单位)在复平面内对应的点在第二象限,则实数m 的取值范围是A .()1,-∞-B .()2,1-C .()+∞,2D .()(),12,-∞+∞3.已知向量()()2,4,,2-==b a m ,且()()b a b a -⊥+,则实数=mA .4-B .4C .2±D .4±4.733x⎛+ ⎝展开式中的常数项是A .189B .63C .42D .215.已知323ln 31343,e ,2===cba ,则A . a b c <<B .a c b <<C .b a c <<D .c a b <<6.函数1ln )(+=x xx f 的图象大致是A B C D7.设曲线1cos ()sin x f x x +=在3π=x 处的切线与直线1y ax =+平行,则实数a 等于A .1-B .23C .2-D .28.“关注夕阳,爱老敬老”,某企业从2012年开始每年向敬老院捐赠物资和现金,下表记录了该企业第x 年(2012年是第一年)捐赠的现金数y (万元):若由表中数据得到y 关于x 的线性回归方程是35.0ˆ+=mx y,则可预测2019年捐赠的现金大约是A .5.95万元B .5.25万元C .5.2万元D .5万元9.执行如图所示的程序框图,如果输入2019=n ,则输出的=SA .40394038B . 40392019C .40372018D .4037403610.若9人已按照一定顺序排成三行三列的方阵,从中任选3人,则至少有两人位于同行或同列的概率是 A .1314 B .47C .37D .11411.已知112ω>,函数)4π+ω2sin(=)(x x f 在区间π3π(,)22内没有最值,则ω的取值范围A .11[,]62B .511,1224⎡⎤⎢⎥⎣⎦C .15,412⎡⎤⎢⎥⎣⎦D .5,112⎡⎤⎢⎥⎣⎦12.在平面直角坐标系中,O 是坐标原点,若两定点,A B满足2OA OB ==,1OAOB ⋅=,则点集{}|,2,,R P OP OAOB λμλμλμ=++≤∈所表示的区域的面积是. A. B . C . D .二、填空题:本大题共4个小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宜宾市高新2010级一诊考试数学(理工农医类)试题参考答案及评分意见说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可比照评分意见制订相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半,如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分. 一、选择题(每小题5分,共50分)二、填空题(每小题5分,共25分) 11.不能; 12.-1; 13. 21; 14. 3; 15. }202|{≥=-≤x x x x 或或. 三、解答题(共75分)16.解:(Ⅰ)等比数列{}n a 的首项211=a ,公比21=q ………………………(1分) n S =n n nq q a 211211)211(211)1(1-=--=--………………………(5分) (Ⅱ)n n a a a b 22212log ...log log +++= =n 21log ...21log 21log 2222+++………………………(6分) )321(n ++++-=………………………(9分) =2)1(+-n n ………………………(11分) 所以数列{}n b 的通项公式2)1(+-=n n b n (12)17.解:(Ⅰ))cos(sin cos )2sin()(x x x x x f +⋅--=ππx x x cos sin cos 2+=………(2分)21)42sin(22)12cos 2(sin 212sin 21cos 2++=++=+=πx x x x x ……(3分)令Z k k x k ∈+<+<+-,224222πππππ所以函数)(x f 的单调增区间为:Z k ∈⎪⎭⎫⎝⎛++-k ,k 8,83ππππ ………………………(5分) 为同理可得函数)(x f 的单调减区间为Z k k k ∈⎪⎭⎫⎝⎛++,85,8ππππ ………………………(6分) (Ⅱ)因为)(A f =1,所以121)42sin(22=++πA 所以22)42sin(=+πA 因为A 为锐角,所以45424πππ<+<A ………………(8分) 所以4342ππ=+A ,所以4π=A ………………(9分) 在△ABC 中,由正弦定理得,3sin4sin 2sin sin ACBAC A BC ==即………(11分)解得6=AC ………………(12分)18.解: (Ⅰ) 记“学生A 、B 、C 中有一人选修课程甲,且无人选修课程乙”为事件R ……(1分)163422)(313=⨯⨯=C R P ………………(5分)答:学生A 、B 、C 中有一人选修课程甲,且无一人选修课程乙的概率为163. ………………(6分) (Ⅱ) 课程丙或丁被这3名学生选修的人数ξ=0、1、2、3 ………………(7分)64842)0(33===ξP , 642442)1(321213=⨯⋅==A C P ξ,6424422)2(322231223=⨯+⨯==A C A C P ξ, 6484)3(312332223=+⋅==A C A C P ξ. …………(11分) 所以 23648364242642416480=⨯+⨯+⨯+⨯=ξE (人). ………………(12分)19.解:(I )设(1)xt e t =≥;则2222111a t y at b y a at at at -'=++⇒=-= ………………(2分) ①当1a ≥时,0y '>⇒1y at b at=++在1t ≥上是增函数………………(3分) 得:当1(0)t x ==时,()f x 的最小值为1a b a++………………(4分)②当01a <<时,12y at b b at=++≥+………………(6分) 当且仅当11(,ln )xat t e x a a====-时,()f x 的最小值为2b +………………(7分)(II )11()()xxx xf x ae b f x ae ae ae '=++⇒=-………………(8分)由题意得:2222212(2)333131(2)222f ae b a ae e f ae b ae ⎧⎧=++==⎧⎪⎪⎪⎪⎪⇔⇔⎨⎨⎨'=⎪⎪⎪-==⎩⎪⎪⎩⎩………………(12分) 20.解:(Ⅰ)设C 方程为)0(12222>>=+b a by a x由已知b=32 离心率222,21c b a a c e +===………………(3分) 得4=a所以,椭圆C 的方程为1121622=+y x ………………(4分) (Ⅱ)①由(Ⅰ)可求得占P 、Q 的坐标为)3,2(P ,)3,2(-Q ,则6||=PQ ,设A (),,11y x B(22,y x ),直线AB 的方程为t x y +=21,代人1121622=+y x 得01222=-++t tx x 由△>0,解得44<<-t ,由根与系数的关系得⎩⎨⎧-=-=+1222121t x x tx x 四边形APBQ 的面积 2213483621t x x S -=-⨯⨯=………………(6分) 故,当312,0max ==S t ………………(7分)②∠APQ=∠BPQ 时,PA 、PB 的斜率之和为0,设直线PA 的斜率为k ,则PB 的斜率为k -,PA 的直线方程为)2(3-=-x k y 与1121622=+y x 联立解得 048)23(4)23(8)43222=--+-++k kx k x k (,2143)32(82k kk x +-=+………………(9分)同理PB 的直线方程)2(3--=-x k y ,可得2243)32(82kkk x ++=+ 所以22122214348,431216kkx x k k x x +-=-+-=+………………(11分) 212121213)2(3)2(x x x k x k x x y y k AB ---++-=--=214824434843161212164)(22332121=--=+-+---=--+=k k kk k k k k k x x k x x k 所以直线AB 的斜率为定值21………………(13分) 21.解:(Ⅰ)321()1,3f x x ax bx =+-+2()2,f x x ax b '∴=+- 由题意(1)121,f a b '∴=+-=2.b a ∴= ① …………………………………………………………(1分).02)(,)(2有两个不等实根方程有极值=-+='∴b ax x x f x f22440,0.a b a b ∴∆=+>∴+> ②由①、②可得,220.20.a a a a +>∴<->或故实数a 的取值范围是),0()2,(+∞--∞∈ a …………………………………(3分 ) (Ⅱ)存在8.3a =- ………………………………………(5分)由(1)可知0)(,2)(2='-+='x f b ax x x f 令,12x a x a ∴=-=-,且),0()2,(+∞--∞∈ a1123)(,)(,2223222=+-+==∴axaxxxfxfxx则取极小值时,632222=-+=∴aaxxx或.……………………………………………………(6分)20,0,0().x a a=-+==若即则舍……………………………………(7分)222222222360,()0,220,40.80,4,4 2.3x ax a f x x ax a ax aa x a a'+-==∴+-=∴-=≠∴=∴-=∴=-<-若又)(,38xfa使得函数存在实数-=∴的极小值为1.………………………………(8分)(Ⅲ)由xxbaxxfxg ln212)()(--+-'=xxbaxbaxxln21222--+--+=xxx ln21--=即xxxxg ln21)(--=故,0)1(12211)(22222>-=+-=-+='xxxxxxxxg则)(xg在),1(+∞上是增函数,故0)1()(=>gxg,所以,)(xg在),1(+∞上恒为正。
.………………………………(10分)(注:只判断符号,未说明理由的,酌情给分)当*Nn∈时,11>+nn,设nnx1+=,则nnnnnnnng1ln211)1(+-+-+=+]ln)1[ln(211111nnnn-+-++-+=]ln)1[ln(2111>-+-++=nnnn即,]ln)1[ln(2111nnnn-+>++.………………………………(12分)上式分别取n的值为1、2、3、……、)1(-n累加得:)111()4131()3121()2111(nn+-+++++++)]1ln(ln3ln4ln2ln3ln1ln2[ln2--++-+-+->nn,(1>n)n n n ln 21)11413121(21>+-+++++∴ ,(1>n )n n n n 11ln 2)1114131211(2++>+-+++++∴ ,(1>n ))11(21ln 1114131211nn n n ++>+-+++++∴ ,(1>n )即,∑=<++ni i n n 11)11(21ln ,(1>n )又当1=n 时,∑==++ni i n n 11)11(21ln ,故∑=≤++ni in n 11)11(21ln ,当且仅当1=n 时取等号。
.……………………(14分)。
