最新-河北省衡水中学2018学年高二下学期第二次调研考试(数学文) 精品
考点10 导数的几何意义-2018版典型高考数学试题解读与变式(解析版)

考点十:导数的几何意义【考纲要求】(1)了解导数概念的实际背景.(2) 通过函数图像直观理解导数的几何意义. (3) 根据导数的定义求基本函数的导数.(4) 能利用给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如)(b ax f +的复合函数)的导数. 【命题规律】导数的运算是导数应用的基础,一般较少直接考查,而导数的几何意义----切线问题是高考考查的热点. 预计2017年的高考将会继续保持稳定,坚持考查导数的几何意义,命题形式会更加灵活、新颖. 【典型高考试题变式】 (一)求函数的导函数例1.【2017浙江高考改编】已知函数()()x 1fx x-2x-1e x 2-⎛⎫=≥ ⎪⎝⎭,求()f x 的导函数. 【答案】(I )()()(12121()221x x x e f x x x ----=>-';【方法技巧归纳】求函数的导函数要做到:1.基本初等函数的导函数相当熟悉;2.导函数的四则运算要熟练.另外,在求导的过程中,要注意对原式进行变形,使得便于我们求导.【变式1】【函数中含有参数,利用某函数值的导数求参数的值】【2015天津卷(文)】已知函数()()ln ,0,f x ax x x =∈+∞ ,其中a 为实数,()f x '为()f x 的导函数,若()13f '= ,则a 的值为 .【答案】3 【解析】因为()()1ln f x a x '=+ ,所以()13f a '==.【变式2】【赋值法在求导得应用,题型变为填空题】【2017江西太原高三模考一(文)改编题】已知函数()()()2102x f f f x e x xe '=+-,则)(x f 的最小值为___________________.【答案】1(二)导数的几何意义例2.【2017天津卷(文)】已知a ∈R ,设函数()ln f x ax x =-的图像在点()()1,1f 处的切线为l ,则l 在y 轴上的截距为 . 【答案】1【解析】(1)f a =,切点为(1,)a ,1()f x a x '=-,则切线的斜率为(1)1f a '=-,切线方程为:(1)(1)y a a x -=--,令0x =得出1y =,l 在y 轴的截距为1.【方法技巧归纳】切线的斜率就是函数在切点处的导数,倾斜值的正切值就是斜率.【变式1】【已知含参函数的切线斜率,求参数的值(或取值范围)】【2017四川乐山第三次调研考试(理)】已知曲线()221x x f x e e ax =-+-存在两条斜率为3的切线,则实数a 的取值范围是( )A. ()3,+∞B. 73,2⎛⎫⎪⎝⎭ C.7,2⎛⎫-∞ ⎪⎝⎭ D. ()0,3 【答案】B 【解析】由题得()222x x f x e e a'=-+,则方程2223x x e e a -+=有两个解,令xt e =,且()2223g t t t a =-+-,则由图象可知,有()0g t >且0∆>,即30a ->且()4830a -->,解得732a <<,故选B.【变式2】【函数的切线斜率与切线的倾斜角之间的关系】【2017安徽宣城六校联考改编题】过函数()3213f x x x =-图象上一个动点作函数的切线,则切线倾斜角的范围为A. 3π0,4⎡⎤⎢⎥⎣⎦ B.π3π0,,π24⎡⎤⎡⎤⋃⎢⎥⎢⎥⎣⎦⎣⎦ C. 3π[,π) 4 D.π3π(,24⎤⎥⎦ 【答案】B【解析】由题意得()22k f x x x ==-'=()2111x --≥-,即tan α1k =≥-,解得πα02≥≥或3παπ4≤≤.即切线倾斜角的范围为π3π0,,π24⎡⎤⎡⎤⋃⎢⎥⎢⎥⎣⎦⎣⎦.故选B. 【变式3】【两个函数的切线垂直求切点的取值范围】【2015陕西卷(理)】设曲线xy e =在点(0,1)处的切线与曲线1(0)y x x =>上点P 处的切线垂直,则P 的坐标为 .【答案】()1,1【变式4】【两个函数的切线平行求参数的值】【2014江苏】在平面直角坐标系中,若曲线(为常数)过点,且该曲线在点处的切线与直线平行,则.【答案】【解析】曲线过点,则①,又,所以②,由①②解得所以.(三)在一点处的切线方程例3.【2017全国1卷(文)】曲线21 y xx=+在点(1,2)处的切线方程为_________________________. 【答案】1y x=+【解析】设()y f x=,则()212f x xx-'=,所以()1211f='-=,所以曲线21y xx=+在点()1,2处的切线方程为()211y x-=⨯-,即1y x=+.【方法技巧归纳】求曲线的切线方程是导数的重要应用之一,用导数求切线方程的关键在于求出斜率,其求法为:设()00,P x y是曲线()y f x=上的一点,则以P为切点的切线方程是()()000y y f x x x'-=-.若曲线()y f x=在点()()00,P x f x处的切线平行于y轴(即导数不存在)时,由切线定义知,切线方程为0x x=.【变式1】【例题中增加函数性质】【2016全国3卷(理)】已知()f x为偶函数,当0x<时,()()ln3f x x x=-+,则曲线()y f x=在点()1,3-处的切线方程是__________.【答案】21y x=--【变式2】【增加例题中函数的参数,求参数的取值】【2017届衡水中学押题卷3(文)改编题】已知函数()()1e xf x bx a=-+(a,Rb∈).若曲线()y f x=在点()()0,0f处的切线方程为y x=,求a,b 的值分别为________.【答案】2,1【解析】函数()f x的定义域为R,()()e1ex xf x b bx=+-'()1e xbx b=+-.因为曲线()y f x=在点()()0,0f处的切线方程为y x=,所以()()00,{01,ff'==得10,{11,ab-=-=解得1,{2.ab==(四)过一点的切线方程例4.【2015全国1卷(理)改编题】已知函数,.(1)当为何值时,轴为曲线的切线.【答案】(Ⅰ);【解析】(Ⅰ)设曲线与轴相切于点,则,,即,解得.因此,当时,轴是曲线的切线.【方法技巧归纳】对于曲线)(xfy=上“过”点),(nm的切线问题,一般要先设切点),(yx,于是切线为))(('mxxfny-=-,再根据切点在曲线上得)(xfy=,切点在切线上得))(('mxxfny-=-.列方程组,可得切点的值.【变式1】【增加例题的难度,求切线的取值范围】【2017甘肃第二次高考诊断考试(理)】若P是函数()()()1ln1f x x x=++图象上的动点,点()1,1A--,则直线AP斜率的取值范围为()A. [)1,+∞B.[]0,1C.(1,e e-⎤⎦D.(1,e-⎤-∞⎦【答案】A切线过点()1,1--,则:()()()()000011ln1ln111x x x x⎡⎤--++=++--⎣⎦,解得:00x=,切线的斜率()ln111k x=++=,综上可得:则直线AP斜率的取值范围为[) 1,+∞.(五)两曲线的公切线例5.【2016全国2卷(理)】若直线y kx b =+是曲线ln 2y x =+的切线,也是曲线()ln 1y x =+的切线,则b = .【答案】1ln2-【解析】ln 2y x =+的切点为()11ln +2x x ,,则它的切线为111ln 1y x x x =⋅++.()ln 1y x =+的切点为()22ln +2x x ,,则它的切线为:()22221ln 111x y x x x x =++-++,所以()122122111ln 1ln 11xx x x x x ⎧=⎪+⎪⎨⎪+=+-⎪+⎩,解得112x =,212x =-,所以1ln 11ln 2b x =+=-.【方法技巧归纳】两曲线有公共切线,一般可以分别求出两曲线的切线,然后说明这两直线重合;或者先求出其中一条曲线的切线,然后说明其也和另一曲线相切.【变式1】【例题中曲线添加参数,求参数的值】【2015全国2卷】已知曲线ln y x x =+在点)1,1(处的切线与曲线1)2(2+++=x a ax y 相切,则a= . 【答案】8【解析】由11y x '=+可得曲线ln y x x =+在点)1,1(处的切线斜率为2,故切线方程为21y x =-,与1)2(2+++=x a ax y 联立得220ax ax ++=,显然0a ≠,所以由 2808a a a ∆=-=⇒=.【变式2】【改编题目问法,两曲线存在公切线求参数范围】【2017河南六市第二次联考(理)】若曲线21:(0)C y ax a =>与曲线2:xC y e =存在公共切线,则a 的取值范围为__________.【答案】2,4e ⎡⎫+∞⎪⎢⎣⎭ 【解析】由y=ax2(a>0),得y ′=2ax ,由y=ex,得y ′=ex ,曲线C1:y=ax2(a>0)与曲线C2:y=ex 存在公共切线,设公切线与曲线C1切于点(x1,ax12),与曲线C2切于点()22,x x e ,则22211212x x e ax ax e x x -==-,可得2x2=x1+2,∴11212x ea x +=,记()122x ef x x +=,则()()1222'4x e x f x x +-=,当x ∈(0,2)时,f ′(x)<0,f(x)递减;当x ∈(2,+∞)时,f ′(x)>0,f(x)递增.∴当x=2时,()2min4e f x =.∴a 的范围是2,4e ⎡⎫+∞⎪⎢⎣⎭ . 【数学思想】 无限逼近的极限思想(1)由()()'()limx f x x f x f x x ∆→+∆-=∆可以知道,函数的导数是函数的瞬时变化率,函数的瞬时变化率是平均变化率的极限,充分说明极限是人们从近似中认识精确的数学方法.极限的实质就是无限近似的量,向着有限的目标无限逼近而产生量变导致质变的结果,这是极限的实质与精髓,也是导数的思想及其内涵. (2)曲线的切线定义,充分体现了运动变化及无限逼近的思想:“两个不同的公共点→两公共点无限接近→两公共点重合(切点)”⇒“割线→切线”.(3)在求曲线的切线方程时,注意两个“说法”:求曲线在点P 处的切线方程和求曲线过点P 的切线方程,在点P 处的切线,一定是以点P 为切点,过点P 的切线,不论点P 在不在曲线上,点P 不一定是切点. 【处理导数的几何意义问题注意点】对于曲线切线方程问题的求解,对函数的求导是一个关键点,因此求导公式,求导法则及导数的计算原则要熟练掌握.对于已知的点,应首先认真审题,对于确定切线的方程问题,要注意区分“该曲线过点P 的切线方程”与“该曲线在点P 处的切线方程”的两种情况,避免出错.从历年高考题看,“该曲线在点P 处的切线方程”问题的考查较为普遍.【典例试题演练】1.【2017宁夏银川一中高三二模(文)】已知在平面直角坐标系中,曲线()ln f x a x x=+在x a =处的切线过原点,则a =A. 1B. eC. 1e D. 0【答案】B2.【2017辽宁沈阳东北育才学校第九次模拟考试(理)】已知函数()xaf x x e=- (0)a >,且()y f x =的图象在0x =处的切线l 与曲xy e =相切,符合情况的切线 A. 有0条 B. 有1条 C. 有2条 D. 有3条 【答案】A【解析】函数f(x)= xax e -的导数为f ′(x)=1−1xa ea ,a>0.易知,曲线y=f(x)在x=0处的切线l 的斜率为1−1a,切点为(0,−1),可得切线的方程为y=(1−1a )x −1.假设l 与曲线y=ex 相切,设切点为(x0,y0),即有e x0=1−1a =(1−1a )x0−1,消去a 得e x0=e x0⋅x0−1,设h(x)=exx −ex −1, 则h ′(x)=exx,令h ′(x)>0,则x>0,所以h(x)在(−∞,0)上单调递减,在(0,+∞)上单调递增, 当x →−∞,h(x )→−1,x →+∞,h(x )→+∞, 所以h(x)在(0,+∞)有唯一解,则e x0>1, 而a>0时,1−1a<1,与e x0>1矛盾,所以不存在. 故选:A.3.【2017湖南长沙长郡中学高三5月模考(理)】设曲线()x f x e x=--(e 为自然对数的底数)上任意一点的切线为1l,总存在曲线()32cos g x ax x=+上某点处切线2l,使得12l l ⊥,则实数a 的取值范围为( )A. []1,2-B. []3,+∞C. 21,33⎡⎤-⎢⎥⎣⎦ D.12,33⎡⎤-⎢⎥⎣⎦【答案】D【解析】因为()()1,32sin x f x e g x a x''=--=-,所以直线12,l l 的斜率分别为()11201,32sin x k e k a x =-+=-,则由题设可得()()10132sin 1x e a x -+-=-,即10132sin 1x a x e -=+,又因为对任意1x ,都有11011x e <<+,故 存在0x 使得0032sin 1a x <-<,即存在0x 使得002sin 312sin x a x <<+,故1232a -≤≤,即1233a -≤≤,应选答案D . 4.【2017安徽蚌埠高三二质检(理)】已知函数()1xf x x a e ⎛⎫=- ⎪⎝⎭,曲线()y f x =上存在两个不同点,使得曲线在这两点处的切线都与y 轴垂直,则实数a 的取值范围是( )A. ()2,e -+∞B. ()2,0e - C. 21,e⎛⎫-+∞ ⎪⎝⎭ D. 21,0e ⎛⎫- ⎪⎝⎭【答案】D 【解析】曲线()y f x =上存在不同的两点,使得曲线在这两点处的切线都与y 轴垂直,()()'10x f x a x e -∴=+-=有两个不同的解,即得()1xa x e -=-有两个不同的解,设()1xy x e -=-,则()'2,2,'0,2,'0x y x e x y x y -=-∴,()1xy x e -=-在(),2-∞上递减,在()2,+∞上递增2x ∴=时,函数取得极小值2,e --又因为当2x >时总有()10xy x e -=-<,所以可得数a 的取值范围是21,0e⎛⎫- ⎪⎝⎭,故选D.5.【2017四川绵阳高三月考(理)】过点()2,1A 作曲线()33f x x x=-的切线最多有( )A .3条B .2条C .1条D .0条 【答案】A6.【2018河北石家庄二中开学考试(理)】已知函数()()21,f x g x x x ==.若直线l 与曲线()(),f x g x 都相切,则直线l 的斜率为__________. 【答案】4-【解析】因为()()21,f x g x x x ==,所以()21‘,f x x =-设曲线()f x 与l 切于点111x x ⎛⎫ ⎪⎝⎭,,则切线斜率211k x =-,故切线方程为()121111y x x x x -=--,即21112y x x x =-+,与()2g x x =联立得:2211120x x x x +-=,因为直线l 与曲线()g x 相切,所以02411221=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛x x ,解得112x =-,故斜率211k 4x =-=-.故答案为: 4-7.【2018广东茂名高三五校联盟9月联考(理)】若函数的图象在点处的切线斜率为,则函数的极小值是__________.【答案】【解析】因为,所以由导数的几何意义可得切线的斜率,故,令可得,则函数的极小值为,应填答案.8.【2017河南新乡三模(文)】若()()2f x f x +-= 33x x ++对R x ∈恒成立,则曲线()y f x =在点()()2,2f 处的切线方程为__________.【答案】1315y x =-(或13150x y --=) 【解析】()()()()()()3323,23f x f x x x f x f x x x +-=++∴-+=-+-+()()()()333233f x x x x x ⎡⎤∴=++--+-+⎣⎦()()()321,31,213f x x x f x x f ''∴=++=+=又()211f =,则曲线()y f x =在点()()2,2f 处的切线方程为()11132y x -=- ,即1315y x =-9.【2017湖南郴州市高三第四次质量检测(文)】若函数()在区间只有一个极值点,则曲线在点处切线的方程为__________.【答案】【解析】由题意可得,所以即在有唯一奇次根.根据根的存在性定理,即,,又因为,所以.,,,所以切线方程为.答案为:x-y+6=0.10.【2018河南周口市中英文学校开学考】曲线()C:sin 2x f x x e =++在0x =处的切线方程为_____.【答案】23y x =+ 【解析】由()sin 2x f x x e =++,得()cos xf x x e ='+,()03f =,切线的斜率为()02k f ='=,故切线方程为23y x =+,故答案为23y x =+.11.【2018贵州贵阳高三8月摸底考】已知函数()()1*n n f x x x n N +=-∈,曲线()y f x =在点()()2,2f 处的切线与y 轴的交点的纵坐标为nb ,则数列{}n b 的前n 项和为__________.【答案】12n n +⋅【解析】对函数求导可得: ()()1'1n nf x nx n x -=-+,则()()()11'221222n n n f n n n --=⨯-+⨯=--⨯,且:()12222n n nf -=-=-,曲线在()()2,2f 处的切线方程为()()12222nn y n x -+=--⨯⨯-,令0x =可得: ()1222n y n -=+⨯,即()1222n n b n -=+⨯,错位相减可得其前n 项和为12n n -⋅.12.【2017湖南省郴州市高三第四次质量检测(文)改编】已知函数()与函数有公共切线.则求的取值范围为_____________. 【答案】13.【2017吉林实验中学八模(理)改编】已知函数()()ln af x x a R x =+∈.(Ⅰ)若函数()f x 在1x =处的切线平行于直线20x y -=,求实数a 的值.【答案】(1)1a =-【解析】试题分析:(1)利用导数的几何意义,得()12f '=, 1a =-;试题解析:(Ⅰ)()21'a fxx x=-,函数()f x在1x=处的切线平行于直线20x y-=.()112,1f a a∴=-=∴=-'.14.【2017陕西省西安市西北工业大学附属中学第八次模拟(理)】已知函数()()1lnt xf x e t x-=-(常数0t>). (Ⅰ)求函数()f x的单调区间;(Ⅱ)若曲线()y f x=与直线y tx=相切,证明:2t<.【答案】(1)()f x的单增区间为()1,+∞,单减区间为()0,1;(2)见解析.【解析】试题分析:(Ⅰ)求出()'f x,()'0f x>得增区间,()'0f x<得减区间;(Ⅱ)设曲线()y f x=与直线y tx=的切点为()()00,x f x,由0011ln t x txx+-=,可得()0001lnxtx x x+=+,()()1lnxr xx x x+=+,其中11,1xt⎛⎫∈+⎪⎝⎭,利用导数研究函数的单调性可得()()12r x r<=,即2t<.(Ⅱ)证明:设曲线()y f x=与直线y tx=的切点为()()00,x f x,因为()()11t xf x t ex-⎛⎫=-⎝'⎪⎭,所以()()011t xf x t e tx-⎛⎫=-=⎪⎝⎭',即()111t xex-=+.因为直线y tx=经过切点()()00,x f x,所以()()01000lnt xf x e t x tx-=-=,于是,有0011ln t x txx+-=,即()0001lnxtx x x+=+.令()()111t xh x ex-=--,则()()121t xh x tex-+'=>,故()h x单增,又()110h=-<,11101th et t⎛⎫+=-->⎪+⎝⎭,所以()h x有唯一零点0x,且11,1xt⎛⎫∈+⎪⎝⎭.再令()()1lnxr xx x x+=+,其中11,1xt⎛⎫∈+⎪⎝⎭,则()()2223ln1lnx x xr xx x x----=<+',故()r x单减,所以()()12r x r<=,即2t<.。
【全国百强校Word】河北省衡水中学2018届高三9月大联考理数试题

726π2抛物线地对称轴地入射光线经抛物线反射后必过抛物线地焦点.已知抛物线24y x =地焦点为F ,一条平行于x 轴地光线从点(3,1)M 射出,经过抛物线上地点A 反射后,再经抛物线上地另一点B 射出,则ABM ∆地周长为( )A .712612+B .926+C .910+D .832612+ 12.已知数列{}n a 与{}n b 地前n 项和分别为n S ,n T ,且0n a >,263n n n S a a =+,*n N ∈,12(21)(21)nnn a n a a b +=--,若*n N ∀∈,n k T >恒成立,则k 地最小值是( )A .17B .149C .49D .8441第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将解析填在答题纸上)13.已知在ABC ∆中,||||BC AB CB =- ,(1,2)AB =,若边AB 地中点D 地坐标为(3,1),点C 地坐标为(,2)t ,则t = .14.已知1()2nx x-(*n N ∈)地展开式中所有项地二项式系数之和、系数之和分别为p 、q ,则64p q +地最小值为 .15.已知x ,y 满足3,,60,x y t x y π+≤⎧⎪⎪≥⎨⎪≥⎪⎩其中2t π>,若sin()x y +地最大值与最小值分别为1,12,则实数t 地取值范围为 .16.在《九章算术》中,将四个面都为直角三角形地三棱锥称之为鳖臑.已知在鳖臑M ABC -中MA ⊥平面ABC ,2MA AB BC ===,则该鳖臑地外接球与内切球地表面积之和为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数21()cos 3sin()cos()2f x x x x ππ=+-+-,x R ∈.(1)求函数()f x 地最小正周期及其图象地对称轴方程;(2)在锐角ABC ∆中,内角A ,B ,C 地对边分别为a ,b ,c ,已知()1f A =-,3a =,sin sin b C a A =,求ABC ∆地面积. 18.如图,在四棱锥E ABCD -中,底面ABCD 为直角梯形,其中//CD AB ,BC AB ⊥,侧面ABE ⊥平面四边形MNPQ 不可能是菱形.21.已知函数()(1)xf x e a x b =-+-(a ,b R ∈),其中e 为自然对数地底数.(1)讨论函数()f x 地单调性及极值;(2)若不等式()0f x ≥在x R ∈内恒成立,求证:(1)324b a +<.请考生在22、23两题中任选一题作答,如果多做,则按所做地第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系中xOy 中,已知曲线C 地参数方程为cos ,sin x t y αα=⎧⎨=⎩(0t >,α为参数),以坐标原点O 为极点,x 轴地正半轴为极轴,取相同地长度单位建立极坐标系,直线l 地极坐标方程为2sin()34πρθ+=.(1)当1t =时,求曲线C 上地点到直线l 地距离地最大值;(2)若曲线C 上地所有点都在直线l 地下方,求实数t 地取值范围.23.选修4-5:不等式选讲已知函数()|21||1|f x x x =-++.(1)解不等式()3f x ≤;(2)记函数()()|1|g x f x x =++地值域为M ,若t M ∈,证明:2313t t t+≥+.衡水金卷2018届全国高三大联考理数解析一、选择题1-5:CBCBA 6-10: ACDAD 11、12:BB二、填空题13.1 14.16 15.57,66ππ⎡⎤⎢⎥⎣⎦16.2482ππ-三、解答题17.解:(1)原式可化为21()cos 3sin cos 2f x x x x =--1cos 231sin 2222x x +=--sin(2)6x π=-sin(2)6x π=--,故其最小正周期22T ππ==,令262x k πππ-=+(k Z ∈),解得23k x ππ=+(k Z ∈),即函数()f x 图象地对称轴方程为23k x ππ=+(k Z ∈).(2)由(1)知()sin(2)6f x x π=--,因为02A π<<,所以52666A πππ-<-<,又()sin(2)6f A A π=--1=-,故262A ππ-=,解得3A π=.由正弦定理及sin sin b C a A =,得29bc a ==,故193sin 24ABC S bc A ∆==.18.解:(1)当12λ=时,//CE 平面BDF .证明如下:连接AC 交BD 于点G ,连接GF .∵//CD AB ,2AB CD =,∴12CG CD GA AB ==.∵12EF FA =,∴12EF CG FA GA ==. ∴//GF CE .又∵CE ⊄平面BDF ,GF ⊂平面BDF ,∴//CE 平面BDF .(2)取AB 地中点O ,连接EO ,则EO ⊥AB .∵平面ABE ⊥平面ABCD ,平面ABE 平面ABCD AB =,且EO AB ⊥,∴EO ⊥平面ABCD .∵//BO CD ,且1BO CD ==,∴四边形BODC 为平行四边形,∴//BC DO . 又∵BC AB ⊥,∴AB OD ⊥.由OA ,OD ,OE 两两垂直,建立如下图所示地空间直角坐标系O xyz -.则(0,0,0)O ,(0,1,0)A ,(0,1,0)B -,(1,0,0)D ,(1,1,0)C -,(0,0,3)E .当1λ=时,有EF FA = ,∴可得13(0,,)22F .∴(1,1,0)BD = ,(1,1,3)CE =- ,33(0,,)22BF = .设平面BDF 地一个法向量为(,,)n x y z = ,则有0,0,n BD n BF ⎧⋅=⎪⎨⋅=⎪⎩ 即0,330,22x y y z +=⎧⎪⎨+=⎪⎩令3z =,得1y =-,1x =,即(1,1,3)n =-.设CE 与平面BDF 所成地角为θ,则|113|1sin |cos ,|555CE n θ--+=<>==⨯ ,∴当1λ=时,直线CE 与平面BDF 所成地角地正弦值为51.19.解:(1)由列联表可知2K 地观测值22()200(50405060) 2.020 2.072()()()()11090100100n ad bc k a b c d a c b d -⨯-⨯==≈<++++⨯⨯⨯,所以不能在犯错误地概率不超过0.15地前提下认为A 市使用网络外卖情况与性别有关.(2)①依题意,可知所抽取地5名女网民中,经常使用网络外卖地有6053100⨯=(人),偶尔或不用网络外卖地有4052100⨯=(人). 则选出地3人中至少有2人经常使用网络外卖地概率为2133233355710C C C P C C =+=.②由22⨯列联表,可知抽到经常使用网络外卖地网民地概率为1101120020=,将频率视为概率,即从A 市市民中任意抽取1人,恰好抽到经常使用网络外卖地市民地概率为1120.由题意得11~(10,)20X B ,∴1111()10202E X =⨯=;11999()10202040D X =⨯⨯=.20.解:(1)由已知,得12c a =,3b =,又222c a b =-,故解得24a =,23b =,所以椭圆C 地标准方程为22143x y +=.(2)由(1),知1(1,0)F -,如图,易知直线MN 不能平行于x 轴,所以令直线MN 地方程为1x my =-,设11(,)M x y ,22(,)N x y ,联立方程2234120,1,x y x my ⎧+-=⎨=-⎩得22(34)690m y my +--=,所以122634m y y m +=+,122934y y m -=+.此时221212||(1)()4MN m y y y y ⎡⎤=++-⎣⎦. 同理,令直线PQ 地方程为1x my =+,设33(,)P x y ,44(,)Q x y ,此时342634m y y m -+=+,342934y y m -=+,此时223434||(1)()4PQ m y y y y ⎡⎤=++-⎣⎦. 故||||MN PQ =,所以四边形MNPQ 是平行四边形.若MNPQ 是菱形,则OM ON ⊥,即0OM ON ⋅=,于是有12120x x y y +=.又1212(1)(1)x x my my =--21212()1m y y m y y =-++,所以有21212(1)()10m y y m y y +-++=,整理得22125034m m --=+,即21250m +=,上述关于m 地方程显然没有实数解,故四边形MNPQ 不可能是菱形.令22()ln (0)g x x x x x =->,则'()(12ln )g x x x =-. 令'()0g x >,得0x e <<;令'()0g x <,得x e >,故()g x 在区间(0,)e 内单调递增,在区间(,)e +∞内单调递减,故max ()()ln 2e g x g e e e e ==-=,即当1a e +=,即1a e =-时,max ()2e g x =.所以22(1)(1)(1)ln(1)2e a b a a a +≤+-++≤,所以(1)24b a e+≤.而3e <,所以(1)324b a +<.22.解:(1)易知曲线C :221x y +=,直线l 地直角坐标方程为30x y +-=. 所以圆心到直线l 地距离33222d ==,∴max 3212d =+.(2)∵曲线C 上地所有点均在直线l 地下方,∴a R ∀∈,有cos sin 30t αα+-<恒成立,∴213t +<.又0t >,∴解得022t <<,∴实数t 地取值范围为(0,22).23.解:(1)依题意,得3,1,1()2,1,213,,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩于是得()3f x ≤1,33,x x ≤-⎧⇔⎨-≤⎩或11,223,x x ⎧-<<⎪⎨⎪-≤⎩或1,233,x x ⎧≥⎪⎨⎪≤⎩解得11x -≤≤.即不等式()3f x ≤地解集为{}|11x x -≤≤.(2)()()|1||21||22||2122|3g x f x x x x x x =++=-++≥---=,当且仅当(21)(22)0x x -+≤时,取等号,∴[3,)M =+∞.原不等式等价于2331t t t -+≥,∵[3,)t ∈+∞,∴230t t -≥,∴2311t t -+≥.又∵31t ≤,∴2331t t t -+≥,∴2313t t t +≥+.。
专题13 利用导数解决函数的极值、最值-学会解题之高三数学万能解题模板(2021版)【原卷版】

学习界的专题13 利用导数解决函数的极值、最值【高考地位】导数在研究函数的极值与最值问题是高考的必考的重点内容,已由解决函数、数列、不等式问题的辅助工具上升为解决问题的必不可少的工具,特别是利用导数来解决函数的极值与最值、零点的个数等问题,在高考中以各种题型中均出现,对于导数问题中求参数的取值范围是近几年高考中出现频率较高的一类问题,其试题难度考查较大.类型一利用导数研究函数的极值例1 已知函数f (x) =+ ln x ,求函数f (x)的极值.x【变式演练1】(极值概念)【西藏日喀则市拉孜高级中学2020 届月考】下列说法正确的是()A.当f '(x0 ) = 0 时,则f (x0 ) 为f (x) 的极大值B.当f '(x0 ) = 0 时,则f (x0 ) 为f (x) 的极小值C.当f '(x0 ) = 0 时,则f (x0 ) 为f (x) 的极值D.当f (x0 ) 为f (x) 的极值且f '(x0 ) 存在时,则有f '(x0 ) = 0【变式演练2】(图像与极值)【百师联盟2020 届高三考前预测诊断联考全国卷1】如图为定义在R 上的函数f (x)=ax3 +bx2 +cx +d (a ≠ 0)的图象,则关于它的导函数y =f '(x)的说法错误的是()A.f '(x)存在对称轴B.f '(x)的单调递减区间为⎛-∞,1 ⎫2 ⎪ ⎝⎭C.f '(x)在(1, +∞)上单调递增D.f '(x)存在极大值【变式演练3】(解析式中不含参的极值)【江苏省南通市2020 届高三下学期高考考前模拟卷】已知函数f (x)=(ax2 +x +1)e x ,其中e是自然对数的底数,a ∈R .(1)当a = 2 时,求f (x )的极值;(2)写出函数f (x )的单调增区间;(3)当a = 0 时,在y 轴上是否存在点P,过点P 恰能作函数f (x)图象的两条切线?若存在,求出所有这样的点;若不存在,请说明理由.【变式演练4】(解析式中含参数的极值)【四川省德阳市2020 届高三高考数学(理科)三诊】已知函数f (x )=ax - 2 ln x - 2 ,g (x )=axe x - 4x .(1)求函数f (x )的极值;(2)当a > 0 时,证明:g (x )- 2 (ln x -x +1)≥ 2 (ln a - ln 2 ).【变式演练5】(由极值求参数范围)【黑龙江省哈尔滨一中2020 届高三高考数学(理科)一模】已知函数学习界的007f ( x ) = x ln x -1 (m + 1) x2 - x 有两个极值点,则实数m 的取值范围为()2A . ⎛ - 1 , 0⎫B . ⎛-1, 1 -1⎫C . ⎛ -∞, 1 -1⎫ )D . (-1, +∞)e ⎪ e⎪ e⎪ ⎝ ⎭ ⎝⎭⎝⎭【变式演练 6】(由极值求其他)【四川省江油中学 2020-2021 学年高三上学期开学考试】已知函数f ( x ) = 1x 3 + ax 2 + bx (a , b ∈ R ) 在 x = -3 处取得极大值为 9.3(1) 求 a , b 的值;(2) 求函数 f (x ) 在区间[-4, 4] 上的最大值与最小值.类型二 求函数在闭区间上的最值万能模板内 容使用场景 一般函数类型解题模板第一步 求出函数 f (x ) 在开区间(a , b ) 内所有极值点;第二步 计算函数 f (x ) 在极值点和端点的函数值;第三步 比较其大小关系,其中最大的一个为最大值,最小的一个为最小值.例 2 【河南省天一大联考 2020 届高三阶段性测试】已知函数 f ( x ) = ln x - x , g ( x ) = ax 2+ 2x (a < 0) .(1) 求函数 f( x ) 在⎡1 , e ⎤上的最值; ⎢⎣ e ⎥⎦(2) 求函数 h( x ) = f (x ) + g (x ) 的极值点.【变式演练 7】(极值与最值关系)【安徽省皖江联盟 2019-2020 学年高三上学期 12 月联考】已知函数 f ( x ) 在区间(a , b ) 上可导,则“函数 f ( x ) 在区间(a , b ) 上有最小值”是“存在 x 0 ∈(a ,b ) ,满足 f '(x 0 ) = 0 ”的⎨ 1 ()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【变式演练 8】(由最值求参数范围)【湖北省武汉市 2020 届高三下学期六月模拟】若函数⎧a ln x - x 2 - 2 (x > 0 )f ( x ) = ⎪x + + a (x < 0) 的最大值为 f (-1) ,则实数a 的取值范围为( )⎩⎪ xA . ⎡⎣0, 2e 2 ⎤⎦B . ⎡⎣0, 2e 3⎤⎦C . (0, 2e 2⎤⎦D . (0, 2e 3⎤⎦【变式演练 9】(不含参数最值)【安徽省江淮十校 2020-2021 学年高三上学期第一次联考】已知函数f (x ) = cos 2 x s in 2x ,若存在实数 M ,对任意 x 1 , x 2 ∈R 都有 f ( x 1 ) - f (x 2 ) ≤ M 成立.则 M 的最小值为()A.3 38B.32C.3 3 4D.2 3 3【变式演练 10】(含参最值)【重庆市经开礼嘉中学 2020 届高三下学期期中】已知函数f (x ) = (x - a - 1)e x -1 - 1x 2 + ax , x > 02(1) 若 f (x ) 为单调增函数,求实数 a 的值;(2) 若函数 f (x ) 无最小值,求整数 a 的最小值与最大值之和.【高考再现】1.【2018 年全国普通高等学校招生统一考试数学(江苏卷)】若函数 ƒ(x ) = 䂸x 3 — t x 䂸 + 1(t C R )在(t h + œ) 内有且只有一个零点,则 ƒ(x )在[ — 1h 1]上的最大值与最小值的和为.2【. 2018 年全国普通高等学校招生统一考试理科数学(新课标 I 卷)】已知函数 ƒ x = 䂸sinx + sin 䂸x ,则 ƒ x的最小值是 .3. 【2020 年高考全国Ⅱ卷理数 21】已知函数 f (x ) = sin 2x sin 2x .3 381 2 n (1) 讨论 f ( x ) 在区间(0,π) 的单调性;(2) 证明: f (x ) ≤ ;(3) 设 n ∈ N *,证明: sin 2x sin 22x sin 24x sin 22nx ≤ 3 . 4n4. 【2020 年高考天津卷 20】已知函数 f (x ) = x3+ k ln x (k ∈ R ) , f ' (x ) 为 f ( x ) 的导函数.(Ⅰ)当 k = 6 时,(i ) 求曲线 y = f ( x ) 在点(1, f (1)) 处的切线方程;(ii )求函数 g (x ) = f (x ) - f '(x ) + 9的单调区间和极值;x(Ⅱ)当 k - 3 时,求证:对任意的 x , x ∈[1, +∞) ,且 x> x , 有 f '( x ) + f ' (x ) > f (x 1 )- f (x 2 ) . 1 2 1 2 2x - x 1 25. 【2018 年全国卷Ⅲ理数】已知函数 ƒ x = 䂸+ x + tx 䂸 ln 1 + x — 䂸x .(1) 若 t = t ,证明:当— 1 ǹ x ǹ t 时,ƒ x ǹ t ;当 x Σ t 时,ƒ x Σ t ;(2) 若 x = t 是 ƒ x 的极大值点,求 t .6. 【2018 年全国普通高等学校招生统一考试文科】设函数 ƒ(x ) = [tx 䂸 — (3t + 1)x + 3t + 䂸]e x .(Ⅰ)若曲线 y = ƒ(x )在点(䂸h ƒ(䂸))处的切线斜率为 0,求 a ;(Ⅱ)若 ƒ(x)在 x = 1 处取得极小值,求 a 的取值范围.7. 【2018 年全国普通高等学校招生统一考试文科数学(天津卷)】设函数 ƒ(x )=(x — t 1)(x — t 䂸)(x — t 3),其中t 1h t 䂸h t 3 C R ,且t 1h t 䂸h t 3是公差为 d 的等差数列.(I )若t 䂸 = t h d = 1h 求曲线 y = ƒ(x )在点(t h ƒ(t ))处的切线方程;(II ) 若 d = 3,求 ƒ(x)的极值;4 4 (III ) 若曲线 y = ƒ(x) 与直线 y =— (x — t 䂸) — 6 3有三个互异的公共点,求d 的取值范围.【反馈练习】1.【2020 届高三 6 月质量检测巩固卷数学(文科)】若函数 f ( x ) = e x (-x 2 + 2x + a )在区间(a , a +1) 上存在最大值,则实数a 的取值范围为()⎛ -1 A ., -1 + 5 ⎫ B . (-1, 2)2 2 ⎪ ⎝ ⎭⎛ -1 C . 2 ⎫ , 2⎪⎛ -1 D .2⎫, -1⎪ ⎝ ⎭⎝⎭2. 【黑龙江省大庆市第四中学 2020 届高三下学期第四次检测】若函数 f (x ) = ae x- 1在其定义域上只有 3x个极值点,则实数a 的取值范围()⎛ e 2 ⎫⎛ e 2 ⎫ A . -∞, - ⎪ (1, +∞)⎝⎭ B . -∞, - ⎪⎝⎭C . ⎛-e , -1 ⎫ (1, +∞)D . ⎛-∞, - 1 ⎫4e 2 ⎪ e ⎪ ⎝ ⎭⎝ ⎭xx2 x3. 【湖北省金字三角 2020 届高三下学期高考模拟】已知函数 f ( x ) = e + - ln x 的极值点为1 ,函数 2g ( x ) = e x + x - 2 的零点为 x ,函数 h ( x ) = ln x的最大值为x ,则( ) 2 2x 3A. x 1 > x 2 > x 3B. x 2 > x 1 > x 3C. x 3 > x 1 > x 2D. x 3 > x 2 > x 14. 【湖北省宜昌一中、龙泉中学 2020 届高三下学期 6 月联考】已知函数(ff (e ) = 1,当 x >0 时,下列说法正确的是()ex )满足 x 2 f '(x ) + 2xf (x ) = 1+ ln x ,① f (x ) 只有一个零点;② f (x ) 有两个零点;- 5 + 5 - 5③ f (x) 有一个极小值点;④ f (x) 有一个极大值点A.①③B.①④C.②③D.②④5.【山东省潍坊市2020届高三6月高考模拟】已知函数f(x)的导函数f'(x)=x4(x-1)3(x-2)2(x-3),则下列结论正确的是()A.f (x)在x = 0 处有极大值B.f (x )在x = 2 处有极小值C. f (x)在[1, 3]上单调递减D.f (x )至少有3 个零点6.【云南省曲靖市2020 届高三年级第二次教学质量监测】已知实数a, b 满足0 ≤a ≤1,0 ≤b ≤ 1 ,则函数f (x)=x3 -ax2 +b2 x +1 存在极值的概率为()A.1B.3C.16 6 3D.37.【云南省红河自治州2019-2020 学年高三第二次高中毕业生复习统一检测】下列关于三次函数f ( x) =ax3 +bx2 +cx +d (a ≠ 0) ( x ∈R) 叙述正确的是()①函数f (x) 的图象一定是中心对称图形;②函数f (x) 可能只有一个极值点;③当x ≠-b时,f (x) 在x =x 处的切线与函数y = f (x) 的图象有且仅有两个交点;0 3a 0④当x ≠-b时,则过点(x, f (x))的切线可能有一条或者三条.0 3a 0 0A.①③B.②③C.①④D.②④8.【2020 届江西省分宜中学高三上学期第一次段考】已知e 为自然对数的底数,设函数f (x)=1 x2 -ax +b ln x 存在极大值点x ,且对于a 的任意可能取值,恒有极大值f (x )< 0 ,则下列结论2 0 0bb ( ) 中正确的是()A. 存在 x 0= ,使得f (x 0 ) < - 12eB. 存在 x 0= ,使得f (x 0 ) > -e 2C.b 的最大值为e 3D.b 的最大值为 2e 2ax 2⎛ 1 , 3⎫9. 【四川省内江市 2020 届高三下学期第三次模拟考试】函数f (x )= 2+(1﹣2a )x ﹣2ln x 在区间 2 ⎪⎝ ⎭内有极小值,则 a 的取值范围是()A . ⎛ -2, -1 ⎫B . ⎛-2, -1 ⎫3 ⎪2 ⎪ ⎝ ⎭⎝ ⎭C . ⎛ -2, - 1 ⎫ ⋃⎛ - 1 , +∞⎫D . ⎛ -2, - 1 ⎫ ⋃ ⎛ - 1 , +∞ ⎫ 3 ⎪ 3 ⎪ 2 ⎪ 2 ⎪ ⎝ ⎭ ⎝ ⎭⎝ ⎭ ⎝ ⎭10.【河北省衡水中学 2019-2020 学年高三下学期期中】已知函数 f (x ) =(x2- a )2- 3 x 2 -1 - b ,当时(从①②③④中选出一个作为条件),函数有 .(从⑤⑥⑦⑧中选出相应的作为结论,只填出一.组.即可)1 3 5 9① a ≤ - ② < a < ③ a = 1 ,-2 < b < 0 ④ a = 1 ,- < b < -2 或b = 0 ⑤4 个极小值点⑥1 个极小值点2 2 2 4⑦6 个零点⑧4 个零点1. 【福建省漳州市 2020 届高三高考数学(文科)三模】已知函数 f (x ) = ( x + 3) e x- 2m , m ∈ R .(1)若 m = 3,求 f ( x ) 的最值;2(2)若当 x ≥ 0 时, f (x - 2) + 2m ≥ 1 mx 2+ 2x +1 ,求 m 的取值范围.e 212. 【安徽省合肥七中、三十二中、五中、肥西农兴中学 2020 届高三高考数学(文科)最后一卷】已知函数 f (x ) = 1 x 2- 2x + a ln x , a > 1 . 2e(1) 讨论 f( x ) 的单调性;(2)若f (x )存在两个极值点x1 、x2 ,求f (x1 )+f (x2 )的取值范围.13.【2020 届安徽省芜湖市高三下学期教育教学质量监测】已知函数f (x)=ae x + 2e -x+(a - 2 )x .(1)若y =f (x )存在极值,求实数 a 的取值范围;(2)设1 ≤a ≤ 2 ,设g (x)= f (x)-(a + 2)cos x 是定义在⎛-∞,π ⎤上的函数.2 ⎥⎝⎦(ⅰ)证明:y =g'(x )在⎛-∞,π ⎤上为单调递增函数( g'(x)是y =g (x )的导函数);2 ⎥⎝⎦ (ⅱ)讨论y =g (x )的零点个数.14.【广东省惠州市2021 届高三上学期第一次调研】已知函数f (x) =x- ln(ax) .a(1)若a > 0 ,求f (x) 的极值;(2)若e x ln x +mx 2 +(1 -e x )x +m ≤ 0 ,求正实数m 的取值范围.15.【北京五中2020 届高三(4 月份)高考数学模拟】设函数f(x)=me x﹣x2+3,其中m∈R.(1)如果f(x)同时满足下面三个条件中的两个:①f(x)是偶函数;②m=1;③f(x)在(0,1)单调递减.指出这两个条件,并求函数h(x)=xf(x)的极值;(2)若函数f(x)在区间[﹣2,4]上有三个零点,求m 的取值范围.16.【辽宁省锦州市渤大附中、育明高中2021 届高三上学期第一次联考】已知函数f (x) =ae x - cos x -x(a ∈R).(1)若 a = 1 ,证明:f (x) ≥ 0 ;(2)若f (x) 在(0,π) 上有两个极值点,求实数 a 的取值范围.17.【西南地区名师联盟2020 届高三入学调研考试】已知函数f (x)=1x3 +bx2 +cx ,b 、c 为常数,且3学习界的007- 1< b < 1, f '(1) = 0 . 2(1)证明: -3 < c < 0 ;(2)若 x 是函数 y = f (x ) - cx 的一个极值点,试比较 f ( x - 4) 与 f (-3) 的大小. 0218.【山东省威海荣成市 2020 届高三上学期期中】某水产养殖公司在一片海域上进行海洋牧场生态养殖, 如图所示,它的边界由圆O 的一段圆弧 PMQ ( M 为此圆弧的中点)和线段 PQ 构成.已知圆O 的半径为12 千米, M 到 PQ 的距离为16 千米.现规划在此海域内修建两个生态养殖区域,养殖区域 R 1 为矩形 ABCD ,养殖区域 R 2 为 A M B ,且 A , B 均在圆弧上,C ,D 均在线段 PQ 上,设∠AOM =α.(Ⅰ)用α分别表示矩形 ABCD 和 A M B 的面积,并确定cos α的范围;(Ⅱ)根据海域环境和养殖条件,养殖公司决定在 R 1 内养殖鱼类,在 R 2 内养殖贝类,且养殖鱼类与贝类单位面积的年产值比为3 : 2 .求当α为何值时,能使年总产值最大.19.【江苏省南通市 2020 届高三下学期高考考前模拟卷】已知函数 f (x ) = ( x - a ) e x + b (a , b ∈ R ) .(1) 讨论函数 f( x ) 的单调性;(2) 对给定的 a ,函数 f( x ) 有零点,求b 的取值范围;(3)当 a = 2 , b = 0 时, F (x ) = f ( x ) - x + ln x ,记 y = F ( x ) 在区间⎛ 1 ,1⎫上的最大值为 m ,且4 ⎪ ⎝ ⎭m ∈[n, n + 1), n ∈Z ,求n 的值.20.【陕西省西安中学2020-2021 学年高三上学期第一次月考】已知函数f ( x) =x -1 -a ln x .(1)当 a = 1 时,求f(x)的最小值;(2)设m 为整数,且对于任意正整数n ,(1+1)(1+1) ⋅⋅⋅ (1+1) <m ,求m 的最小值.2 22 2n。
河北省衡水中学2021届高三下学期第二次调研考试物理试题+Word版含答案

2020—2021学年度下学期高三年级二调考试物理试卷本试卷分第Ⅰ卷(选择题)和第Ⅰ卷(非选择题)两部分。
共8页,共100分,考试时间75分钟。
第Ⅰ卷(选择题 共48分)一、单项选择题(本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.国际单位制(缩写SI )定义了米(m )、秒(s )等7个基本单位,其他单位均可由基本物理量和物理公式导出。
例如,由m 和s 可以导出速度单位-1m s ⋅。
历史上,曾用“米原器”定义米,用平均太阳日定义秒。
但是,以实物或其运动来定义基本单位会受到环境和测量方式等因素的影响,而采用物理常量来定义则可避免这种困扰。
1967年用铯-133原子基态的两个超精细能级间跃迁辐射的频率=9192631770Hz v ∆定义s ;1983年用真空中的光速-1299792458m s c =⋅定义m 。
2018年第26届国际计量大会决定,7个基本单位全部用基本物理常量来定义(对应关系如图,例如,s 对应v ∆,m 对应c )。
新SI 自2019年5月20日(国际计量日)正式实施,这将对科学和技术发展产生深远影响。
下列选项不正确的是 ( )A.7个基本单位全部用物理常量定义,保证了基本单位的稳定性B.用真空中的光速c (1m s -⋅)定义m ,是因为长度l 与速度v 存在l vt =,而s 已定义C.因为普朗克常量h (J s ⋅)的单位中没有kg ,所以无法用它来定义质量单位D.用基本电荷e (C )定义安培(A ),是因为电荷量q 与电流I 存在I q t =,而s 已定义2.甲、乙两质点同时从0x =处出发沿x 轴正方向做直线运动。
甲、乙运动速度v 与位移x 的关系如图所示,其中甲的图线为抛物线的一部分(该抛物线顶点在坐标原点且关于x 轴对称),乙的图线为与x 轴平行的直线。
由图可知,下列说法正确的是 ( )A.甲做加速度为21m s 的匀加速直线运动B.两质点相遇时,甲速度大小为6mC.两质点在3m x =处相遇D.出发后1s ,甲速度大小为3m3.如图所示,质量为M 的正三棱柱横放在两根固定的处于同一水平面的平行光滑杆上,下列判断正确的是( )A.每根杆对棱柱的弹力为12Mg B.两根杆对棱柱的总的作用力为2MgC.若稍微减小两杆的水平距离,每根杆对棱柱的弹力的大小都将增大D.若稍微增大两杆的水平距离,每根杆对棱柱的弹力的大小都不变4.2020年6月23日上午,北斗三号全球卫星导航系统的“收官之星”成功发射,标志着北斗三号全球卫星导航系统全球星座组网部署最后一步完成。
高中物理专项习题-电学实验—高考真题(附答案)
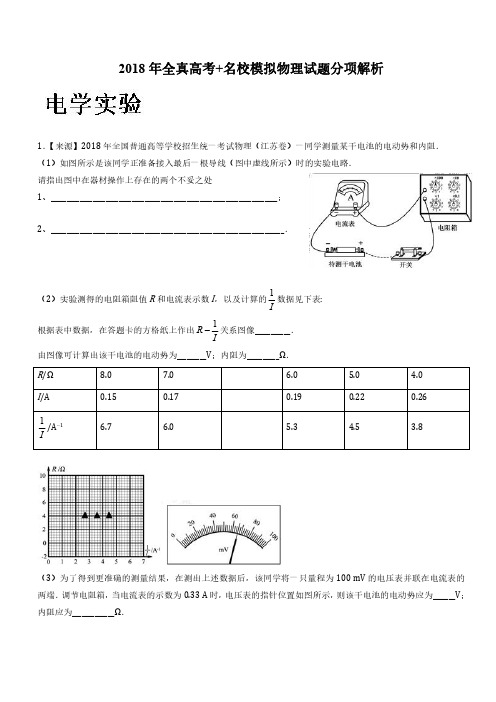
2018年全真高考+名校模拟物理试题分项解析1.【来源】2018年全国普通高等学校招生统一考试物理(江苏卷)一同学测量某干电池的电动势和内阻.(1)如图所示是该同学正准备接入最后一根导线(图中虚线所示)时的实验电路.请指出图中在器材操作上存在的两个不妥之处1、______________________________________________________________________;2、________________________________________________________________________.(2)实验测得的电阻箱阻值R和电流表示数I,以及计算的1I数据见下表:根据表中数据,在答题卡的方格纸上作出1RI 关系图像___________.由图像可计算出该干电池的电动势为_________V;内阻为__________Ω.R/Ω8.07.0 6.0 5.0 4.0I/A0.150.170.190.220.261I/A–1 6.7 6.0 5.3 4.5 3.8(3)为了得到更准确的测量结果,在测出上述数据后,该同学将一只量程为100mV的电压表并联在电流表的两端.调节电阻箱,当电流表的示数为0.33A时,电压表的指针位置如图所示,则该干电池的电动势应为_______V;内阻应为_____________Ω.2.【来源】2018年普通高等学校招生全国统一考试物理(全国II卷)某同学组装一个多用电表。
可用的器材有:μ内阻900Ω);电阻箱R1(阻值范围0~999.9Ω);电阻箱R2(阻值范围0~99999.9Ω);微安表头(量程100A导线若干。
要求利用所给器材先组装一个量程为1mA的直流电流表,在此基础上再将它改装成量程为3V的直流电压表。
组装好的多用电表有电流1mA和电压3V两挡。
回答下列问题:(1)在虚线框内画出电路图并标出R1和R2,其中*为公共接线柱,a和b分别是电流挡和电压挡的接线柱___________。
河北衡水中学2018届高三第十次模考 教师版
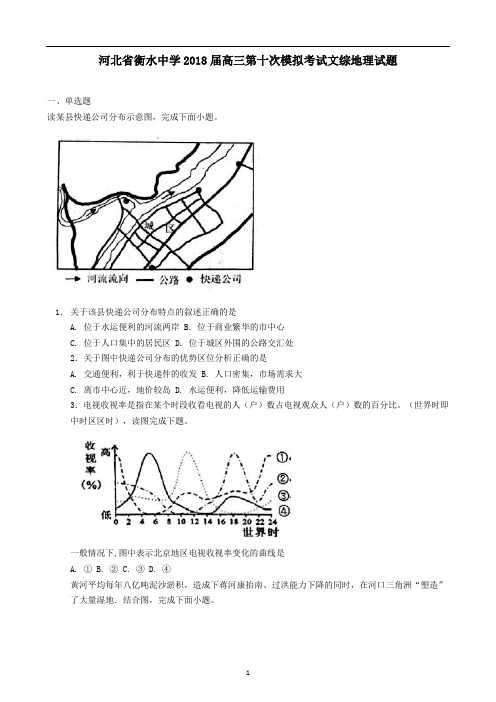
河北省衡水中学2018届高三第十次模拟考试文综地理试题一、单选题读某县快递公司分布示意图,完成下面小题。
1.关于该县快递公司分布特点的叙述正确的是A. 位于水运便利的河流两岸B. 位于商业繁华的市中心C. 位于人口集中的居民区D. 位于城区外围的公路交汇处2.关于图中快递公司分布的优势区位分析正确的是A. 交通便利,利于快递件的收发B. 人口密集,市场需求大C. 离市中心近,地价较岛D. 水运便利,降低运输费用3.电视收视率是指在某个时段收看电视的人(户)数占电视观众人(户)数的百分比。
(世界时即中时区区时),读图完成下题。
一般情况下,图中表示北京地区电视收视率变化的曲线是A. ①B. ②C. ③D. ④黄河平均每年八亿吨泥沙淤积,造成下蒋河康抬南、过洪能力下降的同时,在河口三角洲“塑造”了大量湿地.结合图,完成下面小题。
4.关于黄河泥沙问题的说法.正确的是A. 黄河的年输沙总量和年径流总量的年际变化大并呈递减趋势B. 黄河的年输沙总量和年径流总量的相关性不是很大C. 黄河的年径流总量最大值和年输沙总量最大值出现的年份相同D. 黄河的年汛期径流量制约着年输沙总量的大小5.下列说法正确的是A. 口门外5km内平均水深一定时,新增湿地面积和年入海泥沙量成负相关关系B. 口门外5km内平均水深3m时,5亿—6亿吨入海泥沙将“塑造”5~lOkm2湿地C. 口门外5km内平均水深4m时,增加湿地面积20km2至少需人海泥沙量1O亿吨D. 口门外5km内平均水深5m时,6亿吨年入海泥沙量是湿地面积增加的临界点江苏兴化垛田传统生态系统被联合国粮农组织评定为全球重要农业文化遗产(GIAHS)创造性的将低洼沼泽地改造成岛状耕地,具有独特的水土利用特点。
读垛田农业示意图,回答下面小题。
6.垛田农业主要的生态效益是A. 生物问互生互养,形成良性发展B. 延长产业链,提高产品附加值C. 废弃物充分利用,利于经济发展D. 减少化肥使用,保护生态环境7.垛田农业生产可缓解当地的A. 土地盐碱化B. 水土流失C. 早涝灾害D. 土地污染8.垛田农业为适应时代的需求,从环境、经济效益角度看,最适宜发展A. 休闲观光旅游B. 芋头叶编织C. 鱼类深加工D. 水禽类养殖西伯利亚高原是冬季存在于蒙古——西伯利亚地区对流层下部稳定的强大冷高压,一般选择气压场中1025hpa等压线作为其特征线。
高考数学二轮复习(高考22题)12+4分项练10 圆锥曲线 文
12+4分项练10 圆锥曲线1.(2017·全国Ⅰ)已知F 是双曲线C :x 2-y 23=1的右焦点,P 是C 上一点,且PF 与x 轴垂直,点A 的坐标是(1,3),则△APF 的面积为( ) A.13 B.12 C.23 D.32 答案 D解析 因为F 是双曲线C :x 2-y 23=1的右焦点,所以F (2,0).因为PF ⊥x 轴,所以可设P 的坐标为(2,y P ). 因为P 是C 上一点,所以4-y 2P3=1,解得y P =±3,所以P (2,±3),|PF |=3.又因为A (1,3),所以点A 到直线PF 的距离为1, 所以S △APF =12×|PF |×1=12×3×1=32.故选D.2.(2017届福建省宁德市质检)已知直线l :4x +3y -20=0经过双曲线C :x 2a 2-y 2b2=1的一个焦点,且与其一条渐近线平行,则双曲线C 的实轴长为( ) A .3 B .4 C .6 D .8 答案 C解析 由题意得b a =43,c =5,又a 2+b 2=c 2,所以a =3,2a =6,故选C.3.设P 为双曲线x 2-y 215=1右支上一点,M ,N 分别是圆(x +4)2+y 2=4和(x -4)2+y 2=1上的点,设|PM |-|PN |的最大值和最小值分别为m ,n ,则|m -n |等于( ) A .4 B .5 C .6 D .7 答案 C解析 双曲线的两个焦点为F 1(-4,0),F 2(4,0),分别为两个圆的圆心,半径分别为r 1=2,r 2=1,|PM |max =|PF 1|+2,|PN |min =|PF 2|-1,故|PM |-|PN |的最大值为m =(|PF 1|+2)-(|PF 2|-1)=|PF 1|-|PF 2|+3=5. 同理可得求得n =-1. 则|m -n |=6. 故选C.4.(2017届江西省赣州市二模)已知双曲线x 2a 2-y 2b2=1 (a >0,b >0)的离心率为5,则抛物线x2=4y 的焦点到双曲线的渐近线的距离是( ) A.510 B.55 C.255 D.455答案 B解析 抛物线x 2=4y 的焦点为(0,1),双曲线x 2a 2-y 2b 2=1 (a ,b >0)的离心率为5,所以b a=c 2-a 2a2=e 2-1=2, 双曲线的渐近线方程为y =±b ax =±2x , 则抛物线x 2=4y 的焦点到双曲线的渐近线的距离是11+4=55,故选B. 5.(2017·日照二模)已知双曲线C :x 2a 2-y 2b2=1 (a >0,b >0)的左、右焦点分别为F 1,F 2,左、右顶点分别为A ,B ,虚轴的上、下端点分别为C ,D ,若线段BC 与双曲线的渐近线的交点为E ,且∠BF 1E =∠CF 1E ,则双曲线的离心率为( ) A .1+ 6 B .1+ 5 C .1+ 3 D .1+ 2 答案 C解析 根据双曲线C 的性质可以得到,C (0,b ),B (a,0),F 1(-c,0),双曲线C 的渐近线方程为y =±b a x ,直线BC 方程为y =-ba x +b ,联立⎩⎪⎨⎪⎧y =-ba x +b ,y =ba x ,解得⎩⎪⎨⎪⎧x =a 2,y =b2,即点E ⎝ ⎛⎭⎪⎫a 2,b2,所以E 是线段BC 的中点,又因为∠BF 1E =∠CF 1E ,所以F 1C =F 1B ,而F 1C =c 2+b 2,F 1B =a +c ,故c 2+b 2=(a +c )2,因为a 2+b 2=c 2,所以2a 2+2ac -c 2=0,因为e =ca,即e 2-2e -2=0,所以e =1+3,故选C.6.(2017届黑龙江省哈尔滨师范大学附属中学模拟)双曲线x 2a 2-y 2b2=1 (a >0,b >0)的左、右焦点分别为F 1,F 2,P 为双曲线右支上一点,且PF 1→·PF 2→=0,若∠PF 1F 2∈⎣⎢⎡⎦⎥⎤π12,π6,则双曲线离心率的取值范围是( ) A .[2,3+1] B .[2,23+1] C .[2,2] D .[2,3+1]答案 D解析 由题设可知∠F 1PF 2=90°,所以设∠PF 1F 2=θ, 则|PF 1|=2c cos θ,|PF 2|=2c sin θ, 由双曲线的定义可得2c cos θ-2c sin θ=2a , 即a c=1-sin 2θ,因为θ∈⎣⎢⎡⎦⎥⎤π12,π6,所以2θ∈⎣⎢⎡⎦⎥⎤π6,π3,sin 2θ∈⎣⎢⎡⎦⎥⎤12,32,此时a c=1-sin 2θ∈⎣⎢⎡⎦⎥⎤1-32,12, 所以离心率的取值范围是e ∈[ 2,3+1],故选D.7.(2017届山西省太原市三模)已知点P 在抛物线y 2=x 上,点Q 在圆⎝ ⎛⎭⎪⎫x +122+(y -4)2=1上,则|PQ |的最小值为( ) A.352-1 B.332-1 C .23-1 D.10-1 答案 A解析 设抛物线上点的坐标为P (m 2,m ) (m >0).圆心⎝ ⎛⎭⎪⎫-12,4与抛物线上的点的距离的平方 d 2=⎝⎛⎭⎪⎫m 2+122+(m -4)2=m 4+2m 2-8m +654.令f (m )=m 4+2m 2-8m +654 (m >0),则f ′(m )=4(m -1)(m 2+m +2),由导函数与原函数的关系可得函数在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,函数的最小值为f (1)=454,由几何关系可得|PQ |的最小值为454-1=352-1.故选A. 8.(2017届重庆市巴蜀中学三模)已知双曲线x 24-y 22=1上有不共线三点A ,B ,C ,且AB ,BC ,AC 的中点分别为D ,E ,F ,若满足OD ,OE ,OF 的斜率之和为-1,则1k AB +1k BC +1k AC等于( )A .2B .- 3C .-2D .3答案 C解析 设A (x 1,y 1),B (x 2,y 2),D (x 0,y 0),将A ,B 两点坐标代入双曲线方程,作差并化简得y 1+y 2x 1+x 2=12·x 1-x 2y 1-y 2,即k OD =12k AB ,同理可得k OE =12k BC ,k OF =12k AC ,依题意有k OD +k OE +k OF =12k AB+12k BC +12k AC =-1,即1k AB +1k BC +1k AC =-2.9.(2017·四川省成都市九校联考)已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 为抛物线上一点,PA ⊥l ,A 为垂足,若直线AF 的斜率为-3,则|PF |等于( ) A .4 B .6 C .8 D .8 3 答案 C解析 ∵抛物线方程为y 2=8x ,∴焦点F (2,0),准线l 的方程为x =-2,∵直线AF 的斜率为-3,∴直线AF 的方程为y =-3(x -2),由⎩⎨⎧x =-2,y =-3(x -2),可得A 点坐标为(-2,43),∵PA ⊥l ,A 为垂足, ∴P 点纵坐标为43,代入抛物线方程, 得P 点坐标为(6,43),∴|PF |=|PA |=6-(-2)=8,故选C.10.(2017届江西省南昌市三模)已知F 1,F 2是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且∠F 1PF 2=π4,则椭圆和双曲线的离心率乘积的最小值为( )A.12B.22 C .1 D. 2 答案 B解析 设椭圆和双曲线的离心率分别为e 1,e 2, 设椭圆的长半轴长为a 1,双曲线的实半轴长为a 2⇒⎩⎪⎨⎪⎧|PF 1|+|PF 2|=2a 1,|PF 1|-|PF 2|=2a 2⇒|PF 1|=a 1+a 2,|PF 2|=a 1-a 2⇒4c 2=(a 1+a 2)2+(a 1-a 2)2-2(a 1+a 2)(a 1-a 2)cos π4⇒4c 2=(2-2)a 21+(2+2)a 22⇒4=2-2e 21+2+2e 22≥22-2e 21×2+2e 22=22e 1e 2⇒e 1e 2≥22,故选B. 11.(2017·全国Ⅰ)设A ,B 是椭圆C :x 23+y 2m=1长轴的两个端点.若C 上存在点M 满足∠AMB=120°,则m 的取值范围是( )A .(0,1]∪[9,+∞)B .(0,3]∪[9,+∞)C .(0,1]∪[4,+∞)D .(0,3]∪[4,+∞) 答案 A解析 方法一 设椭圆焦点在x 轴上,则0<m <3,点M (x ,y ). 过点M 作x 轴的垂线,交x 轴于点N ,则N (x,0). 故tan∠AMB =tan(∠AMN +∠BMN )=3+x |y |+3-x |y |1-3+x |y |·3-x|y |=23|y |x 2+y 2-3. 又tan∠AMB =tan 120°=-3,且由x 23+y 2m =1,可得x 2=3-3y 2m,则23|y |3-3y 2m +y 2-3=23|y |(1-3m)y2=- 3. 解得|y |=2m3-m.又0<|y |≤m ,即0<2m3-m ≤m ,结合0<m <3解得0<m ≤1.对于焦点在y 轴上的情况,同理亦可得m ≥9. 则m 的取值范围是(0,1]∪[9,+∞). 故选A.方法二 当0<m <3时,焦点在x 轴上, 要使C 上存在点M 满足∠AMB =120°, 则a b≥tan 60°=3,即3m≥3,解得0<m ≤1.当m >3时,焦点在y 轴上,要使C 上存在点M 满足∠AMB =120°, 则a b≥tan 60°=3,即m3≥3,解得m ≥9.故m 的取值范围为(0,1]∪[9,+∞). 故选A.12.(2017届吉林省实验中学模拟)已知双曲线E :x 2a 2-y 2b2=1 (a >0,b >0)的右顶点为A ,抛物线C :y 2=8ax 的焦点为F ,若在E 的渐近线上存在点P 使得PA ⊥FP ,则E 的离心率的取值范围是( )A .(1,2) B.⎝⎛⎦⎥⎤1,324C .(2,+∞) D.⎣⎢⎡⎭⎪⎫324,+∞ 答案 B解析 双曲线E :x 2a 2-y 2b2=1 (a >0,b >0)的右顶点为A (a ,0),抛物线:y 2=8ax 的焦点F (2a,0),双曲线的渐近线方程为y =±b ax ,可设P ⎝⎛⎭⎪⎫m ,b a m ,即有AP →=⎝ ⎛⎭⎪⎫m -a ,b a m ,FP →=⎝ ⎛⎭⎪⎫m -2a ,b a m ,由PA ⊥FP ,即AP →·FP →=0,即(m -a )(m -2a )+b 2a2m 2=0,化为⎝ ⎛⎭⎪⎫1+b 2a 2m 2-3ma +2a 2=0,由题意可得Δ=9a 2-4⎝ ⎛⎭⎪⎫1+b 2a 2·2a 2≥0,即有a 2≥8b 2=8(c 2-a 2),即8c 2≤9a 2,则e =c a ≤324.由e >1,可得1<e ≤324.故选B.13.已知点F 1,F 2是椭圆C :x 2a 2+y 2b2=1 (a >b >0)的两个焦点,P 为椭圆C 上一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________. 答案 3解析 由PF 1→⊥PF 2→知,∠F 1PF 2=90°, 则由题意,得⎩⎪⎨⎪⎧|PF 1|+|PF 2|=2a ,12|PF 1|·|PF 2|=9,|PF 1|2+|PF 2|2=4c 2,可得4c 2+36=4a 2,即a 2-c 2=9,所以b =3.14.(2017·河北省衡水中学二模)已知点F 1,F 2分别是双曲线C :x 2-y 2b2=1 (b >0)的左、右焦点,O 为坐标原点,点P 在双曲线C 的右支上,且满足|F 1F 2|=2|OP |,tan∠PF 2F 1≥4,则双曲线C 的半焦距的取值范围为____________. 答案 ⎝ ⎛⎦⎥⎤1,173解析 由|F 1F 2|=2|OP |可得△PF 1F 2为直角三角形,∠F 1PF 2=90°,tan∠PF 2F 1≥4,即|PF 1|≥4|PF 2|,|PF 1|2+|PF 2|2=|F 1F 2|2,又|PF 1|-|PF 2|=2a ,得|PF 2|≤23a ,即(|PF 2|+2a )2+|PF 2|2=4c 2化为(|PF 2|+a )2=2c 2-a 2≤⎝ ⎛⎭⎪⎫23a +a 2,可得c ≤173,又双曲线中c >a =1,所以双曲线C 的半焦距的取值范围为⎝ ⎛⎦⎥⎤1,173. 15.(2017届北京市丰台区二模)在平面直角坐标系xOy 中,点M 不与点O 重合,称射线OM 与圆x 2+y 2=1的交点N 为点M 的“中心投影点”. (1)点M (1,3)的“中心投影点”为________;(2)曲线x 2-y 23=1上所有点的“中心投影点”构成的曲线的长度是________.答案 (1)⎝ ⎛⎭⎪⎫12,32 (2)4π3解析 (1)|OM |=12+(3)2=2,|ON |=1, 所以ON →=12OM →,则N 点坐标为⎝ ⎛⎭⎪⎫12,32.(2)双曲线x 2-y 23=1的渐近线为y =±3x ,由“中心投影点”的定义知,中心投影点是单位圆上夹在两渐近线之间的两段圆弧,一条渐近线的倾斜角为π3,因此弧长为2×23π×1=4π3.16.(2017·河南省豫北重点中学联考)已知抛物线C :y 2=4x 的焦点为F ,直线l 与抛物线C 相切于Q 点,P 是l 上一点(不与Q 重合),若以线段PQ 为直径的圆恰好经过F ,则|PF |的最小值是________. 答案 2解析 根据抛物线的对称性设Q (m,2m ), 则k QF =2m m -1,所以直线PF 的方程为y =1-m2m(x -1),当直线l 与抛物线相切于原点O 时,不满足题意,由y 2=4x (x ≠0),取y =2x ,y ′=1x(x ≠0),所以直线l 的方程是y -2m =1m(x -m ),联立⎩⎪⎨⎪⎧y =1-m 2m (x -1),y -2m =1m(x -m ),解得点P 的横坐标x =-1,所以点P 在抛物线的准线上运动,当点P 的坐标是(-1,0)时,|PF |最小,最小值是2.。
衡水中学2018-2019学年度上学期高三年级三调考试历史答案
2018~2019学年度上学期高三历史三调考试答案一、选择题:共48小题,每题1分。
1-10:CCDDD BDADC11-20:ADCBD AAAAB21-30:BCCAD ACBBD31-40:DAADC CBDCA41-48:CBCAC CAA二、本卷共3小题,其中第49题18分,第50题20分,第51题14分,共52分。
49.(1)特点:士绅发挥较大作用;中央的权力逐步延伸到乡村;承担维护社会稳定和征发赋税的职能;通过宗族、乡约进行治理;儒家伦理不断渗入乡村治理。
(8分)(2)变化:传统乡村治理组织趋向解体;乡镇地方自治体系逐渐形成;地方自治事务进一步拓展;乡村治理法制化。
(6分)影响:促进了乡村经济、文化、教育的发展;减轻了政府负担;缓解了社会矛盾;客观上培植了民主革命的力量。
(4分)50.(1)新变化:稻麦等农作物品种不断推广;南方稻麦轮作制普遍应用;主要产粮区域发生转移;外来高产农作物广泛引种。
(6分)影响:农业经济的区域化趋势加强;农产品的商品化程度提高(商品经济的发展或者区域间长途贩运的兴盛);促进了土地资源的开发,缓解了粮食供应压力;使人们的饮食结构发生革命变化。
(6分)(2)特点:农村经济地域发展不平衡;自然经济受到冲击,农民对市场的依赖程度加深。
(4分)成因:自然经济占据主导地位;中国被卷入了资本主义世界市场,中东部遭受冲击更为严重;中国新生产方式发展的冲击。
(4分)51.(1)私有制占据主导地位;商品经济的发展;雕版印刷术和造纸术的发展;宋朝重文,教育和科举考试向社会下层发展。
(6分)(2)特点:以禁令形式保护版权;立法滞后;国人没有形成普遍的版权保护意识。
(4分)原因:专制统治下法制意识淡薄;商品经济不发达;儒家思想重义轻利。
(4分)。
2019年上海市第五十二中学高考数学选择题专项训练(一模)
2019年上海市第五十二中学高考数学选择题专项训练(一模)抽选各地名校试卷,经典试题,有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。
第 1 题:来源:高中数学第二章统计本章整合试卷及答案新人教A版必修3某高级中学有学生270人,其中一年级108人,二、三年级各81人.现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250;②5,9,100,107,111,121,180,195,200,265;③11,38,65,92,119,146,173,200,227,254;④30,57,84,111,138,165,192,219,246,270.关于上述样本的下列结论中,正确的是( )A.②③都不能为系统抽样B.②④都不能为分层抽样C.①④都可能为系统抽样D.①③都可能为分层抽样【答案】D第 2 题:来源:黑龙江省双鸭山市第一中学2019届高三数学上学期第一次月考试题理(含解析)函数其中()的图象如图所示,为了得到的图象,则只需将的图象()A. 向右平移个长度单位B. 向右平移个长度单位C. 向左平移个长度单位D. 向左平衡个长度单位【答案】A【详解】由函数其中()的部分图象可得A=1,,求得ω=2.再根据五点法作图可得,.故把的图象向右平移个长度单位,可得的图象,第 3 题:来源:广西南宁市2016_2017学年高一数学下学期第一次月考试题试卷及答案在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成的角的正弦值为( )A. B. C.D.【答案】D 提示:在平面A1B1C1D1内过点C1作B1D1的垂线,垂足为E,连接BE.⇒C1E⊥平面BDD1B1,∴∠C1BE的正弦值就是所求角的正弦值.∵BC1=,C1E=,∴sin∠C1BE=.第 4 题:来源:山东省泰安市2019届高三数学一轮复习质量检测试卷理(含解析)若复数的实部与虚部互为相反数,则实数A. 3B.C.D.【答案】D【解析】【分析】利用复数乘法的运算法则化简复数,然后利用复数的实部与虚部的和为零,列方程求解即可.【详解】因为,且复数的实部与虚部互为相反数,所以,,解得,故选D.【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查乘法/除法运算,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.第 5 题:来源:甘肃省兰州市2016_2017学年高一数学下学期期末考试试题试卷及答案若,则是第几象限角()A.一或二B.二或三C.三或四D.四或一第 6 题:来源:湖北省宜昌市2017_2018学年高一数学上学期期中试题试卷及答案已知集合,则= A.B. C. D.【答案】B第 7 题:来源:广东省天河区普通高中2017_2018学年高一数学10月月考试题试卷及答案08若奇函数在上为增函数,且有最小值0,则它在上A.是减函数,有最小值0B.是增函数,有最小值0C.是减函数,有最大值0D.是增函数,有最大值0【答案】D第 8 题:来源:湖南省怀化三中2018_2019学年高一数学上学期期中试题.函数在上是增函数,在上是减函数,则()A. B. C. D.的符号不确定【答案】B第 9 题:来源:重庆市万州三中2018_2019学年高二数学下学期期中试题理函数的图象如图所示,下列数值排序正确的是( )A. B.C. D.第 10 题:来源:四川省崇州市2016-2017学年高一数学下学期开学考试试题设,则的大小关系是()A. B.C. D.【答案】A第 11 题:来源:河北省衡水中学2018届高三数学上学期一轮复习周测试题理试卷及答案已知命题有解,命题,则下列选项中是假命题的为()A.B. C.D.【答案】B第 12 题:来源:广东省天河区普通高中2017_2018学年高二数学11月月考试题04 试卷及答案若,,则下列不等式成立的是A. B. C. D.【答案】.A第 13 题:来源: 2019高考数学一轮复习第2章函数的概念与基本初等函数第3讲函数的奇偶性与周期性分层演练文若函数f(x)=ln(ax+)是奇函数,则a的值为( )A.1 B.-1C.±1 D.0【答案】C.因为f(x)=ln(ax+)是奇函数,所以f(-x)+f(x)=0.即ln(-ax+)+ln(ax+)=0恒成立,所以ln[(1-a2)x2+1]=0,即(1-a2)x2=0恒成立,第 14 题:来源:福建省泉州市2017届高考数学模拟试卷(文科)含答案解析若,则=()A.i B.﹣i C.﹣1 D.1【答案】D【考点】A8:复数求模.【分析】利用复数的运算法则、模的计算公式即可得出.【解答】解: ===i,则=1.故选:D.【点评】本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.第 15 题:来源:山东省武城二中2017届高三数学下学期第一次月考试题试卷及答案理若直角坐标平面内两点P,Q满足条件①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则对称点(P,Q)是函数y=f(x)的一个“伙伴点组”(点对(P,Q)与(Q,P)看作同一个“伙伴点组”).则下列函数中,恰有两个“伙伴点组”的函数是___(填空写所有正确选项的序号)①;②;③;④.【答案】②③第 16 题:来源: 2015-2016学年广东省东莞市高二数学下学期期末试卷a 理(含解析)用反证法证明命题:“已知a,b为实数,则方程x2+ax+b=0至少有一个实根”时,要做的假设是()A.方程x2+ax+b=0没有实根B.方程x2+ax+b=0至多有一个实根C.方程x2+ax+b=0至多有两个实根D.方程x2+ax+b=0恰好有两个实根【答案】A【考点】反证法与放缩法.【分析】直接利用命题的否定写出假设即可.【解答】解:反证法证明问题时,反设实际是命题的否定,∴用反证法证明命题“设a,b为实数,则方程x2+ax+b=0至少有一个实根”时,要做的假设是:方程x2+ax+b=0没有实根.故选:A.第 17 题:来源:江西省上饶市玉山县第一中学2018_2019学年高二数学下学期期中试题理(10_19班)若函数的导函数的图像关于原点对称,则的解析式可能为()A.B.C.D.【答案】A第 18 题:来源:重庆市六校联考高一(上)期末数学试卷(含答案解析)若区间[x1,x2]的长度定义为|x2﹣x1|,函数f(x)=(m∈R,m≠0)的定义域和值域都是[a,b],则区间[a,b]的最大长度为()A. B. C. D.3【答案】A【解答】解:函数f(x)=(m∈R,m≠0)的定义域是{x|x≠0},则[m,n]是其定义域的子集,∴[m,n]⊆(﹣∞,0)或(0,+∞).f(x)==﹣在区间[a,b]上时增函数,则有:,故a,b是方程f(x)=﹣=x的同号相异的实数根,即a,b是方程(mx)2﹣(m2+m)x+1=0同号相异的实数根.那么ab=,a+b=,只需要△>0,即(m2+m)2﹣4m2>0,解得:m>1或m<﹣3.那么:n﹣m==,故b﹣a的最大值为,第 19 题:来源: 2017年湖北省宜昌市长阳县高一数学3月月考试题试卷及答案在△ABC中,,c=2,C=600,则A等于() A.1500 B.750 C.1050 D.750或1050【答案】 B第 20 题:来源:湖南省郴州市湘南中学2019届高三数学上学期期中试题理函数的零点所在的大致区间是()A.(0,1) B.(1,2) C.(2,e) D.(3,4)【答案】B第 21 题:来源:河北省石家庄市2017_2018学年高一数学上学期期中试题试卷及答案函数的零点所在区间为( )A. B. C. D.【答案】 C第 22 题:来源:河南省安阳市2017_2018学年高二数学上学期第二次月考试题试卷及答案已知等差数列中,,公差,则使前项和为取最小值的正整数的值是()A.4和 5 B.5和 6 C.6和7 D.7和8【答案】C第 23 题:来源: 2015-2016学年广东省东莞市高二数学下学期期末试卷a 理(含解析)对具有线性相关关系的两个变量y与x进行回归分析,得到一组样本数据(x1,y1),(x2,y2)…(xn,yn),则下列说法中不正确的是()A.若最小二乘法原理下得到的回归直线方程=0.52x+,则y与x具有正相关关系B.残差平方和越小的模型,拟合的效果越好C.在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适D.用相关指数R2来刻画回归效果,R2越小说明拟合效果越好【答案】D【分析】可以用来衡量模拟效果好坏的几个量分别是相关指数,残差平方和和相关系数,只有残差平方和越小越好,其他的都是越大越好.【解答】解:若最小二乘法原理下得到的回归直线方程=0.52x+,b=0.52>0,则y与x具有正相关关系,正确;残差平方和越小的模型,拟合的效果越好,正确;可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.故正确;相关指数R2取值越大,说明残差平方和越小,模型的拟合效果越好,故不正确.故选:D.第 24 题:来源:新疆维吾尔自治区阿克苏市2017_2018学年高二数学上学期第二次月考试题试卷及答案理已知,则“”是“”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】若“”,则,即.所以,充分性成立;若“”,则,有或.必要性不成立.故“”是“”的充分不必要条件.故选A.第 25 题:来源:宁夏石嘴山市2018届高三数学上学期期中试题理用数学归纳法证明“”时,由的假设证明时,如果从等式左边证明右边,则必须证得右边为()A. B.C. D.【答案】D第 26 题:来源:河北省石家庄市2016_2017学年高一数学下学期学情反馈试题(一)理试卷及答案在中,角、、的对边分别为、、,则以下结论错误的为()A.若,则B.C.若,则;反之,若,则D.若,则【答案】D【解析】试题分析:∵,∴由正弦定理,,又∵,为的内角,∴,故,A正确;∵由正弦定理可得,∴,故B正确;在,设外接圆的半径为,若,则,由正弦定理可得,即;若,即有,即,即.则在中,,故C正确;∵,∴,∴或,∴或,∴三角形为直角三角形或等腰三角形,故D错误.故选:D.第 27 题:来源:湖南省长沙市雅礼中学2019届高三数学上学期月考试题二理现有四个函数:①,②,③,④的图像(部分)如下,但顺序打乱了,则按照从左到右将图象对应的序号排列正确的组是A.①③②④ B.②①③④ C.③①④② D.①④②③【答案】D第 28 题:来源: 2017届宁夏银川市高三第二次模拟考试理科数学试卷含答案已知是定义在R上的偶函数,且对恒成立,当时,,则A. B.C. D.【答案】B第 29 题:来源:贵州省思南中学2018_2019学年高二数学下学期期末考试试题理复数z满足,则复数的虚部是()A.1 B.-1 C. D.【答案】C第 30 题:来源:辽宁省沈阳市2018届高三数学11月阶段测试试题理试卷及答案下列判断错误的是()SX010202A.“”是“”的充分不必要条件B.命题“”的否定是“”C.若为真命题,则均为假命题D.命题“若,则”为真命题,则“若,则”也为真命题【答案】C第 31 题:来源:山西省芮城县2017_2018学年高二数学上学期第一次月考试题理试卷及答案已知三棱锥的所有顶点都在球的球面上,为球的直径,且,,为等边三角形,三棱锥的体积为,则球的半径为A. 3B.1C.2D.4【答案】C第 32 题:来源: 2016_2017学年福建省厦门市高二数学试卷及答案下学期期中试题理设a=,b=,,则a、b、c间的大小关系是()A.a>b>c B.b>a>c C.b>c>a D.a>c>b【答案】D第 33 题:来源:高中数学第三章导数及其应用3.1导数3.1.2瞬时速度与导数3.1.3导数的几何意义自我小测新人教B版选修1_120171101235曲线y=x3+2在点处切线的倾斜角为( )A.30° B.45° C.135° D.60°【答案】B第 34 题:来源:广东省深圳市耀华实验学校2018_2019学年高一数学下学期入学考试试题(国际1班)若函数是定义域为上的减函数,则函数的图像大致是 ( ).A. B.C . D.【答案】D第 35 题:来源:湖北省宜昌市2017_2018学年高二数学上学期期中试题理试卷及答案若圆的半径为1,圆心在第二象限,且与直线和轴都相切,则圆的标准方程是()A. B.C. D.【答案】B第 36 题:来源:黑龙江省哈尔滨市2016_2017学年高二数学6月月考试题试卷及答案理.离散型随机变量X的分布列为,则与依次为( )和和和和【答案】D第 37 题:来源: 2017届吉林省长春市朝阳区高三数学下学期第八次模拟考试试题试卷及答案理若,则=(A)(B)1 (C)5 (D)25【答案】B第 38 题:来源:广东省江门市第二中学2017_2018学年高二数学11月月考试题(含解析)数列前项的和为()A. B.C. D.【答案】B【解析】数列前项的和故选B.第 39 题:来源: 2017年河南省焦作市高考数学二模试卷(理科)含答案解析在区间上任选两个数x和y,则y<sinx的概率为()A. B. C. D.【答案】C【考点】几何概型.【分析】该题涉及两个变量,故是与面积有关的几何概型,分别表示出满足条件的面积和整个区域的面积,最后利用概率公式解之即可.【解答】解:在区间上任选两个数x和y,区域的面积为,满足y<sinx的区域的面积为=(﹣cosx)=1,∴所求概率为.故选C.第 40 题:来源:江西省南康中学2018_2019学年高二数学二下学期期中(第二次大考)试题理已知椭圆(a>b>0)的左、右焦点分别为为椭圆上一动点,面积的最大值为,则椭圆的离心率为()A. B.1 C. D.【答案】A。
2019届高三上期末数学分类汇编(18)等差数列与等比数列(含答案)
(山东省德州市2019届高三期末联考数学(理科)试题)4.已知数列为等差数列,且成等比数列,则的前6项的和为()A. 15B.C. 6D. 3【答案】C【解析】【分析】利用成等比数列,得到方程2a1+5d=2,将其整体代入 {a n}前6项的和公式中即可求出结果.【详解】∵数列为等差数列,且成等比数列,∴,1,成等差数列,∴2,∴2=a1+a1+5d,解得2a1+5d=2,∴{a n}前6项的和为2a1+5d)=.故选:C.【点睛】本题考查等差数列前n项和的求法,是基础题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.(福建省宁德市2019届高三第一学期期末质量检测数学理科试题)3.等差数列中,,,则数列的前20项和等于()A. -10B. -20C. 10D. 20【答案】D【解析】【分析】本道题结合等差数列性质,计算公差,然后求和,即可。
【详解】,解得,所以,故选D。
【点睛】本道题考查了等差数列的性质,难度中等。
(江西省新余市2019届高三上学期期末考试数学(理)试题)5.在等差数列中,已知是函数的两个零点,则的前10项和等于( )A. -18B. 9C. 18D. 20【答案】D【解析】【分析】由韦达定理得,从而的前10项和,由此能求出结果.【详解】等差数列中,是函数的两个零点,,的前10项和.故选:D.【点睛】本题考查等差数列的前n项和公式,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.(湖南省长沙市2019届上学期高三统一检测理科数学试题)13.设等差数列的前项和为,且,则__________.【答案】【解析】分析:设等差数列{a n}的公差为d,由S13=52,可得13a1+d=52,化简再利用通项公式代入a4+a8+a9,即可得出.详解:设等差数列{a n}的公差为d,∵S13=52,∴13a1+d=52,化为:a1+6d=4.则a4+a8+a9=3a1+18d=3(a1+6d)=3×4=12.故填12.点睛:本题主要考查等差数列通项和前n项和,意在考查学生等差数列基础知识的掌握能力和基本的运算能力.(湖南省湘潭市2019届高三上学期第一次模拟检测数学(文)试题)3.已知数列是等比数列,其前项和为,,则()A. B. C. 2 D. 4【答案】A【解析】【分析】由题意,根据等比数列的通项公式和求和公式,求的公比,进而可求解,得到答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衡水中学2018—2018学年度第二学期第二次调研考试
高二年级数学试卷(文科)
本试卷分选择题和非选择题两部分,共150分。考试时间120分钟。
一、选择题(每小题5分,共60分。下列每小题所给选项只有一项符合题意,请将正确答案
的序号填涂在答题卡上)
1.设QP,是两个非空实数集合,定义集合},|{QbPabaQP.
若}6,2,1{},5,2,0{QP,则QP中元素的个数是( )
A. 9 B. 8 C. 7 D. 6
2. 设全集RU,}23|{xxxA或,}51|{xxB,
则集合}21|{xx是( )
A.
)()(BCAC
UU
B.)(BACU C.BACU)(
D.BA
3.已知函数)(xf是定义在R上的偶函数,并且在),0[上是单调函数,
若0)1(,2)0(ff,则使得0)(xf的x的取值范围是 ( )
A.)1,0( B.),1( C.),1()1,( D.)1,1(
4. 已知函数)2lg()(bxfx(b为常数),若当1x时,0)(xf恒成立,
则( )
A.1b B.1b C.1b D.1b
5.如果7722107)21(xaxaxaax,
那么721aaa的值等于( )
A. -1 B. 0 C. 2 D.
–2
6. 某人射击1次击中目标的概率为0.6,经过3次射击,此人至少两次击中目标的
概率为( )
A.12581 B.12554 C. 12536 D. 12527
7. 甲袋内装有大小均匀的白球3个,黑球5个,乙袋内装有大小均匀的白球4个,黑球
6
个。
现从甲袋内随机拿出一个球放入乙袋,充分混合后,再从乙袋内随机拿一球放入甲
袋,
则甲袋中白球没有减少的概率( )
A. 447 B. 449 C. 4425 D. 4435
8.有红、黄、绿三色卡片各五张,每种颜色的卡片上分别写有A、B、C、D、E五个字
母,
如果每次取出四张卡片,要求三种颜色齐全,且字母不同,则不同的取法种数为( )
A. 60 B. 90 C. 180 D. 360
9.若2a,则方程03323axx在
(0,2)上恰好有( )个根
A.0 B. 1 C.2 D. 3
10.函数aaxxxf2)(2在区间)1,(上有最小值,则函数xxfxg)()(在
区间),1(上一定( )
A.有最小值 B.有最大值 C. 是减函数 D. 是增函数
11.函数dcxbxxxf23)( 在区间]21[,上是减函数,那么cb有
( )
A.最大值215 B.最大值215 C.最小值215 D.最小值215
12.设函数)10()2)(1()(xxxxxf,则)0(f的值为( )
A.10 B.55 C. 10! D.0
二、填空题(本大题共4小题,每小题5分,共20分。把答案写在答题纸的相应位置)
13.甲、乙两人自相距30米处同时相向运动,甲每分钟走3米;乙第1分钟走2米,
且以后每分钟比前1分钟多走0.5米,则甲和乙开始运动后 分钟相遇.
14.设132a,函数)11(23)(23xbaxxxf的最大值
为1,
最小值为26,则常数ba,的值分别为 和
15.从1,2,3,…,10这十个数中,任取3个不同的数,则这3个数恰好能组成
等差数列的概率为
16.函数251)()(xxfxF的图象在点5x处的切线方程是8xy,
则)5()5(ff的值等于
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17.(本题10分) 在等比数列}{na中,941aa,832aa,
求数列}{na的前6项和6S.
18. (本题12分) 设函数)0()(35acbxaxxf.
(1)若)(xf在1x和)0(00xxx处有不同的极值,且极大值为4,
极小值为1,求0x及实数cba,,的值;
(2) 若)(xf在),2(上单调递增且0)(xf,求ab的最大值.
19.(本题12分)已知)0()(23adcxbxaxxf是定义在R上
的函数, 且)(xf在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求c的值;
(2) 在函数)(xf的图象上是否存在一点),(00yxM,使得)(xf在点M的
切线斜率为b3?若存在,求出点M的坐标;若不存在,请说明理由.
20.(本题12分)七个人排成两排照相,前排3人,后排4人.
(1) 求甲在前排,乙在后排的概率;
(2) 求甲、乙在同一排且相邻的概率;
(3) 求甲、乙之间恰好有一人的概率.
21.(本题12分)口袋里放了12个大小完全一样的小球,其中3
个是红色的,
4个是白色的,5个是蓝色的,现从袋中任意取出4个小球,求:
(1) 取出的小球的颜色至少是两种的概率;
(2) 取出的小球的颜色是三种的概率.
22.(本题12分) 设函数)0(13)(23kxkxxf.
(1) 求函数)(xf的单调区间;
(2) 若函数)(xf在区间(0,2)上单调递减,试求实数k的取值范围;
(3) 若函数)(xf的极小值大于0,试求实数k的取值范围.
高二二调考试数学答案
(文科)
一、BCDBD ADDBD BC
二、
13.5 ; 14.36;1 15.61 ; 16.
-5
三、
17.解:设首项为1a ,公比为q,由题意得:
8,9211311qaqaqaa, 解得:2,11qa,或
2
1
,81qa
则当2,11qa时,636S; 当21,81qa时,4636S
18.解:(1)2435)(bxaxxf ,依题意得:
035)(,035)1(20400bxaxxfbaf
又0,00xa,则1,0350xba,
所以当11x时,0)(xf;当1x或1x时,0)(xf,
故1x时函数有极大值,1x时函数有极小值;
则bacbafcbaf351)1(4)1( 得25,415,49,10cbax
(2) 2435)(bxaxxf,因为)(xf在),2(上单调递增,且
0)(xf
,
所以035)(24bxaxxf在),2(上恒成立。
即253xab在),2(上恒成立,所以453ab ,即ab的最大值为320
19.解:(1) 因为)(xf在(-1,0)和(0,2)上有相反的单调性,
所以0x是)(xf的一个极值点,故0)0(f,
即)(xf0232cbxax有一个解0x,则0c
(2) 令0)(xf,得0232bxax,解得:abxx32,021
因为)(xf在(0,2)和(4,5)上有相反的单调性,
所以4322ab,即36ab,则0ab
假设存在点),(00yxM,则bxf3)(0,即0323020bbxax
由于0)9(4364)3(34)2(22abababbbab
故符合题意的点不存在。
20.解: (1)7277551413AAAAP
(2)215107755AAP;或215)(7722333325442215AAAACAACP
(3)7167755AAP;或71773322142215442215AAACACAACP
21.解: (1)165163165214956114124544CCCP;
(2) 1164951209060412251413152413151423CCCCCCCCCCP
22.解: (1) 当0k时,增区间是)0,(,减区间是),0(;
当0k时,)2(363)(2kxkxxkxxf,
则增区间是)0,(,),2(k,减区间是)2,0(k;
(2) 由(1)得:22k,则k的取值范围是10k;
(3) 当0k时,函数不存在极小值,
当0k时,依题意01128)2(22kkkf,即42k,
则k的取值范围是2k.
