福建省莆田市第二十四中学2017-2018学年高二下学期第一次月考地理试题(解析版)
福建省莆田市第二十四中学2017-2018学年高一下学期期
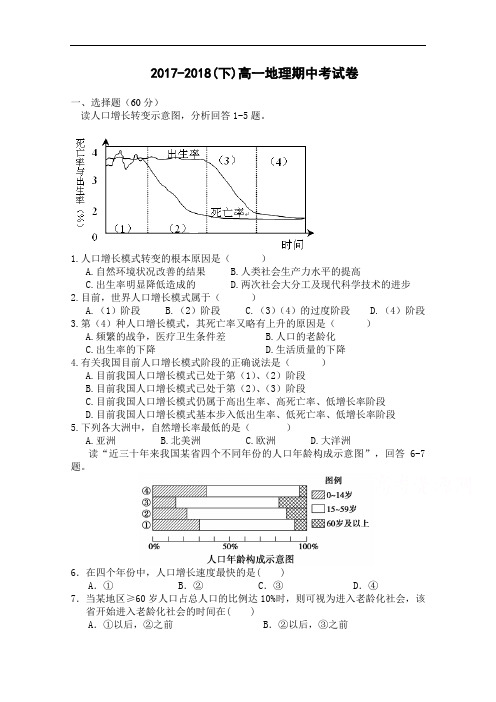
2017-2018(下)高一地理期中考试卷一、选择题(60分)读人口增长转变示意图,分析回答1-5题。
1.人口增长模式转变的根本原因是()A.自然环境状况改善的结果B.人类社会生产力水平的提高C.出生率明显降低造成的D.两次社会大分工及现代科学技术的进步2.目前,世界人口增长模式属于()A.(1)阶段B.(2)阶段C.(3)(4)的过度阶段D.(4)阶段3.第(4)种人口增长模式,其死亡率又略有上升的原因是()A.频繁的战争,医疗卫生条件差B.人口的老龄化C.出生率的下降D.生活质量的下降4.有关我国目前人口增长模式阶段的正确说法是()A.目前我国人口增长模式已处于第(1)、(2)阶段B.目前我国人口增长模式已处于第(2)、(3)阶段C.目前我国人口增长模式仍属于高出生率、高死亡率、低增长率阶段D.目前我国人口增长模式基本步入低出生率、低死亡率、低增长率阶段5.下列各大洲中,自然增长率最低的是()A.亚洲B.北美洲C.欧洲D.大洋洲读“近三十年来我国某省四个不同年份的人口年龄构成示意图”,回答6-7题。
6.在四个年份中,人口增长速度最快的是( ) A.① B.② C.③ D.④7.当某地区≥60岁人口占总人口的比例达10%时,则可视为进入老龄化社会,该省开始进入老龄化社会的时间在( ) A.①以后,②之前 B.②以后,③之前C .③以后,④之前D .④以后,①之前甲市2008年户籍人口出生9.67万人,出生率为0.699%;死亡10.7万人,死亡率为0.773%。
甲市户籍人口这种自然增长态势已持续14年。
下图显示四个地区的人口出生率和死亡率。
据此完成8-9题。
8.甲市可能是( )A.西宁B.延安C.上海D.广州9.①②③④四个地区中,人口再生产与甲市处于同一类型的地区是( )A.①B.②C.③D.④下表是我国第五次人口普查时“江苏省某市迁入人口年龄及性别统计表”,据此回答10-11题。
10. 该市迁入的人口特征有( )①男性人口多于女性人口 ②人口迁移主要受经济因素影响③以青壮年人口为主④与该市原有人口年龄构成相似A. ①②B. ②③C. ①④D. ②④11. 迁入人口对该市的影响有( )①缓和了当地就业紧张的局面 ②制约了该市经济发展③增加了该市被抚养人口 ④加大了城市基础设施的压力A. ①②B. ②③C. ③④D. ②④读“人口迁移示意图”,完成12-1312.若此图表示二战后世界人口迁移的主要方向,则该图可能表示(A.从北美迁往拉美B. C.从非洲迁往西亚D.13..若该图表示近年来我国民工流动的主要方向,则该图表示的可能是()A.从湖南流往广东B.从河北流往山东C.从新疆流往内地D.14.铁路部门为减轻春运的压力,采取上浮票价的方式,造成春运压力的主要原因是()A.铁路运输慢B.C.民工人数多D.为了安全减少了车次15.二战后,德国和沙特阿拉伯都吸引了大量移民。
福建省莆田市第二十四中学2018-2019学年高二上学期开学考试地理试题 含解析
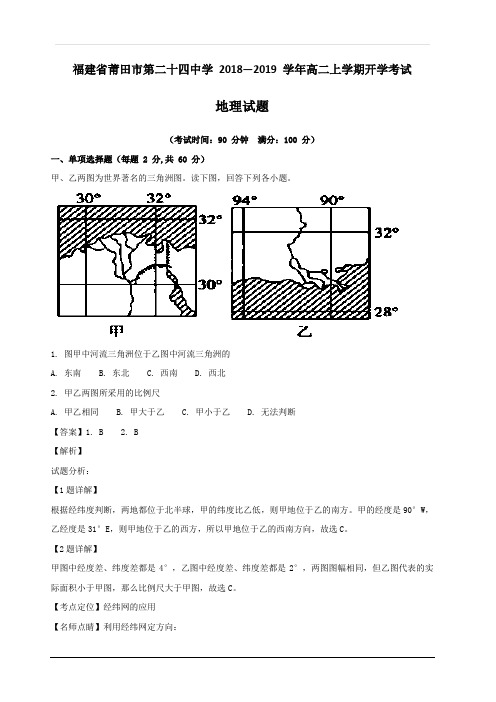
福建省莆田市第二十四中学2018—2019 学年高二上学期开学考试地理试题(考试时间:90 分钟满分:100 分)一、单项选择题(每题 2 分,共 60 分)甲、乙两图为世界著名的三角洲图。
读下图,回答下列各小题。
1. 图甲中河流三角洲位于乙图中河流三角洲的A. 东南B. 东北C. 西南D. 西北2. 甲乙两图所采用的比例尺A. 甲乙相同B. 甲大于乙C. 甲小于乙D. 无法判断【答案】1. B 2. B【解析】试题分析:【1题详解】根据经纬度判断,两地都位于北半球,甲的纬度比乙低,则甲地位于乙的南方。
甲的经度是90°W,乙经度是31°E,则甲地位于乙的西方,所以甲地位于乙的西南方向,故选C。
【2题详解】甲图中经度差、纬度差都是4°,乙图中经度差、纬度差都是2°,两图图幅相同,但乙图代表的实际面积小于甲图,那么比例尺大于甲图,故选C。
【考点定位】经纬网的应用【名师点睛】利用经纬网定方向:理论依据:经线指示南北方向,纬线指示东西方向。
1.方格状经纬网图(1)确定南北方向:在南、北半球的两点,北半球在北,南半球在南;同在北半球,纬度值大者在北;同在南半球,纬度值大者在南。
(2)确定东西方向:同在东经度,经度值大者在东,同在西经度,经度值大者在西。
若分别在东西经,如图所示:若下图中A、B两点经度差<180°时,A在B的西北方向;若下图中A、B两点经度差>180°时,A 在B的东北方向。
2.弧线式经纬网图(以极地经纬网图为例)(1)如图中A、B两点位于同一纬线上,根据自转方向判断B在A的正东方。
(2)B、C位于同一经线上,根据极点位置判断C位于B的正南方。
(3)C、A既不在同一经线上,也不在同一纬线上,根据以上方法分别判断东西、南北方向,可确定C 在A的东南方。
3.不在同一经纬网图上的判断若已知两点不在同一经纬网图上,或只告诉两点的经纬度,需要把两点转绘到同一经纬图上再来判断方向。
福建省莆田市第二十四中学2017-2018学年高二上学期第

福建省莆田市第二十四中学2017-2018学年高二上学期第二次月考(12月)数学(理)试题 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若(2,)3P π--是极坐标系中的一点,则2855(2,),(2,),(2,),(2,2)3333Q R M N k πππππ--,四点中与P 重合的点有( ) A .1个 B .2个 C .3个 D .4个2. 曲线28(x t t y t t =-⎧⎨=-⎩为参数)与x 轴的焦点坐标是( ) A .(8,0),(7,0)- B .(8,0),(7,0)-- C .(8,0),(7,0) D .(8,0),(7,0)-3.已知向量(1,0,1)n =-与平面α垂直,且α经过点(2,3,1)A ,则点(4,3,2)P 到α的距离为( )A .32 B .2C .2 4.设等比数列{}n a 的前n 项和n S ,若243,15S S ==,则6S = ( ) A .31 B .32 C .63D .645. 两直线330x y +-=与610x my ++=平行,则它们之间的距离为( )A .4B D6. 如右图所示,正方体1111ABCD A BC D -中,M 是AB 的中点,则sin ,DB CM为( )A .12 B C .3D .157. 设等差数列{}n a 的前n 项和n S ,且1310670,0,0a a a a a >+><,则满足0n S >的最大自然数n 的值为( ) A .6 B .7 C .12 D .138. 直线1y kx k =-+与椭圆22194x y +=的位置关系为( ) A .相交 B .相切 C .相离 D .不确定9. 已知M 是ABC ∆内的一点,且030AB AC BAC ⋅=∠=,若,MBC MBA ∆∆和MAB ∆的面积分别为1,,2x y ,则14x y+的最小值是( )A .20B .18C .16D .910.已知抛物线2:8C y x =与点(2,2)M -,过C 的焦点且斜率为k 的直线与C 交于,A B 两点,若0MA MB ⋅=,则k = ( )A .12 B.2C.2 11.双曲线的虚轴长4,离心率e =12,F F 分别是它的左右焦点,若过1F 的直线与双曲线的左支交于,A B 两点,且AB 是2AF 与2BF 的等差中项,则为 ( ) A....812.已知直线16(1)()22m x n y +++=与圆22(3)(5x y -+=相切,若对任意的,m n R +∈均有不等式2m n k +≥成立,那么正整数k 的最大值是 ( )A .3B .5C .7D .9第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.直线l的参数方程为3(x tt y =-+⎧⎪⎨=⎪⎩ 为参数),圆C 的参数方程为3cos (3sin x y θθθ=⎧⎨=⎩为参数),则直线l 被圆C 解得弦长为 .14.若抛物线22x y =的顶点是抛物线上的点(0,)A a 距离最近的,则a 的取值范围的 .15.已知抛物线28y x =的准线过双曲线22221(0,0)x y a b a b-=>>的一个焦点,且双曲线的离心率为2,则该双曲线的方程为 .16.已知椭圆22221(0)x y a b a b +=>>上一点A 关于原点的对称点为点,B F 为其右焦点,若AF BF ⊥,设ABF α∠=,且[,]64ππα∈,则该椭圆的离心率e 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在直角坐标系xOy 中,曲线的参数方程为2(1x t y ⎧=-⎪⎨=-⎪⎩为参数),以原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线2C的极坐标方程为ρ= 。
福建省莆田市第二十四中学高二上学期期末考试地理试题(有答案)
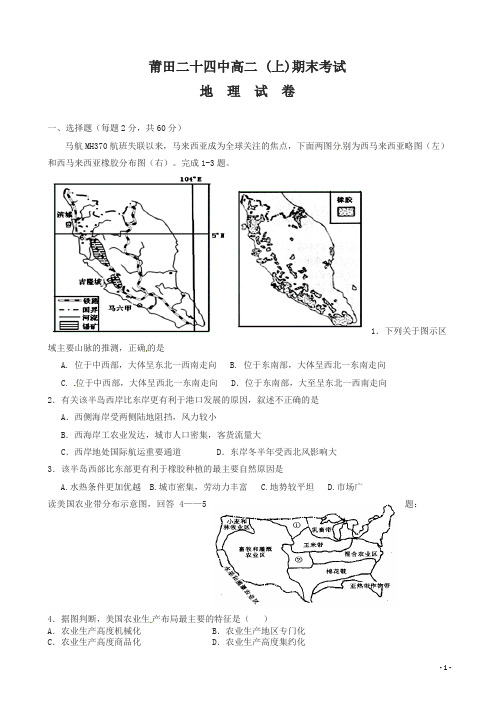
莆田二十四中高二 (上)期末考试地理试卷一、选择题(每题2分,共60分)马航MH370航班失联以来,马来西亚成为全球关注的焦点,下面两图分别为西马来西亚略图(左)和西马来西亚橡胶分布图(右)。
完成1-3题。
1.下列关于图示区域主要山脉的推测,正确的是A. 位于中西部,大体呈东北一西南走向B. 位于东南部,大体呈西北一东南走向C. 位于中西部,大体呈西北一东南走向 D.位于东南部,大至呈东北一西南走向2.有关该半岛西岸比东岸更有利于港口发展的原因,叙述不正确的是A.西侧海岸受两侧陆地阻挡,风力较小B.西海岸工农业发达,城市人口密集,客货流量大C.西岸地处国际航运重要通道 D.东岸冬半年受西北风影响大3.该半岛西部比东部更有利于橡胶种植的最主要自然原因是A.水热条件更加优越B.城市密集,劳动力丰富C.地势较平坦D.市场广读美国农业带分布示意图,回答4——5题:4.据图判断,美国农业生产布局最主要的特征是()A.农业生产高度机械化 B.农业生产地区专门化C.农业生产高度商品化 D.农业生产高度集约化5.图中①、②两地农业生产中存在差异的原因是()A.热量差异 B.水分差异 C.科技差异 D.政策差异读世界某区域图(其中阴影代表海洋),根据图中信息回答6—7题。
6.该岛的地势特征是()A.中间高四周低 B.中间低四周高 C.东南高西北低 D.东南低西北高7.关于该岛的叙述,正确的是()A.受北大西洋暖流影响,地下水水温较高 B.地处亚欧板块和美洲板块的消亡边界C.渔业和旅游业发达 D.大部分地区有极昼现象8.如图反映了欧洲传统民居自大西洋沿岸向东至俄罗斯的墙壁厚度变化规律,形成该规律的主要原因是欧洲自西向东()题。
9.自然带①→②→③→④→⑤→⑥和自然带⑦→⑧→⑨→⑩分布规律分别符合BA.纬度地带和经度地带分异规律B.地方性和垂直地带性规律C.干湿度和纬度地带分异规律D.垂直地带性和地方性规律10.B地绿洲的出现说明其自然带的分布具有A.地带性规律B.非地带性规律C.地带性规律和地方性现象D.垂直地带性规律图3所示区域内自南向北年降水量由约200mm增至500mm左右,沙漠地区年降水量仅50mm左右。
2022-2023学年高二下学期第一次月考A卷(全国通用版)地理试题(解析版)

2022-2023学年高二地理下学期第一次月考A卷(全国通用版)第Ⅰ卷一、选择题:本题共22小题,每小题2分,共44分。
在每小题给出的四个选项中,只有一项符合题目要求。
2022年6月5日上午10时44分07秒在酒泉卫星发射中心发射神舟十四号载人飞船,3名航天员进驻核心舱并在轨驻留6个月,开展空间科学实验与技术试验等工作。
12月4日20时09分,神舟飞船载人飞船返回舱在东风着陆场成功着陆。
据此完成下1-2题。
1.符合航天员驻留期间中国北极黄河站(78°55′N、11°56′E)昼夜长短变化的是()A.B.C.D.2.航天员驻留期间,酒泉卫星发射中心发射塔与山西太原航天发射中心发射塔两地每天正午太阳高度的差值()A.先变大后变小B.先变小后变大C.持续不断变大D.始终保持不变世界奇观“棋盘滩”分布在广西田东县莲花山的一处河道中,长约210米,宽150米,由一块块整齐浮出水面的坚硬石英砂岩组成。
流水顺着岩石节理侵蚀,形成了界线分明的天然“大棋盘”。
图1为棋盘滩景观图,图2示意莲花山地质构造图,据此完成下面3-5题。
3.“棋盘滩”最可能位于图2中的()A.甲地B.乙地C.丙地D.丁地4.推断石英砂岩逐渐演化成“棋盘滩”的地理过程是()A.沉积作用流水侵蚀水平挤压节理发育B.沉积作用水平挤压节理发育流水侵蚀C.变质作用流水侵蚀水平挤压节理发育D.变质作用水平挤压节理发育流水侵蚀5.能正确示意棋盘滩节理构造及其与流水方向关系的是()A.①B.②C.③D.④锋后气团性质一旦发生改变,被更后面的气团追上会形成新的锋面。
此新锋面称为副锋,原锋面称为主锋。
下图示意我国某日局部地区出现的主锋和副锋。
据此完成下面6-7题。
6.导致主锋过境后气团变性的主要原因是()A.冷锋过境,导致气温下降B.地面辐射减弱,导致气温下降C.暖锋过境,导致气温升高D.天气转晴,导致气温升高7.关于近地面①②③三地的判断,正确的是()A.①位于副锋锋后,凤力最大B.②位于主锋锋后,风力最小C.②位于冷锋和暖锋之间D.③位于暖锋锋前,风力最小莫桑比克海峡位于非洲大陆与马达加斯加岛之间。
福建省莆田市二十四中学2017-2018学年高二上学期第二次月考(12月)数学(文)试题(解析版) Word版含解析

福建省莆田市第二十四中学2017-2018学年高二上学期第二次月考(12月)数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 顶点在坐标原点,对称轴为坐标轴,又过点的抛物线方程是()A. B. C. 或 D. 或【答案】D【解析】解答:(1)抛物线的顶点在坐标原点,对称轴是x轴,并且经过点(−2,3),设它的标准方程为y2=−2px(p>0)∴9=4p,解得p=,∴.(2)抛物线的顶点在坐标原点,对称轴是y轴,并且经过点(−2,3),设它的标准方程为x2=2py(p>0)∴4=6p,解得:p=.∴∴抛物线方程是或.故选:D.2. 下列有关命题的叙述:①若为假命题,则为真命题;②“”是“”成立的充分不必要条件;③命题,则;④命题“若,则”的逆命题为真,其中正确的个数是()A. 1B. 2C. 3D. 4【答案】C【解析】①若¬p为假命题,则p为真命题,∴p∨q为真命题,①正确;②由,解得x<−1或x>5,∴“x>5”是“”成立的充分不必要条件,②正确;③命题p:∃x∈R,,则¬p:∀x∈R,,③正确;④命题“若,则a<b”的逆命题为:若“a<b,则”,当m2=0时不成立,是假命题,④错误。
∴正确的个数是3.故选:C.3. 已知集合,则“”是“”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】A==(﹣1,2),若a=1时,B=(﹣1,1)⊆A;当a≤0时,B⊆A;故“a=1”是“B⊆A”的充分不必要条件,故选:A.点睛:认清元素的属性,解决集合问题时,认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.注意元素的互异性.在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误.防范空集.在解决有关A∩B=∅,A⊆B等集合问题时,往往忽略空集的情况,一定先考虑∅是否成立,以防漏解.4. 在极坐标系中,圆的圆心的极坐标是()A. B. C. D.【答案】D【解析】圆ρ=﹣2cosθ即ρ2=﹣2ρcosθ,即 x2+y2+2x=0,即(x+1)2+y2=1,表示以(﹣1,0)为圆心,半径等于1的圆.而点(﹣1,0)的极坐标为(1,π),故选D.5. “”是“曲线为双曲线”的()A. 充分不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】试题分析:当时,,,原方程是双曲线方程;当原方程为双曲线方程时,有;由以上说明可知是“曲线是双曲线”充分而非必要条件.故本题正确选项为A.考点:充分与必要条件,双曲线的标准方程.6. 已知圆,若点在圆外,则直线与圆的位置关系为()A. 相离B. 相切C. 相交D. 不能确定【答案】C【解析】由点P(x0,y0)在圆C:x2+y2=4外,可得x02+y02 >4,求得圆心C(0,0)到直线l:x0x+y0y=4的距离d=<=2,故直线和圆C相交,故选:C.点睛:判断直线与圆的位置关系主要有两种方法:(1)代数方法:联立方程,利用判断二者位置关系,比较繁琐;(2)几何方法:利用圆心到直线的距离与半径的大小关系进行判定,比较简单.7. 已知椭圆的两个交点和短轴的两个端点恰好为一个正方形的四个顶点,则该椭圆的离心率为()A. B. C. D.【答案】D【解析】试题分析:依题意椭圆的焦距和短轴长相等,故,,∴.考点:椭圆的简单几何性质.8. 已知双曲线的左右焦点分别为,以为直径的圆与双曲线渐近线的一个交点为,则此双曲线为()A. B. C. D.【答案】B【解析】∵双曲线的左右焦点分别为,以|F1F2|为直径的圆与双曲线渐近线的一个交点为(1,2),∴由题意知c==,∴a2+b2=5,①又点(1,2)在y=x上,∴,②由①②解得a=1,b=2,∴双曲线的方程为.故选:B.9. 设椭圆和双曲线的公共焦点为,是两曲线的一个公共点,则的值等于()A. B. C. D.【答案】A【解析】由题意知F1(﹣2,0),F2(2,0),解方程组,得.取P点坐标为,,,cos∠F1PF2==.故选A.10. 过抛物线的焦点且倾斜角的直线与抛物线在第一、四象限分别交于两点,则等于()A. B. C. D.【答案】C【解析】设A(x1,y1),B(x2,y2),则|AB|=x1+x2+p==,∴x1+x2=,又x1 x2=,可得x1=,x2=∴=3.故选C.11. 设是椭圆的左右焦点,过作轴的垂线交椭圆四点构成一个正方形,则椭圆的离心率为()A. B. C. D.【答案】B【解析】是椭圆的左右焦点,过作轴的垂线交椭圆四点构成一个正方形,所以(c,c)是椭圆上的点,可得:,a2c2﹣c4+a2c2=a4﹣a2c2,可得e4﹣3e2+1=0.解得e=.故选:B.点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a,b,c的方程或不等式,再根据a,b,c的关系消掉b得到a,c的关系式,建立关于a,b,c的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.12. 已知函数的两个极值点分别为,且,点表示的平面区域内存在点满足,则实数的取值范围是()A. B. C. D.【答案】B【解析】因为的两个极值点满足,所以的两个零点满足,则,即,作出不等式表示的平面区域如图所示;显然当时,的图像经过平面区域;当时,若的图像经过平面区域,须,即,解得,所以实数是范围是.考点:函数的极值、简单的线性规划.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知抛物线的准线过双曲线的一个焦点,且双曲线的离心率为2,则该双曲线的方程为__________.【答案】【解析】由y2=8x准线为x=-2.则双曲线中c=2, ==2,a=1,b=.所以双曲线方程为x2-=1.14. 过点的圆与直线相切与点,则圆的标准方程为__________.【答案】【解析】试题分析:设圆的方程为,解方程得,所以圆的方程为考点:圆的方程15. 在等比数列中,若,则__________.【答案】【解析】由等比数列的性质可得a5a8=a6a7=,∴=()+()=故答案为:点睛:处理等比数列的基本运算题有两个方法:(1)基本量法:建立关于首项与公比的方程组,进而求其它量;(2)性质法:利用等比数列的重要性质直接搭建条件与结论的桥梁,命题者往往从这个角度命题.16. 已知椭圆与抛物线有相同的焦点为原点,点是抛物线上一动点,点在抛物线上,且,则的最小值为__________.【答案】【解析】∵椭圆,a=,b=1,则c2=5﹣1=4,即c=2,则椭圆的焦点为(0,±2),不妨取焦点(0,2),∵抛物线x2=ay,∴抛物线的焦点坐标为(0,),∵椭圆与抛物线有相同的焦点,∴=2,即a=8,则抛物线方程为x2=8y,准线方程为y=﹣2,∵|AF|=4,由抛物线的定义得,∴A到准线的距离为4,y+2=4,即A点的纵坐标y=2,又点A在抛物线上,∴x=±4,不妨取点A的坐标A(4,2);A关于准线的对称点的坐标为B(4,﹣6)则|PA|+|PO|=|PB|+|PO|≥|OB|,即O,P,B三点共线时,有最小值,最小值为|AB|==,故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知函数在处取得极值为。
福建省莆田市第二十四中学高二上学期第二次月考(12月)
福建省莆田市第二十四中学2017-2018学年高二上学期第二次月考(12月)数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 顶点在坐标原点,对称轴为坐标轴,又过点的抛物线方程是()A. B. C. 或 D. 或【答案】D【解析】解答:(1)抛物线的顶点在坐标原点,对称轴是x轴,并且经过点(−2,3),设它的标准方程为y2=−2px(p>0)∴9=4p,解得p=,∴.(2)抛物线的顶点在坐标原点,对称轴是y轴,并且经过点(−2,3),设它的标准方程为x2=2py(p>0)∴4=6p,解得:p=.∴∴抛物线方程是或.故选:D.2. 下列有关命题的叙述:①若为假命题,则为真命题;②“”是“”成立的充分不必要条件;③命题,则;④命题“若,则”的逆命题为真,其中正确的个数是()A. 1B. 2C. 3D. 4【答案】C【解析】①若¬p为假命题,则p为真命题,∴p∨q为真命题,①正确;②由,解得x<−1或x>5,∴“x>5”是“”成立的充分不必要条件,②正确;③命题p:∃x∈R,,则¬p:∀x∈R,,③正确;④命题“若,则a<b”的逆命题为:若“a<b,则”,当m2=0时不成立,是假命题,④错误。
∴正确的个数是3.故选:C.3. 已知集合,则“”是“”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】A==(﹣1,2),若a=1时,B=(﹣1,1)⊆A;当a≤0时,B⊆A;故“a=1”是“B⊆A”的充分不必要条件,故选:A.点睛:认清元素的属性,解决集合问题时,认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件.注意元素的互异性.在解决含参数的集合问题时,要注意检验集合中元素的互异性,否则很可能会因为不满足“互异性”而导致解题错误.防范空集.在解决有关A∩B=∅,A⊆B等集合问题时,往往忽略空集的情况,一定先考虑∅是否成立,以防漏解.4. 在极坐标系中,圆的圆心的极坐标是()A. B. C. D.【答案】D【解析】圆ρ=﹣2cosθ即ρ2=﹣2ρcosθ,即 x2+y2+2x=0,即(x+1)2+y2=1,表示以(﹣1,0)为圆心,半径等于1的圆.而点(﹣1,0)的极坐标为(1,π),故选D.5. “”是“曲线为双曲线”的()A. 充分不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】试题分析:当时,,,原方程是双曲线方程;当原方程为双曲线方程时,有;由以上说明可知是“曲线是双曲线”充分而非必要条件.故本题正确选项为A.考点:充分与必要条件,双曲线的标准方程.6. 已知圆,若点在圆外,则直线与圆的位置关系为()A. 相离B. 相切C. 相交D. 不能确定【答案】C【解析】由点P(x0,y0)在圆C:x2+y2=4外,可得x02+y02 >4,求得圆心C(0,0)到直线l:x0x+y0y=4的距离d=<=2,故直线和圆C相交,故选:C.点睛:判断直线与圆的位置关系主要有两种方法:(1)代数方法:联立方程,利用判断二者位置关系,比较繁琐;(2)几何方法:利用圆心到直线的距离与半径的大小关系进行判定,比较简单.7. 已知椭圆的两个交点和短轴的两个端点恰好为一个正方形的四个顶点,则该椭圆的离心率为()A. B. C. D.【答案】D【解析】试题分析:依题意椭圆的焦距和短轴长相等,故,,∴.考点:椭圆的简单几何性质.8. 已知双曲线的左右焦点分别为,以为直径的圆与双曲线渐近线的一个交点为,则此双曲线为()A. B. C. D.【答案】B【解析】∵双曲线的左右焦点分别为,以|F1F2|为直径的圆与双曲线渐近线的一个交点为(1,2),∴由题意知c==,∴a2+b2=5,①又点(1,2)在y=x上,∴,②由①②解得a=1,b=2,∴双曲线的方程为.故选:B.9. 设椭圆和双曲线的公共焦点为,是两曲线的一个公共点,则的值等于()A. B. C. D.【答案】A【解析】由题意知F1(﹣2,0),F2(2,0),解方程组,得.取P点坐标为,,,cos∠F1PF2==.故选A.10. 过抛物线的焦点且倾斜角的直线与抛物线在第一、四象限分别交于两点,则等于()A. B. C. D.【答案】C【解析】设A(x1,y1),B(x2,y2),则|AB|=x1+x2+p==,∴x1+x2=,又x1 x2=,可得x1=,x2=∴=3.故选C.11. 设是椭圆的左右焦点,过作轴的垂线交椭圆四点构成一个正方形,则椭圆的离心率为()A. B. C. D.【答案】B【解析】是椭圆的左右焦点,过作轴的垂线交椭圆四点构成一个正方形,所以(c,c)是椭圆上的点,可得:,a2c2﹣c4+a2c2=a4﹣a2c2,可得e4﹣3e2+1=0.解得e=.故选:B.点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a,b,c的方程或不等式,再根据a,b,c的关系消掉b得到a,c的关系式,建立关于a,b,c的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.12. 已知函数的两个极值点分别为,且,点表示的平面区域内存在点满足,则实数的取值范围是()A. B. C. D.【答案】B【解析】因为的两个极值点满足,所以的两个零点满足,则,即,作出不等式表示的平面区域如图所示;显然当时,的图像经过平面区域;当时,若的图像经过平面区域,须,即,解得,所以实数是范围是.考点:函数的极值、简单的线性规划.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知抛物线的准线过双曲线的一个焦点,且双曲线的离心率为2,则该双曲线的方程为__________.【答案】【解析】由y2=8x准线为x=-2.则双曲线中c=2, ==2,a=1,b=.所以双曲线方程为x2-=1.14. 过点的圆与直线相切与点,则圆的标准方程为__________.【答案】【解析】试题分析:设圆的方程为,解方程得,所以圆的方程为考点:圆的方程15. 在等比数列中,若,则__________.【答案】【解析】由等比数列的性质可得a5a8=a6a7=,∴=()+()=故答案为:点睛:处理等比数列的基本运算题有两个方法:(1)基本量法:建立关于首项与公比的方程组,进而求其它量;(2)性质法:利用等比数列的重要性质直接搭建条件与结论的桥梁,命题者往往从这个角度命题.16. 已知椭圆与抛物线有相同的焦点为原点,点是抛物线上一动点,点在抛物线上,且,则的最小值为__________.【答案】【解析】∵椭圆,a=,b=1,则c2=5﹣1=4,即c=2,则椭圆的焦点为(0,±2),不妨取焦点(0,2),∵抛物线x2=ay,∴抛物线的焦点坐标为(0,),∵椭圆与抛物线有相同的焦点,∴=2,即a=8,则抛物线方程为x2=8y,准线方程为y=﹣2,∵|AF|=4,由抛物线的定义得,∴A到准线的距离为4,y+2=4,即A点的纵坐标y=2,又点A在抛物线上,∴x=±4,不妨取点A的坐标A(4,2);A关于准线的对称点的坐标为B(4,﹣6)则|PA|+|PO|=|PB|+|PO|≥|OB|,即O,P,B三点共线时,有最小值,最小值为|AB|==,故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知函数在处取得极值为。
2017-2018学年福建省莆田市第二十四中学高一上学期第二次月考(12月)地理试题(pdf版)
福建省莆田市第二十四中学2017-2018学年高一上学期第二次月考(12月)试题 地理学科第Ⅰ卷 (选择题25题,共50分)1.地球上的气压带有:①赤道低气压带 ②副热带高气压带 ③副极地低气压带 ④极地高气压带,同属热力因素形成的气压带是( )A .①②B .①③C .①④D .②③ 2.右图为北半球中高纬环流示意图,判断下列说法正确的是( )A .甲点位于30o N 附近B .乙点位于30oN 附近 C .①地是冷性气流 D .②地盛行西风利用太阳能发电的最佳方式是光伏转换,就是利用太阳光照射到硅材料上产生电流直接发电。
我国有关专家指出:上海没有油田和煤矿,但有两亿平方米的屋顶,不能辜负了屋顶上这片免费的阳光,下图示意屋顶太阳能发电站。
读图完成3-4题。
3.青藏高原是我国太阳能资源最丰富的地区,主要原因是 A .纬度低,太阳高度角大 B .海拔高,距太阳近C .海拔高,大气对太阳辐射削弱作用弱D .深居内陆,晴朗天气多4.大致与青藏高原同纬度的上海也积极推广 “太阳能屋顶计划”,是因为A .上海是我国太阳能资源最丰富的地区B .上海常规能源(煤炭、石油等)短缺,能源需求量大C .太阳能资源清洁、可再生、生产成本低D .上海经济发达,能源蕴藏量大5.若利用楼顶(平顶)自建光伏发电站,电池板与楼顶倾角最小的城市是 A .哈尔滨 B .广州 C .济南 D .北京6.右图是太阳大气层结构示意图,A 、B 、C 是太阳大气层的 三个组成部分。
太阳活动主要类型及其发生的层次组合正 确的是A .A-色球-黑子B .B-光球-耀斑C .C-日冕-耀斑D .A-光球-黑子北京时间2015年9月20日7时01分,我国在太原(112°E )卫星发射中心用全新研制的长征六号运载火箭,成功将20颗卫星顺利送入预定轨道,开创了我国一箭多星发射的新纪录。
据此回答7-8题。
7.长征六号运载火箭将20颗卫星顺利送入预定轨道时,国际标准时(中时区区时)为 A .9月21日0时01分 B .9月20日23时01分AB C 图2 图1C .9月20日15时01分D .9月19日23时01分8.当长征六号运载火箭将20颗卫星顺利送入预定轨道时,湛江(110°E )的地方时为 A .6:21 B . 7:41 C . 6:37 D .6:53 9.在下面四幅图的a 、b 、c 、d 四点中,处于黄昏的是A .aB . bC .cD .d 10.一条河流沿35°N 自西向东流(图3),河中有一沙坝,下列叙述正确的是A .南岸沉积作用强烈B .北岸受冲刷严重C .沙坝将与南岸相连D .沙坝将与北岸相连图4为某地正午太阳高度年变化折线图,读图回答11-12题。
2017-2018学年福建省莆田市第二十四中学高二上学期第二次月考(12月)物理试题 解析版
福建省莆田市第二十四中学 2017-2018 学年高二上学期第二次月考(12 月)试题物理学科一、选择题(本题共 12 小题,每小题 4 分,第 1 题~第 8 题,每小题只有一个选项符合题目要求;第9题~第 12 题,每小题有多个选项符合题目要求,全部选对的得 4 分,选对但选不全的得 2 分,有错选的得 0 分)1. 电动机的电枢阻值为R,电动机正常工作时,两端的电压为U,通过的电流为I,工作时间为 t,下列说法中正确的是( )A. 电动机消耗的电能为U2t/RB. 电动机消耗的电能为I2RtC. 电动机线圈产生的热量为 I2RtD. 电动机线圈产生的热量为UIt【答案】C【解析】试题分析:在计算电功率的公式中,总功率用P=IU来计算,发热的功率用P=I2R来计算,如果是计算纯电阻的功率,这两个公式的计算结果是一样的,但对于电动机等非纯电阻,第一个计算的是总功率,第二个只是计算发热的功率,这两个的计算结果是不一样的.解:A、电动机正常工作时,两端的电压为U,通过的电流为I,工作的时间为t,所以电动机消耗的电能为UIt,所以A正确,B错误;C、电动机为非纯电阻电路线圈产生的热量为I2Rt,不能用来计算,所以C正确,D错误;故选AC.【点评】对于电功率的计算,一定要分析清楚是不是纯电阻电路,对于非纯电阻电路,总功率和发热功率的计算公式是不一样的.2. 如图所示的电路中,L1、L2为“220V、100W”灯泡,L3、L4为“220V,40W”灯泡,现将两端接入电路,其实际功率的大小顺序是()A. P4>P1>P3>P2B. P4>P1>P2>P3C. P1>P4>P2>P3D. P1>P4>P3>P2【答案】B【解析】试题分析:因为四盏灯的电阻关系为,根据P=I2r,则P4>P1>(P2+P3);由于L2L3并联,所以根据可知,P2>P3,所以四盏电灯的实际功率关系为:P4>P1>P2>P3,选项B正确。
福建省莆田二十四中2017-2018学年高二上学期第二次月考数学试卷(文科) Word版含解析
2017-2018学年福建省莆田二十四中高二(上)第二次月考数学试卷(文科)一、选择题(每小题5分共60分)1.下列四个命题中,假命题为()A.∀x∈R,2x>0 B.∀x∈R,x2+3x+1>0C.∃x∈R,lgx>0 D.∃x∈R,2.已知a∈R,则“a>2”是“a2>2a”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件3.抛物线x=﹣2y2的准线方程是()A.B. C. D.4.双曲线=﹣1的渐近线方程是()A.y=±x B.y=±x C.y=±x D.y=±x5.已知命题p:∃x∈R,x﹣2>lgx,命题q:∀x∈R,e x>1,则()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∧(¬q)是真命题D.命题p∨(¬q)是假命题6.椭圆+=1的右焦点到直线y=x的距离是()A.B.C.1 D.7.抛物线y2=10x的焦点到准线的距离是()A.B.5 C.D.108.曲线y=2x3﹣3x+1在点(1,0)处的切线方程为()A.y=4x﹣5 B.y=﹣3x+2 C.y=﹣4x+4 D.y=3x﹣39.若双曲线=1(a>0,b>0)的一个焦点是圆x2+y2﹣10x+24=0的圆心,且虚轴长为6,则双曲线的离心率为()A.B.C.D.10.椭圆+=1的离心率e是()A.B.C.D.11.设P是椭圆+=1上的点,若F1,F2是椭圆的两个焦点,则|PF1|+|PF2|等于()A.4 B.5 C.8 D.1012.直线y=x+1被椭圆x2+2y2=4所截得的弦的中点坐标是()A.()B.(﹣,)C.(,﹣)D.(﹣,)二、填空题(每小题5分共20分)13.写出命题“∃x∈R,x2+x≥0”的否定.14.已知椭圆的中心在原点,焦点在y轴上,若其离心率为,焦距为8,则该椭圆的方程是.15.双曲线的焦点在x轴上,实轴长为4,离心率为3,则该双曲线的标准方程为,渐近线方程为.16.已知点A(0,2)抛物线y2=2px(p>0)的焦点为F,准线为l,线段FA交抛物线与点B,过B做l的垂线,垂足为M,若AM⊥MF,则p=.三、解答题17.求下列函数的导数(1)y=x4﹣2x2+3x﹣1;(2)y=.18.已知命题P:|m+1|≤2成立.命题q:方程x2﹣mx+1=0有实根.若¬p是假命题,p ∧q为假命题,求m的取值范围.19.已知椭圆C: +=1(a>b>0)的上顶点为(0,2),且离心率为.求椭圆C的方程.20.已知函数f(x)=x3﹣3x,求f(x)在x=3处的切线方程.21.求满足下列条件的双曲线的标准方程:(1)与双曲线﹣=1有公共焦点,且过点(3,2);(2)渐近线方程为2x±3y=0,顶点在y轴上,且焦距为2.22.已知抛物线C:y2=4x与直线y=2x﹣4交于A,B两点.(1)求弦AB的长度;(2)若点P在抛物线C上,且△ABP的面积为12,求点P的坐标.2015-2016学年福建省莆田二十四中高二(上)第二次月考数学试卷(文科)参考答案与试题解析一、选择题(每小题5分共60分)1.下列四个命题中,假命题为()A.∀x∈R,2x>0 B.∀x∈R,x2+3x+1>0C.∃x∈R,lgx>0 D.∃x∈R,【考点】全称命题;特称命题.【分析】据指数函数的性质知,可判断A的真假,取当x=﹣2时,可判断B的真假;根据当x=10时,可判断C的真假;解不等式可判断D的真假,进而得到答案.【解答】解:根据指数函数的性质知,当x∈R时,2x>0,故A中“∀x∈R,2x>0”为真命题;当x=﹣2时,x2+3x+1=4﹣6+1=﹣1<0,故B中“∀x∈R,x2+3x+1>0”为假命题;当x=10时,lg10=1>0,故C中“∃x∈R,lgx>0”,故C为真命题;当x=4时,,故D为真命题;故选B.2.已知a∈R,则“a>2”是“a2>2a”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【考点】不等关系与不等式.【分析】我们分别判断“a>2”⇒“a2>2a”与“a2>2a”⇒“a>2”的真假,然后根据充要条件的定义,即可得到答案.【解答】解:∵当“a>2”成立时,a2﹣2a=a(a﹣2)>0∴“a2>2a”成立即“a>2”⇒“a2>2a”为真命题;而当“a2>2a”成立时,a2﹣2a=a(a﹣2)>0即a>2或a<0∴a>2不一定成立即“a2>2a”⇒“a>2”为假命题;故“a>2”是“a2>2a”的充分非必要条件故选A3.抛物线x=﹣2y2的准线方程是()A.B. C. D.【考点】抛物线的简单性质.【分析】由于抛物线y2=﹣2px(p>0)的准线方程为x=,则抛物线x=﹣2y2即y2=﹣x 的准线方程即可得到.【解答】解:由于抛物线y2=﹣2px(p>0)的准线方程为x=,则抛物线x=﹣2y2即y2=﹣x的准线方程为x=,故选:D.4.双曲线=﹣1的渐近线方程是()A.y=±x B.y=±x C.y=±x D.y=±x【考点】双曲线的简单性质.【分析】化方程为标准方程,可得a,b,代入y=可得渐近线方程.【解答】解:化已知双曲线的方程为标准方程,可知焦点在y轴,且a=3,b=2,故渐近线方程为y==故选A5.已知命题p:∃x∈R,x﹣2>lgx,命题q:∀x∈R,e x>1,则()A.命题p∨q是假命题B.命题p∧q是真命题C.命题p∧(¬q)是真命题D.命题p∨(¬q)是假命题【考点】复合命题的真假.【分析】利用函数的性质先判定命题p,q的真假,再利用复合命题真假的判定方法即可得出.【解答】解:对于命题p:例如当x=10时,8>1成立,故命题p是真命题;对于命题q:∀x∈R,e x>1,当x=0时命题不成立,故命题q是假命题;∴命题p∧¬q是真命题.故选:C.6.椭圆+=1的右焦点到直线y=x的距离是()A.B.C.1 D.【考点】椭圆的简单性质;点到直线的距离公式.【分析】根据题意,可得右焦点F(1,0),由点到直线的距离公式,计算可得答案.【解答】解:根据题意,可得右焦点F(1,0),y=x可化为y﹣x=0,则d==,故选B.7.抛物线y2=10x的焦点到准线的距离是()A.B.5 C.D.10【考点】抛物线的简单性质.【分析】根据抛物线的标准方程,可求得p,再根据抛物线焦点到准线的距离是p,进而得到答案.【解答】解:2p=10,p=5,而焦点到准线的距离是p.故抛物线y2=10x的焦点到准线的距离是5故选B8.曲线y=2x3﹣3x+1在点(1,0)处的切线方程为()A.y=4x﹣5 B.y=﹣3x+2 C.y=﹣4x+4 D.y=3x﹣3【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,求得切线的斜率,由点斜式方程,即可得到切线方程.【解答】解:y=2x3﹣3x+1的导数为y′=6x2﹣3,在点(1,0)处的切线斜率为k=3,则在点(1,0)处的切线方程为y﹣0=3(x﹣1),即为y=3x﹣3.故选D.9.若双曲线=1(a>0,b>0)的一个焦点是圆x2+y2﹣10x+24=0的圆心,且虚轴长为6,则双曲线的离心率为()A.B.C.D.【考点】双曲线的简单性质.【分析】求出圆的圆心(5,0),可得c=5,又b=3,由a,b,c的关系,可得a=4,再由离心率公式计算可得离心率.【解答】解:圆x2+y2﹣10x+24=0即为(x﹣5)2+y2=1,可得圆心为(5,0),即有双曲线的c=5,由虚轴长为6,可得b=3,a==4,则双曲线的离心率为e==.故选:A.10.椭圆+=1的离心率e 是( )A .B .C .D .【考点】椭圆的简单性质.【分析】由于椭圆+=1的a 2=36,b 2=20,从而得到a=6,c 2=16,继而可得到的值.【解答】解:由于椭圆的方程为+=1,故a 2=36,b 2=20,从而得到a=6,c 2=16, 即c=4,∴e==,故选:D .11.设P 是椭圆+=1上的点,若F 1,F 2是椭圆的两个焦点,则|PF 1|+|PF 2|等于( )A .4B .5C .8D .10 【考点】椭圆的简单性质.【分析】由椭圆的第一定义知|PF 1|+|PF 2|=2a ,进而求得答案. 【解答】解:由椭圆的第一定义知|PF 1|+|PF 2|=2a=10, 故选D .12.直线y=x +1被椭圆x 2+2y 2=4所截得的弦的中点坐标是( )A .() B .(﹣,) C .(,﹣) D .(﹣,)【考点】直线与圆锥曲线的关系.【分析】将直线y=x +1代入椭圆x 2+2y 2=4中,利用韦达定理及中点坐标公式,即可求得结论.【解答】解:将直线y=x +1代入椭圆x 2+2y 2=4中,得x 2+2(x +1)2=4 ∴3x 2+4x ﹣2=0∴弦的中点横坐标是x==﹣,代入直线方程中,得y=∴弦的中点是(﹣,) 故选B .二、填空题(每小题5分共20分)13.写出命题“∃x∈R,x2+x≥0”的否定∀x∈R,x2+x<0.【考点】命题的否定.【分析】利用特称命题的否定是全称命题,写出结果即可.【解答】解:因为特称命题的否定是全称命题,所以命题“∃x∈R,x2+x≥0”的否定“∀x∈R,x2+x<0”.故答案为:∀x∈R,x2+x<0.14.已知椭圆的中心在原点,焦点在y轴上,若其离心率为,焦距为8,则该椭圆的方程是+=1.【考点】椭圆的标准方程.【分析】依题意可知c,进而根据离心率求得a,进而根据b2=a2﹣c2求得b20,则椭圆方程可得.【解答】解:由题意知,2c=8,c=4,∴e===,∴a=8,从而b2=a2﹣c2=48,∴方程是+=1.故答案为+=115.双曲线的焦点在x轴上,实轴长为4,离心率为3,则该双曲线的标准方程为,渐近线方程为y=.【考点】双曲线的简单性质.【分析】依据题意,求出a、c、b的值,再根据双曲线的焦点在x轴上,求出双曲线的标准方程和渐近线方程.【解答】解:由题意得2a=4,=3,∴a=2,c=6,b===4,双曲线的焦点在x轴上,故该双曲线的标准方程为,渐近线方程为y=,故答案为:,y=.16.已知点A(0,2)抛物线y2=2px(p>0)的焦点为F,准线为l,线段FA交抛物线与点B,过B做l的垂线,垂足为M,若AM⊥MF,则p=.【考点】直线与圆锥曲线的关系.【分析】由抛物线的定义可得BM=BF,又AM⊥MF,根据直角三角形斜边的中点是外心可得故B 为线段AF的中点,求出B的坐标代入抛物线方程求得p值.【解答】解:由抛物线的定义可得BM=BF,F(),又AM⊥MF,故B 为线段AF 的中点,∴B(),把B()代入抛物线y2=2px(p>0)得,1=2p×,∴p=,故答案为.三、解答题17.求下列函数的导数(1)y=x4﹣2x2+3x﹣1;(2)y=.【考点】导数的运算.【分析】根据导数的运算法则计算即可.【解答】解:(1)y=x4﹣2x2+3x﹣1,则y′=4x3﹣4x+3(2)y==1﹣,y′=.18.已知命题P:|m+1|≤2成立.命题q:方程x2﹣mx+1=0有实根.若¬p是假命题,p ∧q为假命题,求m的取值范围.【考点】复合命题的真假.【分析】由绝对值不等式的解法求得p,再由判别式大于等于0,可得q,再由复合命题的真假可得p真,q假,解不等式组,即可得到所求范围.【解答】解:命题P:|m+1|≤2成立即为﹣3≤m≤1,命题q:方程x2﹣mx+1=0有实根,可得△=m2﹣4≥0,解得m≥2或m≤﹣2,¬p是假命题,p∧q为假命题,即为p真,q假,可得解得﹣2<m≤1.则m的取值范围是(﹣2,1].19.已知椭圆C: +=1(a>b>0)的上顶点为(0,2),且离心率为.求椭圆C 的方程.【考点】椭圆的简单性质.【分析】由椭圆的性质可知:焦点在x轴上,b=2,根据椭圆的离心率公式求得a的值,求得椭圆的方程.【解答】解:由题意可知:椭圆的焦点在x轴,且b=2,由离心率公式e====,解得:a=16,故椭圆的标准方程: +=1.20.已知函数f(x)=x3﹣3x,求f(x)在x=3处的切线方程.【考点】利用导数研究曲线上某点切线方程.【分析】首先对f(x)求导,求出x=3处斜率,利用点斜式写出切线方程.【解答】解:对f(x)求导:f'(x)=3x2﹣3,∴x=3 处切线方程的斜率为:f'(3)=24,函数值f(3)=18,∴切线方程过(点3,18),∴切线方程为:y﹣18=24(x﹣3)⇒24x﹣y﹣64=0.21.求满足下列条件的双曲线的标准方程:(1)与双曲线﹣=1有公共焦点,且过点(3,2);(2)渐近线方程为2x±3y=0,顶点在y轴上,且焦距为2.【考点】双曲线的简单性质.【分析】(1)利用与双曲线﹣=1有公共焦点,且过点(3,2),建立方程,即可求出双曲线的标准方程;(2)设双曲线的方程为=1,利用焦距为2,求出m,即可求出双曲线的标准方程.【解答】解:(1)由双曲线﹣=1可求得c2=20.∵两双曲线有公共的焦点,∴a2+b2=20①代入(3,2),可得=1②,由①②可解得:a2=12,b2=8.故所求双曲线的方程为=1;(2)设双曲线的方程为=1,∵焦距为2,∴+=13,∴m=36,∴双曲线的方程为=1.22.已知抛物线C:y2=4x与直线y=2x﹣4交于A,B两点.(1)求弦AB的长度;(2)若点P在抛物线C上,且△ABP的面积为12,求点P的坐标.【考点】直线与圆锥曲线的关系;三角形的面积公式;两点间的距离公式.【分析】(1)利用弦长公式即可求得弦AB的长度;=(2)设点,利用点到直线的距离公式可表示出点P到AB的距离d,S△PAB••d=12,解出即可;【解答】解:(1)设A(x1,y1)、B(x2,y2),由得x2﹣5x+4=0,△>0.由韦达定理有x1+x2=5,x1x2=4,∴|AB|==,所以弦AB的长度为3.(2)设点,设点P到AB的距离为d,则,=••=12,即.∴S△PAB∴,解得y o=6或y o=﹣4∴P点为(9,6)或(4,﹣4).2016年11月9日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建省莆田市第二十四中学 2017-2018 学年 高二下学期第一次月考(3 月)地理试题 一、单项选择题。(共 44 分,每题 4 分) 1. 读图,此时图中甲点时间为( )
A. 3 月 21 日 6 时 B. 3 月 21 日 18 时
C. 9 月 23 日 6 时 D. 9 月 23 日 18 时
【答案】A 【解析】考查光照图的判读。 读图可知,晨昏线与经线圈重合,此时为二分日;联系公转示意图及公转方向可知,此时为春分日;甲位于晨线上,为日出时刻,此时为3月21日6时。故选A。
2. 2011 年 10 月,为安装世界最大的天文望远镜,某天文研究 机构在图所示地区开展天文台的选址工作。
从自然条件来看,该天文台的最佳选址是 A. a 地 B. b 地 C. c 地 D. d 地 【答案】B 【解析】天文台应建在地势较高的地方,要求晴夜多,水汽含量少,且大气宁静度高。因此应选四地中地势较高的b地。 我国是世界重要的苹果生产和浓缩果汁的出口国,据图回答下面小题。
3. 与渤海湾苹果带相比,黄土高原苹果带的优势条 件是
A. 水源丰富 B. 降水充足
C. 昼夜温差大 D. 地势低平
4. 鲁中低山丘陵区苹果树多规划种植在山腰地带, 其主要原因是
A. 利于通风散热 B. 台风影响小
C. 低温、冻害影响小 D. 有良好的排水条件
5. 影响苹果浓缩果汁产业布局的主要区位因素是
A. 原料 B. 市场 C. 交通 D. 气候
【答案】3. C 4. C 5. A 【解析】 3. 本题考查我国的农业生产。第26题,与环渤海苹果带相比,黄土高原地区降水较少,地势较高,故只有
C项正确。 4. 第27题,冬季丘陵低地常有“冷湖效应”,产生逆温,故选择山腰地带,防止冬季的低温、冻害。 5. 第28题,苹果浓缩果汁生产,原料为苹果易腐烂,故属于原料指向型工业。 读“地球表面海陆面积随纬度分布图”,回答下面小题。
6. 地球表面海洋面积比例最大的是( )
A. 北半球中纬度地区 B. 热带地区 C. 南半球中纬度地区 D. 寒带地区
7. 由图可推断,陆地上分布面积最广的气候类型可能是( )
A. 热带草原气候 B. 温带大陆性气候
C. 热带沙漠气候 D. 热带季风气候
【答案】6. B 7. C 【解析】试题分析: 6. 陆地主要集中在北半球和东半球,地球表面的海洋面积比陆地面积大,南极地区主要是陆地,北极地区
主要是海洋。 7. 由图可推断,陆地上分布面积最广的气候类型可能是温带大陆性气候,所以B正确。 考点:经纬网及其地理意义
下图为“世界局部区域不同时间沙尘空间分布图”,读图回答下面小题。
8. 当沙尘扩散如甲所示时,最可能的时间是
A. 1 月 B. 4 月 C. 7 月 D. 10 月
9. 图示沙尘扩散,可能造成的影响是
A. 墨西哥湾沿岸诸国年降水量减少
B. 亚马孙河含沙量剧增
C. 巴西高原干旱程度加剧
D. 美国东南部大气悬浮颗粒物增加
【答案】8. C 9. D 【解析】 8. 据图可知,东北信风带甲的最北位置可以到达北纬30度,所以可以看出气压带和风带随太阳直射点北移,所以是7月,故选C。 9. 沙尘扩散使得墨西哥沿岸降水量增加,A错。亚马孙河含沙量主要取决于流域内的植被覆盖状况,受沙
尘影响不大,B错。巴西高原受来自海洋气流影响,降水增加,C错。根据图示沙尘移动路径可知,沙尘可影响到美国的东南部,所以美国东南部大气悬浮颗粒物增加,D对。故选D。
近读海陆位置分布示意图,回答下面小题。
10. 若图示区域位于北半球,则 P 地气候的成因为( ) A. 夏季受副热带高压控制,冬季受西风带控制 B. 终年受西风带影响 C. 冬夏季风交替控制 D. 受副热带高压或信风带控制 11. 若图示区域位于南半球,则 P 地自然带是( ) A. 亚热带常绿硬叶林带 B. 温带落叶阔叶林带 C. 亚寒带针叶林带 D. 亚热带常绿阔叶林带 【答案】10. A 11. B 【解析】试题分析: 10. 若图示区域位于北半球,则P地为30°N~40°N大陆西岸,为地中海气候,其成因是夏季受副热带高压
控制,冬季受西风带控制;终年受西风带影响为温带海洋性气候;冬夏季风交替控制为季风气候;受副热带高压或信风带控制为热带沙漠气候。 11. 若图示区域位于南半球,则P地位于40°S~60°S大陆西岸,为温带海洋性气候,其对应的自然带为温带
落叶阔叶林。 考点:世界主要地区 二、综合题(56 分) 12. 根据表中资料,分析回答下列问题。 (1)该地位于南北半球的 半球,属于 气候。 (2)该气候类型的成因是 。 (3)该气候类型分布的规律是 。 【答案】(1)南 地中海 (2)气压带和风带的季节性移动 夏季炎热干燥,冬季温和多雨 (3)南北纬 30-40 之间大陆的西岸 【解析】考查世界主要气候类型的分布、特征及成因。 (1)根据表格,该地最热月是1月,最冷月是7月,说明位于南半球。夏季炎热干燥,冬季温和多雨,说明是地中海气候。
(3)该气候类型分布的规律是分布在南北纬30°-40°之间大陆的西岸。 13. 读乌克兰地区图及相关资料,回答下列问题。
资料: 辛菲罗波尔和切尔尼戈夫两城市的气候数据统计 (1)运用资料中的数据,对比分析辛菲罗波尔和切尔尼戈夫两城市气候的差异。 乌克兰地处东欧平原南部,是世界三大黑土分布区之一,黑土面积约占全国的三分之二。19 世纪中期以后,这里逐步成为重要的农业区和商品粮生产基地。20 世纪二、三十年代,该地 区多次发生“黑风暴”现象。 (2)分析回答“黑风暴”现象形成的原因。
乌克兰东部是 20 世纪世界著名的工业区之一,冶金、机械、电力、化学等重工业发达。 (3)简述该地区发展重工业的有利条件。
(4)第聂伯河是乌克兰通航条件好的河流之一,试分析其原因。 (5)乌克兰西部和北部地区与美国中部地区、中国东北地区并称为世界三大商品性玉米产地。 试归纳概括上述三大地区发展玉米生产有利的共性条件。 【答案】 (1)从气温方面看:辛菲罗波尔的年平均气温比切尔尼戈夫高,(2 分)辛菲罗波尔的气温 年较差比切尔尼戈夫小, 从降水方面看:辛菲罗波尔的年降水量比切尔尼戈夫少,辛菲罗波尔比切尔尼戈夫降水 季节变化小。 (2)自然原因:大部分地区为温带大陆性气候,降水较少;风力作用强。人为原因:过度的土地开垦,导致地表植被破坏严重,加剧风力侵蚀作用。 (3)煤炭、水电等能源充足;铁、锰等矿产资源丰富;铁路、港口提供便利的交 通运输条件;(2 分)邻近欧洲经济发达地区,市场广大。 (4)第聂伯河流域地势较平坦,水流平缓;降水较均匀,径流量季节变化不大;流域内以温带草原为主,河流含沙量较低,泥沙淤积程度低。 (5)土地辽阔,地势平坦,有利于大规模机械化生产;水热配合较好(雨热同期),有利于农作 物生长;河流众多,灌溉水源充足;黑土分布广泛,土壤肥力较高;铁路交通发达,运输便 利;周边地区城市众多、乳用养畜业发达,市场需求量大。 【解析】(1)气候的差异关键在于对温度和降水量的分析,一对量的分析、二对变化的描述。从图中数据分析,——平均气温辛菲罗波尔比切尔尼戈夫高,年较差小;辛菲罗波尔的年降水量比切尔尼戈夫少,降水季节变化比切尔尼戈夫小。 (2)分析回答“黑风暴”现象形成的原因要从自然因素及人为因素两方面进行分析。自然原因:大部分地区为温带大陆性气候,降水较少;风力作用强。人为原因:过度的土地开垦,导致地表植被破坏严重,加剧风力侵蚀作用
............ (4)第聂伯河是乌克兰通航条件好的河流之一的原因要从地形对流速的影响及流量大小和季节变化角度考虑。第聂伯河流域位于东欧平原,地势较平坦,水流平缓;受温带海洋性气候的影响,降水较均匀,径流量季节变化不大;流域内以温带草原为主,植被覆盖率高,河流含沙量较低,泥沙淤积程度低。 (5)三大地区发展玉米生产的有利条件主要结合农业区位因素从地形、土壤、机械化、水源、交通、市场等角度分析。三大地区土地辽阔,地势平坦,有利于大规模机械化生产;水热配合较好(雨热同期),有利于农作物生长;河流众多,灌溉水源充足;黑土分布广泛,土壤肥力较高;铁路交通发达,运输便利;周边地区城市众多、乳用养畜业发达,市场需求量大 【点睛】影响河流航运价值大小的因素: 1、地形——平坦,流速缓,易于航运。 2、气候——①降水季节分配均匀,流量稳定有利于航运;②冬季气温高于0℃,无结冰期,通航时间长。 3、土质——土质紧密,水土流失少,河流含沙量小,航道深。 4、经济因素——流经区域经济发达,航运效益好。
