2012高数竞赛A卷试题
华东交大历年高数上册期末试题及答案高等数学(A)12-13上
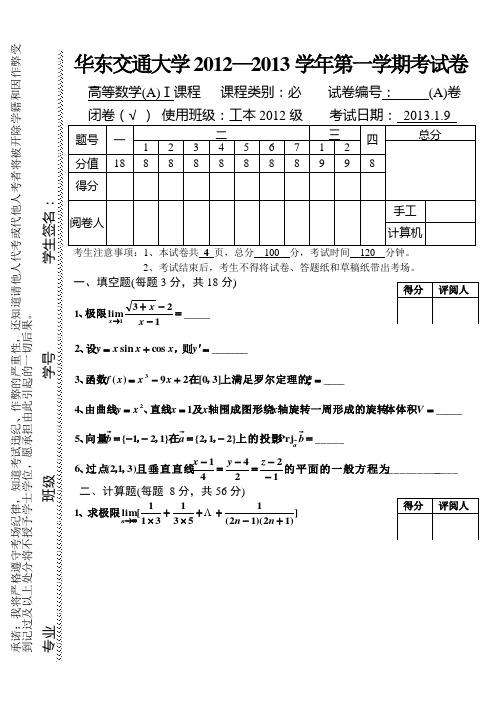
华东交通大学2012—2013学年第一学期考试卷高等数学(A)Ⅰ课程 课程类别:必 试卷编号: (A)卷考生注意事项:1、本试卷共 4 页,总分 100 分,考试时间 120 分钟。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
一、填空题(每题3分,共18分)_____123lim11=--+→x x x 极限、_______ cos sin 2='+=y x x x y 则,设、____]3 0[29)( 33=+-=ξ上满足罗尔定理的,在函数、x x x f_____1 42===V x x x x y 体体积轴旋转一周形成的旋转轴围成图形绕及直线、由曲线、 _____Prj }2 1 2{}1 2 1{ 5=-=--=a上的投影,,在,,向量、______________1224413) 1(2 6的平面的一般方程为且垂直直线,,过点、--=-=-z y x二、计算题(每题 8分,共56分)])12)(12(1531311[lim 1+-++⨯+⨯∞→n n n 求极限、xx xx x x sin 2e e lim 20----→求极限、)0()()ln()sin( 3y x y y x x y xy '==-+,求确定设方程、⎰+x x xd )1(ln 42求不定积分、⎰-x x x d 1 522求不定积分、⎰-2ln 0d 1e 6x x求定积分、的距离:到直线,,求点、212211 )2 1 3( 7-+=-=-z y x L P三、应用题(每题 9分,共18分)的拐点求曲线的极值;求函数,设、)()2( )()1( ln )( 12x f y x f x x x f ==求心脏线的长度;求心脏线围成图形面积,右图设心脏线方程为、)2( )1( )(cos 1 2θ+=r四、证明题(8分)内有且仅有一个实根,在方程证明:,上连续且,在设函数)1 0(01d )(2 1)(]1 0[)( 0=--<⎰xt t f x x f x f。
海南大学经管高数试题(A卷)

海南大学2011-2012学年度第1学期试卷科目:(经管类)《微积分》试题(A卷)姓名:学号:学院:专业班级:时限: 120 分钟考试形式:闭卷笔试所有试卷均配有答题纸,考生应将答案写在答题纸上,写在试卷上一律无效一、选择题:(每题3分,共15分)1、函数)(xf和)(xg相同的是()A . 2()lnf x x=()2lng x x= B. ()f x x=()g x=C. ()f x x=-()g x= D. ()f x= 31xx)x(g-=2、当0→x时,1)sinx(x+是x的().A.高阶无穷小 B.低阶无穷小C.同阶但不等价无穷小 D.等价无穷小3、如图所示函数f(x)的导函数)x('f的图像,关于f(x)的说法,正确的是( )A. 函数y=f(x)在x1点取零点B. 函数y=f(x)在[x1,x2]上单调递增C. 函数f(x)在x2点取极小值D. 函数y=f(x)在(–∞,x1)内单调递增4、若)x (f )x ('F =,则下面正确的是( )A. )x (F dx )x (f =⎰.B. )x (f ]dx )x (f [d =⎰.C.)x (f )'dx )x (f (=⎰. D.c )x (f )x (dF +=⎰5、()()f x dx F x C =+⎰,则()x x e f e dx --⎰=( )A . ()xF e +C B. ()xF e C --+ C. ()xF e C -+ D. ()x F e C x-+二、填空题(每题3分,共15分)6、=→x xsin lim 0x _______,=∞→xx sin x lim ______,=→x x sin 1x lim _______. 7、nx si x (f =),则=)x (f)n ( _____________________________ .8、已知0]b ax 1x 1x [lim 2x =--++∞→,则常数a = ___ ,b = __ .9、⎰dx 2x -1=______________________________________________________.10、设曲线方程为4x x y 2++=,该曲线在点)61(,处的切线方程____________.三 、计算题(每题8分共40分)11、设)a x ln(x y22++=,求dy 。
2012年数学建模A题解题思路

2012年数学建模A题解题思路1. 分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?要分析两组评酒员的评价结果是否有显著性差异,可以使用统计方法进行分析。
一种常用的方法是使用t检验来比较两组平均值的差异,确定是否有统计学意义上的差异。
首先,对于每个评酒员,计算他们对每种葡萄酒的评分的平均值。
然后,对于每组评酒员,计算他们对每种葡萄酒的平均评分的平均值。
接下来,使用t检验来比较两组评酒员对每种葡萄酒的平均评分的平均值是否有显著性差异。
如果t检验的结果显示两组评酒员对某种葡萄酒的评分存在显著性差异,那么可以认为这种葡萄酒的评分更可信的那组评酒员的结果更可信。
1. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
要根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级,可以使用聚类分析或者判别分析等方法。
聚类分析可以根据酿酒葡萄的理化指标和葡萄酒的质量将它们分为几个不同的类别。
这样可以根据每个类别的平均质量评分来进行分级。
判别分析可以建立一个数学模型,根据酿酒葡萄的理化指标预测葡萄酒的质量等级。
这样可以根据酿酒葡萄的理化指标将其进行分级。
1. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。
要分析酿酒葡萄与葡萄酒的理化指标之间的联系,可以使用相关性分析来确定它们之间的相关性。
首先,计算每个理化指标与葡萄酒质量评分之间的相关性系数。
可以使用皮尔逊相关系数或者斯皮尔曼相关系数等方法。
相关性分析的结果可以告诉我们哪些理化指标与葡萄酒质量评分有显著相关性,从而可以了解酿酒葡萄的哪些理化指标对葡萄酒的质量有重要影响。
1. 分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?要分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,可以使用回归分析等方法。
回归分析可以建立一个数学模型,根据酿酒葡萄和葡萄酒的理化指标来预测葡萄酒的质量评分。
这样可以分析每个理化指标对葡萄酒质量的影响程度,并确定哪些指标对葡萄酒的质量影响最为重要。
大学高数竞赛试题及答案

大学高数竞赛试题及答案一、选择题(每题5分,共20分)1. 函数f(x)=x^2-4x+3的零点个数为()。
A. 0B. 1C. 2D. 3答案:C2. 极限lim(x→0) (sin x)/x的值为()。
A. 0B. 1C. -1D. 2答案:B3. 曲线y=x^3-3x+2在点(1,0)处的切线斜率为()。
A. 0B. 1C. -1D. 2答案:B4. 定积分∫(0,1) x^2 dx的值为()。
A. 1/3B. 1/2C. 1D. 2答案:A二、填空题(每题5分,共20分)5. 函数f(x)=x^3-3x+2的极值点为______。
答案:x=16. 函数f(x)=e^x的导数为______。
答案:e^x7. 微分方程y'+2y=e^(-2x)的通解为______。
答案:y=(C-1/2)e^(-2x)+1/28. 函数f(x)=x^2-4x+3的最小值为______。
答案:-1三、解答题(每题15分,共40分)9. 计算极限lim(x→∞) (x^2+3x+2)/(x^3-2x+1)。
答案:lim(x→∞) (x^2+3x+2)/(x^3-2x+1) = lim(x→∞)(1/x+3/x^2+2/x^3)/(1-2/x^2+1/x^3) = 010. 求函数f(x)=x^3-3x+2的导数,并求在x=1处的切线方程。
答案:f'(x) = 3x^2-3f'(1) = 0f(1) = 0切线方程为:y=0四、证明题(每题10分,共20分)11. 证明:对于任意实数x,有e^x > 1+x。
证明:令f(x) = e^x - 1 - x,则f'(x) = e^x - 1。
当x < 0时,f'(x) < 0,f(x)单调递减;当x > 0时,f'(x) > 0,f(x)单调递增。
因此,f(x)的最小值为f(0) = 0。
所以,对于任意实数x,有e^x > 1+x。
2012年数学建模大赛论文A题答案

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):A题我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):曲阜师范大学日照校区参赛队员(打印并签名) :1.王战海2.高延太3.李智超指导教师或指导教师组负责人(打印并签名):黄宝贵日期:2012年09月10日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要确定葡萄酒的质量时一般是通过聘请一批有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄的检测的理化指标会在一定的程度上反映葡萄酒和葡萄的质量。
本论文对葡萄酒的评价问题进行了分析研究,主要判断了已有评价的显著性差异和评价的可信性,分析了如何对酿酒葡萄进行分级,寻找了酿酒葡萄与葡萄酒的理化指标之间的联系,以及解决了酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响等问题,建立了相应的数学模型,并且充分运用MATLAB和SPSS等数学工具,分别就题目所给的为题进行了解答。
11-12重庆理工大学(下)高数期末试题A及答案

重庆理工大学考试试卷2011~ 2012学年第二学期班级 学号 姓名 考试科目 高等数学[(a2)机电] A 卷 闭卷 共 3 页一、判断题(本大题共5小题,每小题2分,共10分)(请在正确说法后面括号内画√,错误说法后面括号内画╳)(1) 若(,,)0x y z a a a a →→=≠,则(,,)||||||yxza a a a a a →→→为平行于向量a →的、长度为1的向量。
( ) (2)22(,)(0,0)3lim6x y xyx y →+=1/2。
( ) (3)⎰+Ldsy x )(22=22 0r d πθ⎰,其中L 为圆周122=+y x 。
( ) (4)若∑∞=1n nu收敛,∑∞=1n nv发散,则)(1∑∞=+n n nv u发散。
( )(5) 设幂级数0nn n a x∞=∑在3x =处收敛,则该级数在1x =-处发散。
( )二、填空题(本大题共10小题,每小题2分,共20分)(6)设向量2a i j k →→→→=-+,42b i j k λ→→→→=-+,则当λ= 时,a →与b →垂直。
(7)xoz 坐标面上的直线1x z =-绕oz 轴旋转而成的圆锥面的方程是 。
(8)直线L :11423zy x =+=-+与平面π:4223x y z --=的关系是 。
(9)设22),(y x y x y x f -=+-,则=),(y x f 。
(10)设363323sin1z x y x y x y =--+,则二阶混合偏导数=)0,1(xy z ___________。
(11)函数22y x z +=在点(3,2)处沿)1,1(=l方向的方向导数为 。
(12)设开区域G 是一个单连通域, 函数P (x , y )及Q (x , y )在G 内具有一阶连续偏导数, 则dy y x Q dx y x P ),(),(+在G 内为某一函数u (x , y )的全微分的充分必要条件是 在G内恒成立。
2012年高中数学竞赛模拟
2012年高中数学竞赛训练(第一次)1、求证:且若,1,0,,,,22222≥++++>e d c b a e d c b a3522222≥++++++++++++++c b a e b a e d a e d c e d c b d c b a证明:()()()1222=≥++⎪⎪⎭⎫ ⎝⎛++∑∑∑a d c b a d c b a 由柯西不等式得: 所以:()即可只要证明:5335)(122≤++⇔≥++∑∑d c b a d c b a ()()()()()()∑∑∑∑++=++≤++2222222d c b a d c b a a d c b a 又有柯西不等式得:()()59359222222≤++⇔≤++∴∑∑d c b a d c b a 得:即可,又由柯西不等式只要证明:()()53-53--12242222≤+⇔≤∑∑∑e a a a e a a 即 ()()()∑∑∑≥++⇔≥+⇔≥+⇔5425422524224224224e e a a e a a e a a()()()()得证!而又由柯西不等式得:5441222222222≥+⇒=+≥⋅+∑∑∑∑ea e ae a求正方体的体积,离恰好是个顶点到一个平面的距、若一个正方体的7,6,5,4,3,2,1082G F E AB B A C D C ,,,,,1111于点分别交平面延长过点为符合题意的平面,如图:设平面ααα因为,的距离分别应为与平面由图可知,点.7,6,5,4,3,2,10,,,,,,,1111αA A D D B B C C列所成的角相等,故由比平面互相平行,所以它们与αAG DC F A E D ,,,11 7:6:5:4:3:2:1::::::1111=F A AG E D DC G B BG E C设正方体棱长为a 4,则a CF a EC a EF a F B a BG a E C 41,17,52,3,2,11======由平面几何知识得故 F EC F EC C CC D C B A CC a S ECF 111111112,,212的底面为四面体知面由于-⊥=上的高,a aa a CC S S d C V V ECFF EC F EC C ECF C 2121421242,2211111=⋅=⋅==--距离,到平面算得点所以由α又因为.2121,2144211所以正方体的体积为棱长为=∴=⇒=a a d 解法2:设单位正方体8个顶点的坐标分别为()()()()()()()()1,1,1,0,1,1,1,0,1,0,0,1,1,1,0,0,1,0,1,0,0,0,0,0若把它们看出二进制的三位数,则恰好为0,1,2,3,4,5,6,7设()()z y x xyz xyz ++=2422为二进制的三位数,则,因平面4x+2y+z=0到点()个顶点的坐标于是,只要令正方体的距离为8,212412424,,222cb ac b ad c b a ++=++++=()()()()()()()()21,21,21,0,21,21,21,0,21,0,0,21,21,21,0,0,21,0,21,0,0,0,0,0为那么,他们到平面4x+2y+z=0的距离就恰好0,1,2,3,4,5,6,7.解法3:题 已知一个正方体八个顶点到一个平面的距离为 0,1,2,3,4,5,6,7 ,求正方体的边长。
高数下册期末a卷考试题及答案
高数下册期末a卷考试题及答案一、单项选择题(每题3分,共30分)1. 函数f(x)=x^3-3x+1的导数是()。
A. 3x^2-3B. 3x^2+3C. x^3-3D. x^3+3x答案:A2. 曲线y=x^2+2x+1在点(1,4)处的切线斜率是()。
A. 2B. 3C. 4D. 5答案:B3. 极限lim(x→0) (sin x)/x的值是()。
A. 0B. 1C. 2D. ∞答案:B4. 函数f(x)=e^x的不定积分是()。
A. e^x + CB. e^(-x) + CC. ln(e^x) + CD. x^e + C答案:A5. 微分方程dy/dx = y/x的通解是()。
A. y = CxB. y = Cx^2C. y = C/xD. y = Cx^(-1)答案:C6. 函数f(x)=ln(x)的二阶导数是()。
A. 1/x^2B. -1/x^2C. 1/xD. -1/x答案:A7. 函数f(x)=x^2-4x+4的极值点是()。
A. x=2B. x=-2C. x=0D. x=4答案:A8. 函数f(x)=x^3-3x+1的拐点是()。
A. x=1B. x=-1C. x=0D. x=2答案:A9. 函数f(x)=x^2+2x+1的最小值是()。
A. 0B. 1C. 2D. 3答案:B10. 函数f(x)=x^3的泰勒展开式在x=0处的前三项是()。
A. 1+3x+3x^2B. 1+x+x^2C. 1+3x+3x^3D. 1+x+x^3答案:D二、填空题(每题4分,共20分)1. 函数f(x)=x^4-4x^2+4的极小值点是x=______。
答案:±√22. 函数f(x)=x^2-6x+8的零点是x=______。
答案:2和43. 函数f(x)=e^x的不定积分是______。
答案:e^x + C4. 函数f(x)=x^3的二阶导数是______。
答案:6x5. 函数f(x)=ln(x)的不定积分是______。
2012高教社杯全国大学生数学建模竞赛A题论文最新的
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍,期刊和其他媒体进行正式或非正式发表等。
)我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话): A1618 所属学校(请填写完整的全名):福州大学参赛队员 (打印并签名) :1.2.3.指导教师或指导教师组负责人 (打印并签名):日期: 2012 年 9 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要本文要解决的是葡萄酒的评价问题,我们利用数理统计的知识,包括显著性差异检验、主成分分析、聚类分析、典型相关分析、逐步线性回归分析等建立数学模型,分别求解。
问题一,由题意知,要分析两组评酒员的评价结果有无显著性差异,需应用《概率统计》中的假设检验知识以及spss 软件中关于两个总体均值的假设检验。
检验结果表明,对于红葡萄酒,由于t >Pr 的值为05.0019.0<,故拒绝原假设0.H ,认为两个红葡萄酒样本总体的均值不相等,同理,对白葡萄酒,t >Pr 的值为05.0017.0<,认为两个白葡萄酒样本总体的均值不相等。
高数下册期末a卷考试题及答案
高数下册期末a卷考试题及答案一、选择题(每题5分,共30分)1. 以下哪个函数不是周期函数?A. \( \sin(x) \)B. \( \cos(x) \)C. \( e^x \)D. \( \tan(x) \)答案:C2. 函数 \( f(x) = x^2 \) 在 \( x=1 \) 处的导数是:A. 0B. 1C. 2D. 3答案:C3. 以下哪个选项是 \( \int_0^1 x^2 dx \) 的正确计算结果?A. \( \frac{1}{3} \)B. \( \frac{1}{2} \)C. \( 1 \)D. \( 2 \)答案:A4. 以下哪个选项是 \( \lim_{x \to 0} \frac{\sin x}{x} \) 的值?A. 0B. 1C. 2D. 3答案:B5. 以下哪个选项是 \( \int \frac{1}{x} dx \) 的原函数?A. \( \ln|x| + C \)B. \( x + C \)C. \( e^x + C \)D. \( \sin x + C \)答案:A6. 以下哪个选项是 \( \int e^x \cos x \, dx \) 的正确积分结果?A. \( \frac{1}{2} e^x (\cos x + \sin x) + C \)B. \( \frac{1}{2} e^x (\cos x - \sin x) + C \)C. \( \frac{1}{2} e^x (\cos x + \sin x) - C \)D. \( \frac{1}{2} e^x (\cos x - \sin x) - C \)答案:B二、填空题(每题5分,共20分)1. 函数 \( f(x) = \ln(x) \) 的定义域是 \( ______ \)。
答案:\( (0, +\infty) \)2. 函数 \( f(x) = \sqrt{x} \) 的导数是 \( ______ \)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华侨大学2012年高等数学竞赛试题(A卷)
第1页 共2页
华侨大学2012年高等数学竞赛试题(A卷)
考试时间:2012年6月2日(星期六) 上午8:30—11:00
境内(外)生 院别 班级 准考证号 姓名 成绩
大题 一 二 三 四 五 六 七
满分 36 10 10 12 15 12 5
得分
一、填空题(本题共12小题,每小题3分,满分36分,把答案直接填在题中的横线上)
1、设222(1)ln2xfxx−=−,且[()]lnfgxx=,则()gxdx=∫ .
2、设(,)zfxyy=,其中f具有二阶连续偏导数,则2zxy∂=∂∂ .
3、设2(,)ln(1)(1)arcsinxfxyxyy=++−,则(,1)xfx= .
4、函数
2
()32fxxx=−+
在区间[3,4]−上的最大值为M= .
5、已知向量rG满足:ra⊥GG,rb⊥GG,且Prj14cr=GG,其中(2,3,1)a=−G,(1,2,3)b=−G,(2,1,2)c=G,
则
r=
G
.
6、二重积分22224sgn(2)xyxydσ+≤+−=∫∫ .
7、极限 ()1lim1234xxxxx→+∞+++= .
8、二次积分2112200ln(1)xdxxydy−++=∫∫ .
9、由球面2224xyzz++=及圆锥面222xyz+=所围成、含有z轴的部分立体的体积V= .
10、已知函数()fx在区间(1,)+∞内可导,且lim[()()]xfxxfxa→+∞′+=,则lim()xfx→+∞= .
11、12011xxdxx−=+∫ .
12、已知
2
0
cos(2)xdxAxπ=+∫,则20sincos
1xxdxxπ=+
∫
.
华侨大学2012年高等数学竞赛试题(A卷)
第2页 共2页
以下各题在答题纸上解答,答题时必须写出详细的解答过程,并在每张答题纸写上:姓名
..、准考证号....
.
二、(本题满分10分) 设函数32ln(1),0;arcsin()6,0;1,0,sin4axaxxxxfxxexaxxxx⎧⎪+<⎪−⎪⎪==⎨⎪+−−⎪>⎪⎪⎩
问:(1)当
a为何值时,()fx在点0x=处连续?(2)当a为何值时,0x
=
是()fx的可去间断点?
三、(本题满分10分)过直线1022270xyzxyz+−=⎧⎨+−=⎩作曲面222327xyz+−=的切平面,求此切平面的方程.
四、 (本题满分12分) 设Σ为曲线(12)0yzeyx⎧=≤≤⎨=⎩绕z轴旋转一周所成的旋转曲面的下侧,利用Gauss
公式计算曲面积分
2
42(1)IzxdydzzdzdxzdxdyΣ=−+−
∫∫
.
五、 (本题满分15分)设函数()ft在区间[0,)+∞上连续,{}2222()(,,)|,0txyzxyztzΩ=++≤≥,
()tΣ
为()tΩ的表面,()Dt为()tΩ在xOy面上的投影区域,()Lt为()Dt的边界曲线.已知当
(0,)t∈+∞
时,恒有
222222222222
()()()()
()()2()LttDttfxyxydsxyzdSfxydxyzdvσΣΩ+++++=++++
∫∫∫∫∫∫∫∫vw
,
求()ft的表达式.
六、(本题满分12分)设非负、具有二阶连续导数的函数
()(0)yyxx=≥满足方程20
xyy
′′′
−+=
;当曲
线
()yyx=过原点时,其与直线1x=及0y=
所围成平面图形D的面积为2,求D绕y轴旋转一周
所得旋转体的体积.
七、(本题满分5分)设函数
()fx在闭区间[]0,1上具有连续导数,且(0)0f=,(1)1f=
,证明
1
10|()()|fxfxdxe−
′
−≥
∫
.
