2014年北京市各城区中考一模数学——代数与几何综合题25题汇总
2014年北京市各城区中考一模数学——四边形计算与证明题19题汇总

G FED CBA A BF D 2014年北京市各城区中考一模数学——四边形计算与证明题汇总1、(2014年门头沟一模)19.如图7,菱形ABCD 的对角线交于O 点,DE ∥AC ,CE ∥BD , (1)求证:四边形OCED 是矩形;(2)若AD =5,BD =8,计算sin DCE ∠的值.2、(2014年丰台一模)19. 如图,在ABCD 中,E F 、分别为边AB CD 、的中点,BD 是对角线,过A 点作AG DB ∥交CB 的延长线于点.G (1)求证:四边形DEBF 是平行四边形;(2)如果90G ∠=°,60C ∠=°,=2BC ,求四边形DEBF 的面积.3、(2014年平谷一模)19.如图,在△ABC 中,D 为AB 边上一点、F 为AC 的中点,过点C 作CE //AB 交DF 的延长线于点E ,连结AE .(1)求证:四边形ADCE 为平行四边形.(2)若EF =22,︒=∠︒=∠4530AED FCD ,,求DC 的长.ADEC BO4、(2014年顺义一模)19.如图,在四边形ABCD 中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB 的长.5、(2014年石景山一模)19.如图,在四边形ABCD 中,2AB =,︒=∠=∠60C A ,DB AB ⊥于点B , 45DBC ∠=︒,求BC 的长.6、(2014年海淀一模)19. 如图,在△ABC 中,∠ACB =90º,∠ABC =30º,BC =AC 为边在△ABC 的外部作等边△ACD ,连接BD . (1)求四边形ABCD 的面积; (2)求BD 的长. DC B AA BCD7、(2014年西城一模)19. 如图,在ABC ∆中,AB AC =,AD 平分BAC ∠,//CE AD 且CE AD =. (1)求证:四边形ADCE 是矩形;(2)若ABC ∆是边长为4的等边三角形,AC ,DE 相交于点O ,在CE 上截取CF CO =,连接OF ,求线段FC 的长及四边形AOFE 的面积。
北京市门头沟区2014年中考数学一模试题

北京市门头沟区2014年中考一模数学试题学校 姓名 准考证号_____________一、选择题(本题共32分,每小题4分) 1.-2的绝对值是A .-2B .2C .12 D . 12- 2. 法国《费加罗报》4月 7日报道,根据来自其他媒体的数据,自从搜索马航失联航班MH370之日起,到目前为止,搜寻费用已超过50 000 000美元,请将50 000 000用科学计数法表示A. 7510⨯B. 8510⨯C. 80.510⨯D. 90.510⨯3. 如图1所示,小红随意在地板上踢键子,则键子恰落在黑色方砖上的概率为A .45 B .35 C .25 D .154. 下列图案中既是中心对称图形也是轴对称图形的是A .B .C .D .5. 小亮和小强进行投飞镖比赛,比赛结束后对他们的成绩进行统计,小亮的平均得分是 9.1环,方差是2.5;小强的平均得分是9.1环,方差是1.9,请问谁的综合技术更稳定些 A .小亮 B .小强 C .都稳定 D .无法判断.考试结束,将本试卷、答题卡和草稿纸一并交回。
BA°图1DA6. 如图2,直线AB∥CD,∠BAE=28О,∠ECD=50О,则∠E=A.68О B.78О C. 92О D.102О7. 一个扇形的圆心角为120°,半径为3,则这个扇形的面积是A.πB.2πC.3πD.4π8.如图3,是由矩形和半圆组成的一个封闭图形,其中AB=8,AD=DE=FC=2,点P由D点出发沿DE→半圆→FC运动,到达C点停止运动.设AP的长为x, △ABP的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是A B. C.D.二、填空题(本题共16分,每小题4分)9. 在函数y=中,自变量x的取值范围是.10. 分解因式29x y y-=____________________.11. 如图4,AB为⊙O的弦,半径OC⊥AB于点D,AB=32,∠A=30°,则⊙O的直径为 .12. 如图5,已知直线l:y=,过点A1(1,0)作x轴的垂线交直线l于点B1,在线段A1B1右侧作等边三角形A1B1C1,过点C1作x轴的垂线交x轴于A2,交直线l于点B2,在线段A2B2右侧作等边三角形A2B2C2,按此作法继续下去则B2的坐标为_______________;B n的坐标为________________.(n为正整数)图3图4图5三、解答题(本题共30分,每小题5分) 13. 计算:(012tan 602014--+o14.求不等式组503512(1)x x x ⎧-<⎪⎨⎪+>-⎩,.的整数..解 15. 已知2430a a --=,求代数式22(1)(1)a a a --+的值.16.如图6,已知点C ,E ,B ,F 在同一直线上,AC ∥DF ,AC =DF ,BC =EF , 求证:AB =DE17.一次函数y kx b =+与反比例函数my x=的图象交于A (1,4),B (-2,n (1)求m 的值;(2)求k 和b 的值;(3)结合图象直接写出不等式0mkx b x-->的解集.18.某建筑集团完成一路段的高架桥铺设任务,在合同期内高效完成了任务,这是记者与该集团工程师的一段对话:工程师:图6通过这段对话,请你求出该建筑集团原来每天铺设的米数.四、解答题(本题共20分,每小题5分)19.如图7,菱形ABCD 的对角线交于O 点,DE ∥AC ,CE ∥BD , (1)求证:四边形OCED 是矩形;(2)若AD =5,BD =8,计算sin DCE 的值.20.如图8,⊙O 的直径AB =4,点P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连结AC .(1)若∠CPA =30°,求PC 的长;(2)若点P 在AB 的延长线上运动,∠CPA 的平分线交AC 于点M . 你认为∠CMP 的大小是否发生变化?若变化,请说明理由;若不变化,求出∠CMP 的大小.21.某市对初三学生的体育成绩进行了一次监测,体育成绩评定分为四个等级:A ,B ,C ,D ;A 代表优秀;B 代表良好;C 代表合格;D 代表不合格,为了准确监测出全区体育成绩的真实水平,特别从农村、县镇、城市三地抽取5000人作为检测样本,相关数据如下扇形统计图和条形统计图(1)请你通过计算补全条形统计图;E记者: 图7图8(2)若该市今年有100000人参加中考体育考试,请你估算一下今年大约有多少学生中考体育考试成绩能在合格以上.22. 折纸是一种传统的手工艺术,也是很多人从小就经历的事,在折纸中,蕴涵许多数学知识,我们还可以通过折纸验证数学猜想.如下图把一张直角三角形纸片按照图①~④的过程折叠后展开,便得到一个新的图形—“叠加矩形”。
2014年北京市中考数学试卷(含答案和解析)

2014年北京市中考数学试卷(含答案和解析)2014年北京市中考数学试卷一、选择题(本题共32分,每小题4分)1.(4分)2的相反数是()A。
2B。
-2C。
D。
2.(4分)据报道,某小区居民XXX改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨。
将300 000用科学记数法表示应为()A。
0.3×10^6B。
3×10^5C。
D。
3×10^43.(4分)如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是()A。
B。
C。
D。
4.(4分)如图是几何体的三视图,该几何体是()A。
圆锥B。
圆柱C。
正三棱柱D。
正三棱锥5.(4分)某篮球队12名队员的年龄如表:年龄(岁)。
18.19.20.21人数。
5.4.1.2则这12名队员年龄的众数和平均数分别是()A。
18,19B。
19,19C。
18,19.5D。
19,19.56.(4分)园林队在某公园进行绿化,中间休息了一段时间。
已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图,则休息后园林队每小时绿化面积为()A。
4平方米B。
5平方米C。
8平方米D。
100平方米7.(4分)如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为()A。
2B。
4C。
D。
88.(4分)已知点A为某封闭图形边界上一定点,动点P 从点A出发,沿其边界顺时针匀速运动一周。
设点P运动的时间为x,线段AP的长为y。
表示y与x的函数关系的图象大致如图,则该封闭图形可能是()A。
B。
C。
D。
二、填空题(本题共16分,每小题4分)9.(4分)分解因式:ax^4-9ay^2=_________。
10.(4分)在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为_________m。
11.(4分)如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数y=f(x)(k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为_________。
2014年北京市17区中考数学一模试题汇编7.选择压轴8题
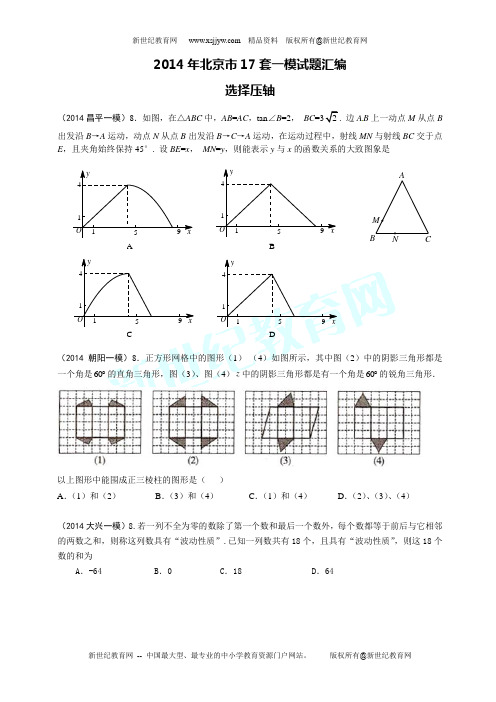
2014年北京市17套一模试题汇编选择压轴(2014昌平一模)8.如图,在△ABC 中,AB =AC ,tan ∠B =2, BC =32. 边A B 上一动点M 从点B 出发沿B →A 运动,动点N 从点B 出发沿B →C →A 运动,在运动过程中,射线MN 与射线BC 交于点E ,且夹角始终保持45°. 设BE =x , MN =y ,则能表示y 与x 的函数关系的大致图象是ABC D459yOx11459yOx11459yOx11459yOx11(2014朝阳一模)8.正方形网格中的图形(1)-(4)如图所示,其中图(2)中的阴影三角形都是一个角是60︒的直角三角形,图(3)、图(4)z 中的阴影三角形都是有一个角是60︒的锐角三角形.以上图形中能围成正三棱柱的图形是( )A .(1)和(2)B .(3)和(4)C .(1)和(4)D .(2)、(3)、(4)(2014大兴一模)8.若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有18个,且具有“波动性质”,则这18个数的和为A .-64B .0C .18D .64AB CMN(2014东城一模)8. 在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为(4,3).平行于对角线AC 的直线m 从原点O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边分别交于点M ,N ,直线m 运动的时间为t (秒).设△OMN 的面积为S ,则能反映S 与t 之间函数关系的大致图象是123456789-1-1-21234567tSO123456789-1-1-21234567tSO 123456789-1-1-21234567tSO123456789-1-1-21234567tSOA B C D(2014房山一模)8.如图1,菱形ABCD 的对角线交于点O ,AC=2BD ,点P 是AO 上一个动点,过点P 作AC 的垂线交菱形的边于M ,N 两点.设AP =x ,△OMN 的面积为y , 表示y 与x 的函数关系的图象大致如图2所示,则菱形的周长为A. 2 B .23 C . 4 D . 25(2014丰台一模)8. 如图,在矩形ABCD 中,AB=4cm ,23AD =cm ,E 为CD 边上的中点,点P 从点A 沿折线AE EC -运动到点C 时停止,点Q 从点A 沿折线AB BC -运动到点C 时停止,它们运动的速度都是s cm /1.如果点P ,Q 同时开始运动,设运动时间为)(s t ,APQ ∆的面积为)(2cm y ,则y 与t 的函数关系的图象可能是A .B .C .D .图1 图2MN BD O ACPyx18112OQPEDCBAPAED CB(2014海淀一模)8.如图,点P 是以O 为圆心,AB 为直径的半圆的中点,2AB =,等腰直角三角板45︒角的顶点与点P 重合,当此三角板绕点P 旋转时,它的斜边和直角边所在的直线与直径AB 分别相交于C 、D 两点.设线段AD 的长为x ,线段BC 的长为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( ).O PA BC DA B C D(2014怀柔一模)8.在矩形ABCD 中,AB=23,BC=6,点E 为对角线AC 的中点,点P 在边BC 上,连接PE 、PA.当点P 在BC 上运动时,设BP=x ,△APE 的周长为y ,下列图象中,能表示y 与x 的函数关系的图象大致是2121yx O2121yx O2121yxO2121yxO B yx4681012142468102OA yxO 4681012142468102 Dyx4681012142468102OCyx4681012142468102OEFDBACP(2014门头沟一模)8.如图3,是由矩形和半圆组成的一个封闭图形,其中AB=8,AD=DE=FC=2,点P由D点出发沿DE→半圆→FC运动,到达C点停止运动.设AP的长为x, △ABP的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是A B. C. D.(2014密云一模)8..如右图,MN⊥PQ,垂足为点O,点A、C在直线MN上运动,点B、D在直线PQ上运动.顺次连结点A、B、C、D,围成四边形ABCD。
2014东城初三一模数学答案
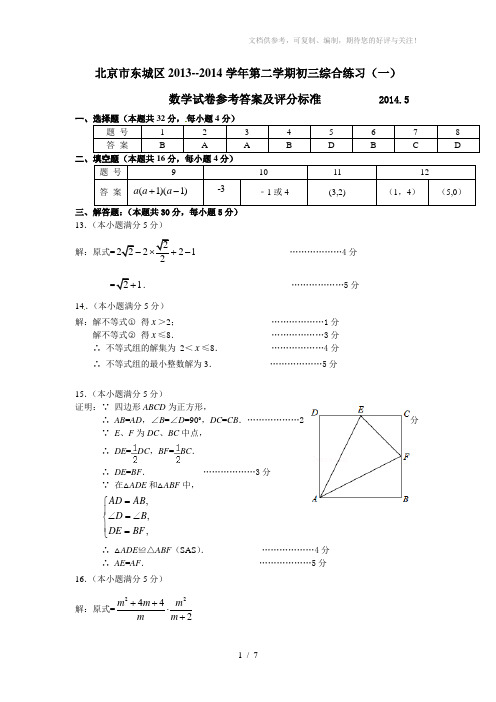
北京市东城区2013--2014学年第二学期初三综合练习(一) 数学试卷参考答案及评分标准 2014.5一、选择题(本题共32分,每小题4分)题 号 1 2 3 4 5 6 7 8 答 案 B AABD BC D二、填空题(本题共16分,每小题4分)题 号 91011 12答 案(1)(1)a a a +--3﹣1或4(3,2)(1,4)(5,0)三、解答题:(本题共30分,每小题5分) 13.(本小题满分5分) 解:原式=2222212-⨯+- ………………4分 =21+. ………………5分 14.(本小题满分5分)解:解不等式○1 得x >2; ………………1分 解不等式○2 得x ≤8. ………………3分 ∴ 不等式组的解集为 2<x ≤8. ………………4分∴ 不等式组的最小整数解为3. ………………5分 15.(本小题满分5分)证明:∵ 四边形ABCD 为正方形,∴ AB =AD ,∠B =∠D =90°,DC =CB .………………2分∵ E 、F 为DC 、BC 中点,∴ DE =DC ,BF =BC .∴ DE =BF . ………………3分 ∵ 在△ADE 和△ABF 中,,,,AD AB D B DE BF =⎧⎪∠=∠⎨⎪=⎩∴ △ADE ≌△ABF (SAS ). ………………4分 ∴ AE =AF . ………………5分 16.(本小题满分5分)解:原式=22442m m m m m ++⋅+=22(2)2m m m m +⋅+ =22m m +. ………………3分 ∵ m 是方程22410x x +-=的根,∴ 22410m m +-=. ∴ 2122m m +=. ………………………5分 17.(本小题满分5分)解:设甲种商品应购进x 件,乙种商品应购进y 件. ………………………1分根据题意,得 1605101100.x y x y +=⎧⎨+=⎩………………………3分解得 10060.x y =⎧⎨=⎩………………………4分答:甲种商品购进100件,乙种商品购进60件. ………………………5分18.(本小题满分5分)解:(1)过点B 作BC ⊥x 轴于点C .由勾股定理可得 5OB =.………1分 ∵ OA=OB ,∴ 点A 的坐标为(5,0). ………2分设直线AB 的解析式为 y kx b =+.可求直线AB 的解析式为210y x =-+.………3分(2)将等腰△AOB 沿x 轴正方向平移5个单位,能使点B 落在反比例函数32y x=(x >0)的图象上. ………5分四、解答题(本题共20分,每小题5分) 19.(本小题满分5分)(1)证明:由折叠的性质可得:∠ANM =∠CNM . ∵ 四边形ABCD 是矩形, ∴ AD ∥BC .∴ ∠ANM =∠CMN . ∴ ∠CMN =∠CNM .∴ CM =CN . ………2分(2)解:过点N 作NH ⊥BC 于点H ,则四边形NHCD 是矩形. ∴ HC =DN ,NH =DC .∵ △CM N 的面积与△CDN 的面积比为3:1, ∴ MC =3ND =3HC .∴ MH =2HC .设DN =x ,则HC =x ,MH =2x , ∴CM =3x =CN ,在Rt △CDN 中,DC =2x =4,∴ 2x =.∴ HM =2.在Rt △MNH 中,MN =2281626MH NH +=+=.20.(本小题满分5分) 解:(1)90÷30%=300(名),一共调查了300名学生.(2)艺术的人数:300×20%=60名,其它的人数:300×10%=30名;补全折线图如图.(3)体育部分所对应的圆心角的度数为:×360°=48°.(4)1800×=480(名).答:1800名学生中估计最喜爱科普类书籍的学生人数为480.21.(本小题满分5分)解:(1)∵AB 是⊙O 的直径,∴∠ADB =∠ADC =90°.∵∠B =∠AED =∠CAD ,∠C =∠C ,90.C CAD C B ︒∴∠+∠=∠+∠=∴∠BAC =∠ADC =90°.∴AC 是⊙O 的切线.………………2分 (2)可证△ADC ∽△BAC .∴AC CDBC AC =.即AC 2=BC ×CD =36. 解得 AC =6. ∵点E 是BD 的中点, ∴∠DAE =∠BAE .∵∠CAF =∠CAD +∠DAE =∠ABF +∠BAE =∠AFD , ∴CA =CF =6,∴DF =CA ﹣CD =2.………………5分22.(本小题满分5分)解: (1)∠B +∠D =180°(或互补). ………………1分 (2)∵ AB =AC ,∴ 把△ABD 绕A 点逆时针旋转90°至△ACG ,可使AB与AC 重合. ………………2分 ∠B =∠ACG , BD=CG , AD=AG∵ △ABC 中,∠BAC =90°,∴ ∠ACB +∠ACG =∠ACB +∠B =90°. 即∠ECG =90°.∴ EC 2+CG 2=EG 2.………………3分 在△AEG 与△AED 中,∠EAG =∠EAC +∠CAG =∠EAC +∠BAD =90°-∠EAD =45°=∠EAD . 又∵AD =AG ,AE =AE ,∴ △AEG ≌△AED . ………………4分 ∴ DE =EG . 又∵CG =BD ,∴ BD 2+EC 2=DE 2.∴ 5DE =.………………5分五、解答题:(本题共22分,第23题7分,第24题7分,第25题8分) 23.(本小题满分7分) 解:(1)证明:()()()22=41433=21,m m m m ∆+-+-所以方程有两个不等实根. ………………2分()()()21212412141212.213,1+.111,01,1 2.1,3,1.13331.m m m m x mmm m mx x x x my m m +±-+±-=∴>∴<<∴+<>∴==+⎛⎫∴=-+=- ⎪⎝⎭两根分别为………………5分(3)作出函数3(1)m m>y=-的图象,并将图象在直线2m =左侧部分沿此直线翻折,所得新图形如图所示.易知点,A B 的坐标分别为3(3,3),(2,).2A B --当直线 过点 A 时,可求得 过点B 时,可求得 因此,……………7分24. (本小题满分7分)解: (1) ∠QEP = 60 °.………………1分 (2) ∠QEP = 60 °.证明: 如图1,以∠DAC 是锐角为例.∵ △ABC 是等边三角形,∴ AC =BC ,∠ACB =60°.()21,=210.m m >∴∆->2y m b =+9,b =-11,2b =-119.2b -<<-文档供参考,可复制、编制,期待您的好评与关注! 21G QPEDCBAGQPEDCBA12345678910-1-2-1-2-3-412345xyOA BCDN 1N 2N 3N 4E又由题意可知,CP =CQ ,∠PCQ =6O °. ∴ ∠ACP =∠BCQ . ∴ △ACP ≌△BCQ . ∴ ∠APC =∠Q .设PC 与BQ 交于点G , 图1 ∵ ∠1=∠2,∴ ∠Q EP =∠PCQ =60°. ………………4分 (3)由题意可求,∠APC =30°,∠PCB =45°. 又由(2)可证 ∠QEP =60°. ∴ 可证QE 垂直平分PC ,△GBC 为等腰直角三角形. ∵ AC =4,∴ 22GC =,26GQ =.∴ 2622BQ =-. ………………7分25.(本小题满分8分) 解:(1)由题意可求点A (2,0),点B (0,1).过点C 作CE ⊥x 轴,易证△AOB ≌△ECA .∴ OA =CE =2,OB =AE =1.∴ 点C 的坐标为(3,2). ………………1分 将点A (2,0),点C (3,2)代入212y x bx c =-++,220,93 2.2b c b c -++=⎧⎪⎨-++=⎪⎩文档供参考,可复制、编制,期待您的好评与关注!解得9,27.b c ⎧=⎪⎨⎪=-⎩∴二次函数的解析式为219722y x x =-+-. ………………2分 (2)令2197022x x -+-=,解得7D x =. ∴ D 点坐标为(7,0).可求 5,25,5AC CD AD ===. ∴ △ACD 为直角三角形,∠ACD =90°. 又∵ ∠BAC =90°,∴ AB ∥CD . ………………4分(3)如图,由题意可知,要使得以A ,B ,M ,N 四点构成的四边形为平行四边形,只需要点N 到x 轴的距离与点B 到x 轴的距离相等. ∵ B 点坐标为(0,1), ∴ 点N 到x 轴的距离等于1. 可得2197122x x -+-=和2197122x x -+-=-. 解这两个方程得12349-179+179339332222x x x x +-====∴ 点N 的坐标分别为9-1721),9172-,1)9332+-1),9-332,-1). ………8分。
2014中考数学模拟测试题数与代数部分

第 1 页 共 4 页 2014中考数学模拟测试题数与代数部分 一、选择题(10×3’=30’) 1.下列四个数中,负数是( ) A. -2 B. 2-2 C. 1-2 D. 2-2 2.若x是2的相反数,||3y,则xy的值是( )A.5 B.1 C.1或5 D.1或5 3.下列计算正确的是( ) A.33 B.030 C.331 D.39 4.下面的多项式中,能因式分解的是( ) A.nm2 B. 12mm C. nm2 D.122mm
5.若分式12xx的值为0,则( ) A. x=-2 B. x=0 C. x=1或x=-2 D. x=1 6.在算式()□()的□中填上运算符号,使结果最大,这个运算符号是( ) A.加号 B.减号 C.乘号 D.除号 7.雅西高速公路于2012年4月29日正式通车,西昌到成都全长420千米,一辆小汽车和一辆客车同时从西昌、成都两地相向开出,经过2.5小时相遇,相遇时,小汽车比客车多行驶70千米,设小汽车和客车的平均速度分别为x千米/小时和y千米/小时,则下列方程组正确的是( )
A.702.52.5420xyxyB.702.52.5420xyxyC.702.52.5420xyxyD.2.52.54202.52.570xyxy
8.已知关于x的一元二次方程20xbxc的两根分别为121,2xx,则b与c的值分别为( ) A.1,2bc B.1,2bc C.1,2bc D.1,2bc
9.不等式组215,3112xxx的解集在数轴上表示正确的是( )
(A). (B) . (C) . (D) . 10.如图(5)所示,已知A(21,y1),B(2,y2)为反比例函数y=x1图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( ) A.(21,0) B.(1,0) C.(23,0) D.(25,0) 二、填空题(6×4’=24’)
2014-2015学年北京市大兴区初三一模数学试题(含答案)
5.考试结束,将本试卷、答题卡和草稿纸一并交回. 一、选择题(本题共 30 分,每小题 3 分)
下面各题均有四个选项,其中只有一个 ..是符合题意的.
1.今年我区初中毕业生学业考试的考生总数为
4768 人,这个数据用科学记数法表示为
A. 47.68 102
B. 4.768 10 4
C. 0.4768 104
接圆.
( 1)试判断直线 AB与⊙ O的位置关系,并说明理由;
1 ( 2)若 AC= 4,tan ∠ DAC=2,求⊙ O的半径.
D
C
O
P
A
B
26.数学课上,老师要求同学们在扇形纸片
OAB 上画出一个正方形,使得正方形的四个顶
点分别落在扇形半径 OA 、OB 和弧 AB 上 .有一部分同学是这样画的: 如图 1,先在扇形 OAB
求证: AC+BC> 2AD;
D
C
22.列方程或方程组解应用题: 某服装商预测一种应季衬衫能畅销市场,
A
E
B
就用 8000 元购进一批衬衫, 面市后果然供不应求,
服装商又用 17600 元购进了第二批这种衬衫, 所购数量是第一批购进数量的 2 倍,但单价贵
了 8 元。商家销售这种衬衫时每件售价都是 100 元,很快售完。在这两笔生意中,商家共盈
D. 4.768 1ຫໍສະໝຸດ 32 .如果 a 为有理数,且 a a ,那么 a 是
A.负数
B .正数
C .非正数
D .非负数
3.一个口袋中有 4 个白球, 5 个红球, 6 个黄球,每个球除颜色外都相同,搅匀后随机从袋
中摸出一个球,这个球是黄球的概率是
1 A.
15
《二次函数》检测练习—25代数几何函数综合题(较难)
《二次函数》检测练习—25代数几何函数综合题(较难)
《二次函数》检测练习—25 代数几何函数综合题(较难)
附:周老师工作室数学辅导资料目录
一、全国中考专题训练
①全国中考函数专题训练资料
②全国中考动态问题专题训练
二、北京中考综合训练
①北京中考数学综合能力训练资料(一)(针对目标分数96分)
②北京中考数学综合能力训练资料(二)(针对目标分数106分)
③北京中考数学综合能力训练资料(三)(针对目标分数115分)
④北京中考数学综合能力训练资料(四)---北京中考数学模拟试
卷及中考真题100题解析
三、基础知识能力训练资料:
①全等三角形
②一次函数
③轴对称
④勾股定理
⑤反比例函数
⑥四边形
⑦一元二次方程
⑧旋转
⑨圆
⑩相似
⑾二次函数
⑿锐角三角函数(解直角三角形)
北京市2o14年中考数学试题及答案
北京市2o14年中考数学试题及答案北京市2014年中考数学试题及答案一、选择题(每题3分,共30分)1. 以下哪个数是最小的正整数?A. 0B. 1C. 2D. 3答案:B2. 一个数的相反数是-3,那么这个数是?A. 3B. -3C. 0D. 6答案:A3. 以下哪个选项是正确的不等式?A. 3 > 2B. 3 < 2C. 3 = 2D. 3 ≥ 2答案:A4. 计算下列表达式的结果:(2x - 3) + (4x + 5) = ?A. 6x + 2B. 6x - 2C. 2x + 2D. 2x - 2答案:A5. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 20π厘米C. 25π厘米D. 30π厘米答案:C6. 如果一个角的补角是120°,那么这个角的度数是?A. 60°B. 30°C. 45°D. 90°答案:A7. 以下哪个图形是轴对称图形?A. 平行四边形B. 梯形C. 等腰三角形D. 不规则多边形答案:C8. 一个数的平方根是2,那么这个数是?A. 4B. -4C. 2D. -2答案:A9. 以下哪个选项是正确的比例关系?A. 3:4 = 6:8B. 3:4 = 6:9C. 3:4 = 9:12D. 3:4 = 9:8答案:C10. 一个数的立方是-8,那么这个数是?A. 2B. -2C. 4D. -4答案:B二、填空题(每题3分,共15分)11. 一个数的绝对值是5,那么这个数可能是_________。
答案:±512. 计算下列表达式的结果:(-2)^3 = _________。
答案:-813. 一个直角三角形的两个锐角的度数分别是30°和60°,那么这个三角形的斜边与较短直角边的比是_________。
答案:214. 一个数的倒数是1/4,那么这个数是_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 1 页 共 17 页 2014年北京市各城区中考一模数学——代数与几何综合题汇总 1、(2014年门头沟一模)25.概念:点P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小
值叫做线段a与线段b的“理想距离”.已知O(0,0),A(3,1),B(m,n),C(m,n+2)是平面直角坐标系中四点. (1) 根据上述概念,根据上述概念,完成下面的问题(直接写答案)
① 当m=23,n=1时,如图13-1,线段BC与线段OA的理想距离是 ; ② 当m=23,n=2时,如图13-2,线段BC与线段OA的理想距离为 ; ③ 当m=23,若线段BC与线段OA的理想距离为3,则n的取值范围是 . (2)如图13-3,若点B落在圆心为A,半径为1的圆上,当n≥1时,线段BC与线段OA的理想距离记为d,则d的最小值为 (说明理由) (3)当m的值变化时,动线段BC与线段OA的距离始终为1,线段BC的中点为G,求点G随线段BC运动所走过的路径长是多少?
备用图 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 2 页 共 17 页
2、(2014年丰台一模)25. 在平面直角坐标系xOy中,抛物线2yaxc与x轴交于点A(-2,0)和点B,与y轴交于点C(0,23),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移
动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒. (1)求该抛物线的解析式; (2)在整个运动过程中,是否存在某一时刻,使得以A,P,Q为顶点的三角形与△AOC相似?如果存在,请求出对应的t的值;如果不存在,请说明理由. (3)在y轴上有两点M(0,m)和N(0,m+1),若要使得AM+MN+NP的和最小,请直接写出相应的m、t的值以及AM+MN+NP的最小值.
备用图 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 3 页 共 17 页 y
xy
xAB
CN
备用图N
C
BA
OO
3、(2014年平谷一模)25.在平面直角坐标系中,已知抛物线y=-12x2+bx+c (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限. (1)如图,若该抛物线过A,B两点,求b,c的值; (2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与直线AC交于另一点Q. ①点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M,P,Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时,求点M的坐标; ②取BC的中点N,连接NP,BQ.当PQNP+BQ取最大值时,点Q的坐标为________. 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 4 页 共 17 页
4、(2014年顺义一模)25.设pq,都是实数,且pq.我们规定:满足不等式pxq≤≤的实数x的所有取值的全体叫做闭区间,表示为pq,.对于一个函数,如果它的自变量x与函数值y满足:当pxq≤≤时,有pyq≤≤,我们就称此函数是闭区间pq,上的“闭函数”.
(1)反比例函数2014yx是闭区间12014,上的“闭函数”吗?请判断并说明理由; (2)若一次函数0ykxbk是闭区间mn,上的“闭函数”,求此函数的解析式; (3)若实数c,d满足cd,且2d,当二次函数2122yxx是闭区间cd,上的“闭函数”时,求cd,的值. 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 5 页 共 17 页
5、(2014年石景山一模)25.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”Sah. 例如:三点坐标分别为)2,1(A,)1,3(B,)2,2(C,则“水平底”5a,“铅垂高”4h,“矩面积”20Sah. (1)已知点)2,1(A,)1,3(B,),0(tP. ①若A,B,P三点的“矩面积”为12,求点P的坐标; ②直接写出A,B,P三点的“矩面积”的最小值.
(2)已知点)0,4(E,)2,0(F,)4,(mmM,)16,(nnN,其中0m,0n. ①若E,F,M三点的“矩面积”为8,求m的取值范围; ②直接写出E,F,N三点的“矩面积”的最小值及对应n的取值范围. 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 6 页 共 17 页
6、(2014年海淀一模)25. 对于平面直角坐标系 xOy中的点P(a,b),若点P的坐标为(bak,kab)(其中k为常数,且0k),则称点P为点P的“k属派生点”. 例如:P(1,4)的“2属派生点”为P(1+42,214),即P(3,6). (1)①点P(-1,-2)的“2属派生点”P的坐标为____________
;
②若点P的“k属派生点” P的坐标为(3,3),请写出一个符合条件的点P的坐标____________;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为P点,且△OPP为等腰直角三角形,则k的值
为____________;
(3)如图, 点Q的坐标为(0,43),点A在函数43yx(0x)的图象上,且点A是点B的“3属派生点”,当线段B Q最短时,求B点坐标. 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 7 页 共 17 页
7、(2014年西城一模)25. 定义1:在ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为ABC的“有向面积”。“有向面积”用S表示,例如图1中,ABCABCSS
,图2中,ABCABCSS。
定义2:在平面内任取一个ABC和点P(点P不在ABC的三边所在直线上),称有序数组(PBCS,PCAS,PABS)为点P关于ABC的“面积坐标”,记作()PBCPCAPABPSSS,,,例如图3中,菱形ABCD的边长为2,=60ABC,则3ABCS,点D关于ABC的“面积坐标”()DBCDCADABDSSS,,为(333)D,,。在图3中,我们知道ABCDBCDABDCASSSS,利用“有向面积”,我们也可以
把上式表示为:ABCDBCDABDCASSSS。 应用新知:(1)如图4,正方形ABCD的边长为1,则ABCS ,点D关于ABC的“面积坐标”是 ;
探究发现:(2)在平面直角坐标系xOy中,点(02)A,,(10)B,.
①若点P是第二象限内任意一点(不在直线AB上),设点P关于ABO的“面积坐标”为()Pmnk,,,试探究mnk与ABOS之间有怎样的数量关系,并说明理由; ②若点()Pxy,是第四象限内任意一点,请直接写出点P关于ABO的“面积坐标”(用xy,表示); 解决问题:(3)在(2)的条件下,点(10)C,,(01)D,,点Q在抛物线224yxx上,求当QABQCDSS
的值最小时,点Q的横坐标。
A B C 图1 A B C 图2 图3 A B C D B C D A 2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 8 页 共 17 页 8、(2014年通州一模)25.如图,在平面直角坐标系xOy中,半圆的圆心点A在x轴上,直径OB=8,点C是半圆上一点,60COA,二次函数khxay2)(的图象经过点A、B、C.动点P和点Q同时从
点O出发,点P以每秒1个单位的速度从O点运动到点C,点Q以每秒两个单位的速度在OB上运动,当点P运动到点C时,点Q随之停止运动.点D是点C关于二次函数图象对称轴的对称点,顺次连接点D、P、Q,
设点P的运动时间为t秒,△DPQ的面积为y. (1)求二次函数khxay2)(的表达式; (2)当120DQP时,直接写出....点P的坐标; (3)在点P和点Q运动的过程中,△DPQ的面积存在最大值吗?如果存在,请求出此时的t值和△DPQ面积的最大值;如果不存在,请说明理由.
备用图 y
xQDCABO
P
yxQDCABO
P2014年北京市各城区中考一模数学——代数与几何综合题汇总 第 9 页 共 17 页
9、(2014年东城一模)25.在平面直角坐标系xOy中,直线112yx分别与x轴,y轴交于过点A,B,点C是第一象限内的一点,且AB=AC,AB⊥AC,抛物线212yxbxc经过A,C两点,与x轴的另一交点为D. (1)求此抛物线的解析式; (2)判断直线AB与CD的位置关系,并证明你的结论;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,B,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
