上海重点中学2010学年第一学期期中考试高三数学试卷(理科答案)
上海市青浦高级中学2024-2025学年高三上学期9月考试数学试卷(含答案)

上海市青浦高级中学2024学年第一学期9月质量检测高三 数学试卷考试时间:120分钟 满分:150分一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)1.直线的倾斜角大小为__________.2.在的展开式中,含项的系数为__________.3.已知集合,集合,则__________.4.若关于x ,y 的方程组有唯一解,则实数a 满足的条件是__________.5.已知x ,,则“”是“”的____________________条件.6.已知,的最小值为__________.7.从1,2,3,4,5这五个数字中任意选取两个不同的数字组成一个两位数,则这个两位数是偶数的概率为__________.8.已知函数,且,则方程的解是__________.9.已知集合,,若,则m 的取值范围是__________.10.甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为,各局比赛的结果都相互独立,第1局甲当裁判,则前4局中乙恰好当一次裁判的概率是__________.11.设O 为坐标原点,P 是以F 为焦点的抛物线上任意一点,M 是线段PF 上的点且,则直线OM 斜率的取值范围是__________.12.对于定义在D 上的函数,若同时满足:(1)对任意的,均有;(2)对任意的,存在,且,使得成立,则称函数10x +=51x x ⎛⎫+ ⎪⎝⎭3x 211x A x x ⎧⎫=≤⎨⎬-⎩⎭{1,0,1,2,3}B =-A B = 2436x y x ay +=⎧⎨+=⎩y ∈R ||||||x y x y -=+0xy <1ab =2249a b +()21xf x -=+2log (1),0()(),0x x g x f x x +≥⎧=⎨-<⎩()2g x =5322A x x ⎧⎫=-≤⎨⎬⎩⎭{13,}B x m x m m =+≤≤∈R ∣A B A = 1222(0)y px p =>4PM MF = ()y f x =x D ∈()()0f x f x -+=1x D ∈2x D ∈21x x ≠-()()1122f x x x f x -=-()y f x =为“等均”函数.下列函数中:①;②;③;④,“等均”函数的序号是__________.二、选择题(本大题共有4题,满分18分.第13-14题每题4分,第15-16题每题5分)13.若实数a ,b 满足,则下列不等式中恒成立的是()A .B.C .D .14.在2022北京冬奥会单板滑雪U 型场地技巧比赛中,6名评委给A 选手打出了6个各不相同的原始分,经过“去掉其中一个最高分和一个最低分”处理后,得到4个有效分,则经处理后的4个有效分与6个原始分相比,一定会变小的数字特征是()A .平均数B .中位数C .众数D .方差15.如图所示,在正方体中,M 是棱上一点,若平面与棱交于点N ,则下列说法中正确的是( )A .存在平面与直线垂直B .四边形可能是正方形C .不存在平面与直线平行D .任意平面与平面垂直16.已知无穷数列的各项均为实数,为其前n 项和,若对任意正整数都有,则下列各项中可能成立的是( )A .,,,…,为等差数列,,,,…,为等比数列B .,,,…,为等比数列,,,,…,为等差数列C .,,,…,为等差数列,,,…,,…为等比数列D .,,,…,为等比数列,,,…,,…为等差数列三、解答题(本大题共有5题,满分78分)17.(本题满分14分,本题共有2个小题,第1小题满分6分,第2小题满分8分)如图,在四棱锥中,平面ABCD ,底面ABCD 为梯形,,,()f x x =1()1x f x x -=+2()f x x =()sin f x x =0a b >>22a b +>22a b +<a b +>a b +<1111ABCD A B C D -1AA 1MBD 1CC 1MBND 1BB 1MBND 1MBND 11A C 1MBND 1ACB {}n a n S 2024k >1k k S S +>1a 3a 5a 21n a -2a 4a 6a 2n a 1a 3a 5a 21n a -2a 4a 6a 2n a 1a 2a 3a 2024a 2024a 2025a n a 1a 2a 3a 2024a 2024a 2025a n a P ABCD -PD ⊥//AB CD 60BAD ∠=︒,.(1)在侧面PBC 中能否作出一条线段,使其与AD 平行?如果能,请写出作图过程并给出证明;如果不能,请说明理由;(2)若四棱锥的体积是,求直线BP 与平面PCD 所成角的大小.18.(本题满分14分,本题共有2个小题,第1小题满分7分,第2小题满分7分)记为数列的前n 项和,已知,是公差为的等差数列.(1)求的通项公式;(2)证明:.19.(本题满分14分,本题共有2个小题,第1小题满分7分,第2小题满分7分)汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间),当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车.某种算法(如下图所示)将报警时间划分为4段,分别为准备时间、人的反应时间、系统反应时间、制动时间,相应的距离分别为、、、.当车速为v (米/秒),且时,通过大数据统计分析得到下表(其中系数k 随地面湿滑程度等路面情况而变化,)阶段0、准备1、人的反应2、系统反应3、制动时间秒秒2AD AB ==4CD =P ABCD -n S {}n a 11a =n n S a ⎧⎫⎨⎬⎩⎭13{}n a 121112na a a +++< 0t 1t 2t 3t 0d 1d 2d 3d [0,33.3]v ∈[0.5,0.9]k ∈0t 10.8t =20.2t =3t距离米米(1)请写出报警距离d (米)与车速v (米/秒)之间的函数关系式,并求时,若汽车达到报警距离时人和系统均不采取任何制动措施,仍以此速度行驶,则汽车撞上固定障碍物的最短时间.(精确到0.1秒)(2)若要求汽车不论在何种路面情况下行驶,报警距离均小于80米,则汽车的行驶速度应限制在多少米/秒以下?合多少千米/小时〈精确到1千米/小时〉?20.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)已知椭圆的左、右焦点分别为、、点在椭圆上,且.(1)求椭圆的方程;(2)过点作斜率为k 的直线l 交椭圆于M 、N 两点,若,O 为坐标原点,求直线l 的方程;(3)点P 、Q 为椭圆上的两个动点,O 为坐标原点,若直线OP 、OQ 的斜率之积为,求证:为定值.21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)设函数,直线l 是曲线在点处的切线.(1)当,求单调区间;(2)求证:l 不经过;(3)当时,设点,,,B 为l 与y 轴的交点,与分别表示和的面积.是否存在点A 使得成立?若存在,这样的点A 有几个?020d =1d 2d 23120d v k=()d v 0.9k =2222:1(0)x y a b a b Γ+=>>1F 2F T ⎛- ⎝124TF TF +=Γ(1,0)Γ35OM ON ⋅=- Γ14-22||||OP OQ +()ln(1)(0)f x x k x k =++≠()y f x =(,())(0)t f t t >1k =-()f x (0,0)1k =(,())(0)A t f t t >(0,())C f t (0,0)O ACO S △ABO S △ACO △ABO △215ACO ABO S S =△△上海市青浦高级中学2024学年第一学期9月质量检测高三 数学试卷考试时间:120分钟 满分:150分一、填空题(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)1.2.53.4.5.必要不充分6.127.8.39.10.1112.①③二、选择题(本大题共有4题,满分18分,第13-14题每题4分,第15-16题每题5分)13.C 14.D 15.D 16.C三、解答题(本大题共有5题,满分78分)17.(本题满分14分,本题共有2个小题,第1小题满分6分,第2小题满分8分)解:(1)不能.因为梯形ABCD 中,,,,所以AD 不平行于BC ,则AD 与BC 必相交于一点,设为M ,面,在侧面PBC 中不能作AD 的平行线.(2)过点B 作于H ,连接PH ,因为平面ABCD ,平面ABCD ,所以,所以平面PCD ,所以PH 是BE 在平面PCD 内的射影,所以是直线BP 与平面PCD 所成角,因为中,,,所以是等边三角形,所以,,又因为,所以,所以,所以中,,又因为四棱锥的体积是所以,解得,所以中,,,直线BP 与平面PCD 所成角大小是18.(本题满分14分,本题共有2个小题,第1小题满分7分,第2小题满分7分)π6{1,0}-6a ≠2543m ≤58//AB CD 2AB =4CD =AD ∴ PBC M =∴BH CD ⊥PD ⊥BH ⊂PD PH ⊥BH ⊥BPH ∠ABD △2AB AD ==60BAD ∠=︒ABD △60ADB ∠=︒2BD =//AB CD 120ADC ∠=︒60BDC ∠=︒Rt BDH △BH =1DH =P ABCD -111(2332V Sh h ==⋅+=2h =Rt BPH △PH ==BH =tan BH BPH PH ∠===arctan解:(1),当时,,作差,累加得,满足,.(2),.19.(本题满分14分,本题共有2个小题,第1小题满分7分,第2小题满分7分)解:(1)由题意得,,当时,,(秒).(2)根据题意,要求对于任意,恒成立,即对于任意,,即恒成立,由得,,即,解得,(米/秒),(千米/小时),汽车的行驶速度应限制在20米/秒以下,合72千米/小时.20.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)解:(1)椭圆的左右焦点分别为、,点在椭圆上,且.,椭圆的方程.(2)设,,2233n n n n S n n S a a ++=⇒=2n ≥1113n n n S a --+=111n n a n a n -+=-1(1)2n a n n a +=1a n a (1)2n n n a +∴=11121n a n n ⎛⎫=- ⎪+⎝⎭1211112121na a a n ⎛⎫∴+++=-< ⎪+⎝⎭ 0123()d v d d d d =+++21()2020d v v v k ∴=++0.9k =2()2018v d v v =++20()1112 3.118v t v v =++≥+=+=[0.5,0.9]k ∈()80d v <[0.5,0.9]k ∈21208020v v k ++<2160120k v v <-[0.5,0.9]k ∈111,201810k ⎡⎤∈⎢⎥⎣⎦2160110v v ∴<-2106000v v +-<3020v -<<020v ∴≤<360020721000⨯=∴ 2222:1(0)x y a b a bΓ+=>>1F 2F T ⎛- ⎝Γ124TF TF +=21a b =⎧⎨=⎩∴2214x y +=()11,M x y ()22,N x y根据题意得,,与联立,整理可得,根据韦达定理可得①②将①代入②,解得,即直线l 的方程为或.(3)证明:设直线,联立方程组,得,,又直线,同理可得,为定值.21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)解:(1)当时,,得的单调增区间是,单调减区间是.(2),,,整理得,假设l 过原点,,设,,(1)y k x =-2214x y +=22(1)14y k x x y =-⎧⎪⎨+=⎪⎩()2222148440k x k x k +-+-=212221228144414k x x k k x x k ⎧+=⎪⎪+⎨-⎪=⎪+⎩()()()()22212121212121231115OM ON x x y y x x k x k x k x x k x x k ⋅=+=+--=+-++=- 1k =±1y x =-1y x =-+:OP y kx =2244y kx x y =⎧⎨+=⎩22414x k =+()()222222241||114k OP x y k x k +∴=+=+=+1:4OQ y x k=-222161||41k OQ k +=+2222222244161205||||5414141k k k OP OQ k k k +++∴+=+==+++1k =-()(1)1x f x x x'=>-+()f x (0,)+∞(1,0)-()ln(1)(0)f x x k x k =++≠()11k f x x∴'=++:[ln(1)]1()1k l y t k t x t t ⎛⎫∴-++=+- ⎪+⎝⎭1ln(1)(0)11k kt y x k t k t t⎛⎫=+-++≠ ⎪++⎝⎭ln(1)0*1t t t -⇒++=+()ln(1)1t F t t t=+-+2211()01(1)(1)t F t t t t '=-=>+++所以在上严格增,,与*式矛盾.所以l 不经过原点.(3),,由(2)知时,,,,,设,,,极大值,极小值,又,所以在上有两个零点.存在点A 使得且点A 有两个.()F t (0,)+∞()0F t ∴>ln(1)1t t t∴+>+(,ln(1))A t t t ++(0,ln(1))C t t ++1k =0,ln(1)1t B t t ⎛⎫+- ⎪+⎝⎭215ACO ABO S S = △△112||||15||||22OC AC OB AC ∴⨯⋅=⨯2||15||OC OB ∴=15()213ln(1)1t g t t t t =-+++(0)t >222294(21)(4)()(1)(1)t t t t g t t t -+--'==++13613ln 022g ⎛⎫=-> ⎪⎝⎭(4)2013ln 50g =-<40(8)1613ln 903g =-+>()g t (0,)+∞∴215ACO ABO S S =△△。
北京市第十五中学2024-2025学年高三上学期期中考试数学试卷(解析)

北京十五中高三年级数学期中考试试卷本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题纸上,在试卷上作答无效.第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}23A x x =-≤≤,{1B x x =<-或}4x >,那么集合A B = ( )A. {}21x x -≤<- B. {3x x ≤或x ≥4}C. {}24x x -≤< D. {}13x x -≤≤【答案】A 【解析】【分析】由集合交集的定义即可得到答案.【详解】因为{}23A x x =-≤≤,{1B x x =<-或}4x >,所以{}21A B x x ⋂=-≤<-故选:A.2. 在复平面内,复数z 满足(1)2i z -=,则z =( )A. −1−i B. −1+i C. 1i - D. 1i+【答案】D 【解析】【分析】由题意利用复数的运算法则整理计算即可求得最终结果.【详解】由题意可得:z =21−i=2(1+i )(1−i )(1+i )=2(1+i )2=1+i .故选:D.3. 下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是( )A. ()sin f x x = B. 2()f x x =C. 3()f x x= D. 3()f x x =【答案】D 【解析】【分析】逐个判断各个选项中函数的单调性和奇偶性即可..【详解】解:对于A 项,函数()sin f x x =为周期函数,在(0,+∞)上不是增函数,故A 项错误,对于B 项,函数2()f x x =是偶函数,故B 项错误,对于C 项,函数3()f x x=是奇函数,且在(0,+∞)上单调递减,故C 项错误,对于D 项,函数3()f x x =是奇函数,且在R 上单调递增,故D 项正确,故选:D.4. 若0m n <<,则下列结论正确的是( )A. 22log log m n > B. 0.50.5log log m n> C. 1122m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D. 22m n>【答案】B 【解析】【分析】根据指数函数、对数函数的单调性,逐一分析选项,即可得答案.【详解】对于A :因为2log y x =在(0,+∞)上为增函数,且0m n <<,所以22log log m n <,故A 错误;对于B :因为0.5log y x =在(0,+∞)上为减函数,且0m n <<,所以0.50.5log log m n >,故B 正确;对于C :因为1()2x y =在R 上为减函数,且0m n <<,所以1122m n⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,故C 错误;对于D :因为2xy =在R 上为增函数,且0m n <<,所以22m n <,故D 错误,故选:B5. 若α是第二象限角,且1tan 2α=-,则πcos 2α⎛⎫+= ⎪⎝⎭( )A.B. C.D. 【答案】D 【解析】【分析】利用同角三角函数的关系求出sin α,结合诱导公式得到结果.【详解】∵α是第二象限角,∴sin 0,cos 0αα><.∵22sin 1tan ,sin cos 1cos 2a a a a a ==-+=,∴sin α=∴πcos sin 2αα⎛⎫+=-= ⎪⎝⎭故选:D.6. 设等差数列{}n a 的前n 项和为n S ,且2822a a +=-,11110S =-,则n S 取最小值时,n 的值为( )A. 14 B. 15C. 16D. 15或16【答案】D 【解析】【分析】由题意按等差数列的通项公式及求和公式列出含1a 和d 的方程组,解出1a 和d ,再利用求和公式写出n S ,进而求出n S 取最小值时n 的值即可.【详解】由题意知:281122110a a S +=-⎧⎨=-⎩,则1117221155110a d a d a d +++=⎧⎨+=-⎩,解得1151a d =-⎧⎨=⎩,所以22131131********n S n n n ⎛⎫=-=-- ⎪⎝⎭()*N n ∈,所以当15n =或16时,n S 取最小值.故选:D.7. 已知单位向量,a b ,则“a b ⊥”是“任意R λ∈都有a b a b -λ=λ+r r r r ”( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C 【解析】【分析】根据题意,利用向量的线性运算法则,结合充分条件、必要条件的判定方法,即可求解.【详解】由单位向量,a b ,且a b ⊥时,可得1,0a b a b ==⋅= ,则a b b -λ==+==r r r ,所以a b a b -λ=λ+r r r r,即充分性成立;的反正,对于单位向量,a b,若a b a b -λ=λ+r r r r 成立,可得22222222a a b b a a b b -λ⋅-λ=λ+λ⋅+r r r r r r r r ,即221221a b a b -λ⋅-λ=λ+λ⋅+r r r r ,解得0a b ⋅= ,所以a b ⊥,即必要性成立,所以a b ⊥ 是a b a b -λ=λ+rr r r 成立的充分必要条件.故选:C.8. 设函数()21cos cos 2f x x x x =-,则下列结论错误的是( )A. ()f x 的一个周期为πB. ()y f x =的图象关于直线43x π=对称C. 将函数cos2y x =的图象向左平移6π个单位可以得到函数()f x 的图象D. ()f x 在,2ππ⎛⎫⎪⎝⎭上单调递减【答案】D 【解析】【分析】由题可得()cos(23f x x π=+,再利用余弦函数的性质即得.【详解】∵()211+cos21cos cos cos(2)2223x f x x x x x x π=-=-=+,∴函数的最小正周期为π,故A 正确,当43x π=时,233x ππ+=,故B 正确,将函数cos2y x =的图象向左平移6π个单位可以得到函数cos2(cos(2)63y x x ππ=+=+,故C 正确,当,2x ππ⎛⎫∈⎪⎝⎭时,47,2333x πππ⎛⎫ ⎪⎝+⎭∈,函数先增后减,故D 错误.故选:D.9. 在ABC V 中,2π3A =,D 为边BC 上一点,若AD AB ⊥,且1AD =,则ABC V 面积的最小值为( )A.B.C.D. 【答案】B 【解析】【分析】利用等面积法建立,b c 边的等量关系,再利用基本不等式求bc 的最小值即可求解.【详解】如图,由已知2π3A =,AD AB ⊥,且1AD =,ABC V 的面积112πsin sin 223ABC S bc A bc ===△,又11π11sin 22622ABC ABD ADC S S S c b c b ⎛⎫=+=+=+ ⎪⎝⎭,2c b =+≥=83bc ≥,当且仅当2b c =,即b c ==时等号成立,所以ABC S 故选:B.10. 如图,曲线C 为函数5sin (0)2y x x π=≤≤的图象,甲粒子沿曲线C 从A 点向目的地B 点运动,乙粒子沿曲线C 从B 点向目的地A 点运动.两个粒子同时出发,且乙的水平速率为甲的2倍,当其中一个粒子先到达目的地时,另一个粒子随之停止运动.在运动过程中,设甲粒子的坐标为(,)m n ,乙粒子的坐标为(,)u v ,若记()n v f m -=,则下列说法中正确的是( )A. ()f m 在区间(,)2ππ上是增函数B. ()f m 恰有2个零点C. ()f m 的最小值为2-D. ()f m 的图象关于点5(,0)6π中心对称【答案】B 【解析】【分析】由题意得到()22sin sin 1=+-f m m m 逐项判断.【详解】解:由题意得:5sin ,sin sin 2cos 22π⎛⎫===-= ⎪⎝⎭n m v u m m ,所以()2sin cos 22sin sin 1=-=-=+-f m n v m m m m ,由502550222m m πππ⎧≤≤⎪⎪⎨⎪≤-≤⎪⎩得504π≤≤m ,令sin =t m ,则221y t t =+-,因为sin =t m 在(,)2ππ上递减,221y t t =+-在()0,1上递增,所以()f m 在区间(,)2ππ上是减函数,故A 错误;令()22sin sin 10=+-=f m m m ,得1sin 2=m 或sin 1=-m ,解得6m π=或56m π=,故B 正确;因为2219212,[48⎛⎫=+-=+-∈ ⎪⎝⎭y t t t t ,所以()f m 的最小值为98-,故C 错误;因为2219212,[48⎛⎫=+-=+-∈ ⎪⎝⎭y t t t t ,关于14t =-对称,是轴对称图形,所以()f m 不可能关于点5(,0)6π中心对称,故D 错误;故选:B第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分.11.函数()f x =________.【答案】[2,+∞)【解析】【详解】分析:根据偶次根式下被开方数非负列不等式,解对数不等式得函数定义域.详解:要使函数()f x 有意义,则2log 10x -≥,解得2x ≥,即函数()f x 的定义域为[2,+∞).点睛:求给定函数的定义域往往需转化为解不等式(组)的问题.12. 612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为________ (用数字作答)【答案】160-【解析】【分析】根据题意,由题意可得二项式展开式的通项公式,代入计算,即可得到结果.【详解】因为612x x ⎛⎫- ⎪⎝⎭展开式的通项公式为()()6261661C 22C rr rr r r r T x x x --+⎛⎫=⋅-=-⋅ ⎪⎝⎭,令260r -=可得3r =,则展开式中的常数项为()330462C 160T x =-⋅⋅=-.故答案为:160-13. 设向量()(),11,2a m b == ,,且222a b a b +=+ ,则m=_________.【答案】-2【解析】【详解】试题分析:由题意得222(1)+315 2.m m m +=++⇒=-考点:向量的模14. 对于函数()ln21xf x x =-和()ln ln(21)g x x x =--,给出下列三个结论:①设()f x 的定义域为M ,()g x 的定义域为N ,则N 是M 的真子集.②函数()g x 的图像在1x =处的切线斜率为0.③函数()f x 的图像关于点1,ln 24⎛⎫-⎪⎝⎭对称.其中所有正确结论的序号是______.【答案】①③【解析】【分析】对于①,根据对数函数的定义域,建立不等式组,结合真子集,可得答案;对于②,利用导数的几何意义,由函数解析式求导,建立方程,可得答案;对于③,利用中点坐标公式,结合函数解析式,可得答案.【详解】对于①,由题意得,函数()f x 的定义域M =x |x 2x−1>0=(−∞,0)∪+∞,函数()g x 的定义域12N x x ⎧⎫=⎨⎬⎩⎭.所以N 是M 的真子集,则①正确.对于②,12()21g x x x '=--,则在1x =处的切线斜率12(1)1121k g '==-=--,则②错误.对于③只需验证:当1212x x +=时,121212121212((lnln ln 2ln 22121)42()1)x x x x f x f x x x x x x x +=+==----++,则③正确.故答案为:①③.15. 中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹, 用于装点生活或配合其他民俗活动的民间艺术, 剪纸具有广泛的群众基础, 交融于各族人民的社会生活, 是各种民俗活动的重要组成部分, 其传承赓 (gêng) 续的视觉形象和造型格式, 蕴涵了丰富的文化历史信息, 是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下: 取一张半径为 1 的圆形纸片,记为O ,在O 内作内接正方形,接着在该正方形内作内切圆,记为1O ,并裁剪去该正方形与内切圆之间的部分 (如图所示阴影部分),记为一次裁剪操作,L ,重复上述裁剪操作n 次,最终得到该剪纸,则第2024次操作后,所有被裁剪部分的面积之和为______________.【答案】()202414π12⎛⎫-- ⎪⎝⎭【解析】【分析】设n O 的半径为n R,分析正方形边长与半径的关系可得1n n R R +=,进而可得n O 的面积为π2n S =,再分析第n 次裁剪操作的正方形边长,进而可得每次操作减去的面积,再求和即可.【详解】设n O 的半径为n R,则1R =,1n O +n R,即1n n R R +=,故12112nn nn R R -⎛⎫=== ⎪⎝⎭,n O 的面积为1ππ22nnS ⎛⎫== ⎪⎝⎭,又第n 次裁剪操作的正方形边长为12122nn R ⎛⎫= ⎪⎝⎭,故第n 次裁剪操作裁剪掉的面积为1222221111ππ2222n n n n⎛⎫-⨯⨯- ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫-⨯=-⨯ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21π4π222n n n --=-=,所以第n 次裁剪操作后,裁剪掉的面积之和为()()211114π...4π12222nn ⎛⎫⎛⎫-+++=--⎪ ⎪⎝⎭⎝⎭,所以第2024次操作后,所有被裁剪部分的面积之和为()202414π12⎛⎫--⎪⎝⎭.故答案为:()202414π12⎛⎫--⎪⎝⎭.【点睛】方法点睛:数列求和的常用方法:(1)对于等差等比数列,利用公式法可直接求解;(2)对于{}n n a b 结构,其中{}n a 是等差数列,{b n }是等比数列,用错位相减法求和;(3)对于{}n n a b +结构,利用分组求和法;(4)对于11n n a a +⎧⎫⎨⎬⎩⎭结构,其中{}n a 是等差数列,公差为()0d d ≠,则111111n n nn a a d a a ++⎛⎫=- ⎪⎝⎭,利用裂项相消法求和.三、解答题共5小题,共85分.解答应写出文字说明,演算步骤或证明过程.16. 已知函数()πsin sin 3f x x x ⎛⎫=++⎪⎝⎭.(1)求()f x 的最小正周期和单调增区间;(2)若π6x =是函数()(0)y f x ϕϕ=+>的一个零点,求ϕ的最小值.【答案】(1)2π,2ππ2π,2π33k k ⎡⎤-++⎢⎥⎣⎦,k ∈Z(2)2π3【解析】【分析】(1)利用三角函数恒等变换的公式,化简函数()f x ,进而求得函数的最小正周期和单调增区间;(2)由条件可得πsin 03ϕ⎛⎫+= ⎪⎝⎭,结合0ϕ>,求得答案.【小问1详解】由函数π13π()sin sin sin sin sin 3226f x x x x x x x x x ⎛⎫⎛⎫=++=++==+ ⎪ ⎪⎝⎭⎝⎭,所以函数()f x 的最小正周期为2πT =.由πππ2π2π262k x k -+≤+≤+,Z k ∈,得2ππ2π2π33k x k -+≤≤+,Z k ∈,所以函数()f x 的单调增区间为2ππ2π,2π33k k ⎡⎤-++⎢⎥⎣⎦,Z k ∈.【小问2详解】因为π6x =是函数()(0)y f x ϕϕ=+>的一个零点,ππ066ϕ⎛⎫++= ⎪⎝⎭,即πsin 03ϕ⎛⎫+= ⎪⎝⎭,所以ππ3k ϕ+=,Z k ∈,即ππ3k ϕ=-+,Z k ∈,又因为0ϕ>,所以ϕ的最小值为2π3.17. 在△ABC 中,6a =,1cos 3=-C ,三角形面积为,求:(1)b 和c 的值;(2)sin()A B -的值.【答案】(1)2b =,c =(2【解析】【分析】(1)由1cos 3=-C 求得sin C =即可求出b ,利用余弦定理即可求出c ;(2)利用正弦定理可求得sin A =sin B =,结合同角三角函数的基本关系可得cos A =,cos B =,再利用两角差的正弦公式展开,代入求解即可.【小问1详解】在ABC 中,因为1cos 03C =-<,所以π,π2C ⎛⎫∈ ⎪⎝⎭,sin C ==。
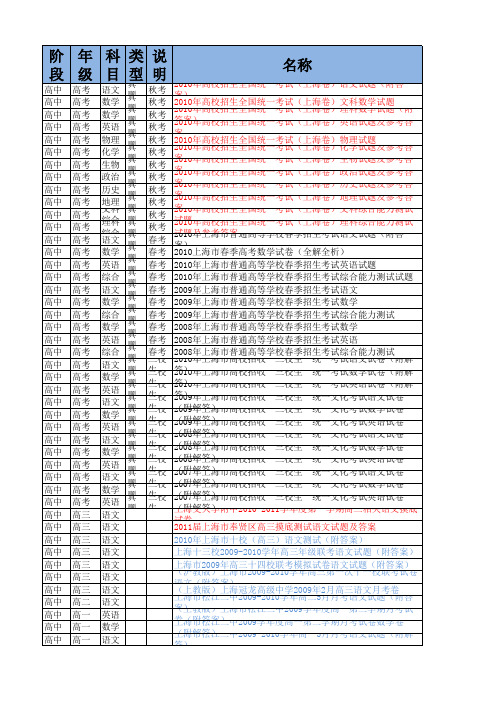
上海市高中初中试卷下载地址列表一
2.答答题要求,所有答题必须涂(选择题)或写(非选择题)在答题纸上,做在试卷上一律不得分。
3.答2.答题前,务必在答题纸上填写准考证号和姓名,并将核对后的条形码贴在指定位置上。
4.考试时间150分3.答题纸与试卷在试题编号上是一一对应的,答题时应特别注意,不能错位。
笔 墨 的 超 越
阅读下文,完成第1—6题。
(16分)
一 阅读80分
间150分钟。
试卷满分150分。
①毛笔、墨是中国书法和绘画的主要工具,原本并无奇特之处,不过分别是由兽毛与熏烧的越
熏烧的烟灰制作而成的。
但是,在中国的书画艺术史上,它们始终扮演着不可或缺的角色。
上海市东华大学附属奉贤致远中学2023-2024学年高一上学期期中考试数学含答案(可编辑)

东华致远2023学年第一学期期中教学评估高一数学 试卷考试时间:120分钟 满分150分一、填空(1~6题每题4分,7~12题每题5分)1. 已知集合A ={a 2−2a,1},若3∈A ,则实数a 的值是 ___________.2. 分式不等式1x >1的解集为 __________.3. 已知x,y ∈R ,则“x >1且y >1”是“x +y >2”的 ___________ 条件.4. 将√a √a3>0)化为有理数指数幂的形式为 ___________.5. 设x >0,y >0,且x +y =18,则xy 的最大值为 ____________.6. 已知对数函数y =log a x(a >0且a ≠1)的图像经过点(3,2), 若点P(b,4)为此函数图像上的点,则实数b = ____________.7. 若log 53=a ,5b =2,用含有a ,b 的代数式表示log 26为 ___________. 8. 关于x 的方程|x −a |+|x −a −1|=1的解为 ____________.9. 用反证法证明时,命题“实数a,b,c 中至少有1个数是偶数”的否定是 ______________. 10. 若函数y =(a 2−3a +3)a x 是指数函数,则 a = ____________.11. 若不等式(a 2−1)x 2−(a −1)x −1<0的解集为R ,则实数a 的取值范围是 ____________. 12. 对于数集X ={﹣1,x 1,x 2,x 3,⋯,x n },其中0<x 1<x 2<x 3<⋯<x n ,n ≥2,定义点集 Y ={(s ,t) | s ∈X ,t ∈X},若对于任意(s 1,t 1)∈Y ,存在(s 2,t 2)∈Y ,使得s 1s 2+t 1t 2=0,则称集合X 具有性质P 。
2024-2025学年上海市宝山区高三上学期教学质量监测数学试卷(含答案)

2024-2025学年上海市宝山区高三上学期教学质量监测数学试卷考生注意:1.本试卷共21题,满分150分,考试时间120分钟;2.本试卷包括试题卷和答题纸两部分,答题纸另页,正反面;3.在本试题卷上答题无效,必须在答题纸上的规定位置按照要求答题;4.可使用符合规定的计算器答题.一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得分,否则一律得零分).1. 集合,则 .Z =-=B A ),1,1(=B A 2. 函数的最小正周期为.12+=x y cos 3. 设为虚数单位,若为纯虚数,则实数 .i (2)(21)i a a -+-a =4. 在的展开式中的系数为.5)2(+x 3x 5. 已知为实数,且函数是偶函数,则 .b a 、]4,[,12b x ax x y ∈++==-b a 6.某运动员在某次男子米气手枪射击比赛中的得分数据(单位:环)为:10,,,,,,,,,,,,则这组数据的第6.99.92.94.99.91.102.107.96.93.90.104.10百分位数为25.7. 已知关于正整数的方程,则该方程的解为.x 5512112--=x x C C 8. 若,且,则 .m b a ==49211=+ba =m 9. 过双曲线的左焦点作圆的切线,切点为. 延长切线交双曲线的116922=-y x F 922=+y x M 右支于点,为坐标原点,点为线段的中点,则 .P O T FP =||OT 10. 将棱长为的正四面体绕着它的某一条棱旋转一周所得的几何体的体积为.211. 某物流公司为了扩大业务量,计划改造一间高为米,底面积为平方米,且背面靠墙624的长方体形状的仓库. 因仓库的背面靠墙,无须建造费用,设仓库前面墙体的长为米(x ). 现有甲、乙两支工程队参加竞标,甲队的报价方案为:仓库前面新建墙体每平46x ≤≤方米元,左右两面新建墙体每平方米元,屋顶和地面以及其他共计元;乙队40030028800给出的整体报价为元(). 不考虑其他因素,若乙队要确保竞标成功,42610k x ⨯⨯(1+0k >则实数的取值范围是.k 12. 已知平面向量满足:,,且对任意的单位向量满足b a 、1||=a )2,1(||∈=m bc ,则的最大值为 .(用含的式子表示)6||||≤⋅+⋅c b c a b a ⋅m 二、选择题(本大题共有4题,满分18分,第13~14题每题4分,第15~16题每题5分,每题都给出四个结论,其中有且仅有一个结论是正确的,必须把答题纸上相应题序内的正确结论代号涂黑,选对得相应满分,否则一律得零分).13.设,则“”是“”的( )0>ab b a >ba 11<A .充分非必要条件 B .必要非充分条件C .充要条件D .既非充分也非必要条件14. 下列函数中,在区间上是严格增函数且存在零点的是( )()∞+,0A .B .C .D .xe y =2+=x y xy 21log -=()22-=x y15. 如图,正四棱柱的底面边长为,1111D C B A ABCD -ABCD 1为上任意一点,为中点,若棱上至少存在E ADF 1CC 11D C 一点使得,则棱长的最大值为( )P PF PE ⊥1AA A.B .C .D .2212216.设的三边长分别为,面积为.若,n n n A B C △n n n a b c 、、n S n (为正整数)11112b c a -=其中,,,,则( )1114c a >1n n a a +=114n n n b c a +=+114n n n c b a +=+A. 为严格减数列 {}n S B. 为严格增数列{}n S C. 为严格增数列,为严格减数列21{}-n S 2{}n S D. 为严格减数列,为严格增数列21{}-n S 2{}n S 3、解答题(本大题共有5题,满分78分,解答下列各题必须在答题纸的规定区域(对应的题号)内写出必要的步骤).17.(本题满分14分,第1小题满分7分,第2小题满分7分)如图,四棱锥中,底面为矩形,,且该四ABCD P -ABCD 43====AB AD PB PA ,棱锥的体积为.54(1) 证明:平面;ABCD PAB 底面⊥(2) 求异面直线和所成角的余弦值.PC AB 18.(本题满分14分,第1小题满分8分,第2小题满分6分)在中,已知.ABC ∆bc a c b +=+222(1) 若且,求的面积;sin 2sin C B =,2=b ABC ∆(2) 若求的取值范围.,1=+c b a 19.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)甲乙两人轮流掷质地均匀的骰子,每人每次掷两颗.(1) 甲掷一次,求两颗骰子点数不同的概率;(2) 甲乙各掷一次,求甲的点数和恰好比乙的点数和大的概率;7(3) 若第一次掷出点数之和大于的人为胜者,同时比赛结束;否则,由另一人继续投掷,6直到比赛结束. 例如,甲乙先后轮流掷出的点数之和为:、、、,此时乙为胜者. 设5437甲先投掷,求甲最终获胜的概率.20.(本题满分16分,第1小题满分4分,第2小题满分4分,第3小题满分8分)已知椭圆:,直线经过椭圆的右顶点且与椭圆交于另一点,设线段Γ13922=+y x l ΓP A 的中点为.AP M (1) 求椭圆的焦距和离心率;Γ(2) 若,求直线的方程;31-=OM k AP (3) 过点再作一条直线与椭圆交于点,线段的中点为. 若,则直线P ΓB BP N ON OM ⊥是否经过定点?若经过定点,求出定点坐标;若不经过定点,请说明理由.AB 21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分).已知都是定义在实数集上的可导函数.对于正整数,当分别(),()y f x y g x ==k m n 、是和的驻点时,记,若,则称和满足性()y f x =()y g x =||x m n ∆=-x k ∆≤()f x ()g x ()P k 质;当,且时,记,若,则称和12x x R ∈、12()()g x g x ≠1212()()()()f x f x yg x g x -∆=-y k ∆≥()f x 满足性质.()g x ()Q k (1) 若,,判断和是否满足性质,并说明理由;()21f x x =+()g x x =()f x ()g x (2)Q (2) 若,,且和满足性质,求实数的取值范围;2()(1)f x x =-1()x ax g x e+=()f x ()g x (1)P a (3) 若的最小正周期为4,且,.当时,()y f x =(1)(1)g f -=-(1)(1)g f =[1,3]x ∈-的驻点与其两侧区间的部分数据如下表所示:()y f x =x1-(1,1)-1(1,3)3'()f x 0+-0()f x 极小值1-极大值1极小值1-已知和满足性质,请写出的充要条件,并说明理由.()f x ()g x ()Q k ()()f x g x =答案一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.2.3.4.5.6.{}0π24045.97.或 8.9. 10. 11.12.1365π2⎪⎭⎫⎝⎛320,())2151,22m m m m ⎧∈-⎪⎨-⎪∈⎩,,二、选择题(本大题共有4题,满分18分,第13~14题每题4分,第15~16题每题5分)13.14.15.16.C C A B三、解答题(本大题共有5题,满分78分)17.(本题满分14分,第1小题满分7分,第2小题满分7分)(1)证明:设该四棱锥的高为,则体积......1分 h 54433131=⨯⨯=⨯=h h S V 底从而...............................................................2分5=h 等腰中,设边的中点为,易知PAB ∆AB E AB PE ⊥在中,,所以...................................................... 4分PAE R ∆t 2,3==AE PA 5=PE 所以该四棱锥的高为即为.........................................5分h 5=PE 即,又ABCD PE 底面⊥PABPE 面⊆所以面..................................................7分ABCD PAB 底面⊥(2)因为,CD AB //所以即为异面直线和所成的角或其补角;.......................9分PCD ∠PC AB 由(1)知平面,且ABCD PAB 底面⊥ABABCD PAB =底面平面矩形中,,所以,从而..............10分ABCD AB CB ⊥PAB CB 面⊥PB CB ⊥中,,所以...............................11分PBC R ∆t 3==BC PB 23=PC 同理可得.......................................................12分23=PD 中,PCD ∆4,23===CD PD PC 由余弦定理可得..............13分3242321816182222=⨯⨯-+=⋅-+=∠CD PC PD CD PC PCD cos 所以异面直线和所成角的余弦值为...........................14分PC AB 32另解:(空间向量法)以的中点为为原点,、为轴建立空间坐标系,AB E EB EP z x 、则()()()()0,3,20,020,0,250,0C A B P ,,,,,-所以........................................9分()()5,3,2,0,0,4-==PC AB......13分(公式2分,数值2分)3245948AB PC,cos =⋅++所以异面直线和所成角d 余弦值为.............................14分PC AB 3218.(本题满分14分,第1小题满分8分,第2小题满分6分)解:(1)由正弦定理得,又,从而.......................2分2sin sin ==BC b c 2=b 4=c 由得,........................4分bc a c b +=+2222122cos 222==-+=bc bc bc a c b A 从而.................................................................5分3π=A 所以的面积......................8分ABC ∆323sin 4221sin 21=⨯⨯⨯==πA bc S (公式2分,结果1分)(2)................................9分()bc bc c b bc c b a 3132222-=-+=-+=由平均值不等式,当且仅当时取等号.................11分4122=⎪⎭⎫⎝⎛+≤c b bc 21==c b 从而,所以..............................................12分414312=-≥a 21≥a 又因为中,,从而.......................................13分ABC ∆a c b >+1<a 所以的范围是........................................................14分a ⎪⎭⎫⎢⎣⎡121,19.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)解:(1)甲掷一次,两颗骰子点数相等的概率为.....................2分61666=⨯所以两颗骰子点数不同的概率为;..................................4分15166-=(2)解:甲的点数和恰好比乙的点数和大点的情形如下表:7甲的点数乙的点数甲的点数和乙的点数和、、、(3,6)(4,5)(5,4)(6,3)(1,1)92、、(4,6)(5,5)(6,4)、(1,2)(2,1)103、(5,6)(6,5)、、(1,3)(2,2)(3,1)114(6,6)、、、(1,4)(2,3)(3,2)(4,1)125.......8分所以;..................................10分44132231456324⨯+⨯+⨯+⨯==P 另解:设掷一次两颗骰子的点数和为,则X 12...,4,3,2,=X 则()();3616611122=⨯⨯====X P X P ()();181662113=⨯====X P X P ()();121663104=⨯====X P X P()();9166495=⨯====X P X P ()();36566586=⨯====X P X P .................................................8分();616667=⨯==X P 所以甲的点数和恰好比乙的点数和大7点的概率为...............................10分32453619118112112118191361=⨯+⨯+⨯+⨯(3)由(2)可知掷两颗骰子点数和大于的概率为6 (12)()1273611811219136561127=+++++==∑=i X P i 分若甲第一轮获胜,概率为1271=P 若甲第二轮获胜,即第一轮投掷后两人的点数和都不大于,概率为;612712522⨯⎪⎭⎫ ⎝⎛=P 若甲第三轮获胜,即前两轮投掷后两人的点数和都不大于,概率为 (612)712543⨯⎪⎭⎫ ⎝⎛=P 由以上可得,若甲第轮获胜,即前轮投掷后两人的点数和都不大于,概率为()1≥n n 1-n 6..................................14分1271251271252212⨯⎪⎭⎫⎝⎛=⨯⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛=--n n n P 于是,组成一个以为首项,为公比的无穷等比数列.nP P P P ,...,,321,1272125⎪⎭⎫⎝⎛所以甲最终获胜的总概率为...........16分17121251127 (2)321=⎪⎭⎫⎝⎛-=+++++n P P P P 20.(本题满分16分,第1小题满分4分,第2小题满分4分,第3小题满分8分)解:(1)由得........................2分3,3==b a 622=-=b a c 所以焦距,.............................................3分622=c离心率...............................................4分36==a c e (2),设直线的方程()0,3P AP 3+=ty x 与椭圆:联立得...........................5分Γ13922=+y x ()06322=++ty y t 因为点与点不重合,所以可得点......................6分M P ⎪⎭⎫⎝⎛+-+33,3922t t t M 于是由得...........................................7分3193-=-=t k OM 1=t 直线的方程............................................8分AP 03=--y x (3)①当直线斜率存在时,设方程为:,与椭圆:联立得:AB m kx y +=Γ13922=+y x ...........................................9分()093613222=-+++m kmx x k设()()2211,,,y x B y x A 由韦达定理得............................................10分⎪⎪⎩⎪⎪⎨⎧+-=+-=+13931362221221k m x x k km x x 且,化简得()()093134362222>-+-=∆m k m k 03922<--k m 又,从而()0,3P ⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛+2,23,2,232211y x N y x M 由可得,从而ON OM ⊥0=⋅ON OM ()()0332121=+++y y x x 将代换,m kx y +=()()()()0332121=+++++m kx m kx x x 整理得:()()()0931221212=++++++m x x km x x k韦达定理代入化简得.029922=+-m km k ,所以.............................12分()()0323=--m k m k k m k m 233==或当时,直线经过点,舍;................................13分k m 3=AB ()0,3-当时,此时成立,直线经过定点......14分k m 23=0394922<--k k AB ⎪⎭⎫⎝⎛-0,23②当直线斜率不存在时,设,则AB ()()n m B n m A -,,,⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛+2,23,2,23n m N n m M 代入得0=⋅ON OM ()223+=m n 与联立得解得13922=+n m 09922=++m m 23-=m 此时直线也经过点............................... ..........16分AB ⎪⎭⎫⎝⎛-0,23综上,直线经过定点.AB ⎪⎭⎫⎝⎛-0,2321.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分).解:(1).......................2分12122121(21)(21)2()22x x x x y x x x x +-+-∆===≥--所以和是满足性质. .......................................4分()f x ()g x (2)Q (2)由可知,驻点...................................5分'()2(1)f x x =-1m =又1'()xa axg x e --=当时,不存在驻点;0a =()g x 当时,的驻点..................................... .....7分0a ≠()g x 1a n a-=由题意可知,.......................................... ......8分111a a--≤解得.................................................10分(,1][1,)a ∈-∞-+∞(3)的充要条件是......................................11分()()f x g x =1k =首先证明必要性:当时,由题意可知不是常函数,所以()()f x g x =()f x 1212()()1()()f x f x y g x g x -∆==-因为和满足性质,所以,所以,()f x ()g x ()Q k y k ∆≥1k ≤又是正整数,故..................................... ......12分k 1k =其次证明充分性:由题意可知,,,且1()1f x -≤≤(1)(1)1g f -=-=-(1)(1)1g f ==1212()()1()()f x f x g x g x -≥-①当()时,41x k ≠±k Z ∈可知.()(1)g x g ≠-否则,若存在,有041()x k k Z ≠±∈0()(1)1g x g =-=-因为,所以与已知矛盾.01()1f x -<<000()(1)|()1|1()(1)2f x f f xg x g --=<-同理,.............................................. ......14分()(1)g x g ≠故()(1)()1()11()(1)()1|()1|f x f f x f x g x g g x g x --++==≥--++所以,即|()1|()1g x f x +≤+()2()()f xg x f x --≤≤同理,,得()(1)()11()1()(1)()1|()1|f x f f x f xg x g g x g x ---==≥---()()2()f x g x f x ≤≤-所以.......................................................16分()()f x g x =②当()时,41x k =-k Z ∈(41)1f k -=-任意,有,又由①可知,(1,1)t ∈-1()1f t -<<()()f tg t =若存在有,则,)1,1(,0-∈∈t Z k )()14(0t g k g =-)(1,1)14(-∈-k g 所以)1()14(-≠-g k g 由已知,其中(41)(1)1(41)(1)f k fg k g ---≥---1)1()14(-=-=-f k f 于是有,矛盾,所以10≥)()14(t g k g ≠-所以,(41)()1()1()1(41)()(41)()|(41)()|f k f t f t f tg k g t g k g t g k f t ----+==≥------得1(41)12()g k f t -≤-≤+因为,所以,从而,即.1()1f t -<<112()3f t -<+<(41)1g k -=-(41)(41)g k f k -=-③当()时,41x k =+k Z ∈(41)1f k +=任意,有,同理可得(1,1)t ∈-1()1f t -<<)()14(t g k g ≠+所以,(41)()1()1()1(41)()(41)()|(41)()|f k f t f t f tg k g t g k g t g k f t +---==≥+-+-+-得12()(41)1f tg k -+≤+≤因为,所以,从而,即.1()1f t -<<312()1f t -<+<(41)1g k +=-(41)(41)g k f k +=+综上,.....................................................18分()()f x g x =(3)另解:(反证法)由题意可知,,,且.1()1f x -≤≤(1)(1)1g f -=-=-(1)(1)1g f ==1212()()1()()f x f x g x g x -≥-②任意时,可知.(1,1)x ∈-()(1)g x g ≠-否则,若存在,使0(1,1)x ∈-0()(1)1g x g =-=-因为,所以与已知矛盾.01()1f x -<<000()(1)|()1|1()(1)2f x f f xg x g --=<-同理,.............................................. ......14分()(1)g x g ≠②先证任意时,有.(1,1)x ∈-()()f x g x =反证,若存在,使.0(1,1)x ∈-00()()f x g x ≠若时,001()()f x g x >>则与已知矛盾.0000()(1)()11()(1)()1f x f f xg x g g x --=<--若时,001()()f x g x -<<则与已知矛盾.0000()(1)()11()(1)()1f x f f xg x g g x --+=<--+由于,,(1)(1)1g f -=-=-(1)(1)1g f ==可得,任意时,有................................16分[]1,1x ∈-()()f x g x =③下证任意时,有.()(,1)1,x ∈-∞-⋃+∞()()f x g x =反证,若存在,使.()0(,1)1,x ∈-∞-⋃+∞00()()f x g x ≠由于,可得存在满足.1()1f x -≤≤[]1,1m ∈-0()()()f x f m g m ==则与已知矛盾.0000()()01()()()()f x f mg x g m g x f x -=<--综上,.....................................................18分()()f x g x =。
人教A版数学高二弧度制精选试卷练习(含答案)2

人教A 版数学高二弧度制精选试卷练习(含答案)学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知扇形的周长是5cm ,面积是322cm ,则扇形的中心角的弧度数是( ) A .3B .43C .433或 D .2【来源】江西省九江第一中学2016-2017学年高一下学期期中考试数学(文)试题 【答案】C2.已知扇形的周长为8cm ,圆心角为2,则扇形的面积为( ) A .1B .2C .4D .5【来源】四川省双流中学2017-2018学年高一1月月考数学试题 【答案】C3.《掷铁饼者》 取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为4π米,肩宽约为8π米,“弓”所在圆的半径约为1.25米,你估测一下掷铁饼者双手之间的距离约为( )1.732≈≈)A .1.012米B .1.768米C .2.043米D .2.945米【来源】安徽省五校(怀远一中、蒙城一中、淮南一中、颍上一中、淮南一中、涡阳一中)2019-2020学年高三联考数学(理)试题 【答案】B4.已知扇形的周长为4,圆心角所对的弧长为2,则这个扇形的面积是( ) A .2B .1C .sin 2D .sin1【来源】福建省泉州市南安侨光中学2019-2020学年高一上学期第二次阶段考试数学试题 【答案】B5.已知α是第三象限角,且cos cos22αα=-,则2α是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角【来源】2012人教A 版高中数学必修四1.2任意角的三角函数练习题 【答案】B6.如图,2弧度的圆心角所对的弦长为2,这个圆心角所对应的扇形面积是( )A .1sin1B .21sin 1C .21cos 1D .tan1【来源】广西河池市高级中学2017-2018学年高一下学期第二次月考数学试题 【答案】B7.半径为10cm ,面积为2100cm 的扇形中,弧所对的圆心角为( ) A .2 radB .2︒C .2π radD .10 rad【来源】第一章滚动习题(一) 【答案】A8.若一扇形的圆心角为72︒,半径为20cm ,则扇形的面积为( ). A .240πcmB .280πcmC .240cmD .280cm【来源】陕西省西安市长安区第一中学2016-2017学年高一下学期第一次月考数学试题 【答案】D9.如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为1S ,正八边形外侧八个扇形(阴影部分)面积之和为2S ,则12S S =( )A .34B .35C .23D .1【来源】广西省南宁市马山县金伦中学、武鸣县华侨中学等四校2017-2018学年高一10月月考数学试题. 【答案】B10.在-360°到0°内与角1250°终边相同的角是( ) . A .170° B .190° C .-190°D .-170°【来源】2012人教A 版高中数学必修四1.1任意角和弧度制练习题(一)(带解析) 【答案】C11.下列各角中,终边相同的角是 ( ) A .23π和240o B .5π-和314oC .79π-和299π D .3和3o【来源】新疆伊西哈拉镇中学2018-2019学年高一上学期第二次月考数学试题 【答案】C12.已知2弧度的圆心角所对的弧长为2,则这个圆心角所对的弦长是( ) A .sin 2B .2sin 2C .sin1D .2sin1【来源】广东省东莞市2018-2019学年高一第二学期期末教学质量检查数学试题 【答案】D13,弧长是半径的3π倍,则扇形的面积等于( ) A .223cm πB .26cm πC .243cm πD .23cm π【来源】河北省隆华存瑞中学(存瑞部)2018-2019学年高一上学期第二次数学试题 【答案】D14.如图所示,用两种方案将一块顶角为120︒,腰长为2的等腰三角形钢板OAB 裁剪成扇形,设方案一、二扇形的面积分别为12S , S ,周长分别为12,l l ,则( )A .12S S =,12l l >B .12S S =,12l l <C .12S S >,12l l =D .12S S <,12l l =【来源】浙江省省丽水市2018-2019学年高一下学期期末数学试题 【答案】A15.已知sin sin αβ>,那么下列命题成立的是( ) A .若,αβ是第一象限角,则cos cos αβ> B .若,αβ是第二象限角,则tan tan αβ> C .若,αβ是第三象限角,则cos cos αβ> D .若,αβ是第四象限角,则tan tan αβ>【来源】正定中学2010高三下学期第一次考试(数学文) 【答案】D16.半径为1cm ,中心角为150°的角所对的弧长为( )cm . A .23B .23π C .56D .56π 【来源】宁夏石嘴山市第三中学2018-2019学年高一5月月考数学试题 【答案】D 17.设5sin 7a π=,2cos 7b π=,2tan 7c π=,则( ) A .a b c <<B .a c b <<C .b c a <<D .b a c <<【来源】2008年高考天津卷文科数学试题 【答案】D18.扇形的中心角为120o )A .πB .45πC D 2【来源】辽宁省大连市第八中学2016-2017学年高一下学期期中考试数学试题【答案】A19.若扇形的周长为8,圆心角为2rad ,则该扇形的面积为( ) A .2B .4C .8D .16【来源】河南省洛阳市2018-2019学年高一下学期期中考试数学试卷 【答案】B20.-300° 化为弧度是( ) A .-43πB .-53πC .-54πD .-76π【来源】2014-2015学年山东省宁阳四中高一下学期期中学分认定考试数学试卷(带解析) 【答案】B21.一个扇形的面积为3π,弧长为2π,则这个扇形的圆心角为( ) A .3π B .4π C .6π D .23π 【来源】湖北省荆门市2017-2018学年高一(上)期末数学试题 【答案】D22.《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=12(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为23π,弦长为的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中3π≈,1.73≈)A .15B .16C .17D .18【来源】湖北省2018届高三5月冲刺数学(理)试题 【答案】B23.下列各式不正确的是( ) A .-210°=76π-B .405°=49πC .335°=2312πD .705°=4712π【来源】河南信阳市息县第一高级中学、第二高级中学、息县高中2018-2019学年高一下学期期中联考数学(文)试题 【答案】C24.下列函数中,最小正周期为π2的是( )A .y =sin (2x −π3)B .y =tan (2x −π3)C .y =cos (2x +π6) D .y =tan (4x +π6)【来源】20102011年山西省汾阳中学高一3月月考数学试卷 【答案】B25.已知扇形的周长为12cm ,圆心角为4rad ,则此扇形的弧长为 ( ) A .4cmB .6cmC .8cmD .10cm【来源】江西省玉山县一中2018-2019学年高一(重点班)下学期第一次月考数学(理)试卷 【答案】C二、填空题26.已知扇形的圆心角18πα=,扇形的面积为π,则该扇形的弧长的值是______.【来源】上海市黄浦区2018-2019学年高一下学期期末数学试题 【答案】3π 27.若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的底面半径为_______ . 【来源】上海市浦东新区川沙中学2018-2019学年高二下学期期末数学试题 【答案】128.一个扇形的弧长与面积的数值都是5,则这个扇形中心角的弧度数为__________. 【来源】河南省灵宝市实验高中2017-2018学年高一下学期第一次月考考数学试题 【答案】5229.已知圆锥的侧面展开图是一个扇形,若此扇形的圆心角为65π、面积为15π,则该圆锥的体积为________.【来源】上海市杨浦区2019-2020学年高三上学期期中质量调研数学试题 【答案】12π30.圆O 的半径为1,P 为圆周上一点,现将如图放置的边长为1的正方形(实线所示 ,正方形的顶点A 和点P 重合)沿着圆周顺时针滚动,经过若干次滚动,点A 第一次回到点P 的位置,则点A 走过的路径的长度为 .【来源】2015届山东省日照市高三3月模拟考试理科数学试卷(带解析)31.已知扇形的圆心角为1弧度,扇形半径为2,则此扇形的面积为______. 【来源】上海市复兴高级中学2018-2019学年高一下学期3月份质量检测数学试题 【答案】232.一个球夹在120°的二面角内,且与二面角的两个面都相切,两切点在球面上的最短距离为π,则这个球的半径为_______ .【来源】上海市七宝中学2017-2018学年高二下学期期中数学试题 【答案】333.用半径为,面积为cm 2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 则该容器盛满水时的体积是 .【来源】2012届江苏省泗阳中学高三上学期第一次调研考试数学试卷(实验班) 【答案】31000cm 3π34.《九章算术》是体现我国古代数学成就的杰出著作,其中(方田)章给出的计算弧田面积的经验公式为:弧田面积12=(弦⨯矢+矢2),弧田(如图阴影部分)由圆弧及其所对的弦围成,公式中“弦”指圆弧所对弦的长,“矢”等于半径长与圆心到弦的距离之差,现有弧长为43π米,半径等于2米的弧田,则弧所对的弦AB 的长是_____米,按照上述经验公式计算得到的弧田面积是___________平方米.【来源】山东省济南市2018-2019学年高一下学期期末学习质量评估数学试题【答案】1235.设扇形的半径长为2cm ,面积为24cm ,则扇形的圆心角的弧度数是 【来源】2013-2014学年山东济南商河弘德中学高一下学期第二次月考数学试卷(带解析) 【答案】236.已知一个圆锥的展开图如图所示,其中扇形的圆心角为120o ,弧长为2π,底面圆的半径为1,则该圆锥的体积为__________.【来源】2018年春高考数学(文)二轮专题复习训练:专题三 立体几何【答案】337.现用一半径为10cm ,面积为280cm π的扇形铁皮制作一个无盖的圆锥形容器(假定衔接部分及铁皮厚度忽略不计,且无损耗),则该容器的容积为__________3cm . 【来源】江苏省苏州市2018届高三调研测试(三)数学试题 【答案】128π38.已知扇形的周长为6,圆心角为1,则扇形的半径为___;扇形的面积为____. 【来源】浙江省宁波市镇海区镇海中学2018-2019学年高一上学期期中数学试题 【答案】2 2 39.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论用角度制还是用弧度制度量一个角,它们与扇形所在半径的大小无关; ④若sin sin αβ=,则α与β的终边相同;⑤若cos 0θ<,则θ是第二或第三象限的角. 其中正确的命题是______.(填序号)【来源】江苏省南通市启东中学2018-2019学年高二5月月考数学(文)试题 【答案】③40.设扇形的周长为4cm ,面积为21cm ,则扇形的圆心角的弧度数是________. 【来源】广东省中山市第一中学2016-2017学年高一下学期第一次段考(3月)数学(理)试题 【答案】2三、解答题41.已知扇形AOB 的周长为8.(1)若这个扇形的面积为3,求其圆心角的大小.(2)求该扇形的面积取得最大时,圆心角的大小和弦长AB .【来源】2015-2016学年四川省雅安市天全中学高一11月月考数学试卷(带解析) 【答案】(1)或;(2);.42.已知一扇形的中心角是120︒,所在圆的半径是10cm ,求: (1)扇形的弧长; (2)该弧所在的弓形的面积【来源】福建省福州市平潭县新世纪学校2019-2020学年高一上学期第二次月考数学试题【答案】(1)203π;(2)1003π-43.某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O 为圆心的两个同心圆弧和延长后通过点AD 的两条线段围成.设圆弧AB 、CD 所在圆的半径分别为()f x 、R 米,圆心角为θ(弧度).(1)若3πθ=,13r =,26=r ,求花坛的面积;(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD 的长度为多少时,花坛的面积最大?【来源】江苏省泰州市泰州中学2019~2020学年高一上学期期中数学试题 【答案】(1)292m π(2)当线段AD 的长为5米时,花坛的面积最大44.已知一个扇形的周长为30厘米,求扇形面积S 的最大值,并求此时扇形的半径和圆心角的弧度数.【来源】上海市华东师范大学第二附属中学2018-2019学年高一上学期期末数学试题 【答案】()2rad α= 152r =45.如图所示为圆柱形大型储油罐固定在U 型槽上的横截面图,已知图中ABCD 为等腰梯形(AB ∥DC ),支点A 与B 相距8m ,罐底最低点到地面CD 距离为1m ,设油罐横截面圆心为O ,半径为5m ,56D ∠=︒,求:U 型槽的横截面(阴影部分)的面积.(参考数据:sin530.8︒≈,tan56 1.5︒≈,3π≈,结果保留整数)【来源】上海市闵行区七宝中学2019-2020学年高一上学期9月月考数学试题 【答案】202m46.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”某教师根据这首词的思想设计如下图形,已知CE l ⊥,DF l ⊥,CB CD =,AD BC ⊥,5DF =,2BE =,AD =则在扇形BCD 中随机取一点求此点取自阴影部分的概率.【来源】山西省阳泉市2018-2019学年高一第一学期期末考试试题数学试题【答案】1)4(P A π=-47.某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由试卷第11页,总11页 扇形OAD 挖去扇形OBC 后构成的).已知10, (0<<10)OA=OB =x x ,线段BA 、CD与弧BC 、弧AD 的长度之和为30米,圆心角为θ弧度.(1)求θ关于x 的函数解析式;(2)记铭牌的截面面积为y ,试问x 取何值时,y 的值最大?并求出最大值.【来源】上海市黄浦区2018届高三4月模拟(二模)数学试题【答案】(1)210(010)10x x x θ+=<<+;(2)当52x =米时铭牌的面积最大,且最大面积为2254平方米. 48.已知一扇形的圆心角为()0αα>,所在圆的半径为R .(1)若90,10R cm α==o ,求扇形的弧长及该弧所在的弓形的面积;(2)若扇形的周长是一定值()0C C >,当α为多少弧度时,该扇形有最大面积?【来源】2019高考备考一轮复习精品资料 专题十五 任意角和弧度制及任意角的三角函数 教学案【答案】(1)2550π-;(2)见解析49.已知在半径为10的圆O 中,弦AB 的长为10.(1)求弦AB 所对的圆心角α(0<α<π)的大小;(2)求圆心角α所在的扇形弧长l 及弧所在的弓形的面积S .【来源】(人教A 版必修四)1.1.2弧度制(第一课时)同步练习02【答案】(1)π3(2)10π3;50(π3−√32) 50.已知在半径为6的圆O 中,弦AB 的长为6,(1)求弦AB 所对圆心角α的大小;(2)求α所在的扇形的弧长l 以及扇形的面积S.【来源】江西省玉山县一中2018-2019学年高一(重点班)下学期第一次月考数学(文)试卷【答案】(1)3π ;(2)2l π= ,6S π=。
上海市上海师范大学附属嘉定高级中学2024-2025学年高一上学期期中考试数学试卷(无答案)
上大嘉高2024学年第一学期期中考试高一年级数学学科试卷命题人:石云 审题人:姜楠 2024年11月(本试卷考试时间:120分钟,满分150分)一、填空题(本大题满分54分)本大题共有12题,只要求直接填写结果,前6题每题得4分,后6题每题得5分.1.方程组的解集是______.2.命题“若,则”是_____命题.(填“真”或“假”)3.陈述句“且”的否定形式为______.4.已知集合,,若,则______.5.关于的方程的解集为______.6.不等式的解集为______.7.已知,则函数的最大值为______.8.关于的不等式恒成立,则实数的取值范围是______.9.已知正实数,满足,则的最小值为______.10.若集合有且仅有两个不同的子集,则实数______.11.为实数,且不等式有解,则实数的取值范围是______.12.已知关于的不等式的解集为,求不等式的解集______.二、选择题(本大题满分18分)本大题共有4题,13、14每题4分,15、16每题5分.13.已知,,则等于( )A .B.C .D .14.已知,则“”是“”的( )条件A .充分不必要B .必要不充分C .充要D 既不充分也不必要15.已知集合,,则下列结论正确的是( )251x y x y +=⎧⎨-=⎩a b >11a b <1x >1y >{}1,2A ={},3B a ={}2A B = a =x 2log 532x =25123x x x +≥++x ∈R ()4y x x =-x 210ax ax ++>a a b 121a b+=2a b +(){}21320,A x a x x x =-+-=∈R a =x 53x x m -+-<m x 20ax bx c ++≥1,23⎡⎤-⎢⎥⎣⎦20cx bx a ++<23x =25y =222y x +9+452ab ∈R a b >33a b >(){},20A x y x ay a =++=(){},10B x y ax ay =+-=A .存在,使的B .当时,C .当时,D .对任意的,都有16.设,,,,,均为非零实数,方程和的解集分别为,则“”是“的( )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件三、解答题(本大题满分78分)本大题共有5题,解答下列各题必须写出必要的步骤.17.(本题满分14分)已知集合,.若,且,求实数及的值.18.(本题满分14分,第1小题满分7分,第2小题满分7分)已知集合,集合.(1)若,求、及:(2)若,求实数的取值范围.19.(本题满分14分,第1小题满分7分,第2小题满分7分)设集合.(1)求证:,,();(2)用反证法证明10不是集合的元素.20.(本题满分18分,第1小题满分8分,第2小题满分10分)设函数,其中,.(1)解关于的不等式:(2)当时,关于的不等式恒成立.求的取值范围.21.(本题满分18分,本题共有3个小题,第1小题4分,第2小题6分,第3小题8分.)若集合,满足,则称为集合的一种分拆,并规定:当且仅当时,与为集合的同一种分拆:(1)集合的不同分拆种数为多少?(2)集合的不同分拆种数为多少?a ∈R A =∅1a =-13,22A B ⎛⎫=- ⎪⎝⎭ A B =∅ 1a =a ∈R A B≠1a 1b 1c 2a 2b 2c 21110a x b x c ++=22220a x b x c ++=,M N 111222a b c a b c ==n M N ={}2230A x x x =-->{}20B x x px q =++≤A B =R [)2,1A B =-- p q 2112x A x x ⎧⎫-=<⎨⎬+⎩⎭{}2B x x a =-<2a =A B A B B A ⊆a {}22,,A x x m n m n ==-∈∈Z Z 11A ∈12A ∈21k A +∈k ∈Z A ()y f x =()()233f x x a x a =-++a ∈R x ()0f x <[)4,x ∈+∞x ()9f x ≥-a 1A 2A 12A A A = ()12,A A A 12A A =()12,A A ()21,A A A {},A a b ={},,A a b c =(3)由上述两题归纳一般的情形:集合的不同分拆种数为多少?(不必证明){}123,,,,n A a a a a =⋅⋅⋅。
山东省青岛第十九中学2024-2025学年高三上学期期中考试数学试题(含答案)
青岛十九中2024-2025学年度第一学期期中模块检测高三数学试题2024.11说明:1.本试卷分第I 卷和第II 卷.满分150分.答题时间120分钟.2.请将第I 卷题目的答案选出后用2B 铅笔涂在答题纸对应题目的代号上;第II 卷用黑色签字笔将正确答案写在答题纸对应的位置上,答在试卷上作废.第I 卷(选择题,共58分)一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,复数z 对应的点的坐标是,则z 的共轭复数( )A. B. C. D.2.若,,,则a ,b ,c 的大小关系为( )A. B. C. D.3.已知,则等于( )A. B. C. D.4.我国古代数学名著《九章算术》对立体几何问题有着深入的研究,其中谈到的“堑堵”是指底面为直角三角形且侧棱垂直于底面的三棱柱.现有堑堵如图所示,其中,若,平面将堑堵分成了两部分,这两部分体积比值为( )A. B. C. D.5.在中,,,,P 为所在平面内的动点,且.则的最大值为( )A.12B.C.6.已知函数,若对于任意实数k ,总存在实数,使得成立,则实数a 的取值范围是( )(-z =11-1-+1-log e a π=23b =131(ec -=a c b <<b a c<<c a b<<a b c<<1cos 2sin θθ-=tan θ4343-23-23AC BC ⊥14AA AC BC ===11A BC 1:11:21:31:4ABC △90A ∠=︒3AC =4AB =ABC △1PC =PA PB +721)+122()log (23)f x ax x =++0x 0()f x k =A. B. C. D.7.已知三棱锥的四个顶点都在球O 的球面上,,,O 的表面积为( )A.B.C.D.8.已知函数的部分图象如图所示,关于该函数有下列四个说法错误的是( )A.的图象关于点对称B.的图象关于直线对称C.的图象可由的图象向左平移个单位长度得到D.若方程在上有且只有两个极值点,则t 的最大值为二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列不等式恒成立的是( )A., B.,C., D.,10.已知向量,,则下列命题为真命题的是( )A.若,则B.若,则C.的最大值为6D.若,则11.如图,正方体棱长为2,P ,Q 分别是棱,棱BC 的中点,点M 是其侧面上的动点(含边界),下列结论正确的是( )11,3⎡⎫-⎪⎢⎣⎭(1,)-+∞1,3⎡⎫+∞⎪⎢⎣⎭10,3⎡⎤⎢⎥⎣⎦P ABC -4PA PB PC ===2AB BC ==AC =64π340π327π421π2()cos()f x A x ωϕ=+π(0,0,)2A ωϕ>><()f x 4π(,0)3()f x 5π12x =-()f x π2sin(2)6y x =-π2()()(0)g x f tx t =>5π(0,)61310222a b ab +≥(,)a b ∈R 2a b +≤(0,0)a b >>b m b a m a +<+(0,0)a b m >>>131x x +≥-(1)x >(cos ,sin )a θθ=(3,4)b =- //a b 4tan 3θ=-a b ⊥ 3sin 5θ=a b -()0a a b ⋅-=a b -= 1111ABCD A B C D -1CC 11ADD AA.沿正方体的表面从点A 到点PB.过点A ,P ,Q 的平面截该正方体所得的截面面积为C.当时,点M 的轨迹长度为D.保持PM 与垂直时,点M第II 卷(非选择题,共92分)三、填空题:本题共3小题,每小题5分,共15分.12.已知角的终边上一点,且,则________.13.如图,在平行四边形ABCD 中,E 为CD 的中点,P 为线段AE 上一点,且满足,则________.14.设函数和的定义域为D ,若存在非零实数,使得,则称函数和在D 上具有性质P .现有四组函数:①,;②,;③,;④,.其中具有性质P 的是________.(写出所有满足条件的函数的序号)四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)设函数(1)求函数的最小正周期,并解不等式;(2)先将图象上所有点的横坐标伸长为原来的2倍,纵坐标不变;再向左平移个单位;最后向下平移个单位得到函数的图象.若对,不等式恒成立,求实数m 的取值范98PM =2π31BD α(P x cos α=x =23BP mBA BC =+m =()f x ()g x c D ∈()()0f c g c +=()f x ()g x ()f x x =2()g x x =()2x f x -=()e x g x =-2()f x x =-()2x g x =()f x x =()sin g x x =π()sin()4f x x x =+()f x ()1f x ≥()f x π412()g x ππ,63x ⎡⎤∀∈⎢⎥⎣⎦()0m g x +<围.16.(15分)如图,在三棱锥中,为P 在平面ABC 内的射影点,已知,,,,.(1)请以、为基底表示,并证明.(2)求证平面PAC .17.(15分)在中,角A ,B ,C 的对边分别为a ,b ,c..(1)求角C 的大小;(2)若的面积,求c ;(3)若的平分线交AB 于D ,且,求的面积S 的最小值.18.(17分)如图,PD 垂直于梯形ABCD 所在平面,,F 为PA 的中点,,,四边形PDCE 为矩形.(1)求证:平面DEF ;(2)求平面ABCD 与平面BCP 的夹角的余弦值;(3)求点F 到平面BCP 的距离.19.(17分)凸函数是数学中一个值得研究的分支,它包括数学中大多数重要的函数,如,等.记为的导数.现有如下定理:在区间I 上为凸函数的充要条件为.(1)证明:函数为上的凸函数;(2)已知函数.①若为上的凸函数,求a 的最小值;P ABC -P 'AB =4BC =3AC =PA =230P A P B P C '''++=BA BC BP 'BP AC '⊥PB ⊥ABC △sin cos cos )B A B A -=sin C ABC △S =3r =ACB ∠2CD =ABC △90ADC BAD ∠=∠=︒PD =112AB AD CD ===//AC 2x e x ()f x ''()y f x '=()f x ()0()f x x I ''≥∈31()f x x x=-(1,)+∞2()2ln ln ()g x ax x x x a =--∈R ()g x [1,)+∞②在①的条件下,当a 取最小值时,证明:,在上恒成立.31()22(32)(31)x xx g x x -+≥+-+[1,)+∞青岛十九中2024-2025学年度第一学期期中模块检测高三数学试题答案一、单项选择题 1-5 DABBC 6-8 DAC 二、多项选择题 9. ABD 10. ACD 11. CD 三、填空题 12.13. 14.①③四、解答题15.(1)由可得令,故,,解得,.故不等式的解为;(2)将图象上所有点的横坐标伸长为原来的2倍,纵坐标不变;可得,再向左平移个单位,可得;最后向下平移个单位得到函数,当,由于在单调递增,故,所以,由于,故,即.16.(1)如图:中:延长到,使;23π()sin()4f x x x =+21cos 21π1())sin sin cos sin 2)2242xf x x x x x x x x x -==+=+=-+()1f x ≥π1π1sin(2)424x x -+≥⇒-≥ππ3π2π22π444k x k +≤-≤+k ∈Z ππππ42k x k +≤≤+k ∈Z ππππ,42xk x k k ⎭+≤≤+∈⎧⎫⎨⎬⎩Z ()f x π142y x =-+π412y x =+12()g x x =ππ,63x ⎡⎤∀∈⎢⎥⎣⎦()g x x =ππ,63x ⎡⎤∈⎢⎥⎣⎦()g x x =∈()g x ⎡-∈⎢⎣()0m g x +<min (())m g x <-m <ABC △P A 'A '2P A P A '''=延长到,使.因为,所以,所以点为的重心.所以所以.又因为即.因为.所以.(2)如图:因为平面ABC ,平面ABC ,所以;又,,平面,,所以平面,又平面,所以.又因为,所以,所以;在中,,,所以.又,所以,所以P B 'B '3P B P B '''=230P A P B P C '''++= 0P A P B P C '''''++= P 'A B C ''△11()3()923333B P B A B C BP P A P B P C P B BP P A BP P C BP ''''''''''''''''''=+⇒=-+-⇒=+++⇒322()BP P A P C BA BP BC BP '''''=+=-+- 116236BP BA BC BP BA BC ''=+⇒=+ 222222AC BC BA AC BC BA AC BC BA BC BA=-⇒=-⇒=+-⋅ 91316210BC BA BC BA =+-⋅⇒⋅=11()()36BP AC BA BC BC BA '⋅=+⋅- 2211(2)(2131610)066BA BC BC BA =-++⋅=-⨯++= BP AC '⊥PP '⊥AC ⊂PP AC '⊥BP AC '⊥PP 'BP '⊂BPP 'PP BP P '''= AC ⊥BPP 'BP ⊂BPP 'AC BP ⊥1121()3636P A BA BP BA BA BC BA BC ''=-=-+=- 22222111(168)(161316810)4363636P A BA BC BA BC BA BC '=-=+-⋅=⨯+-⨯= 2P A '=Rt PP A '△AP =2AP '=PP '===1136BP BA BC '=+22221111()(44)(41316410)3363636BP BA BC BA BC BA BC '=+=++⋅=⨯++⨯= BP '=在中,,所以.在中,,,因为,所以.又平面PAC ,,所以平面PA C.17.(1,可得,,即因,则.(2)由等面积法可得:,即:,所以①,②,在中,由余弦定理得,即③,由①②③解得:;(3)如图,因CD 平分,故,在中,设,则,在中,由正弦定理,得,则,在中,由正弦定理,得,则,Rt P BP '△BP '=PP '=BP =Rt ABP △BP =AP =AB =222BP AP AB +=BP AP ⊥,AP AC ⊂AC AP A = BP ⊥o sin sin c s cos si n )B A B A C -=)sin A B C +=sin C C =tan C =0πC <<π3C =11sin ()22S ab C r a b c ==++3()2a b c =++=a b c ++=40ab =ABC △2222cos c a b ab C =+-2222()3c a b ab a b ab =+-=+-c =ACB ∠1π26ACD BCD ACB ∠=∠=∠=ABC △(0)AD m m c =<<BD c m =-ACD △2πsin sin 6mA =1sin m A =BCD △2πsin sin 6c mB -=1sin c m B -=得,故有(*).在中,由正弦定理,得,则,得代入(*)式,可得,即.,当且仅当”.于是,即18.【详解】(1)令,连接FG,由四边形PDCE为矩形,得为PC中点,又为PA中点,则,又平面DEF,平面DEF;所以平面DEF.(2)由PD垂直于梯形ABCD所在平面,,得直线DA,DC,DP两两垂直,以为坐标原点,直线DA,DC,DP分別为x,y,z轴建立空间直角坐标系,则,,,,,设平面BCP的法向量,则,令,得,由轴平面ABCD,得平面ABCD的法向量,则所以平面ABCD与平面BCP.(3)由(2)知:,则,而平面BCP的法向量,所以点到平面BCP的距离.1sinc mB=+11sin sincA B=+ABC△sin sina bA B==sin sina bA B==1sin1sinAB⎧=⎪⎪⎨⎪=⎪⎩11()ca b=+11a b+=11a b=+≥163ab≥a b===1sin2ABCS ab C ab==≥△ABC△CP DE G=G F//AC FGFG⊂AC⊂///AC90ADC∠=︒D(1,1,0)B(0,2,0)C P(1,1,0)BC=-(0,CP=-(,,)n x y z=20BC n x yCP n y⎧⋅=-+=⎪⎨⋅=-+=⎪⎩1y=n=z⊥(0,0,1)m=cos,m nm nm n⋅〈〉==1(2F1(,0,2PF=n=F11224PF ndn⋅===19.(1)因为,则,因为,又,所以,故在区间上恒成立,即函数为上的凸函数.(2)①因为,所以,,由题知在区间上恒成立,即在区间上恒成立,令,则在区间上恒成立,令,对称轴为,所以当时,取到最大值,最大值为1,所以,得到,所以的最小值为.②由(1)知,令,则,令,则在区间恒成立,当且仅当时取等号,所以在区间上单调递增,得到,当且仅当时取等号,即在区间恒成立,31()f x x x=-232(31)()()x f x x x --'=-42632(631)()(1)x x f x x x -+''=-4222156316()048x x x -+=-+>(1,)x ∈+∞63(1)0x x ->42632(631)()0(1)x x f x x x -+''=>-(1,)+∞31()f x x x=-(1,)+∞2()2ln ln ()g x ax x x x a =--∈R 1()22ln 2g x ax x x'=---221()2g x a x x '=-+221()20g x a x x ''=-+≥[1,)+∞2212a x x ≥-[1,)+∞1(0,1]t x =∈222a t t ≥-(0,1]22y t t =-1t =1t =22y t t =-21a ≥12a ≥a 1221()2ln ln ()2g x x x x x a =--∈R 21()()22ln ln 22H x g x x x x x x x =+=--+11()2ln 222ln H x x x x x x x '=--+=-1()2ln m x x x x=--222222121(1)()10x x x m x x x x x-+-'=-+==≥[1,)+∞1x =1()2ln m x x x x=--[1,)+∞()(1)0m x m ≥=1x =1()2ln 0H x x x x'=--≥[1,)+∞当且仅当时取等号,即在区间上单调递增,所以,令,令,得到,则在区间上恒成立,即在区间上单调递减,所以,即当,,当且仅当时取等号,所以,在上恒成立.1x =21()2ln ln 22H x x x x x x =--+[1,)+∞15()(1)222H x H ≥=+=31()2(32)(31)x x x F x -=+-+312x t =-≥2(1)(2)t y t t =+-+22220(2)t y t t --'=<+-[2,)+∞2(1)(2)t y t t =+-+[2,)+∞252(21)(22)2y ≤+=-+[1,)x ∈+∞315()2(32)(31)2x x x F x -=+≤-+1x =31()22(32)(31)x x x g x x -+≥+-+[1,)+∞。
2023—2024学年上海市华东师范大学附属周浦中学高三上学期期中考试数学试卷
2023—2024学年上海市华东师范大学附属周浦中学高三上学期期中考试数学试卷一、填空题1. 已知集合,则 ____________2. 的二项展开式中的系数为 ____________3. 复数满足为虚数单位),则= _____ .4. 物体位移s和时间t满足函数关系,则当时,物体的瞬时速度为 ______ .5. 将5个人排成一排,若甲和乙须排在一起,则有 __________ 种不同的排法.(用数字作答)6. 现利用随机数表法从编号为00,01,02,…,18,19的20支水笔中随机选取6支,选取方法是从下列随机数表第1行的第9个数字开始由左到右依次选取两个数字,则选出来的第6支水笔的编号为 ______ .95226000 49840128 66175168 39682927 43772366 27096623 92580956 43890890 06482834 59741458 29778149 646089257. 若向量,,则在方向上的投影向量的坐标为______ .8. 若存在,使得,则实数a的取值范围 ______ .9. 已知向量,满足,,则 ______ .10. 设点P是以原点为圆心的单位圆上的动点,它从初始位置出发,沿单位圆按逆时针方向转动角后到达点,然后继续沿单位圆按逆时针方向转动角到达.若点的横坐标为,则点的纵坐标为______ .11. 《九章算术》将上下两个平行平面为矩形的六面体称为刍童.如图几何体是一个刍童,其上下底面都为正方形,边长分别为6和2,侧面是全等的等腰梯形,梯形的高为,则该几何体的体积为 ______ .12. 若函数在上是严格单调函数,则实数a的取值范围为 _____________ .二、单选题13. 下列函数中,既是奇函数又是减函数的是()A.B.C.D.14. “”是“事件A与事件互相独立”()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件15. 了解某些细菌、病毒的生存条件、繁殖习性等对于预防该细菌、病毒引起的疾病传播有重要的意义.科研团队在培养基中放入一定量某种菌落进行研究,设经过时间x(单位:min),菌落的覆盖面积为y(单位:).团队提出如下假设:①当时,;②y随x的增加而增加,且增加的速度越来越快.则下列选项中,符合团队假设的模型是()A.B.C.D.16. 在单位正方体中,点P在线段上,点Q线段上.①二面角的大小为定值;②长度的最小值为.对于以上两个命题,下列判断正确的是()A.①正确,②正确B.①正确,②错误C.①错误,②正确D.①错误,②错误三、解答题17. 为了鼓励消费,某地发放了以“爱购**”为主题的消费券,一张消费券价值50元,使用方式为:消费满100元后,结账时该券抵50元.(1) A商家在中秋节期间举行促销活动,每件商品按原价6折销售.若买一件原价为300元的商品,则在结账时使用了一张消费券后,还应付多少元?(2)小明在B商家选购时看中了一件88元的商品和一件打5折的特价商品,但特价商品的折扣不能与消费券同时使用,若该特价商品原价的范围在元,试判断小明是否会使用消费券?并说明理由.18. 某班共50名学生,根据他们一次平时测试成绩绘制了如图所示的频率分布直方图.已知分数为的矩形面积为0.16.(1)求分数在内的学生人数并计算这次测试的平均成绩;(2)以频率估计概率,已知在全校学生中采用分层抽样在和范围内共抽取了5人,求从这5人中随机选取2人,这2人中至少有1人分数在内的概率.19. 已知的内角A、B、C所对的边分别为a、b、c,面积为S.(1)若,,求C;(2)若,,求S的最大值.20. 如图,在三棱锥中,平面平面BCD,,,H为BD的中点,,.(1)求证:;(2)求异面直线BC与AD所成角的大小.(3)若,求三棱锥外接球的体积.21. 设.(1)求证:直线与曲线相切;(2)设点P在曲线上,点Q在直线上,求的最小值;(3)若正实数a,b满足:对于任意,都有,求的最大值.。
2023-2024学年上海高一第一学期数学期中期末考试 专题05 期末解答压轴题(解析版)
专题05期末解答压轴题新定义题型1.(2023上·上海徐汇·高一统考期末)已知函数()y f x =,x D ∈,若存在常数k (0k >),使得对定义域D 内的任意12,x x (12x x ≠),都有()()1212f x f x k x x -≤-成立,则称函数()y f x =在其定义域D 上是“k -利普希兹条件函数”(1)判断函数①y x =,②3y x =是否是“1-利普希兹条件函数”,若是,请给出证明;若不是,请说明理由;(2)若函数y x =(14x ≤≤)是“k -利普希兹条件函数”,求常数k 的最小值;(3)若()y f x =是定义在闭区间[]0,1上的“2-利普希兹条件函数”,且(0)(1)f f =,求证:对任意的[]12,0,1x x ∈都有()()121f x f x -≤.【答案】(1)y x =是,3y x =不是(2)12(3)证明见解析【分析】(1)证明()()1212f x f x x x -≤-即可判断y x =,举出反例即可判断3y x =;(2)分离参数,将不等式变为关于12,x x 的不等式,结合定义域即可求得常数k 的最小值;(3)对任意的[]12,0,1x x ∈都有()()12f x f x m -≤,只需要()()12max f x f x m -≤即可,根据新定义求出()()12max f x f x -即可得出答案.【解析】(1)对于函数()y f x x ==,不妨设12x x >,则()()1212f x f x x x -=-,符合题意,所以函数y x =是“1-利普希兹条件函数”,对于函数()3y f x x ==,因为()()21721f f -=>-,所以函数3y x =不是“1-利普希兹条件函数”;(2)若函数()f x x =(14x ≤≤)是“k -利普希兹条件函数”,则对定义域[]1,4内任意12,x x (12x x ≠),均有()()1212f x f x k x x -≤-,即1212x x k x x -≤-,设12x x >,则1212x x k x x -≤-,即121k x x ≤+,因为2114x x ≤<≤,所以1211142x x <<+,所以12k ≥所以k 的最小值为12;(3)设12x x ≥,当1212x x -≤时,因为()y f x =是定义在闭区间[]0,1上的“2-利普希兹条件函数”,所以()()121212212f x f x x x -≤-≤⨯=,当1212x x ->时,由[]12,0,1x x ∈,得12112x x <-≤,故()()()()()()121212(1)(0)(1)(0)f x f x f x f f f x f x f f f x -=-+-≤-+-()()1212212221x x x x ≤-+=--≤恒成立,综上所述,()()121f x f x -≤,【点睛】关键点点睛:本题考查了函数新定义问题,解决本题的关键在于理解“k -利普希兹条件函数”.2.(2023上·上海杨浦·高一复旦附中校考期末)若定义在区间[],a b 上的函数()y f x =满足:存在常数M ,使得对任意的12n a x x x b =≤≤⋅⋅⋅≤=,都有()()()()()()12231n n f x f x f x f x f x f x M --+-+⋅⋅⋅+-≤成立,则称()y f x =为一个有界变差函数,并将满足条件的M 的最小值称为()y f x =的全变差.(1)判断函数()()311f x x x =--≤≤,和()[][]R 0,0,1Q 1,0,1Q x D x x ⎧∈⋂⎪=⎨∈⋂⎪⎩ð(Q 为有理数集)是否为有界变差函数;(无需说明理由)(2)求函数()()414g x x x x=+≤≤的全变差;(3)证明:函数()2log 4xh x x x=+是[]1,4上的有界变差函数.【答案】(1)3()f x x =-是有界变差函数,()D x 不是有界变差函数;(2)2;(3)证明见解析.【分析】(1)根据已知定义判断即可;(2)根据全变差定义结合单调性,把差的绝对值去掉求解可得;(3)根据有界变差函数定义结合单调性,把差的绝对值去掉求解可得;【解析】(1)由3()f x x =-在[1,1]-上递减,令121...1n x x x -=≤≤≤=,则23121()()()()...()()n n f x f x f x f x f x f x --+-++-=121231()()()()...()()()()(1)(1)2n n n f x f x f x f x f x f x f x f x f f --+-++-=-=--=,显然,存在2M ≥,使任意的12n a x x x b =≤≤⋅⋅⋅≤=,都有()()()()()()12231n n f x f x f x f x f x f x M --+-+⋅⋅⋅+-≤成立,所以3()f x x =-为一个有界变差函数;对于()D x ,令120...1n x x x =≤≤≤=,所得i x *(1,N )i n n ≤≤∈中有理数、无理数都有可能为无限个,若12,,...,n x x x 以无理数、有理数成对依次出现时12312()()()()...()()n n f x f x f x f x f x f x --+-++-随n 的变大趋向于正无穷大,所以()D x 不是一个有界变差函数.(2)对任意的11221.....4.n m m x x x x x +=≤≤≤≤≤≤==,()g x 在[]1,2上单调递减,所以()()()()121...m m g x g x g x g x -≥≥≥≥,即()()()()()()12231...mm g x g x g x g x g x g x --+-++-()()()()()()()()122311...m m m g x g x g x g x g x g x g x g x -=-+-++-=-,()g x 在[]2,4上单调递增,所以()()()()11n n m m g x g x g x g x -+≥≥≥≥ ,即()()()()()()1112...m n n n n m g x g x g x g x g x g x --+--+-++-()()()()()()()()2111...n n n n m n m m g x g x g x g x g x g x g x g x --+-=-+-++-=-,所以()()()()()()12231...n n g x g x g x g x g x g x --+-++-()()()()()()1222214n m g x g x g x g g g =+-=+-=,所以,存在2M ≥使()()()()()()12231n n g x g x g x g x g x g x M --+-+⋅⋅⋅+-≤成立,则称()y g x =为一个有界变差函数,M 的最小值2称为()y g x =的全变差.(3)由(2)知:()g x 在[]1,4上是一个有界变差函数,令1()()p x g x =,则111()()|()()|||()()i i i i i i g x g x p x p x g x g x -----=,而在[]1,4上()54g x ≥≥,所以111|()()||()()|16i i i i p x p x g x g x ---≤-,即11221|()()||()()|1616nn i i i i i i M p x p x g x g x --==-≤-=∑∑,故()p x 是有界变差函数;又2()log q x x =在[]1,4上递增且值域为[0,2],任意1214n x x x =≤≤≤= ,则()()()12...n q x q x q x ≤≤≤,所以12|()()|n i i i q x q x -=-∑()()()()1412n q x q x q q =-=-=,故存在2M ≥使12|()()|ni i i q x M q x -=-≤∑,则()q x 是有界变差函数,令()()()h x q x p x =⋅,则11122|()()||()()()()|nn ii i i i i i i h x h xq x p x q x p x ---==-=-∑∑1112|()[()()]()[()()]|ni i i i i i i q x p x p x p x q x q x ---==-+-∑,由上可设1|()|,|()|i i q x N p x L -≤≤且,N L 均为常数,故111222|()()||()()||()()|nn nii i i i i i i i h x h xN p x p x L q x q x ---===-≤-+-∑∑∑,而()p x 、()q x 均为有界变差函数,所以()()()h x q x p x =⋅2log 4xx x=+为有界变差函数.【点睛】关键点点睛:根据有界变差函数的定义,结合相关函数的单调性判断无限细分后区间端点函数值差的绝对值小于某一常数是否恒成立.3.(2023上·上海浦东新·高一上海南汇中学校考期末)设函数()f x 的定义域为D ,若函数()f x 满足条件:存在[],a b D ⊆,使()f x 在[],a b 上的值域为[],ma mb (其中(]0,1)m ∈,则称()f x 为区间[],a b 上的“m 倍缩函数”.(1)证明:函数()3f x x =为区间11,22⎡⎤-⎢⎥⎣⎦上的“14倍缩函数”;(2)若存在[],R a b ⊆,使函数()()2log 2xf x t =+为[],a b 上的“12倍缩函数”,求实数t 的取值范围;(3)给定常数0k >,以及关于x 的函数()1kf x x=-,是否存在实数,()a b a b <,使()f x 为区间[],a b 上的“1倍缩函数”.若存在,请求出,a b 的值;若不存在,请说明理由.【答案】(1)证明见解析;(2)1(0,)4;(3)答案见解析.【分析】(1)利用函数()f x 的单调性,求出()f x 的值域,再结合定义判断作答.(2)利用函数()f x 的单调性,求出()f x 的值域,结合定义构造方程,再利用方程有两个不等的正根求解作答.(3)根据给定条件,可得0a >,再分类去绝对值符号,结合单调性求出值域即可求解作答.【解析】(1)函数3()f x x =在R 上单调递增,则3()f x x =在区间11[,]22-上的值域为11[,]88-,显然有111111(),842842-=⨯-=⨯,所以函数()3f x x =为区间11[,]22-上的“14倍缩函数”.(2)因为函数2x u t =+在R 上单调递增,当0u >时,函数2log y u =在(0,)+∞上单调递增,因此函数2()log (2)xf x t =+是定义域上的增函数,因为函数2()log (2)xf x t =+为[],a b 上的“12倍缩函数”,则函数()f x 在[],a b 上的值域为11[,]22a b ,于是得1()21()2f a a f b b⎧=⎪⎪⎨⎪=⎪⎩,即,()a b a b <是方程1()2f x x =的两个不等实根,则方程12221log (2)22(2)(2)02x xxx x t x t t +=⇔+=⇔-+=有两个不等实根,令(2)0x z =>,则关于z 的一元二次方程20z z t -+=有两个不等的正实根,因此Δ140100t t =->⎧⎪>⎨⎪>⎩,解得104t <<,当104t <<时,函数()f x 恒有意义,所以实数t 的取值范围是1(0,)4.(3)常数0k >,函数()1kf x x=-的定义域为(,0)(0,)-∞+∞ ,并且()0f x ≥,假定存在实数,()a b a b <,使()f x 为区间[],a b 上的“1倍缩函数”,则函数()f x 在区间[],a b 上的值域为[],a b ,由[,](,0)(0,)a b ⊆-∞+∞ ,及[,][0,)a b ⊆+∞知0a b <<,因为函数1k y x =-在[],a b 上单调递增,即111k k k a x b-≤-≤-,若101k ka b -<<-,即0a k b <<<,则函数()f x 在区间[],a b 上的值域中有数0,矛盾,若10k b -≤,即0a b k <<≤,当[,]x a b ∈时,()1kf x x=-在[,]a b 上单调递减,有()()f a b f b a =⎧⎨=⎩,即11ka bk ba⎧-=⎪⎪⎨⎪-=⎪⎩,整理得k b ab k a ab -=⎧⎨-=⎩,显然无解,若10k a -≥,即k a b ≤<,当[,]x a b ∈时,()1kf x x=-在[,]a b 上单调递增,有()()f a a f b b =⎧⎨=⎩,即,()a b a b <是方程()f x x =的两个不等实根且a k ≥,而方程210kx x x k x-=⇔-+=,于是得方程2()0g x x x k =-+=在[,)k +∞上有两个不等实根,从而2Δ140()012k g k k k=->⎧⎪⎪=≥⎨⎪>⎪⎩,解得14k <,而0k >,即有104k <<,解方程20x x k -+=得:12114114,22k kx x --+-==,所以当104k <<时,存在实数,()a b a b <,使()f x 为区间[],a b 上的“1倍缩函数”,114114,22k ka b --+-==,当14k ≥时,不存在实数,()a b a b <,使()f x 为区间[],a b 上的“1倍缩函数”.【点睛】思路点睛:涉及函数新定义问题,理解新定义,找出数量关系,联想与题意有关的数学知识和方法,再转化、抽象为相应的数学问题作答.4.(2023上·上海徐汇·高一位育中学校考期末)若函数()f x 的定义域为R ,且对12,x x ∀∈R ,都有()()()1212f x x f x f x +≤⋅,则称()f x 为“J 形函数”(1)当()1f x x =+时,判断()f x 是否为“J 形函数”,并说明理由;(2)当()22f x x =+时,证明:()f x 是“J 形函数”;(3)如果函数()2x f x a =+为“J 形函数”,求实数a 的取值范围.【答案】(1)否,理由见解析;(2)证明见解析;(3)1a ≥或0a =.【分析】(1)作差可得()()()121212f x x f x f x x x +-⋅=-,根据12,x x 的任意性,无法判断该式符号,即可说明;(2)作差可得()()()1212f x x f x f x +-⋅()22212122x x x x =----,即可证明得出结论;(3)代入化简可得()12122x x f x x a ++=+,()()1212212222x x x x f x x a a ++++=+.由“J 形函数”的概念整理化简可得,()12122x xa -+≥,进而即可得出实数a 的取值范围.【解析】(1)解:()f x 不是“J 形函数”,理由如下:当()1f x x =+时,有()111f x x =+,()221f x x =+,()12121f x x x x +=++,则()()()1212f x x f x f x +-⋅()()1212111x x x x ++-++=12x x =-.因为12,x x ∈R ,所以12x x -与0的关系不确定,不能得出()()()12120f x x f x f x +-⋅≤,所以()f x 不是“J 形函数”.(2)证明:当()22f x x =+时,有()2112f x x =+,()2222f x x =+,()()22212121212222f x x x x x x x x +=++=+++,则()()()()2222221212121222224f x f x x x x x x x ⋅=++=+++,所以()()()1212f x x f x f x +-⋅212222121222x x x x x x =----()22212122x x x x =----,显然有()()()121220f x x f x f x +-⋅≤-≤对12,x x ∀∈R 恒成立,所以有()()()1212f x x f x f x +≤⋅对12,x x ∀∈R 恒成立,所以()f x 是“J 形函数”.(3)解:由已知可得()112x f x a =+,()222x f x a =+,()12122x x f x x a ++=+,所以()()121222x x f x f x a a ⋅=+⋅+()12122222x x x x a a +=+++.因为函数()2x f x a =+为“J 形函数”,所以有()12121222222x x x x x x a a a +++≤+++,即()121212202222x x x x x x a a a ++++≤+≤+.由1220x x a ++≥,可得0a ≥;由()12121222222x x x x x x a a a +++≤+++可得,()12222x x a a a ≤++.当0a =时,该式恒成立,满足;当0a >时,有()12122x xa -+≥恒成立.因为12220x x +>,所以1a ≥.综上可得,1a ≥或0a =.【点睛】关键点点睛:本题考查函数中的新定义问题,解题关键是能够充分理解“J 形函数”的本质是函数值的大小关系的比较问题,从而利用作差法,整理化简()()()1212f x x f x f x +-⋅.只要得出()()()12120f x x f x f x +-⋅≤恒成立,即可说明()f x 是“J 形函数”.5.(2023上·上海徐汇·高一上海市西南位育中学校考期末)已知()f x 定义域为R 的函数,S ⊆R ,若对任意1212,,x x x x S ∈-∈R ,均有()()12f x f x S -∈,则称()f x 是S 关联.(1)判断函数()()12112f x xg x x =-=-、是否是[)1,+∞关联,并说明理由:(2)若()f x 是{}2关联,当[)0,2x ∈时,()2f x x x =-,解不等式:()02f x ≤≤;(3)判断“()f x 是{}2关联”是“()f x 是[]1,2关联”的什么条件?试证明你的结论.【答案】(1)函数()21f x x =-是[)1,+∞关联,函数1()12g x x =-不是[)1,+∞关联,理由见解析(2){|13x x ≤≤或}0x =(3)必要不充分条件,证明见解析【分析】(1)根据给定的定义为[)1,+∞时,求12()()f x f x -的取值区间即可判断作答.(2)根据给定条件,可得(2)()2f x f x +-=,再结合已知函数分段解不等式并求并集作答.(3)利用给定的定义,利用推理证明命题的充分性和必要性作答.【解析】(1)函数()21f x x =-是[)1,+∞关联,证明如下:任取12,x x ∈R ,若12[1,)-∈+∞x x ,则()()()[)121222,[1,)f x f x x x -=-∈+∞⊂+∞,()()()12122[1,)f x f x x x ∴-=-∈+∞所以函数()21f x x =-是[)1,+∞关联;函数1()12g x x =-不是[)1,+∞关联,证明如下::若12[1,)-∈+∞x x ,则121211()()(),22⎡⎫-=-∈+∞⎪⎢⎣⎭f x f x x x ,所以函数1()12g x x =-不是[)1,+∞关联;(2)因()f x 是{}2关联,则122x x -=,有12()()2f x f x -=,即(2)()2f x f x +-=,当[)0,2x ∈时,22111(),2244⎛⎫⎡⎫=-=--∈- ⎪⎪⎢⎝⎭⎣⎭f x x x x ,而()02f x ≤≤,即202≤-≤x x ,解得12x ≤≤或10x -≤≤,所以不等式的解集为{|12x x ≤<或}0x =,当[2,22),,0x n n n Z n ∈+∈≠时,()2112224f x x n n ⎛⎫=---+ ⎪⎝⎭,所以当[2,4)x ∈时,2577()(2)2,4244⎛⎫⎡⎫=-+=-+∈ ⎪⎪⎢⎝⎭⎣⎭f x f x x ,而0()2f x ≤≤,得2570224⎛⎫≤-+≤ ⎪⎝⎭x ,解得23x ≤≤,所以不等式的解集为{}|23x x ≤≤,当0n <时,()0f x <或当2n ≥时,()2f x >,此时不等式0()2f x ≤≤无解;综上得13x ≤≤或0x =,所以不等式2()3f x ≤≤的解集为{|13x x ≤≤或}0x =,.(3)“()f x 是{}2关联”是“()f x 是[]1,2关联”的必要不充分条件,证明如下,易得函数,()1,x x Zf x x x Z ∈⎧=⎨-∉⎩是{}2关联,但1 2.112≤-≤时2)(2.1()0f f <-,所以函数()f x 不是[1,2]关联;所以充分性不成立;当函数()f x 是[1,2]关联时,即2112x x ≤-≤,21)1(()2f x f x -≤≤,则有1(2)(1)2f x f x -≤++≤,)1(1()2f x f x -≤+≤,即有)2(2()4f x f x -≤+≤,又1(2)2x x ≤+-≤,则有)1(2()2f x f x -≤+≤,于是得(2)()2f x f x +-=,从而得()()21212,=2x x f x f x -=-,即函数()f x 是{2}关联;所以“()f x 是{}2关联”是“()f x 是[]1,2关联”的必要不充分条件.【点睛】思路点睛:涉及函数新定义问题,理解新定义,找出数量关系,联想与题意有关的数学知识和方法,再转化、抽象为相应的数学问题作答.抽象函数6.(2023上·上海浦东新·高一上海市建平中学校考期末)已知函数()f x 在定义域D 上是严格增函数.(1)若()221f x x x =+--,求()f x 的值域;(2)若()[]12241log ,,(04)214x x x f x D t t t x+-=++=-<<++的值域为[],m n ,求m n +的值;(3)若()0,D =+∞,且对定义域D 内任意自变量x 均有()()11f x f f x x ⎛⎫⋅+= ⎪⎝⎭成立,试求()f x 的解析式.【答案】(1)[2,2]-;(2)4;(3)()152f x x-=.【分析】(1)先求出函数的定义域,然后根据函数的单调性可求出函数的最值,从而可求出函数的值域;(2)根据函数在D 上是严格增函数,可得()12241log 214t t t m f t t --++=-=+++-,()12241log 214t t tn f t t +-==++++,然后相加化简可得答案;(3)由已知可得111()()11()f f x f f f x x x f x x ⎛⎫ ⎪⎛⎫⎛⎫+⋅++=⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪+⎝⎭,则有()11()1()f f f x f x x f x x ⎛⎫ ⎪⎛⎫++= ⎪ ⎪⎝⎭ ⎪+⎝⎭,再根据其单调性和已知条件可得()111()x f x f x x+=+,从而可求出()f x 的解析式.【解析】(1)由22010x x +≥⎧⎨-≥⎩,解得11x -≤≤,因为22y x =+和1y x =--在[1,1]-上均为增函数,所以()221f x x x =+--在[1,1]-上为增函数,所以min ()(1)221(1)2f x f =-=-+---=-,max ()(1)222f x f ==+=,所以()f x 的值域为[2,2]-;(2)因为()[]12241log ,,(04)214x x xf x D t t t x+-=++=-<<++的值域为[],m n ,且()f x 在定义域D 上是严格增函数,所以()12241log 214t t t m f t t --++=-=+++-,()12241log 214t t tn f t t+-==++++,所以()()m n f t f t +=-+112224241log 1log 214214t t t t t tt t -++-+-=++++++-++1222442log 212144t t t t t t t ++-⎛⎫=+++⋅ ⎪++-+⎝⎭22(21)2log 211t t +=+++224=+=;(3)因为对定义域D 内任意自变量x 均有()()11f x f f x x ⎛⎫⋅+= ⎪⎝⎭成立,所以111()()11()f f x f f f x x x f x x ⎛⎫ ⎪⎛⎫⎛⎫+⋅++=⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪+⎝⎭,所以()()111()()1()f x f fx f f f x f x x x f x x ⎛⎫ ⎪⎛⎫⎛⎫⋅+⋅++= ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪+⎝⎭,所以()11()1()f f f x f x x f x x ⎛⎫ ⎪⎛⎫++= ⎪ ⎪⎝⎭ ⎪+⎝⎭,因为函数()f x 在定义域D 上是严格增函数,所以11()1()f f x x x f x x⎛⎫++= ⎪⎝⎭+,所以()111()xf x f x x+=+,所以()()()()()()211f x f x xf x f x xf x f x x x ⎡⎤++=+=+⎢⎥⎣⎦,所以()()210xf x f x x --=,解得()152f x x±=,因为函数()f x 在定义域D 上是严格增函数,所以()152f x x-=.7.(2023上·上海松江·高一上海市松江二中校考期末)若函数f (x )满足:对于任意正数s ,t ,都有()0f s >,()0f t >,且()()()f s f t f s t +<+,则称函数f (x )为“L 函数”.(1)试判断函数()2h x x =是否是“L 函数”,并说明理由;(2)若函数()()3131x xg x a -=-+-为“L 函数”,求实数a 的取值范围;(3)若函数f (x )为“L 函数”,且()11f =,求证:对任意()()1*2,2N k k x k -∈∈,都有()2x f x >.【答案】(1)是“L 函数”,理由见解析;(2)[1,1]-;(3)证明见解析.【分析】(1)根据“L 函数”的定义分析判断即可;(2)由()g x 为“L 函数”,可得()0g t >,则3t a <,得1a ≤,()()()g s g t g s t +<+可得30s t a ++>,得10a +≥,从而可求出实数a 的取值范围;(3)由函数f (x )为“L 函数”,可得(2)2()f s f s >,即(2)2()f s f s >,则112(2)(2)(2)(2)2()(2)(2)()k k k k k k f s f s f s f s f s f s f s f s ---=⋅⋅⋅⋅⋅⋅>,再结合111()(2)(2)(2)k k k f x f x f f --->-+>可证得结论.【解析】(1)对于()2h x x =,当0,0t s >>时,()20h t t =>,()20h s s =>,因为()()()222()20h s h t h s t s t s t st +-+=+-+=<,所以()()()h s h t h s t +<+,所以()2h x x =是“L 函数”;(2)当0,0t s >>时,由()()3131x xg x a -=-+-是“L 函数”,得()()31310t t g t a -=-+->,即(31)(3)0t t a -->对一切正数t 恒成立,因为310t ->,所以3t a <对一切正数t 恒成立,所以1a ≤,由()()()g s g t g s t +<+,得3331(3331)0s t s t s t s t a +------++--+>,所以(31)(31)(3)0s t s t a +--+>,因为(31)(31)0s t -->,所以30s t a ++>,由30s t a ++>对一切正数,s t 恒成立,所以10a +≥,即1a ≥-,综上可知,实数a 的取值范围为[1,1]-;(3)因为函数f (x )为“L 函数”,所以对于任意正数,s t 都有()0f s >,()0f t >,且()()()f s f t f s t +<+,令s t =,可知(2)2()f s f s >,即(2)2()f s f s >,所以对于正整数k 与正数s 都有112(2)(2)(2)(2)2()(2)(2)()k k k k k k f s f s f s f s f s f s f s f s ---=⋅⋅⋅⋅⋅⋅>,对任意()()1*2,2N k k x k -∈∈,可得()()1*12,2N k k k x--∈∈,因为(1)1f =,所以11112()(2)(2)(2)2(1)22k k k k k x f x f x f f f ---->-+>≥=>.【点睛】关键点点睛:此题考查函数的新定义,解题的关键是对函数新定义的正确理解,然后结合已知条件求解即可,考查理解能力和运算能力,属于较难题.8.(2023上·上海闵行·高一统考期末)已知函数()y F x =的定义域为D ,t 为大于0的常数,对任意x D ∈,都满足()()()2F x t F x t F x ++->,则称函数()y F x =在D 上具有“性质A ”.(1)试判断函数2x y =和函数2y x =-是否具有“性质A ”(无需证明);(2)若函数()y f x =具有“性质A ”,且()102f f ⎛⎫> ⎪⎝⎭,求证:对任意n ∈N ,都有()()1f n f n >+;(3)若函数()y g x =的定义域为R ,且具有“性质A ”,试判断下列命题的真假,并说明理由,①若()y g x =在区间(),0∞-上是严格增函数,则此函数在R 上也是严格增函数;②若()y g x =在区间(),0∞-上是严格减函数,则此函数在R 上也是严格减函数.【答案】(1)函数2x y =不具有“性质A ”,函数2y x =-具有“性质A ”(2)证明见解析(3)命题①为假命题,命题②为真命题,理由见解析【分析】(1)利用作差法结合“性质A ”的定义判断可得出结论;(2)利用“性质A ”的定义结合不等式()102f f ⎛⎫> ⎪⎝⎭可推导出()1102f n f n ⎛⎫+-+< ⎪⎝⎭,()102f n f n ⎛⎫+-< ⎪⎝⎭,利用不等式的基本性质可证得结论成立;(3)取()2g x x =-可判断命题①为假命题,对命题②,对任意的1t 、2t ∈R 且12x x <,取210t x x =->,根据“性质A ”的定义结合基本不等式的性质、单调性的定义证得()()12g x g x >,即可证得结论成立.【解析】(1)解:函数2x y =不具有“性质A ”,函数2y x =-具有“性质A ”,理由如下:设()2xp x =,()2q x x =-,对任意的0t >,()()()()222222222x t x t x x t tp x t p x t p x +--++--=+-⋅=+-()222220x t t ->⨯⋅-=,所以,()()()2p x t p x t p x ++-<,所以,函数2x y =不具有“性质A ”,对任意的0t >,()()()()()22222220q x t q x t q x x x t x t t ++--=-+--=<,所以,()()()2q x t q x t q x ++->,所以,函数2y x =-具有“性质A ”.(2)证明:因为函数()y f x =具有“性质A ”,对任意的0t >,()()()2f x t f x t f x ++->,所以,()()()()f x f x t f x t f x -->+-,又因为()102f f ⎛⎫> ⎪⎝⎭,所以,()()()1130011222f f f f f f ⎛⎫⎛⎫⎛⎫>->->-> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()()1111222f n f n f n f n f n f n ⎛⎫⎛⎫⎛⎫>-->+->+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以,()()1021102f n f n f n f n ⎧⎛⎫+-< ⎪⎪⎪⎝⎭⎨⎛⎫⎪+-+< ⎪⎪⎝⎭⎩,由不等式的可加性可得()()10f n f n +-<,故对任意的N n ∈,()()1f n f n +<.(3)解:命题①是假命题,命题②是真命题,理由如下:对于命题①,取函数()2g x x =-,由(1)可知,函数()g x 具有“性质A ”,函数()2g x x =-在区间(),0∞-上是严格增函数,但该函数在R 上不单调;对于命题②,对任意的0t >,对任意的x ∈R ,()()()2g x t g x t g x ++->,所以,()()()()g x t g x g x g x t -->-+,对任意的1t 、2t ∈R 且12x x <,取210t x x =->,必存在1k ≥且N k ∈,满足()2201x kt x k t >->-+,因为函数()y g x =在区间(),0∞-上是严格减函数,所以,()()()221g x kt g x k t -<-+,即()()()2210g x kt g x k t ---+<,所以,()()()()()()()()222222011g x k t g x kt g x kt g x k t g x t g x <-+--<----<<-- ,故()()()()22120g x t g x g x g x <--=-,即()()12g x g x >,故函数()y g x =在R 上是严格减函数.所以,命题②为真命题.【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的:遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.9.(2022上·上海宝山·高一上海市吴淞中学校考期末)若函数()f x 满足:对于任意正数,s t ,都有()()0,0f s f t >>,且()()()f s f t f s t +<+,则称函数()f x 为“L 函数”.(1)试判断函数()21f x x =与()122f x x =是否是“L 函数”;(2)若函数()()3131x xg x a -=-+-为“L 函数”,求实数a 的取值范围;(3)若函数()f x 为“L 函数”,且()11f =,求证:对任意()()12,2N *k kx k -∈∈,都有()122x f x f x x⎛⎫->- ⎪⎝⎭.【答案】(1)21()f x x =是“L 函数”.2()f x x =不是“L 函数”.(2)[11]-,(3)见解析【解析】试题分析:利用“L 函数”的定义判断函数21()f x x =符合要求,而2()f x x =不符合要求(只需举一个反例说明);函数()()3131x xg x a -=-+-为“L 函数”,则()g x 满足“L 函数”的定义,当0,0t s >>时,()0,()0,()()()g s g t g s g t g s t >>+<+成立;根据要求可以求出a 的范围;令s t =得(2)2()f s f s >,即(2)2()f s f s >,故对于正整数k 与正数s ,都有()()()()()()()()1122222222k k k kk k f sf s f sf s f s f s f s f s ---=⋅⋅⋅> ,()()12,2N *k kx k -∈∈,则()112,2kk x--∈,利用(1)1f =,借助()()()1122k k f x f x f -->-+及()111122kk f f f x x --⎛⎫⎛⎫<-- ⎪ ⎪⎝⎭⎝⎭借助不等关系证明.试题解析:(1)对于函数()21f x x =,当0,0t s >>时,()()22110,0f t t f s s =>=>,又()()()()22211120f t f s f t s t s t s ts +-+=+-+=-<,所以()()()111f s f t f s t +<+,故()21f x x =是“L 函数”.对于函数()2f x x =,当1t s ==时,()()()22222f t f s f t s +=>=+,故()2f x x =不是“L 函数”.(2)当0,0t s >>时,由()()3131x xg x a -=-+-是“L 函数”,可知()()31310t t g t a -=-+->,即()()3130t ta -->对一切正数t 恒成立,又310t ->,可得3t a <对一切正数t 恒成立,所以1a ≤.由()()()g t g s g t s +<+,可得()+333133310s ts t s t s t a ------++--+>,故()()()31313+0s t s t a +-->,又()()31310t s-->,故3+0s t a +>,由3+0s t a +>对一切正数,s t 恒成立,可得10a +≥,即1a ≥-.综上可知,a 的取值范围是[]11-,.(3)由函数()f x 为“L 函数”,可知对于任意正数,s t ,都有()()0,0f s f t >>,且()()()f s f t f s t +<+,令s t =,可知()()22f s f s >,即()()22f s f s >,故对于正整数k 与正数s ,都有()()()()()()()()1122222222k k k k k k f sf s f sf s f s f s f s f s ---=⋅⋅⋅> ,对任意()()12,2N *k kx k -∈∈,可得()112,2kk x--∈,又()11f =,所以()()()()()111122222122k k k k k xf x f x f f f ---->-+>≥=>,同理()()()11111112222212k k k k kf f f f f x x x -----⎛⎫⎛⎫<--<≤=< ⎪ ⎪⎝⎭⎝⎭,故()1f x f x ⎛⎫->⎪⎝⎭22x x -.【点睛】本题为自定义信息题,根据题目所提供的信息,要严格遵循“L 函数”的定义解题,首先判断两个函数是否符合“L 函数”的定义,说明是“L 函数”,需要按定义严格证明,说明不是只需举一反例;第二步函数()g x 是“L 函数”,则满足定义,利用满足的条件,借助恒成立条件和最值原理求出参数的范围.零点问题10.(2022上·上海浦东新·高一上海市进才中学校考期末)已知函数()f x 的定义域为()0,∞+,若存在常数0T >,使得对任意()0,x ∈+∞,都有()()f Tx f x T =+,则称函数()f x 具有性质()P T .(1)若函数()f x 具有性质()2P ,求()122f f ⎛⎫- ⎪⎝⎭的值(2)设()log a f x x =,若01a <<,求证:存在常数0T >,使得()f x 具有性质()P T (3)若函数()f x 具有性质()P T ,且()f x 的图像是一条连续不断的曲线,求证:函数()f x 在()0,∞+上存在零点.【答案】(1)()1242f f ⎛⎫-= ⎪⎝⎭(2)证明见解析(3)证明见解析【分析】(1)对任意()0,x ∈+∞,都有()()22f x f x =+,代入2x =和12x =即可得出答案;(2)设()log a g x x x =-,利用零点存在性定理即可证得结论;(3)先转化为()()nf T x f x nT =+,然后令1x =得,()()1nf T f nT =+,分情况利用零点存在性定理证得结论.【解析】(1)函数()f x 具有性质()2P ,所以对任意()0,x ∈+∞,都有()()22f x f x =+,令2x =,得()()212f f =+,令12x =,得()1122f f ⎛⎫=+ ⎪⎝⎭,所以()1242f f ⎛⎫-= ⎪⎝⎭.(2)证明:函数()f x 具有性质()P T 的充要条件为存在0T >,使得()log log a a Tx x T =+,即log a T T =,设()log a g x x x =-,因为()110g =-<,()10g a a =->,所以在区间(),1a 上函数()g x 存在零点0x ,取0T x =,则log a T T =,得函数()f x 具有性质()P T .(3)设n N *∈,因为()()f Tx f x T =+,所以()()nf T x f x nT =+,令1x =得,()()1nf T f nT =+,①若()10f =,则函数()f x 存在零点若()10f <,当()01f n T>-时,()00nf T >,所以此时函数()f x 在区间()0,+∞上存在零点②因为()n x f x f nTT ⎛⎫=+ ⎪⎝⎭所以()()1nf T f nT-=-若()10f >,当()01f n T>时,()00nf T -<,所以此时函数()f x 在区间()0,+∞上存在零点.综上,函数()f x 在()0,∞+上存在零点.11.(2023上·上海浦东新·高一校考期末)已知函数21()4f x x ax =++,()ln g x x =-.(1)若函数[()]g f x 的定义域为R ,求实数a 的取值范围;(2)若函数[()]g f x 在(1,)+∞上单调递减,求实数a 的取值范围;(3)用min{,}m n 表示m ,n 中的最小值,设函数()min{(),()}(0)h x f x g x x =>,讨论()h x 零点的个数.【答案】(1)()1,1-;(2)5[,)4-+∞;(3)答案见解析.【解析】(1)由对数函数的性质及函数的定义域为R ,利用判别式,列出不等式,即可求解;(2)由函数21[()]ln()4=-++g f x x ax ,结合对数函数的性质和复合函数的单调性的判定方法,列出不等式组,即可求解;(3)根据函数()min{(),()}(0)h x f x g x x =>,先分1x >,1x =和01x <<三种情况讨论,再结合二次函数的性质,分∆<0,0∆=和0∆>三种情况讨论,即可求解.【解析】(1)由题意,函数21[()]ln()4=-++g f x x ax ,因为该函数的定义域为R ,则2104x ax ++>对任意x R ∈恒成立,可得210a ∆=-<,解得11a -<<,即实数a 的取值范围()1,1-.(2)由函数21[()]ln()4=-++g f x x ax ,若[()]g f x 在(1,)+∞上单调递减,则问题等价于()0f x >在(1,)+∞上恒成立,且()f x 在(1,)+∞上单调递增,即5(1)0412f a a ⎧=+≥⎪⎪⎨⎪-≤⎪⎩,解得54a ≥-,所以实数a 的取值范围是5[,)4-+∞.(3)当1x >时,()ln 0g x x =-<,所以当1x >时,min{(),()}()0≤<f x g x g x ,所以()h x 在(1,)+∞上没有零点;当1x =时,(1)0g =,5(1)4f a =+,若504a +≥即54a ≥-时,(1)min{(1),(1)}(1)0h f g g ===,此时1x =是函数()h x 的一个零点;若504+<a 即54a <-时,(1)min{(1),(1)}(1)0h f g f ==<,此时1x =不是函数()h x 的一个零点;当01x <<时,因为()ln 0g x x =->,则函数()h x 的零点个数等价于函数()f x 的零点个数,①当210a ∆=-<,即11a -<<时,()0f x >,则()min{(),()}0=>h x f x g x ,函数()h x 在(0,1)上没有零点;②当0∆=即1a =±时,函数()f x 有且只有一个零点,若1a =,由()0f x =可得1(0,1)2=-∉x ,则函数()h x 在(0,1)上没有零点;若1a =-,由()0f x =可得12x =,则函数()h x 在(0,1)上有1个零点;③当0∆>,即1a <-或1a >时,函数()f x 有两个零点,不妨设为12,x x 且12x x <,当1a >时,120x x a +=-<,12104=>x x ,所以120x x <<,则()f x 在(0,1)上没有零点;当1a <-时,120x x a +=->,12104=>x x ,所以120x x <<,当5(1)04=+≤f a 即54a ≤-时,1(0)04=>f ,所以(0)(1)0f f <,则101x <<,21x ≥,所以此时()f x 在(0,1)上有且只有一个零点;当(1)0f >,即514a -<<-时,对称轴15(,)228=-∈a x ,且(0)0f >,(1)0f >所以1201x x <<<,()f x 在(0,1)上有两个零点,综上所述:当54a <-或1a >-时,()h x 有一个零点;当54a =-或1a =-时,()h x 有两个零点;当514a -<<-时,()h x 有三个零点.【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解12.(2023上·上海徐汇·高一南洋中学校考期末)设k ∈R ,函数()y f x =的表达式为()243f x x x =-+,函数()y g x =的表达式为()1g x kx =+,()()y f x g x =-有四个零点,设为()12341234,,,x x x x x x x x <<<.(1)求实数k 的取值范围;(2)求22221234x x x x k+++的取值范围.【答案】(1)1,03⎛⎫- ⎪⎝⎭(2)182,3⎛⎫-∞- ⎪⎝⎭【分析】(1)根据题意,做出图像,结合图像即可得到k 的取值范围;(2)根据题意,利用韦达定理,求得2214x x +,2223x x +和k 的关系,将目标式转化为关于k 的函数,借助对勾函数的单调性,即可求得结果.【解析】(1)根据题意,令2430x x -+=,解得1x =或3x =,不妨设()()()1,03,0,0,,1A B C 做图如下:又直线BC 的斜率为13-,数形结合可知,要满足题意,1,03k ⎛⎫∈- ⎪⎝⎭;(2)由题意可知,14,x x 为方程2431x x kx -+=+,即()2420x k x -++=的两根,当1,03k ⎛⎫∈- ⎪⎝⎭时,()2480k ∆=+->,则41414,2x x k x x +=+=,故()()2422244111244x x x x x x k +=+-=+-;23,x x 为方程2431x x kx -+-=+,即()2440x k x +-+=的两根,当1,03k ⎛⎫∈- ⎪⎝⎭时,()24160k ∆=-->,则23234,4x x k x x +=-=,故()()2222232323248x x x x x x k +=+-=--;则22221234x x x x k +++22201012,,03k k k k k +⎛⎫⎛⎫==+∈- ⎪ ⎪⎝⎭⎝⎭,令()1012,,03f x x x x ⎛⎫⎛⎫=+∈- ⎪ ⎪⎝⎭⎝⎭,由对勾函数单调性可知()f x 在1,03⎛⎫- ⎪⎝⎭上单调递减,又118233f ⎛⎫-=- ⎪⎝⎭,故()f x ∈182,3⎛⎫-∞- ⎪⎝⎭,即22221234x x x x k+++的取值范围为182,3⎛⎫-∞- ⎪⎝⎭.13.(2023上·上海松江·高一校考期末)已知函数()()22,0f x ax ax b a b =-+≥在[]1,3x ∈时有最大值4和最小值0,设()()f xg x x=.(1)求实数a ,b 的值;(2)若不等式()22log log 0g x k x -≤在[]4,8x ∈上恒成立,求实数k 的取值范围;(3)若关于x 的方程()22131021xxmg m -+-+=-有三个不同的实数解,求实数m 的取值范围.【答案】(1)1a =,1b =(2)4,9⎡⎫+∞⎪⎢⎣⎭(3)()1,+∞【分析】(1)根据题意得0a >,再根据二次函数单调性列方程求解即可;(2)由题知2221log 2log 0log x k x x+--≤在[]4,8x ∈上恒成立,设2log t x =,进而得2212111k t t t ⎛⎫≥+-=- ⎪⎝⎭,在[]2,3t ∈上恒成立,再求最值即可得答案;(3)用换元法化简方程()22131021xx mg m -+-+=-为一元二次方程的形式,结合指数型函数的图象、一元二次方程根的分布的知识求得m 的取值范围.【解析】(1)解:()()2221f x ax ax b a x b a =-+=-+-,(),0a b ≥因为,当0a =时,()f x b =,为常函数,不满足题意;所以,0a >,()()21f x a x b a =-+-在[]1,3x ∈上单调递增,因为函数()()22,0f x ax ax b a b =-+≥在[]1,3x ∈时有最大值4和最小值0,所以()()10334f b a f a b ⎧=-=⎪⎨=+=⎪⎩,解得1a b ==,所以1a =,1b =.(2)解:由(1)知()221f x x x =-+,()()12f x g x x x x==+-,因为不等式()22log log 0g x k x -≤在[]4,8x ∈上恒成立,所以2221log 2log 0log x k x x+--≤在[]4,8x ∈上恒成立,设2log t x =,则[]2,3t ∈,所以,120t kt t +--≤,在[]2,3t ∈上恒成立,所以2212111k t t t ⎛⎫≥+-=- ⎪⎝⎭,在[]2,3t ∈上恒成立,因为[]2,3t ∈,所以111,32t ⎡⎤∈⎢⎥⎣⎦,所以,当113t =时,211t ⎛⎫- ⎪⎝⎭取得最大值,最大值为211394⎛⎫-= ⎪⎝⎭,所以,2212111k t t t ⎛⎫≥+-=- ⎪⎝⎭,在[]2,3t ∈上恒成立,则49k ≥,所以k 的取值范围是4,9⎡⎫+∞⎪⎢⎣⎭.(3)解:方程()22131021xx m g m -+-+=-等价于122123102121xx x m m -+-+-+=--,即()()2211321120x x m m --+-++=,210x-≠,令21xt -=,则方程化为()()213120t m t m -+++=,()0t ≠,因为方程()22131021xxmg m -+-+=-有三个不同的实数解,所以,画出21xt =-的图像如下图所示,所以()()213120t m t m -+++=,()0t ≠,有两个根1t 、2t ,且1201t t <<<或101t <<,21t =.记()()()21312h t t m t m =-+++,所以,()()0120110h m h m ⎧=+>⎪⎨=-<⎪⎩,即121m m ⎧>-⎪⎨⎪>⎩,此时1m >或()()()012011013012h m h m m ⎧⎪=+>⎪⎪=-=⎨⎪-+⎪<-<⎪⎩得1211133m m m ⎧>-⎪⎪=⎨⎪⎪-<<⎩,此时m 无解,综上,1m >,即实数m 的取值范围()1,+∞【点睛】本题第三问解题的关键在于令21xt -=,进而结合题意,数形结合得()()213120t m t m -+++=,()0t ≠,有两个根1t 、2t ,且1201t t <<<或101t <<,21t =,再根据零点存在性定理求解即可.二次函数(包括含绝对值)、对勾函数14.(2022上·上海徐汇·高一上海市第二中学校考期末)对于定义域为D 的函数y=f (x ),如果存在区间[m ,n]⊆D ,同时满足:①f (x )在[m ,n]内是单调函数;②当定义域是[m ,n]时,f (x )的值域也是[m ,n].则称[m ,n]是该函数的“和谐区间”.(1)证明:[0,1]是函数y=f (x )=x 2的一个“和谐区间”.(2)求证:函数()53y g x x ==-不存在“和谐区间”.(3)已知:函数()()221aa x y h x a x+-==(a ∈R ,a≠0)有“和谐区间”[m ,n],当a 变化时,求出n﹣m 的最大值.【答案】(1)证明见解析;(2)证明见解析;(3).【解析】试题分析:(1)根据二次函数的性质,在区间[]0,1上单调递增,且值域也为[]0,1满足“和谐区间”的定义,即可得到结论;(2)该问题是一个确定性问题,从正面证明有一定的难度,故可采用反证法来进行证明;(3)设[],m n 是已知函数定义域的子集,我们可以用a 表示出n m -的取值,转化为二次函数的最值问题后,根据二次函数的性质,可以得到答案.试题解析:(1)y=x 2在区间[0,1]上单调递增.又f (0)=0,f (1)=1,值域为[0,1],区间[0,1]是y=f (x )=x 2的一个“和谐区间”.(2)设[m ,n]是已知函数定义域的子集.故函数在[m ,n]上单调递增.若[m ,n]是已知函数的“和谐区间”,则故m 、n 是方程的同号的相异实数根.x 2﹣3x+5=0无实数根,函数不存在“和谐区间”.(3)设[m ,n]是已知函数定义域的子集.x≠0,故函数在[m ,n]上单调递增.若[m ,n]是已知函数的“和谐区间”,则故m 、n 是方程,即222()10a x a a x -++=的同号的相异实数根.,m ,n 同号,只须,即a >1或a <﹣3时,已知函数有“和谐区间”[m ,n],当a=3时,n ﹣m 取最大值考点:1.函数的单调性的性质;2.集合的关系;3.二次函数的图象和性质.【方法点晴】(1)根据二次函数的性质,我们可以得出区间上单调递增,且值域也为满足“和谐区间”的定义,即可得到结论.(2)该问题是一个确定性问题,从正面证明有一定的难度,故可采用反证法来进行证明,即先假设区间为函数的“和谐区间”,然后根据函数的性质得到矛盾,进而得到假设不成立,原命题成立.(3)设是已知函数定义域的子集,我们可以用a 表示出的取值,转化为二次函数的最值问题后,根据二次函数的性质,可以得到答案.15.(2023上·上海徐汇·高一上海中学校考期末)设S ,T 是R 的两个非空子集,如果函数()y f x =满足:①(){}T f x x S =∈;②对任意1x ,2x S ∈,当12x x <时,恒有()()12f x f x <,那么称函数()y f x =为集合S 到集合T 的“保序同构函数”.(1)写出集合A =R 到集合{R ,B x x =∈且}0x >的一个保序同构函数(不需要证明);(2)求证:不存在从整数集Z 的到有理数集Q 的保序同构函数;(3)已知存在正实数s 和t 使得函数()21xf x x m =+-是集合[]0,s 到集合[]0,t 的保序同构函数,求实数m 的取值范围和s 的最大值(用m 表示).【答案】(1)()2xf x =(2)见解析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 上海重点中学2010学年第一学期期中考试 高三数学试卷(理科)
考生注意:本试卷共有20道试题,满分150分,考试时间120分钟 一.填空题(本大题满分40分)本大题共有10题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若3112nnCP,则正整数n的值为______10____.
2.函数31(0)xyx的反函数是 3log(1)(2)yxx . 3.记nxx)12(的展开式中第m项的系数为mb,若432bb,则n的值为_____5_____. 4.方程2cos2(lg16)2lg4x的解集为 {|,}6xxkkZ . 5.在平面直角坐标系xoy中,以ox轴为始边作两个锐角,,它们的终边分别与单位圆相
交于A、B两点,已知A、B的横坐标分别为225,105.则tan()的值为____3___. 6.已知函数21fxx,gxx,若存在Rx使fxbgx成立,则实数b的取值范围是__________(,0)(4,)__________. 7.不等式9log()10xx的解集是__________[1,0)___________.
8.已知函数34(2)()2(2)1xxfxxx,则当()1fx时,自变量x的取值范围是__________5(,1][,3]3_________. 9.已知函数2()4sin4cos1fxxxa,若关于x的方程()0fx在区间
324,
上有实数解,则实数a的取值范围是_______[4,5]________. 10.设fx是定义在R上的奇函数,且对于任意的xR,110fxfx恒成立,当0,1x时,2fxx.若方程fxax恰好有5个不同的解,则实数a的取值范围
是________222,375
_______. 2
二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,将代表答案的小方格涂黑,选对得5分,否则一律得零分. 11.若}|{},12|{2xyyNxyxM,则M,N两个集合的关系是( D ) A.{(1,1)}MN B.MN=Φ C.NM D.MN 12.“(5)0xx成立”是“14x成立”的( A ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件
13.在ABC中,,,abc分别是角,,ABC的对边,且2cos22Abcc,则ABC是( B )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰三角形或直角三角形 14.已知二次函数()()()fxxaxb(其中ab)的图像如下面右图所示,则函数()xgxab的图像是 ( A )
三.解答题(本大题满分90分)本大题共有6题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤. 15.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知集合}1|2||{xxA,集合}221|{xxxB,集合|1Cxaxa. (1)求A∪B; (2)若BC,求实数a的取值范围.
解:(1){||2|1}{|1Axxxx或3}x, „„„„„„„„2分
}221|{xxxB=}52xx „„„„„„„„4分 所以A∪B=}21{xxx或. „„„„„„„„6分 (2)因为BC,所以521aa或,„„„„„„„„„10分 因此实数a的取值范围是51aa或. „„„„„„„„„12分
16.(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分. 在ABC中,510cos,cos,2510ABAB.
f (x) 3
(1)求角C; (2)求ABC的面积. 解:(1)由5cos5A,10cos10B,得02AB、,,
所以23sinsin.510AB, „„„„4分 因为2coscos[()]cos()coscossinsin2CABABABAB,„6分 又0C, 故.4C „„„„ 8分 (2)根据正弦定理得sin6 sinsinsin10ABACABBACCBC, „„„„11分 所以ABC的面积为ABCS16sin.25ABACA „„„„14分 17.(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分. 已知函数2()2sincos23sin3444xxxfx. (1)求函数()fx的最小正周期及最值;
(2)令5π()3gxfx,判断函数()gx的奇偶性,并加以证明. 解:(1)2()sin3(12sin)24xxfxsin3cos22xxπ2sin23x. „4分 ()fx的最小正周期2π4π12T. „„„„„„6分
当πsin123x时,()fx取得最小值2;当πsin123x时,()fx取得最大值2. „„„„„„8分 (2)由(1)知π()2sin23xfx.又5π()3gxfx.
15πππ()2sin2sin23322xgxx
4
BC
DA
π2sin22x
2cos2x. „„„„„„11分
()2cos2cos()22
xxgxgx
. „„„„„„13分
函数()gx是偶函数. „„„„„„14分
18.(本题满分14分)本题共有2个小题,第1小题满分9分,第2小题满分5分. 现建造一条防洪堤,其断面为等腰梯形,腰与底边成角为060(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为36平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段与两腰长的和)要最小. (1)求外周长l的最小值,此时防洪堤高h为多少?
(2)如防洪堤的高限制在]32,3[范围内,则外周长l的最小应为多少米?
【解】(1)依题意有36)(21hBCAD,hBChBCAD33260cot20
所以hhBChBC3336),3322(21 „„„3分
所以 26363333660sin220hhhhhBCABl „„„6分 当hh363,即6h时等号成立. 所以外围的周长的最小值为26米,此时堤高6h米.------------9分 (2)由(1)知)6(3hhl, 因为函数)6(3hhl在]32,3[递增. „„„„„„11分 所以当3h时,min63(3)533l(米) „„13分 故外周长最小应为53米. „„14分
19.(本题满分18分)本题共有2个小题,第1小题满分10分,第2小题满分8分. 请认真阅读并思考以下五个命题: 5
①若函数)(xf的图像与其反函数)(1xf的图像存在公共点,则该公共点必在直线xy
上.
②函数1()21xfxm是奇函数的充要条件是12m. ③若定义在R上的函数()fx满足13()()22fxfx和(1)()fxfx,则函数()fx一定是偶函数. ④已知函数)(xf在(,)上是增函数,若Rba,,且0ab,则()()()(fafbfafb.
⑤设函数12)(xmxxf的图像关于直线xy对称,则函数)(xf在区间)1(,上是减函数. (1)请你将五个命题中真命题的序号全部选择出来,并选择其中一个加以证明; (2)请你将五个命题中假命题的序号全部选择出来,并选择其中一个加以证明. 解:(1)真命题的序号是③④⑤. „„3分 ③的证明:由(1)()fxfx得(1)()fxfx, ∴(2)[(1)1](1)[()]()fxfxfxfxfx.
又由13()()22fxfx得()(2)fxfx,∴()()fxfx,∴函数()fx是偶函数. 故命题③是真命题.
④的证明:因为)(xf在R上是增函数,且abba,所以)()()()(afbfbfaf. 同向相加得)()()()(bfafbfaf. 故命题④是真命题.
⑤的证明:由12)(xmxxf得mxxxf2)(1. 依题意知,函数)(xf与其反函数)(1xf是同一函数,∴1m. ∴12)(xxxf. 设则且,,),1(,2121xxxx1221121212223()()()011(1)(1)xxxxfxfxxxxx, ∴函数12)(xxxf在),1(上是减函数. 故命题⑤是真命题. „„10分
(2)假命题的序号是①②. „„12分 ①的证明:取xxf161)(,则xxf1611log)(.
