备战中考数学专题题库∶旋转的综合题附答案解析
2020年中考数学一轮专项复习——图形的旋转问题中考真题汇编(含详细解答)
2020年中考数学一轮专项复习——图形的旋转问题中考真题汇编一.选择题1.(2019•济南)下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是()A.赵爽弦图B.笛卡尔心形线C.科克曲线D.斐波那契螺旋线2.(2019•湘潭)如图,将△OAB绕点O逆时针旋转70°到△OCD的位置,若∠AOB =40°,则∠AOD=()A.45°B.40°C.35°D.30°3.(2019•大连)下列所述图形中,既是轴对称图形又是中心对称图形的是()A.等腰三角形B.等边三角形C.菱形D.平行四边形4.(2019•内江)如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A 顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为()A.1.6 B.1.8 C.2 D.2.6 5.(2019•河北)对于题目:“如图1,平面上,正方形内有一长为12、宽为6的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数n.”甲、乙、丙作了自认为边长最小的正方形,先求出该边长x,再取最小整数n.甲:如图2,思路是当x为矩形对角线长时就可移转过去;结果取n=13.乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取n=14.丙:如图4,思路是当x为矩形的长与宽之和的倍时就可移转过去;结果取n=13.下列正确的是()A.甲的思路错,他的n值对B.乙的思路和他的n值都对C.甲和丙的n值都对D.甲、乙的思路都错,而丙的思路对6.(2019•毕节市)下面摆放的图案,从第二个起,每个都是前一个按顺时针方向旋转90°得到,第2019个图案中箭头的指向是()A.上方B.右方C.下方D.左方7.(2019•孝感)如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P',则P'的坐标为()A.(3,2)B.(3,﹣1)C.(2,﹣3)D.(3,﹣2)8.(2019•荆门)如图,Rt△OCB的斜边在y轴上,OC=,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B',则B点的对应点B′的坐标是()A.(,﹣1)B.(1,﹣)C.(2,0)D.(,0)9.(2019•河南)如图,在△OAB中,顶点O(0,0),A(﹣3,4),B(3,4),将△OAB 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为()A.(10,3)B.(﹣3,10)C.(10,﹣3)D.(3,﹣10)10.(2019•贵港)若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n 的值是()A.1 B.3 C.5 D.7 11.(2019•宜昌)如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是()A.(﹣1,2+)B.(﹣,3)C.(﹣,2+) D.(﹣3,)12.(2019•张家界)如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019,那么点A2019的坐标是()A.(,﹣)B.(1,0)C.(﹣,﹣)D.(0,﹣1)13.(2019•呼和浩特)已知正方形的对称中心在坐标原点,顶点A、B、C、D按逆时针依次排列,若A点的坐标为(2,),则B点与D点的坐标分别为()A.(﹣2,),(2,﹣)B.(﹣,2),(,﹣2)C.(﹣,2),(2,﹣)D.(,)()14.(2019•荆州)在平面直角坐标系中,点A的坐标为(1,),以原点为中心,将点A 顺时针旋转30°得到点A',则点A'的坐标为()A.(,1)B.(,﹣1)C.(2,1)D.(0,2)15.(2019•青岛)如图,将线段AB先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A′B′,则点B的对应点B′的坐标是()A.(﹣4,1)B.(﹣1,2)C.(4,﹣1)D.(1,﹣2)16.(2019•舟山)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA'B'C',再作图形OA'B'C'关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是()A.(2,﹣1)B.(1,﹣2)C.(﹣2,1)D.(﹣2,﹣1)17.(2019•聊城)如图,在等腰直角三角形ABC中,∠BAC=90°,一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B,将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,下列结论中错误的是()A.AE+AF=AC B.∠BEO+∠OFC=180°C.OE+OF=BC D.S四边形AEOF=S△ABC 18.(2019•天津)如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是()A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC二.填空题19.(2019•营口)如图,△ABC是等边三角形,点D为BC边上一点,BD=DC=2,以点D为顶点作正方形DEFG,且DE=BC,连接AE,AG.若将正方形DEFG绕点D 旋转一周,当AE取最小值时,AG的长为.20.(2019•包头)如图,在△ABC中,∠CAB=55°,∠ABC=25°,在同一平面内,将△ABC绕A点逆时针旋转70°得到△ADE,连接EC,则tan∠DEC的值是.21.(2019•梧州)如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP 的长是.22.(2019•河池)如图,在平面直角坐标系中,A(2,0),B(0,1),AC由AB绕点A 顺时针旋转90°而得,则AC所在直线的解析式是.23.(2019•贺州)如图,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE 交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为.24.(2019•邵阳)如图,将等边△AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将等边△AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是.25.(2019•武汉)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE 与BC交于点P,可推出结论:PA+PC=PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=.点O是△MNG 内一点,则点O到△MNG三个顶点的距离和的最小值是.26.(2019•宿迁)如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB 边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为.27.(2019•随州)如图,在平面直角坐标系中,Rt△ABC的直角顶点C的坐标为(1,0),点A在x轴正半轴上,且AC=2.将△ABC先绕点C逆时针旋转90°,再向左平移3个单位,则变换后点A的对应点的坐标为.28.(2019•哈尔滨)如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为.29.(2019•海南)如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE,直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF,连结EF.若AB =3,AC=2,且α+β=∠B,则EF=.30.(2019•山西)如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC 内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为cm.三.解答题31.(2019•济南)小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(一)猜测探究在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC相等的角度,得到线段AN,连接NB.(1)如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;(2)如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(二)拓展应用如图3,在△A1B1C1中,A1B1=8,∠A1B1C1=60°,∠B1A1C1=75°,P是B1C1上的任意点,连接A1P,将A1P绕点A1按顺时针方向旋转75°,得到线段A1Q,连接B1Q.求线段B1Q长度的最小值.32.(2019•阜新)如图,△ABC在平面直角坐标系中,顶点的坐标分别为A(﹣4,4),B (﹣1,1),C(﹣1,4).(1)画出与△ABC关于y轴对称的△A1B1C1.(2)将△ABC绕点B逆时针旋转90°,得到△A2BC2,画两出△A2BC2.(3)求线段AB在旋转过程中扫过的图形面积.(结果保留π)33.在下面的网格中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣3,0),(﹣1,﹣1).(1)请在图中画出平面直角坐标系,并直接写出点A的坐标.(2)将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A′B'C′.(3)接写出在上述旋转过程中,点A所经过的路径长.34.如图1,在Rt△ABC中,∠ACB=90°,∠B=30°,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且PC<BC,连接MP交AC于点H.将射线MP绕点M逆时针旋转60°交线段CA的延长线于点D.(1)找出与∠AMP相等的角,并说明理由.(2)如图2,CP=BC,求的值.(3)在(2)的条件下,若MD=,求线段AB的长.35.(2019•日照)如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上,AG=CH,直线GH绕点O逆时针旋转α角,与边AB、CD分别相交于点E、F(点E不与点A、B重合).(1)求证:四边形EHFG是平行四边形;(2)若∠α=90°,AB=9,AD=3,求AE的长.36.(2019•遵义)将在同一平面内如图放置的两块三角板绕公共顶点A旋转,连接BC,DE.探究S△ABC与S△ADE的比是否为定值.(1)两块三角板是完全相同的等腰直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图①)(2)一块是等腰直角三角板,另一块是含有30°角的直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图②)(3)两块三角板中,∠BAE+∠CAD=180°,AB=a,AE=b,AC=m,AD=n(a,b,m,n为常数),S△ABC:S△ADE是否为定值?如果是,用含a,b,m,n的式子表示此定值(直接写出结论,不写推理过程),如果不是,说明理由.(图③)37.(2019•辽阳)如图1,△ABC(AC<BC<AC)绕点C顺时针旋转得△DEC,射线AB交射线DE于点F.(1)∠AFD与∠BCE的关系是;(2)如图2,当旋转角为60°时,点D,点B与线段AC的中点O恰好在同一直线上,延长DO至点G,使OG=OD,连接GC.①∠AFD与∠GCD的关系是,请说明理由;②如图3,连接AE,BE,若∠ACB=45°,CE=4,求线段AE的长度.38.(2019•本溪)在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系:;(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.①如图b,猜想并证明线段OM和线段ON之间的数量关系;②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).参考答案一.选择题1.解:A、不是轴对称图形,是中心对称图形,故此选项错误;B、是轴对称图形,不是中心对称图形,故此选项错误;C、是轴对称图形,是中心对称图形,故此选项正确;D、不是轴对称图形,不是中心对称图形,故此选项错误;故选:C.2.解:∵△OAB绕点O逆时针旋转70°到△OCD的位置,∴∠BOD=70°,而∠AOB=40°,∴∠AOD=70°﹣40°=30°.故选:D.3.解:A、等腰三角形是轴对称图形,不是中心对称图形,故本选项错误;B、等边三角形是轴对称图形,不是中心对称图形,故本选项错误;C、菱形既是轴对称图形,又是中心对称图形,故本选项正确;D、平行四边形不是轴对称图形,是中心对称图形,故本选项错误.故选:C.4.解:由旋转的性质可知,AD=AB,∵∠B=60°,AD=AB,∴△ADB为等边三角形,∴BD=AB=2,∴CD=CB﹣BD=1.6,故选:A.5.解:甲的思路正确,长方形对角线最长,只要对角线能通过就可以,但是计算错误,应为n=14;乙的思路与计算都正确;丙的思路与计算都错误,图示情况不是最长;故选:B.6.解:如图所示:每次旋转4个图形为一个周期,2019÷4=504…3,则第2019个图案中箭头的指向与第3个图案方向一致,箭头的指向是下方.故选:C.7.解:作PQ⊥y轴于Q,如图,∵P(2,3),∴PQ=2,OQ=3,∵点P(2,3)绕原点O顺时针旋转90°得到点P'相当于把△OPQ绕原点O顺时针旋转90°得到△OP'Q′,∴∠P′Q′O=90°,∠QOQ′=90°,P′Q′=PQ=2,OQ′=OQ=3,∴点P′的坐标为(3,﹣2).故选:D.8.解:如图,在Rt△OCB中,∵∠BOC=30°,∴BC=OC=×=1,∵Rt△OCB绕原点顺时针旋转120°后得到△OC′B',∴OC′=OC=,B′C′=BC=1,∠B′C′O=∠BCO=90°,∴点B′的坐标为(,﹣1).故选:A.9.解:∵A(﹣3,4),B(3,4),∴AB=3+3=6,∵四边形ABCD为正方形,∴AD=AB=6,∴D(﹣3,10),∵70=4×17+2,∴每4次一个循环,第70次旋转结束时,相当于△OAB与正方形ABCD组成的图形绕点O顺时针旋转2次,每次旋转90°,∴点D的坐标为(3,﹣10).故选:D.10.解:∵点P(m﹣1,5)与点Q(3,2﹣n)关于原点对称,∴m﹣1=﹣3,2﹣n=﹣5,解得:m=﹣2,n=7,则m+n=﹣2+7=5.故选:C.11.解:如图,作B′H⊥y轴于H.由题意:OA′=A′B′=2,∠B′A′H=60°,∴∠A′B′H=30°,∴AH′=A′B′=1,B′H=,∴OH=3,∴B′(﹣,3),故选:B.12.解:∵四边形OABC是正方形,且OA=1,∴A(0,1),∵将正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1,∴A1(,),A2(1,0),A3(,﹣),…,发现是8次一循环,所以2019÷8=252 (3)∴点A2019的坐标为(,﹣)故选:A.13.解:如图,连接OA、OD,过点A作AF⊥x轴于点F,过点D作DE⊥x轴于点E,易证△AFO≌△OED(AAS),∴OE=AF=,DE=OF=2,∴D(,﹣2),∵B、D关于原点对称,∴B(﹣,2),故选:B.14.解:如图,作AE⊥x轴于E,A′F⊥x轴于F.∵∠AEO=∠OFA′=90°,∠AOE=∠AOA′=∠A′OF=30°∴∠AOE=∠A′,∵OA=OA′,∴△AOE≌△A′OF(AAS),∴OF=OE=,A′F=AE=1,∴A′(,1).故选:A.15.解:将线段AB先向右平移5个单位,点B(2,1),连接OB,顺时针旋转90°,则B'对应坐标为(1,﹣2),故选:D.16.解:∵点C的坐标为(2,1),∴点C′的坐标为(﹣2,1),∴点C″的坐标的坐标为(2,﹣1),故选:A.17.解:连接AO,如图所示.∵△ABC为等腰直角三角形,点O为BC的中点,∴OA=OC,∠AOC=90°,∠BAO=∠ACO=45°.∵∠EOA+∠AOF=∠EOF=90°,∠AOF+∠FOC=∠AOC=90°,∴∠EOA=∠FOC.在△EOA和△FOC中,,∴△EOA≌△FOC(ASA),∴EA=FC,∴AE+AF=AF+FC=AC,选项A正确;∵∠B+∠BEO+∠EOB=∠FOC+∠C+∠OFC=180°,∠B+∠C=90°,∠EOB+∠FOC=180°﹣∠EOF=90°,∴∠BEO+∠OFC=180°,选项B正确;∵△EOA≌△FOC,∴S△EOA=S△FOC,∴S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=S△ABC,选项D正确.故选:C.18.解:∵将△ABC绕点C顺时针旋转得到△DEC,∴AC=CD,BC=CE,AB=DE,故A错误,C错误;∴∠ACD=∠BCE,∴∠A=∠ADC=,∠CBE=,∴∠A=∠EBC,故D正确;∵∠A+∠ABC不一定等于90°,∴∠ABC+∠CBE不一定等于90°,故B错误故选:D.二.填空题(共12小题)19.解:过点A作AM⊥BC于M,∵BD=DC=2,∴DC=4,∴BC=BD+DC=2+4=6,∵△ABC是等边三角形,∴AB=AC=BC=6,∵AM⊥BC,∴BM=BC=×6=3,∴DM=BM﹣BD=3﹣2=1,在Rt△ABM中,AM===3,当点E在DA延长线上时,AE=DE﹣AD.此时AE取最小值,在Rt△ADM中,AD===2,∴在Rt△ADG中,AG===8;故答案为:8.20.解:由旋转的性质可知:AE=AC,∠CAE=70°,∴∠ACE=∠AEC=55°,又∵∠AED=∠ACB,∠CAB=55°,∠ABC=25°,∴∠ACB=∠AED=100°,∴∠DEC=100°﹣55°=45°,∴tan∠DEC=tan45°=1,故答案为:121.解:连接BD交AC于O,如图所示:∵四边形ABCD是菱形,∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,∴OB=AB=1,∴OA=OB=,∴AC=2,由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,∴CE=AC﹣AE=2﹣2,∵四边形AEFG是菱形,∴EF∥AG,∴∠CEP=∠EAG=60°,∴∠CEP+∠ACD=90°,∴∠CPE=90°,∴PE=CE=﹣1,PC=PE=3﹣,∴DP=CD﹣PC=2﹣(3﹣)=﹣1;故答案为:﹣1.22.解:∵A(2,0),B(0,1)∴OA=2,OB=1过点C作CD⊥x轴于点D,则易知△ACD≌△BAO(AAS)∴AD=OB=1,CD=OA=2∴C(3,2)设直线AC的解析式为y=kx+b,将点A,点C坐标代入得∴∴直线AC的解析式为y=2x﹣4.故答案为:y=2x﹣4.23.解:作FM⊥AD于M,FN⊥AG于N,如图,易得四边形CFMD为矩形,则FM=4,∵正方形ABCD的边长为4,点E是CD的中点,∴DE=2,∴AE==2,∵△ADE绕点A顺时针旋转90°得△ABG,∴AG=AE=2,BG=DE=2,∠3=∠4,∠GAE=90°,∠ABG=∠D=90°,而∠ABC=90°,∴点G在CB的延长线上,∵AF平分∠BAE交BC于点F,∴∠1=∠2,∴∠2+∠4=∠1+∠3,即FA平分∠GAD,∴FN=FM=4,∵AB•GF=FN•AG,∴GF==2,∴CF=CG﹣GF=4+2﹣2=6﹣2.故答案为6﹣2.24.解:作BH⊥y轴于H,如图,∵△OAB为等边三角形,∴OH=AH=2,∠BOA=60°,∴BH=OH=2,∴B点坐标为(2,2),∵等边△AOB绕点O顺时针旋转180°得到△A′OB′,∴点B′的坐标是(﹣2,﹣2).故答案为(﹣2,﹣2).25.(1)证明:如图1,在BC上截取BG=PD,在△ABG和△ADP中,∴△ABG≌△ADP(SAS),∴AG=AP,BG=DP,∴GC=PE,∵∠GAP=∠BAD=60°,∴△AGP是等边三角形,∴AP=GP,∴PA+PC=GP+PC=GC=PE∴PA+PC=PE;(2)解:如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,∴∠GMO=∠DME在△GMO和△DME中∴△GMO≌△DME(SAS),∴OG=DE∴NO+GO+MO=DE+OE+NO∴当D、E、O、M四点共线时,NO+GO+MO值最小,∵∠NMG=75°,∠GMD=60°,∴∠NMD=135°,∴∠DMF=45°,∵MG=.∴MF=DF=4,∴NF=MN+MF=6+4=10,∴ND===2,∴MO+NO+GO最小值为2,故答案为2,26.解:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动将△EFB绕点E旋转60°,使EF与EG重合,得到△EFB≌△EHG从而可知△EBH为等边三角形,点G在垂直于HE的直线HN上作CM⊥HN,则CM即为CG的最小值作EP⊥CM,可知四边形HEPM为矩形,则CM=MP+CP=HE+EC=1+=故答案为.27.解:∵点C的坐标为(1,0),AC=2,∴点A的坐标为(3,0),如图所示,将Rt△ABC先绕点C逆时针旋转90°,则点A′的坐标为(1,2),再向左平移3个单位长度,则变换后点A′的对应点坐标为(﹣2,2),故答案为:(﹣2,2).28.解:∵将△ABC绕点C逆时针旋转得到△A′B′C,∴AC=A'C=3,∠ACB=∠ACA'=45°∴∠A'CB=90°∴A'B==故答案为29.解:由旋转的性质可得AE=AB=3,AC=AF=2,∵∠B+∠BAC=90°,且α+β=∠B,∴∠BAC+α+β=90°∴∠EAF=90°∴EF==故答案为:30.解:过点A作AG⊥DE于点G,由旋转知:AD=AE,∠DAE=90°,∠CAE=∠BAD=15°,∴∠AED=∠ADG=45°,在△AEF中,∠AFD=∠AED+∠CAE=60°,在Rt△ADG中,AG=DG==3cm,在Rt△AFG中,GF==cm,AF=2FG=2cm,∴CF=AC﹣AF=(10﹣2)cm,故答案为:(10﹣2)cm.三.解答题(共8小题)31.解:(一)(1)结论:∠NAB=∠MAC,BN=MC.理由:如图1中,∵∠MAN=∠CAB,∴∠NAB+∠BAM=∠BAM+∠MAC,∴∠NAB=∠MAC,∵AB=AC,AN=AM,∴△NAB≌△MAC(SAS),∴BN=CM.故答案为∠NAB=∠MAC,BN=CM.(2)如图2中,①中结论仍然成立.理由:∵∠MAN=∠CAB,∴∠NAB+∠BAM=∠BAM+∠MAC,∴∠NAB=∠MAC,∵AB=AC,AN=AM,∴△NAB≌△MAC(SAS),∴BN=CM.(二)如图3中,在A1C1上截取A1N=A1B1,连接PN,作NH⊥B1C1于H,作A1M⊥B1C1于M.∵∠C1A1B1=∠PA1Q,∴∠QA1B1=∠PA1N,∵A1A=A1P,A1B1=AN,∴△QA1B1≌△PA1N(SAS),∴B1Q=PN,∴当PN的值最小时,QB1的值最小,在Rt△A1B1M中,∵∠A1B1M=60°,A1B1=8,∴A1M=A1B1•sin60°=4,∵∠MA1C1=∠B1A1C1﹣∠B1A1M=75°﹣30°=45°,∴A 1C1=4,∴NC 1=A1C1﹣A1N=4﹣8,在Rt△NHC1,∵∠C1=45°,∴NH=4﹣4,根据垂线段最短可知,当点P与H重合时,PN的值最小,∴QB1的最小值为4﹣4.32.解:(1)如图,△A l B1C1为所作;(2)如图,△A2BC2为所作;(3)AB==3,所以线段AB在旋转过程中扫过的图形面积==π.33.解:(1)如图,A点坐标为(﹣2,3);(2)如图,△A′B′C′为所作;(2)如图,OA==,所以点A所经过的路径长==π.△A2B2C2为所作;点A2的坐标为(﹣1,﹣1).34.解:(1)∠D=∠AMP.理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°.∴∠D+∠DMA=60°.由旋转的性质知,∠DMA+∠AMP=60°.∴∠D=∠AMP;(2)如图,过点C作CG∥BA交MP于点G.∴∠GCP=∠B=30°,∠BCG=150°.∵∠ACB=90°,点M是AB的中点,∴CM=AB=BM=AM.∴∠MCB=∠B=30°.∴∠MCG=120°.∵∠MAD=180°﹣60°=120°.∴∠MAD=∠MCG.∵∠DMG﹣∠AMG=∠AMC﹣∠AMG,∴∠DMA=∠GMC.在△MDA与△MGC中,∴△MDA≌△MGC(ASA).∴AD=CG.∵CP=BC.∴CP=BP.∵CG∥BM,∴△CGP∽△BMP.∴==.设CG=AD=t,则BM=3t,AB=6t.在Rt△ABC中,cos B==.∴BC=3t.∴==;(3)如图,由(2)知△CGP∽△BMP.则MD=MG=.∵CG∥MA.∴∠CGH=∠AMH.∵∠GHC=∠MHA,∴△GHC∽△MHA.∴===.∴HG=MG=×=.∴MH=﹣=.由(2)知,CG=AD=t,则BM=AM=CA=3t.∴CH=t,AH=t.∵∠MHA=∠DHM,∠HMA=∠D.∴△MHA∽△DHM.∴=.∴MH2=AH•DH,即()2=t t.解得t1=,t2=﹣(舍去).∴AB=6t=2.35.证明:(1)∵对角线AC的中点为O∴AO=CO,且AG=CH∴GO=HO∵四边形ABCD是矩形∴AD=BC,CD=AB,CD∥AB∴∠DCA=∠CAB,且CO=AO,∠FOC=∠EOA ∴△COF≌△AOE(ASA)∴FO=EO,且GO=HO∴四边形EHFG是平行四边形;(2)如图,连接CE∵∠α=90°,∴EF⊥AC,且AO=CO∴EF是AC的垂直平分线,∴AE=CE,在Rt△BCE中,CE2=BC2+BE2,∴AE2=(9﹣AE)2+9,∴AE=536.解:(1)结论:S△ABC:S△ADE=定值.理由:如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.∵∠BAE=∠CAD=90°,∴∠BAC+∠EAD=180°,∠BAC+∠CAG=180°,∴∠DAE=∠CAG,∵AB=AE=AD=AC,∴==1.(2)如图2中,S△ABC:S△ADE=定值.理由:如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.不妨设∠ADC=30°,则AD=AC,AE=AB,∵∠BAE=∠CAD=90°,∴∠BAC+∠EAD=180°,∠BAC+∠CAG=180°,∴∠DAE=∠CAG,∴==.(3)如图3中,如图2中,S△ABC:S△ADE=定值.理由:如图1中,作DH⊥AE于H,CG⊥BA交BA的延长线于G.∵∠BAE+∠CAD=180°,∴∠BAC+∠EAD=180°,∠BAC+∠CAG=180°,∴∠DAE=∠CAG,∵AB=a,AE=b,AC=m,AD=n∴==.37.解:(1)如图1,AF与CD的交点记作点N,由旋转知,∠ACB=∠DCE,∠A=∠D,∴∠BCE=∠ACD,∵∠ACD=180°﹣∠A﹣∠ANC,∠AFD=180°﹣∠D﹣∠DNF,∠ANC=∠DNF,∴∠ACD=∠AFD,∴∠AFD=∠BCE,故答案为:∠AFD=∠BCE;(2)①∠AFD=∠GCD或∠AFD+∠GCD=180°,理由:如图2,连接AD,由旋转知,∠CAB=∠CDE,CA=CD,∠ACD=60°,∴△ACD是等边三角形,∴AD=CD,∵∠AMC=∠DMF,∴△ACM∽△DFM,∴∠ACD=∠AFD,∵O是AC的中点,∴AO=CO,∵OD=OG,∠AOD=∠COG,∴△AOD≌△COG(SAS),∴AD=CG,∴CG=CD,∴∠GCD=2∠ACD=120°,∴∠AFD=∠GCD或∠AFD+∠GCD=180°,故答案为:∠AFD=∠GCD或∠AFD+∠GCD=180°;②由①知,∠GCD=120°,∠ACD=∠BCE=60°,∴∠GCA=∠GCD﹣∠ACD=60°,∴∠GCA=∠BCE,∵∠GCB=∠GCA+∠ACB,∠ACE=∠BCE+∠ACB,∴∠GCB=∠ACE,由①知,CG=CD,CD=CA,∴CG=CA,∵BC=EC=4,∴△GCB≌△ACE(SAS),∴BC=CE=4,∴GB=AE,∵CG=CD,OG=OD,∴CO⊥GD,∴∠COG=∠COB=90°在Rt△BOC中,BO=BC•sin∠ACB=2,CO=BC•cos∠ACB=2,在Rt△GOC中,GO=CO•tan∠GCA=2,∴GB=CO+BO=2+2,∴AE=2+2.38.解:(1)结论:∠ECO=∠OAC.理由:如图1中,连接OE.∵∠BCD=90°,BE=ED,BO=OA,∵CE=ED=EB=BD,CO=OA=OB,∴∠OCA=∠A,∵BE=ED,BO=OA,∴OE∥AD,OE=AD,∴CE=EO.∴∠EOC=∠OCA=∠ECO,∴∠ECO=∠OAC.故答案为:∠OCE=∠OAC.(2)如图2中,∵OC=OA,DA=DB,∴∠A=∠OCA=∠ABD,∴∠COA=∠ADB,∵∠MON=∠ADB,∴∠AOC=∠MON,∴∠COM=∠AON,∵∠ECO=∠OAC,∴∠MCO=∠NAO,∵OC=OA,∴△COM≌△AON(ASA),∴OM=ON.②如图3﹣1中,当点N在CA的延长线上时,∵∠CAB=30°=∠OAN+∠ANO,∠AON=15°,∴∠AON=∠ANO=15°,∴OA=AN=m,∵△OCM≌△OAN,∴CM=AN=m,在Rt△BCD中,∵BC=m,∠CDB=60°,∴BD=m,∵BE=ED,∴CE=BD=m,∴EM=CM+CE=m+m.如图3﹣2中,当点N在线段AC上时,作OH⊥AC于H.∵∠AON=15°,∠CAB=30°,∴∠ONH=15°+30°=45°,∴OH=HN=m,∵AH=m,∴CM=AN=m﹣m,∵EC=m,∴EM=EC﹣CM=m﹣(m﹣m)=m﹣m,综上所述,满足条件的EM的值为m+m或m﹣m.。
中考数学压轴题之旋转(中考题型整理,突破提升)及详细答案

在△ DAG 与△ DCG 中, ∵ AD=CD,∠ ADG=∠ CDG,DG=DG, ∴ △ DAG≌ △ DCG. ∴ AG=CG. 在△ DMG 与△ FNG 中, ∵ ∠ DGM=∠ FGN,FG=DG,∠ MDG=∠ NFG, ∴ △ DMG≌ △ FNG. ∴ MG=NG 在矩形 AENM 中,AM=EN. 在 Rt△ AMG 与 Rt△ ENG 中, ∵ AM=EN, MG=NG, ∴ △ AMG≌ △ ENG. ∴ AG=EG ∴ EG=CG. (3)(1)中的结论仍然成立.
4.如图(1)所示,将一个腰长为 2 等腰直角△ BCD 和直角边长为 2、宽为 1 的直角△ CED 拼在一起.现将△ CED 绕点 C 顺时针旋转至△ CE’D’,旋转角为 a. (1)如图(2),旋转角 a=30°时,点 D′到 CD 边的距离 D’A=______.求证:四边形 ACED′ 为矩形; (2)如图(1),△ CED 绕点 C 顺时针旋转一周的过程中,在 BC 上如何取点 G,使得 GD’=E’D;并说明理由.
【答案】(1)详见解析;(2)FE·sin( -90°) 【解析】 【分析】 (1)由四边形 ABCD 是平行四边形得 AF∥ BE,所以∠ FAE=∠ BEA,由折叠的性质得 ∠ BAE=∠ FAE,∠ BEA=∠ FEA,所以∠ BAE=∠ FEA,故有 AB∥ FE,因此四边形 ABEF 是平行四 边形,又 BE=EF,因此可得结论; (2)根据点 M 在线段 BE 上和 EC 上两种情况证明∠ ENG=90°- ,利用菱形的性质得到
备考2019年中考数学考点过关练习:图形的旋转综合(含答案)

备考2019年中考数学考点过关练习:图形的旋转综合一.选择题1.如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数为()A.55°B.75°C.85°D.90°2.下列图形:①平行四边形;②矩形;③菱形;④等边三角形中,是中心对称图形的有()A.①②③B.②③④C.①②④D.①②③④3.如图,在△ABC中,∠C=20°,将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC 交于点F,则∠AFB的度数是()A.60°B.70°C.80°D.90°4.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有()个是正确的.①∠DAF=45°②△ABE≌△ACD③AD平分∠EDF④BE2+DC2=DE2A.4B.3C.2D.15.如图,在等腰直角△ABC中,∠ACB=90°,D为△ABC内一点,将线段CD绕点C逆时针旋转90°后得到CE,连接BE,若∠DAB=10°,则∠ABE是()A.75°B.78°C.80°D.92°6.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△ABC,M是BC 的中点,P是A’B’的中点,连接PM.若BC=4,∠BAC=30°,则线段PM的最大值是()A.8B.6C.4D.5),C(﹣2,0).将△7.在平面直角坐标系xOy中,点O(0,0),A(2,0),B(0,OAB绕点O顺时针旋转α(0°<α<360°)得到△OA′B′((其中点A旋转到点A′的位置),设直线AA′与直线BB′相交于点P,则线段CP长的最小值是()A.B.C.2D.8.如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF的长为()A.B.C.D.9.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=116°,则∠α的大小是()A .64°B .36°C .26°D .22°10.如图①,正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的,如图②,移动正方形A 的位置,使正方形B 的一个顶点与正方形A 的对称中心重合,则重叠部分面积是正方形B 面积的()A .二.填空题B .C .D .11.如图,△ABC 为等边三角形,D 是△ABC 内一点,将△ABD 绕点A 按逆时针方向旋转到△ACP 位置,则∠PAD =°.12.如图,在△ABC 中,∠C =90°,AC =3cm ,AB =5cm ,将△ABC 绕点B 顺时针旋转60°得到△FBE ,则点E 与点C 之间的距离是cm .13.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C顺时针旋转得到△A'B'C,D是A'B'的中点,连接BD,若BC=2,∠ABC=60°,则线段BD的最大值为.14.如图,将矩形ABCD绕点B顺时针旋转90°至EBGF的位置,连接AC,EG,取AC,EG 的中点M,N连接MN,若AB=8,BC=6,则MN=.15.如图,将△ABC的边AB绕着点A顺时针旋转α(0°<α<90°)得到AB′,边AC绕着点A逆时针旋转β(0°<β<90°)得到AC′,联结B′C′,当α+β=60°时,我们称△AB′C′是△ABC的“双旋三角形”,如果等边△ABC的边长为a,那么它所得的“双旋三角形”中B′C′=(用含a的代数式表示).16.如图,正方形ABCD的边长为,点E是正方形ABCD内一点,将△BCE绕着点C顺时针旋转90°,点E的对应点F和点B,E三点在一条直线上,BF与对角线AC相交于点G,若DF=6,则GF的长为.17.如图,AB =AC ,∠CAB =90°,∠ADC =45°,AD =1,CD =3,则BD =.18.在平面直角坐标系中,点P (x ,y )经过某种变换后得到点P '(﹣y +1,x +2),我们把点P '(﹣y +1,x +2)叫做点P (x ,y )的终结点.已知点P 1的终结点为P 2,点P 2的终结点为P 3,点P 3的终结点为P 4,这样依次得到P 1、P 2、P 3、P 4、…P n 、…,若点P 1的坐标为(2,0),则点P 2019的坐标为.19.如图,将△ABC 的边AB 绕着点A 顺时针旋转α(0°<α<90°)得到AB ′,边AC 绕着点A 逆时针旋转β(0°<β<90°)得到AC ,连接B ′C ′,当α+β=60°时,我们称△AB ′C ’是△ABC 的“双展三角形”,已知一直角边长为2的等腰直角三角形,那么它的“双展三角形”的面积为.20.如图,将△ABC 绕点C 顺时针旋转90°得到△EDC ,若点A 、D 、E 在同一条直线上,∠ACD =70°,则∠EDC 的度数是.三.解答题21.将一副三角尺的直角重合放置(∠B =30°,∠C =45°),如图1所示,(1)图1中∠BEC 的度数为;(2)三角尺AOB 的位置保持不动,将三角尺COD 绕其直角顶点O 顺时针方向旋转:①当旋转至图2所示位置时,恰好OD ∥AB ,求此时∠AOC 的大小;②若将三角尺COD 继续绕O 旋转,直至回到图1位置,在这一过程中,是否会存在△COD 其中一边能与AB 平行?如果存在,请你画出图形,并直接写出相应的∠AOC 的大小;如果不存在,请说明理由.22.在四边形ABCD 中,AB ∥CD ,∠ABC =60°,AB =BC =4,CD =3.(1)如图1,求△BCD 的面积;(2)如图2,M 是CD 边上一点,将线段BM 绕点B 逆时针旋转60°,可得线段BN ,过点N 作NQ ⊥BC ,垂足为Q ,设NQ =n ,BQ =m ,求n 关于m 的函数解析式.(自变量m 的取值范围只需直接写出)23.如图,将一个直角三角形纸片AOB ,放置在平面直角坐标系中,点A (3,3),点B (3,0),点O (0,0),将△AOB 沿OA 翻折得到△AOD (点D 为点B 的对应点).(Ⅰ)求OA 的长及点D 的坐标:(Ⅱ)点P 是线段OD 上的点,点Q 是线段AD 上的点.①已知OP =1,AQ =,R 是x 轴上的动点,当PR +QR 取最小值时,求出点R 的坐标及点D 到直线RQ 的距离;②连接BP ,BQ ,且∠PBQ =45°,现将△OAB 沿AB 翻折得到△EAB (点E 为点O 的对应点),再将∠PBQ 绕点B 顺时针旋转,旋转过程中,射线BP ,BQ 交直线AE 分别为点M ,N ,最后将△BMN 沿BN 翻折得到△BGN (点G 为点M 的对应点),连接EG ,若的坐标(直接写出结果即可).,求点M24.如图,把直角三角形ABC 按逆时针方向旋转到△EBD 的位置,使得A 、B 、D 三点在一直线上.(1)旋转中心是哪一点?旋转角是多少度?(2)AC 与DE 的位置关系怎样?请说明理由.25.将一副直角三角尺按图1摆放,其中∠C =90°,∠EDF =90°,∠B =60°,∠F =45°,等腰直角三角尺的直角边DF 恰好垂直平分AB ,与AC 相交于点G ,BC =4(1)求DG 的长;(2)如图2.将△DEF 绕点D 按顺时针方向旋转,直角边DF 经过点C ,另一直角边DE 与AC 相交于点H ,分别过点H ,D 作AB ,BC 的垂线,垂足分别为点M ,N .猜想HM 与CN 之间的数量关系,并证明;(3)如图3,在旋转的过程中,若△DEF 两边DE ,DF 与△ABC 两边AC ,BC 分别交于K 、cm .T 两点,则KT 的最小值为.26.如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.(1)判断A E、BE、BC之间的数量关系(直接写出结果,不必证明);(2)如图2,过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角a(0°<a<<144°)得到△AE'F',连结CE',BF′,求证:CE'=BF':(3)在(2)的旋转过程中,当a=时,CE'∥AB?(请直接写出结果).27.如图,将等边△ABC绕点C顺时针旋转90°得到△EFC,∠ACE的平分线CD交EF于点D,连接AD、AF.(1)求∠CFA度数;(2)求证:AD∥BC.28.如图1,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转,得到△ADE,旋转角为α(0°<α<90°),连接BD交CE于点F.(1)如图2,当α=45°时,求证:CF=EF;(2)在旋转过程中,①问(1)中的结论是否仍然成立?证明你的结论;②连接CD,当△CDF为等腰直角三角形时,求tan的值.29.综合与实践数学活动:在综合与实践活动课上,老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动,探究线段长度的有关问题.动手操作:如图1,在直角三角形纸片ABC中,∠BAC=90°,AB=6,AC=8.将三角形纸片ABC进行以下操作:第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;第二步:将△ABC沿折痕DE展开,然后将△DEC绕点D逆时针方向旋转得到△DFG,点E,C的对应点分别是点F,G,射线GF与边AC交于点M(点M不与点A重合),与边AB交于点N,线段DG与边AC交于点P.数学思考:(1)求DC的长;(2)在△DEC绕点D旋转的过程中,试判断MF与ME的数量关系,并证明你的结论;问题解决:(3)在△DEC绕点D旋转的过程中,探究下列问题:①如图2,当GF∥BC时,求AM的长;②如图3,当GF经过点B时,AM的长为;③当△DEC绕点D旋转至DE平分∠FDG的位置时,试在图4中作出此时的△DFG和射线GF,并直接写出AM的长.(要求:尺规作图,不写作法,保留作图痕迹,标记出所有相应的字母)30.如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD、CE的交点.(1)判断线段BD与CE的关系,并证明你的结论;(2)若AB=8,AD=4,把△ADE绕点A旋转,①当∠EAC=90°时,求PB的长;②求旋转过程中线段PB长的最大值.参考答案一.选择题1.解:根据旋转的性质可知:∠C=∠A=110°,在△COD中,∠COD=180°﹣110°﹣40°=30°.旋转角∠AOC=85°,所以∠α=85°﹣30°=55°.故选:A.2.解:平行四边形,矩形,菱形是中心对称图形.故选:A.3.解:∵△ABC绕点A顺时针旋转60°得△ADE,∴∠CAE=60°,∵∠C=20°,∴∠AFC=100°,∴∠AFB=80°.故选:C.4.解:由旋转可知:△BAE≌△CAF,∴∠BAE=∠CAF,∴∠EAF=∠BAC=90°,∵∠EAD=45°,∴∠EAD=∠FAD=45°,∴AD平分∠EAF,∵AD=AD,AE=AF,∴△DAE≌△DAF(SAS),故①③正确,∴DE=DF,∵∠ACF∠B=∠ACB=45°,∴∠DCF=90°,∴DF2=CD2+CF2,∵DF=DE,BE=CF,∴BE2+CD2=DE2,故④正确,无法判断△ABE≌△ACD,故②错误.故选:B.5.解:∵△ABC是等腰直角三角形,∴∠ABC=∠BAC=45°.∴∠DAC=45°﹣10°=35°.在△BEC和△ADC中∴△BCE≌△ACD(SAS).∴∠EBC=∠DAC=35°.∴∠ABE=∠EBC+∠DAC=80°.故选:C.6.解:如图连接PC.在Rt△ABC中,∵∠A=30°,BC=4,∴AB=8,根据旋转不变性可知,A′B′=AB=8,∴A′P=PB′,∴PC=A′B′=4,∵CM=BM=2,又∵PM≤PC+CM,即PM≤6,∴PM的最大值为3(此时P、C、M共线).故选:B.7.解:∵△OAB是直角三角形,点P在以AB为直径的圆上运动,∵A(2,0),B(0,),∴AB=4,AB的中点为(1,),∵C(﹣2,0),∴CP的最小值为2故选:B.8.解:如图,连接BE,CE,过E作EG⊥BC于G,由旋转可得,AB=AE=1=AD,AC=AF,∠BAC=∠EAF=45°=∠DAC,∴∠CAE=∠FAD,∴△ADF≌△AEC(SAS),∴DF=CE,由旋转可得,AB=AE=1,∠BAE=60°,∴△ABE是等边三角形,∴BE=1,∠ABE=60°,∴∠EBG=30°,∴EG=BE=,BG=∴CG=1﹣∴Rt△CEG,中,CE====,﹣2;==,∴DF=故选:A.,9.解:如图设BC交C′D′于K.在四边形ABKD ′中,∵∠B =∠D ′=90°,∠BKD ′=∠1=116°,∴∠BAD ′=180°﹣116°=64°,∵∠BAD =90°,∴∠DAD ′=90°﹣64°=26°,故选:C .10.解:设正方形B 对角线的交点为O ,如图1,设正方过点O 作边的垂线,则OE =OM ,∠EOM =90°,∵∠EOF +∠EON =90°,∠MON +∠EON =90°,∴∠EOF =∠MON ,在△OEF 和△OMN 中,∴△OEF ≌△OMN (ASA ),∴阴影部分的面积=S 四边形NOEP +S △OEF =S 四边形NOEP +S △OMN =S 四边形MOEP =S 正方形CTKW ,即图1中阴影部分的面积=正方形B 的面积的四分之一,同理图2中阴影部分烦人面积=正方形A 的面积的四分之一,∵图①,正方形A 的一个顶点与正方形B 的对称中心重合,重叠部分面积是正方形A 面积的,∴正方形B 的面积=正方形A 的面积的2倍,∴图2中重叠部分面积是正方形B 面积的,故选:D .二.填空题(共10小题)11.解:∵△ABC 为等边三角形,∴∠BAC =60°,∵将△ABD 绕点A 按逆时针方向旋转到△ACP ,∴∠DAP =∠BAC =60°,故答案为:60.12.解:连接EC ,即线段EC 的长是点E 与点C 之间的距离,在Rt △ACB 中,由勾股定理得:BC =∵将△ABC 绕点B 顺时针旋转60°得到△FBE ,∴BC =BE ,∠CBE =60°,∴△BEC 是等边三角形,∴EC =BE =BC =4cm ,故答案为:4.13.解:连接CD ,==4(cm ),在Rt △ABC 中,∵∠ACB =90°,BC =2,∠ABC =60°,∴∠A =30°,∴AB =A ′B ′=2BC =4,∵DB ′=DA ′,∴CD =A ′B ′=2,∴BD ≤CD +CB =4,∴BD 的最大值为4,14.解:连接BM、BN,在Rt△ABC中,利用勾股定理可得AC=10,∵M为AC中点,∴BM=AC=5.∵矩形ABCD绕点B顺时针旋转90°至EBGF的位置,∴BM=BN,且∠MBN=90°,∴MN=BM=5.故答案为5.15.解:∵△ABC为等边三角形,∴AB=AC=a,∠BAC=60°,∵△AB′C′是△ABC的“双旋三角形”,∴α+β=60°,AB′=AB=a,AC′=AC=a,∴∠B′AC=120°,∴∠B′=∠C′=30°,作AH⊥B′C′于H,如图,则B′H=C′H,在Rt△AB′H中,AH=AB′=a,∴B′H=AH=a,a.∴B′C′=2A′H=16.解:作CH ⊥BF 于H ,GK ⊥BC 于K .∵四边形ABCD 是正方形,∴CB =CD ,∠BCD =90°,∵∠ECF =90°,∴∠BCD =∠ECF ,∴∠BCE =∠DCF ,∵CE =CF ,∴△BCE ≌△DCF (SAS ),∴BE =DF =6,∵CE =CF ,∠ECF =90°,CH ⊥EF ,∴EH =HF ,∴CH =HE =HF ,设CH =HE =HF =a ,在Rt △BCH 中,∵BC 2=BH 2+CH 2,∴50=(6+a )2+a 2,解得a =1或﹣7(舍弃),∴CH =HE =HF =1,BF =8,∵tan ∠CBH =∴8k =5∴k =∴BG =,,=5==,设GK =k ,BK =7k ,则GK =CK =k ,k =,∴FG=BF﹣BG=8﹣故答案为.=,17.解:如图,过点A作AE⊥AD交CD于E,连接BE.∵∠DAE=90°,∠ADE=45°,∴∠ADE=∠AED=45°,∴AE=AD=1,DE=,∵∠DAE=∠BAC=90°,∴∠BAE=∠CAD,∵AB=AC,∴△BAE≌△CAD(SAS),∴CD=BE=3,∠AEB=∠ADC=45°,∴∠BED=90°,∴BD=故答案为.==.18.解:根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,而2019=4×504+3,所以点P2019的坐标与点P3的坐标相同,为(﹣3,3).故答案为(﹣3,3).19.解:如图1中,当△AB′C′是△ABC的“双展三角形”时,作C′D⊥B′A交B′A的延长线于D,在C′D上取一点F,使得FA=FC,连接AF.∵B ∠B ′AC ′=60°+45°=105°,∴∠DAC ′=75°,∵∠D =90°,∴∠DC ′A =15°,∵FA =FC ′,∴∠FAC =∠FC ′A =15°,∴∠AFD =∠FAC +∠FC ′A =30°,设AD =x ,则AF =FC ′=2x .DF =∵AB =BC =2,∠B =90°,∴AC =AC ′=2,x ,在Rt △ADC ′中,则有x 2+(解得x =x +2x )2=(2)2,﹣1(负根已经舍弃),∴DC ′=2x +x =+1,+1.∴S △AB ′C ′=•AB ′•C ′D =如图2中,当△A ′BC ′是△ABC 的“双展三角形”时,作C ′D ⊥B ′A 交A ′B 的延长线于D .由题意:∠A ′BC ′=60°+90°=150°,∴∠C ′BD =30°,∴C ′D =BC ′=1,∴S △A ′BC ′=•BA ′•C ′D =1,综上所述,满足条件的故答案为+1或1.+1或1.20.解:由题意可知:CA =CE ,∠ACE =90°,∴∠E =∠CAE =45°,∵∠ACD =70°,∴∠DCE =20°,∴∠EDC =180°﹣∠E ﹣∠DCE =180°﹣45°﹣20°=115°,故答案为115°.三.解答题(共10小题)21.解:(1)∠CAE =180°﹣∠BAO =180°﹣60°=120°,∴∠BEC =∠C +∠CAE =45°+120°=165°,故答案为:165°.(2)①∵OD ∥AB ,∴∠BOD =∠B =30°,又∠BOD +∠BOC =90°,∠AOC +∠BOC =90°,∴∠AOC =∠BOD =30°.′②存在,如图1,当AB ∥OC 时,则∠COB =∠B =30°,∴∠AOC =90°+30°=120°;如图2,当AB ∥CD 时,延长DO 交AB 于D ′,∴∠AD ′O =∠D =45°,∴∠AOD ′=75°,∴∠AOC =∠AOD ′+90°=165°;如图3,当AB ∥OD 时,∠DOB =∠B =30°,∴∠AOC =∠DOB =30°;如图4,当AB∥OD时,∠AOD=∠A=60°,∴∠AOC=90°+60°=150°;如图5,当AB∥OC时,∴∠AOC=∠A=60°;如图6,当AB∥CD时,∠1=∠A=60°,∴∠AOC=60°﹣45°=15°;综上所述,∠AOC的度数为:15°,30°,60°,120°,150°,165°.22.解:(1)过点D作DE⊥BC,则∠DEB=90°.∵AB∥CD,∴∠ABC=∠DCE=60°.∴在Rt△CDE中,∠CDE=30°.∴CE=CD=.∴DE==.∴△BCD的面积为BC DE=×4×=(2)方法一:连接AN,∵线段BM绕点B逆时针旋转60°得到线段BN,∴NB=MB,∠NBM=60°.∵∠MBC+∠MBA=∠MBA+∠NBA.∴∠MBC=∠NBA,∵AB=BC,∴△MBC≌△NBA(SAS).∴∠NAB=∠BCM=120°.连接AC,∵∠ABC=60°,AB=BC,∴△ABC为等边三角形.∴∠BAC=∠ACB=60°.∴∠NAB+∠BAC=180°.∴N,A,C三点在一条直线上.∵NQ=n,BQ=m,∴CQ=4﹣m.∵NQ⊥BC,∴∠NQC=90°.∴在Rt △NQC 中,NQ =CQ •tan ∠NCQ .∴n =即n =﹣(4﹣m ).m +4.所以n 关于m 的函数解析式为:n =﹣m +4(≤m ≤2).方法二:∵线段BM 绕点B 逆时针旋转60°得到线段BN ,∴NB =BM ,∠NBM =60°.∵∠MBC +∠MBA =∠MBA +∠NBA .∴∠MBC =∠NBA ,∵AB =BC ,∴△MBC ≌△NBA .∴∠NAB =∠BCM =120°.设AB 与NQ 交于H 点,∵NQ ⊥BC ,∴∠HQB =90°.∵∠ABC =60°,∴∠BHQ =∠NHA =30°.∴∠HNA =180°﹣30°﹣120°=30°.∴NA =AH .∴在Rt △BHQ 中,HQ =BQ •tan ∠HBQ =又∵BH =2m ,∴AH =4﹣2m .过点A 作AG ⊥NH ,∴NG =GH .m .在Rt△AGH中,GH=AH cos∠AHN=∴NH=2GH=4∵NQ=N H+HQ,∴n=﹣﹣2(4﹣2m)=2﹣m,m.m+4.所以n关于m的函数解析式为:n=﹣m+4(≤m≤2).23.解:(Ⅰ)如图1中,∵A(3,3),B(3,0),∴AB=OB=3,∠ABO=90°,∴∠BOA=45°,∵将△AOB沿OA翻折得到△AOD,∴∠AOD=∠AOB=45°,∴∠BOD=90°,∴点D在y轴的正半轴上,∴D(0,3).(Ⅱ)①如图1中,作点P关于点O的对称点K,连接KQ交OB于R′,此时PR′+QR′的值最小.作DH⊥QK于H.由题意:K (0,﹣1),Q (,3).∴直线KQ 的解析式为y =∴R ′(,0),x ﹣1,令y =0,得到x =,∵DH ⊥KQ ,∴直线KQ 的解析式为y =﹣x +3,由,解得,∴H (∴DH =∴R ′(,),=.,0),点D 到直线KQ 的距离为②如图2中,易证△ABM ≌△EBG (SAS ),∴∠BAM =∠BEC =45°,∵∠AEB =45°,∴∠GEN =90°,∵,∴可以假设EN =12k ,EG =5k ,则NG =MN =13k ,∵AM =EG =5k ,∴5k +13k +12k =3∴k =∴AM =,,,作MH ⊥AB 于H ,∵∠MAH =45°,AM =∴AH =MH =,可得M (,).24.解:(1)直角三角形ABC 按逆时针方向旋转到△EBD 的位置,∴旋转中心是点B ,旋转角是90°;(2)AC ⊥DE ,理由:延长DE 交AC 于F ,∵把直角三角形ABC 按逆时针方向旋转到△EBD 的位置,∴∠C =∠D ,∠DBE =∠ABC =90°,∴∠C +∠A =∠D +∠A =90°,∴∠DFA =90°,∴AC ⊥DE .,25.解:(1)如图1中,在Rt △ABC 中,∵∠C =90°,BC =4∴AB =2BC =8,,∠CAB =30°∵DF 垂直平分线段AB ,∴AD =DB =4,×=4.在Rt △ADG 中,DG =AD tan30°=4(2)结论:CN =理由:如图2中,HM .∵∠ACB =90°,AD =DB ,∴CD =DA =DB ,∵∠B =60°,∴△BDC 是等边三角形,∴∠DCB =∠CDB =60°,∵∠ACB =∠CDH =90°,∴∠MDH =∠HCD =30°,∴CD =DH ,∵∠DHM =∠DCN =60°,∠DMH =∠DNC =90°,∴△DMH ∽△DNC ,∴==,∴CN =HM .(3)如图3中,连接CD .∵∠KCT =∠KDT =90°,∴∠KCT +∠KDT =180°,∴K ,D ,T ,C 四点共圆,∴KT 是该圆的直径,当CD 是该圆的直径时,KT 的长最短,此时KT =CD =AB =426.解:(1)∵∠A =36°,AB =AC ,∴∠ABC =∠C =(180°﹣36°)=72°,∵BE 平分∠ABC ,∴∠ABE =∠CBE =×72°=36°,∴∠BEC =∠A +∠ABE =36°+36°=72°,∴∠ABE =∠A ,∠BEC =∠C ,∴AE =BE ,BE =BC ,∴AE =BE =BC ,故答案为:AE =BE =BC ;(2)证明:∵AB =AC ,EF ∥BC ,∴AE =AF ,由旋转的性质得,∠E ′AC =∠F ′AB ,AE ′=AF ′,在△CAE ′和△BAF ′中,,∴△CAE ′≌△BAF ′(SAS ),∴CE ′=BF ′;.(3)解:由(1)可知AE=BC,由旋转知,AE'=AE,∴AE'=BC,如图,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,①当点E'与点M重合时,∵CM∥AB,∴四边形ABCM是等腰梯形,∴∠BAM=∠ABC=72°,又∵∠BAC=36°,∴α=∠CAM=36°;②当点E′与点N重合时,∵CE′∥AB,∴∠AMN=∠BAM=72°,∵AM=AN,∴∠ANM=∠AMN=72°,∴∠MAN=180°﹣72°×2=36°,∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,综上所述,当旋转角为36°或72°时,CE′∥AB.故答案为:36°或72°.27.解:(1)∵△ABC是等边三角形∴∠ACB=60°,BC=AC∵等边△ABC绕点C顺时针旋转90°得到△EFC ∴CF=BC,∠BCF=90°,AC=CE∴CF=AC∵∠BCF=90°,∠ACB=60°∴∠ACF=∠BCF﹣∠ACB=30°∴∠CFA=(180°﹣∠ACF)=75°(2)∵△ABC和△EFC是等边三角形∴∠ACB=60°,∠E=60°∵CD平分∠ACE∴∠ACD=∠ECD∵∠ACD=∠ECD,CD=CD,CA=CE,∴△ECD≌△ACD(SAS)∴∠DAC=∠E=60°∴∠DAC=∠ACB∴AD∥BC28.(1)证明:如图2中,∵∠EAC=∠DAB,AE=AC,AD=AB,∴∠AEC=∠ACE=∠ADB=∠ABD,∵∠ADB=∠CDF,∴∠FDC=∠FCD,∴FD=FC,∵∠EDC=90°,∴∠DEF+∠ECD=90°,∠FDE+∠FDC=90°,∴∠FED=∠FDE,∴FE=FD,∴EF=FC.(2)①解:如图1中,结论仍然成立.理由:连接AF.∵∠FCA=∠ABF,∴A,B,C,F四点共圆,∴∠AFC+∠ABC=180°,∵∠ABC=90°,∴∠AFC=90°,∴AF⊥EC,∵AE=AC,∴EF=CF.②如图3﹣1中,当CF=CD,∠FCD=90°时,连接AF,作CH⊥BF于H.设CF=CD=a.则DE==a,DF=a,∵CF=CD,CH⊥DF,∴HF=HD,∴CH=DF=∴BC=DE=∴BH=a,a,=a,∵AE=AC,EF=CF,∴AF平分∠EAC,∵A,B,C,F四点共圆,∴∠CAF=∠CBH=α,∴tanα===.如图3﹣2中,当DF=DC,∠CDF=90°时,作DH⊥CF于H,连接AF.设CD=DF=m.则CF =EF =∴DE =BC =∴BD =∴tan α=a ,DH =CF ===2a ,=.a ,a ,29.解:(1)如图1中,∵DE ⊥AC ,∴∠DEC =∠A =90°,∴DE ∥AB ,∵AE =EC ,∴BD =DC ,在Rt △ABC 中,∵AB =6,AC =8,∴BC =∴CD =BC =5.(2)结论:MF =ME .理由:如图1中,连接DM ,==10,∵∠DFM =∠DEM =90°,DM =DM ,DF =DE ,∴Rt △DMF ≌Rt △DME (HL ),∴MF =ME .(3)①如图2中,作AH ⊥BC 于H ,交FG 于K .易知AH =∴DF =KH =3,=,四边形DFKH 是矩形,∴AK =AH ﹣KH =,∵KM ∥CH ,∴=,∴=,∴AM =3.②如图3中,∵DG =DB =DC ,∴∠G =∠DBG ,∵∠G =∠C ,∴∠MBC =∠C ,∴BM =MC ,设BM =MC =x ,在Rt △ABM 中,∵BM 2=AB 2+AM 2,∴62+(8﹣x )2=x 2,∴x =,∴AM=AC﹣CM=8﹣故答案为.=.③尺规作图如图4﹣1所示.作DR平分∠CDF,在DR上截取DG=DC,分别以D,G为圆心,DE,CE为半径画弧,两弧交于点F,△DFG即为所求.如图4﹣1中,连接DM,设DG交AC于T,作TH⊥CD于H,作DK平分∠CDG交TH于K,作KJ⊥DG于J.易证△DEM≌△DHK(AAS),推出EM=HK,只要求出HK即可.∵TE⊥DE,TH⊥DC,DG平分∠CDE,∴TE=TH,设TE=TH=x,在Rt△TCH中,x2+22=(4﹣x)2,∴x=,∴DT==,∵DK平分∠CDT,KJ⊥DT,KH⊥CD,∴KJ=KH,设KJ=KH=y,在Rt△KTJ中,y2+(﹣3)2=(﹣y)2,∴y=3∴EM=3﹣6,﹣6,∴AM=AE﹣EM=4﹣(3﹣6)=10﹣3.30.解:(1)结论:BD=CE,BD⊥CE.理由如图1中,∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,∴AB=AC,AD=AE,∠DAB=∠CAE,在△ADB和△AEC中,,∴△ADB≌△AEC(SAS),∴BD=CE.∠ACE=∠ABD设CP与AB交于点O,∵∠AOC=∠BOP∴∠BPC=∠OAC=90°∴BD⊥CE;(2)解:a:如图2中,当点E在AB上时,BE=AB﹣AE=4.∵∠EAC=90°,∴CE===4,同(1)可证△ADB≌△AEC.∴∠DBA =∠ECA .∵∠PEB =∠AEC ,∴△PEB ∽△AEC .∴∴==,,,∴PB =b :如图3中,当点E 在BA 延长线上时,BE =AB +AE =12.∵∠EAC =90°,∴CE ==4,同(1)可证△ADB ≌△AEC .∴∠DBA =∠ECA .∵∠PEB =∠AEC ,∴△PEB ∽△AEC .∴∴==,,,或.∴PB =∴PB 的长为(3)a 、如图4中,以A 为圆心AD 为半径画圆,当CE 在⊙A 下方与⊙A 相切时,PB 的值最小.理由:此时∠BCE最小,因此PB最小,(△PBC是直角三角形,斜边BC为定值,∠BCE 最小,因此PB最小)∵AE⊥EC,∴EC==4,由(1)可知,△ABD≌△ACE,∴∠ADB=∠AEC=90°,BD=CE=4∴∠ADP=∠DAE=∠AEP=90°,∴四边形AEPD是矩形,∴PD=AE=4,∴PB=BD﹣PD=4﹣4.,b、如图5中,以A为圆心,AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.理由:此时∠BCE最大,因此PB最大,(△PBC是直角三角形,斜边BC为定值,∠BCE 最大,因此PB最大)∵AE⊥EC,∴EC===4,同(1)可证△ADB≌△AEC∴∠ADB =∠AEC =90°,BE =CE =4∴∠ADP =∠DAE =∠AEP =90°,∴四边形AEPD 是矩形,∴P D =AE =4,∴PB =BD +PD =4∴PB 最大值是4+4.+4;,。
中考数学压轴题之初中数学 旋转(中考题型整理,突破提升)及详细答案

中考数学压轴题之初中数学旋转(中考题型整理,突破提升)及详细答案一、旋转1.阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.(1)在图1中证明小胖的发现;借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).【答案】(1)证明见解析;(2)证明见解析;(3)∠EAF =12 m°.【解析】分析:(1)如图1中,欲证明BD=EC,只要证明△DAB≌△EAC即可;(2)如图2中,延长DC到E,使得DB=DE.首先证明△BDE是等边三角形,再证明△ABD≌△CBE即可解决问题;(3)如图3中,将AE绕点E逆时针旋转m°得到AG,连接CG、EG、EF、FG,延长ED到M,使得DM=DE,连接FM、CM.想办法证明△AFE≌△AFG,可得∠EAF=∠FAG=12 m°.详(1)证明:如图1中,∵∠BAC=∠DAE,∴∠DAB=∠EAC,在△DAB和△EAC中,AD AE DAB EAC AB AC ⎧⎪∠∠⎨⎪⎩===,∴△DAB ≌△EAC ,∴BD=EC .(2)证明:如图2中,延长DC 到E ,使得DB=DE .∵DB=DE ,∠BDC=60°,∴△BDE 是等边三角形,∴∠BD=BE ,∠DBE=∠ABC=60°,∴∠ABD=∠CBE ,∵AB=BC ,∴△ABD ≌△CBE ,∴AD=EC ,∴BD=DE=DC+CE=DC+AD .∴AD+CD=BD .(3)如图3中,将AE 绕点E 逆时针旋转m°得到AG ,连接CG 、EG 、EF 、FG ,延长ED 到M ,使得DM=DE ,连接FM 、CM .由(1)可知△EAB ≌△GAC ,∴∠1=∠2,BE=CG ,∵BD=DC ,∠BDE=∠CDM ,DE=DM ,∴△EDB ≌△MDC ,∴EM=CM=CG ,∠EBC=∠MCD ,∵∠EBC=∠ACF,∴∠MCD=∠ACF,∴∠FCM=∠ACB=∠ABC,∴∠1=3=∠2,∴∠FCG=∠ACB=∠MCF,∵CF=CF,CG=CM,∴△CFG≌△CFM,∴FG=FM,∵ED=DM,DF⊥EM,∴FE=FM=FG,∵AE=AG,AF=AF,∴△AFE≌△AFG,∴∠EAF=∠FAG=12 m°.点睛:本题考查几何变换综合题、旋转变换、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会利用“手拉手”图形中的全等三角形解决问题,学会构造“手拉手”模型,解决实际问题,属于中考压轴题.2.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2考点:四边形综合题3.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=12MC,∴EG=CG.(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.4.(1)如图①,在矩形ABCD 中,对角线AC 与BD 相交于点O ,过点O 作直线EF ⊥BD ,交AD 于点E ,交BC 于点F ,连接BE 、DF ,且BE 平分∠ABD .①求证:四边形BFDE 是菱形;②直接写出∠EBF 的度数;(2)把(1)中菱形BFDE 进行分离研究,如图②,点G 、I 分别在BF 、BE 边上,且BG=BI ,连接GD ,H 为GD 的中点,连接FH 并延长,交ED 于点J ,连接IJ 、IH 、IF 、IG.试探究线段IH 与FH 之间满足的关系,并说明理由;(3)把(1)中矩形ABCD 进行特殊化探究,如图③,当矩形ABCD 满足AB=AD 时,点E 是对角线AC 上一点,连接DE 、EF 、DF ,使△DEF 是等腰直角三角形,DF 交AC 于点G.请直接写出线段AG 、GE 、EC 三者之间满足的数量关系.【答案】(1)①详见解析;②60°.(2)IH =3FH ;(3)EG 2=AG 2+CE 2.【解析】【分析】(1)①由△DOE ≌△BOF ,推出EO =OF ,∵OB =OD ,推出四边形EBFD 是平行四边形,再证明EB =ED 即可.②先证明∠ABD =2∠ADB ,推出∠ADB =30°,延长即可解决问题.(2)IH =3FH .只要证明△IJF 是等边三角形即可.(3)结论:EG 2=AG 2+CE 2.如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,先证明△DEG ≌△DEM ,再证明△ECM 是直角三角形即可解决问题.【详解】(1)①证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,OB =OD ,∴∠EDO =∠FBO ,在△DOE 和△BOF 中,EDO FBO OD OBEOD BOF ∠∠⎧⎪⎨⎪∠∠⎩=== ,∴△DOE ≌△BOF ,∴EO =OF ,∵OB =OD ,∴四边形EBFD 是平行四边形,∵EF ⊥BD ,OB =OD ,∴EB =ED ,∴四边形EBFD 是菱形.②∵BE 平分∠ABD ,∴∠ABE =∠EBD ,∵EB =ED ,∴∠EBD =∠EDB ,∴∠ABD =2∠ADB ,∵∠ABD +∠ADB =90°,∴∠ADB =30°,∠ABD =60°,∴∠ABE =∠EBO =∠OBF =30°,∴∠EBF =60°.(2)结论:IH =3FH .理由:如图2中,延长BE 到M ,使得EM =EJ ,连接MJ .∵四边形EBFD 是菱形,∠B =60°,∴EB =BF =ED ,DE ∥BF ,∴∠JDH =∠FGH ,在△DHJ 和△GHF 中,DHG GHF DH GHJDH FGH ∠∠⎧⎪⎨⎪∠∠⎩=== , ∴△DHJ ≌△GHF ,∴DJ =FG ,JH =HF ,∴EJ =BG =EM =BI ,∴BE =IM =BF ,∵∠MEJ =∠B =60°,∴△MEJ 是等边三角形,∴MJ =EM =NI ,∠M =∠B =60°在△BIF 和△MJI 中,BI MJ B M BF IM ⎧⎪∠∠⎨⎪⎩===,∴△BIF ≌△MJI ,∴IJ =IF ,∠BFI =∠MIJ ,∵HJ =HF ,∴IH ⊥JF ,∵∠BFI +∠BIF =120°,∴∠MIJ +∠BIF =120°,∴∠JIF =60°,∴△JIF 是等边三角形,在Rt △IHF 中,∵∠IHF =90°,∠IFH =60°,∴∠FIH =30°,∴IH =3FH .(3)结论:EG 2=AG 2+CE 2.理由:如图3中,将△ADG 绕点D 逆时针旋转90°得到△DCM ,∵∠FAD +∠DEF =90°,∴AFED 四点共圆,∴∠EDF =∠DAE =45°,∠ADC =90°,∴∠ADF +∠EDC =45°,∵∠ADF =∠CDM ,∴∠CDM +∠CDE =45°=∠EDG ,在△DEM 和△DEG 中,DE DE EDG EDM DG DM ⎧⎪∠∠⎨⎪⎩=== , ∴△DEG ≌△DEM ,∴GE =EM ,∵∠DCM =∠DAG =∠ACD =45°,AG =CM ,∴∠ECM =90°∴EC 2+CM 2=EM 2,∵EG =EM ,AG =CM ,∴GE 2=AG 2+CE 2.【点睛】考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质,等边三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,学会转化的思想思考问题.5.在平面直角坐标系中,已知点A(0,4),B(4,4),点M,N是射线OC上两动点(OM<ON),且运动过程中始终保持∠MAN=45°,小明用几何画板探究其中的线段关系.(1)探究发现:当点M,N均在线段OB上时(如图1),有OM2+BN2=MN2.他的证明思路如下:第一步:将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.第二步:证明△APM≌△ANM,得MP=MM.第一步:证明∠POM=90°,得OM2+OP2=MP2.最后得到OM2+BN2=MN2.请你完成第二步三角形全等的证明.(2)继续探究:除(1)外的其他情况,OM2+BN2=MN2的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)新题编制:若点B是MN的中点,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).【答案】(1)见解析;(2)结论仍然成立,理由见解析;(3)见解析.【解析】【分析】(1)将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.证明△APM≌△ANM,再利用勾股定理即可解决问题;(2)如图2中,当点M,N在OB的延长线上时结论仍然成立.证明方法类似(1);(3)如图3中,若点B是MN的中点,求MN的长.利用(2)中结论,构建方程即可解决问题.【详解】(1)如图1中,将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.∵点A(0,4),B(4,4),∴OA=AB,∠OAB=90°,∵∠NAP=∠OAB=90°,∠MAN=45°,∴∠MAN=∠MAP,∵MA=MA,AN=AP,∴△MAN≌△MAP(SAS).(2)如图2中,结论仍然成立.理由:如图2中,将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.∵∠NAP=∠OAB=90°,∠MAN=45°,∴∠MAN=∠MAP,∵MA=MA,AN=AP,∴△MAN≌△MAP(SAS),∴MN=PM,∵∠ABN=∠AOP=135°,∠AOB=45°,∴∠MOP=90°,∴PM2=OM2+OP2,∴OM2+BN2=MN2;(3)如图3中,若点B是MN的中点,求MN的长.设MN=2x,则BM=BN=x,∵OA=AB=4,∠OAB=90°,∴OB=2,∴OM=2﹣x,∵OM2+BN2=MN2.∴(42﹣x)2+x 2=(2x)2,解得x =﹣22+26或﹣22﹣26(舍弃)∴MN =﹣42+46.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质和判定,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考压轴题.6.如图1,在Rt △ABC 中,∠ACB =90°,AC =BC .点D 、E 分别在AC 、BC 边上,DC =EC ,连接DE 、AE 、BD .点M 、N 、P 分别是AE 、BD 、AB 的中点,连接PM 、PN 、MN .(1)PM 与BE 的数量关系是 ,BE 与MN 的数量关系是 .(2)将△DEC 绕点C 逆时针旋转到如图2的位置,判断(1)中BE 与MN 的数量关系结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;(3)若CB =6.CE =2,在将图1中的△DEC 绕点C 逆时针旋转一周的过程中,当B 、E 、D 三点在一条直线上时,求MN 的长度.【答案】(1)1,22PM BE BE MN ==;(2)成立,理由见解析;(3)MN 17﹣117【解析】【分析】(1)如图1中,只要证明PMN 的等腰直角三角形,再利用三角形的中位线定理即可解决问题;(2)如图2中,结论仍然成立,连接AD 、延长BE 交AD 于点H .由ECB DCA ≅,推出BE AD =,DAC EBC ∠=∠,即可推出BH AD ⊥,由M 、N 、P 分别AE 、BD 、AB 的中点,推出//PM BE ,12PM BE =,//PN AD ,12PN AD =,推出PM PN =,90MPN ∠=︒,可得2222BE PM MN ===; (3)有两种情形分别求解即可.【详解】(1)如图1中,∵AM =ME ,AP =PB ,∴PM ∥BE ,12PM BE =, ∵BN =DN ,AP =PB , ∴PN ∥AD ,12PN AD =, ∵AC =BC ,CD =CE ,∴AD =BE ,∴PM =PN ,∵∠ACB =90°,∴AC ⊥BC ,∴∵PM ∥BC ,PN ∥AC ,∴PM ⊥PN , ∴△PMN 的等腰直角三角形,∴2MN PM =, ∴122MN BE =⋅, ∴2BE MN =,故答案为12PM BE =,2BE MN =. (2)如图2中,结论仍然成立.理由:连接AD 、延长BE 交AD 于点H .∵△ABC 和△CDE 是等腰直角三角形,∴CD =CE ,CA =CB ,∠ACB =∠DCE =90°,∵∠ACB ﹣∠ACE =∠DCE ﹣∠ACE ,∴∠ACD =∠ECB ,∴△ECB ≌△DCA ,∴BE =AD ,∠DAC =∠EBC ,∵∠AHB =180°﹣(∠HAB +∠ABH )=180°﹣(45°+∠HAC +∠ABH )=∠180°﹣(45°+∠HBC +∠ABH )=180°﹣90°=90°,∴BH ⊥AD ,∵M 、N 、P 分别为AE 、BD 、AB 的中点,∴PM ∥BE ,12PM BE =,PN ∥AD ,12PN AD =, ∴PM =PN ,∠MPN =90°, ∴22222BE PM MN MN ==⨯=. (3)①如图3中,作CG ⊥BD 于G ,则2CG GE DG ===,当D 、E 、B 共线时,在Rt △BCG 中,()22226234BG BC CG =-=-= ∴342BE BG GE =-=∴21712MN BE ==. ②如图4中,作CG ⊥BD 于G ,则2CG GE DG ===当D 、E 、B 共线时,在Rt △BCG 中,()22226234BG BC CG =-=-=, ∴342BE BG GE =+=+,∴21712MN BE ==+. 综上所述,MN =17﹣1或17+1.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.7.已知正方形 ABCD 中,E 为对角线 BD 上一点,过 E 点作 EF ⊥BD 交 BC 于 F ,连接 DF ,G 为 DF 中点,连接 EG ,CG .(1) 求证:EG =CG ;(2) 将图①中△BEF 绕 B 点逆时针旋转 45∘,如图②所示,取 DF 中点 G ,连接 EG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3) 将图①中△BEF 绕 B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).【答案】解:(1)CG=EG(2)(1)中结论没有发生变化,即EG=CG .证明:连接AG ,过G 点作MN ⊥AD 于M ,与EF 的延长线交于N 点.在△DAG与△DCG中,∵ AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG.∴ AG=CG.在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG.∴ MG=NG在矩形AENM中,AM=EN.在Rt△AMG 与Rt△ENG中,∵ AM=EN, MG=NG,∴△AMG≌△ENG.∴ AG=EG∴ EG=CG.(3)(1)中的结论仍然成立.【解析】试题分析:(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.还知道EG⊥CG;试题解析:解:(1)证明:在Rt△FCD中,∵G为DF的中点,∴,同理,在Rt△DEF中,,∴CG=EG;(2)(1)中结论仍然成立,即EG=CG;连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点,如图所示:在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DC=DC,∴△DAG≌△DCG,∴AG=CG,在△DMG与△FNG中,∵∠DGM=∠FGN,DG=FG,∠MDG=∠NFG,∴△DMG≌△FNG,∴MG=NG,在矩形AENM中,AM=EN.,在Rt△AMG与Rt△ENG中,∵AM=EN,MG=NG,∴△AMG≌△ENG,∴AG=EG,∴EG=CG,(3)(1)中的结论仍然成立,即EG=CG且EG⊥CG。
中考专题数学解答组与旋转有关的类比探究题
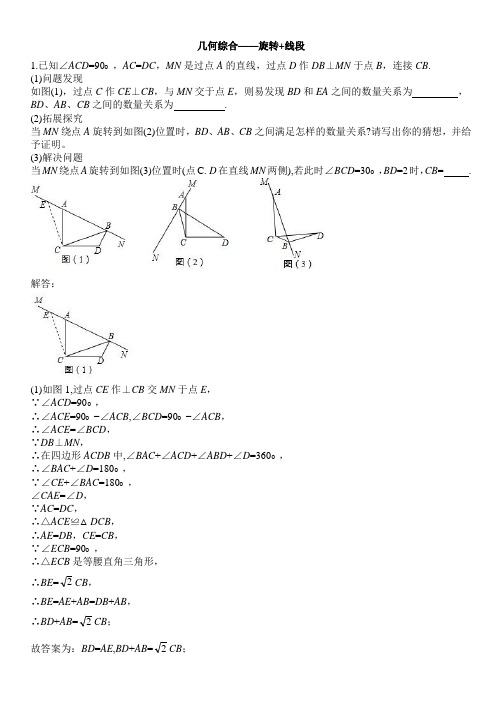
几何综合——旋转+线段1.已知∠ACD=90∘,AC=DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB.(1)问题发现如图(1),过点C作CE⊥CB,与MN交于点E,则易发现BD和EA之间的数量关系为,BD、AB、CB之间的数量关系为.(2)拓展探究当MN绕点A旋转到如图(2)位置时,BD、AB、CB之间满足怎样的数量关系?请写出你的猜想,并给予证明。
(3)解决问题当MN绕点A旋转到如图(3)位置时(点C. D在直线MN两侧),若此时∠BCD=30∘,BD=2时,CB= .解答:(1)如图1,过点CE作⊥CB交MN于点E,∵∠ACD=90∘,∴∠ACE=90∘−∠ACB,∠BCD=90∘−∠ACB,∴∠ACE=∠BCD,∵DB⊥MN,∴在四边形ACDB中,∠BAC+∠ACD+∠ABD+∠D=360∘,∴∠BAC+∠D=180∘,∵∠CE+∠BAC=180∘,∠CAE=∠D,∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∵∠ECB=90∘,∴△ECB是等腰直角三角形,∴BE=AE+AB=DB+AB,(2)如图2,过点C作⊥CB交MN于点E,∵∠ACD=90∘,∴∠ACE=90∘+∠ACB,∠BCD=90∘+∠ACB,∴∠ACE=∠BCD,∵DB⊥MN,∴∠CAE=90∘−∠AFB,∠D=90∘−∠CFD,∵∠AFB=∠CFD,∴∠CAE=∠D,∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∵∠ECB=90∘,∴△ECB是等腰直角三角形,∴BE=AE−AB=DB−AB,(3)如图3,过点C作⊥CB交MN于点E,∵∠ACD=90∘,∴∠ACE=90∘−∠DCE,∠BCD=90∘−∠DCE,∴∠ACE=∠BCD,∵DB⊥MN,∴∠CAE=90∘−∠AFC,∠D=90∘−∠CFD,∵∠AFB=∠BFD,∴∠CAE=∠D,∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∵∠ECB=90∘,∴△ECB是等腰直角三角形,∴BE=AB−AE=AB−DB,∵△BCE为等腰直角三角形,∴∠BEC=∠CBE=45∘,∵∠ABD=90∘,∴∠DBH=45∘过点D作DH⊥BC,∴△DHB是等腰直角三角形,2.如图所示,平行四边形ABCD中,∠B=60∘,将一块含60∘的直角三角板如图放置在平行四边形ABCD 所在平面内旋转,且60∘角的顶点始终与点C重合,角的两边所在的两直线分别交线段AB、AD于点E、F(不包括线段的端点).(1)问题发现:如图1,若平行四边形ABCD为菱形,试猜想线段AE、AF、AC之间的数量关系,请证明你的猜想。
备战中考数学旋转-经典压轴题

一、旋转 真题与模拟题分类汇编(难题易错题)1.在等边△AOB 中,将扇形COD 按图1摆放,使扇形的半径OC 、OD 分别与OA 、OB 重合,OA =OB =2,OC =OD =1,固定等边△AOB 不动,让扇形COD 绕点O 逆时针旋转,线段AC 、BD 也随之变化,设旋转角为α.(0<α≤360°)(1)当OC ∥AB 时,旋转角α=度;发现:(2)线段AC 与BD 有何数量关系,请仅就图2给出证明.应用:(3)当A 、C 、D 三点共线时,求BD 的长.拓展:(4)P 是线段AB 上任意一点,在扇形COD 的旋转过程中,请直接写出线段PC 的最大值与最小值.【答案】(1)60或240;(2) AC=BD ,理由见解析;(3)13+12或1312;(4)PC 的最大值=3,PC 的最小值31.【解析】 分析:(1)如图1中,易知当点D 在线段AD 和线段AD 的延长线上时,OC ∥AB ,此时旋转角α=60°或240°.(2)结论:AC =BD .只要证明△AOC ≌△BOD 即可.(3)在图3、图4中,分别求解即可.(4)如图5中,由题意,点C 在以O 为圆心,1为半径的⊙O 上运动,过点O 作OH ⊥AB 于H ,直线OH 交⊙O 于C ′、C ″,线段CB 的长即为PC 的最大值,线段C ″H 的长即为PC 的最小值.易知PC 的最大值=3,PC 的最小值31.详解:(1)如图1中,∵△ABC 是等边三角形,∴∠AOB =∠COD =60°,∴当点D 在线段AD 和线段AD 的延长线上时,OC ∥AB ,此时旋转角α=60°或240°.故答案为60或240;(2)结论:AC =BD ,理由如下:如图2中,∵∠COD =∠AOB =60°,∴∠COA =∠DOB .在△AOC 和△BOD 中,OA OB COA DOB CO OD =⎧⎪∠=∠⎨⎪=⎩,∴△AOC ≌△BOD ,∴AC =BD ;(3)①如图3中,当A、C、D共线时,作OH⊥AC于H.在Rt△COH中,∵OC=1,∠COH=30°,∴CH=HD=12,OH=32.在Rt△AOH中,AH=22OA OH-=132,∴BD=AC=CH+AH=1132+.如图4中,当A、C、D共线时,作OH⊥AC于H.易知AC=BD=AH﹣CH=131-.综上所述:当A、C、D三点共线时,BD的长为1312+或1312-;(4)如图5中,由题意,点C在以O为圆心,1为半径的⊙O上运动,过点O作OH⊥AB于H,直线OH交⊙O于C′、C″,线段CB的长即为PC的最大值,线段C″H的长即为PC的最小值.易知PC的最大值=3,PC的最小值=3﹣1.点睛:本题考查了圆综合题、旋转变换、等边三角形的性质、全等三角形的判定和性质、勾股定理、圆上的点到直线的距离的最值问题等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,利用辅助圆解决最值问题,属于中考压轴题.2.如图,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P'CB的位置.(1)设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P'CB的过程中边PA所扫过区域(图中阴影部分)的面积;(2)若PA=2,PB=4,∠APB=135°,求PC的长.【答案】(1) S阴影=(a2-b2);(2)PC=6.【解析】试题分析:(1)依题意,将△P′CB逆时针旋转90°可与△PAB重合,此时阴影部分面积=扇形BAC的面积-扇形BPP'的面积,根据旋转的性质可知,两个扇形的中心角都是90°,可据此求出阴影部分的面积.(2)连接PP',根据旋转的性质可知:BP=BP',旋转角∠PBP'=90°,则△PBP'是等腰直角三角形,∠BP'C=∠BPA=135°,∠PP'C=∠BP'C-∠BP'P=135°-45°=90°,可推出△PP'C是直角三角形,进而可根据勾股定理求出PC的长.试题解析:(1)∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,∴△PAB≌△P'CB,∴S△PAB=S△P'CB,S阴影=S扇形BAC-S扇形BP P′=(a2-b2);(2)连接PP′,根据旋转的性质可知:△APB≌△CP′B,∴BP=BP′=4,P′C=PA=2,∠PBP′=90°,∴△PBP'是等腰直角三角形,P'P2=PB2+P'B2=32;又∵∠BP′C=∠BPA=135°,∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,即△PP′C是直角三角形.PC==6.考点:1.扇形面积的计算;2.正方形的性质;3.旋转的性质.3.小明在矩形纸片上画正三角形,他的做法是:①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF,把纸片展平;②沿折痕BG折叠纸片,使点C落在EF上的点P 处,再折出PB、PC,最后用笔画出△PBC(图1).(1)求证:图1中的PBC是正三角形:(2)如图2,小明在矩形纸片HIJK上又画了一个正三角形IMN,其中IJ=6cm,且HM=JN.①求证:IH=IJ②请求出NJ的长;(3)小明发现:在矩形纸片中,若一边长为6cm,当另一边的长度a变化时,在矩形纸片上总能画出最大的正三角形,但位置会有所不同.请根据小明的发现,画出不同情形的示意图(作图工具不限,能说明问题即可),并直接写出对应的a的取值范围.【答案】(1)证明见解析;(2)①证明见解析;②1233)3<a<3,a>3【解析】分析:(1)由折叠的性质和垂直平分线的性质得出PB=PC,PB=CB,得出PB=PC=CB即可;(2)①利用“HL”证Rt△IHM≌Rt△IJN即可得;②IJ上取一点Q,使QI=QN,由Rt△IHM≌Rt△IJN知∠HIM=∠JIN=15°,继而可得∠NQJ=30°,设NJ=x,则IQ=QN=2x、3,根据IJ=IQ+QJ求出x即可得;(3)由等边三角形的性质、直角三角形的性质、勾股定理进行计算,画出图形即可.(1)证明:∵①对折矩形纸片ABCD(AB>BC),使AB与DC重合,得到折痕EF∴PB=PC∵沿折痕BG折叠纸片,使点C落在EF上的点P处∴PB=BC∴PB=PC=BC∴△PBC是正三角形:(2)证明:①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ 是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ =⎧⎨=⎩∴Rt △MHI ≌Rt △JNI (HL )∴HI=IJ②在线段IJ 上取点Q ,使IQ=NQ∵Rt △IHM ≌Rt △IJN ,∴∠HIM=∠JIN ,∵∠HIJ=90°、∠MIN=60°,∴∠HIM=∠JIN=15°,由QI=QN 知∠JIN=∠QNI=15°,∴∠NQJ=30°,设NJ=x ,则IQ=QN=2x ,QJ=22=3QN NJ -x ,∵IJ=6cm ,∴2x+3x=6,∴x=12-63,即NJ=12-63(cm ).(3)分三种情况:①如图:设等边三角形的边长为b ,则0<b≤6,则tan60°=3=2ab,∴a=32b,∴0<b≤632=33;②如图当DF与DC重合时,DF=DE=6,∴a=sin60°×DE=632=33,当DE与DA重合时,a=643sin603==︒,∴33<a<43;③如图∵△DEF是等边三角形∴∠FDC=30°∴DF=643cos303==︒∴a>3点睛:本题是四边形的综合题目,考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识;本题综合性强,难度较大.4.如图1,ABCD和AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将ABCD固定不动,AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.探究一:(1)在图2的情形下,求旋转角α的度数;探究二:(2)如图3,当AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;探究三:(3)如图1,连接CF,BF,在旋转过程中△BCF的面积是否存在最大的情形,如果存在,求出最大面积,如果不存在,请说明理由.【答案】(1)α=120°;(2)四边形CDFM是菱形,证明见解析;(3)存在△BCF的面积最大的情形,S△BCF =332a2.【解析】试题分析:(1)由平行四边形的性质知∠D=∠B,AB=CD=a,可得∠D=∠DEC,由等角对等边知CD=CE,由AE=AB=a,AD=BC=2a,可得DE=CE,即可证得△CDE是等边三角形,∠D=60°,由两直线平行,同位角相等可得∠DAB=120°,即可求得α;(2)由旋转的性质以及∠B=60°,可得△ABE是等边三角形,由平行线的判定以及两组对边分别平行的四边形是平行四边形可证四边形ABEM是平行四边形,再由由一组邻边相等的平行四边形是菱形即可得证;(3)当点F到BC的距离最大时,△BCF的面积最大,由于点F始终在以A为圆心AF为半径的圆上运动,故当FG与⊙A相切时,点F到BC的距离最大,过点A作AH⊥BC于点H,连接AF,由题意知∠AFG=90°.由∠ABH=∠G=60°,AB=a,AG=2a,可得AH、AF的值.可求得点F到BC的最大距离.进而求得S△BCF的值.试题解析:(1)∵四边形ABCD是平行四边形,∴∠D=∠B,AB=CD=a,∵∠AEF=∠B,∠AEF=∠DEC,∴∠D=∠DEC,∴CD=CE,∵AE=AB=a,AD=BC=2a,∴DE=CE.,∴CD=CE=DE,∴△CDE是等边三角形,∴∠D=60°,∵CD∥AB,∴∠D+∠DAB=180°,∴∠DAB=120°,∴α=120°.;(2)四边形CDFM是菱形.证明:由旋转可得AB=AE,∵∠B=60°,∴△ABE是等边三角形,∴∠BAE=60°,∴∠BAG=∠BAE+∠GAE=60°+120°=180°,∴点G,A,B在同一条直线上,∴ME ∥AB,BE∥AM,∴四边形ABEM是平行四边形,∴AM=AB=ME,∴CD=DM=MF,∵CD ∥AB∥MF,∴四边形CDFM是平行四边形,∵∠D= 60°,CD=DM,∴△CDM是等边三角形,∴CD=DM,∴四边形CDFM是菱形;(3)存在△BCF的面积最大的情形.∵CB的长度不变,∴当点F到BC的距离最大时,△BCF的面积最大.∵点F始终在以A为圆心AF为半径的圆上运动,∴当FG与⊙A相切时,点F到BC的距离最大,如图,过点A作AH⊥BC于点H,连接AF,则∠AFG=90°.∵∠ABH=∠G=60°,AB=a,AG=2a,∴AH=AB×sin60°=32a,AF=AG×sin60°=3 a.∴点F到BC的最大距离为3a+ 32a=332a.∴S△BCF=12×2a×332a=332a2.点睛:此题考查了旋转的洗澡那个会、平行四边形的判定和性质、菱形的判定和性质,三角形的面积的求法,关键是运用旋转前后,图形的对应边相等、对应角相等的性质解题.5.如图2,边长为2的等边△ABC内接于⊙O,△ABC绕圆心O顺时针方向旋转得到△,A′C′分别与AB、AC交于E、D点,设旋转角度为.(1)当=,△A′B′C′与△ABC出现旋转过程中的第一次完全重合;(2)当=60°时(如图1),该图()A.是中心对称图形但不是轴对称图形B.是轴对称图形但不是中心对称图形C.既是轴对称图形又是中心对称图形D.既不是轴对称图形也不是中心对称图形(3)如图2,当,△ADE的周长是否会发生变化,如会变化,说明理由,如不会变化,求出它的周长.【答案】(1)120°;(2)C;(3)△的周长不变.【解析】【分析】(1)根据等边三角形的中心角为120°可直接求解;(2)根据题意可知,当=60°时,点A、、B、、C、为⊙O的六等分点,,所有的三角形都是正三角形,由此可得到所有图形即是轴对称图形,又是中心对称图形;(3)得到结论:周长不发生变化,连接A,根据弦相等,则它们所对的弧相等的性质可得,即,再根据等弧所对的圆周角相等,得,由等角对等边的性质可得,同理,因此可求△的周长==.【详解】解:(1)120°.如图,可根据等边三角形的性质直接根据三角形的内角和求得∠O=120°;(2)C(3)△的周长不变;理由如下:连接AA′,∵,∴,∴,∴,∴,同理,,∴△的周长=.即考点:正多边形与圆,圆周角定理6.如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.同时转动两个转盘,当转盘停止后,计算指针所指区域内的数字之和.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.(1)请你通过画树状图或列表的方法分析,并求指针所指区域内的数字和小于10的概率;(2)小亮和小颖小亮和小颖利用它们做游戏,游戏规则是:指针所指区域内的数字和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.你认为该游戏规则是否公平?请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.【答案】(1)13;(2)不公平.【解析】试题分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.(2)判断游戏的公平性,首先要计算出游戏双方赢的概率,概率相等则公平,否则不公平.试题解析:(1)共有12种等可能的结果,小于10的情况有4种,所以指针所指区域内的数字和小于10的概率为13.(2)不公平,因为小颖获胜的概率为;小亮获胜的概率为512.小亮获胜的可能性大,所以不公平.可以修改为若这两个数的和为奇数,则小亮赢;积为偶数,则小颖赢.考点:1.游戏公平性;2.列表法与树状图法.7.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,当点P 在BC 延长线上时,若∠BPO =15°,BP =4,请求出BQ 的长.【答案】(1)BQ =CP ;(2)成立:PC =BQ ;(3)434-.【解析】试题分析:(1)结论:BQ =CP .如图1中,作PH ∥AB 交CO 于H ,可得△PCH 是等边三角形,只要证明△POH ≌△QPB 即可;(2)成立:PC =BQ .作PH ∥AB 交CO 的延长线于H .证明方法类似(1);(3)如图3中,作CE ⊥OP 于E ,在PE 上取一点F ,使得FP =FC ,连接CF .设CE =CO =a ,则FC =FP =2a ,EF 3,在Rt △PCE 中,表示出PC ,根据PC +CB =4,可得方程62)24a a +=,求出a 即可解决问题;试题解析:解:(1)结论:BQ =CP .理由:如图1中,作PH ∥AB 交CO 于H .在Rt △ABC 中,∵∠ACB =90°,∠A =30°,点O 为AB 中点,∴CO =AO =BO ,∠CBO =60°,∴△CBO 是等边三角形,∴∠CHP =∠COB =60°,∠CPH =∠CBO =60°,∴∠CHP =∠CPH =60°,∴△CPH 是等边三角形,∴PC =PH =CH ,∴OH =PB ,∵∠OPB =∠OPQ +∠QPB =∠OCB +∠COP ,∵∠OPQ =∠OCP =60°,∴∠POH =∠QPB ,∵PO =PQ ,∴△POH ≌△QPB ,∴PH =QB ,∴PC =BQ .(2)成立:PC =BQ .理由:作PH ∥AB 交CO 的延长线于H .在Rt △ABC 中,∵∠ACB =90°,∠A =30°,点O 为AB 中点,∴CO =AO =BO ,∠CBO =60°,∴△CBO 是等边三角形,∴∠CHP =∠COB =60°,∠CPH =∠CBO =60°,∴∠CHP =∠CPH =60°,∴△CPH 是等边三角形,∴PC =PH =CH ,∴OH =PB ,∵∠POH =60°+∠CPO ,∠QPO =60°+∠CPQ ,∴∠POH =∠QPB ,∵PO =PQ ,∴△POH ≌△QPB ,∴PH =QB ,∴PC =BQ .(3)如图3中,作CE ⊥OP 于E ,在PE 上取一点F ,使得FP =FC ,连接CF .∵∠OPC =15°,∠OCB =∠OCP +∠POC ,∴∠POC =45°,∴CE =EO ,设CE =CO =a ,则FC =FP =2a ,EF 3a ,在Rt △PCE 中,PC 22PE CE +22(23)a a a ++=62)a ,∵PC +CB =4,∴(62)24a a =,解得a =4226,∴PC =434,由(2)可知BQ =PC ,∴BQ =434.点睛:此题考查几何变换综合题、旋转变换、等边三角形的判定和性质全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.8.如图,已知Rt △ABC 中,∠ACB =90°,AC =BC ,D 是线段AB 上的一点(不与A 、B 重合).过点B 作BE ⊥CD ,垂足为E .将线段CE 绕点C 顺时针旋转90︒,得到线段CF ,连结EF .设∠BCE 度数为α.(1)①补全图形;②试用含α的代数式表示∠CDA .(2)若3EF AB = ,求α的大小. (3)直接写出线段AB 、BE 、CF 之间的数量关系.【答案】(1)①答案见解析;②45α︒+;(2)30α=︒;(3)22222AB CF BE =+.【解析】试题分析:(1)①按要求作图即可;②由∠ACB=90°,AC=BC ,得∠ABC=45°,故可得出结论;(2)易证FCE ∆∽ ACB ∆,得3CF AC =FA ,得△AFC 是直角三角形,求出∠ACF=30°,从而得出结论;(3)222A 22B CF BE =+.试题解析:(1)①补全图形.②∵∠ACB=90°,AC=BC ,∴∠ABC=45°∵∠BCE=α ∴∠CDA=45α︒+(2)在FCE ∆和ACB ∆中,45CFE CAB ∠=∠=︒ ,90FCE ACB ∠=∠=︒ ∴ FCE ∆∽ ACB ∆ ∴ CF EF AC AB = 3EF AB = ∴ 32CF AC = 连结FA .90,90FCA ACE ECB ACE ∠=︒-∠∠=︒-∠∴ FCA ECB ∠=∠=α在Rt CFA ∆中,90CFA ∠=︒,3cos FCA ∠= ∴ 30FCA ∠=︒即30α=︒.(3)22222AB CF BE =+。
2020-2021九年级中考数学初中数学 旋转解答题压轴题提高专题练习附答案
2020-2021九年级中考数学初中数学 旋转解答题压轴题提高专题练习附答案一、旋转1.在△ABC 中,AB=AC ,∠BAC=α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD 。
(1)如图1,直接写出∠ABD 的大小(用含α的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE 的形状并加以证明;(3)在(2)的条件下,连结DE ,若∠DEC=45°,求α的值。
【答案】(1)1302α︒-(2)见解析(3)30α=︒ 【解析】解:(1)1302α︒-。
(2)△ABE 为等边三角形。
证明如下:连接AD ,CD ,ED ,∵线段BC 绕点B 逆时针旋转60︒得到线段BD ,∴BC=BD ,∠DBC=60°。
又∵∠ABE=60°,∴1ABD 60DBE EBC 302α∠=︒-∠=∠=︒-且△BCD 为等边三角形。
在△ABD 与△ACD 中,∵AB=AC ,AD=AD ,BD=CD ,∴△ABD ≌△ACD (SSS )。
∴11BAD CAD BAC 22α∠=∠=∠=。
∵∠BCE=150°,∴11BEC 180(30)15022αα∠=︒-︒--︒=。
∴BEC BAD ∠=∠。
在△ABD 和△EBC 中,∵BEC BAD ∠=∠,EBC ABD ∠=∠,BC=BD ,∴△ABD ≌△EBC (AAS )。
∴AB=BE 。
∴△ABE 为等边三角形。
(3)∵∠BCD=60°,∠BCE=150°,∴DCE 1506090∠=︒-︒=︒。
又∵∠DEC=45°,∴△DCE 为等腰直角三角形。
∴DC=CE=BC 。
∵∠BCE=150°,∴(180150)EBC 152︒-︒∠==︒。
而1EBC 30152α∠=︒-=︒。
∴30α=︒。
中考数学专卷2020届中考数学总复习(27)图形的旋转-精练精析(1)及答案解析
图形的变化——图形的旋转1一.选择题(共9小题)1.如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为()A.(a﹣2,b)B.(a+2,b)C.(﹣a﹣2,﹣b)D.(a+2,﹣b)2.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70° B.65° C.60° D.55°3.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B.C.D.π4.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为()A.6 B.4 C.3 D.35.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()A. B.C.D.6.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30° B.60° C.90° D.150°7.如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为()A.2﹣B.C.﹣1 D.18如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB.6πC.3πD.1.5π9.如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于()A.30° B.40° C.50° D.60°二.填空题(共8小题)10.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=_________ .11如图,将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E 的对应点为F,则∠EAF的度数是_________ .12.如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为_________ .13.如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=,则图中阴影部分的面积等于_________ .14.如图,在△A BC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为_________ .15如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是_________ .16.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为_________ .17如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A 顺时针旋转到位置①可得到点P1,此时AP1=;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+;…,按此规律继续旋转,直至得到点P2014为止.则AP2014=_________ .三.解答题(共7小题)18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.19.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.20.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).(1)画出△ABC关于y轴对称的△A1B1C1;(2)画出△ABC关于原点O成中心对称的△A2B2C2.21.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为_________ cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.22.正方形ABCD中,E是CD边上一点,(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是_________ ,∠AFB=∠_________(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.23.(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2,PC=5,求∠BQC的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.24.如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.(1)证明:△ABE≌△C1BF;(2)证明:EA1=FC;(3)试判断四边形ABC1D的形状,并说明理由.图形的变化——图形的旋转1参考答案与试题解析一.选择题(共9小题)1.如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为()A.(a﹣2,b)B.(a+2,b)C.(﹣a﹣2,﹣b)D.(a+2,﹣b)考点:坐标与图形变化-旋转.专题:压轴题.分析:先根据图形确定出对称中心,然后根据中点公式列式计算即可得解.解答:解:由图可知,△ABC与△A′B′C′关于点(﹣1,0)成中心对称,设点P′的坐标为(x,y),所以,=﹣1,=0,解得x=﹣a﹣2,y=﹣b,所以,P′(﹣a﹣2,﹣b).故选C.点评:本题考查了坐标与图形变化﹣旋转,准确识图,观察出两三角形成中心对称,对称中心是(﹣1,0)是解题的关键.2如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70°B.65°C.60°D.55°考点:旋转的性质.专题:几何图形问题.分析:根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.解答:解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,∴AC=A′C,∴△ACA′是等腰直角三角形,∴∠CAA′=45°,∴∠A′B′C=∠1+∠CAA′=20°+45°=65°,由旋转的性质得∠B=∠A′B′C=65°.故选:B.点评:本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.3.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B C.D.π考点:旋转的性质;弧长的计算.专题:几何图形问题.分析:利用锐角三角函数关系得出BC的长,进而利用旋转的性质得出∠BCB′=60°,再利用弧长公式求出即可.解答:解:∵在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,∴cos30°=,∴BC=ABcos30°=2×=,∵将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,∴∠BCB′=60°,∴点B转过的路径长为:=π.故选:B.点评:此题主要考查了旋转的性质以及弧长公式应用,得出点B转过的路径形状是解题关键.4.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为()A. 6 B4C3D.3考点:旋转的性质.专题:几何图形问题.分析:利用直角三角形的性质得出AB=4,再利用旋转的性质以及三角形外角的性质得出AB′=2,进而得出答案.解答:解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∴∠CAB=30°,故AB=4,∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,∴AB=A′B′=4,AC=A′C,∴∠CAA′=∠A′=30°,∴∠ACB′=∠B′AC=30°,∴AB′=B′C=2,∴AA′=2+4=6.故选:A.点评:此题主要考查了旋转的性质以及直角三角形的性质等知识,得出AB′=B′C=2是解题关键.5.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()A.B C D.考点:旋转的性质;正方形的性质.专题:几何图形问题.分析:连接AC1,AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1,进而求出DC1=OD,根据三角形的面积计算即可.解答:解:连接AC1,∵四边形AB1C1D1是正方形,∴∠C1AB1=×90°=45°=∠AC1B1,∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,∴∠B1AB=45°,∴∠DAB1=90°﹣45°=45°,∴AC1过D点,即A、D、C1三点共线,∵正方形ABCD的边长是1,∴四边形AB1C1D1的边长是1,在Rt△C1D1A中,由勾股定理得:AC1==,则DC1=﹣1,∵∠AC1B1=45°,∠C1DO=90°,∴∠C1OD=45°=∠DC1O,∴DC1=OD=﹣1,∴S△ADO=×OD•AD=,∴四边形AB1OD的面积是=2×=﹣1,故选:C.点评:本题考查了正方形性质,勾股定理等知识点,主要考查学生运用性质进行计算的能力,题目比较好,但有一定的难度.6.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30°B60°C.90°D.150°考点:旋转的性质.专题:几何图形问题.分析:根据直角三角形两锐角互余求出∠A=60°,根据旋转的性质可得AC=A′C,然后判断出△A′AC是等边三角形,根据等边三角形的性质求出∠ACA′=60°,然后根据旋转角的定义解答即可.解答:解:∵∠ACB=90°,∠ABC=30°,∴∠A=90°﹣30°=60°,∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上,∴AC=A′C,∴△A′AC是等边三角形,∴∠ACA′=60°,∴旋转角为60°.故选:B.点评:本题考查了旋转的性质,直角三角形两锐角互余,等边三角形的判定与性质,熟记各性质并准确识图是解题的关键.7.如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为()A.2﹣B.C.﹣1 D.1考点:旋转的性质.分析:连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD﹣C′D计算即可得解.解答:解:如图,连接BB′,∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,∴AB=AB′,∠BAB′=60°,∴△ABB′是等边三角形,∴AB=BB′,在△ABC′和△B′BC′中,,∴△ABC′≌△B′BC′(SSS),∴∠ABC′=∠B′BC′,延长BC′交AB′于D,则BD⊥AB′,∵∠C=90°,AC=BC=,∴AB==2,∴BD=2×=,C′D=×2=1,∴BC′=BD﹣C′D=﹣1.故选:C.点评:本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出BC′在等边三角形的高上是解题的关键,也是本题的难点.8.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB6πC.3πD.1.5π考点:旋转的性质;弧长的计算.专题:计算题.分析:根据弧长公式列式计算即可得解.解答:解:的长==1.5π.故选:D.点评:本题考查了旋转的性质,弧长的计算,熟记弧长公式是解题的关键.9.如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于()A.30°B.40°C.50°D.60°考点:旋转的性质.专题:计算题.分析:先根据平行线的性质得∠DCA=∠CAB=65°,再根据旋转的性质得∠BAE=∠CAD,AC=AD,则根据等腰三角形的性质得∠ADC=∠DCA=65°,然后根据三角形内角和定理计算出∠CAD=180°﹣∠ADC﹣∠DCA=50°,于是有∠BAE=50°.解答:解:∵DC∥AB,∴∠DCA=∠CAB=65°,∵△ABC绕点A旋转到△AED的位置,∴∠BAE=∠CAD,AC=AD,∴∠ADC=∠DCA=65°,∴∠CAD=180°﹣∠ADC﹣∠DCA=50°,∴∠BAE=50°.故选:C.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.二.填空题(共8小题)10.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=55°.考点:旋转的性质.分析:根据题意得出∠ACA′=35°,则∠A′=90°﹣35°=55°,即可得出∠A的度数.解答:解:∵把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D,∠A′DC=90°,∴∠ACA′=35°,则∠A′=90°﹣35°=55°,则∠A=∠A′=55°.故答案为:55°.点评:此题主要考查了旋转的性质以及三角形内角和定理等知识,得出∠A′的度数是解题关键.11.如图,将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,则∠EAF的度数是60°.考点:旋转的性质;等边三角形的性质.专题:计算题.分析:根据等边三角形的性质以及旋转的性质得出旋转角,进而得出∠EAF的度数.解答:解:∵将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,∴旋转角为60°,E,F是对应点,则∠EAF的度数为:60°.故答案为:60°.点评:此题主要考查了等边三角形的性质以及旋转的性质,得出旋转角的度数是解题关键.12如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为12﹣4.考点:旋转的性质;菱形的性质.分析:根据菱形的性质得出DO的长,进而求出S正方形DNMF,进而得出S△ADF即可得出答案.解答:解:如图所示:连接AC,BD交于点E,连接DF,FM,MN,DN,∵将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形,∠BAD=60°,AB=2,∴AC⊥BD,四边形DNMF是正方形,∠AOC=90°,BD=2,AE=EC=,∴∠AOE=45°,ED=1,∴AE=EO=,DO=﹣1,∴S正方形DNMF=2(﹣1)×2(﹣1)×=8﹣4,S△ADF=×AD×AFsin30°=1,∴则图中阴影部分的面积为:4S△ADF+S正方形DNMF=4+8﹣4=12﹣4.故答案为:12﹣4.点评:此题主要考查了菱形的性质以及旋转的性质,得出正确分割图形得出DO的长是解题关键.13.如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=,则图中阴影部分的面积等于﹣1 .考点:旋转的性质;等腰直角三角形.专题:压轴题.分析:根据题意结合旋转的性质以及等腰直角三角形的性质得出AD=BC=1,AF=FC′=AC′=1,进而求出阴影部分的面积.解答:解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=,∴BC=2,∠C=∠B=∠CAC′=∠C′=45°,∴AD⊥BC,B′C′⊥AB,∴AD=BC=1,AF=FC′=AC′=1,∴图中阴影部分的面积等于:S△AFC′﹣S△DEC′=×1×1﹣×(﹣1)2=﹣1.故答案为:﹣1.点评:此题主要考查了旋转的性质以及等腰直角三角形的性质等知识,得出AD,AF,DC′的长是解题关键.14.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 6 .考点:旋转的性质;相似三角形的判定与性质.专题:几何图形问题.分析:利用平行线的性质以及旋转的性质得出△CAD∽△B′A′C,再利用相似三角形的性质得出AD的长,进而得出BD的长.解答:解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,∵CB′∥AB,∴∠B′CA′=∠D,∴△CAD∽△B′A′C,∴=,∴=,解得AD=8,∴BD=AD﹣AB=8﹣2=6.故答案为:6.点评:此题主要考查了旋转的性质以及相似三角形的判定与性质等知识,得出△CAD∽△B′A′C是解题关键.15.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是2π.考点:旋转的性质.分析:首先计算出圆的面积,根据图示可得阴影部分面积为半圆的面积,进而可得答案.解答:解:∵AB=4,∴BO=2,∴圆的面积为:π×22=4π,∴阴影部分的面积是:×4π=2π,故答案为:2π.点评:此题主要考查了旋转的性质,关键是掌握圆的面积公式.16.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为2﹣.考点:旋转的性质.专题:几何图形问题.分析:利用正方形和旋转的性质得出A′D=A′E,进而利用勾股定理得出BD的长,进而利用锐角三角函数关系得出DE的长即可.解答:解:由题意可得出:∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD中,AD=1,∴AB=A′B=1,∴BD=,∴A′D=﹣1,∴在Rt△DA′E中,DE==2﹣.故答案为:2﹣.点评:此题主要考查了正方形和旋转的性质以及勾股定理、锐角三角函数关系等知识,得出A′D的长是解题关键.17.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A 顺时针旋转到位置①可得到点P1,此时AP1=;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+;…,按此规律继续旋转,直至得到点P2014为止.则AP2014=1342+672.考点:旋转的性质.专题:规律型.分析:由已知得AP1=,AP2=1+,AP3=2+;再根据图形可得到AP4=2+2;AP5=3+2;AP6=4+2;AP7=4+3;AP8=5+3;AP9=6+3;每三个一组,由于2013=3×671,则AP2013=(2013﹣671)+671,然后把AP2013加上即可.解答:解:AP1=,AP2=1+,AP3=2+;AP4=2+2;AP5=3+2;AP6=4+2;AP7=4+3;AP8=5+3;AP9=6+3;∵2013=3×671,∴AP2013=(2013﹣671)+671=1342+671,∴AP2014=1342+671+=1342+672.故答案为:1342+672.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.三.解答题(共7小题)18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.考点:旋转的性质;含30度角的直角三角形;直角三角形斜边上的中线;菱形的判定.专题:几何图形问题.分析:(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.解答:解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,∴AC=DC,∠A=60°,∴△ADC是等边三角形,∴∠ACD=60°,∴n的值是60;(2)四边形ACFD是菱形;理由:∵∠DCE=∠ACB=90°,F是DE的中点,∴FC=DF=FE,∵∠CDF=∠A=60°,∴△DFC是等边三角形,∴DF=DC=FC,∵△ADC是等边三角形,∴AD=AC=DC,∴AD=AC=FC=DF,∴四边形ACFD是菱形.点评:此题主要考查了菱形的判定以及旋转的性质和直角三角形斜边上的中线等于斜边的一半等知识,得出△DFC是等边三角形是解题关键.19如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.考点:旋转的性质;正方形的判定;平移的性质.专题:几何图形问题.分析:(1)根据旋转和平移可得∠DEB=∠ACB,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.解答:(1)解:FG⊥ED.理由如下:∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,∵CG∥EB,∴∠BCG=∠CBE=90°,∴∠BCG=90°,∴四边形BCGE是矩形,∵CB=BE,∴四边形CBEG是正方形.点评:此题主要考查了图形的旋转和平移,关键是掌握新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.20在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).(1)画出△ABC关于y轴对称的△A1B1C1;(2)画出△ABC关于原点O成中心对称的△A2B2C2.考点:作图-旋转变换;作图-轴对称变换.专题:作图题.分析:(1)根据网格结构找出点A、B、C关于y轴对称的点A1、B1、C1的位置,然后顺次连接即可;(2)根据网格结构找出点A、B、C关于原点对称的点A2、B2、C2的位置,然后顺次连接即可.解答:解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示.点评:本题考查了利用旋转变换作图,利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.21.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为4cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.考点:几何变换综合题.专题:几何综合题.分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案;(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,此时DP+EP值为最小,进而得出答案;(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.解答:解:(1)∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm,∵∠ACD=30°,∠DAC=90°,AC=12cm,∴CD=AC÷cos30°=12÷=12×=8(cm),∵点E为CD边上的中点,∴AE=DC=4cm.故答案为:4;(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE,∴△ADE为等边三角形,∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°,∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′,∴点E,D′关于直线AC对称,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′,∵△ADE是等边三角形,AD=AE=4,∴DD′=2×AD×=2×6=12,即DP+EP最小值为12cm;(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=4,在△ABD′和△CBD′中,,∴△ABD′≌△CBD′(SSS),∴∠D′BG=45°,∴D′G=GB,设D′G长为xcm,则CG长为(6﹣x)cm,在Rt△GD′C中x2+(6﹣x)2=(4)2,解得:x1=3﹣,x2=3+(不合题意舍去),∴点D′到BC边的距离为(3﹣)cm.点评:此题主要考查了全等三角形的判定与性质和锐角三角函数关系以及等边三角形的判定与性质等知识,利用垂直平分线的性质得出点E,D′关于直线AC对称是解题关键.22.正方形ABCD中,E是CD边上一点,(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是BF ,∠AFB=∠AED(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.考点:旋转的性质;全等三角形的判定与性质;勾股定理;正方形的性质.分析:(1)直接根据旋转的性质得到DE=BF,∠AFB=∠AED;(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2,然后利用等相等代换即可得到BM2+DN2=MN2.解答:解:(1)∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,∵DE=BF,∠AFB=∠AED.故答案为BF,AED;(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,∵∠PAQ=45°,∴∠PAE=45°,∴∠PAQ=∠PAE,在△APE和△AP Q中∵,∴△APE≌△APQ,∴PE=PQ,而PE=PB+BE=PB+DQ,∴DQ+BP=PQ;(3)∵四边形ABCD为正方形,∴∠ABD=∠ADB=45°,如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,则∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,∵∠MBA+∠KBA=45°+45°=90°,∴△BMK为直角三角形,∴BK2+BM2=MK2,∴BM2+DN2=MN2.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了三角形全等的判定与性质、正方形的性质以及勾股定理.23.(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A 与点C重合,点P的对应点是Q.若PA=3,PB=2,PC=5,求∠BQC的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.考点:旋转的性质;等边三角形的性质;勾股定理的逆定理;正方形的性质.分析:(1)根据题意得出△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,进而得出∠PBQ=90°,再利用勾股定理得出∠PQC的度数,进而求出∠BQC的度数;(2)由题意可得出:△ABP绕点B顺时针方向旋转60°,才使点A与C重合,进而得出∠PP'C=90°,即可得出∠BPA的度数.解答:解:(1)连接PQ.由旋转可知:,QC=PA=3.又∵ABCD是正方形,∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,即∠PBQ=90°,∴∠PQB=45°,PQ=4.则在△PQC中,PQ=4,QC=3,PC=5,∴PC2=PQ2+QC2.即∠PQC=90°.故∠BQC=90°+45°=135°.(2)将此时点P的对应点是点P′.由旋转知,△APB≌△CP′B,即∠BPA=∠BP′C,P′B=PB=5,P′C=PA=12.又∵△ABC是正三角形,∴△ABP绕点B顺时针方向旋转60°,才使点A与C重合,得∠PBP′=60°,又∵P′B=PB=5,∴△PBP′也是正三角形,即∠PP′B=60°,PP′=5.因此,在△PP′C中,PC=13,PP′=5,P′C=12,∴PC2=PP′2+P′C2.即∠PP′C=90°.故∠BPA=∠BP′C=60°+90°=150°.点评:此题主要考查了旋转的性质以及勾股定理逆定理和正方形的性质等知识,熟练利用勾股定理逆定理得出是解题关键.24.如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.(1)证明:△ABE≌△C1BF;(2)证明:EA1=FC;(3)试判断四边形ABC1D的形状,并说明理由.考点:旋转的性质;全等三角形的判定与性质;等腰三角形的性质;菱形的判定.分析:(1)利用全等三角形的判定结合ASA得出答案;(2)利用全等三角形的性质对边相等得出答案;(3)首先得出四边形ABC1D是平行四边形,进而利用菱形的判定得出即可.解答:(1)证明:∵等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,∴AB=BC1=A1B=BC,∠ABE=∠C1BF,∠A=∠C1=∠A1=∠C,在△ABE和△C1BF中,,∴△ABE≌△C1BF(ASA);(2)证明:∵△ABE≌△C1BF,∴EB=BF.又∵A1B=CB,∴A1B﹣EB=CB﹣BF,∴EA1=FC;(3)答:四边形ABC1D是菱形.证明:∵∠A1=∠C=30°,∠ABA1=∠CBC1=30°,∠A1=∠C=∠ABA1=∠CBC1.∴AB∥C1D,AD∥BC1,∴四边形ABC1D是平行四边形∵AB=BC1,∴四边形ABC1D是菱形.点评:此题主要考查了旋转的性质、全等三角形的判定与性质以及菱形的判定等知识,利用旋转的性质得出对应边关系是解题关键.。
中考数学专题复习卷:轴对称、平移与旋转(含解析)
轴对称、平移与旋转一、选择题1.下列图形中一定是轴对称图形的是()A. B. C. D.【答案】D【解析】A、40°的直角三角形不是轴对称图形,故不符合题意;B、两个角是直角的四边形不一定是轴对称图形,故不符合题意;C、平行四边形是中心对称图形不是轴对称图形,故不符合题意;D、矩形是轴对称图形,有两条对称轴,故符合题意,故答案为:D.【分析】把一个图形沿着一条直线折叠,直线两旁的部分能完全重合的图形就是轴对称图形;根据轴对称图形的定义,再一一判断即可。
2.下列图形中,是轴对称图形但不是中心对称图形的是()A. 正三角形B. 菱形C. 直角梯形D. 正六边形【答案】C【解析】:A.正三角形是轴对称图形,不是中心对称图形,故正确,A符合题意;B.菱形既是轴对称图形,又是中心对称图形,故错误,B不符合题意;C.直角梯形既不是轴对称图形,也不是中心对称图形,故错误,C不符合题意;D.正六边形既是轴对称图形,又是中心对称图形,故错误,D不符合题意;故答案为:A.【分析】根据轴对称图形和中心对称图形定义一一判断对错即可得出答案.3.将抛物线y=-5x +l向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为().A. y=-5(x+1) -1B. y=-5(x-1) -1C. y=-5(x+1) +3D. y=-5(x-1) +3【答案】A【解析】:将抛物线y=-5x+l向左平移1个单位长度,得到的抛物线解析式为:y=-5(x+1)2+1再向下平移2个单位长度得到的抛物线为:y=-5(x-1)+1-2即y=-5(x+1)-1故答案为:A【分析】根据二次函数图像的平移规律:上加下减,左加右减,将抛物线y=ax2向上或向下平移m个单位,再向左或向右平移n个单位即得到y=a(x±n)2±m。
根据平移规则即可得出平移后的抛物线的解析式。
即可求解。
4.在平面直角坐标系中,点关于原点对称的点的坐标是()A.B.C.D.【答案】C【解析】:点关于原点对称的点的坐标为(3,5)故答案为:C【分析】根据关于原点对称点的坐标特点是横纵坐标都互为相反数,就可得出答案。
备考2021年中考数学复习专题:图形的变换_平移、旋转变换_旋转的性质,综合题专训及答案
,在中,,,点延长线上一点,且,连接MP交AC于点H.将射线MP绕点M逆时针旋转交线段找出与相等的角,并说明理由,,求的值)的条件下,若,求线段(2020武汉.中考模拟) 已知平行四边形ABCD.逆时针旋转到的式子表示的值:的图象上,点为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)(1)求点A、B的坐标;:经过A'M,求△OA'M的面积;(2020杭州.中考模拟) 如图1,O为正方形如图一,菱形与菱形的顶点重合,点在对角线上,且.(1)的值为;将菱形绕点按顺时针方向旋转角(),如图二所示,试探究线段与之间的数量关菱形在旋转过程中,当点,,三点在一条直线上时,如图三所示,连接并延长,交于点,若,,则的长为(2020绍兴.中考模拟) 在正方形ABCD中,点E,F分别在边BC,CD上,且∠(2020如皋.中考模拟)11OAB OCD OA=OB OC=OD①的值为;断的值及∠OB= ,请直接写中,,绕点顺时针旋转,它的两边分别交(或它们的延长线)于点 .当绕点旋转到时(如图),易证 .(1)当绕点旋转到时(如图2),线段和之间有怎样的数量关系?写出.当绕点旋转到如图的位置时,线段和之间又有怎样的数量关系?请直接写出(2020武汉.中考模拟) 如图(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC,则,的值变化,当(2020安顺.中考真卷) 如图,四边形是正方形,点O为对角线的中点(1)问题解决:如图①,连接,分别取,的中点P,,则与的数量关系是是将图①中的绕点按顺时针方向旋转得到的三角形,连接,的中点,连接, .的形状,并证明你的结论;是将图①中的绕点A按逆时针方向旋转得到的三角形,连接,的中点,连接, .若正方形的边长为的面积DOE= 。
1M F= 和直线MH x NFMHO的面积;>k如图①,点为正方形内一点,,将绕点按顺时针方向旋转,得到(点的对应点为点),延长交于点,连接.1的形状,并说明理由;,请猜想线段与的数量关系并加以证明;,,请直接写出的长.轴交于点B,连接AB,将△OAB绕着点B顺时针旋转得到△(1)用配方法求抛物线的对称轴并直接写出A,1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、旋转 真题与模拟题分类汇编(难题易错题) 1.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,
G为DF中点,连接EG,CG.
(1)请问EG与CG存在怎样的数量关系,并证明你的结论; (2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立 【解析】 【分析】 (1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG. (2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.
(3)结论依然成立. 【详解】 (1)CG=EG.理由如下:
∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,
同理.在Rt△DEF中,EG=12FD,∴CG=EG. (2)(1)中结论仍然成立,即EG=CG. 证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点. 在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;
在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG(ASA),∴MG=NG. ∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在
△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),
∴AG=EG,∴EG=CG. 证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,
∴MF∥CD∥AB,∴EF⊥MF.
在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE ∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.
∵MG=CG,∴EG=12MC,∴EG=CG.
(3)(1)中的结论仍然成立.理由如下: 过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N. 由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC ∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.
∵G为CM中点,∴EG=CG,EG⊥CG
【点睛】 本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.
2.已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别
与BC、DC的延长线交于点E、F,连接EF,设CE=a,CF=b. (1)如图1,当a=42时,求b的值; (2)当a=4时,在图2中画出相应的图形并求出b的值; (3)如图3,请直接写出∠EAF绕点A旋转的过程中a、b满足的关系式. 【答案】(1)42;(2)b=8;(3)ab=32. 【解析】 试题分析:(1)由正方形ABCD的边长为4,可得AC=42 ,∠ACB=45°. 再CE=a=42,可得∠CAE=∠AEC,从而可得∠CAF的度数,既而可得 b=AC; (2)通过证明△ACF∽△ECA,即可得; (3)通过证明△ACF∽△ECA,即可得. 试题解析:(1)∵正方形ABCD的边长为4,∴AC=42 ,∠ACB=45°.
∵CE=a=42,∴∠CAE=∠AEC=452=22.5°,∴∠CAF=∠EAF-∠CAE=22.5°,
∴∠AFC=∠ACD-∠CAF=22.5°,∴∠CAF=∠AFC,∴b=AC=CF=
42;
(2)∵∠FAE=45°,∠ACB=45°,∴∠FAC+∠CAE=45°,∠CAE+∠AEC=45°,∴∠FAC=∠AEC.
又∵∠ACF=∠ECA=135°,∴△ACF∽△ECA,∴ACCFECCA,∴42442CF,∴CF=8,即b=8.
(3)ab=32.
提示:由(2)知可证△ACF∽△ECA,∴∴ACCFECCA,∴4242ba,∴ab=32.
3.如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE; (2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
【答案】(1)证明见解析;(2)△PMN是等边三角形.理由见解析;(3)△PMN周长的最小值为3,最大值为15. 【解析】 分析:(1)由∠BAC=∠DAE=120°,可得∠BAD=∠CAE,再由AB=AC,AD=AE,利用SAS即可判定△ABD≌△ADE;(2)△PMN是等边三角形,利用三角形的中位线定理可得PM=12CE,PM∥CE,PN=12BD,PN∥BD,同(1)的方法可得BD=CE,即可得PM=PN,所
以△PMN是等腰三角形;再由PM∥CE,PN∥BD,根据平行线的性质可得∠DPM=∠DCE,∠PNC=∠DBC,因为∠DPN=∠DCB+∠PNC=∠DCB+∠DBC, 所以
∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,再由∠BAC=120°,可得∠ACB+∠ABC=60°,即可得
∠MPN=60°,所以△PMN是等边三角形;(3)由(2)知,△PMN是等边三角形,
PM=PN=12BD,所以当PM最大时,△PMN周长最大,当点D在AB上时,BD最小,PM最小,求得此时BD的长,即可得△PMN周长的最小值;当点D在BA延长线上时,BD最大,PM的值最大,此时求得△PMN周长的最大值即可. 详解: (1)因为∠BAC=∠DAE=120°, 所以∠BAD=∠CAE,又AB=AC,AD=AE, 所以△ABD≌△ADE; (2)△PMN是等边三角形. 理由:∵点P,M分别是CD,DE的中点,
∴PM=12CE,PM∥CE,
∵点N,M分别是BC,DE的中点,
∴PN=12BD,PN∥BD,
同(1)的方法可得BD=CE, ∴PM=PN,
∴△PMN是等腰三角形,
∵PM∥CE,∴∠DPM=∠DCE,
∵PN∥BD,∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC, ∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC =∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=120°,∴∠ACB+∠ABC=60°,
∴∠MPN=60°,
∴△PMN是等边三角形.
(3)由(2)知,△PMN是等边三角形,PM=PN=12BD, ∴PM最大时,△PMN周长最大,
∴点D在AB上时,BD最小,PM最小,
∴BD=AB-AD=2,△PMN周长的最小值为3;
点D在BA延长线上时,BD最大,PM最大, ∴BD=AB+AD=10,△PMN周长的最大值为15.
故答案为△PMN周长的最小值为3,最大值为15 点睛:本题主要考查了全等三角形的判定及性质、三角形的中位线定理、等边三角形的判定,解决第(3)问,要明确点D在AB上时,BD最小,PM最小,△PMN周长的最小;点D在BA延长线上时,BD最大,PM最大,△PMN周长的最大值为15.
4.如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋
转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E. (1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE; (2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____; (3)在(1)的条件下,若CD=6,S△BCE=2S△ACD
,求AE的长.
【答案】(1)见解析 (2)AD=BE+DE (3)8 【解析】 试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证; (2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形
的即可证明AF=BE,从而得到AD=BE+DE; (3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解. 试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,
∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,
∵CECFACFBCEACBC
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即
AD+BE=DE;
(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又
∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,
