全国2018-2019学年高二数学选修2-1讲义:第1部分 第1章 1.2 第二课时 含逻辑联结词的命题的真假判断
1.3 简单的逻辑联结词 课件 (新人教选修2-1).

(4) P : {0} q : {0} (1) “P或q”为真,“p且q”为假,“非p”为 解: “P或q”为假,“p且q”为假,“非p”为 真 (2) 真 “P或q”为真,“p且q”为真,“非p”为 (3) 假 “P或q”为真,“p且q”为假,“非p”为 (4) 假
◆巩固结论:例题、习题
ks5u精品课件
课堂流程图
研究“非p”命题
设疑激趣
活动探究
研究“p且q”命题 研究“p或q”命题
巩固提高激趣 ?
非p,p且q,p或q
1.复合命题的构成形式有哪些? 2.观察下列几个命题,指出它们的构成形式,并判 P且q,真 断其真假 P或q,真 ①杨利伟、聂海胜是我国的第一代航天员;
ks5u精品课件
“p或q”形式复合命题当p、 “p且q”形式复合命题当p 结论 “非p”形式复合命题的真 q同为假时为假,其他情 、q同为真时为真,其 况为真; 他情况为假; 假与p的真假相反 复合命题的真假判断(真值表)
P 真 真 q 真 假 非p P且q P或q
假
真
假
真
真
假
假
真
假
真
假
假
真
假
ks5u精品课件
逻 辑 联 结 词(二)
ks5u精品课件
教材分析
1.教材地位: 本节内容把原来分散在高中 数学各章中的逻辑知识集中起来 讲解,作为高中数学学习的基础与 工具,有助于学生思维能力与良好 个性品质的培养,对提高数学素养 起到积极的作用.
ks5u精品课件
教材分析
2.教学目标
知识目标:
(1).理解逻辑联结词“或”“且”“非” 的含义; (2).判断复合命题的真假。
(完整版)高二数学(理科)选修2-1知识点总结,推荐文档
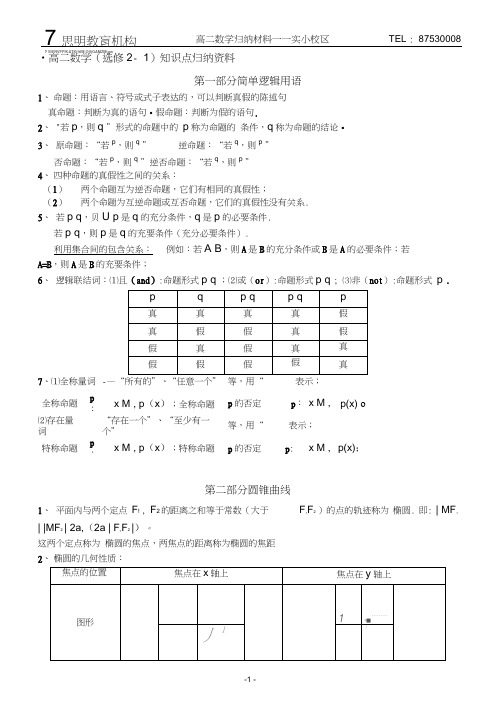
? SlENVFPlKATKiftlM OfljGAMZMigw•高二数学(选修2- 1)知识点归纳资料第一部分简单逻辑用语1、 命题:用语言、符号或式子表达的,可以判断真假的陈述句 真命题:判断为真的语句•假命题:判断为假的语句.2、 "若p ,则q ”形式的命题中的 p 称为命题的 条件,q 称为命题的结论•3、 原命题:“若p ,则q ”逆命题:“若q ,则p ”否命题:“若p ,则q ”逆否命题:“若q ,则p ” 4、 四种命题的真假性之间的关系: (1) 两个命题互为逆否命题,它们有相同的真假性;(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.5、 若p q ,贝U p 是q 的充分条件,q 是p 的必要条件.若p q ,则p 是q 的充要条件(充分必要条件). 利用集合间的包含关系: 例如:若A B ,则A 是B 的充分条件或B 是A 的必要条件;若A=B ,则A 是B 的充要条件;6、 逻辑联结词:⑴且(and ):命题形式p q ;⑵或(or ):命题形式p q ; ⑶非(not ):命题形式 p .7、⑴全称量词--—“所有的”、“任意一个” 等,用“ 表示;全称命题 p:x M , p (x );全称命题 p 的否定p : x M , p(x) o⑵存在量词“存在一个”、“至少有一个”等,用“表示;特称命题 p:x M , p (x );特称命题 p 的否定 p :x M , p(x);第二部分圆锥曲线1、 平面内与两个定点 F ! , F 2的距离之和等于常数(大于F ,F 2)的点的轨迹称为 椭圆. 即: | MF ,| |MF 2| 2a,(2a | F ,F 2|)。
这两个定点称为 椭圆的焦点,两焦点的距离称为椭圆的焦距 2、 椭圆的几何性质:3、平面内与两个定点i , 2的距离之差的绝对值等于常数(小于1)的点的轨迹称为双曲线•即:|| MF i | | MF2 II 2a,(2a IF1F2I)。
高中数学__选修2-1简单的逻辑联结词课件

思考:命题 p∨q的真假如何确定? 观察下列三组命题,命题p∨q的真假与p、q 的真假有什么联系? P:27是7的倍数; q:27是9的倍数; p∨q :27是7的倍数或是9的倍数. P:等腰梯形对角线垂直; q:等腰梯形对角线平分; p∨q:等腰梯形对角线垂直或平分. P:三边对应成比例的两个三角形相似; q:三角对应相等的两个三角形相似; p∨q:三边对应成比例或三角对应相等的两 个三角形相似.
P:等腰三角形两腰相等; q:等腰三角形三条中线相等; p∧q:等腰三角形两边相等且三条中线相等. P:6是奇数; q:6是素数; p∧q:6是奇数且是素数.
命题p∧q的真假判断方法:
填空:一般地,我们规定:当p,q都是真命 题时,p∧q是 真命题 ;当p,q 两个命题 中有一个命题是假命题时,p∧q是 假命题 . 一句话概括: 全真为真,有假即假. p q p∧q
真
真 真 假 假
真 假 真 假
假 假
假
活动探究 探究:逻辑联结词“且”的含义与集合 中学过的哪个概念的意义相同呢?
对“且”的理解,可联想到集合中 “交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”, 是指“x∈A”、“x∈B”这两个条件都 要满足的意思
例题分析
例1:将下列命题用“且”联结成新命题,并判 断他们的真假: (1)p:平行四边形的对角线互相平分, q:平行四边形的对角线相等; (2)p:菱形的对角线互相垂直, q:菱形的对角线互相平分; (3)p:35是15的倍数, q:35是7的倍数.
命题p∨q的真假判断方法:
一般地,我们规定:当p,q两个命题中 有 一 个命题是真命题时,p∨q是 真 命题; 当p,q两个命题都是假命题时,p∨q 是 假 命题.
最新人教版高二数学选修2-1电子课本课件【全册】

0002页 0106页 0174页 0257页 0341页 0457页 0479页 0520页 0545页 0585页 0608页 0637页 0734页
第一章 常用逻辑用语 1.2 充分条件与必要条件 1.4 全称量词与存在量词 复习参考题 2.1 曲线与方程 探究与发现 为什么截口曲线是椭圆 2.3 双曲线 2.4 抛物线 阅读与思考 复习参考题 3.1 空间向量及其运算 3.2 立体几何中的向量方法 复习参考题
最新人教版高二数学选修2-1电子 课本课件【全册】
探究与发现 为什么截口曲线 是椭圆
最新人教版高二数学选修2-1电子 课本课件【全册】
信息技术应用 用《几何画板 》探究点的轨迹:椭圆
最新人教版高二数学选修2-1电子 课本课件【全册】
最新人教版高二数学选修2-1电子 课本课件【全册】
2.1 曲线与方程
最新人教版高二数学选修2-1电子 课本课件【全册】
2.2 椭圆
第一章 常用逻辑用语
最新人教版高二数学选修2-1电子 课本课件【全册】
1.1 命题及其关系
最新人教版高二数学选修2-1电子 课本课件【全册】
1.2 充分条件与必要条件
小结
最新人教版高二数学选修2-1电子 课本课件【全册】
复习参考题
最新人教版高二数学选修2-1电子 课本课件【全册】
第二章 圆锥曲线与方程
最新人教版高二数学选修2-1电子 课课件【全册】
1.3 简单的逻辑联结词
最新人教版高二数学选修2-1电子 课本课件【全册】
1.4 全称量词与存在量词
最新人教版高二数学选修2-1电子 课本课件【全册】
人教版高二数学选修2-1全套精美课件

复习参考题
人教版高二数学选修2-1全套精美 课件
第二章 圆锥曲线与方程
人教版高二数学选修2-1全套精美 课件
第一章 常用逻辑用语
人教版高二数学选修2-1全套精美 课件
1.1 命题及其关系
人教版高二数学选修2-1全套精美 课件
1.2 充分条件与必要条件
人教版高二数学选修2-1全套精 美课件目录
0002页 0115页 0173页 0208页 0231页 0303页 0345页 0388页 0456页 0574页 0658页 0660页 0694页
第一章 常用逻辑用语 1.2 充分条件与必要条件 1.4 全称量词与存在量词 复习参考题 2.1 曲线与方程 探究与发现 为什么截口曲线是椭圆 2.3 双曲线 2.4 抛物线 阅读与思考 复习参考题 3.1 空间向量及其运算 3.2 立体几何中的向量方法 复习参考题
人教版高二数学选修2-1全套精美 课件
1.3 简单的逻辑联结词
人教版 全称量词与存在量词
人教版高二数学选修2-1全套精美 课件
小结
苏教版2018-2019高二数学新学案选修2-1:第一章 常用逻辑用语 §4 4.1~4.2

§4 逻辑联结词“且”“或”“非”4.1 逻辑联结词“且”4.2 逻辑联结词“或”学习目标 1.了解联结词“且”“或”的含义.2.会用联结词“且”“或”联结或改写某些数学命题,并判断其命题的真假.知识点一 “且”思考 观察三个命题:①5是10的约数;②5是15的约数;③5是10的约数且是15的约数,它们之间有什么关系?答案 命题③是将命题①②用“且”联结得到的新命题.梳理 (1)定义:一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题“p且q”.(2)当p,q都是真命题时,p且q是真命题;当p,q两个命题中有一个命题是假命题时,p且q是假命题.将命题p和命题q以及p且q的真假情况绘制为命题“p且q”的真值表如下:p q p且q真真真真假假假真假假假假命题“p且q”的真值表可简单归纳为“同真则真”.知识点二 “或”思考 观察三个命题:①3>2;②3=2;③3≥2,它们之间有什么关系?答案 命题③是命题①②用逻辑联结词“或”联结得到的新命题.梳理 (1)定义:一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题“p或q”.(2)当p,q两个命题有一个命题是真命题时,p或q是真命题;当p,q两个命题都是假命题时,p或q是假命题.将命题p和命题q以及p或q的真假情况绘制为命题“p或q”的真值表如下:p q p或q真真真真假真假真真假假假命题“p或q”的真值表可简单归纳为“假假才假”.1.逻辑联结词“且”“或”只能出现在命题的结论中.(×)2.“p且q为假命题”是“p为假命题”的充分条件.(×)3.当p,q都为假命题时,p且q才为假命题.(×)4.若p:sin x≥2,q:任意x∈R,x2-x+1>0,则p或q为假命题.(×)类型一 含有“且”“或”命题的构成命题角度1 简单命题与复合命题的区分例1 指出下列命题的形式及构成它的命题.(1)向量既有大小又有方向;(2)矩形有外接圆或有内切圆;(3)2≥2.考点 “且”“或”的概念题点 把命题写成“p且q”或“p或q”的形式解 (1)是p且q形式命题.其中p:向量有大小,q:向量有方向.(2)是p或q形式命题.其中p:矩形有外接圆,q:矩形有内切圆.(3)是p或q形式命题.其中p:2>2,q:2=2.反思与感悟 不含有逻辑联结词的命题是简单命题;由简单命题与逻辑联结词“或”“且”构成的命题是复合命题.判断一个命题是简单命题还是复合命题,不能仅从字面上看它是否含有“或”“且”等逻辑联结词,而应从命题的结构来看是否用逻辑联结词联结两个命题.如“四边相等且四角相等的四边形是正方形”不是“且”联结的复合命题,它是真命题,而用“且”联结的命题“四边相等的四边形是正方形且四角相等的四边形是正方形”是假命题.跟踪训练1 命题“菱形对角线垂直且平分”为________形式复合命题.考点 “且”的概念题点 把命题写成“p且q”的形式答案 p且q命题角度2 用逻辑联结词构造新命题例2 分别写出下列命题的“p且q”“p或q”形式的命题.(1)p:梯形有一组对边平行,q:梯形有一组对边相等;(2)p:-1是方程x2+4x+3=0的解,q:-3是方程x2+4x+3=0的解.考点 “且”“或”的概念题点 把命题写成“p且q”或“p或q”的形式解 (1)p或q:梯形有一组对边平行或有一组对边相等.p且q:梯形有一组对边平行且有一组对边相等.(2)p或q:-1或-3是方程x2+4x+3=0的解.p且q:-1和-3是方程x2+4x+3=0的解.反思与感悟 用逻辑联结词“或”“且”联结p,q构成新命题时,在不引起歧义的前提下,可以把p,q中的条件或结论合并.跟踪训练2 指出下列命题的形式及构成它的简单命题.(1)96是48与16的倍数;(2)不等式x 2-x -2>0的解集是{x |x <-1或x >2}.考点 “且”“或”的概念题点 把命题写成“p 且q ”或“p 或q ”的形式解 (1)p 且q :p :96是48的倍数;q :96是16的倍数.(2)p 或q :p :不等式x 2-x -2>0的解集是{x |x <-1},q :不等式x 2-x -2>0的解集是{x |x >2}.类型二 “p 且q ”和“p 或q ”形式命题的真假判断例3 分别指出“p 或q ”“p 且q ”的真假.(1)p :函数y =sin x 是奇函数;q :函数y =sin x 在R 上单调递增;(2)p :直线x =1与圆x 2+y 2=1相切;q :直线x =与圆x 2+y 2=1相交.12考点 “p 且q ”和“p 或q ”形式命题真假性判断题点 判断“p 且q ”和“p 或q ”形式命题的真假解 (1)∵p 真,q 假,∴“p 或q ”为真,“p 且q ”为假.(2)∵p 真,q 真,∴“p 或q ”为真,“p 且q ”为真.反思与感悟 形如p 或q ,p 且q 命题的真假根据真值表判定.跟踪训练3 分别指出由下列各组命题构成的“p 或q ”“p 且q ”形式的命题的真假.(1)p :是无理数,q :π不是无理数;3(2)p :集合A =A ,q :A ∪A =A ;(3)p :函数y =x 2+3x +4的图像与x 轴有公共点,q :方程x 2+3x -4=0没有实数根.考点 “p 且q ”和“p 或q ”形式命题真假性判断题点 判断“p 且q ”和“p 或q ”形式命题的真假解 (1)∵p 真,q 假,∴“p 或q ”为真,“p 且q ”为假.(2)∵p 真,q 真,∴“p 或q ”为真,“p 且q ”为真.(3)∵p 假,q 假,∴“p 或q ”为假,“p 且q ”为假.类型三 已知复合命题的真假求参数范围例4 已知p :方程x 2+mx +1=0有两个不相等的负根,q :方程4x 2+4(m -2)x +1=0无实数根,若p 或q 为真,p 且q 为假,求m 的取值范围.考点 “p 或q ”“p 且q ”形式命题真假性的判断题点 由“p 或q ”“p 且q ”形式命题的真假求参数的取值范围解 因为p :方程x 2+mx +1=0有两个不相等的负根,所以Error!所以m >2.因为q :方程4x 2+4(m -2)x +1=0无实数根,所以Δ<0,即16(m-2)2-16<0,所以16(m2-4m+3)<0,所以1<m<3.因为p或q为真,p且q为假,所以p为真,q为假或者p为假,q为真.即Error!或Error!解得m≥3或1<m≤2.所以m的取值范围为{m|m≥3或1<m≤2}.引申探究本例中若将“p且q为假”改为“p且q为真”,求实数m的取值范围.解 同例得当p为真命题时,m>2,当q为真命题时,1<m<3.因为p或q为真,p且q为真,所以p,q均为真命题,即Error!解得2<m<3,所以m的取值范围为(2,3).反思与感悟 应用逻辑联结词求参数范围的四个步骤(1)分别求出命题p,q为真时对应的参数集合A,B;(2)讨论p,q的真假;(3)由p,q的真假转化为相应的集合的运算;(4)求解不等式或不等式组得到参数的取值范围.跟踪训练4 已知p:(x+2)(x-3)≤0,q:|x+1|≥2,若“p且q”为真,则实数x的取值范围是________.考点 “p且q”形式命题真假性的判断题点 由“p且q”形式命题的真假求参数的取值范围答案 [1,3]解析 由(x+2)(x-3)≤0,解得-2≤x≤3.由|x+1|≥2,解得x≥1或x≤-3.∵“p且q”为真,∴Error!解得1≤x≤3,则实数x的取值范围是[1,3].1.已知p:2+3=5,q:5<4,则下列判断正确的是( )A .p 为假命题B .q 为真命题C .p 或q 为真命题D .p 且q 为真命题考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 判断“p 且q ”“p 或q ”形式命题的真假答案 C解析 由题意,知p 为真命题,q 为假命题.2.由下列各组命题构成的新命题“p 或q ”“p 且q ”都为真命题的是( )A .p :4+4=9,q :7>4B .p :a ∈{a ,b ,c },q :{a }⊆{a ,b ,c }C .p :15是质数,q :8是12的约数D .p :2是偶数,q :2不是质数考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 判断“p 且q ”“p 或q ”形式命题的真假答案 B3.已知命题p ,q ,若p 为真命题,则( )A .p 且q 必为真B .p 且q 必为假C .p 或q 必为真D .p 或q 必为假考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 判断“p 且q ”“p 或q ”形式命题的真假答案 C解析 p 或q ,一真则真,故必有p 或q 为真.4.已知p :函数y =sin x 的最小正周期为,q :函数y =sin2x 的图像关于直线x =π对称,π2则p 且q 是________命题.(填“真”或“假”)考点 “p 且q ”形式命题真假性的判断题点 判断“p 且q ”形式命题的真假答案 假解析 由题意,知命题p 为假命题,命题q 也是假命题,故p 且q 是假命题.5.已知命题p :函数f (x )=(x +m )(x +4)为偶函数;命题q :方程x 2+(2m -1)x +4-2m =0的一个根大于2,一个根小于2,若p 且q 为假,p 或q 为真,求实数m 的取值范围.考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 由“p 且q ”“p 或q ”形式命题的真假求参数的取值范围解 若命题p 为真,则由f (x )=x 2+(m +4)x +4m ,得m +4=0,解得m =-4.设g (x )=x 2+(2m -1)x +4-2m ,其图像开口向上,若命题q为真,则g(2)<0,即22+(2m-1)×2+4-2m<0,解得m<-3.由p且q为假,p或q为真,得p假q真或p真q假.若p假q真,则m<-3且m≠-4;若p真q假,则m无解.所以实数m的取值范围为(-∞,-4)∪(-4,-3).1.判断不含有逻辑联结词的命题构成形式关键是:弄清构成它的命题条件、结论.2.对用逻辑联结词联结的复合命题的真假进行判断时,首先找出构成复合命题的简单命题,判断简单命题的真假,然后分析构成形式,根据构成形式判断复合命题的真假.一、选择题1.“p 且q 是真命题”是“p 或q 是真命题”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件考点 “p 或q ”“p 且q ”形式命题真假性的判断题点 判断“p 或q ”“p 且q ”形式命题的真假答案 A解析 p 且q 是真命题⇒p 是真命题,且q 是真命题⇒p 或q 是真命题;p 或q 是真命题⇏p 且q 是真命题.2.命题p :函数y =log a (ax +2a )(a >0且a ≠1)的图像必过定点(-1,1),命题q :如果函数y =f (x )的图像关于(3,0)对称,那么函数y =f (x -3)的图像关于原点对称,则有( )A .“p 且q ”为真B .“p 或q ”为假C .p 真q 假D .p 假q 真考点 “p 或q ”“p 且q ”形式命题真假性的判断题点 判断“p 或q ”“p 且q ”形式命题的真假答案 C解析 由命题p 知,ax +2a =a ,解得x =-1,故过定点(-1,1),而命题q 为假命题.3.设命题p :函数y =sin2x 的最小正周期为;命题q :函数y =cos x 的图像关于直线x =π2对称,则下列判断正确的是( )π2A .p 为真B .q 为真C .p 且q 为假D .p 或q 为真考点 “p 且q ”形式命题真假性的判断题点 判断“p 且q ”形式命题的真假答案 C解析 函数y =sin2x 的最小正周期为=π,故p 为假命题;x =不是y =cos x 的对称轴,2π2π2命题q 为假命题,故p 且q 为假.故选C.4.p :方程x 2+2x +a =0有实数根,q :函数f (x )=(a 2-a )x 是增函数,若“p 且q ”为假命题,“p 或q ”为真命题,则实数a 的取值范围是( )A .a >0B .a ≥0C .a >1D .a ≥1考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 由“p 且q ”“p 或q ”形式命题的真假求参数的取值范围答案 B解析 ∵方程x 2+2x +a =0有实数根,∴Δ=4-4a ≥0,解得a ≤1.∵函数f (x )=(a 2-a )x 是增函数,∴a 2-a >0,解得a <0或a >1.∵p 且q 为假命题,p 或q 为真命题,∴p ,q 中一真一假.①当p 真q 假时,得0≤a ≤1;②当p 假q 真时,得a >1.由①②,得所求实数a 的取值范围是a ≥0.5.命题p :“x >0”是“x 2>0”的必要不充分条件,命题q :△ABC 中,“A >B ”是“sin A >sin B ”的充要条件,则( )A .p 真q 假B .p 且q 为真C .p 或q 为假D .p 假q 真考点 “p 或q ”“p 且q ”形式命题真假性的判断题点 判断“p 或q ”“p 且q ”形式命题的真假答案 D解析 命题p 假,命题q 真.6.命题p :点P 在直线y =2x -3上;q :点P 在曲线y =-x 2上,则使“p 且q ”为真命题的一个点P 的坐标是( )A .(0,-3) B .(1,2)C .(1,-1)D .(-1,1)考点 “p 且q ”形式命题真假性的判断题点 判断“p 且q ”形式命题的真假答案 C解析 点P (x ,y )满足Error!解得P (1,-1)或P (-3,-9),故选C.7.已知p :x 2-2x -3<0;q :<1,若p 且q 为真,则x 的取值范围是( )1x -2A .(-1,2) B .(-1,3)C .(3,+∞)D .(-∞,2)考点 “p 且q ”形式命题真假性的判断题点 由“p 且q ”形式命题的真假求参数的值答案 A解析 由命题p ,得-1<x <3,当q 为真命题时,得x <2或x >3,因为p 且q 为真命题,所以Error!即-1<x <2.二、填空题8.设p :2x +y =3,q :x -y =6,若p 且q 为真命题,则x =________,y =________.考点 “p 且q ”形式命题真假性的判断题点 由“p 且q ”形式命题的真假求参数的值答案 3 -3解析 若p 且q 为真命题,则p ,q 均为真命题,所以有Error!解得Error!9.若“x ∈[2,5]或x ∈{x |x <1或x >4}”是假命题,则x 的取值范围是________.考点 “p 或q ”形式命题真假性的判断题点 由“p 或q ”形式命题的真假求参数的取值范围答案 [1,2)解析 x ∈[2,5]或x ∈(-∞,1)∪(4,+∞),即x ∈(-∞,1)∪[2,+∞),由于命题是假命题,所以1≤x <2,即x ∈[1,2).10.设p :关于x 的不等式a x >1的解集是{x |x <0},q :函数y =lg(ax 2-x +a )的定义域为R ,如果p 和q 有且仅有一个为真,则a 的取值范围为______________.考点 “p 或q ”形式命题真假性的判断题点 由“p 或q ”形式命题的真假求参数的取值范围答案 ∪(0,12][1,+∞)解析 若p 真,则0<a <1,若p 假,则a ≥1或a ≤0.若q 真,有Error!即a >.12若q 假,则a ≤,又p 和q 有且仅有一个为真,12所以当p 真q 假时,0<a ≤,12当p 假q 真时,a ≥1.综上所述,a ∈∪.(0,12][1,+∞)三、解答题11.判断下列复合命题的真假.(1)等腰三角形顶角的平分线平分底边并且垂直于底边;(2)不等式x 2-2x +1>0的解集为R 且不等式x 2-2x +2≤1的解集为∅.考点 “p 且q ”形式命题真假性的判断题点 判断“p 且q ”形式命题的真假解 (1)这个命题是“p 且q ”形式的复合命题,其中p :等腰三角形顶角的平分线平分底边,q :等腰三角形顶角的平分线垂直于底边,因为p 真q 真,则“p 且q ”为真,所以该命题是真命题.(2)这个命题是“p 且q ”形式的复合命题,其中p :不等式x 2-2x +1>0的解集为R ,q :不等式x 2-2x +2≤1的解集为∅.因为p 假q 假,所以“p 且q ”为假,故该命题为假命题.12.已知p :c 2<c 和q :对任意x ∈R ,x 2+4cx +1>0,若p 或q 为真,p 且q 为假,求实数c 的取值范围.考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 由“p 且q ”“p 或q ”形式命题的真假求参数的取值范围解 由不等式c 2<c ,得0<c <1.由对任意x ∈R ,x 2+4cx +1>0,得(4c )2-4<0,得-<c <.1212由已知,得p 和q 必有一个为真、一个为假.当p 真q 假时,≤c <1;当q 真p 假时,-<c ≤0.1212故实数c 的取值范围是∪(-12,0][12,1)13.设p :函数f (x )=lg(ax 2-4x +a )的定义域为R ;q :设a =(2x 2+x ,-1),b =(1,ax +2),不等式a ·b >0对任意x ∈(-∞,-1)恒成立.如果p 或q 为真命题,p 且q 为假命题,求实数a 的取值范围.考点 “p 或q ”“p 且q ”形式命题真假性的判断题点 由“p 或q ”“p 且q ”形式命题的真假求参数的取值范围解 若p 为真命题,则ax 2-4x +a >0对x ∈R 都成立,当a =0时,f (x )=lg(-4x )的定义域不为R ,不合题意,当a ≠0时.则(-4)2-4a 2<0且a >0,即Error!解得a >2.若q 为真命题,则由a ·b >0对任意x ∈(-∞,-1)恒成立,知2x 2+x -(ax +2)>0,即a >2x -+1对任意x ∈(-∞,-1)恒成立,则a >max .2x (2x -2x +1)令g (x )=2x -+1,可知g (x )在(-∞,-1)上是增函数,当x =-1时取得最大值,g (x )2x max =1.故a ≥1.又p 或q 为真命题,p 且q 为假命题,则p ,q 中一个为真命题,另一个为假命题.若p 真q 假,则Error!无解;若p 假q 真,则Error!则1≤a ≤2.综上,实数a 的取值范围为[1,2].四、探究与拓展14.命题p :1是集合{x |x 2<a }中的元素;命题q :2是集合{x |x 2<a }中的元素.若“p 且q ”是真命题,则a 的取值范围为________.考点 “p 且q ”形式命题真假性的判断题点 “p 且q ”形式命题的真假求参数的取值范围答案 (4,+∞)解析 由p 为真命题,得a >1,由q 为真命题,得a >4.因为p 且q 为真命题,所以Error!解得a >4.15.已知p :(x +1)(x -5)≤0,q :1-m ≤x ≤1+m (m >0).(1)若p 是q 的充分条件,求实数m 的取值范围;(2)若m =5,p 或q 为真命题,p 且q 为假命题,求实数x 的取值范围.考点 “p 且q ”“p 或q ”形式命题真假性的判断题点 由“p 且q ”“p 或q ”形式命题的真假求参数的取值范围解 (1)由(x +1)(x -5)≤0,得-1≤x ≤5,∵p 是q 的充分条件,∴Error!解得m ≥4.(2)当m =5时,q :-4≤x ≤6.根据已知,p ,q 一真一假,当p 真q 假时,Error!无解;当p 假q 真时,Error!解得-4≤x <-1或5<x ≤6.综上,实数x 的取值范围是[-4,-1)∪(5,6].。
2018-2019学年度高二数学人教A版选修2-1课件:2.1.1 曲线与方程2.1.2 求曲线的方程
课标要求
素养达成
1.了解曲线与方程的对应关系. 2.进一步感受数形结合的基本思想. 通过对曲线与方程的学习,培养学生 3.掌握求曲线方程的基本方法(直接 分析、判断、归纳的逻辑思维能力 法),了解求曲线方程的其他方法(待 与抽象思维的能力. 定系数法、定义法、参数法等).
因此,尽管动点C的坐标都满足方程x2+y2=1,但以方程x2+y2=1的解为坐标的 点不都在动点C的轨迹上.
方法技巧
解决此类问题要从两方面入手:(1)曲线上的点的坐标都是
这个方程的解,即直观地说“点不比解多”称为纯粹性;(2)以这个方程的
解为坐标的点都在曲线上,即直观地说“解不比点多”,称为完备性,只有
(2)求曲线方程时应注意的四个问题 ①注意选坐标系:如果原题中没有确定坐标系,首先选取适当的坐标系. ②注意隐含条件:要仔细分析曲线的特征,注意揭示其隐含的条件,列出等 式,此步骤有时也可以省略. ③注意运算的等价性:化简的过程中,注意运算的合理性与准确性,尽量避 免“失解”或“增解”. ④注意验证剔除:说明可以省略不写,若有特殊情况,可以适当说明,如某 些点虽然其坐标满足方程,但不在曲线上,可以通过限定方程中x(或y)的
点和解一一对应,才能说曲线是方程的曲线,方程是曲线的方程.
即时训练1-1:设方程f(x,y)=0的解集非空,如果命题“坐标满足方程f(x,y)=0
的点都在曲线C上”是不正确的,那么下列命题正确的是(
(A)坐标满足方程f(x,y)=0的点都不在曲线C上 (B)曲线C上的点的坐标都不满足方程f(x,y)=0
新知探求
知识点 曲线与方程
2018-2019学年高二数学苏教版选修2-1讲义:第1部分 第1章 1.3 1.3.2 含有一个量词的命题的否定
1.3.2含有一个量词的命题的否定[对应学生用书P14]观察下列几个命题:(1)p:有些三角形是直角三角形;(2)q:所有的质数都是奇数;(3)r:所有的人都睡觉;(4)s:有些实数的相反数比本身大.问题1:哪些是全称命题,哪些是存在性命题?提示:(1)、(4)是存在性命题,(2)、(3)是全称命题.问题2:试对它们进行否定.提示:(1)任意的三角形都不是直角三角形.(2)有些质数不是奇数.(3)有的人不睡觉.(4)任意实数的相反数都不大于本身.问题3:它们的否定有什么规律?提示:全称命题的否定是存在性命题;存在性命题的否定是全称命题.1.全称命题的否定全称命题的否定是存在性命题,“∀x∈M,p(x)”的否定为“∃x∈M,綈p(x)”.2.存在性命题的否定存在性命题的否定是全称命题,“∃x∈M,p(x)”的否定为“∀x∈M,綈p(x)”.对全称命题与存在性命题进行否定的方法:(1)确定所给命题类型,分清是全称命题还是存在性命题;(2)改变量词:把全称量词换为恰当的存在量词;把存在量词换为恰当的全称量词;(3)否定性质:原命题中的“是”“有”“存在”“成立”等更改为“不是”“没有”“不存在”“不成立”等.[对应学生用书P15][例1] 判断下列命题的真假,并写出它们的否定. (1)对任意x ∈R ,x 3-x 2+1≤0; (2)所有能被5整除的整数都是奇数; (3)对任意的x ∈Q ,13x 2+12x +1是有理数.[思路点拨] 几个命题均为全称命题,可先判断真假,再变换量词、否定结论、写出其否定.[精解详析] (1)当x =2时,23-22+1=5>0,故(1)是假命题. 命题的否定:存在x ∈R ,x 3-x 2+1>0.(2)10能被5整除,10是偶数,故(2)是假命题. 命题的否定:存在一个能被5整除的整数不是奇数.(3)有理数经过加、减、乘运算后仍是有理数,故(3)是真命题. 命题的否定:存在x ∈Q ,13x 2+12x +1不是有理数.[一点通]1.全称命题的否定:全称命题的否定是一个存在性命题,给出全称命题的否定时既要否定全称量词,又要否定性质,所以找出全称量词,明确命题所提供的性质是解题的关键.2.常见词语的否定:1.指出下列命题的形式,写出下列命题的否定:(1)所有的矩形都是平行四边形;(2)每一个素数都是奇数;(3)∀x∈R,x2-2x+1≥0.解:(1)∀x∈M,p(x),否定:存在一个矩形不是平行四边形,∃x∈M,綈p(x).(2)∀x∈M,p(x),否定:存在一个素数不是奇数,∃x∈M,綈p(x).(3)∀x∈M,p(x),否定:∃x∈R,x2-2x+1<0,∃x∈M,綈p(x).2.判断下列命题的真假,并写出这些命题的否定:(1)三角形的内角和为180°;(2)每个二次函数的图像都开口向下;(3)任何一个平行四边形的对边都平行;(4)负数的平方是正数.解:(1)是全称命题且为真命题.命题的否定:三角形的内角和不全为180°,即存在一个三角形且它的内角和不等于180°.(2)是全称命题且为假命题.命题的否定:存在一个二次函数的图像开口不向下.(3)是全称命题且为真命题.命题的否定:存在一个平行四边形的对边不都平行.(4)是全称命题且为真命题.命题的否定:某个负数的平方不是正数.[例2]写出下列存在性命题的否定,并判断其否定的真假:(1)有些实数的绝对值是正数;(2)某些平行四边形是菱形;(3)∃x0,y0∈Z,使得2x0+y0=3.[思路点拨]它们的否定是全称命题,解题时既要改变量词,也要否定结论,最后判断其真假.[精解详析](1)命题的否定是:“所有实数的绝对值都不是正数”.由于|-2|=2,因此命题的否定为假命题.(2)命题的否定是:“每一个平行四边形都不是菱形”.由于菱形是平行四边形,因此命题的否定是假命题.(3)命题的否定是:“∀x,y∈Z,2x+y≠3”.因为当x=0,y=3时,2x+y=3,因此命题的否定是假命题.[一点通]1.存在性命题的否定是全称命题,要否定存在性命题“∃x∈M,p(x)成立”,需要验证对M中的每一个x,均有p(x)不成立,也就是说“∀x∈M,綈p(x)成立”.2.要证明存在性命题是真命题,只需要找到使p(x)成立的条件即可.3.只有“存在”一词是量词时,它的否定才是“任意”,当“存在”一词不是量词时,它的否定是“不存在”.例如:三角形存在外接圆.这个命题是全称命题,量词“所有的”被省略了,所以,这个命题的否定是:有些三角形不存在外接圆.3.写出下列命题的否定,并判断其真假:(1)p:∃x0∈R,x20+1<0;(2)p:至少有一个实数x,使x3+1=0.解:(1)綈p:∀x∈R,x2+1≥0,真命题.(2)綈p:∀x∈R,x3+1≠0∵x=-1时,x3+1=0,∴綈p为假命题.4.判断下列命题的真假,并写出这些命题的否定:(1)存在一条直线在y轴上有截距;(2)存在二次函数的图像与x轴相交;(3)存在一个三角形,它的内角和小于180°;(4)存在一个四边形没有外接圆.解:(1)与y轴平行的直线在y轴上没有截距,其他直线在y轴上都有截距,所以,此命题是真命题.命题的否定是:所有的直线在y轴上没有截距;(2)对于二次函数y =ax 2+bx +c (a ≠0),当Δ≥0时,函数图像与x 轴有交点,所以,此命题是真命题,命题的否定是:所有二次函数的图像与x 轴不相交;(3)任何三角形内角和都等于180°.所以,此命题是假命题.命题的否定是:任何三角形的内角和不小于180°;(4)对角不互补的四边形就没有外接圆,所以,此命题是真命题.命题的否定是:任何四边形都有外接圆.[例3] 若全称命题“对任意x ∈[-1,+∞),x 2-2ax +2≥a 恒成立”是真命题,求实数a 的取值范围.[思路点拨] 由于此全称命题是真命题,所以可以推出a 的值,求出在x ∈[-1,+∞)时,f (x )min ≥a ,利用一元二次不等式与二次函数的关系解题.[精解详析] 法一:由题意,对任意x ∈[-1,+∞),令f (x )=x 2-2ax +2≥a 恒成立. 所以f (x )=(x -a )2+2-a 2可转化为对任意x ∈[-1,+∞),f (x )min ≥a 成立,即对任意x ∈[-1,+∞),f (x )min =⎩⎪⎨⎪⎧2-a 2,a ≥-1,(1+a )2+2-a 2,a <-1. 由f (x )的最小值f (x )min ≥a ,知a ∈[-3,1]. 所以实数a 的取值范围是[-3,1].法二:x 2-2ax +2≥a ,即x 2-2ax +2-a ≥0. 令f (x )=x 2-2ax +2-a ,所以全称命题转化为对任意x ∈[-1,+∞),f (x )≥0恒成立. 所以Δ≤0,或⎩⎪⎨⎪⎧Δ=4a 2-4(2-a )>0,a <-1,f (-1)≥0,即-2≤a ≤1,或-3≤a <-2.所以-3≤a ≤1. 综上,所求实数a 的取值范围是[-3,1].[一点通] 对任意x ∈[-1,+∞),f (x )≥a ,只需f (x )min ≥a .也可等价转化为对任意x ∈[-1,+∞),x 2-2ax +2-a ≥0恒成立,结合一元二次不等式的解集与二次函数图像间的关系求解.5.若命题:“∃x ∈k ,m <4sin x +cos x ”是真命题,求m 的取值范围. 解:∵4sin x +cos 2x =-2sin 2x +4sin x +1 =-2(sin x -1)2+3, 又x ∈R 时,-1≤sin x ≤1, ∴4sin x +cos 2x ∈[-5,3]. 则当m <3时,该命题为真命题. ∴m 的取值范围为(-∞,3).6.若方程ax 2+2x -1=0至少有一个正实数根,求实数a 的取值范围. 解:当a =0时,方程变为:2x -1=0,x =12>0满足条件.当a ≠0时,若方程ax 2+2x -1=0至少有一个正实数根. 则Δ=4+4a ≥0,则a ≥-1.又因x =0时,ax 2+2x -1=-1<0恒成立. 故a ≥-1时,一定有正实根. 综上:a 的取值范围为[-1,+∞).对含有一个量词的命题的否定要遵循以下步骤: (1)确定命题类型,是全称命题还是存在性命题.(2)改变量词:把全称量词改为恰当的存在量词;把存在量词改为恰当的全称量词. (3)否定结论:原命题中的“是”“有”“存在”“成立”等改为“不是”“没有”“不存在”“不成立”等.(4)无量词的全称命题要先补回量词再否定.[对应课时跟踪训练(六)]1.(重庆高考改编)命题“对任意x ∈R ,都有x 2≥0”的否定是_________________. 解析:因为“∀x ∈M ,p (x )”的否定是“∃x ∈M ,綈p (x )”故“对任意x ∈R ,都有x 2≥0”的否定是“存在x ∈R ,使得x 2<0”.答案:存在x ∈R ,使得x 2<02.命题“∃x ∈∁R Q ,x 3∈Q ”的否定是________________. 解析:存在性命题的否定是全称命题. 答案:∀x ∈∁R Q ,x 3∉Q3.命题“∀x ∈R ,x 2-x +3>0”的否定是_______________________________. 解析:全称命题的否定是存在性命题. 答案:∃x ∈R ,x 2-x +3≤04.命题“所有能被2整除的整数都是偶数”的否定是______________________. 解析:此命题是一个全称命题,全称命题的否定是存在性命题.故该命题的否定是:“存在能被2整除的整数不是偶数”.答案:存在能被2整除的整数不是偶数5.若命题“∃x ∈R ,使得x 2+(a -1)x +1≤0”为假命题,则实数a 的取值范围是________. 解析:该命题p 的否定是綈p :“∀x ∈R ,x 2+(a -1)x +1>0”,即关于x 的一元二次不等式x 2+(a -1)x +1>0的解集为R ,由于命题p 是假命题,所以綈p 是真命题,所以Δ=(a -1)2-4<0,解得-1<a <3,所以实数a 的取值范围是(-1,3).答案:(-1,3)6.设语句q (x ):cos ⎝⎛⎭⎫x -π2=sin x : (1)写出q ⎝⎛⎭⎫π2,并判定它是不是真命题;(2)写出“∀a ∈R ,q (a )”,并判断它是不是真命题. 解:(1)q ⎝⎛⎭⎫π2:cos ⎝⎛⎭⎫π2-π2=sin π2, 因为cos 0=1,sin π2=1,所以q ⎝⎛⎭⎫π2是真命题.(2)∀a ∈R ,q (a ):cos ⎝⎛⎭⎫a -π2=sin a , 因为cos ⎝⎛⎭⎫a -π2=cos ⎝⎛⎭⎫π2-a =sin a , 所以“∀a ∈R ,q (a )”是真命题.7.写出下列命题的否定,并判断其真假:(1)p :不论m 取何实数,方程x 2+x -m =0必有实数根; (2)q :存在一个实数x ,使得x 2+x +1≤0;(3)r :等圆的面积相等,周长相等.解:(1)这一命题可以表述为p :“对所有的实数m ,方程x 2+x -m =0有实数根”,其否定形式是綈p :“存在实数m ,使得x 2+x -m =0没有实数根”.当Δ=1+4m <0,即m <-14时,一元二次方程没有实数根,所以綈p 是真命题.(2)这一命题的否定形式是綈q :对所有实数x ,都有x 2+x +1>0.利用配方法可以验证綈q 是一个真命题.(3)这一命题的否定形式是綈r :存在一对等圆,其面积不相等或周长不相等,由平面几何知识知綈r 是一个假命题.8.∀x ∈[-1,2],使4x -2x +1+2-a <0恒成立,求实数a 的取值范围.解:已知不等式化为22x -2·2x +2-a <0.① 令t =2x ,∵x ∈[-1,2],∴t ∈⎣⎡⎦⎤12,4,则不等式①化为:t 2-2t +2-a <0,即a >t 2-2t +2,原命题等价于:∀t ∈⎣⎡⎦⎤12,4,a >t 2-2t +2恒成立,令y =t 2-2t +2=(t -1)2+1,当t ∈⎣⎡⎦⎤12,4时,y max =10.所以只须a >10即可.即所求实数a 的取值范围是(10,+∞).。
2018-2019学年北师大版选修2-1 1.4逻辑联结词“且”“或”“非” 课件(20张)
1.正确理解逻辑联结词“且”“或”“非”的 含义和表示.(重点) 2.会判断用“且”“或”“非”联结成新命题 的真假.(难点)
探究点1
联结词“且”
下列三个命题之间有什么关系?
1(1)菱形的对角线互相垂直; (2)菱形的对角线互相平分; (3)菱形的对角线互相垂直且平分; 答案:命题(3)是由命题(1)(2)使用联结词“且”
(假命题)
思考: 如果p且q为真命题,那么p或q一定为真命题吗? 反之,如果p或q为真命题,那么p且q一定是真命题吗?
p 真 真 假 假 真 假 真 假 q p且q 真 假 假 假 真 p或q
真 真
假
1.命题“x=±3是方程∣x∣=3的解”中(
A.没有使用任何一种联结词 B.使用了逻辑联结词“非” C.使用了逻辑联结词 “或” D.使用了逻辑联结词“且”
(3)命题“正数或0的平方根是实数”是 p∨q 的形
式.
5.已知命题p:0不是自然数;q: 是无理 数,写出命题“p∧q”“p∨q”并判断 其真假. 解:p∧q:0不是自然数且 假命题.
是无理数, 是无理数,
p∨q:0不是自然数或
真命题.
含逻辑联结词“且”“或”的命题真假的判断: 确定形式→判断真假. 判断p且q的真假:有假则假. 判断p或q的真假:有真则真.
(2)p∧q:12是3的倍数且是4的倍数.
由于p是真命题,q是真命题,所以p∧q是真命题.
(3)p∧q:π>3且π <2. 是假命题。
例2
用逻辑联结词“且”改写下列命题,并判断
它们是质数.
解:(1)改写为:1是奇数且1是质数.由于“1是质数”
是假命题,所以该命题为假命题.
高二数学选修2-1课件:1.3_简单的逻辑联结词(新人教A版)
若p为真,则﹁p为假.
思考2:对于命题p、q,如何确定 ﹁p∧q,﹁p∨q的真假? 当且仅当p为假命题,q为真命题时, ﹁p∧q为真命题;
当且仅当p为真命题,q为假命题时, ﹁p∨q为假命题.
思考3:命题﹁(p∧q)和﹁(p∨q)分别等 价于什么命题?
﹁(p∧q)=﹁p∨﹁q; ﹁(p∨q)=﹁p∧﹁q.
思考2:一般地,对一个命题p全盘否定, 就得到一个新命题,记作﹁p,读作“非 p”或“p的否定”,那么﹁p的否定是什 么?
﹁p的否定是p 思考3:命题p与﹁p的真假有什么关系? p与﹁p必有一个是真命题, 另一个是假命题.
练习:写出下列命题的否定,并判明真假. 1.矩形的对角线相等且相互平分;
作业:
P18练习:1,2 ,3. 习题1.3A组:3.
当且仅当p、q都是假命题时,p∨q为假 命题.
3.逻辑联结词不只是“且”与“或”, 其中“非”也是一个常用的逻辑联结词, 对此,我们再作些理论分析.
探究(一):逻辑联结词“非” 思考1:下列各组语句是命题吗?它们之 间有什么关系?并判明真假. 真 (1)35能被5整除, 假 35不能被5整除; (2)函数y=lgx是偶函数, 假 函数y=lgx不是偶函数; 真 真 (3)|a|≥0, 假 |a|<0; (4)方程x2-4=0无实根, 假 真 方程x2-4=0有实根.
新知拓展
已知p:方程x mx 1 0有两个不等
2
负实根;q:方程4 x 4(m 2) 1 0
2
无实根,若p q为真,p q为假,求 m的取值范围.
m 3或1 m 2例 已知p:函数 f ( x) (a a) x 在
2
R上单调递减,q:函数 y lg( ax x a )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23第二课时 含逻辑联结词的命题的真假判断[对应学生用书P10]含逻辑联结词的命题的真假判断[例1] 分别指出下列各组命题构成的“p∧q”“p∨q”“綈p”形式的命题的真假:(1)p:6<6,q:6=6;(2)p:函数y=x2+x+2的图像与x轴没有公共点.
q:不等式x2+x+2<0无解;
(3)p:函数y=cos x是周期函数.q:函数y=cos x是奇函数.[思路点拨] 先判断命题p、q的真假,再判断“p∧q”“p∨q”“綈p”的真假.[精解详析] (1)∵p为假命题,q为真命题,∴p∧q为假命题,p∨q为真命题,綈p为真命题.(2)∵p为真命题,q为真命题,∴p∧q为真命题,p∨q为真命题,綈p为假命题.(3)∵p为真命题,q为假命题,∴p∧q为假命题,p∨q为真命题,綈p为假命题.[一点通] 判断含逻辑联结词的命题的真假的步骤:
(1)确定复合命题的构成形式,是“p∧q”、“p∨q”还是“綈p”形式;(2)判断其中简单命题p,q的真假; (3)根据真值表判断含逻辑联结词的命题的真假.
1.分别指出由下列各组命题构成的“p或q”“p且q”的形式的命题的真假:(1)p:a2+1≥1,q:2>3;
(2)p:2+2=5,q:3>2;(3)p:1∈{1,2},q:{1}⊆{1,2};(4)p:∅⊆{0},q:∅={0}.解:pqp或qp且q
(1)真假真假
(2)假真真假23(3)真真真真(4)真假真假
2.分别指出下列命题的构成形式及各命题的真假:(1)全等三角形周长相等或对应角相等;(2)9的算术平方根不是-3;(3)垂直于弦的直径平分这条弦并且平分弦所对的两段弧.解:(1)这个命题是p∨q的形式,其中p:全等三角形周长相等,q:全等三角形对应角相等,因为p真q真,所以p∨q为真.
(2)这个命题是綈p的形式,其中p:9的算术平方根是-3,因为p假,所以綈p为真.
(3)这个命题是p∧q的形式,其中p:垂直于弦的直径平分这条弦,q:垂直于弦的直径平分这条弦所对的两段弧,因为p真q真,所以p∧q为真.
含有逻辑联结词的命题的综合应用[例2] 已知p:函数y=x2+mx+1在(-1,+∞)上单调递增,q:函数
y=4x2+4(m-2)x+1大于零恒成立.若p或q为真,p且q为假,求m的取值范围.
[思路点拨] 由p或q为真,p且q为假,可判断p和q一真一假,进而求m的范围.
[精解详析] 若函数y=x2+mx+1在(-1,+∞)上单调递增,则-≤-1,解得
m2
m≥2,即p:m≥2;若函数y=4x2+4(m-2)x+1恒大于零,则Δ=16(m-2)2-16<0,解得1因为p或q为真,p且q为假,所以p、q一真一假,当p真q假时,由Error!得m≥3,当p假q真时,由Error!得1综上可知,m的取值范围是{m|m≥3或1[一点通] 231.含有逻辑联结词的命题p∧q、p∨q的真假可以用真值表来判断,反之根据命题p∧q、p∨q的真假也可以判断命题p、q的真假.2.解答这类问题的一般步骤:(1)先求出构成命题p∧q、p∨q的命题p、q成立时参数需满足的条件;(2)其次根据命题p∧q、p∨q的真假判定命题p、q的真假;(3)根据p、q的真假求出参数的取值范围.
3.命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;命题q:函数f(x)
=-(5-2a)x是减函数,若p或q为真,p且q为假,求实数a的取值范围.解:由Δ=4a2-16<0,得-2
故命题p:-2由5-2a>1,得a<2,故命题q:a<2.若p或q为真,p且q为假,则①p真,q假.则由Error!得a∈∅.②p假,q真.Error!
∴a<-2.综上可知,符合条件的a的取值范围为(-∞,-2)4.已知a>0,且a≠1,设p:函数y=loga(x+1)在x∈(0,+∞)内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点,“p或q”为真,“p且q”为假,求实数a的取值范围.解:当0<a<1时,函数y=loga(x+1)在(0,+∞)内单调递减;当a>1时,函数
y=loga(x+1)在(0,+∞)内不是单调递减的.
曲线y=x2+(2a-3)x+1与x轴交于不同的两点等价于(2a-3)2-4>0,即a<或a>12
.52
(1)若p为真且q为假,即函数y=loga(x+1)在(0,+∞)内单调递减,曲线23y=x2+(2a-3)x+1与x轴不交于不同的两点,则a∈(0,1)∩,[12,52]
即a∈.[12,1)(2)若p为假且q为真,即函数y=loga(x+1)在(0,+∞)内不是单调递减的,曲线y=x2+(2a-3)x+1与x轴交于不同的两点,则a∈(1,+∞)∩,即a∈((0,12)∪(52,+∞))
.(52,+∞)
综上可知,a的取值范围为∪.[12,1)(52,+∞)
1.含逻辑联结词的综合问题,一般会出现“p或q”为真,“p或q”为假,“p且q”为真,“p且q”为假等这些条件,解题时应先将这些条件翻译成p,q的真假,p,q 的真假有时是不确定的,需要讨论,然后当它们为假时,取其补集即可.2.相关结论:使“p或q”为真的参数范围为使命题p,q分别为真的参数范围的并集,使“p且q”为真的参数范围为使命题p、q分别为真的参数范围的交集.
[对应课时跟踪训练(四)] 1.若p是真命题,q是假命题,则下列说法错误的是________.①p∧q是真命题 ②p∨q是假命题 ③綈p是真命题 ④綈q是真命题解析:p是真命题,则綈p是假命题.q是假命题,则綈q是真命题.故p∧q是假命题,p∨q是真命题.
答案:①②③2.已知命题p:若a>1,则ax>logax恒成立;命题q:在等差数列{an}中,m+n=p+q是am+an=ap+aq成立的充分不必要条件(m,n,p,q∈N*),则下面为真命题的是________.①(綈p)∧(綈q);②(綈p)∨(綈q);③p∨(綈q);④p∧q.解析:当a=1.1,x=2时,
ax=1.12=1.21,logax=log1.12>log1.11.21=2,23此时,ax
命题q,由等差数列的性质,当m+n=p+q时,an+am=ap+aq成立,当公差d=0时,由am+an=ap+aq不能推出m+n=p+q成立,故q是真命题.故綈p是真命题,綈q是假命题,所以p∧q为假命题,p∨(綈q)为假命题,(綈p)∧(綈q)为假命题,(綈p)∨((綈q)为真命题.答案:② 3.已知命题p:不等式ax+b>0的解集为Error!,命题q:关于x的不等式(x-a)(x-b)<0的解集为{x|a________.解析:命题p是假命题,因为当a<0或a=0时解集与已知不同;命题q也是假命题,因为不知道a,b的大小关系.所以只有非p是真命题.
答案:非p4.已知命题p:所有自然数都是正数,命题q:正数的对数都是正数,则下列命题中为真命题的是________.(填序号)①綈p且q;②p或q;③綈p且綈q;④綈p或綈q.解析:因为命题p为假命题,命题q为假命题,所以綈p且綈q为真命题,綈p或綈q为真命题.答案:③④5.(湖北高考改编)在一次跳伞训练中,甲、乙两位学员各跳一次.设命题p是“甲降落在指定范围”,q 是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为________.①(綈p)∨(綈q);②p∨(綈q);③(綈p)∧(綈q);④p∨q.解析:由题意可知,“至少有一位学员没有降落在指定范围”意味着“甲没有或乙没有降落在指定范围”,使用“非”和“或”联结词即可表示该复合命题为(綈p)∨(綈q).
答案:①6.写出下列各组命题构成的“p或q”、“p且q”以及“非p”形式的命题,并判断它们的真假.23(1)p:是有理数,q:是整数;55(2)p:不等式x2-2x-3>0的解集是(-∞,-1),
q:不等式x2-2x-3>0的解集是(3,+∞).
解:(1)p或q:是有理数或是整数;55
p且q:是有理数且是整数;55非p:不是有理数.5
因为p假,q假,所以p或q为假,p且q为假,非p为真.(2)p或q:不等式x2-2x-3>0的解集是(-∞,-1)或不等式x2-2x-3>0的解集是(3,+∞);p且q:不等式x2-2x-3>0的解集是(-∞,-1)且不等式x2-2x-3>0的解集是
(3,+∞);非p:不等式x2-2x-3>0的解集不是(-∞,-1).因为p假,q假,所以p或q假,p且q假,非p为真.7.命题p:实数x满足x2-4ax+3a2<0(a>0),命题q:实数x满足Error!
(1)若a=1,且p∧q为真,求实数x的取值范围;(2)若q⇒綈p,求实数a的取值范围.解:(1)由于a=1,则x2-4ax+3a2<0⇔x2-4x+3<0⇔1所以p:1解不等式组Error!得2所以q:2由于p∧q为真,所以p,q均是真命题,解不等式组Error!得2所以实数x的取值范围是(2,3).(2)綈p:x2-4ax+3a2≥0,a>0,
x2-4ax+3a2≥0⇔(x-a)(x-3a)≥0⇔
x≤a或x≥3a,
