99_泵与风机习题课
流体力学泵与风机的课后习题

流体力学泵与风机的课后习题泵与风机的结构1、指出离心式风机主要部件名称2、指出轴流泵主要部件名称3、在下列热力发电厂的泵与风机序号中选择至少两个正确序号填入下面各题的空白处。
(a)锅炉给水泵 (b)汽轮机凝结水泵 (c)循环水泵(d)送风机 (e)引风机 (f)排粉风机 (g)烟气循环风机1)热力发电厂的泵与风机中 可以采用轴流式;2)热力发电厂的泵与风机中 应注意防磨、防积灰和防腐蚀;3)热力发电厂的泵与风机中 输送的是饱和热水,应采取防汽蚀措施。
4、简述热力发电厂主要有哪些风机?根据所输送的气体性质说明它们在结构上应注意哪些问题?5、轴端密封的方式有几种?它们各自是起到怎样的密封作用?各有何特点?泵与风机的叶轮理论1、转速n=1500r/min的离心风机,叶轮内径D1=480mm。
叶片进口处空气相对速度ω1=25m/s,与圆周速度的夹角为β1=60°,试绘制空气在叶片进口处的速度三角形。
答案:2、有一离心泵转速为1450r/min,其叶轮的进口尺寸为:宽度 ,直径 ,安装角 。
假设有无限多叶片且叶片为无限薄,不考虑叶片厚度对流道断面的影响。
(1)设液体径向流入叶轮,计算叶轮的理论流量。
(2)转速不变,理论流量增大20%,设进口相对流动角仍等于安装角,计算绝对速度的圆周分速度,并说明它的方向是否与圆周速度方向一致。
分析:按照题目已知条件,要计算叶轮理论流量,应想到它等于叶轮进口流道断面面积与进口径向分速度的乘积,进口流道断面面积很容易看出如何计算,进口径向分速度需根据进口速度三角形进行计算,那么就要进一步找出速度三角形的三个参数,从题意中已知了相对流动角 ,容易看出圆周速度如何计算,剩下的一个条件是什么呢?其实,“设液体径向流入叶轮”隐含了一个条件,它意味着进口绝对速度方向为径向,而径向总是与圆周速度方向垂直,所以进口绝对流动角 。
解:(1) 由题意知:、。
(m/s)画出速度三角形(图略),由图知:(m/s) 理论流量为:(m3/s)(2) 由题意知:,圆周速度不变为m/s,流量增大20%,相应的也增大20%(因为叶轮进口流道断面面积不变),即 m/s画出速度三角形(图略),由图知:m/s其方向与圆周速度的方向相反。
《泵与风机》课程试题汇集-3含答案

《泵与风机》课程试题汇集-3一、单项选择题(共15分,每小题1分)1.风机管路特性方程p c='ϕq v2中,p c是表示当管路所输送的流量为q v时,由此管路输送( )气体所需的机械能。
A.单位时间经管路B.单位重量C.单位质量D.单位体积2.圆盘摩擦损失属于( )A.机械损失B.容积损失C.流动损失D.既属于机械损失,又属于流动损失3.某台风机在转速不变时,当输送的空气温度增加时,其全压( )A.增加B.不变C.降低D.先增加后降低4.风机产生旋转失速及喘振的主要原因是其性能曲线为驼峰型,上述的风机的性能曲线是指( )A.q v—p曲线B.q v—P 曲线C.q v—η线曲D.包括q v—p、q v—P、q v—η曲线在内5.两台同性能风机串联运行,串联工作点参数为qv串、p串,改为其中一台单独运行时(管路特性曲线不变),工作点参数为q v单、p单。
则串联与单台工作点间的关系为( ) A. p串=2 p串, q v串= q v单 B. p串<2 p单, q v串>q v单C. p串<2 p单, q v串= q v单D. p串=2 p单, q v串>q v单6.下列各项的值,哪个越大越不易汽蚀?( )A.HgB.HsC.ΔhaD.Δhr7.泵原动机的输入功率为( )A. ρgqvH1000B.ρηgqvH1000C.ρηηgqvHtm1000D.ρηηηgqvHtm g10008.某台水泵在转速不变时,当输送的水温度增加时,其轴功率( )A.增加B.降低C.不变D.先降低,后增加9.对β2e>90°的前弯式叶片,q vT-H T∞的关系曲线为( )A.水平直线B.自左向右上升的直线C.自左向右下降的直线D.自左向右下降的曲线10.当出现轴向涡流时,叶片的出口速度三角形发生变化,下面哪一种变化是正确的?( )A.出口绝对速度的圆周分量变大B.出口绝对速度的圆周分量变小C.出口绝对速度的轴向分量变大D.出口绝对速度的轴向分量变小12.锅炉给水泵是把除氧器内的水压送至锅炉汽包内,当除氧器液面压强在运行中变化时,随着除氧器内液面压力的不断升高,锅炉给水泵的流量q v和扬程H也将不断变化,其变化规律是( )A.q v增大、H升高B.q v减小、H降低C.q v增大、H降低D.q v减小、H升高13.离心式泵与风机是由原动机带动叶轮旋转,( ),从而使流体获得能量。
流体力学泵与风机_课后题答案详解

流体力学泵与风机部分习题答案 2-15解:(1)当1γ为空气 21p p = ()A B p h z p =++γ ()h z p p p B A +=-=∆γ 3.010008.9⨯⨯= kpa pa 94.22940== (2)当1γ为油 31p p =()z H h p p A +++=γ1 ()H h p p B γγ++=13H h z H h p p p p p B A γγγγγ--+++-=-=∆131h z h 1γγγ-+=1.090002.010008.91.010008.9⨯-⨯⨯+⨯⨯= kpa pa 04.22040== 2-16 解:21p p =()211h h H p p M +++=水γ 212h h p p a 汞油γγ++=()2121h h p h h H p a M 汞油水γγγ++=+++()2.010008.96.1378502.05.110008.998011⨯⨯⨯+⨯=++⨯⨯+-h h 26656785098002.098005.1980098011+=+⨯+⨯+-h h 1960147009802665619501--+=hm h 63.51= 2-28解:()21h h p -=γ()()()b h h h b h h h h P 02210212145sin 45sin 21-+--=γγ ()()145sin 22310008.9145sin 232310008.92100⨯-⨯⨯+⨯-⨯-⨯⨯⨯= kN N 65.343465022510008.9==⨯⨯=()()()Pbl h h h bl h h h h l D D D 2022110212145sin 45sin 21-+--=γγ m 45.222510008.9222210008.92322210008.9=⨯⨯⨯⨯⨯+⨯⨯⨯=2-32 解:b h h b h h P 02202145sin 2145sin γγ+= 2222210008.9212222110008.9⨯⨯⨯⨯⨯+⨯⨯⨯⨯=kN N 8576.1106.1108572810008.9==⨯⨯=Ph h b h h h h b h h l D 02102202102145sin 3245sin 2145sin 245sin ⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=γγ 2810008.92372410008.9222410008.9⨯⨯⨯⨯⨯+⨯⨯⨯=2613= 26722613=-=p lT P G l T l P l G ⨯=⨯+⨯22672810008.9162.19⨯=⨯⨯⨯+⨯T kN T 31.10134.27481.9=+= 2-41解:245sin 0=⨯=r hb h h P x ⨯⨯⋅⋅=21γ 4212210008.9⨯⨯⨯⨯⨯=kN N 2.3939200==V P z γ=b r r r⎪⎭⎫⎝⎛⨯⨯⨯-=00245cos 45sin 2136045πγ 4212281214.310008.92⨯⎪⎭⎫ ⎝⎛⨯⨯-⨯⨯⨯⨯= kN N 344.2222344==kN P 1.45344.222.3922=+=03057.0arctan 2.39344.22arctan arctan≈===x z P P α3-3解:(1)s m v d Q /0049.010025.04432323=⋅⋅=⋅=ππs kg Q /9.4=ρ(2)s m v d d v /625.032131=⎪⎪⎭⎫⎝⎛= s m v d d v /5.232232=⎪⎪⎭⎫ ⎝⎛=3-5解:s m h m Q /778.2/1000033==s m d Qv /2042≤=π所以,177.04=≥πv Qd 所以,mm m d 45045.0== 此时,s m d Q d Qv /4.1763585.0112.114422====ππ3-6解:22543212054d d A A A A A ππ======22114012021d d A A ππ=⋅="=' 22224012021d d A A ππ=⋅="='22334012021d d A A ππ=⋅="='22444012021d d A A ππ=⋅="='22554012021d d A A ππ=⋅="='2214014d d ππ=d d 1011=d r 10211= 2224034d d ππ=d d 1032= d r 10232= 2234054d d ππ=d d 1053= d r 10253= 2244074d d ππ=d d 1074= d r 10274=2254094d d ππ=d d 1035=d r 10235= ()()54321254321220240u u u u u d u u u u u d Q G ++++=++++==πρπρρ3-7解:干管前端的质量流量为:42562.2211111d A v Q πρρ⨯⨯==()s kg /128544.005.042562.22=⨯⨯⨯=πs kg Q Q Q /064272.02132===ρρρ ()s m A Q v /247.2204.043.2064272.022222=⋅⋅==πρρ()s m A Q v /05.18045.0424.2064272.023333=⋅⋅==πρρ 3-10解:将基准面建立在B 点经过的水平面上,列能量方程:gv p z gv p z 222222221111αγαγ++=++其中,m z 2.11= m p 5.11=γ s m v /21= s m v d d v /5.4122212== 121==αα gp g 25.40225.12.1222++=++γ871.125.4225.12.1222=-++=gg p γ 3-11解:将2点所在的水平面作为基准面,列能量方程: gv p z gv p z 222222221111αγαγ++=++31=z 02=zγγ21p p =s m v /31=gv p g p 2023322221++=++γγ s m gh v /2.83222=+=32.822112=⎪⎪⎭⎫ ⎝⎛=d d v v 所以,m d 12.02= 3-14解:以水面为基准面,列0-0和D-D 的能量方程:gv p z gv p z DD DD 22220000αγαγ++=++00=z00=γp02200=gv α 4-=D z0=γDpgv DD 2040002α++-=++ 所以,422=gv DD α,即,s m v D /85.88.924=⋅⋅=所以,s m v d Q D /017368.085.805.044322=⋅⋅==ππ81:1:2:24422==A D DD A A d d gv gv αα列0-0和A-A 断面的能量方程:gv p z gv p z AA AA 22220000αγαγ++=++8147000++-=++γAp 所以,8147-=γAp 所以,kpa p A 1.68= 列0-0和B-B 断面的能量方程:gv p z gv p z BB BB 22220000αγαγ++=++kpa p B 484.08.9814-=⋅-= 列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 22220000αγαγ++=++kpa p C 1.208.98142-=⨯⎪⎭⎫ ⎝⎛+-=0=D p3-18解:将基准面建在管道所在的水平面上,列能量方程:21222222111122-+++=++l h gv p z gv p z αγαγ128.998.0008.9490222+++=++g v α9.3222=gv s m v /74.82= 3-19 解:(1)(a )将基准面建在A 所在的水平面上,列0-0和C-C 断面的能量方程:gv p z gv p z CC CC 2222000αγαγ++=++gv CC 2000042α++=++422=gv CC α s m v C /85.88.98=⨯=1:4:2:22222==B C CC B B s s gv gv αα122=gv BB α s m v /43.48.921=⨯= 且 B A v v =(b )(c )gv p z gv p z AA AA 22220000αγαγ++=++10004++=++γAp3=γAp kpa p A 4.29=(2)(a )2122000022-+++=++l CC CC h gv p z gv p z αγαγ其中,gv g v h l 2324222121+=-g v g v g v 223200004222222++++=++54222=g v 所以,s m v /96.32= s m v v /96.12121==(b )(c )gv g v p z g v p z 2222212111120000+++=++αγαγ 5300041++=++γp5341-=γp kpa p 32.331= gv g v g v p z g v p z 223242222222222220000++++=++αγαγ5423545400042⋅++++=++γp kpa p 76.112=3-20 解:()()212221221122-++=--++l a p v p z z v p ργγρs m d Qv /38.2005.014.34202.042221=⨯⨯⨯==πs m d Qv /19.1005.014.3402.04222=⨯⨯==π2423222121v v p l ρρ+=-()()242322222122212211v v v p z z v p a ρρργγρ+++=--++22214v v =()()8.930306.02.1224232300212221221⨯+---+++=v v v v p ρρρρ()()8.930306.02.12424212230022222222⨯+---+++=v v v v ρρρρ8.9606.019.1026.0133002⨯⨯-⨯⨯+= pa 16.352= mm p h 6.449.716.3521===γ3-22解:s kN h kN G /048944.0/2.176==s m GQ /1347.77.08.910048944.033=⨯⨯==γs m d Q d Qv /09.914.31347.7444222=⨯===ππ()2122221122-++=-++l a p v p H v p ργγρ其中,01≈v ,pa h p 988.9101010331=⨯⨯⨯==-γ()γgv d H H 2035.0209.97.008.97.02.1098222+⨯+=⨯⨯-++-()8.97.08.9209.9035.0209.97.008.97.02.109822⨯⨯⨯+⨯+=⨯⨯-++-H HH H 0122.19.289.498+=+-所以,m H 64.32=()212211212212-++=-++l M M a p v p H v p ργγρ()8.97.08.9209.9164.322035.0209.97.064.328.97.02.12109822⨯⨯⨯+⨯+=⨯⨯-++-M p 科技52.169.28968.7998++=+-M p 所以,pa p M 45.63-=3-263-28解:列连续性方程:s m D Qv /18.34.014.344.04221=⨯⨯==π s m d Q v /96.501.014.344.04222=⨯⨯==π列能量方程: g v p z g v p z 222222221111αγαγ++=++ g v g v p 222112221ααγ-=m 98.1318.9218.396.5022=⨯-= kpa p 404.12938.998.1311=⨯=列动量方程:()12v vQ F -=∑ρ ()12222144v v Q R d p D p -=-⨯-⨯ρππ()18.396.504.04.04404.12932-⨯=-⨯⨯R πkN R 339.14378.474.04.04404.12932=⨯-⨯⨯=π kN R 94.1112=3-33解:列能量方程:g v p z g v p z 222222221111αγαγ++=++ 其中,5321=v v 2221259v v = g v g v 209.0205.1222211αα++=++gv g v 225926.02222-= s m v /3.42= s m v /58.21=()12v v Q F -=∑ρ()1222212121v v Q R b h b h -=--ργγ 其中,s m Q /644.45.12.158.23=⨯⨯= 72.1644.410009.0108.9215.1108.9212323⨯⨯=-⨯⨯⨯-⨯⨯⨯R N R 2.480=4-2 (1) m mm d 1.0100== s kg Q /10=ρs m Q Q /01.03==ρρs m d Q v /274.11.014.301.04422=⨯⨯==π s m /10519.126-⨯=ν 8387110519.11.0274.1Re 6=⨯⨯==-νvd (紊流) (2) s kg Q /10=ρ s m Q Q /011765.0850103===ρρ s m d Q v /4987.11.014.3011765.04422=⨯⨯==π s m /1014.124-⨯=ν 13151014.11.04987.1Re 4=⨯⨯==-νvd 4-3 解:m d 3.0= C T 020= s m /107.1526-⨯=νs m d v /1067.1043.0107.152000Re 36max --⨯=⨯⋅=⋅=ν s m A v Q /103947.743.014.31067.1043323max max --⨯=⨯⨯⨯=⋅= h kg Q /9.3136002.1103947.73=⨯⨯⨯=-ρ4-4 解:212=d d 4212221==d d v v 222111Re 2214Re ===ννd v d v 所以,2Re Re 21= 4-12 紊流粗糙区,5106Re ⨯> νvd=Re ,所以,s m d v /14.325.010308.1106Re 65=⨯⨯⨯==-ν s m d v Q /154.0425.014.314.34322=⨯==π 4-13 s m s L Q /2.0/20031==s m d Q v /076433.44211==π 661107791.010308.125.0076433.4Re ⨯=⨯⨯==-νvd s L Q /202= s m v /4076433.02=4210791.7Re ⨯=s L Q /53= s m v /1019.03= 43109478.1Re ⨯=查尼氏图,得到, 5106Re ⨯=u 4104Re ⨯=l123Re Re Re Re Re <<<<u l ,所以,1Q 属于紊流粗糙区,2Q 属于紊流过渡区,3Q 属于紊流光滑区,(1) 对于1Q ,采用希弗林松公式,02326.025.0105.011.011.025.0325.01=⎪⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=-d K λm g v d l h f 888.78.92076433.425.010002326.0222111=⨯⨯⨯==λ (2) 对于2Q ,采用阿公式,02547.010791.76825.0105.011.0Re 6811.025.04325.02=⎪⎪⎭⎫ ⎝⎛⨯+⨯=⎪⎭⎫ ⎝⎛+=-d K λ m g v d l h f 086.08.924076433.025.010002547.0222222=⨯⨯⨯==λ(3) 对于3Q ,采用布公式02678.05.194773164.0Re 3164.025.025.03===λ m g v d l h f 005676.08.9244076433.025.010002678.0222333=⨯⎪⎭⎫ ⎝⎛⨯⨯==λ 4-15 5102Re ⨯=u 4000Re =lm d 05.0= m K 31025.0-⨯= s m d v u /028.405.010007.1102Re 65max =⨯⨯⨯==-νs L d v Q /905.7405.014.3028.4422max max =⨯==π 26min 10056.805.010007.14000Re --⨯=⨯⨯==d v l ν s L s m d v Q /1581.0/1001581.0405.014.310056.8432222min min =⨯=⨯⨯==--π 4-21 (1) a d d =21 2211av v = gv d l d v g v d l g v d l h f 2642Re 64221111211121111νλ=== 4212221211ad d v v h h f f == 19.1=a (2)75.425.12275.12122225.0225.0225.021125.0125.0125.021123164.023164.0a d d v v gv d l d v g v d l d v h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛==νν 16.1=a (3)25.525.11222122225.0221125.01211211.0211.0a d d v v g v d l d K g v d l d K h h f f =⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛= 14.1=a 4-24 解:s m Q /002742.0602329.03=⨯=s m d Q v /3972.105.014.3002742.04422=⨯⨯==π 629.022=⎪⎭⎫ ⎝⎛+g v d l ζλ ()629.08.923972.162=⨯+ζ 3151.0=ζ 4-26 解:(1) 突然缩小375.03145.7815.015.0121=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζmm m g v h j 5.760765.08.922375.022211==⨯==ζ (2)5.02=ζmm m g v h j 102102.08.9225.022222==⨯==ζ (3)1693145.781122213=⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=A A ζ mm m h j 115115.08.92216923==⨯= (4)14=ζ mm m h j 204204.08.922124==⨯= 4-27 解:()()gv v g v v h h m m j j 222121-+-=''+' ()()()()02212221=-+--=''+'gv v g v v h h m m vm j j 所以,221v v v m += 此时,()j j j h gv v g v v v g v v v h h 2221222222121212211=-=⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛+-=''+' 4-29 解:s m h m Q /1044.4/16333-⨯== s m d Q v /2624.205.014.31044.44423211=⨯⨯⨯==-π s m d Q v /5656.01.014.31044.44423222=⨯⨯⨯==-π m g v v p p h j 140674.08.925656.02624.28.910001739.522222121=⨯-+⨯⨯-=-+-=γ g v h j 2211ζ= 5387.01=ζ gv h j 2222ζ= 619.82=ζ5-17 解:5.6082.014.32.12.01002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 7.30422.014.32.12.05002.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 973671.014.32.11.05002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=d d l S p πρλ 3.101018973677.30425.608321=++=++=p p p p S S S S 22211/91.227215.03.101018m N Q S p p =⨯==22222/1.258616.03.101018m N Q S p p =⨯==5-25 解:()()⎪⎩⎪⎨⎧=++=++=1021520232322223221SQ Q Q S SQ Q Q S SQ 610=S解得,s m Q /10472.4331-⨯= s m Q /1041.2332-⨯= s m Q /1063.0333-⨯=5-27 解:94.10348.92.014.32.020002.08842412111=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 8.206988.91.014.31.0100025.08842422222=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 78.37258.92.014.32.072002.08842432333=⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=g d d l S πλ 038035.087.14311705.321111211=+=+='S S S 所以,25.6911='S 1)()H Q S S =+'231s m S S H Q /10186.604417163331-⨯==+'=2)H SQ =2 H Q S =⎪⎭⎫ ⎝⎛'221 1325133831432=+'=-'=S S S S gd πζ ()1.25688.92.014.31325142=⨯⨯⨯=ζ 5-28 解:286.1368.93.014.383.020002.084242=⨯⨯⨯⨯==g d d l S AB AB AB AB πλ 029.1098.93.014.383.016002.084242=⨯⨯⨯⨯==g d d l S AC AC AC AC πλ 34.328.94.014.384.020002.084242=⨯⨯⨯⨯==g d d l S AD AD AD AD πλ 772.818.93.014.383.012002.084242=⨯⨯⨯⨯===g d d l S S BC BC BC CD BC πλ 5108.2⨯=A p2AB AB A Q S p γ= s m S p Q AB A AB /457868.08.91000286.136108.235=⨯⨯⨯==γ 2AD AD A Q S p γ= s m S p Q AD A AD /93993.08.9100034.32108.235=⨯⨯⨯==γ ()()222BC BC BC AC A Q S Q S p += ()s m S S p Q Q BC AC A CD BC /23488.043=+==γs m Q Q Q BC AB /69275.022=+= s m Q Q Q CD AD /17481.123=+=s m Q Q Q /86756.13321=+= 22/2.44m kN Q S p BC BC C ==γ。
泵与风机杨诗成,习题及答案(6)
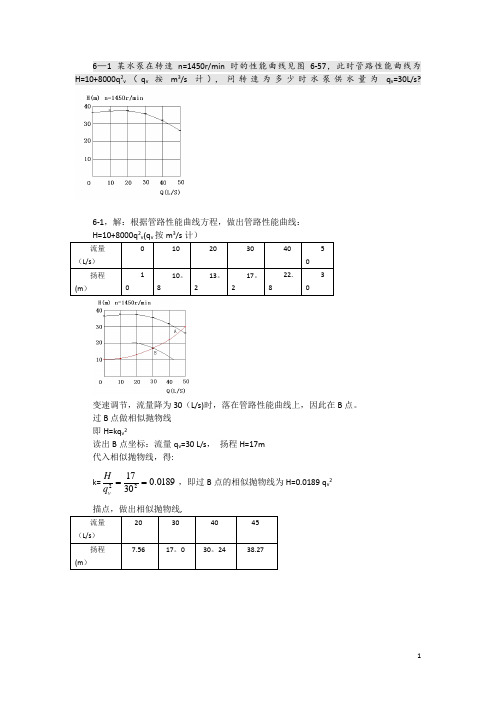
6—1 某水泵在转速n=1450r/min 时的性能曲线见图6-57,此时管路性能曲线为H=10+8000q 2v (q v 按m 3/s 计),问转速为多少时水泵供水量为q v =30L/s?6-1,解:根据管路性能曲线方程,做出管路性能曲线: 23流量(L/s )102030405扬程(m )110。
813。
217。
222.830变速调节,流量降为30(L/s)时,落在管路性能曲线上,因此在B 点。
过B 点做相似抛物线 即H=kq v 2读出B 点坐标:流量q v =30 L/s , 扬程H=17m 代入相似抛物线,得: k=0189.0301722==v q H ,即过B 点的相似抛物线为H=0.0189 q v 2 流量(L/s )20 30 40 45 扬程(m )7.5617。
030。
2438.27如图:与原性能曲线相交于C 点,则C 、B 两点相似。
C 点坐标:流量q v =41 L/s , 扬程H=32m 根据相似定律得:22121⎪⎪⎭⎫ ⎝⎛=n n H H min /1989173214501212r H H n n =⨯==也可以通过:2121n n q q = min /1982304114501212r q q n n =⨯==6—2 某离心风机在转速为n 1=1450r/min 时,p-q v 曲线见图6—58,管路性能曲线方程为p=20q 2v 。
若采用变转速的方法,使风机流量变为q 2v =27 000m 3/h ,此时风机转速应为多少?2流量(m 3/s )246810风压(Pa )832720128200管路性能曲线与相似抛物线重合,因此,A 、B 两点相似, A (8。
3,1380),B (2。
74,150)22121⎪⎪⎭⎫ ⎝⎛=n n p p min /478138015014501212r p p n n =⨯==6—3 某离心泵转速为n 1=950r/min,其性能曲线见图6—59,问当n 2=1450r/min 时,水泵流量改变了多少?6-3转速改变后,满足相似定律根据图,知道原来转速下的工作点:(46,87)1212n n q q = ∴s m n n q q /2.7095014504631212=⨯=⨯= 6-46—4 一台离心风机性能曲线见图6-60,管路性能曲线方程为p=20q 2v .若把流量调节到q v =6m 3/s,采用出口节流和变速两种调节方法,则采用两种调节方法后风机的轴功率各为多少?若风机按每年运行7500h 计算,变速调节每年要比节流调节节省多少电能?流量(m 3/s )246810风压(Pa )832720128200变速调节在B点工作:B(6m3/s,700Pa),由于变速调节效率曲线随之移动,即效率与原工作点相同。
泵与风机第四版(何川 郭立君)课后习题答案

由 HT =
ctg 2 a u 2 v 2u / v 2 m 6.04 37.31 / 38.8 0.806
2 a 128.85 (数据有问题,离心泵出口安装角应是锐角,即后弯式叶片)
1-7 有一离心式风机,叶轮外径 D2 =600mm,叶轮出口宽度 b2 =150mm,叶片出 口安装角 2 a =30°,转速 n=1450r/min。设空气在叶轮进口处无预旋,空气密度
b 为多 t
v1 wa v a 5.8 (m/s)
由题知轴向进入 v1u 0 ,所以 w1u u 。 w2u u v 2u 21.25 2.3 18.95 (m/s)
பைடு நூலகம்rctg
2v1 w1u w2u
2 5.8 16.09 arctg 21 . 25 18 . 95
Dn 3.14 0.38 2 1450
60
=
60
57.67 (m/s)
v1 wa =33.5(m/s) v2u = p 692.8 = 10.01 (m/s) u 1.2 57.67
由题知轴向进入 v1u 0 ,所以 w1u u 。 w2u u v 2u 57.67 10.01 47.66 (m/s)
流体力学泵与风机 课后习题讲解

150
1-8.如 图 所 示 盛 水U 形 管, 静 止 时, 两 支 管 水 面 距 离 管 口 均 为h, 当U 形 管 绕OZ 轴 以 等 角 速 度ω 旋 转 时, 求 保 持 液 体 不 溢 出 管 口 的 最 大 角 速 度ωmax 。
解:由 液 体 质 量 守 恒 知, 管 液 体 上 升 高 度 与 管 液 体 下 降 高 度 应 相 等,且 两 h 者 液 面 同 在 一 等 压 面 上, 满 足 等 压 面 方
在 液 面 上 为 大 气 压, dp0
ac3 o 0 d x 0 s ( g as3 i0 ) n d 0 z 0
将 以 上 关 系 代 入 平 衡 微 分 方 程, 得:
ac3 o 0 d x 0 s ( g as3 i0 ) n d 0 z 0
dz
aco3s0 0
dxtangasi3 n0 00.269
程: 2r 2 z C 2g
液 体 不 溢 出, 要 求 zIzII2 h
, 程
以得:r1a,
r2b 分
别
代
入
等
压面
方
z
I
II
a
b
a>b
gh 2 a2 b2
gh max2 a2b2
作业解答
1-10.一个圆锥体绕其铅直中心轴等速旋转,锥体与固定壁的间距为δ=1mm, 全部为润滑油充满,μ=0.1Pa.s ,当旋转角速度ω=16s-1,锥体底部半径R= 0.3m,高H=0.5m时,求:作用于圆锥的阻力矩。
此 力 即 为 射 流 对 平 板 的 作 用 力P1, 此 外, 平板另一侧所受到的静止油液的总压力
P 2g2h2A 20.8g2h d 42 2
流体力学泵与风机 蔡增基 课后习题答案
得 µ =0.105pa.S 10. 一圆锥体绕其铅直中心轴等速旋转, 锥体与固定壁间的距离 δ
= 1mm ,全部为
润滑油( µ =0.1pas)充满,当旋转速度
ω = 16 s −1
,锥 体 底 部 半 径 R=0.3m ,高
H=0.5m 时,求作用于圆锥的阻力矩。 解: dT 其中 dA
dl = dr sin θ
1
10%,问此时 µ 增加多少? 解: µ = ρυ = γυ
g
= (1 − 10%)(1 + 15%)
γ 0υ 0 γ υ = 1.035 0 0 g g
所以 µ 增加了 3.5% 7.水平方向运动的木板,其速度为 1m/s,平板浮在油面上 ,
δ = 10mm
,油的 µ =0.09807pa.s。求作用于平板单位面积上
5.在封闭水箱中, 水深 h = 1.5m 的 A 点上安 装一压力表,其中表距 A 点 Z=0.5m 压 力表读数为 4.9kN / m 2 ,求水面相对压强及 其真空度。
6
解: p0 + γh = M + γZ
内科大流体力学泵与风机蔡增基_课后习题答案(2)
论
1. 流体的容重及密度有何区别及联系? 解: γ
=ρg
ρ 是流体的本身属性。 γ
还与 g 有关。
2. 已知水的密度 ρ = 1000kg/m 3 ,求其容重。 若有这样的水 1L, 它的质量和重力各是多少? 解: γ = ρ g=1000×9.807=9807N/m 3 m= ρ v=1000×0.001=1kg G=mg=1×9.807=9.807N
8
p0 + γh + γ Hg ∆h = 0 p0 = −9.807 × 1.22 − 133.375 × 0.203 = −38kpa pv = γ Hg ∆h = 133.375 × 0.203 = 27 kpa
11. 管路上安装一 U 形 测压管,测得 h1 = 30cm,h2 = 60cm ,
4
流体静力学
1. 试求图(a),( b),( c)中,A,B,C 各点相对压强,图
中 p0 是绝对压强,大气压强 p a
= 1atm 。
解: ( a) (b)
p = ρgh = 1000 × 9.807 × 7 = 68650 pa = 68.65kpa
p = p 0 + ρgh − 1atm = 100000 + 1000 × 9.807 × 3 − 101325 = 28096 pa = 28.1kpa
h = 2.5m 处安装一测压表
M ,试求 M 的
7
读数。 解:
p M = γ Hg ∆h + γh = 133.375 × 0.1 + 9.807 × 2.5 = 37.86kpa
8. 已 知 水 深 h=1.2m , 水 银 柱 高 度 h p
= 240mm
泵与风机部分思考题及习题答案
泵与风机部分思考题及习题答案泵与风机(思考题答案)绪论3.泵与风机有哪些主要的性能参数?铭牌上标出的是指哪个⼯况下的参数?答:泵与风机的主要性能参数有:流量、扬程(全压)、功率、转速、效率和汽蚀余量。
在铭牌上标出的是:额定⼯况下的各参数5.离⼼式泵与风机有哪些主要部件?各有何作⽤?答:离⼼泵叶轮:将原动机的机械能传递给流体,使流体获得压⼒能和动能。
吸⼊室:以最⼩的阻⼒损失引导液体平稳的进⼊叶轮,并使叶轮进⼝处的液体流速分布均匀。
压出室:收集从叶轮流出的⾼速流体,然后以最⼩的阻⼒损失引⼊压⽔管或次级叶轮进⼝,同时还将液体的部分动能转变为压⼒能。
导叶:汇集前⼀级叶轮流出的液体,并在损失最⼩的条件下引⼊次级叶轮的进⼝或压出室,同时在导叶内把部分动能转化为压⼒能。
密封装置:密封环:防⽌⾼压流体通过叶轮进⼝与泵壳之间的间隙泄露⾄吸⼊⼝。
轴端密封:防⽌⾼压流体从泵内通过转动部件与静⽌部件之间的间隙泄漏到泵外。
离⼼风机叶轮:将原动机的机械能传递给流体,使流体获得压⼒能和动能蜗壳:汇集从叶轮流出的⽓体并引向风机的出⼝,同时将⽓体的部分动能转化为压⼒能。
集流器:以最⼩的阻⼒损失引导⽓流均匀的充满叶轮⼊⼝。
进⽓箱:改善⽓流的进⽓条件,减少⽓流分布不均⽽引起的阻⼒损失。
9.试简述活塞泵、齿轮泵及真空泵、喷射泵的作⽤原理?答:活塞泵:利⽤⼯作容积周期性的改变来输送液体,并提⾼其压⼒。
齿轮泵:利⽤⼀对或⼏个特殊形状的回转体如齿轮、螺杆或其他形状的转⼦。
在壳体内作旋转运动来输送流体并提⾼其压⼒。
喷射泵:利⽤⾼速射流的抽吸作⽤来输送流体。
真空泵:利⽤叶轮旋转产⽣的真空来输送流体。
第⼀章1.试简述离⼼式与轴流式泵与风机的⼯作原理。
答:离⼼式:叶轮⾼速旋转时产⽣的离⼼⼒使流体获得能量,即流体通过叶轮后,压能和动能都得到提⾼,从⽽能够被输送到⾼处或远处。
流体沿轴向流⼊叶轮并沿径向流出。
轴流式:利⽤旋转叶轮、叶⽚对流体作⽤的升⼒来输送流体,并提⾼其压⼒。
泵与风机答案 何川
泵与风机(课后习题答案)第一章1-1有一离心式水泵,其叶轮尺寸如下:1b =35mm, 2b =19mm, 1D =178mm, 2D =381mm, 1a β=18°,2a β=20°。
设流体径向流入叶轮,如n=1450r/min ,试画出出口速度三角形,并计算理论流量,V T q 和在该流量时的无限多叶片的理论扬程T H ∞。
解:由题知:流体径向流入叶轮 ∴1α=90° 则:1u =1n60D π=317810145060π-⨯⨯⨯=13.51 (m/s )1V =1m V =1u tg 1a β=13.51⨯tg 18°=4.39 (m/s )∵1V q =π1D 1b 1m V =π⨯0.178⨯4.39⨯0.035=0.086 (3m /s ) ∴2m V =122Vq D b π=0.0860.3810.019π⨯⨯=3.78 (m/s ) 2u =2D 60n π=338110145060π-⨯⨯⨯=28.91 (m/s ) 2u V ∞=2u -2m V ctg 2a β=28.91-3.78⨯ctg20°=18.52 (m/s )T H ∞=22u u V g∞=28.9118.529.8⨯=54.63 (m )1-2有一离心式水泵,其叶轮外径2D =220mm,转速n=2980r/min ,叶片出口安装角2a β=45°,出口处的轴面速度2m v =3.6m/s 。
设流体径向流入叶轮,试按比例画出出口速度三角形,并计算无限多叶片叶轮的理论扬程T H ∞,又若环流系数K=0.8,流动效率h η=0.9时,泵的实际扬程H 是多少? 解:2u =2D 60n π=0.22298060π⨯⨯=34.3 (m/s )∵2m V =3.6 m/s 2a β=45°∴2w =22sin mav β=5.09 (m/s ) 画出出口速度三角形 2u V ∞=2u -2m V ctg 2a β=34.31-3.6⨯ctg45°=30.71 (m/s ) ∵1α=90°T H ∞=22u u V g∞=34.3130.719.8⨯=107.5 (m)实际扬程H=K T H =K h ηT H ∞=0.8⨯0.9⨯107.5=77.41 (m)1-3有一离心式水泵,叶轮外径2D =360mm ,出口过流断面面积2A =0.0232m ,叶片出口安装角2a β=30°,流体径向流入叶轮,求转速n=1480r/min ,流量,V T q =86.8L/s 时的理论扬程T H 。
