2015秋华师大版数学九上246《图形与坐标》练习题2
华师大版-数学-九年级上册-24.6图形与坐标 完整版

24.6图形与坐标一、选择题1.(2009年江苏)如图,在55⨯方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是()A.先向下平移3格,再向右平移1格B.先向下平移2格,再向右平移1格C.先向下平移2格,再向右平移2格D.先向下平移3格,再向右平移2格【关键词】平移【答案】D2.(2009年湖北孝感)如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1,则B′点的坐标为()A.33()22,B.33()22,C.13()22,D.31(,)22【关键词】图形的变换【答案】A二、填空题1.(2009年吉林省)如图,OAB△的顶点B的坐标为(4,0),把OAB△沿x轴向右平移得到CDE△,如果1,CB=那么OE的长为.【关键词】平移,平面直角坐标系内的平移【答案】7三、解答题1.(2009年浙江宁波)如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(80)-,,xyA DO C B E直线BC 经过点(86)B -,,(06)C ,,将四边形OABC 绕点O 按顺时针方向旋转α度得到四边形OA B C ''',此时直线OA '、直线B C ''分别与直线BC 相交于点P 、Q . (1)四边形OABC 的形状是 , 当90α=°时,BPBQ的值是 ; (2)①如图2,当四边形OA B C '''的顶点B '落在y 轴正半轴时,求BPBQ的值; ②如图3,当四边形OA B C '''的顶点B '落在直线BC 上时,求OPB '△的面积.(3)在四边形OABC 旋转过程中,当0180α<≤°时,是否存在这样的点P 和点Q ,使12BP BQ =?若存在,请直接写出点P 的坐标;若不存在,请说明理由.【关键词】相似三角形有关的计算和证明 【答案】解:(1)矩形(长方形);47BPBQ =. (2)①POC B OA ''∠=∠,PCO OA B ''∠=∠90=°,COP A OB ''∴△∽△. CP OC A B OA ∴=''',即668CP =,92CP ∴=,72BP BC CP =-=.同理B CQ B C O '''△∽△,CQ B C C Q B C '∴=''',即10668CQ -=, 3CQ ∴=,11BQ BC CQ =+=. 722BP BQ ∴=. ) (图3)(图2) (备用图)(第10题)②在OCP △和B A P ''△中,90OPC B PA OCP A OC B A ''∠=∠⎧⎪'∠=∠=⎨⎪''=⎩,°,, (AAS)OCP B A P ''∴△≌△.OP B P '∴=. 设B P x '=,在Rt OCP △中, 222(8)6x x -+=,解得254x =. 125756244OPB S '∴=⨯⨯=△. (3)存在这样的点P 和点Q ,使12BP BQ =. 点P的坐标是19P ⎛⎫- ⎪⎝⎭,2764P ⎛⎫- ⎪⎝⎭,. 对于第(3)题,我们提供如下详细解答,对学生无此要求. 过点Q 画QH OA '⊥于H ,连结OQ ,则QH OC OC '==,12POQ S PQ OC =△,12POQ S OP QH =△, PQ OP ∴=.设BP x =,12BP BQ =, 2BQ x ∴=,① 如图1,当点P 在点B 左侧时,3OP PQ BQ BP x ==+=,在Rt PCO △中,222(8)6(3)x x ++=,解得11x=,21x =. 9PC BC BP ∴=+=19P ⎛⎫∴-- ⎪⎝⎭.②如图2,当点P 在点B 右侧时,OP PQ BQ BP x ∴==-=,8PC x =-.在Rt PCO△中,222(8)6x x-+=,解得254x=.PC BC BP∴=-257844=-=,2764P⎛⎫∴-⎪⎝⎭,.综上可知,存在点13962P⎛⎫--⎪⎝⎭,,2764P⎛⎫-⎪⎝⎭,,使12BP BQ=.2.(2009年浙江义乌)如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原。
华师大版初中数学九年级上册《23.6 图形与坐标》同步练习卷(含答案解析
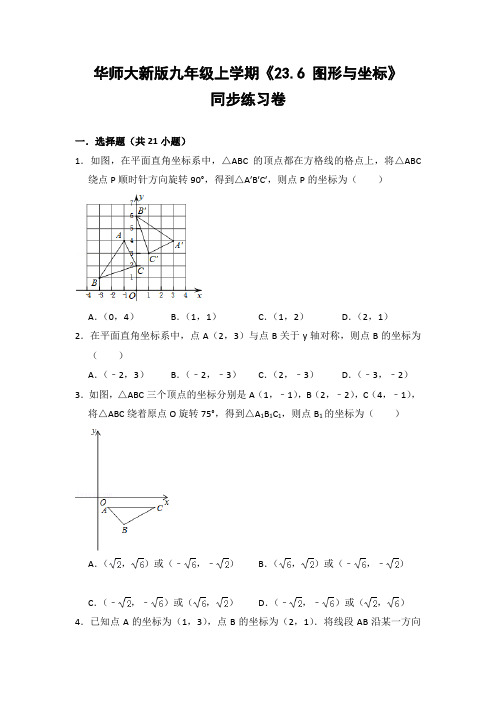
华师大新版九年级上学期《23.6 图形与坐标》同步练习卷一.选择题(共21小题)1.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC 绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为()A.(0,4)B.(1,1)C.(1,2)D.(2,1)2.在平面直角坐标系中,点A(2,3)与点B关于y轴对称,则点B的坐标为()A.(﹣2,3)B.(﹣2,﹣3)C.(2,﹣3)D.(﹣3,﹣2)3.如图,△ABC三个顶点的坐标分别是A(1,﹣1),B(2,﹣2),C(4,﹣1),将△ABC绕着原点O旋转75°,得到△A1B1C1,则点B1的坐标为()A.(,)或(﹣,﹣)B.(,)或(﹣,﹣)C.(﹣,﹣)或(,)D.(﹣,﹣)或(,)4.已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为()A.(5,3)B.(﹣1,﹣2)C.(﹣1,﹣1)D.(0,﹣1)5.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为()A.(1,1)B.(0,)C.()D.(﹣1,1)6.若点A(a+1,b﹣2)在第二象限,则点B(﹣a,1﹣b)在()A.第一象限B.第二象限C.第三象限D.第四象限7.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是()A.﹣5B.﹣3C.3D.18.在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是()A.(4,1)B.(﹣1,4)C.(﹣4,﹣1)D.(﹣1,﹣4)9.如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是()A.(﹣2,3)B.(3,﹣1)C.(﹣3,1)D.(﹣5,2)10.在平面直角坐标系xOy中,将点N(﹣1,﹣2)绕点O旋转180°,得到的对应点的坐标是()A.(1,2)B.(﹣1,2)C.(﹣1,﹣2)D.(1,﹣2)11.如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(﹣5,2),(﹣2,﹣2),(5,﹣2),则点D的坐标为()A.(2,2)B.(2,﹣2)C.(2,5)D.(﹣2,5)12.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是()A.(1,0)B.(,)C.(1,)D.(﹣1,)13.如图,正方形OABC在平面直角坐标系中,点A的坐标为(2,0),将正方形OABC绕点O顺时针旋转45°,得到正方形OA′B′C′,则点C′的坐标为()A.(,)B.(﹣,)C.(,)D.(2,2)14.如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是()A.(5,0)B.(8,0)C.(0,5)D.(0,8)15.如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是()A.(﹣,1)B.(﹣1,)C.(﹣1,)或(1,﹣)D.(﹣,1)或(1,﹣)16.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是()A.(2,2)B.(1,2)C.(﹣1,2)D.(2,﹣1)17.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是()A.(﹣3,2)B.(2,﹣3)C.(1,﹣2)D.(﹣1,2)18.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为()A.(2,2)B.(﹣2,4)C.(﹣2,2)D.(﹣2,2)19.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是()A.(2,5)B.(5,2)C.(2,﹣5)D.(5,﹣2)20.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为()A.(1,﹣1)B.(﹣1,﹣1)C.(,0)D.(0,﹣)21.将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为()A.(,﹣1)B.(1,﹣)C.(,﹣)D.(﹣,)二.填空题(共29小题)22.如图,等边三角形的顶点A(1,1),B(3,1),规定:“先以x轴为对称轴作△ABC的轴对称图形,再将其向左平移2个单位”为一次变换.第一次变换后,与点C对应的顶点坐标为;如果这样连续经过2018次变换后,与点C对应的顶点坐标为.23.如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2018次后,顶点B的坐标为.24.如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(﹣1,0),将线段AB沿x轴的正方向平移,若点B的对应点的坐标为B'(2,0),则点A的对应点A'的坐标为.25.在如图所示的象棋盘上,若“将”位于点(1,﹣2)上,“象”位于点(3,﹣2)上,则“炮”位于点上.26.如图,△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为.27.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为.28.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为.29.如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为.30.如图,在正方形网格中画的是某校的平面示意图,若花坛与教学楼的坐标分别为(3,﹣2),(6,1),则实验楼的坐标是.31.如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α(0°<α<180°),使点A仍在双曲线上,则α=.32.如图,点B在x的正半轴上,且BA⊥OB于点B,将线段BA绕点B逆时针旋转60°到BB′的位置,且点B′的坐标为(1,).若反比例函数y=(x>0)的图象经过A点,则k=.33.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,﹣1)和(﹣3,1),那么“卒”的坐标为.34.如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为.35.如图,在正方形OABC中,O为坐标原点,点C在y轴正半轴上,点A的坐标为(2,0),将正方形OABC沿着OB方向平移OB个单位,则点C的对应点坐标为.36.如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC 与△A'B'C'关于点P成中心对称,则点A'的坐标为.37.如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为.38.若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为.39.如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为.40.如图,△ABO中,AB⊥OB,AB=,OB=1,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为.41.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),那么第一架轰炸机C的平面坐标是.42.如图所示,坐在象棋棋盘上建立直角坐标系,使“帅”位于点(﹣2,﹣2),“马”位于点(1,﹣2),则“兵”位于点.43.如图,将△AOB绕点O逆时针旋转90°,得到△A′OB′.若点A的坐标为(a,b),则点A′的坐标为.44.如图,正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,则点C的坐标为.45.如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P 的坐标为.46.如图,在方格纸上建立的平面直角坐标系中,Rt△ABC关于y轴对称的图形为Rt△DEF,则点A的对应点D的坐标是.47.菱形OCAB在平面直角坐标系中的位置如图所示,点O的坐标是(0,0),点A在y轴的正半轴上,点P是菱形对角线的交点,点C坐标是(,3)若把菱形OCAB绕点A逆时针旋转90°,则点P的对应点P′的坐标是.48.平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOB=60°,AO=1,AC=2,把平行四边形AOBC绕点O逆时针旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为.49.如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是两直线y1=2x+6、y2=2x﹣6中某条上的一点,若△APD是等腰Rt△,则点D的坐标为.50.如图,点A向左平移4个单位长度得到点A′,则点A′的坐标是.华师大新版九年级上学期《23.6 图形与坐标》同步练习卷参考答案与试题解析一.选择题(共21小题)1.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC 绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为()A.(0,4)B.(1,1)C.(1,2)D.(2,1)【分析】选两组对应点,连接后作其中垂线,两中垂线的交点即为点P.【解答】解:由图知,旋转中心P的坐标为(1,2),故选:C.【点评】本题主要考查坐标与图形的变化﹣旋转,解题的关键是掌握旋转变换的性质.2.在平面直角坐标系中,点A(2,3)与点B关于y轴对称,则点B的坐标为()A.(﹣2,3)B.(﹣2,﹣3)C.(2,﹣3)D.(﹣3,﹣2)【分析】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”解答.【解答】解:点A(2,3)关于y轴对称点的坐标为B(﹣2,3).故选:A.【点评】本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.3.如图,△ABC三个顶点的坐标分别是A(1,﹣1),B(2,﹣2),C(4,﹣1),将△ABC绕着原点O旋转75°,得到△A1B1C1,则点B1的坐标为()A.(,)或(﹣,﹣)B.(,)或(﹣,﹣)C.(﹣,﹣)或(,)D.(﹣,﹣)或(,)【分析】根据题意只研究点B的旋转即可,OB与x轴夹角为45°,分别按顺时针和逆时针旋转75°后,与y轴负向、x轴正向分别夹角为30°,由此计算坐标即可.【解答】解:由点B坐标为(2,﹣2)则OB=,且OB与x轴、y轴夹角为45°当点B绕原点逆时针转动75°时,OB1与x轴正向夹角为30°则B1到x轴、y轴距离分别为,,则点B1坐标为(,);同理,当点B绕原点顺时针转动75°时,OB1与y轴负半轴夹角为30°,则B1到x轴、y轴距离分别为,,则点B1坐标为(﹣,﹣);故选:C.【点评】本题为坐标旋转变换问题,考查了图形旋转的性质、特殊角锐角三角函数值,解答时注意分类讨论和确定象限符号.4.已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为()A.(5,3)B.(﹣1,﹣2)C.(﹣1,﹣1)D.(0,﹣1)【分析】根据点A、点A的对应点的坐标确定出平移规律,然后根据规律求解点B的对应点的坐标即可.【解答】解:∵A(1,3)的对应点的坐标为(﹣2,1),∴平移规律为横坐标减3,纵坐标减2,∵点B(2,1)的对应点的坐标为(﹣1,﹣1).故选:C.【点评】本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,本题根据对应点的坐标确定出平移规律是解题的关键.5.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为()A.(1,1)B.(0,)C.()D.(﹣1,1)【分析】根据图形可知:点B在以O为圆心,以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.【解答】解:∵四边形OABC是正方形,且OA=1,∴B(1,1),连接OB,由勾股定理得:OB=,由旋转得:OB=OB1=OB2=OB3=…=,∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,∴B1(0,),B2(﹣1,1),B3(﹣,0),…,发现是8次一循环,所以2018÷8=252 (2)∴点B2018的坐标为(﹣1,1)故选:D.【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.也考查了坐标与图形的变化、规律型:点的坐标等知识,解题的关键是学会从特殊到一般的探究规律的方法,属于中考常考题型.6.若点A(a+1,b﹣2)在第二象限,则点B(﹣a,1﹣b)在()A.第一象限B.第二象限C.第三象限D.第四象限【分析】直接利用第二象限横纵坐标的关系得出a,b的符号,进而得出答案.【解答】解:∵点A(a+1,b﹣2)在第二象限,∴a+1<0,b﹣2>0,解得:a<﹣1,b>2,则﹣a>1,1﹣b<﹣1,故点B(﹣a,1﹣b)在第四象限.故选:D.【点评】此题主要考查了点的坐标,正确记忆各象限内点的坐标符号是解题关键.7.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是()A.﹣5B.﹣3C.3D.1【分析】根据关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变,据此求出m、n的值,代入计算可得.【解答】解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,∴1+m=3、1﹣n=2,解得:m=2、n=﹣1,所以m+n=2﹣1=1,故选:D.【点评】本题主要考查关于x、y轴对称的点的坐标,解题的关键是掌握两点关于y轴对称,纵坐标不变,横坐标互为相反数.8.在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是()A.(4,1)B.(﹣1,4)C.(﹣4,﹣1)D.(﹣1,﹣4)【分析】直接利用关于x轴对称点的性质,横坐标不变纵坐标改变符号进而得出答案.【解答】解:∵点B的坐标是(4,﹣1),点A与点B关于x轴对称,∴点A的坐标是:(4,1).故选:A.【点评】此题主要考查了关于x轴对称点的性质,正确把握横纵坐标的关系是解题关键.9.如图,在平面直角坐标系中,△ABC位于第一象限,点A的坐标是(4,3),把△ABC向左平移6个单位长度,得到△A1B1C1,则点B1的坐标是()A.(﹣2,3)B.(3,﹣1)C.(﹣3,1)D.(﹣5,2)【分析】根据点的平移的规律:向左平移a个单位,坐标P(x,y)⇒P(x﹣a,y),据此求解可得.【解答】解:∵点B的坐标为(3,1),∴向左平移6个单位后,点B1的坐标(﹣3,1),故选:C.【点评】本题主要考查坐标与图形的变化﹣平移,解题的关键是掌握点的坐标的平移规律:横坐标,右移加,左移减;纵坐标,上移加,下移减.10.在平面直角坐标系xOy中,将点N(﹣1,﹣2)绕点O旋转180°,得到的对应点的坐标是()A.(1,2)B.(﹣1,2)C.(﹣1,﹣2)D.(1,﹣2)【分析】根据题意可知点N旋转以后横纵坐标都互为相反数,从而可以解答本题.【解答】解:在平面直角坐标系xOy中,将点N(﹣1,﹣2)绕点O旋转180°,得到的对应点的坐标是(1,2),故选:A.【点评】本题考查坐标与图形变化﹣旋转,解答本题的关键是明确题意,利用旋转的知识解答.11.如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(﹣5,2),(﹣2,﹣2),(5,﹣2),则点D的坐标为()A.(2,2)B.(2,﹣2)C.(2,5)D.(﹣2,5)【分析】依据四边形ABCD是平行四边形,即可得到BD经过点O,依据B的坐标为(﹣2,﹣2),即可得出D的坐标为(2,2).【解答】解:∵点A,C的坐标分别为(﹣5,2),(5,﹣2),∴点O是AC的中点,∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,∴BD经过点O,∵B的坐标为(﹣2,﹣2),∴D的坐标为(2,2),故选:A.【点评】本题主要考查了坐标与图形变化,图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.12.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是()A.(1,0)B.(,)C.(1,)D.(﹣1,)【分析】根据平移的性质得出平移后坐标的特点,进而解答即可.【解答】解:因为点A与点O对应,点A(﹣1,0),点O(0,0),所以图形向右平移1个单位长度,所以点B的对应点B'的坐标为(0+1,),即(1,),故选:C.【点评】此题考查坐标与图形变化,关键是根据平移的性质得出平移后坐标的特点.13.如图,正方形OABC在平面直角坐标系中,点A的坐标为(2,0),将正方形OABC绕点O顺时针旋转45°,得到正方形OA′B′C′,则点C′的坐标为()A.(,)B.(﹣,)C.(,)D.(2,2)【分析】先根据点A的坐标求出正方形的边长,再根据旋转可得点C′在第一象限的平分线上,然后求解即可.【解答】解:∵点A的坐标为(2,0),∴正方形OABC的边长为2,∵正方形OABC绕点O顺时针旋转45°,得到正方形OA′B′C′,∴点C′在第一象限的平分线上,∴点C′的横坐标为2×=,纵坐标为为2×=,∴点C′的坐标为(,).故选:A.【点评】本题考查了坐标与图形变化﹣旋转,正方形的性质,熟记性质并判断出点C′的位置是解题的关键.14.如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是()A.(5,0)B.(8,0)C.(0,5)D.(0,8)【分析】直接利用勾股定理得出AB的长,再利用旋转的性质得出OB′的长,进而得出答案.【解答】解:∵A(3,0),B(0,4),∴AO=3,BO=4,∴AB==5,∴AB=AB′=5,故OB′=8,∴点B′的坐标是(8,0).故选:B.【点评】此题主要考查了勾股定理以及坐标与图形的性质,正确得出AB′的长是解题关键.15.如图,矩形ABCD的边BC在x轴上,点A在第二象限,点D在第一象限,AB=2,OD=4,将矩形ABCD绕点O旋转,使点D落在x轴上,则点C对应点的坐标是()A.(﹣,1)B.(﹣1,)C.(﹣1,)或(1,﹣)D.(﹣,1)或(1,﹣)【分析】根据矩形的性质得到CD=AB=2,∠DCO=90°,根据已知条件得到∠DOC=60°,OC=2,①当顺时针旋转至△OD′C′时,过C′作C′E⊥OD′于E,②当逆时针旋转至△OD″C″时,如图,过C″作C″E⊥OD″于F,解直角三角形即可得到结论.【解答】解:在矩形ABCD中,∵CD=AB=2,∠DCO=90°,∵OD=4,∴∠DOC=60°,OC=2,①当顺时针旋转至△OD′C′时,如图,∠D′OC′=∠DOC=60°,OC′=OC=2,过C′作C′E⊥OD′于E,则OE=OC′=1,C′E=OC′=,∴C′(1,﹣),②当逆时针旋转至△OD″C″时,如图,∠D″OC″=∠DOC=60°,OC″=OC=2,过C″作C″E⊥OD″于F,则OF=OC″=1,C″F=OC′=,∴C″(﹣1,),综上所述:点C对应点的坐标是(1,﹣),(﹣1,),故选:C.【点评】本题考查了坐标与图形变换﹣旋转,矩形的性质,解直角三角形,正确的作出辅助线是解题的关键.16.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是()A.(2,2)B.(1,2)C.(﹣1,2)D.(2,﹣1)【分析】根据旋转变换的性质得到旋转变换后点A的对应点坐标,根据平移的性质解答即可.【解答】解:∵点C的坐标为(﹣1,0),AC=2,∴点A的坐标为(﹣3,0),如图所示,将Rt△ABC先绕点C顺时针旋转90°,则点A′的坐标为(﹣1,2),再向右平移3个单位长度,则变换后点A′的对应点坐标为(2,2),故选:A.【点评】本题考查的是坐标与图形变化旋转和平移,掌握旋转变换、平移变换的性质是解题的关键.17.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(﹣2,3),先把△ABC向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是()A.(﹣3,2)B.(2,﹣3)C.(1,﹣2)D.(﹣1,2)【分析】首先利用平移的性质得到△A1B1C1,进而利用关于x轴对称点的性质得到△A2B2C2,即可得出答案.【解答】解:如图所示:点A的对应点A2的坐标是:(2,﹣3).故选:B.【点评】此题主要考查了平移变换以及轴对称变换,正确掌握变换规律是解题关键.18.如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为()A.(2,2)B.(﹣2,4)C.(﹣2,2)D.(﹣2,2)【分析】作BC⊥x轴于C,如图,根据等边三角形的性质得OA=OB=4,AC=OC=2,∠BOA=60°,则易得A点坐标和O点坐标,再利用勾股定理计算出BC=2,然后根据第二象限点的坐标特征可写出B点坐标;由旋转的性质得∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,则点A′与点B重合,于是可得点A′的坐标.【解答】解:作BC⊥x轴于C,如图,∵△OAB是边长为4的等边三角形∴OA=OB=4,AC=OC=1,∠BOA=60°,∴A点坐标为(﹣4,0),O点坐标为(0,0),在Rt△BOC中,BC==2,∴B点坐标为(﹣2,2);∵△OAB按顺时针方向旋转60°,得到△OA′B′,∴∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,∴点A′与点B重合,即点A′的坐标为(﹣2,2),故选:D.【点评】本题考查了坐标与图形变化﹣旋转:记住关于原点对称的点的坐标特征;图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°;解决本题的关键是正确理解题目,按题目的叙述一定要把各点的大致位置确定,正确地作出图形.19.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是()A.(2,5)B.(5,2)C.(2,﹣5)D.(5,﹣2)【分析】由线段AB绕点O顺时针旋转90°得到线段A′B′可以得出△ABO≌△A′B′O′,∠AOA′=90°,作AC⊥y轴于C,A′C′⊥x轴于C′,就可以得出△ACO≌△A′C′O,就可以得出AC=A′C′,CO=C′O,由A的坐标就可以求出结论.【解答】解:∵线段AB绕点O顺时针旋转90°得到线段A′B′,∴△ABO≌△A′B′O′,∠AOA′=90°,∴AO=A′O.作AC⊥y轴于C,A′C′⊥x轴于C′,∴∠ACO=∠A′C′O=90°.∵∠COC′=90°,∴∠AOA′﹣∠COA′=∠COC′﹣∠COA′,∴∠AOC=∠A′OC′.在△ACO和△A′C′O中,,∴△ACO≌△A′C′O(AAS),∴AC=A′C′,CO=C′O.∵A(﹣2,5),∴AC=2,CO=5,∴A′C′=2,OC′=5,∴A′(5,2).故选:B.【点评】本题考查了旋转的性质的运用,全等三角形的判定及性质的运用,等式的性质的运用,点的坐标的运用,解答时证明三角形全等是关键.20.如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为()A.(1,﹣1)B.(﹣1,﹣1)C.(,0)D.(0,﹣)【分析】根据菱形的性质,可得D点坐标,根据旋转的性质,可得D点的坐标.【解答】解:菱形OABC的顶点O(0,0),B(2,2),得D点坐标为(1,1).每秒旋转45°,则第60秒时,得45°×60=2700°,2700°÷360=7.5周,OD旋转了7周半,菱形的对角线交点D的坐标为(﹣1,﹣1),故选:B.【点评】本题考查了旋转的性质,利用旋转的性质是解题关键.21.将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为()A.(,﹣1)B.(1,﹣)C.(,﹣)D.(﹣,)【分析】先根据题意画出点A′的位置,然后过点A′作A′C⊥OB,接下来依据旋转的定义和性质可得到OA′的长和∠COA′的度数,最后依据特殊锐角三角函数值求解即可.【解答】解:如图所示:过点A′作A′C⊥OB.∵将三角板绕原点O顺时针旋转75°,∴∠AOA′=75°,OA′=OA.∴∠COA′=45°.∴OC=2×=,CA′=2×=.∴A′的坐标为(,﹣).故选:C.【点评】本题主要考查的是旋转的定义和性质、特殊锐角三角函数值的应用,得到∠COA′=45°是解题的关键.二.填空题(共29小题)22.如图,等边三角形的顶点A(1,1),B(3,1),规定:“先以x轴为对称轴作△ABC的轴对称图形,再将其向左平移2个单位”为一次变换.第一次变换后,与点C对应的顶点坐标为(0,﹣﹣1);如果这样连续经过2018次变换后,与点C对应的顶点坐标为(﹣4034,+1).【分析】根据轴对称判断出点C变换后在x轴下方或上方,然后求出点C纵坐标,再根据平移的距离求出点C变换后的横坐标,最后写出坐标即可.【解答】解:∵△ABC是等边三角形,BC=3﹣1=2,∴点C到x轴的距离为1+2×=+1,其横坐标为2,∴C(2,+1),∴第1次变换后,与点C对应的顶点在x轴的下方,其坐标为(0,﹣﹣1),∵第2018次变换后的三角形在x轴上方,∴点C的纵坐标为+1,其横坐标为2﹣2018×2=﹣4034,∴经过2018次变换后,点C的坐标是(﹣4034,+1),故答案为:(0,﹣﹣1),(﹣4034,+1).【点评】本题考查了坐标与图形变化,平移和轴对称变换,以及等边三角形的性质的运用,确定出连续2018次这样的变换得到三角形在x轴上方是解题的关键.23.如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2018次后,顶点B的坐标为(0,﹣3).【分析】由点B的旋转周期为6知点B旋转2018次后的坐标与旋转2次后的坐标相同,再结合图形得出点B旋转2次后的坐标即可得.【解答】解:由题意知点B旋转=6次后与点B重合,即点B的旋转周期为6,∵2018÷6=336…2,∴点B旋转2018次后的坐标与旋转2次后的坐标相同,如图,∵∠AOB=60°,∴∠BOC=120°,则两次旋转都点B落在y轴的负半轴,且OB=3,所以点B的坐标为(0,﹣3).故答案为:(0,﹣3).【点评】本题主要考查坐标与图形的变化﹣旋转,根据题意得出点B的旋转周期为6及旋转的性质是解题的关键.24.如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(﹣1,0),将线段AB沿x轴的正方向平移,若点B的对应点的坐标为B'(2,0),则点A的对应点A'的坐标为(3,2).【分析】根据平移的性质即可得到结论.【解答】解:∵将线段AB沿x轴的正方向平移,若点B的对应点B′的坐标为(2,0),∵﹣1+3=2,∴0+3=3∴A′(3,2),故答案为:(3,2)【点评】本题考查了坐标与图形变化﹣平移.解决本题的关键是正确理解题目,按题目的叙述一定要把各点的大致位置确定,正确地作出图形.25.在如图所示的象棋盘上,若“将”位于点(1,﹣2)上,“象”位于点(3,﹣2)上,则“炮”位于点(﹣2,1)上.【分析】直接利用已知点位置进而得出原点位置进而得出“炮”的位置.【解答】解:如图所示:“炮”位于点:(﹣2,1).故答案为:(﹣2,1).【点评】此题主要考查了坐标确定位置,正确得出原点的位置是解题关键.26.如图,△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(﹣,).【分析】过B1作B1C⊥y轴于C,由把△ABO绕点O逆时针旋转120°后得到△A1B1O,根据旋转的性质得到∠BOB1=120°,OB1=OB=,解直角三角形即可得到结果.【解答】解:过B1作B1C⊥y轴于C,∵把△ABO绕点O逆时针旋转120°后得到△A1B1O,∴∠BOB1=120°,OB1=OB=,∵∠BOC=90°,∴∠COB1=30°,∴B1C=OB1=,OC=,∴B1(﹣,).故答案为:(﹣,).【点评】本题考查了坐标与图形变化﹣旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标是解题的关键.27.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为(4,2).【分析】利用DB=1,B(4,0),得出△AOB沿x轴向右平移了3个单位长度,再利用平移中点的变化规律求解即可.【解答】解:∵点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,DB=1,∴OD=3,∴△AOB沿x轴向右平移了3个单位长度,∴点C的坐标为:(4,2).故答案为:(4,2).【点评】此题主要考查了坐标系中点、线段的平移规律,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.28.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…,按这样的规律进行下去,第4个正方形的边长为.【分析】根据勾股定理求出AD,进而得到AB的长度,利用三角形相似的判定,证明△ABA1∽△DOA,得出BA1的长度,进而得到CA1的长度,同理可得第三个正方形,第四个正方形的边长.【解答】解:∵点A的坐标为(1,0),点D的坐标为(0,3),∴OA=1,OD=3,∵∠AOD=90°,∴AD==,∠ODA+∠OAD=90°,∵四边形ABCD是正方形,∴∠BAD=∠ABC=90°,AB=AD=,∴∠ODA1=90°,∠OAD+∠BAA1=90°,∴∠ODA=∠BAA1,∴△ABA1∽△DOA,∴,即,解得:BA1=,∴CA1=,同理,可得:C1A2=,∴第4个正方形的边长为=,故答案为:.【点评】本题主要考查了点的规律,综合运用了正方形的性质、勾股定理、相似三角形的性质和判定等知识,能熟练运用三角形的性质和判定求出相关线段的长度是解决此题的关键.29.如图,已知等边三角形OAB的顶点O(0,0),A(0,3),将该三角形绕点O顺时针旋转,每次旋转60°,则旋转2017次后,顶点B的坐标为(,﹣).【分析】由点B的旋转周期为6知点B旋转2017次后的坐标与旋转1次后的坐标相同,再结合图形解直角三角形得出点B旋转1次后的坐标即可得.【解答】解:由题意知点B旋转=6次后与点B重合,即点B的旋转周期为6,∵2017÷6=336…1,∴点B旋转2017次后的坐标与旋转1次后的坐标相同,如图,OB绕点O顺时针旋转60°得到OB1,过点B1作B1C⊥x轴,。
华师大版-数学-九上-23.6.2 图形的变换与坐标 作业

23.6.2图形的变换与坐标一、选择题:1.如图所示,将点A向右平移多少个单位长度可得到点B ( )A.3个单位长度B.4个单位长度;C.5个单位长度D.6个单位长度2.如1.图所示,将点A向下平移5个单位长度后,将重合于图中的( )A.点C B.点F C.点D D.点E3.如1.图所示,将点A向右平移3个单位长度,再向下平移5个单位长度,得到A′,将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B′,则A′与B′相距( ) A.4个单位长度 B.5个单位长度;C.6个单位长度 D.7个单位长度4.如1.图所示,点G(−2,−2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G′,则G′的坐标为( )A.(6,5) B.(4,5) C.(6,3) D.(4,3)二、填空题:1.已知△ABC,A(−3,2),B(1,1),C(−1,−2),现将△ABC平移,使点A到点(1,−2) 的位置上,则点B,C的坐标分别为______,________.2.已知点A(−4,−6),将点A先向右平移4个单位长度,再向上平移6个单位长度,得到A′,则A′的坐标为________.3.已知平面内两点M,N,如果它们平移的方式相同,那么它们之间的相对位置是_________.4.正方形的四个顶点中,A(−1,2),B(3,2),C(3,−2),则第四个顶点D的坐标为_________.5.△ABC中,如果A(1,1),B(−1,−1),C(2,−1),则△ABC的面积为________.三、基础训练:如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),求A′,B′,C′的坐标.四、提高训练:坐标平面内有4个点A(0,2),B(−1,0),C(1,−1),D(3,1).(1)建立坐标系,描出这4个点;(2)顺次连接A,B,C,D,组成四边形ABCD,求四边形ABCD的面积.五、探索发现:如图所示,△BCO是△BAO经过某种变换得到的,则图中A与C的坐标之间的关系是什么?如果△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?参考答案:一、1.B2.D3.A4.D二、1.(5,−3) (3,−6)2.(0,0)3.不变4.(−1,−2) 5.3三、A′(2,3),B′(1,0),C′(5,1).四、(1)略(2)四边形ABCD的面积为6.5.五、A与C的横坐标相同,纵坐标互为相反数,N点的坐标为(x,−y).。
华师大版九年级数学上册课件:23.6.2图形的变换与坐标

均互为相反数
1观察:(1)由点B到点A
是怎样移动得到的?他们的
坐标有何关系?
y
(2)在图中,你还能
看到哪些点的移动?
B ( -3 , 2)
1 01
C (-3, -2 )
A ( 3, 2 )
x
D ( 3 , -2
2、如果是⊿AOB 向右移动3个单位长度,得到 ⊿A ’O’ B ’ ,各顶点的坐标又有什么变化?你能 用自已的语言归纳这个规律吗?
(1)
12 、如图1矩形ABOC的长OB=3,宽AB=2,则点A的坐标为__。
13、如果点P(a-3,a+4)在第二象限,则a的取值范围是_____。
14、点A(a,-4)到两坐标轴的距离相- 等,则a=_______.
课前训练题答案:
1、 -3 3、 0, 3 5、 5, 2 5 7、 6,27
23.6.2 图形的变换与坐标
课前训练 1、方程 x2 3x 0 一次项的系数是 .
2、方程 x2 25 的根是
。
3.方程 x2 3x 的根是_____。
4 、最简二次根式 x 2 与 3 是同类二次根式,则x的值是____。 4.计算: 25 =_____。 20 =______。
6、相似三角形的相似比是2﹕3,则周长比是__________.
Y
A
A’
0
O’ B B’ X
规律(1)左右移动时,横坐标左减右加,纵坐标不变: 3、你能画图说明⊿AOB向左移动时,对应点的坐标 又有什么规律吗?
4小组讨论:将 你⊿能A探OB索向出上图或形向上下下移移动动几的个规单律位吗长?度, Y 4A
0
2
4B
X
-5
华师大版数学九上24.5画相似图形同步测试

文档从互联网中收集,已重新修正排版,word格式支持编辑,如有帮助欢迎下载支持。
24.5 画相似图形
一、基础训练:(每小题15分,共45分)
1.如图所示,将下列图形按相似比为3:2 画出它的相似图形.
2.如图所示,将下列图形分别分成四小块,使它们的形状、大小完全相同,并且与原图形相似,应怎样分?(画出大致图形即可)
3.如图所示,把图(1)中的图形在图(2)中放大(形状完全一样).
二、提高训练:(每小题12分,共36分)
1.某出版社一位编辑在设计一本书的封面时,想把封面划分为四个矩形,其中左上角矩形与右下角矩形相似(如图所示),给人一种和谐的感觉, 这样的两个相似矩形是怎样画出来的?
2.如图所示,小芳用画正方形的办法画出下列一组图案, 你能按规律继续画下去吗?想想其中有哪些相似图形?
3.用木条制成如图所示的形状,A,B,C三点钉上钉子,在D和D′处加上粉笔, 当用D′画图时,在D处的笔同时也画出一个图形,请问: 这样画上的两个图形是相似图形吗?
三、中考题与竞赛题:(共19分)
在方格纸中,每个小格的顶点叫做格点,以
格点连线为边的三角形叫做格点三角形,请你
在如图所示的10×10的方格纸中,画出两个相
似但不全等的格点三角形,并加以说明,要求所
画的三角形是钝角三角形,并标明相应的字母.
参考答案
一、1.略 2.如图所示
3.略.
二、1.解:如图所示,作对角线AC,在AC上取一点P,过P作EF∥BC,作G H∥AB
∴矩形AEPG和矩形CFPH是两个相似矩形
2.略.
3.相似.
三、提示:以边为主要条件,利用三边成比例来画.
1word格式支持编辑,如有帮助欢迎下载支持。
华师大版-数学-九年级上册- 24.6 图形与坐标(一)

24.6 图形与坐标(一)1.如图,A、B、C三点分别代表邮局、医院、学校中的某一处,邮局和医院均在学校的北偏西方向,邮局又在医院的北偏东方向,那么图中A点应该是__________,B点是_________,C点是_______________.2.如图是某市动物园的平面示意图,借助于刻度尺和量角器解决下列问题:(1)百鸟园在大门的北偏东________度的方向上,它到大门的图上距离约为________cm;(2)熊猫馆在大门的北偏_____ _____度的方向上,到大门的图上距离约为________cm;(3)驼峰在大门的南偏_____ ______度的方向上,它到大门的图上距离约为_______cm.3.下面是红旗乡的行政区域图,试借助刻度尺和量角器解决如下问题:(1)建立适当的直角标系,用坐标表示各村的位置;(2)用方位角表示各村与大山镇所在地的位置关系.4.如图所示,为A市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度).请用两种方式表示出图中各个景点的位置.5.如图县某校的平面示意图,其比例尺为1:5 000,借助刻度尺、量角器解答下列问题:(1)以旗杆为原点,用一个角度和距离指出其余各点的具体位置;(2)如果用(0,0)表示教学楼的位置,且小正方形边长为1个单位长度,水平向右和竖直向上方向取为正值,你能写出其余各点的具体位置吗?6.如图是小明家周边地区的平面示意图,借助刻度尺、量角器解决如下问题:(1)某楼位于小明家的南偏东66度的方向,到小明家的实际距离约为350米,说出这一地点的名称;(2)相对小明家的位置,说出书店所在的位置.7.如图(比例尺为 l:l 000,单位:km),用刻度尺、量角器解答下列问题:(1)剧场位于纪念堂的北偏东多少度方向上?图中到纪念堂的距离约为多少厘米?实际距离呢?(2)立交桥位于城楼的北偏西多少度方向上?到图中城楼的距离是多少?实际距离是多少?(3)城楼正北方向上的公园实际距离城楼多少米?(4)商场的位置如何表示?8.如图是某市2路公交车的行车路线.(1)若该车从镇江路驶往西镇,请用坐标表示出该车的行车路线;(2)请说出镇江路在西镇的什么方位.9.如图是我市某区的旅游风景区,请用两种方式表示出图中各景点的位置.(可用刻度尺、量角器帮助解决)10.如图是一个公园的示意图,请用两种方式表示出猴山、大象馆、海洋世界、虎豹园的位置.11.以你所在学校的旗杆为中心,设计描述学校大门、食堂、实验室、教室位置的一种方法.参考答案1.邮局医院学校 2~8.略 9~11.略。
华师大版九年级上册课件:23.6.2图形的变换与坐标
6、相似三角形的相似比是2﹕3,则周 号用(5,24)表示,则(6,27)表示
小红坐在第__排___号。
8、点A(3,-2)关于 x 轴对称的点是_____。
9、点A(3,4)关于 y 轴对称的点是_____。
A
y C
10、P(2,3)关于原点对称的点是_____。 B O x
Y
A
6
C
2
D 0
2
B
6
X
规律: 横坐标和纵坐标都缩小相同的倍数
课堂小结:
1、本节课我学会了……
2、我的体会是……
快乐小测:
1、画出⊿ABC向下平移4个单位后的图形 2 、画出⊿ABC关于原点对称的图形 3、以O为位似中心,将⊿ABC放大2倍
Y
B4
A
C
O
-4 -2
24
X
-4
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月28日星期一2022/2/282022/2/282022/2/28 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年2月2022/2/282022/2/282022/2/282/28/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/282022/2/28February 28, 2022 •4、享受阅读快乐,提高生活质量。2022/2/282022/2/282022/2/282022/2/28
5、将⊿AOB沿着x轴对折,得到⊿A ’ OB, 画图并说明对应顶点有什么变化?
Y
A
华师大版-数学 九年级上册 练习-23.6 图形与坐标
23.6图形与坐标23.6.1用坐标确定位置1.确定物体的位置的常用方法:(1)用__坐标__确定物体的所在的位置;(2)用__经纬度__确定物体所在的位置;(3)用__角度__和__距离__确定物体所在的位置.2.所有的平面图形都可以看成是__点__的集合,因此可以通过确定有关__点__的位置(坐标),进而确定一个平面图形的位置.知识点1:用坐标确定一个物体的位置1.如图,是小刚画的一张脸,他对妹妹说,如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( A )A.(1,0)B.(-1,0)C.(-1,1)D.(1,-1)2.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( C )A.(-1,1)B.(-2,-1)C.(-3,1) D.(1,-2),第2题图),第3题图)3.如图,小明在云南省地图上设定临沧市的坐标为(-1,0),昆明市的坐标为(1,1),请帮助小明确定出香格里拉的坐标为__(-1,4)__.知识点2:用经、纬度表示地理位置4.能够大致表示我国首都北京这个地点位置的是( D )A.北纬39.9度B.东经116.3度C.河北衡水的正北方向D.东经116.3度,北纬39.9度知识点3:用方向角表示位置5.海事救灾船前去救援某海域失火货轮,需要确定( C )A.方向角B.距离C.方向角和距离D.失火轮船的国籍6.如图,图书馆相对于大门的位置是__北偏东56°,3_km__;操场相对于大门的位置是__北偏西34°,6_km__;车站相对于大门的位置是__正南,4_km__.知识点4:用坐标确定一个平面图形的位置7.如图,矩形ABCD中,A(-4,1),B(0,1),C(0,3),则点D坐标为__(-4,3)__.,第7题图),第8题图) 8.如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为__(3,2),(-2,3)__.9.如果长方形的长为8,宽为6,以长方形的两条对称轴为坐标轴建立平面直角坐标系,那么下面哪个点不是长方形的顶点( D )A.(4,-3) B.(-4,3)C.(4,3) D.(0,3)10.长方形ABCD的长为6,宽为4,建立平面直角坐标系,使其中B点的坐标为(-3,-2),并写出其他三个顶点的坐标.解:A(-3,2)C(3,-2)D(3,2)11.张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图),若以大门为坐标原点,其他四个景点大致用坐标表示肯定错误的是( C )A.熊猫馆(1,4)B.猴山(6,0)C.百鸟园(5,-3)D.驼峰(3,-2)12.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( B )A.点A B.点B C.点C D.点D,第12题图),第13题图)13.小李在平面直角坐标系中画了一张示意图,分别标出了学校、工厂、体育馆、百货商店的大致位置.如果张大爷从工厂向南走150米,再向西走250米,再向南走350米,再向东走200米,最终到达的地点是( D )A.学校B.工厂C.体育馆D.百货商店14.如图,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标C,F的位置表示为C(6,120°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( D )A.A(5,30°) B.B(2,90°)C.D(4,240°) D.E(3,60°),第14题图),第15题图) 15.如图所示的零件中(各角都是直角),把D定为坐标原点,DF所在直线为x轴,建立直角坐标系,则其它点的坐标为:A (__-1,3__),B (__-1,0__),C (__-2,0__),E (__0,3__),F (__2,0__),G (__2,-1__),H (__-2,-1__). 16.在坐标系中描出下列四个点:A (-1,0),B (0,3),C (3,3),D (6,0),并用线段依次连接起来.(1)你得到的是什么图形?(2)计算所得的图形的面积.解:(1)梯形 (2)图形的面积为(3+7)×32=15(平方单位)17.建立适当的平面直角坐标系,标出学校、医院、超市、车站的位置.医院:从学校向东走200 m ,再向北走250 m ;超市:从学校向西走100 m ,再向北走50 m ;车站:从学校向南走400 m ,再向东走200 m.解:如图,以学校为坐标原点,东西方向所在直线为x 轴,南北方向所在直线为y 轴,建立直角坐标系,以50 m 的长为1个单位,描出各点18.在如图所示的海域中,有各种目标,根据要求填空:(1)对于我军潜艇来说,在南偏东60°方向上有哪些目标:__敌舰A 和小岛__;(2)敌舰B 在我军潜艇的__正东__方向上,现距我军潜艇图上距离为2 cm ,距我军潜艇的实际距离是__200_km __;(3)敌舰C 距我军潜艇的图上距离为1 cm ,沿我军潜艇北偏东30°的方向以60 km/h 的速度逃跑,我军潜艇将沿__北偏东30°__方向,至少以__90_km/h__速度出击,才能将敌舰击沉,且没有触礁的危险.(暗礁距我军潜艇的图上距离为3 cm)23.6.2图形的变换与坐标1.(1)点(x,y)沿x轴向右或向左平移a个单位后所得到的点的坐标为__(x+a,y)__或__(x-a,y)__.(2)点(x,y)沿y轴向上或向下平移b个单位后所得到的点的坐标为__(x,y+b)__或__(x,y-b)__.(3)图形的平移,点的坐标变化规律可简化为:右__加__左__减__,上__加__下__减__.2.点P(x,y)关于x轴对称的点P1的坐标为__(x,-y)__,关于y轴对称的点P2的坐标为__(-x,y)__,关于原点对称的点P3的坐标为__(-x,-y)__.3.一般地,在平面直角坐标系中,如果以原点为位似中心,新图形与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为__(kx,ky)或(-kx,-ky)__.知识点1:用坐标表示图形的平移1.在平面直角坐标系中,△ABC的三个顶点坐标分别是A(4,5),B(1,2),C(4,2),将△ABC向左平移5个单位后,A点的对应点A′的坐标是( B )A.(0,5)B.(-1,5)C.(9,5) D.(-1,0)2.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( A )A.(0,1) B.(6,1)C.(0,-3) D.(6,-3)3.在平面直角坐标系中,线段AB的两个端点的坐标分别为A(-2,1),B(1,3),将线段AB经过平移后得到线段A′B′,若点A的对应点为A′(3,2),则点B的对应点B′的坐标是__(6,4)__.知识点2:用坐标表示图形的轴对称4.(2014·海南)如图,△ABC与△DFE关于y轴对称,已知A(-4,6),B(-6,2),E(2,1),则点D的坐标为( B )A.(-4,6) B.(4,6)C.(-2,1) D.(6,2),第4题图),第6题图)5.(2014·来宾)将点P(-2,3)向右平移3个单位得到点P 1,点P 2与点P 1关于原点对称,则P 2的坐标是( C )A .(-5,-3)B .(1,-3)C .(-1,-3)D .(5,-3)6.(2014·牡丹江)如图,把△ABC 经过一定的变换得到△A′B′C′,如果△ABC 上点P 的坐标为(x ,y),那么这个点在△A′B′C′中的对应点P′的坐标为( B )A .(-x ,y -2)B .(-x ,y +2)C .(-x +2,-y )D .(-x +2,y +2)知识点3:用坐标表示图形的位似变化7.如图,将△AOB 缩小得到△COD ,则△AOB 与△COD 的相似比是__2∶1__.,第7题图) ,第8题图)8.(2014·武汉)如图,线段AB 两个端点的坐标分别为A(6,6),B(8,2),以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的12后得到线段CD ,则端点C 的坐标为( A ) A .(3,3) B .(4,3)C .(3,1)D .(2,1)9.在平面直角坐标系中,已知点E (-4,2),F (-2,-2),以原点O 为位似中心,相似比为12,把△EFO 缩小,则点E 的对应点E ′的坐标是( D ) A .(-2,1) B .(-8,4)C .(-8,4)或(8,-4)D .(-2,1)或(2,-1)10.在平面直角坐标系中,将线段OA 向左平移2个单位,点O ,A 的对应点分别为点O 1,A 1,若点O (0,0),A (1,4),则点O 1,A 1的坐标分别是( D )A .(0,0),(1,4)B .(0,0),(3,4)C .(-2,0),(1,4)D .(-2,0),(-1,4)11.(2014·日照)如图,在直角坐标系中,矩形OABC 的顶点O 在坐标原点,边OA 在x 轴上,OC 在y 轴上,如果矩形OA′B′C′与矩形OABC 关于点O 位似,且矩形OA′B′C 的面积等于矩形OABC 面积的14,那么点B′的坐标是( D ) A .(-2,3) B .(2,-3)C .(3,-2)或(-2,3)D .(-2,3)或(2,-3),第11题图) ,第13题图)12.(2014·宜宾)在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B ,则点B 关于x 轴的对称点C 的坐标是__(2,-2)__.13.(2014·荆门)如图,正方形OABC 与正方形ODEF 是位似图形,点O 为位似中心,相似比为1∶2,点A 的坐标为(0,1),则点E 的坐标是__(2,2)__.14.(2014·钦州)如图,△A ′B ′C ′是△ABC 经过某种变换后得到的图形,如果△ABC 中有一点P 的坐标为(a ,2),那么变换后它的对应点Q 的坐标为__(a +5,-2)__.,第14题图) ,第15题图)15.如图,原点O 是△ABC 和△A ′B ′C ′的位似中心,点A (1,0)与A ′(-2,0)是对应点,△ABC 的面积是32,则△A ′B ′C ′的面积是__6__. 16.(2014·湘潭)在边长为1的小正方形网格中,△AOB 的顶点均在格点上.(1)B 点关于y 轴的对称点坐标为__(-3,2)__;(2)将△AOB 向左平移3个单位长度得到△A 1O 1B 1,请画出△A 1O 1B 1;(3)在(2)的条件下,A 1的坐标为__(-2,3)__.解:(2)图略17.(2014·龙东)如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形;(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形;(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.解:(1)图略(2)图略(3)旋转中心坐标(0,-2)18.(2014·巴中)如图,在平面直角坐标xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)请画出△ABC关于x轴对称的△A1B1C1;(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,请画出△A2B2C2;(3)求△A1B1C1与△A2B2C2的面积比,即S△A1B1C1∶S△A2B2C2=__1∶4__.(不写解答过程,直接写结果)解:(1)图略(2)图略(3)∵将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A2,B2,C2,∴△A1B1C1与△A2B2C2的相似比为1∶2,∴S△A1B1C1∶S△A2B2C2=1∶4.故答案为1∶4。
24.6 图形与坐标 课件(华师大版九年级上册) (3)
若沿y轴向下平 移3个单位呢?
思考与探索
• 图中,△AOB关于x轴的轴对称图形是 △A′OB.对应顶点的坐标有什么变化?
A″
△AOB关于y 轴的轴对称图 形呢?
B″
试一试
• 请在右图的直角坐标 系中画一个平行四边 形,写出它的四个顶 点的坐标,然后画出 这个四边形关于x轴的 对称图形,写出对称 图形四个顶点的坐标, 观察对应顶点的坐标 有什么变化.
学科网
巩固提高
1、已知下列点的坐标,在平面直角坐标系中 正确标出这些点并且依次把它们连结起来 ,观察得到的图形,你觉得它像什么? (0,2),(0,0),(1,3),(2,3),(3,2), (3,0),(1,-1),(2,-1),(1,-3),(0, -1), (-1,-3),(-2,-1),(-1,-1),(-3,0), (-3,2),(-2,3),(0,0).
情境导入
• 在同一直角坐标系中,图形 经过平移、旋转、轴对称、 放大或缩小之后,点的坐标 会如何变化呢?
zxxkw 学科网
例 如图,△AOB沿x轴向右平移3个单位 之后,得到△A′O′B′.三个顶点的 坐标有什么变化呢? 解:△AOB的三个 顶点的坐标是: A(2, 4)、O(0, 0)、B(4, 0). 平移之后的 △A′O′B′ 对应的顶点是: A′(5, 4)、O′(3, 0)、B′(7, 0).
(0,2),(0,0),(1,3),(2,3),(3,2),
·· · · · ·
(第 1 题)
2.将图中的△ABC作下列运动,画出相应的 图形,指出三个顶点的坐标所发生的变化. (1)沿y轴正向平移2个单位; (2)关于y轴对称; (3)以B点为位似中心,放大到2倍.
学科网 学科网
华师大版-数学-九年级上册-24.6 图形与坐标(1) 作业
华师大版九年级(上)第二十四章第六节24.6 图形与坐标作业一、积累·整合1.在图12的网络中,描述右边图形的缩小图。
2.下面是小于所在学校的平面示意图,其中各点分别表示:A(大门);B(教学楼);C、(宿舍);D、(食堂);E(操场);F(卫生室);G(国旗),请你选择适当的坐标系,使所标的点尽量多的在坐标轴上,(1)根据坐标系描述食堂、宿舍、教学楼的位置;(2)其它各点中,哪一点距卫生室(F)最近?(3)现确定一图书馆的准确位置:使得与B、D、C三点的距离都相等,请标出此出,并说明理由。
如图所示,在右边的方格中分别画出边长之比为2:1,4:3,3:1的相似图形.5.试作四边形,使它和已知的四边形位似比等于1:2,位似中心为O使两个图形在点O同侧。
6.如图所示,形状相同的图形有哪些?(只需说出两种)二、拓展·应用7.将图中的△ABC作下列运动,画出相应的图形,指出三个顶点坐标所发生的变化。
AB CDEA1B1C1D1E1(1)沿y轴正面平移2个单位。
(2)关于y轴对称。
8.如果三角形的每条边都扩大为原来的5倍,那么三角形的每个角( )(A)都扩大为原来的5倍(B)都扩大为原来的10倍(C)都扩大为原来的25倍(D)都与原来相等三、探索·创新9.在直角坐标系中描出点O (0,0)、A (1,2)、B (2, 4)、C (3,2)、D (4,0).先用线段顺次连接点O, A、B,C, D,然后再用线段连结A、C两点.(1)你得到了一个什么图形?(2)填写表1,在直角坐标系中描出点O,、A1、B1、C1、D1,并按同样的方式连结各点.你得到一个什么图形?填写表2,你又得到一个什么图形?填写表3呢?(3)在上述的图个图形中,哪两个图形的形状相同?【答案与解析】1、略2、以FE直线为X轴,BG直线为Y轴(1)D(4,0) C(4,0)B(0,6)(2)A距F 最近 D距F最远(3)图书馆H(2,3)3.略4.略5.略6.略7.(1)A(0,0),B(3,1),C(2,3) (2)A(0,-2),B(-3,-1),C(-2,1)8.D 9.略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015秋华师大版数学九上24.6《图形与坐标》word练习题2
24、6、2 图形的变换与坐标
◆随堂检测
1、如图,在平面直角坐标系中,请按下列要求分别作出△ABC变换后的图形(图中每个小正方
形的边长为个单位),并写出变换后△ABC各顶点的坐标、
(1)向右平移个单位;(2)关于轴对称、
2、如图方格纸中每个小方格都就是边长为1 个单位的正方形,在建立平面直角坐标系后,
ABC的顶点在格点上,点B的坐标为(5,-4),请您作出ABC,使ABC与ABC关于y
轴对
称,并写出B的坐标、
◆
典例分析
三角形的顶点坐标分别就是A(2,2),B(4,2),C(6,4),试将△ABC缩小,使缩小后的△DEF与
△ABC对应边比为1∶ 2、
解:将A(2,2),B(4,2),C(6,4)三点的横坐标、纵坐标都缩小为原来的得D(1,1),
E(2,1),F(3,2)后,顺次连结D,E,F,D,即可得到缩小后的△DEF
、如图、
◆课下作业
●拓展提高
1、如图,铅笔图案的五个顶点的坐标分别就是
(0,1),(4,1),(5,1、5),(4,2),(0,2)、将图案向下平
移2个单位长度,则平移后相应5个点的坐标分别
2015秋华师大版数学九上24.6《图形与坐标》word练习题2
为 、
2、将点A (3 , l)绕原点O按顺时针方向旋转900到点B,则点B的坐标就是 、
3、 △ABC在平面直角坐标系中的位置如图所示、
(1)作出△ABC关于轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1与△A2B2C2,它们就是否关于某直线对称?若就是,请在图上画出这条对称
轴、
4、下图就是益阳市行政区域图,图中益阳市区所在地用坐标表示为(2,0),安化县城所在地用
坐标表示为(-2,-1),那么南县县城所在地用坐标表示为 、
5、右图就是永州市几个主要景点示意图,根据图中信息可确定九疑山的中
心位置C点的坐标为 、
6、如图,将边长为1的正三角形OAP沿轴正方向连续翻转2008次,点依
次落在点1232008PPPP,,,...,的位置,则点2008P的横坐标
为 、
7、如图,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A、B、C作循环对称跳动,
即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳
到点N关于C的对称点处,…、如此下去。
(1)在图中画出点M、N,并写出点M、N的坐标:_____________
LL
1
P
A
O
y
x
P
安化
益阳
南县
2015秋华师大版数学九上24.6《图形与坐标》word练习题2
(2)求经过第2008次跳动之后,棋子落点与点P的距离。
8、在平面直角坐标系中按下列要求作
图、
(1)作出三象限中的小鱼关于轴的对
称图形;
(2)将(1)中得到的图形再向右平移6
个单位长度、
9、以如图所示的方格纸中,每个小正方形的边长为1,如果以MN所在的直线为Y轴,以小正
方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则这时C点的坐标
可能就是( )
A、(1,3) B
、(2,-1)
C、2,1) D
、(3,1)
●体验中考
1、(2009年吉林省)如图,OAB△的顶点的坐标为(4,0),把OAB△沿轴向右平移得到
CDE△,如果1,CB那么OE
的长为 、
O
x
y
第11题图
2015秋华师大版数学九上24.6《图形与坐标》word练习题2
参考答案:
随堂检测:
1、 变换后的图形如图、变换后△ABC各顶点的坐标分别
为:(1)A(7,1),B(6,3),C(2,2);(2)A(-1,-1),B(-2,-3),C(-6,-2)、
2、作图(略)
点B的坐标为(-5,-4)
拓展提高:
1、(0,-1),(4,-1),(5,-0、5),(4,0),(0,0)
2、(1,-3)
3、(1)如图, A1(0,4),B1(2,2),C1(1,1)、
(2)如图,A2(6,4),B2(4,2),C2(5,1)、
(3)如图,△A1B1C1与△A2B2C2关于直线3x轴对称、
4、(3,4)
5、(3,1)
6、2008
7、解:(1)M(-2,0),N(4,4)(画图略) …4分
(2)棋子跳动3次后又回点P处,所以经过第2008次跳
动后,棋子落在点M处,
∴PM=2222OMOP=22=22
答:经过第2008次跳动后,棋子落点与P点的距离
2015秋华师大版数学九上24.6《图形与坐标》word练习题2
为22、
8、注:关于x轴对称的点的横坐标不变,纵坐标就是原坐标的相反数,图形向右平移,纵坐标
不变,横坐标加6即可;做以上图形时,只需做出几个关键点的相应的对应点,在顺次连接即
可。
9、B
体验中考:
1、7
