1_平面基本性质第三课时上课
高一数学平面的基本性质1
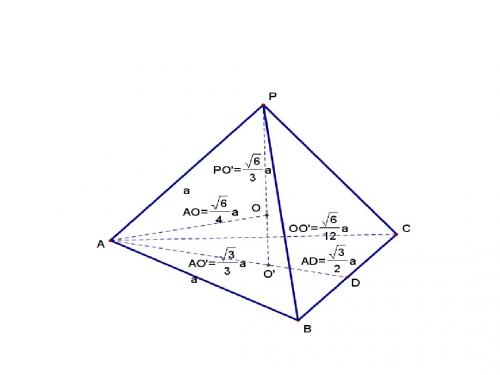
公理1 如果一条直线上的两点在一个平面内, 那么这条直线在这个平面内.
(两点确定一条直线)
应用:
1、判断直线是否在平面内的依据。
2、检验一个面是否是平面。
公理2 过不在一条直线上的三点,有且只 有一个平面
A, B, C不共线 A, B, C确定一平面
过A、B、C 三点的平面可记作“平面ABC ”.
(不共线的三点确定一个平面) “有”——存在性
这是确定平面的依据之一
“只有”——唯一性
公理3 如果两个不重合的平面有一个公共点, 那么它们有且只有一条过该点的公共直线.
P l且 P l
注意: 1.以后说到两个平面,如不特 别说明都是指两个不重合的平 面。
2.这是判定两平面相交以及 它们的交点共线的依据。
b
即:两平行直线确定一个平面
C
练习
l b B, 1.已知直线 a , b 相交,且 l a A,
b、 l 三线共面. 求证: a 、
2.三条直线相交于一点,过每两条相交直线作一个平面. 最少可以作几个平面?最多可以作几个平面? 若三条直线相交于三点呢?
; /2016-12/16/content_9227222.htm 海尔开放式创新模式再升级 HOPE创新合伙人计划发布
两个不重合的平面,只要它们有公共点,
叫做这两个平面的交线。
它们 就是相交的位置关系,交集是一条直线,
表示两平面相交的画法
画两平面相交,当其中一个平面被另一个平面遮住时, 应把被遮住的部分画成虚线或不画。
1.正方体的各顶点如图所示,正方体的三个面所在 平面 AC 1 1, A 1 B, B 1C ,分别记作 、、 , 试用适当的符号填空.
平面的基本性质教案

课题:9.1平面的基本性质(一)教学目标:知识目标:(1)了解平面的概念,掌握平面的画法及表示法(2)掌握平面的基本性质及它们的作用能力目标:(3)会用文字语言、图形语言、符号语言表示点、线、面的位置关系(4)能够画出水平放置的平面的直观图(5)培养学生的空间想象能力情感目标:(6)渗透数学来源于实践又服务于实践的辩证观点(7)在数学学习活动中获得成功的体验,建立自信心教学重点与难点重点:(1)平面的概念。
“平面”是教材中只作描述说明,而不定义的最原始的基本概念,应让学生结合实例弄清平面的含义,认真体会平面与平面无大小之分,无厚薄之别,仅有位置上的不同。
(2)会正确画图表示两相交平面的位置关系(3)会用文字语言、图形语言、符号语言表示点、线、面的位置关系,并熟记它们,达到能得心应手运用他们的程度。
难点:(1)理解平面的无限延展性;(2)集合概念的符号语言的正确使用。
授课类型:新授课课时安排:1课时教学方法与教学手段:讲授法多媒体辅助教学教学过程一、创设情景导入新课:首先来讨论一个问题:“给你6根火柴棒能拼出四个三角形吗?”现在老师这里有6根火柴棒,想来尝试的同学请举手。
好,**同学请上来(可以不用把六根火柴棒放在同一个平面里考虑)做得非常好,大家看下,这是什么图形,这不是平面图形,是立体几何图形,大家想一下就知道这个问题在平面中是解决不了的,解决这个问题就需要运用立体几何知识。
那么今天我们就来学习与立体几何有关的知识,(立体几何章节中的第一节)——平面的基本性质二、讲解新课:平面的画法:首先让学生观察光滑的桌面、平静的湖面,象这些桌面、平静的湖面都给我们以平面的形象师:生活中还有哪些留给我们平面的形象呢?生:黑板、地面、镜面、海平面师:对,象这些镜面、桌面、黑板面、地面、海平面等都给我们以平面的印象那平面具有什么特点?生:平坦、光滑师:对,那还具什么特点?生:、、、、同学们有没发现镜面、桌面、地面、海平面,逐渐增大,但还是平面,说明平面还具有“无限延展”的特点下面我们来归纳总结下平面的特点(看PPT)(平面具有“平”、“无限延展”、“无厚薄”的特点。
“平面的基本性质”教案

平面的基本性质教案一、教学目标知识与技能:1. 理解平面的基本性质,掌握平面的定义和特征。
2. 学会使用平面几何图形进行推理和证明。
过程与方法:1. 通过观察和操作,培养学生的空间想象力。
2. 运用小组合作、讨论交流等方法,提高学生的合作能力和口头表达能力。
情感态度价值观:1. 培养学生对数学的兴趣和好奇心。
2. 培养学生的逻辑思维能力和解决实际问题的能力。
二、教学重点与难点重点:1. 平面的定义和特征。
2. 平面几何图形的推理和证明。
难点:1. 理解平面的无限延展性和不可度量性。
2. 掌握平行线的性质和判定。
三、教学准备教师准备:1. 平面的定义和特征的相关教学素材。
2. 平面几何图形的推理和证明的案例。
学生准备:1. 了解一些基本的几何概念。
2. 准备笔记本和文具。
四、教学过程1. 导入:利用现实生活中的实例,如桌面、黑板等,引导学生观察和体验平面的存在。
提出问题:“你们认为平面是什么?”让学生发表自己的观点。
2. 探究:引导学生通过观察和操作平面几何图形,如正方形、长方形等,探讨平面的基本性质。
让学生尝试用自己的语言描述平面的特征,如无限延展性、不可度量性等。
3. 证明:利用反证法,让学生尝试证明平面的基本性质。
例如,证明平面是无限延展的,可以让学生假设平面有边界,通过推理和逻辑分析,得出矛盾的结论,从而证明平面的无限延展性。
4. 应用:给出一些平面几何图形的推理和证明案例,让学生运用所学的平面性质进行分析和解决问题。
如平行线的性质和判定,可以让学生观察和分析实际生活中的实例,如马路上的交通标志等。
五、作业布置1. 完成课后练习题,巩固所学知识。
2. 观察生活中的平面实例,拍摄照片或绘制图片,下节课分享。
教学反思:课后对教学效果进行反思,观察学生对平面基本性质的理解程度,以及他们在实际问题中的运用能力。
根据学生的反馈,调整教学方法和策略,以提高教学效果。
六、教学拓展1. 利用多媒体展示平面几何图形的动态变化,如正方形变为长方形的过程,让学生直观地感受平面的性质。
中职数学 10.1-平面的基本性质

即: A∈且B∈ AB
A B
AB
B
A
作用:用于判定线在面内
结论2 :空间中线与面的位置关系
直线a在平面内 记作:a 直线a在平面外 记作:a
强调:
空间中点与线(面)只有∈和 关系
空间中线与面只有 与 的关系
推导符号“”的使用:
条件结论
a和b确定一平面.
a//b
a和b确定一平面.
作用:用于确定一个平面.
A
B C
Aa
aP
b
a
b
公理3:若两个不重合平面有一个公共点, 则它们有且只有一条过该点的公共直线。
即: P∈且P∈ I=l且P∈l
}{ P∈
I=l
P∈
P∈l
作用:用于证明点在线上或多点共线
结论1:空间中点与线、点与面的位置关系
条件结论
} 条件1 结论
条件2
B
A
C
A、B、C不共线 A、B、C确定一个平面
作用:用于确定一个平面.
确定一平面还有哪些方法?
公理2.不共线的三点确定一个平面.
A
B C
推论1.一条直线和直线外一点确定一个平面。 推论2.两条相交直线确定一个平面。 推论3.两条平行直线确定一个平面。
思考4:如图所示,两个平面、,若相交 于一点,则会发生什么现象?
l
P
公理3:若两个不重合平面有一个公共点, 则它们有且只有一条过该点的公共直线。
即: P∈且P∈ I=l且P∈l
}{ P∈
I=l
P∈
P∈l
作用:用于证明点在线上或多点共线.
【全程复习方略】2013版高中数学 7.3平面的基本性质及两直线位置关系课件 理 新人教B版
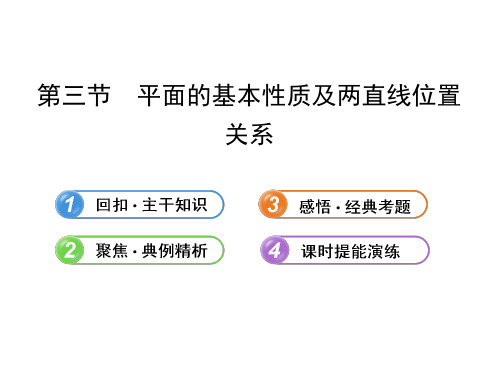
答案:①④⑤
【阅卷人点拨】通过阅卷数据分析与总结,我们可以得到以下 误区警示和备考建议: 在解答本题时有以下几点容易造成失误:
误 区 警
一是作图不精确,从而导致对④判断失误;
二是对异面直线概念理解不清造成失误; 三是对⑤的直观理解不够,不会结合图形,直觉不 灵敏而造成失误.
示
备 考 建 议
对于本类问题的解答,还有几点容易造成失误,备考时
2
故GH∥BC且GH=BC, 所以四边形BCHG是平行四边形.
②C,D,F,E四点共面.理由如下: 由BE∥AF且BE=
1 AF,G是FA的中点知, 2
BE∥GF且BE=GF,
所以四边形EFGB是平行四边形, 所以EF∥BG. 由①知BG∥CH,所以EF∥CH,故EC,FH共面. 又点D在直线FH上,所以C,D,F,E四点共面.
(3)如图,取BC的中点O,连接MO、NO, 则 OM 1 AC,ON 1 BD,
2 2
在△MON中,MN<OM+ON= ∴④正确.
1 (AC+BD). 2
答案:(1)异面、平行或相交 (2)3或4 (3)④
平面的基本性质及其应用
【方法点睛】 考查平面基本性质的常见题型及解法 (1)判断所给元素(点或直线)是否能确定唯一平面问题,关键是 分析所给元素是否具有确定唯一平面的条件.
(D)PN∥面BDC
【解题指南】结合图形,根据有关的知识逐一进行判断.注意
本题选择的是错误选项!
【规范解答】选C.因为四边形PQMN为正方形,所以PQ∥MN, 又PQ 平面ADC,MN⊂平面ADC,所以PQ∥平面ADC.
又平面BAC∩平面DAC=AC,所以PQ∥AC.
同理可证QM∥BD.由PQ∥AC,QM∥BD,PQ⊥QM可得AC⊥BD,故A
14.1 平面及其基本性质

二、典型习题
(一)概念的辨析 1.判断下列命题的真假,真的打“√”,假的打“×”
(1)可画一个平面,使它的长为4cm,宽为2cm。( )
(2)一条直线把它所在的平面分成两部分, 一个平面把空间分成两部分.
()
(3)一个平面的面积为20 cm2.
()
(4) 一条直线和任意一点确定一个平面
()
2、在下列命题正确的是(
• 2、习题14.1A组1 习题14.1B组1,2
• 3、画一个正方体
2.根据下列符号表示的语句,说出有关 点、线、面的关系,并画出图形.
(2)l , m A
(3) l
思考题:
几位同学一次野炊活动,带去一张折叠方桌, 不小心弄坏了桌脚,有一生提议可将几根一样长的 木棍,在等高处用绳捆扎一下作桌脚(如图所示),
类比思考:
如果两个不重合的平面有公共点,其公共点有多少个?
如图,把三角板的一个角立 在课桌面上,三角板所在的 平面与桌面所在的平面是否 只相交于一点B?为什么?
BB
两相交平面的公共部分的特点:有无穷多点, 而且是直线。
公理2 如果两个平面有一个公共点,那么 它们有且只有一条经过这个点的公共直线.
P l, Pl
同理,P∈平面CBD. ∴P在平面ABD与平面CBD的交线BD上, 即B、D、P三点在同一条直线上.
题型: 证明多线共面
【例3】求证:两两相交且不共点的四条直线在同一平面内.
分析 由题知,四条直线两两相交且不共点,故有两种情况:一种是三条交 于一点,另一种是任何三条都不共点,故分两种情况证明. 要证明四线共面,先根据公理2的推论证两条直线共面,然后再证第三条直 线在这个平面内,同理第四条直线也在这个平面内,故四线共面.
平面的基本性质教案
学生活动
感悟与改进
通 过学 生演 示引 出平 面的概念
学生自主推导,教师适,根据情况进行 点评
在平面α上(外) ,记作 A∈α(A∉α) ;若直线 a 在平面α内,记做 a⊂α,若直线 a 不在平面α内, 记做 a⊄α。这里的“⊂、∈”借用了集合的符号, 其含义仍然与集合符号的意义一致。 (2)公理一:若一条直线上有两个点在一个 教师提出问题,学生思 平面内,则该直线上所有的点都在这个平面内。即 考,提高认知,强化理 A∈α,B∈α ⇒ AB ⊂ α。 解 说明:此时即直线在平面内,或者说平面经过 直线。公理一是判定直线在平面内的依据。 位置关系 点 p 在直线 AB 上 点 C 不在直线 AB 上 点 M 在平面 AC 上 点 A1 不在平面 AC 上 直线 AB 与直线 BC 交于 点B 直线 AB 在平面 AC 上 直线 AA1 不在平面 AC 上 3、两个平面相交的依据(这里所指的两个平面都 是指不重合的平面) : (1)当一条直线 a 既在平面α内,又在平面 β内,即α和β有一条公共的直线 a,则称α与β 相交,交线是 a,记做α∩β=a。 (2)公理二:如果两个平面有一个公共点, 那么它们有且只有一条通过这个点的公共直线。 即 教师提出问题,学生练 习。知识应用意识与能 A∈α,A∈β ⇒ α∩β=a 且 A∈a。 “公理二” 说明: ①若两个平面有一个公共点, 力的培养 则必定还有第二个、第三个……,必有无限多个公 共点,所有这些公共点都在同一条直线上,反之, 该直线上的每一点都是两个平面的公共点。因此, 两平面若有公共点,则必有公共直线。②两平面若 相交,则有且只有一条交线。 [课堂检测]:课本 22 页 1,2,3,4 板书 设计 教师提出问题,学生练 习,在思维训练过程中 提高认知,强化理解, 增强能力。 符号表示
高中数学《平面的基本性质》教案
高中数学《平面的基本性质》教案一、教学目标1. 让学生理解并掌握平面的基本性质,包括平面的定义、平面的表示方法、平面的性质等。
2. 培养学生运用平面几何知识解决实际问题的能力。
3. 提高学生的逻辑思维能力和空间想象力。
二、教学内容1. 平面的定义:平面是无限延展、无厚度的二维空间。
2. 平面的表示方法:用字母“α”、“β”等表示平面。
3. 平面的性质:(1)平面上的点与直线的关系:任意一点在平面内,都可以用平面内的直线表示。
(2)平面上的直线与直线的关系:平面内的任意两条直线,要么相交于一点,要么平行。
(3)平面上的直线与点的关系:平面内的任意一点,要么在给定直线上,要么不在给定直线上。
三、教学重点与难点1. 教学重点:平面的定义、表示方法和平面的性质。
2. 教学难点:平面的性质中直线与直线、直线与点的关系的理解和应用。
四、教学方法1. 采用问题驱动法,引导学生通过思考和讨论,自主探究平面的基本性质。
2. 利用几何画板或实物模型,直观展示平面的性质,帮助学生建立空间想象。
3. 设计适量练习题,让学生在实践中巩固知识。
五、教学过程1. 导入:通过生活中的实例,如平面地图、桌面等,引出平面的概念。
2. 新课导入:介绍平面的表示方法,讲解平面的性质。
3. 课堂讲解:详细讲解平面的性质,引导学生理解直线与直线、直线与点的关系。
4. 例题讲解:分析并解决典型例题,让学生掌握平面几何的应用。
5. 课堂练习:学生自主完成练习题,巩固所学知识。
6. 总结与拓展:对本节课内容进行总结,提出更高层次的问题,激发学生兴趣。
7. 课后作业:布置适量作业,让学生进一步巩固平面几何知识。
六、教学评估1. 课堂提问:通过提问了解学生对平面基本性质的理解程度。
2. 练习题解答:检查学生课后练习题的完成情况,评估其对知识的掌握程度。
3. 小组讨论:观察学生在小组讨论中的表现,了解其合作能力和解决问题的能力。
七、教学反思1. 反思教学内容:根据学生的反馈,调整教案内容,使之更符合学生的认知水平。
《4.1.2平面的基本性质》教学设计教学反思-2023-2024学年中职数学高教版21拓展模块一上册
《平面的基本性质》教学设计方案(第一课时)一、教学目标1. 理解平面的基本性质,包括平面的定义、平面的基本性质及推论。
2. 能够应用平面的基本性质进行简单的推理和证明。
3. 培养逻辑推理和空间想象力。
二、教学重难点1. 教学重点:理解并掌握平面的基本性质及推论。
2. 教学难点:从二维空间的角度出发,培养空间想象力,进行推理和证明。
三、教学准备1. 准备教学PPT,包含图片、动画和相关概念的解释。
2. 准备一些简单的教具,如纸张、图钉等,用于演示和解释平面的基本性质。
3. 准备一些练习题,供学生练习和巩固所学知识。
4. 安排一次课前预习,让学生对平面的基本性质有一定的了解。
四、教学过程:1. 导入新课通过生活中的实例引导学生观察平面的基本性质,引起学生兴趣,明确学习目标。
例如:在平面内绘制一个矩形花坛的平面图,并标注各个角点。
请学生观察平面图中的点、线、面的关系,引导学生发现平面性质的应用价值。
2. 探索新知学生分小组讨论并探索平面的基本性质,教师给予必要的提示和引导。
通过多媒体演示、实物展示等多种方式,帮助学生理解平面的基本性质。
例如:使用三角板和直尺,演示直线的平行性和不平行性;使用平行四边形纸张,演示其两组对边平行的性质。
3. 师生互动鼓励学生大胆提出问题,共同讨论解决,加强师生互动,增强学生的学习热情。
教师对课堂内容进行总结,强调重点和难点,并布置适当的练习题以巩固所学知识。
例如:请学生举出生活中应用平面的实例,并解释其原理。
4. 布置作业(1) 完成课后练习题;(2) 预习下一节内容,提出自己的问题。
5. 课堂小结回顾本节课的主要内容,强调平面的基本性质及其应用价值,鼓励学生继续探索数学世界的奥秘。
教学设计方案(第二课时)一、教学目标1. 理解平面的公理及其推论在日常生活中的应用。
2. 能够用平面的公理及推论解决一些实际问题。
3. 培养逻辑推理和数学应用能力。
二、教学重难点1. 教学重点:理解并掌握平面的公理及其推论。
【中职】9.1 平面的基本性质
巩固知识 典型例题
例3 在长方体 ABCD A1B1C1D1中,画出由A、C、D1 三点所确定的平面γ与长方体的表面的交线.
解 点 A、D1 为平面 与平面 A1D的公共点, 点 A、C 为平面 与平面 BD 的公共点,
点 C、D1 为平面 与平面 C1D 的公共点.
分别将这三个点两两连接,得到直线 AD1、AC、CD1
立
立体几何
体
立体几何
几
立体几何
9.1何.1~9.1.2 平面的基本性质
【教学目标】 知识目标: (1)了解平面的概念、平面的基本性质; (2)掌握平面的表示法与画法.平面图形与立体图形的
直观画法。 能力目标: (1)画出平面及两个相交平面的直观图; (2)利用平面的性质和三个结论,解释生活空间的一些
z D
例2 画长为 4 cm,宽为 3 cm, A
高为 2 cm 的长方体的直观图.
D
A
y C
B
C
B x
(1) 用例 1 的方法画一个长为 4 cm,宽为 3 cm 的长方形的 直观图ABCD.
(2) 过 A 做 z 轴,使之垂直与 x 轴.在 z 轴上截取 AA = 2 cm. (3) 过点 B,C,D 分别作 z 轴的平行线 BB ,CC ,DD ,
(2) 在立体图形中,过 x 轴或 y 轴的交点取 z 轴,并
使 z 轴垂直于 x 轴和 y 轴. 过 x 轴或 y 轴的交点 作 z 轴对应的z 轴,且 z 轴垂直于 x 轴. (3) 图形中平行于 z 轴的线段画成平行于 z 轴的线段,
且长度不变. (4) 连接有关线段,擦去有关辅助线.
作边长为 4cm 的正方体的直观图.
练习:求证:三角形一定是平面图形
