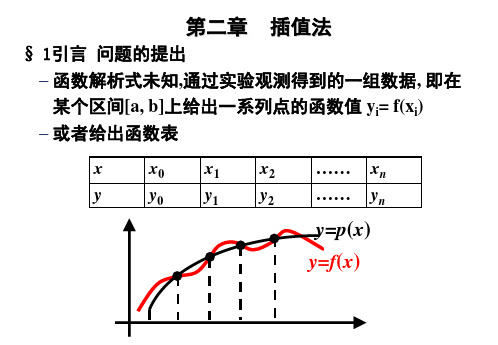
数值分析第二章
合集下载
清华第五版数值分析第二章课件

证 设所求的插值多项式为
Pn(x)=a0+a1x+a2x2+...+anxn
则由插值条件式Pn(xi)=yi (i=0,1, ..., n) 可得关于系数
a0 ,a1 , …,an的线性代数方程组
上页 下页
n a0 a1 x0 an x0 y0 n a0 a1 x1 an x1 y1 n a0 a1 xn an xn yn 此方程组有n+1个方程, n+1个未知数, 其系数行列式是 范德蒙(Vandermonde)行列式:
由式 n+1(xk)=0 和式 Pn(xk)=yk ( k=0,1,…,n ),以及
Rn ( x ) f ( x ) Pn ( x ) K ( x )n1 ( x )
可知:x0 , x1, , xn 和 x 是(t) 在区间[a,b]上的 n+2个 互异零点, 因此根据罗尔 (Rolle) 定理, 至少存在一点 =(x) (a,b),使 ( n 1) f ( ) ( n1) 即 K ( x) ( ) 0 ( n 1)! 所以
f ( n1) ( ) Rn ( x ) f ( x ) Pn ( x ) n 1 ( x ) ( n 1)!
上页 下页
2.2 拉格朗日插值
Lagrange 法1736-1813
上页
下页
2.2.2 拉格朗日插值多项式
利用拉格朗日基函数l i(x), 构造次数不超过n的多项式
一性有
l ( x) x
i 0 i
n
k i
x ,
k
k 0,1, , n
特别当k=0时,就得到
数值分析第五版第二章_插值法
于是
Ak
1
(x
j 0 j k
n
k
xj)
代入上式,得
(x x
l k ( x)
j 0 j k n
n
j
)
j 0 jk n
x xj xk x j
(x
j 0 j k
k
xj)
称
l k ( x) 为关于基点
x i 的n次插值基函数(i=0,1,…,n)
( x x0 )(x x2 ) ( x x0 )(x x1 ) ( x x1 )(x x2 ) P( x) y0 y1 y2 ( x0 x1 )(x0 x2 ) ( x1 x0 )(x1 x2 ) ( x2 x0 )(x2 x1 )
容易看出,P(x)满足条件
( x 0 , y0 ), ( x1 , y1 ), ( x 2 , y2 ) 的抛物线 y P( x) 近似代替曲线
y f ( x) ,如下图所示。因此也称之为抛物插值。
P(x)的参数 a0 , a1 , a 2
直接由插值条件决定, 即
y
a0 , a1 , a2满足下面
O
y=L2(x) y0 x0 y1 x1 y1 x2 y=f(x) x
( x x0 )(x x1 ) l 2 ( x) ( x2 x0 )(x2 x1 )
这样构造出来的 l0 ( x),l1 ( x),l2 ( x) 称为抛物插值的基函数 取已知数据 y0 , y1 , y 2 作为线性组合系数,将基函数
l0 ( x),l1 ( x),l2 ( x) 线性组合可得
a n x0 n a n 1 x0 n 1 a1 x0 a 0 f ( x0 ) n n 1 a n x1 a n 1 x1 a1 x1 a 0 f ( x1 ) a x n a x n 1 a x a f ( x ) n 1 n 1 n 0 n n n
数值分析-第二章-距离空间

a
b g(x) q dx 1/ q
a
其中 f (x) p , g(x) q在[a,b]上可积分。
特别的 p=q=2 时,称为 Cauchy 不等式
特别的,当 n=1 时, (x, y) x y , 当 n=2 时, (x, y) (x1 y1)2 (x2 y2 )2
如果在 R2 中,定义 d(x, y) x1 y1 x2 y2 ,
例2 有理数空间 Q 按欧氏距离是不完备的距离空间。
例 3 距离空间l2 和 L2[a,b]按通常意义下的距离是完备的。
例 4 C[a,b]按 (x, y) max x(t) y(t) 是完备的距离空间; t[ a ,b ]
C[a,b]按
1(x,
y)
b
a
x(t)
y(t ) dt
是不完备的距离空间
间 Q 是等距同构的,所以实数空间 R1 是有理数空间 Q
的完备化空间。
例2
C[a,b]按距离
(x,
y)
b
a
x(t)
y(t)
dt
是不完备的,
但C[a,b] L1[a,b],且C[a,b]在L1[a,b]中稠密,故 L1[a,b]是
C[a,b]的完备化距离空间。
同理,C[a,b]按距离
( x,
y)
则l p 是距离空间,常称为 p 方可和的空间。
特别的,当 p=2,l 2 称为平方可和距离空间。
§2.2 收敛概念
1) 定义(收敛点列) 设 X 是一个距离空间,{x n}是
X 中点列, x X 。若 n 时, (xn, x) 0 (即 0, N, 当n N时, (xn, x) )
补充不等式
1)Minkowski 不等式
数值分析课件 第二章2.2

(1) 当r =1时称为线性收敛,此时C < 1; (2) 当r =2 时称为二次收敛,或平方收敛; (3) 当r =1,C=0时称为超线性收敛.
二分法线性收敛; 不动点迭代中,若 ( x* ) 0 则线性收敛
r (r 1)阶收敛一定是超线性收
2 k
敛,反之不一定成立。
k 2k
数 值 分 析
第二章
解非线性方程的数值方法
一、 二分法 二、 迭代法
三、 Newton法
二、 迭代法 1 迭代法的基本思想 对给定方程f(x)=0,可以用各种方法转化成等 (2.1) 价方程 x ( x ) * * * * 若x 是f(x)的根,即若 f ( x ) 0 ,则有 x ( x ) 称x*为函数 ( x ) 的一个不动点.
( p ) ( k )
p!
( xk x * ) p
* p
xk 1 x
*
( p ) ( k )
p!
( xk x )
ek 1 1 ( p) * lim p (x ) k e p! k
2 例2.9 将方程 x 2 0化为等价形式 x ( x ), x 分别取 x0 1, 用迭代法求其根,并验 证次此迭代
*
由此得迭代公式
yk ( xk ),
xk 1
L yk ( yk xk ) 1 L
如何求L?
再令 y0 ( x0 ), z0 ( y0 ) 得到 * * * * y0 x L( x0 x ), z0 x L( y0 x )
y0 x x0 x ( y0 x0 ) * x x0 * * z0 2 y0 x0 z0 x y0 x
数值分析第二章答案

∑
n
i=1
ln x i = 0
θ
∧
= −
n
∑ ∑
n
n
i=1
ln x i n
θ
= =
解之得:
i=1
ln x i
(2)母体 X 的期望
E (x) =
∫
+∞ −∞
xf ( x ) d x =
∫
1 0
θ xθ dx =
θ θ +1
而样本均值为:
1 n X = ∑ xi n i =1 令E ( x) = X 得 θ =
x e 2σ 1 n
d x = 2 x ) =
∫
+ ∞ 0
x 2σ
e
−
x σ
d x = − x e ) = 1 ⋅ nσ n
−
x σ
+ ∞
+
0
∫
+ ∞ 0
e
−
x σ
d x =
E (σ ) = E (
∑
n
i=1
i
1 n
∑
n
E ( x
i=1
i
= σ
所以
σ=
∧
1 n ∑ xi σ n i=1 为 的无偏估计量。
∧
X 1− X
5.。解:其似然函数为:
L (σ ) = ∏
i =1
n
1 ⋅e 2σ
−
xi σ
=
1 ⋅e (2σ ) n 1 σ
n i =1
−
1 σ
∑ xi
i =1
n
ln L (σ ) = − n ln(2σ ) − 得: σ =
∧
数值分析计算方法第二章作业

第二章作业题答案
1.当x=1,-1,2时,f(x)=0,-3,4,求f(x)的二次差值多项式 (1)用单项式基底 (2)用拉格朗日插值基底
(1)解:设 f(x)abxcx2 则a+b+c=0 a-b+c=-3 a+2b+4c=4
解得
a7,b3,c5 326
所以 f(x)73x5x2
解:由p(0)=0,p(1)=1,p(2)=1,我们可以得出
P 2 ( x ) ( x ( 1 1 ) ) ( ( x 2 ) 2 ) 0 ( 1 ( x ) 0 ( ) x ( 1 2 2 ) ) 1 ( ( 2 x ) ) ( ( 2 x 1 1 ) ) 1 1 2 x 2 3 2 x
将 p'(0)0,p'(1)1 代入到上式中,得出
a 3 ,b 1
4
4
从而有 P4(x)1 4x43 2x39 4x2
p ( x 0 ) f ( x 0 ) , P '( x 0 ) f '( x 0 ) , P ''( x 0 ) f ''( x 0 ) ,p ( x 1 ) f ( x 1 )
解:设 P ( x ) f( x 0 ) f'( x 0 ) ( x x 0 ) f''2 ( x ! 0 )( x x 0 ) 2 a ( x x 0 ) 3
解:设P(x)= ax3bx2cxd
则 P'(x)3ax22bxc
d 0 代入已知条件,得到: c 1
abcd 1 3a 2b c 2
解得a=1,b=-1,c=1,d=0
所以P(x)= x3 x2 x
1.当x=1,-1,2时,f(x)=0,-3,4,求f(x)的二次差值多项式 (1)用单项式基底 (2)用拉格朗日插值基底
(1)解:设 f(x)abxcx2 则a+b+c=0 a-b+c=-3 a+2b+4c=4
解得
a7,b3,c5 326
所以 f(x)73x5x2
解:由p(0)=0,p(1)=1,p(2)=1,我们可以得出
P 2 ( x ) ( x ( 1 1 ) ) ( ( x 2 ) 2 ) 0 ( 1 ( x ) 0 ( ) x ( 1 2 2 ) ) 1 ( ( 2 x ) ) ( ( 2 x 1 1 ) ) 1 1 2 x 2 3 2 x
将 p'(0)0,p'(1)1 代入到上式中,得出
a 3 ,b 1
4
4
从而有 P4(x)1 4x43 2x39 4x2
p ( x 0 ) f ( x 0 ) , P '( x 0 ) f '( x 0 ) , P ''( x 0 ) f ''( x 0 ) ,p ( x 1 ) f ( x 1 )
解:设 P ( x ) f( x 0 ) f'( x 0 ) ( x x 0 ) f''2 ( x ! 0 )( x x 0 ) 2 a ( x x 0 ) 3
解:设P(x)= ax3bx2cxd
则 P'(x)3ax22bxc
d 0 代入已知条件,得到: c 1
abcd 1 3a 2b c 2
解得a=1,b=-1,c=1,d=0
所以P(x)= x3 x2 x
数值分析第二章 线性方程组的数值解法
(2.2)
a11 x1 a12 x2 a1n xn b1 a22 x2 a2 n xn b2 ann xn bn
(2.3)
2.顺序高斯消去法
a11 x1 a12 x2 a13 x3 a1n xn a1, n 1 a 21 x1 a 22 x2 a 23 x3 a 2 n xn a 2, n 1 a n1 x1 a n 2 x2 a n 3 x3 a nn xn a n , n 1
(1) a12 (1) a 22
(1) an 2
0
(1) a1 n (1) a2 n (1) a nn
?
A( 1 )
(1) (1) (1) a11 a12 a1 n (1) (1) (1) a21 a22 a2 n (1) (1) (1) an 2 ann a n1
(k ) (k ) m a 用 ik ik / akk 乘第k行
加到第i行中,得到
a (1) a (1) 1k 11 (k ) akk 0 0
(1) (1) x a1 b 1 n 1 (k ) (k ) (k ) akk 1 akn xk bk ( k 1) . ( k 1) ( k 1) x ak 1k 1 ak 1n k 1 bk 1 ( k 1) ( k 1) x ( k 1) ank 1 ann n b n (1) a1 k 1
写出原方程组的增广矩阵:
0.0120 0.0100 0.1670 0.6781 1.000 0.8334 5.910 12.10 1200 4.200 981.0 3200
《数值分析》第二讲插值法PPT课件
1 xn xn2 xnn Vandermonde行列式
即方程组(2)有唯一解 (a0, a1, , an)
所以插值多项式
P (x ) a 0 a 1 x a 2 x 2 a n x n
存在且唯一
第二章:插值
§2.2 Lagrange插值
y
数值分析
1、线性插值
P 即(x)ykx yk k 1 1 x yk k(xxk)
l k ( x k 1 ) 0 ,l k ( x k ) 1 ,l k ( x k 1 ) 0 l k 1 ( x k 1 ) 0 ,l k 1 ( x k ) 0 ,l k 1 ( x k 1 ) 1
lk1(x)(x(k x 1 x xk k))x x ((k 1x k x 1k )1) lk(x)((xx k x xk k 1 1))((x xkxx k k1)1)
第二章:插值
数值分析
3、Lagrange插值多项式
令 L n ( x ) y 0 l 0 ( x ) y 1 l 1 ( x ) y n l n ( x )
其中,基函数
lk (x ) (x ( k x x x 0 ) 0 ) (( x x k x x k k 1 1 ) )x x k ( ( x x k k 1 ) 1 ) (( x x k x n x )n )
因此 P (x ) lk (x )y k lk 1 (x )y k 1
且
P (x k ) y k P (x k 1 ) y k 1
lk(x), lk1(x) 称为一次插值基函数
数值分析
第二章:插值
2、抛物线插值 令
y (xk , yk )
f (x)
lk1(x)(x(k x 1 x xk k))x x ((k 1x k x 1k )1) p( x) (xk1,yk1)
数值分析-第二章(2)
知识回顾: 知识回顾:向量与矩阵的范数
向量范数: 向量范数 范数
矩阵范数
;
称为B的谱半径
相容矩阵范数
称为与向量范数相容的矩阵范数, 称为与向量范数相容的矩阵范数,如果
对任意向量x成立
MATLAB中 输出A的p-范数
矩阵范数性质
(1 ) (2 ) (3 ) (4 )
A ≥ 0, A = 0⇔ A = O
⋯
Bk x = λ k x ;
,
Bk x = λ ⋅ x
k
所以当
k
k →∞
不收敛到零向量。根据引理1, {B x} 不收敛到零向量。
{B }
k
不收敛到零矩阵, 不收敛到零矩阵,矛盾于( 矛盾于(1)。
(2) ⇒ (3)
对任
ε > 0,存在一种矩阵范数
B ε ≤ ρ ( B) + ε
⋅ ε使
由(2),
为方程组的近似解。 为方程组的近似解。
Gauss-Seidel 迭代
x
( k +1) i
= (bi − ∑ aij x
j =1
i −1
( k +1) j
−
∑
j =i +1
n
n
aij x (jk ) ) / aii , i = 1, 2,⋯ , n
xi( k +1) = (bi − ∑ aij x (jk ) −
Ax=b >>x=A\b (核心: 核心:列主元Gauss消去) PA=LU LUx=Pb Ux=y; Ly=Pb
适合中、 适合中、小规模问题
迭代法
Jacobi Gauss-Seidel SOR 收敛性、 收敛性、收敛速度
数值分析课后第二章习题解答
6 应用牛顿迭代法于方程 x – a = 0, 导出求立方根 3 解:令 f(x) = x – a,则牛顿迭代公式
3
3
a 的迭代公式, 并讨论其收敛阶。
x n +1 = x n −
故迭代函数为
3 xn −a 2 a = xn + 2 2 3 3x n 3xn
ϕ ( x) =
而
a 2 x+ 2 3 3x
x − 1 , ϕ ′( x ) =
−1 2 ( x − 1) 3
,在 x0 = 1.5 附近有 | ϕ ′( x) |≥ 1 成立,故
迭代格式不收敛; (3) ϕ ( x ) = 1 + x , ϕ ′( x ) =
3 2
− 2x 33 (1 + x 2 ) 2
,在 x0 = 1.5 附近有 | ϕ ′( x) |< 1 成立,故
反复递推,得
( xn − 2 ) 2 ( xn + 2 ) 2 ]2 = L = [
2
x n +1 − 2 x n +1 + 2
令
=
( xn − 2 ) 2 ( xn + 2 ) 2
=[
x n −1 − 2 x n −1 − 2 x0 − 2 x0 + 2
= q2
n
x0 − 2 x0 + 2
]2
n +1
x0>0,均收敛于 2 。
证明:对迭代格式,得 x n +1 =
1 2 ( xn + 2) ,等式两端同减 2 ,并进行配方,得 2 xn 1 x n +1 − 2 = ( xn − 2 ) 2 2 xn x n +1 + 2 = 1 ( xn + 2 ) 2 2 xn
