《理论力学》第九章 质点动力学 习题解
《理论力学》第九章质点动力学

目
CONTENCT
录
• 质点动力学的基本概念 • 质点的运动分析 • 质点的动力学方程 • 刚体的动力学 • 相对论力学简介
01
质点动力学的基本概念
质点和质点系
质点
具有质量的点,没有大小和形状 ,是理论力学中最基本的理想化 模型。
质点系
由两个或多个质点组成的系统, 可以是一个物体或多个物体。
质点运动的基本参数
位移
质点在空间中的位置变化。
速度
质点在单位时间内通过的位移,表示质点的运动快 慢和方向。
加速度
质点速度的变化率,表示质点速度变化的快慢和方 向。
质点动力学的基本定律
牛顿第一定律(惯性定律)
一个不受外力作用的质点将保持静止状态或匀速直线运动状态。
牛顿第二定律
质点的加速度与作用力成正比,与质量成反比,即F=ma。
自然坐标系中的运动分析
总结词
自然坐标系是一种以质点所在位置的切线方向为基准的描述方法,常用于分析曲线运动。在自然坐标系中,质点 的运动分析需要考虑切向和法向的运动。
详细描述
在自然坐标系中,质点的位置由曲线上的弧长$s$和对应的角度$alpha$确定。切向的运动由切向速度$v_t$描述, 而法向的运动由法向加速度$a_n$描述。在自然坐标系中,质点的运动分析需要考虑切向和法向的物理量,以便 更准确地描述质点的运动状态。
描述质点角动量和角动量矩随时间变化的物理定理
详细描述
质点的角动量定理指出,质点所受合外力矩的冲量等于其角动量的变化量。公式表示为 Mt=L,其中M为合外力矩,t为时间,L为质点的角动量。角动量矩定理则描述了质点 绕定轴转动的动量矩变化规律,公式表示为L=Iω,其中L为动量矩,I为转动惯量,ω
理论力学练习册及答案
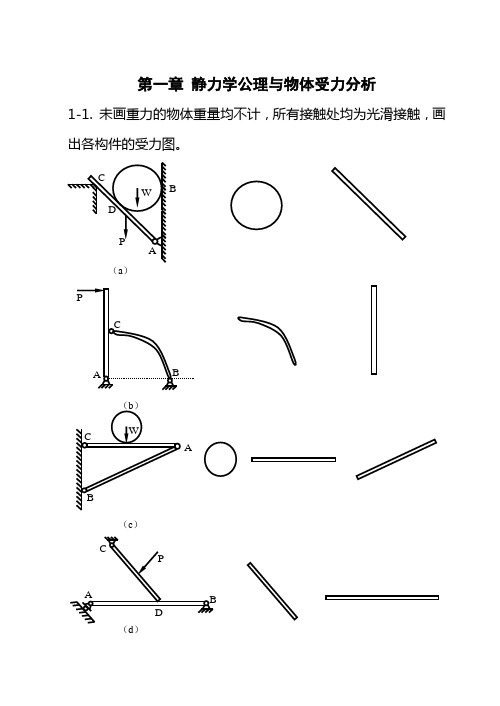
8-8.图示机构中,设当OA与水平线成450角的瞬时,曲柄OA有反时针方向的匀角速度ω=25 rad/s,连杆AB水平,扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解:将力系向A点简化,并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋,
作用点为:
3-2.已知A(1,0,1),B(0,1,2)(长度单位为米),F= kN。求力F对x、y、z轴的矩?
解:
3-3.如图所示,长方体边长为a、b、c,力F沿BD,试计算力F对AC轴之矩MAC(F)
解:力F对C点的矩为:
4-3.置于铅垂面内的均质正方形簿板重P= 100kN,与地面间的摩擦系数f= 0.5,欲使簿板静止不动,求作用在点A的力F的最大值?
4-4.折梯放在水平地面上,其两脚与地面的摩擦系数分别为fA= 0.2,fB= 0.6,折梯一边AC的中点D上有一重为P= 500N的重物,折梯重量不计,问折梯能否平衡?如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1.在如图所示中,已知ω、。在图上标示出A、B两的速度、加速度。
6-2.在如图所示的平面机构中,半径为r的半圆盘在A和B处与杆铰接,已知 , ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3.在如图所示的平面机构中,齿轮1紧固在杆AC上, ,齿轮1与半径为r2的齿轮2啮合,齿轮2可绕O2轴转动,。设 , ,试确定 时,轮2的角速度和角加速度。
解:动点取曲柄OA上A点,
理论力学课件 第九章动量定理,质点和质点系动量定理

5、解方程。
ω
O2
e
O1 θ
例9-3 如图所示,电动机外壳固
定在水平基础上,定子、转子的
质量分别为m1、m2。设定子质心 位 于 转 轴中 心 O1 , 由 于 制 造 误 差,转子质心O2 到O1的距离为
e,已知转子以匀角速度ω 转
动。求: 基础对电机总的水平和
铅垂反力
偏心转子
解:1、研究对象
如何建立受力和运动的关系?
建立运动特征量的变化与 力系作用量的关系
第9章 动量定理
第9章 动量定理
现代跳高为什么采用背越式?
9.1 质点和质点系动量定理
一、基本概念
1 质心
∑ rvC =
m i rvi m
∑ xC =
mi xi m
∑ yC =
mi yi m
∑ zC =
mi zi m
9.1 质点和质点系动量定理
x
m1g
Fx
M O Fy
Fx = −m2ω2e cosωt Fy = −m2ω 2e sin ωt + (m1 + m2 )g
由主动力直接引起的静约束力
Fx静 = 0
Fy静 = (m1 + m2 )g
由质点系运动引起的动约束力
vy
ω
O2
e
O1 θ m2 g
x
m1g
Fx
M O Fy
Fx动 = −m2ω 2e cosωt
9.1 质点和质点系动量定理
思考题:两个相同的均质杆 AB 和 AD 用铰链连接,每个杆的质量为m ,长
为L,在屏幕面内运动。已知铰链A的速度为u,两个杆的角速度为ω(转向
如图),求该瞬时系统的动量。
理论力学 质点动力学

第8章质点动力学
[例8-1]桥式起重机跑车吊挂一质量为m的重物,沿水平横梁作
ν
匀速运动,速度为,重物中心至悬挂点距离为l。
突然刹车,
重物因惯性绕悬挂点O向前摆动,求钢丝绳的最大拉力。
解:1)以重物为研究对象2)受力分析mg
F T
a n a t 3)运动分析4)牛顿第二定律
ϕ
sin mg ma t −=ϕ
cos mg F ma T n −=∑=t
t F ma ∑=n
n F ma 5)补充方程
ϕsin mg dt
dv
m −=ϕcos 2
mg F l
v
m T −=
mg
F T
a n a t ϕsin mg dt
dv
m −=ϕcos 2
mg F l
v
m T −=0<dt
dv 重物减速
=ϕ0
max v v =max
T T , 0F F ==时ϕ)
1(20
max
T gl
v
mg F +=
a n
F N
a t
a n
ma
mg
F N
a t a n
mg
O
解释非惯性系一些物理现象
飞机急速爬高时
飞行员的黑晕现象
爬升时:a > 5g
惯性参考系——地球
非惯性参考系——飞机
动点——血流质点
牵连惯性力向下,从心脏流向头部的血流受阻,造成大脑缺血,形成黑晕现象。
飞行员的黑晕与红视现象
在北半球的弹道偏右;在南半球的弹道偏左
a
C
F
IC。
9 质点动力学的基本方程自测题

Page 1 of 2 Created by JiangFang, School of Technology, BJFU(a )(b )(c )xO第九章 质点动力学的基本方程 自测题1. 判断正误(1)只要知道作用在质点上的力,那么质点在任一瞬时的运动状态就可以确定。
( ) (2) 一个质点只要有运动,就一定有力的作用,而且运动方向就是它受力的方向。
( ) (3)在同一地点、同一坐标系内,以相同大小的初速度0v 斜抛两质量相同的小球,若不计空气阻力,则两者的运动微分方程一定相同。
( ) (4)质点受到的力越大,其运动的速度就越大。
( ) (5)在惯性参考系中,不论初始条件如何变化,只要质点不受力的作用,则该质点应保持静止或匀速直线运动状态。
( )2. 选择题(1)求解质点动力学问题时,质点的初始条件是用来 。
A .分析力的变化规律 B. 建立质点运动微分方程 C. 确定积分常数 D. 分离积分变量(2)三个质量相同的质点,在相同的力F 作用下。
若初始位置都在坐标原点O (如图所示),但初速度不同,则三个质点的运动微分方程 , 三个质点的运动轨迹 。
A .相同 B. 不同 C. 无法确定(3) 距地面高为H 的质点M ,具有水平初速度0v ,则该质点落地时的水平距离l 与成正比。
A .HB.C. 2H D. 3HPage 2 of 2 Created by JiangFang, School of Technology, BJFUxO(4)一铅垂上抛的小球,可视为质点,已知质量为m ,空气阻力v R k −=(k 为常数),则对图示坐标轴Ox ,小球的运动微分方程为 。
A. x k mg x m−= B. x k mg x m −−= C. x k mg x m+−= D. x k mg x m +=(5)如图,已知A 物重20N ,B 物重30N ,不计滑轮C 、D 的质量,并忽略各处的摩擦,则绳水平段的拉力为 。
理论力学质点动力学的运动方程

消去t, 得轨迹方程 由初始条件:t=0时,q0=0,
代入上式得
如果已知这种变化即可确定球与棒的相互作用力。
分析: 由(1)、(2)式可得:
3m 的绳上,绳的另一端系在固定点O,并与铅直线成
角。
作用下从甲板上起飞
y
eA mk 2
cos
k v0
x
1
这是第二类基本问题。
例10-3 一圆锥摆,如图所示。质量m=0.1kg的 小球系于长l=0.3m 的绳上,绳的另一端系在固定点O,
1661年牛顿进入了剑桥大学的三一学院,1665年 获文学学士学位。在大学期间他全面掌握了当时的数 学和光学。1665-1666的两年期间,剑桥流行黑热病, 学校暂时停办,他回到老家。这段时间中他发现了二 项式定律,开始了光学中的颜色实验,即白光由7种 色光构成的实验。而且由于一次躺在树下看到苹果落 地开始思索地心引力问题。在30岁时,牛顿被选为皇 家学会的会员,这是当时英国最高科学荣誉。
初始条件为
a a t 0 :x 0 y 0 0 ,v 0 x v 0 c o s,v 0 y v 0 s i n
确定出积分常数为:
a a C 1 v 0 c o s,C 2 v 0 s i n ,C 3 C 4 0
于是物体的运动方程为:
xv0tcoas
y
v0t
1 2
gt2
轨迹方程为:
有 mr 2 F l 2 r2 l
得 F mr 2 2 l 2 r 2
这属于动力学第一类问题。
例10-2 质量为m的质点带有电荷e,以速度v0进入强 度按E=Acoskt变化的均匀电场中,初速度方向与电场强
度垂直,如图所示。质点在电场中受力 F eE 作用。
习题第9章5答案

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
第9章 质点系动量定理

2
质点系动量定理
质点系整体运动状 态的物理量(动量 、动量矩、动能)
质点系动力 学普遍定理
作用于质点系的力 系特征量(主矢、 主矩、功)
质点系动力学普遍定理包括动量定理、动量矩定 理、动能定理及其推论。
3
质点系动量定理
二、质点系的质心
磅秤指示数会不会发生变化
9
质点系动量定理
隔板
抽去隔板后将会
水池
? 发生什么现象
水
光滑台面
10
质点系动量定理
偏心转子电机
? 为什么会左右运动 ? 这种运动有何规律 ? 会不会上下跳动 ? 有何工程应用
11
质点系动量定理
§9-1 动量定理
一、动量
1.质点的动量 ——质点的质量与速度的乘积 mv。
z 瞬时矢量;
倾角均为45°。则此时机构的动量 p大小为( )。
31
质点系动量定理
§9-2 质心运动定理
∑ 质点系的动量定理: d p = F e dt
将 p = m v C 代入,并当质点系质量不变时,有
∑ m aC = F e
或
——质心运动定理
∑ m &r&C = F e
即:质点系的质量与其质心加速度的乘积,等于作用于
质点系动量定理
理论力学
基 础 部 分 — 动力学
第9 章 质点系动量定理
2012年11月13日
1
质点系动量定理
质点系动力学普遍定理概述
一、质点系动力学普遍定理的特征
理论上: n个质点构成的质点系动力学问题,可通过 建立3n个微分方程联立求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 第九章 质点动力学 习题解 [习题9-1] 质量为kgm2的质点沿空间曲线运动,其运动方程为:324ttx,ty5,24tz。求st1时作用于该质点的力。
解: (1)求加速度 23238)4(ttttdtddtdxvx
tttdtddtdvaxx68)38(2 )/(2168|221smatx
5)5(tdtddtdyvy
0)5(dtddtdvayy
0|1tya 344)2(ttdtddtdzvz
2312)4(ttdtddtdvazz
)/(12112|221smatz
(2)求作用在质点上的力 )(422|1NmaFtxx
)(002|1NmaFtyy
)(24122|1NmaFtzz
力的大小: )(331.242404222222NFFFFzyx 力的方向角: 2
054.80331.244arccosarccos
F
Fx
090331.240arccosarccos
F
Fy
046.9331.2424arccosarccos
F
Fz
力的作用点: )(3114|321mxt
)(515|1myt
)(121|41mzt
即在F作用点在M(3,-5,-1)。
[习题9-2] 某质量为kg5的质点在jtitF)2sin(100)2cos(90(F以N计)作用下运动,已知当0t时,cmx40,cmy50,00•x,scmy/100•。试求该质点的运动方程。 解:
由jtitF)2sin(100)2cos(90可知: )2cos(90tFx )2sin(100tFy )2cos(90tmaFxx
)2cos(9022tdtxdm )2cos(90522tdtxd )2cos(1822tdtxd )2()2cos(9tdtdt
dx 3
1)2sin(9Ctdtdx 1)2sin(9Ctx•
0)02sin(9|1100••CCxxt
)2sin(9tdtdx
)2()2sin(29tdtx
2)2cos(29Ctx )(04.0)()(5.429)02cos(29|22200mmCmCCxxt
)(46.45.404.02mC
)(46.4)2cos(29mtx )2sin(100tFy
)2sin(10022tdtydm )2sin(100522tdtyd )2sin(2022tdtyd )2()2sin(10tdt
dt
dy
3)2cos(10Ctdtdy 3)2cos(10Cty•
smsmCCyyt/1.0/)10()02cos(10|3300•• 1.0103C )/(9.93smC 9.9)2cos(10•ty 4
0v
030
m1地面
mg
Ox
y
9.9)2cos(10tdt
dy
dttdty9.9)2()2cos(5
49.9)2sin(5Ctty )(05.009.9)02sin(5|4400mCCyyt
)(05.09.9)2sin(5mtty
[习题9-3] 水管喷头从m1高处以sm/13的速度向外喷水,水管与水平线夹角为030。求水能达到的最大高度H及水平距离d。 解:水珠的受力如图所示。
)/(231330cos00smvvx
2313dtdx
12
313Ctx
002313|110CCxt
tx2313 tgtvvy8.95.630sin00 tdtdy8.95.6
229.45.6Ctty
)(109.405.6|2220mCCyt
19.45.62tty 水珠达到最高点时,竖向速度为0。 08.95.6tdtdyvy 5
)(663.08.9/5.6st 水珠所能达到的最大高度为: )(16.31633.09.4663.05.62maxmyH 水珠着地时所经过的时间为: 019.45.62tty
019.45.62tt 015.69.42tt 不合,舍去。),(139.0)(47.19.42)1(9.44)5.6(5.62sst
水珠所能达到的最大水平距离为: )(55.1647.12313maxmxd
x-t与y-t曲线
-2024681012141618
00.20.40.60.811.21.41.6tx/y
xy 6
ABm1030
C
Bv
Bm1030
C
Bv
ABT
gmB
ntAABT
gmA
ANAF
[习题9-4] 通过光滑圆环C的绳索将物体A与B相连,已知kgmA5.7,kgmB0.6,物体A与水平面的摩擦因素6.0f,在图示瞬时,物体B具有朝右上方的速度smvB/2。若在此时突然剪断墙与物体间的绳子,求该瞬时物体A的加速度Aa 解: (1)求AB间绳子的拉力 以B为研究对象,其受力如图所示。
nBinamF
CBvmgmTBBBAB2030cos
)(92.74)12866.08.9(6)30cos(202NCBvgmTBBAB 以A为研究对象,其受力如图所示。
)/(11.45.78.95.76.092.742smmfNTaAAABA (→)
[习题9-5] 倾角为030的楔形斜面以2/.4sma的加速度向右运动,质量为kgm5的小小球A用软绳维系置于斜面上,试求绳子的拉力及斜面的压力,并求当斜面的加速度达到多大时绳子的拉力为零? 解: (1)求绳子的拉力T及斜面的压力N 以小球为研究对象,其受力如图所示。 7
A030
aA
030
a
NTG
xy
maTN0030cos30sin 452321TN 403TN…………(1)
030cos30sin00GNT
8.952321NT 983NT…………(2)
(1)代入(2)得: 98)340(3TT 98)3340TT
)(18.7434098NT )(44.5218.7732.140340NTN (2)求当斜面的加速度达到多大时绳子的拉力为零 maTN0030cos30sin
aTN52321 aTN103…………(1) 8
rzA
A
mg
n
tbz
'tF
'nF
NF
030cos30sin00GNT 8.952321NT 983NT…………(2)
(1)代入(2)得: 98310(3TaT 983310TaT
431098aT
令T=0得: 031098a
)/(658.5310982sma 故,当)/(658.52sma时,绳子的拉力为零。 [习题9-6] 水平转台以匀角加速度从静止开始绕z轴转动,转台上与转轴距离为r处放置一质量为m的物块A,物块与转台间的摩擦因素为f,求经过多少时间后,物块开始在转台上滑动。
解: 以物块A为研究对象(抽象为一质点),其受力如图所示。 0mgFFNb
