2006年普通高等学校招生全国统一考试文试题答案(重庆卷)

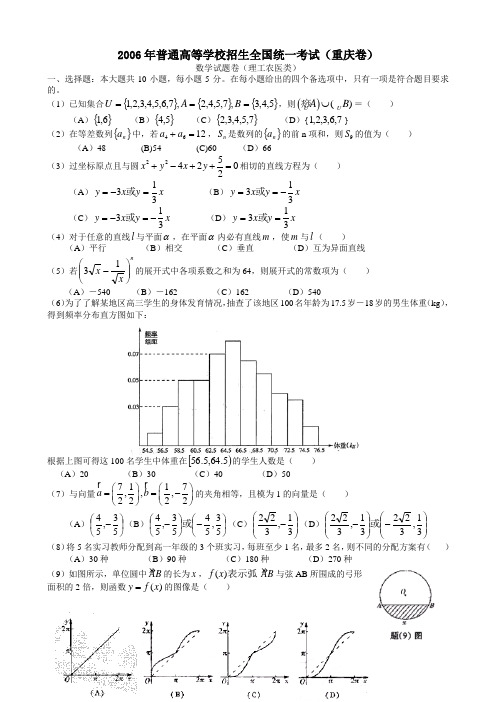
2006年普通高等学校招生全国统一考试（重庆卷）数学试题（文史类）答案一、选择题：每小题5分，满分60分． 1．Ｄ 2．Ｄ 3．Ｃ 4．Ｄ 5．Ｂ 6．Ｃ 7．Ｃ 8．Ｄ 9．Ｂ 10．Ｂ 11．Ａ 12．Ａ二、填空题：每小题4分，满分16分． 13．2-14．21-n15．(2)+，∞16．12a >三、解答题：满分74分． 17．（本小题13分） 解：（Ⅰ）由互斥事件有一个发生的概率公式和独立事件同时发生的概率公式，所求概率为33311116326p ⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．（Ⅱ）这是136n p ==，的独立重复试验，故所求概率为2233155(2)C 6672P ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭． 18．（本小题13分）解：（Ⅰ）1()cos 2sin 2222f x x x a ωω=+++πsin 232x a ω⎛⎫=+++ ⎪⎝⎭． 依题意得πππ2632ω+=·． 解得12ω=．（Ⅱ）由（Ⅰ）知，π()sin 32f x x a ⎛⎫=+++ ⎪⎝⎭． 又当π5π36x ⎡⎤∈-⎢⎥⎣⎦，时，π7π036x ⎡⎤+∈⎢⎥⎣⎦，，故1πsin 123x ⎛⎫-+ ⎪⎝⎭≤≤，从而()f x 在π5π36⎡⎤-⎢⎥⎣⎦，上取得最小值12a -+．因此，由题设知122a -++= 故12a =．19．（本小题12分）解：（Ⅰ）求导得2()3f x x '=-63ax b +．由于()f x 的图象与直线1210x y +-=相切于点(111)-，，所以(1)11f =-，(1)12f '=-，即1331136312.a b a b -+=-⎧⎨-+=-⎩，解得13a b ==-，． （Ⅱ）由13a b ==-，得22()3633(23)3(1)(3)f x x ax b x x x x '=-+=--=+-． 令()0f x '>，解得1x <-或3x >；又令()0f x '<，解得13x -<<．所以当(1)x ∈--，∞时，()f x 是增函数；当(3)x ∈+，∞时，()f x 也是增函数，但(13)x ∈-，时，()f x 是减函数．20．（本小题12分）解法一：（Ⅰ）由1AD D G ∥知11C GD ∠为异面直线AD 与1C G 所成的角．连接1C F ．因为AE 和1C F 分别是平行平面11ABB A 和11CC D D 与平面1AEC G 的交线，所以1AE C F ∥，由此可得1D F BE == 再由1FDG FDA △∽△得1DG = 在11Rt C DG △中，由1111C D DG =，得11π6C GD ∠=． （Ⅱ）作11D H C G ⊥于H ，连接FH ．由三垂线定理知1FH C G ⊥，故1DH F ∠为二面角11F C G D --即二面角11A C G A --的平面角． 在1Rt GHD △中，由1DG =1π6D GH ∠=得1D H = EＢＡ ＣＤＦ1B1A 1D1CHG答（20）图1从而111tan 2D FD HF D H===． 解法二：（Ⅰ）由1AD D G ∥知11C GD ∠为异面直线AD 与1C G 所成的角． 因为1EC 和AF 是平行平面11BB C C 与11AA D D 与 平面1AEC C 的交线， 所以1EC AF ∥．由此可得111π4AGA EC B ∠=∠=，从而111AG AA =，于是1DG = 在11Rt C DG △中，由111C D =，1DG =11π6C GD ∠=． （Ⅱ）在11AC G △中，由11π4C A G ∠=，11π6A GC ∠=知11AC G ∠为钝角．作11A H GC ⊥交1GC 的延长线于H ，连接AH ．由三垂线定理知GH AH ⊥，故1AHA ∠为二面角11A C G A --的平面角．在1Rt A HG △中，由11AG =，1π6A GH ∠=得112A H =．从而111tan 2AA AHA A H===． 解法三：（Ⅰ）以1A 为原点，11111A B A D A A ，，所在直线分别为x 轴，y 轴和z 轴建立如图所示的空间直角坐标系．于是，1(01)(110)1)A C D ，，，，，(101)(010)E AD = ，，，，，，1(011)EC =- ，，．因为1EC 和AF 分别是平行平面11BB C C 和11AA D D 与平面1AEC G 的交线，所以1EC AF ∥，答（20）图3ＢＡ ＣＤＦ1B 1A1D1C GH 答（20）图2 E设(00)G y ，，，则(01)AG y =-，，．由1EC AG ∥得1y =1y =．故(010)G ，，1(C G =-． 设异面直线AD 与1C G 所成的角的大小为θ，则11cos AD C G AD C Gθ==·· 从而π6θ=． （Ⅱ）作11A H C G ⊥于H ，由三垂线定理知A H G H ⊥，故1AHA ∠为二面角11A C G A --的平面角．设(0)H a b ，，，则1(0)A H a b = ，，，1(110)C H a b =--，，． 由11A H C G ⊥得110A H C G =·，由此得0a =． ① 又由1H C G ，，共线得11C H C G ∥，从而11a -=-1)0b +-=． ②联立①和②得3144a b ==，．故H ⎝⎭．由1A H ==11A A =得111tan 2A A AHA A H=== ． 21．（本小题12分）解：（Ⅰ）因为()f x 是奇函数，所以(0)0f =，即102ba-+=+，解得1b =． 从而有121()2x x f x a+-+=+．又由(1)(1)f f =--知1121241a a-+-+=-++，解得2a =．（Ⅱ）解法一：由（Ⅰ）知12111()22221x x x f x +-+==-+++．由上式易知()f x 在()-+，∞∞上为减函数，又因()f x 是奇函数，从而不等式22(2)(2)0f t t f t k -+-<等价于222(2)(2)(2)f t t f t k f t k -<--=-+．因()f x 是减函数，由上式推得2222t t t k ->-+． 即对一切t ∈R 有2320t t k -->．从而判别式4120k ∆=+<，解得13k <-． 解法二：由（Ⅰ）知121()22x x f x +-+=+．又由题设条件得2222222121212102222t tt kt t t k ---+-+-+-++<++．即2222212212(22)(21)(22)(21)0tk tttt tk-+--+-+-+++-+<，故2320t t k -->．上式对一切t ∈R 均成立，从而判别式4120k ∆=+<，解得13k <-． 22．（本小题12分）证明：（Ⅰ）对任意固定的1n ≥，因为焦点(01)F ，，所以可设直线n n A B 的方程为1n y k x -=，将它与抛物线方程24x y =联立得2440n x k x --=，由一元二次方程根与系数的关系得4n n x s =-．（Ⅱ）对任意固定的1n ≥，利用导数知识易得抛物线24x y =在n A 处的切线的斜率2n n A x =．故24x y =在n A 处的切线方程为()2n n n x y y x x -=-． ① 类似地，可求得24x y =在n B 处的切线方程为()2n n n s y t x s -=- ②由②减去①得2222n n n n n n x s x s y t x ---=-+，从而22224422n n n n n nx s x s x s x ---=-+， 2224n n n nx s x s x --=-，2n n x s x +=． ③将③代入①并注意4n n x s =-得交点n C 的坐标为12n n x s +⎛⎫- ⎪⎝⎭，．由两点间的距离公式得22222224242224442n n n n n n nn n x s x s x x FC x x ⎛⎫+⎛⎫=+=++=++=+ ⎪ ⎪⎝⎭⎝⎭． 从而22n n nx FC x =+． 现在2n n x =．利用上述已证结论并由等比数列求和公式得，12n FC FC FC +++…12121111()22n n x x x x x x ⎛⎫=+++++++ ⎪ ⎪⎝⎭ (22111)1(222)22222n n ⎛⎫=+++++++ ⎪⎝⎭…… 11(21)(22)221n n n n -+-+=-+-=-+．。