2019-2020年高考数学大题专题练习——立体几何(一)

合集下载

专题3.1 以立体几何中探索性问题为背景的解答题——新高考数学专项练习题附解析

专题三压轴解答题第一关以立体几何中探索性问题为背景的解答题【名师综述】利用空间向量解决探索性问题立体几何中的探索性问题立意新颖，形式多样，近年来在高考中频频出现，而空间向量在解决立体几何的探索性问题中扮演着举足轻重的角色，它是研究立体几何中的探索性问题的一个有力工具，应用空间向量这一工具，为分析和解决立体几何中的探索性问题提供了新的视角、新的方法．下面借“题”发挥，透视有关立体几何中的探索性问题的常见类型及其求解策略，希望读者面对立体几何中的探索性问题时能做到有的放矢，化解自如．1.以“平行”为背景的存在判断型问题典例1 （2019·山东省实验中学高考模拟）如图所示的矩形ABCD中，AB=12AD=2，点E为AD边上异于A，D两点的动点，且EF//AB，G为线段ED的中点，现沿EF将四边形CDEF折起，使得AE与CF的夹角为60°，连接BD，FD．(1)探究：在线段EF上是否存在一点M，使得GM//平面BDF，若存在，说明点M的位置，若不存在，请说明理由；(2)求三棱锥G—BDF的体积的最大值，并计算此时DE的长度．【名师指点】本题是直线和平面平行的存在性问题，这种问题可以利用空间直角坐标系，通过建系设点，利用空间向量求解，如果利用传统立体几何的方法，就需利用分析法，利用直线和平面平行的性质定理寻求点的位置．【举一反三】如图所示,在四棱锥中,四边形是正方形,点分别是线段的中点.（1）求证：;（2）线段上是否存在一点,使得面面,若存在，请找出点并证明;若不存在,请说明理由.类型2 以“垂直”为背景的存在判断型问题典例2 如图，在四棱锥中，四边形为平行四边形，，为中点,（1）求证：平面；（2）若是正三角形，且.(Ⅰ)当点在线段上什么位置时，有平面？(Ⅱ)在(Ⅰ)的条件下，点在线段上什么位置时，有平面平面？【名师指点】以直线和平面垂直、直线和直线垂直为背景的垂直问题，可以通过建立空间直角坐标系，通过直线的方向向量与平面的法向量共线或者直线方向向量垂直求得，也可以利用传统立体几何知识利用分析的方法，确定线、面垂直关系来求解．【举一反三】【北京市通州区2018-2019学年第一学期高三年级期末考试】如图，在三棱柱中，底面，△ABC是边长为的正三角形，，D，E分别为AB，BC的中点．（Ⅰ）求证：平面；（Ⅱ）求二面角的余弦值；（Ⅲ）在线段上是否存在一点M ，使平面？说明理由.类型3 以“角”为背景的探索性问题典例3 （2019·山东高三月考）如图，在四棱锥S ABCD -中，四边形ABCD 是矩形，SAD ∆是等边三角形，平面SAD ⊥平面ABCD ，1AB =，E 为棱SA 上一点，P 为AD 的中点，四棱锥S ABCD -的体积为233.（1）若E 为棱SA 的中点，F 是SB 的中点，求证：平面∥PEF 平面SCD ；（2）是否存在点E ，使得平面PEB 与平面SAD 所成的锐二面角的余弦值为30？若存在，确定点E 的位置；若不存在，请说明理由.【名师指点】与“两异面直线所成的角、直线与平面所成的角和二面角”有关的存在性问题，常利用空间向量法解决，可以避开抽象、复杂地寻找角的过程，只要能够准确理解和熟练应用夹角公式，就可以把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等．事实说明，空间向量法是证明立体几何中存在性问题的强有力的方法．【举一反三】（2019·山东枣庄八中高三月考（理））如图，直三棱柱111-ABC A B C 中，120ACB ∠=且12AC BC AA ===，E 是棱1CC 上动点，F 是AB 中点.（Ⅰ）当E 是中点C 1C 时，求证：CF 平面 AE 1B ；（Ⅱ）在棱1CC 上是否存在点E ，使得平面AE 1B 与平面ABC 所的成锐二面角为6π，若存在，求CE 的长，若不存在，请说明理由.【精选名校模拟】1. （·山东高考模拟（理））如图，在四棱锥P ABCD -中，,AD PCD PD CD ⊥⊥平面，底面ABCD 是梯形，//,1,2,AB DC AB AD PD CD AB Q ====为棱PC 上一点. (Ⅰ)若点Q 是PC 的中点，证明：//PQ PAD 平面； (Ⅱ)PQ PC λ=试确定λ的值使得二面角Q BD P --为60°. 2. （2019·夏津第一中学高三月考）如图所示，等腰梯形ABCD 中，AB CD ∥，2AD AB BC ===，4CD =，E 为CD 中点，AE 与BD 交于点O ，将ADE 沿AE 折起，使点D 到达点P 的位置（P ∉平面ABCE ）．（1）证明：平面POB ⊥平面ABCE ；（2）若6PB =，试判断线段PB 上是否存在一点Q （不含端点），使得直线PC 与平面AEQ 所成角的正弦值为15，若存在，求出PQ OB 的值；若不存在，说明理由．3. （2018·山东济南外国语学校高三月考（理））如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，60,90DAB ADP ∠=︒∠=︒，平面ADP ⊥平面ABCD ，点F 为棱PD 的中点．（Ⅰ）在棱AB 上是否存在一点E ，使得AF 平面PCE ，并说明理由；（Ⅱ）当二面角D FC B --的余弦值为24时，求直线PB 与平面ABCD 所成的角．【答案】（1）见解析（2）60︒4. （2019·北京北师大实验中学高三月考）如图所示，在四棱锥P ABCD -中，底面四边形ABCD 为正方形，已知PA ⊥平面ABCD ，2AB =，2PA =.（1）证明：BD PC ⊥；（2）求PC 与平面PBD 所成角的正弦值；（3）在棱PC 上是否存在一点E ，使得平面BDE ⊥平面BDP ？若存在，求PEPC的值并证明，若不存在，说明理由.5.【黑龙江省哈尔滨市第六中学2019届高三上学期期末考试】如图，在棱长为2的正方体中，点分别是棱上的动点，且.（1）求证：；（2）当三棱锥的体积取得最大值时，求二面角的正切值． 6. 【湖北省2019届高三联考测试】如图，在四棱锥中，，，，且PC=BC=2AD=2CD=2，.（1）平面；（2）在线段上，是否存在一点，使得二面角的大小为？如果存在，求的值；如果不存在，请说明理由.7. 【福建省龙岩市2019届高三第一学期期末教学质量检查】如图，四边形是边长为2的正方形，平面平面，且.（1）证明：平面平面；（2）当，且与平面所成角的正切值为时，求二面角的正弦值.8. 【福建省厦门市2019届高三年级第一学期期末质检】如图，在四棱锥中，平面，四边形为平行四边形，且，.（1）证明：平面；（2）当直线与平面所成角的正切值为时，求二面角的余弦值.9. 【北京市朝阳区2018-2019高三数学期末考试】如图，三棱柱的侧面是平行四边形，，平面平面，且分别是的中点.（1）求证：平面；（2）当侧面是正方形，且时，（ⅰ）求二面角的大小；（ⅱ）在线段上是否存在点，使得？若存在，指出点的位置；若不存在，请说明理由.10. 如图，在多面体ABCDMN 中，四边形ABCD 为直角梯形， //AB CD ， 22AB =， BC DC ⊥，2BC DC AM DM ====，四边形BDMN 为矩形.（1）求证：平面ADM ⊥平面ABCD ；（2）线段MN 上是否存在点H ，使得二面角H AD M --的大小为4π？若存在，确定点H 的位置并加以证明.11. 在三棱锥P ABC -中， AB AC =， D 为BC 的中点， PO ⊥平面ABC ，垂足O 落在线段AD 上，已知4,3,2,1BC PO AO OD ====. （1）证明： AP BC ⊥；（2）在线段AP 上是否存在一点M ，使得二面角A MC B --为直二面角？若存在，求出AM 的长；若不存在，请说明理由.12 【安徽省江南十校2019届高三第二次大联考】如图，已知四边形中，对角线，，为等边三角形.（1）求面积的最大值；（2）当的面积最大时，将四边形沿折起成直二面角，在上是否存在点使直线与平面所成的角满足：，若不存在，说明理由；若存在，指出点的位置.13. 【云南省昆明市2019届高三1月复习诊断测试】如图，在四棱锥中，底面是平行四边形，平面，，，是棱上的一点.（1）若平面，证明：；（2）在（1）的条件下，棱上是否存在点，使直线与平面所成角的大小为？若存在，求的值；若不存在，请说明理由.14. 【河南省开封市2019届高三上学期第一次模拟考试】如图所示，是边长为2的正方形，平面，且.（Ⅰ）求证：平面平面；（Ⅱ）线段上是否存在一点，使二面角所成角的余弦值为？若存在，请找出点的位置；若不存在，请说明理由.15.如图，五面体11A BCC B -中，14AB =，底面ABC 是正三角形，2AB =，四边形11BCC B 是矩形，二面角1A BC C --为直二面角．（1）D 在AC 上运动，当D 在何处时，有1//AB 平面1BDC ，并说明理由；（2）当1//AB 平面1BDC 时，求二面角1C BC D --余弦值．专题三压轴解答题第一关以立体几何中探索性问题为背景的解答题【名师综述】利用空间向量解决探索性问题立体几何中的探索性问题立意新颖，形式多样，近年来在高考中频频出现，而空间向量在解决立体几何的探索性问题中扮演着举足轻重的角色，它是研究立体几何中的探索性问题的一个有力工具，应用空间向量这一工具，为分析和解决立体几何中的探索性问题提供了新的视角、新的方法．下面借“题”发挥，透视有关立体几何中的探索性问题的常见类型及其求解策略，希望读者面对立体几何中的探索性问题时能做到有的放矢，化解自如．2.以“平行”为背景的存在判断型问题典例1 （2019·山东省实验中学高考模拟）如图所示的矩形ABCD中，AB=12AD=2，点E为AD边上异于A，D两点的动点，且EF//AB，G为线段ED的中点，现沿EF将四边形CDEF折起，使得AE与CF的夹角为60°，连接BD，FD．(1)探究：在线段EF上是否存在一点M，使得GM//平面BDF，若存在，说明点M的位置，若不存在，请说明理由；(2)求三棱锥G—BDF的体积的最大值，并计算此时DE的长度．【答案】（1）见解析；（2）33,2【解析】（1）取线段EF的中点M，有GM∥平面BDF．证明如下：如图所示，取线段EF的中点M，∵G为线段ED的中点，M为线段EF的中点，∴GM为△EDF的中位线，故GM∥DF，又GM⊄平面BDF，DF⊂平面BDF，故GM∥平面BDF；（2）∵CF ∥DE ，且AE 与CF 的夹角为60°，故AE 与DE 的夹角为60°，即60AED ∠=︒，过D 作DP ⊥AE 交AE 于P ，由已知得DE ⊥EF ，AE ⊥EF ，∴EF ⊥平面AED ， EF ⊥DP,又AE EF=E,∴DP ⊥平面AEFB ，即DP 为点D 到平面ABFE 的距离，且3DP x =，设DE ＝x ，则AE ＝BF ＝4﹣x ，由（1）知GM ∥DF ，G BDF M BDF D MBF V V V ---===11131(4)3322MBF S DP x x ⎡⎤⋅⋅=⨯⨯⨯-⨯⎢⎥⎣⎦()24333(4)x x x x -+=-⋅=，当且仅当4﹣x ＝x 时等号成立，此时x ＝DE ＝2．故三棱锥G ﹣BDF 的体积的最大值为33，此时DE 的长度为2．【名师指点】本题是直线和平面平行的存在性问题，这种问题可以利用空间直角坐标系，通过建系设点，利用空间向量求解，如果利用传统立体几何的方法，就需利用分析法，利用直线和平面平行的性质定理寻求点的位置．【举一反三】如图所示,在四棱锥中,四边形是正方形,点分别是线段的中点.（1）求证：;（2）线段上是否存在一点,使得面面,若存在，请找出点并证明;若不存在,请说明理由. 【解析】（1）证明：由四边形为正方形可知，连接必与相交于中点故∵面∴面（2）线段上存在一点满足题意，且点是中点理由如下：由点分别为中点可得：∵面∴面由（1）可知，面且故面面类型2 以“垂直”为背景的存在判断型问题典例2 如图，在四棱锥中，四边形为平行四边形，，为中点,（1）求证：平面；（2）若是正三角形，且.(Ⅰ)当点在线段上什么位置时，有平面？(Ⅱ)在(Ⅰ)的条件下，点在线段上什么位置时，有平面平面？【解析】（1）证明：连接,,=，因为ABCD是平行四边形，则为中点，连接，又为中点，面，面平面.（2）解(Ⅰ)当点在线段中点时，有平面取中点，连接，又，又，，平面，又是正三角形，平面(Ⅱ)当时，有平面平面过作于，由(Ⅰ)知，平面，所以平面平面易得【名师指点】以直线和平面垂直、直线和直线垂直为背景的垂直问题，可以通过建立空间直角坐标系，通过直线的方向向量与平面的法向量共线或者直线方向向量垂直求得，也可以利用传统立体几何知识利用分析的方法，确定线、面垂直关系来求解．【举一反三】【北京市通州区2018-2019学年第一学期高三年级期末考试】如图，在三棱柱中，底面，△ABC是边长为的正三角形，，D，E分别为AB，BC的中点．（Ⅰ）求证：平面；（Ⅱ）求二面角的余弦值；（Ⅲ）在线段上是否存在一点M，使平面？说明理由.【解析】（Ⅰ）证明：在三棱柱中，因为底面，CD⊂平面ABC，所以．又为等边三角形，为的中点，所以．因为，所以平面；（Ⅱ）取中点，连结，则因为，分别为，的中点，所以．由（Ⅰ）知，，如图建立空间直角坐标系．由题意得，，，,,,,，，．设平面法向量，则即令，则，．即．平面BAE法向量．因为，，，所以由题意知二面角为锐角，所以它的余弦值为.（Ⅲ）解：在线段上不存在点M，使平面．理由如下．假设线段上存在点M，使平面．则，使得．因为，所以．又，所以．由（Ⅱ）可知，平面法向量，平面，当且仅当，即，使得．所以解得．这与矛盾．所以在线段上不存在点M ，使平面．类型3 以“角”为背景的探索性问题典例3 （2019·山东高三月考）如图，在四棱锥S ABCD -中，四边形ABCD 是矩形，SAD ∆是等边三角形，平面SAD ⊥平面ABCD ，1AB =，E 为棱SA 上一点，P 为AD 的中点，四棱锥S ABCD -的体积为23.（1）若E 为棱SA 的中点，F 是SB 的中点，求证：平面∥PEF 平面SCD ；（2）是否存在点E ，使得平面PEB 与平面SAD 30E 的位置；若不存在，请说明理由.【答案】（1）证明见解析；（2）存在，点E 位于AS 的靠近A 点的三等分点. 【解析】（1）证明：因为E 、F 分别是SA 、SB 的中点，所以EF AB ∥，在矩形ABCD 中，AB CD ∥，所以EF CD ∥，又因为E 、P 分别是SA 、AD 的中点，所以∥EP SD ，又因为EF CD ∥，EF EP E ⋂=，,EF EP ⊂平面PEF ，,SD CD ⊂平面SCD ，所以平面∥PEF 平面SCD .（2）解：假设棱SA 上存在点E 满足题意. 在等边三角形SAD 中，P 为AD 的中点，于是SP AD ⊥，又平面SAD ⊥平面ABCD ，平面SAD ⋂平面ABCD AD =，SP ⊂平面SAD ，所以SP ⊥平面ABCD ，所以SP 是四棱锥S ABCD -的高，设AD m =，则SP =，ABCD S m =矩形，所以1133S ABCD ABDD V S SP m -=⋅==矩形所以2m =，以P 为坐标原点，PA 所在直线为x 轴，过点P 与AB 平行的直线为y 轴，PS 所在直线为z 轴，建立如图所示的空间直角坐标系.则()0,0,0P ，()1,0,0A ，()1,1,0B，(S ，设(()()01AE AS λλλλ==-=-≤≤，()()1,0,0PE PA AE λ=+=+-()1λ=-，()1,1,0PB =，设平面PEB 的一个法向量为()1,,n x y z =，有()1110n PE x z n PB x y λ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，令3x λ=，则()13,,1n λλ=-，易知平面SAD 的一个法向量()20,1,0n =，所以12122123cos ,721n n n n n n λλλ-⋅==-+30=，因为01λ≤≤，所以13λ=，所以存在点E ，位于AS 的靠近A 点的三等分点.【名师指点】与“两异面直线所成的角、直线与平面所成的角和二面角”有关的存在性问题，常利用空间向量法解决，可以避开抽象、复杂地寻找角的过程，只要能够准确理解和熟练应用夹角公式，就可以把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等．事实说明，空间向量法是证明立体几何中存在性问题的强有力的方法．【举一反三】（2019·山东枣庄八中高三月考（理））如图，直三棱柱111-ABC A B C 中，120ACB ∠=且12AC BC AA ===，E 是棱1CC 上动点，F 是AB 中点.（Ⅰ）当E 是中点C 1C 时，求证：CF 平面 AE 1B ；（Ⅱ）在棱1CC 上是否存在点E ，使得平面AE 1B 与平面ABC 所的成锐二面角为6π，若存在，求CE 的长，若不存在，请说明理由.【答案】（1）见解析；（2）1CE =.【解析】（1）取1AB 中点G ，连结EG FG 、，则FG ∥1BB 且112FG BB =. 因为当E 为1CC中点时，CE ∥1BB 且112CE BB =，所以FG ∥CE 且FG = CE .所以四边形CEGF 为平行四边形，CF ∥EG ，又因为1CF AEB ⊄平面，1EG AEB ⊂平面，所以//CF 平面1AEB ；（2）假设存在满足条件的点E ，设()01CE λλ=≤≤.以F 为原点，向量1FB FC AA 、、方向为x 轴、y 轴、z 轴正方向，建立空间直角坐标系. 则()3,0,0A -，()13,0,2B ，()0,1,E λ，平面ABC 的法向量()0,0,1m =，平面1AEB 的法向量()333,3n λ=--，，()23cos 23991m n m n m nλ⋅===++-，，解得1λ=，所以存在满足条件的点E ，此时1CE =.【精选名校模拟】1. （·山东高考模拟（理））如图，在四棱锥P ABCD -中，,AD PCD PD CD ⊥⊥平面，底面ABCD 是梯形，//,1,2,AB DC AB AD PD CD AB Q ====为棱PC 上一点. (Ⅰ)若点Q 是PC 的中点，证明：//PQ PAD 平面； (Ⅱ)PQ PC λ=试确定λ的值使得二面角Q BD P --为60°. 【答案】（1）见解析（2）36【解析】 (Ⅰ)取PD 的中点M ，连接AM ，M Q ，Q PC点是的中点，∴M Q∥CD，1.2MQ CD=又AB∥CD，1,2AB CD QM=则∥AB，QM＝AB，则四边形ABQM是平行四边形.BQ∴∥AM.又AM⊂平面PAD，BQ⊄平面PAD，BQ∴∥平面PAD.（Ⅱ）解：由题意可得DA，DC，DP两两垂直，以D为原点，DA，DC，DP所在直线为,,x y z轴建立如图所示的空间直角坐标系，则P(0，1，1)，C(0，2，0)，A(1，0，0)，B(1，1，0).令()()()000000,,,,,1,0,2,1.Q x y z PQ x y z PC=-=-则()()000,,,10,2,1,PQ PC x y zλλ=∴-=-()0,2,1.Qλλ∴-又易证BC⊥平面PBD，()1,1,0.n PBD∴=-是平面的一个法向量设平面QBD的法向量为(),,,m x y z=(),0,0,2210,.0,1x yx ym DBy z z ym DQλλλλ=-⎧+=⎧⎧⋅=⎪⎨⎨⎨+-==⋅=⎩⎩⎪-⎩则有即解得令21,1,1,.1y mλλ⎛⎫==-⎪-⎝⎭则60Q BD P 二面角为--，21cos,,22221m n m n m nλλ⋅∴===⎛⎫⋅+ ⎪-⎝⎭解得3 6.λ=±Q 在棱PC 上，01,3 6.λλ<<∴=-2. （2019·夏津第一中学高三月考）如图所示，等腰梯形ABCD 中，AB CD ∥，2AD AB BC ===，4CD =，E 为CD 中点，AE 与BD 交于点O ，将ADE 沿AE 折起，使点D 到达点P 的位置（P ∉平面ABCE ）．（1）证明：平面POB ⊥平面ABCE ；（2）若6PB =PB 上是否存在一点Q （不含端点），使得直线PC 与平面AEQ 所成角的正弦值为155，若存在，求出PQ OB 的值；若不存在，说明理由．【答案】（1）证明见解析（215【解析】（1）证明：连接BE ，在等腰梯形中ABCD ，2AD AB BC ===，4CD =，E 为中点， ∴四边形ABED 为菱形，∴BD AE ⊥，∴OB AE ⊥，OD AE ⊥，即OB AE ⊥，OP AE ⊥，且OBOP O =，OB ⊂平面POB ，OP ⊂平面POB ，∴AE ⊥平面POB ．又AE ⊂平面ABCE ，∴平面POB ⊥平面ABCE ．（2）由（1）可知四边形ABED 为菱形，∴2AD DE ==，在等腰梯形ABCD 中2AE BC ==，∴PAE △正三角形， ∴3OP =3OB =∵6PB =，∴222OP OB PB +=，∴OP OB ⊥．由（1）可知OP AE ⊥，OB AE ⊥，以O 为原点，OE ，OB ，OP 分别为x 轴，y 轴，为z 轴，建立空间直角坐标系O xyz -，由题意得，各点坐标为()0,0,3P ，()1,0,0A -，()0,3,0B，()2,3,0C ，()1,0,0E ，∴(3,3PB =-，(3,3PC =-，()2,0,0AE =，设()01PQ PB λλ=<<，()1,333AQ AP PQ AP PB λλλ=+=+=，设平面AEQ 的一个法向量为(),,n x y z =，则00n AE n AQ ⎧⋅=⎨⋅=⎩，即()203330x x y λλ=⎧⎪⎨++=⎪⎩，取0x =，1y =，得1z λλ=-，∴0,1,1n λλ⎛⎫= ⎪-⎝⎭，设直线PC 与平面AEQ 所成角为θ，π0,2θ⎡⎤∈⎢⎥⎣⎦，则15sin cos ,5PC nPC n PC nθ⋅===，即2331511011λλλλ+-=⎛⎫+ ⎪-⎝⎭化简得：24410λλ-+=，解得12λ=， ∴存在点Q 为PB 的中点时，使直线PC 与平面AEQ 所成角的正弦值为155． 3. （2018·山东济南外国语学校高三月考（理））如图，在四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，60,90DAB ADP ∠=︒∠=︒，平面ADP ⊥平面ABCD ，点F 为棱PD 的中点．（Ⅰ）在棱AB 上是否存在一点E ，使得AF 平面PCE ，并说明理由；（Ⅱ）当二面角D FC B --的余弦值为2时，求直线PB 与平面ABCD 所成的角．【答案】（1）见解析（2）60︒ 【解析】（Ⅰ）在棱AB 上存在点E ，使得//AF 平面PCE ，点E 为棱AB 的中点．理由如下：取PC 的中点Q ，连结EQ 、FQ ，由题意，//FQ DC 且12FQ CD =， //AE CD 且12AE CD =，故//AE FQ 且AE FQ =.所以，四边形AEQF 为平行四边形.所以，//AF EQ ，又EQ ⊥平面PEC ，AF ⊥平面PEC ，所以，//AF 平面PEC . （Ⅱ）由题意知ABD ∆为正三角形，所以ED AB ⊥，亦即ED CD ⊥，又90ADP ∠=︒，所以PD AD ⊥，且平面ADP ⊥平面ABCD ，平面ADP ⋂平面ABCD AD =，所以PD ⊥平面ABCD ，故以D 为坐标原点建立如图空间直角坐标系，设FD a =，则由题意知()0,0,0D ，()0,0,F a ，()0,2,0C ，)3,1,0B，()0,2,FC a =-，()3,1,0CB =-，设平面FBC 的法向量为(),,m x y z =，则由m FCm CB⎧⋅=⎨⋅=⎩得2030y azx y-=⎧⎪⎨-=⎪⎩，令1x=，则3y=，23z=，所以取231,3,m⎛⎫= ⎪⎪⎝⎭，显然可取平面DFC的法向量()1,0,0n=，由题意：22cos,41213m na==++，所以3a=.由于PD⊥平面ABCD，所以PB在平面ABCD内的射影为BD，所以PBD∠为直线PB与平面ABCD所成的角，易知在Rt PBD∆中，tan3PDPBD aBD∠===，从而60PBD∠=︒，所以直线PB与平面ABCD所成的角为60︒.4. （2019·北京北师大实验中学高三月考）如图所示，在四棱锥P ABCD-中，底面四边形ABCD为正方形，已知PA⊥平面ABCD，2AB=，2PA=.（1）证明：BD PC⊥；（2）求PC与平面PBD所成角的正弦值；（3）在棱PC上是否存在一点E，使得平面BDE⊥平面BDP？若存在，求PEPC的值并证明，若不存在，说明理由.【答案】（1）证明见解析；（210；（3）存在，23PEPC=，理由见解析【解析】（1）如图，连接AC交BD于点O，由于PA⊥平面ABCD，BD⊂平面ABCD所以PA BD⊥，即BD PA⊥由于BD PA ⊥，BD AC ⊥，PA AC A =，所以BD ⊥平面PAC又因为PC ⊂平面PAC ，因此BD PC ⊥ （2）由于PA ⊥平面ABCD ，AB平面ABCD ，AD ⊂平面ABCD ，所以PA AB ⊥，PA AD ⊥又AB AD ⊥，所以PA ，AB ，AD 两两垂直，因比，如图建立空间直角坐标系A xyz -(2,0,0)B ，(2,2,0)C ，(0,2,0)D，P因此(2,2,PC =，(2,0,PB =，(0,2,PD =设平面PBD 的法向量为(,,)m x y z =，则00m PB m PD ⎧⋅=⎨⋅=⎩即2020x y ⎧=⎪⎨=⎪⎩ 取1x =，1y =，z =，则(1,1,2)m =设直线PC 与平面PBD 所成角为θ，10sin |cos ,|=||10||||m PC m PC m PC θ⋅=<>=⋅（3）存在，设[0,1]PEPCλ=∈，则(2,2))E λλλ- 则(22,2))BE λλλ=--，(2,2,0)BD =-设平面BDE 的法向量为(,,)n a b c =，则0n BE n BD ⎧⋅=⎨⋅=⎩，即2(1)2(1)0220a b a bλλλ⎧-+-=⎪⎨-+=⎪⎩，即1a λ=-，1b λ=-，2)c λ=-则(1,12))n λλλ=---，若平面BDE ⊥平面BDP ，则0m n ⋅=即1(1)1(1)2)0λλλ⋅-+⋅-+-=，则2[0,1]3λ=∈ 因此在棱PC 上存在点E ，使得平面BDE ⊥平面BDP ，23PE PC =5.【黑龙江省哈尔滨市第六中学2019届高三上学期期末考试】如图，在棱长为2的正方体中，点分别是棱上的动点，且.（1）求证：；（2）当三棱锥的体积取得最大值时，求二面角的正切值．【解析】设AE＝BF＝x．以D为原点建立空间直角坐标系，得下列坐标：D（0，0，0），A（2，0，0），B （2，2，0），C（0，2，0），D1（0，0，2），A1（2，0，2），B1（2，2，2），C1（0，2，2），E（2，x，0），F（2﹣x，2，0）．（1）因为，，所以．所以A1F⊥C1E．（2）因为，所以当S△BEF取得最大值时，三棱锥B1﹣BEF的体积取得最大值．因为，所以当x＝1时，即E，F分别是棱AB，BC的中点时，三棱锥B1﹣BEF的体积取得最大值，此时E，F坐标分别为E（2，1，0），F（1，2，0）．设平面B1EF的法向量为，则得取a＝2，b＝2，c＝﹣1，得．显然底面ABCD的法向量为．设二面角B1﹣EF﹣B的平面角为θ，由题意知θ为锐角．因为，所以，于是．所以，即二面角B1﹣EF﹣B的正切值为．6. 【湖北省2019届高三联考测试】如图，在四棱锥中，，，，且PC=BC=2AD=2CD=2，.（1）平面；（2）在线段上，是否存在一点，使得二面角的大小为？如果存在，求的值；如果不存在，请说明理由.【解析】（1）∵在底面中，，且∴，∴又∵，，平面，平面∴平面又∵平面∴∵，∴又∵，，平面，平面∴平面（2）方法一：在线段上取点，使则又由（1）得平面∴平面又∵平面∴作于又∵，平面，平面∴平面又∵平面∴又∵∴是二面角的一个平面角设则，这样，二面角的大小为即即∴满足要求的点存在，且方法二：取的中点，则、、三条直线两两垂直∴可以分别以直线、、为、、轴建立空间直角坐标系且由（1）知是平面的一个法向量设则，∴，设是平面的一个法向量则∴令，则，它背向二面角又∵平面的法向量，它指向二面角这样，二面角的大小为即即∴满足要求的点存在，且7. 【福建省龙岩市2019届高三第一学期期末教学质量检查】如图，四边形是边长为2的正方形，平面平面，且.（1）证明：平面平面；（2）当，且与平面所成角的正切值为时，求二面角的正弦值.【解析】（1）由题设知，平面平面，交线为.因为，平面，所以平面，因此，又，，所以平面.而平面，所以平面平面.（2）以为坐标原点，的方向为轴正方向建立如图所示的直角坐标系，则有，过点作于，设，则.因为，所以，，由题设可得，即，解得或，因为，所以，所以，.由，知是平面的法向量，，.设平面的法向量为，则取得，设二面角为，则，因为，.综上，二面角的正弦值为.8. 【福建省厦门市2019届高三年级第一学期期末质检】如图，在四棱锥中，平面，四边形为平行四边形，且，.（1）证明：平面；（2）当直线与平面所成角的正切值为时，求二面角的余弦值. 【解析】（1）证明：由已知，得，在中，，∴，即，∵平面，平面，∴，又∵，平面，平面，∴平面（2）∵平面，∴为直线与平面所成角，∴，∴，在中，，取的中点，连结，则，∵平面，平面，∴，又∵，平面，平面，∴平面，以点为坐标原点，建立如图空间直角坐标系，则，，，，∴，，设平面的法向量为，则，取，解得，又平面的法向量为，∴.∴二面角的余弦值为.9. 【北京市朝阳区2018-2019高三数学期末考试】如图，三棱柱的侧面是平行四边形，，平面平面，且分别是的中点.（1）求证：平面；（2）当侧面是正方形，且时，（ⅰ）求二面角的大小；（ⅱ）在线段上是否存在点，使得？若存在，指出点的位置；若不存在，请说明理由.【解析】证明：（1）取中点，连，连.在△中，因为分别是中点，所以，且.在平行四边形中，因为是的中点，所以，且.所以，且.所以四边形是平行四边形.所以.又因为平面，平面，所以平面.（2）因为侧面是正方形，所以.又因为平面平面，且平面平面，所以平面.所以.又因为，以为原点建立空间直角坐标系，如图所示. 设，则，.（ⅰ）设平面的一个法向量为.由得即令，所以. 又因为平面，所以是平面的一个法向量.所以.由图可知，二面角为钝角，所以二面角的大小为. （ⅱ）假设在线段上存在点，使得.设，则.因为，又，所以.所以.故点在点处时，有10. 如图，在多面体ABCDMN 中，四边形ABCD 为直角梯形， //AB CD ， 22AB =， BC DC ⊥，2BC DC AM DM ====，四边形BDMN 为矩形.（1）求证：平面ADM ⊥平面ABCD ；（2）线段MN 上是否存在点H ，使得二面角H AD M --的大小为4π？若存在，确定点H 的位置并加以证明.【解析】（1）证明：由平面几何的知识，易得2BD =， 2AD =，又22AB =，所以在ABD ∆中，满足222AD BD AB +=，所以ABD ∆为直角三角形，且BD AD ⊥. 因为四边形BDMN 为矩形，所以BD DM ⊥. 由BD AD ⊥， BD DM ⊥， DM AD D ⋂=，可得 BD ADM ⊥平面. 又BD ABD ⊂平面，所以平面ADM ⊥平面ABCD .（2）存在点H ，使得二面角H AD M --为大小为，点H 为线段AB 的中点.事实上，以D 为原点， DA 为x 轴， DB 为y 轴，过D 作平面ABCD 的垂线为z 轴，建立空间直角坐标系D xyz -，则()()()0,0,0,2,0,0,0,2,0D A B , ()1,0,1M ，设(),,H x y z ,由MH MN DB λλ==，即()()1,,10,2,0x y z λ--=，得()1,2,1H λ. 设平面ADH 的一个法向量为()1111,,n x y z =，则，即，不妨设11y =，取()10,1,2n λ=-. 平面ADM 的一个法向量为()20,1,0n =. 二面角H AD M --为大小为于是.解得或（舍去）.所以当点H 为线段MN 的中点时，二面角H AD M --为大小为.11. 在三棱锥P ABC -中， AB AC =， D 为BC 的中点， PO ⊥平面ABC ，垂足O 落在线段AD 上，已知4,3,2,1BC PO AO OD ====. （1）证明： AP BC ⊥；（2）在线段AP 上是否存在一点M ，使得二面角A MC B --为直二面角？若存在，求出AM 的长；若不存在，请说明理由.法二：如图，以O 为原点，分别以过O 点与DB 共线同向的向量， OD ， OP 方向上的单位向量为单位正交基建立空间直角坐标系O xyz -，则()()()()()0,0,0,0,2,0,2,1,0,2,1,0,0,0,3,O A B C P --()()()0,2,3,4,0,0,2,3,0AP BC AC ==-=-∴0AP BC ⋅= ∴AP BC ⊥ ∴AP BC ⊥（2）假设M 点存在，设AM AP λ=， (),,M x y z ，则(),2,AM x y z =+，∴()(),2,0,2,3x y z λ+=，∴0{22 3x y z λλ=+==，∴()0,22,3M λλ-， ∴()2,23,3BM λλ=--设平面MBC 的法向量为()1111,,n x y z =，平面APC 的法向量为()2222,,n x y z = 由110{n BM n BC ⋅=⋅=得()111122330{40x y z x λλ-+-+=-=，令11y =，可得1320,1,3n λλ-⎛⎫= ⎪⎝⎭，由220{n AC n AP ⋅=⋅=得2222230{230x y y z -+=+=，令16y =，可得()29,6,4n =-，若二面角A MC B --为直二面角，则120n n ⋅=，得326403λλ--⋅=，解得613λ=，∴613AM =故线段AP 上是否存在一点M ，满足题意， AM 的长为613. 12 【安徽省江南十校2019届高三第二次大联考】如图，已知四边形中，对角线，，为等边三角形.（1）求面积的最大值；（2）当的面积最大时，将四边形沿折起成直二面角，在上是否存在点使直线与平面所成的角满足：，若不存在，说明理由；若存在，指出点的位置. 【解析】（1）在中，记，，则由余弦定理：，（当且仅当时，上式取等号）此时，，的面积的最大值为.（2）由（1）知，，，设存在，在三棱锥中，取的中点，连接，易知.作于，由平面平面平面.故在平面上的投影为.与平面所成的角为，由.设，得，，故.故存在，且，满足题意.（2）另解：由（1），，设存在，则在三棱锥中，取的中点，连接，易求.以为坐标原点，为轴，为轴，为轴建立空间直角坐标系，平面的法向量为，设，得，得，又.由.故存在，且，满足题意.13. 【云南省昆明市2019届高三1月复习诊断测试】如图，在四棱锥中，底面是平行四边形，平面，，，是棱上的一点.（1）若平面，证明：；（2）在（1）的条件下，棱上是否存在点，使直线与平面所成角的大小为？若存在，求的值；若不存在，请说明理由.【解析】（1）连接交于，连接，则是平面与平面的交线.因为平面，平面，所以.又因为是中点，所以是的中点.所以.（2）由已知条件可知，所以，以为原点，为轴，为轴，为轴建立空间直角坐标系.。

2019-2020年高考数学一轮复习高考大题专项练4高考中的立体几何

2019-2020年高考数学一轮复习高考大题专项练4高考中的立体几何1.如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=,三棱锥P-ABD的体积V=,求点A到平面PBC的距离.2.如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.(1)求证:PC⊥AD;(2)证明在PB上存在一点Q,使得A,Q,M,D四点共面;(3)求点D到平面PAM的距离.3.如图所示,△ABC为正三角形,CE⊥平面ABC,BD∥CE,CE=CA=2BD,M是EA的中点.求证:(1)DE=DA.(2)平面BDM⊥平面ECA.4.如图,在底面是菱形的四棱柱ABCD-A1B1C1D1中,∠ABC=60°,AA1=AC=2,A1B=A1D=2,点E在A1D上.(1)证明:AA1⊥平面ABCD;(2)当为何值时,A1B∥平面EAC,并求出此时三棱锥D-AEC的体积.5.(2017山东,文18)由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.6.如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6.顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.(1)证明:G是AB的中点;(2)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.7.(2017天津,文17)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP与BC所成角的余弦值;(2)求证:PD⊥平面PBC;(3)求直线AB与平面PBC所成角的正弦值.参考答案高考大题专项练四高考中的立体几何1.(1)证明设BD与AC的交点为O,连接EO.因为四边形ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.又EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.(2)解V=PA·AB·AD=AB,由V=,可得AB=.作AH⊥PB交PB于H,由题设知BC⊥平面PAB,所以BC⊥AH.故AH⊥平面PBC.又AH=.所以点A到平面PBC的距离为.2.(1)证法一取AD中点O,连接OP,OC,AC,依题意可知△PAD,△ACD均为正三角形,所以OC⊥AD,OP⊥AD.又OC∩OP=O,OC⊂平面POC,OP⊂平面POC,所以AD⊥平面POC.又PC⊂平面POC,所以PC⊥AD.证法二连接AC,依题意可知△PAD,△ACD均为正三角形,又M为PC的中点,所以AM⊥PC,DM⊥PC.又AM∩DM=M,AM⊂平面AMD,DM⊂平面AMD,所以PC⊥平面AMD.又AD⊂平面AMD,所以PC⊥AD.(2)证明当点Q为棱PB的中点时,A,Q,M,D四点共面,证明如下:取棱PB的中点Q,连接QM,QA,又M为PC的中点,所以QM∥BC,在菱形ABCD中AD∥BC,所以QM∥AD,所以A,Q,M,D四点共面.(3)解点D到平面PAM的距离即点D到平面PAC的距离,由(1)可知PO⊥AD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO⊂平面PAD,所以PO⊥平面ABCD,即PO为三棱锥P-ACD的体高.在Rt△POC中,PO=OC=,PC=,在△PAC中,PA=AC=2,PC=,边PC上的高AM=,所以△PAC的面积S△PAC=PC·A M=,设点D到平面PAC的距离为h,由V D-PAC=V P-ACD,得S△PAC·h=S△ACD·PO,又S△ACD=×22=,所以·h=,解得h=,所以点D到平面PAM的距离为. 3.证明(1)取CE的中点F,连接DF.∵CE⊥平面ABC,∴CE⊥BC.∵BD∥CE,BD=CE=CF=FE,∴四边形FCBD是矩形,∴DF⊥EC.又BA=BC=DF,∴Rt△DEF≌Rt△ADB,∴DE=DA.(2)取AC中点N,连接MN,NB,∵M是EA的中点,∴MN CE.由BD CE,且BD⊥平面ABC,可得四边形MNBD是矩形,于是DM⊥MN.∵DE=DA,M是EA的中点,∴DM⊥EA.又EA∩MN=M,∴DM⊥平面ECA,而DM⊂平面BDM,∴平面BDM⊥平面ECA.4.(1)证明因为底面ABCD是菱形,∠ABC=60°,所以AB=AD=AC=2.在△AA1B中,由A+AB2=A1B2,知AA1⊥AB.同理,AA1⊥AD.又因为AB∩AD于点A,所以AA1⊥平面ABCD.(2)解当=1时,A1B∥平面EAC.证明如下:连接BD交AC于O,当=1,即点E为A1D的中点时,连接OE,则OE∥A1B,所以A1B∥平面EAC.设AD的中点为F,连接EF.则EF∥AA1,所以EF⊥平面ACD,且EF=1,可求得S△ACD=.所以V E-ACD=×1×,即V D-AEC=V E-ACD=.5.证明(1)取B1D1的中点O1,连接CO1,A1O1,由于ABCD-A1B1C1D1是四棱柱,所以A1O1∥OC,A1O1=OC,因此四边形A1OCO1为平行四边形,所以A1O∥O1C.又O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1.(2)因为AC⊥BD,E,M分别为AD和OD的中点,所以EM⊥BD,又A1E⊥平面ABCD,BD⊂平面ABCD,所以A1E⊥BD,因为B1D1∥BD,所以EM⊥B1D1,A1E⊥B1D1.又A1E,EM⊂平面A1EM,A1E∩EM=E, 所以B1D1⊥平面A1EM,又B1D1⊂平面B1CD1,所以平面A1EM⊥平面B1CD1.6.(1)证明因为P在平面ABC内的正投影为D,所以AB⊥PD.因为D在平面PAB内的正投影为E,所以AB⊥DE.所以AB⊥平面PED,故AB⊥PG.又由已知可得,PA=PB,从而G是AB的中点.(2)解在平面PAB内,过点E作PB的平行线交PA于点F,F即为E在平面PAC内的正投影.理由如下:由已知可得PB⊥PA,PB⊥PC,又EF∥PB,所以EF⊥PA,EF⊥PC.因此EF⊥平面PAC,即点F为E在平面PAC内的正投影.连接CG,因为P在平面ABC内的正投影为D,所以D是正三角形ABC的中心.由(1)知,G是AB的中点,所以D在CG上,故CD=CG.由题设可得PC⊥平面PAB,DE⊥平面PAB,所以DE∥PC,因此PE=PG,DE=PC.由已知,正三棱锥的侧面是直角三角形且PA=6,可得DE=2,PE=2.在等腰直角三角形EFP中,可得EF=PF=2.所以四面体PDEF的体积V=×2×2×2=.7.(1)解如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得AP=,故cos∠DAP=.所以,异面直线AP与BC所成角的余弦值为.(2)证明因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.又因为BC∥AD,所以PD⊥BC.又PD⊥PB,所以PD⊥平面PBC.(3)解过点D作AB的平行线交BC于点F,连接PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,由已知,得CF=BC-BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得DF==2,在Rt△DPF中,可得sin∠DFP=.所以,直线AB与平面PBC所成角的正弦值为.。

专题08-1立体几何问题第一季-2019年领军高考数学(理)压轴题必刷题(解析版)

专题08-1立体几何问题第一季1．正三棱柱中,所有棱长均为2,点分别为棱的中点,若过点作一截面,则截面的周长为（）A．B．C．D．【答案】B【解析】在正三棱柱中，延长和交于点M，连接，交于点，分别连接，则过点的截面为四边形，如图所示，由，可得，由，则，解得，则，在直角中，，则，在直角中，，则，在直角中，，则，在中，，由余弦定理可得，即，所以截面的周长为，故选B.2．设正方体的棱长为，为的中点，为直线上一点，为平面内一点，则，两点间距离的最小值为（）A．B．C．D．【答案】B【解析】结合题意，绘制图形结合题意可知OE是三角形中位线，题目计算距离最短，即求OE与两平行线的距离，，所以距离d，结合三角形面积计算公式可得，解得，故选B。

3．如图，在棱长为2的正方体中，分别是棱的中点，是底面内一动点，若直线与平面不存在公共点，则三角形的面积的最小值为A．B．1 C．D．【答案】C【解析】延展平面，可得截面,其中分别是所在棱的中点，直线与平面不存在公共点，所以平面,由中位线定理可得,在平面内，在平面外，所以平面,因为与在平面内相交，所以平面平面,所以在上时，直线与平面不存在公共点，因为与垂直，所以与重合时最小，此时，三角形的面积最小，最小值为，故选C.4．已知四面体，，则该四面体外接球的半径为（）学科_网A．1 B．C．D．【答案】B【解析】设为的中点，由于三角形为直角三角形，故其外心为点，则球心在点的正上方，设球心为，作出图像如下图所示.其中，.由余弦定理得，.设外接球的半径为.在三角形中，由勾股定理得①.在三角形中，由余弦定理得②.在三角形中，由余弦定理可知，由于，则，所以，所以③.联立①②③可得.故选B.5．如图，在三棱锥A-BCD中，平面ABC⊥平面BCD，△BAC与△BCD均为等腰直角三角形，且∠BAC=∠BCD=90°，BC=2，点P是线段AB上的动点，若线段CD上存在点Q，使得异面直线PQ与AC成30°的角，则线段P A长的取值范围是（）A．B．C．D．【答案】B【解析】以C为原点，CD为轴，CB为轴，过C作平面BCD的垂线为轴，建立空间直角坐标系，则，设，则，6．已知在长方体ABCD-A1B1C1D1中，AB=2，BC=2，CC1=3，长方体每条棱所在直线与过点C1的平面α所成的角都相等，则直线AC与平面α所成角的余弦值为（）A．或1 B．或0 C．或0 D．或1【答案】A在直角△EGC1中，，GC1＝2，，∴sin．∴直线AC与平面α所成角的余弦值为1，，故选：A．7．已知直三棱柱中的底面为等腰直角三角形，，点，分别是边，上动点，若直线平面，点为线段的中点，则点的轨迹为A．双曲线的一支（一部分）B．圆弧（一部分）C．线段（去掉一个端点）D．抛物线的一部分【答案】C【解析】如图作平面PQRK∥平面BCC1B1，可得到点M，N为平面PQRK与边，的交点，取MN的中点D，由对称性可知，在梯形NQRM中，D到底面ABC的距离DF始终为三棱柱高的一半，故Q落在到底面ABC距离为三棱柱高的一半的平面上，且与底面ABC平行.又D在底面的投影F始终在底面BC的高线AE上，即Q落在过底面BC的高线且与底面垂直的平面上，所以Q在两个面的交线上，又只能落在柱体内，故为线段OH，又直线平面，所以去掉O点，故选C.8．已知点在同一个球面上，，若四面体体积的最大值为10，则这个球的表面积是A．B．C．D．【答案】B【解析】由，可知，则球心在过中点与面垂直的直线上，因为面积为定值，所以高最大时体积最大，根据球的几何性质可得，当过球心时体积最大，因为四面体的最大体积为10，所以，可得，在中，，，得，球的表面积为，故选B.学科_网9．已知过球面上三点、、的截面到球心距离等于球半径的一半，且，，则球面面积为（）A．B．C．D．【答案】C10．有四根长都为2的直铁条，若再选两根长都为的直铁条，使这六根铁条端点处相连能够焊接成一个对棱相等的三棱锥形的铁架，则此三棱锥体积的取值范围是A．B．C．D．【答案】B【解析】构成三棱锥的两条对角线长为a，其他各边长为2，如图所示，AD=BC=a,此时0＜a＜2．取BC中点为E,连接AE,DE,易得：BC⊥平面ADE,∴，当且仅当4即时，等号成立，∴此三棱锥体积的取值范围是故选：11．已知正三棱锥P—ABC（顶点在底面的射影是底面正三角形的中心）的侧面是顶角为30°腰长为2的等腰三角形，若过A的截面与棱PB，PC分别交于点D和点E，则截面△ADE周长的最小值是（）A．B．2C．D．2【答案】D【解析】将三棱锥的侧面展开,如图则将求截面周长的最小值,转化成计算的最短距离,结合题意可知=,,所以,故周长最小值为,故选D.12．过棱长为1的正方体的一条体对角线作截面，则截得正方体的截面面积的最小值是A．1 B．C．D．【答案】D【解析】如图：在正方体中，取的中点,连接,过的平面截得正方体的截面中，当截面为菱形时，截面面积最小，,故选D.学_科网13．已知球是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）的外接球，，，点在线段上，且，过点作球的截面，则所得截面圆面积的取值范围是（）A．B．C．D．【答案】B【解析】画出图象如下图所示，其中是球心，是等边三角形的中心.根据等边三角形中心的性质有，，设球的半径为，在三角形中，由勾股定理得，即，解得，故最大的截面面积为.在三角形中，，由余弦定理得.在三角形中，,过且垂直的截面圆的半径，故最小的截面面积为.综上所述，本小题选B.14．正三棱锥的底面边长为，高为，它在六条棱处的六个二面角（侧面与侧面或者侧面与底面）之和记为，则在从小到大的变化过程中，的变化情况是（）A．一直增大B．一直减小C．先增大后减小D．先减小后增大【答案】D15．已知中，，，将绕BC旋转得，当直线PC与平面P AB所成角的正弦值为时，P、A两点间的距离是（）A．2 B．4 C．D．【答案】C【解析】画出图像如下图所示.设是的中点，则，过作交于，连接.由于，所以平面，所以，故平面，所以，结合，证得平面.故是直线与平面所成的角.故，.设，则，在直角三角形中，利用面积公式有，解得，即，故,.16．如图，在△ABC中，∠C=90°，PA⊥平面ABC，AE⊥PB于E，AF⊥PC于F，AP=AB=2，∠EAF=α，当α变化时，则三棱锥P﹣AEF体积的最大值是（）A．B．C．D．【答案】C【解析】在中，，，底面，得，平面，可得，平面，平面，且面，三棱锥的高为定值，平面平面，中，，，∴当，即时，有最大值为，此时，三棱锥的体积的最大值为，故选C．17．如图所示，四边形ABCD为边长为2的菱形，∠B=60°，点E,F分别在边BC,AB上运动(不含端点)，且EF//AC，沿EF把平面BEF折起，使平面BEF⊥底面ECDAF，当五棱锥B-ECDAF的体积最大时，EF的长为（）A．1 B．C．D．【答案】B【解析】由可知三角形为等边三角形，设，等边三角形的高为，面积为，所以五边形的面积为，故五棱锥的体积为.令，解得，且当时，单调递增，时，单调递减，故在时取得极大值也即是最大值.故选B. 18．正方体ABCD－A1B1C1D1的棱长为1，平面A1B1C1D1内的一动点P，满足到点A1的距离与到线段C1D1的距离相等，则线段PA长度的最小值为（）A．B．C．D．【答案】C【解析】如图，以A1D1的中点为原点，以A1D1为x轴建立如图所示的空间直角坐标系，则．由于动点P到点A1的距离与到线段C1D1的距离相等，所以点P在以点A1为焦点、以C1D1为准线的抛物线上．由题意得，在平面内，抛物线的方程为，设点P的坐标为，则，所以，又，所以当时，有最小值，且．故选C．19．如图，设梯形所在平面与矩形所在平面相交于，若，，，则下列二面角的平面角大小为定值的是( )A．B．C．D．【答案】D【解析】如图，在等腰梯形中,过作于，作于,连接,在梯形中,由，可得，由三角形直角三角形，且，可得，则，，即，则平面，为二面角的平面角，同理可得为二面角的平面角，平面平面，则二面角的平面角为，与均为等腰三角形，，，，即二面角为，故选D.20．如图，已知三棱锥，记二面角的平面角为，直线与平面所成的角为，直线与所成的角为，则（）A．B．C．D．【答案】A【解析】不妨设三棱锥D-ABC是棱长为2的正四面体，取AB中点E，DC中点M，AC中点M，连结DE、CE、MN、EN，过D作DO⊥CE，交CE于O，连结AO，则∠DEC=α，∠DAO=β，∠MNE=γ，∴，，∴，取BC中点E，连结DE、AE，则DE⊥BC，AE⊥BC，又DE∩AE=E，∴BC⊥平面AED，∴BC⊥AD，∴γ=90°．∴γ≥α≥β．学_科网故选：A．。

2019版二轮复习数学(理)全国版专题三第二讲大题考法——立体几何

第二讲大题考法——立体几何[典例感悟][典例1] (2018·全国卷Ⅱ)如图，在三棱锥P -ABC 中，AB ＝BC ＝22，P A ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且二面角M -P A -C 为30°，求PC 与平面P AM 所成角的正弦值.[解] (1)证明：因为P A ＝PC ＝AC ＝4，O 为AC 的中点，所以PO ⊥AC ，且PO ＝2 3. 连接OB ，因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2.所以PO 2＋OB 2＝PB 2，所以PO ⊥OB . 又因为OB ∩AC ＝O ，所以PO ⊥平面ABC .(2)以O 为坐标原点，OB ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系O -xyz .由已知得O (0,0,0)，B (2,0,0)，A (0，－2,0)，C (0,2,0)，P (0,0，23)，AP ―→＝(0,2,23)．取平面P AC 的一个法向量OB ―→＝(2,0,0)．设M (a,2－a,0)(0<a ≤2)，则AM ―→＝(a,4－a,0)．设平面P AM 的法向量为n ＝(x ，y ，z )．由⎩⎪⎨⎪⎧AP ―→·n ＝0，AM ―→·n ＝0，得⎩⎪⎨⎪⎧2y ＋23z ＝0，ax ＋(4－a )y ＝0，令y ＝3a ，得z ＝－a ，x ＝3(a －4)，所以平面P AM 的一个法向量为n ＝(3(a －4)，3a ，－a )，所以cos 〈OB ―→，n 〉＝23(a －4)23(a －4)2＋3a 2＋a2.由已知可得|cos 〈OB ―→，n 〉|＝cos 30°＝32，所以23|a －4|23(a －4)2＋3a 2＋a 2＝32，解得a ＝43或a ＝－4(舍去)．所以n ＝⎝⎛⎭⎫－833，433，－43.又PC ―→＝(0,2，－23)，所以cos 〈PC ―→，n 〉＝833＋8334＋12·643＋163＋169＝34.所以PC 与平面P AM 所成角的正弦值为34.[典例2] (2016·全国卷Ⅲ)如图，四棱锥P -ABCD 中，P A ⊥底面ABCD ，AD ∥BC ，AB ＝AD ＝AC ＝3，P A ＝BC ＝4，M 为线段AD 上一点，AM ＝2MD ，N 为PC 的中点．(1)证明MN ∥平面P AB ；(2)求直线AN 与平面PMN 所成角的正弦值.[解] (1)证明：由已知得AM ＝23AD ＝2.取BP 的中点T ，连接AT ，TN ，由N 为PC 的中点知TN ∥BC ，TN ＝12BC ＝2.又AD ∥BC ，故TN 綊AM ，所以四边形AMNT 为平行四边形，于是MN ∥AT . 因为MN ⊄平面P AB ，AT ⊂平面P AB ，所以MN ∥平面P AB . (2)取BC 的中点E ，连接AE .由AB ＝AC 得AE ⊥BC ，从而AE ⊥AD ，且AE ＝AB 2－BE 2＝AB 2－⎝⎛⎭⎫BC 22＝ 5.以A 为坐标原点，AE ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系A -xyz . 由题意知P (0,0,4)，M (0,2,0)，C (5，2,0)，N ⎝⎛⎭⎫52，1，2，PM ―→＝(0,2，－4)，PN ―→＝⎝⎛⎭⎫52，1，－2，AN ―→＝⎝⎛⎭⎫52，1，2.设n ＝(x ，y ，z )为平面PMN 的法向量，则⎩⎪⎨⎪⎧n ·PM ―→＝0，n ·PN ―→＝0，即⎩⎪⎨⎪⎧2y －4z ＝0，52x ＋y －2z ＝0，可取n ＝(0,2,1)．于是|cos 〈n ，AN ―→〉|＝|n ·AN ―→||n ||AN ―→|＝8525.所以直线AN 与平面PMN 所成角的正弦值为8525.[类题通法]1．证明空间位置关系要抓两点一是平面图形中的平行与垂直关系，这是证明空间线面平行与垂直关系的起点，特别是三角形、梯形中的平行与垂直关系；二是准确利用空间线、面平行与垂直的判定与性质定理，尤其是定理中的条件要记全、记准，切忌因记漏条件或错用定理等导致出错．2．利用空间向量求线面角的解题模型[对点训练](2018·唐山模拟)如图，在四棱锥P -ABCD 中，PC ⊥底面ABCD ，ABCD 是直角梯形，AB ⊥AD ，AB ∥CD ，AB ＝2AD ＝2CD ，E 是PB 的中点．(1)求证：平面EAC ⊥平面PBC ； (2)若二面角P -AC -E 的余弦值为63，求直线P A 与平面EAC 所成角的正弦值．解：(1)证明：因为PC ⊥平面ABCD ，AC ⊂平面ABCD ，所以AC ⊥PC . 因为AB ＝2AD ＝2CD ，所以AC ＝BC ＝2AD ＝2CD ，所以AC 2＋BC 2＝AB 2，故AC ⊥BC . 又BC ∩PC ＝C ，所以AC ⊥平面PBC . 因为AC ⊂平面EAC ，所以平面EAC ⊥平面PBC .(2)如图，以C 为原点，CB ―→，CA ―→，CP ―→的方向分别为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系，并设CB ＝2，CP ＝2a (a >0)．则C (0,0,0)，A (0,2,0)，B (2,0,0)，P (0,0,2a )，则E (1,0，a )，CA ―→＝(0,2,0)，CP ―→＝(0,0,2a )，CE ―→＝(1,0，a )，易知m ＝(1,0,0)为平面P AC 的一个法向量．设n ＝(x ，y ，z )为平面EAC 的法向量，则n ·CA ―→＝n ·CE ―→＝0，即⎩⎪⎨⎪⎧2y ＝0，x ＋az ＝0，取x ＝a ，则z ＝－1，n ＝(a,0，－1)．依题意，|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝a a 2＋1＝63，则a ＝ 2.于是n ＝(2，0，－1)，P A ―→＝(0,2，－22)．设直线P A 与平面EAC 所成角为θ，则sin θ＝|cos 〈P A ―→，n 〉|＝|P A ―→·n ||P A ―→||n |＝23，即直线P A 与平面EAC 所成角的正弦值为23.[典例1] (2018·全国卷Ⅲ)如图，边长为2的正方形ABCD 所在的平面与半圆弧C D 所在平面垂直，M 是C D 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)当三棱锥M -ABC 体积最大时，求平面MAB 与平面MCD 所成二面角的正弦值.[解] (1)证明：由题设知，平面CMD ⊥平面ABCD ，交线为CD .因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，所以BC ⊥DM .因为M 为CD 上异于C ，D 的点，且DC 为直径，所以DM ⊥CM .又BC ∩CM ＝C ，所以DM ⊥平面BMC .因为DM ⊂平面AMD ，所以平面AMD ⊥平面BMC .(2)以D 为坐标原点，DA ―→的方向为x 轴正方向，建立如图所示的空间直角坐标系D -xyz .当三棱锥M -ABC 的体积最大时，M 为CD 的中点．由题设得D (0,0,0)，A (2,0,0)，B (2,2,0)，C (0,2,0)，M (0,1,1)，AM ―→＝(－2，1,1)，AB ―→＝(0,2,0)，DA ―→＝(2,0,0)，设n ＝(x ，y ，z )是平面MAB 的法向量，则⎩⎪⎨⎪⎧n ·AM ―→＝0，n ·AB ―→＝0，即⎩⎪⎨⎪⎧－2x ＋y ＋z ＝0，2y ＝0.可取n ＝(1,0,2)，又DA ―→是平面MCD 的一个法向量，所以cos 〈n ，DA ―→〉＝n ·DA ―→|n ||DA ―→|＝55，sin 〈n ，DA ―→〉＝255.所以平面MAB 与平面MCD 所成二面角的正弦值是255.[典例2] (2017·全国卷Ⅰ)如图，在四棱锥P -ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°.(1)证明：平面P AB ⊥平面P AD ；(2)若P A ＝PD ＝AB ＝DC ，∠APD ＝90°，求二面角A -PB -C 的余弦值.[解] (1)证明：由已知∠BAP ＝∠CDP ＝90°，得AB ⊥AP ，CD ⊥PD . 因为AB ∥CD ，所以AB ⊥PD . 又AP ∩PD ＝P ，所以AB ⊥平面P AD . 又AB ⊂平面P AB ，所以平面P AB ⊥平面P AD .(2)在平面P AD 内作PF ⊥AD ，垂足为F .由(1)可知，AB ⊥平面P AD ，故AB ⊥PF ，可得PF ⊥平面ABCD .以F 为坐标原点，F A ―→的方向为x 轴正方向，|AB ―→|为单位长度，建立如图所示的空间直角坐标系F -xyz .由(1)及已知可得A ⎝⎛⎭⎫22，0，0，P ⎝⎛⎭⎫0，0，22，B ⎝⎛⎭⎫22，1，0，C ⎝⎛⎭⎫－22，1，0. 所以PC ―→＝⎝⎛⎭⎫－22，1，－22，CB ―→＝(2，0,0)，P A ―→＝⎝⎛⎭⎫22，0，－22，AB ―→＝(0,1,0)．设n ＝(x 1，y 1，z 1)是平面PCB 的法向量，则⎩⎪⎨⎪⎧ n ·PC ―→＝0，n ·CB ―→＝0，即⎩⎪⎨⎪⎧－22x 1＋y 1－22z 1＝0，2x 1＝0.所以可取n ＝(0，－1，－2)．设m ＝(x 2，y 2，z 2)是平面P AB 的法向量，则⎩⎪⎨⎪⎧ m ·P A ―→＝0，m ·AB ―→＝0，即⎩⎪⎨⎪⎧22x 2－22z 2＝0，y 2＝0.所以可取m ＝(1,0,1)．则cos 〈n ，m 〉＝n ·m |n ||m |＝－23×2＝－33. 由图知二面角A -PB -C 为钝角，所以二面角A -PB -C 的余弦值为－33. [类题通法]利用空间向量求二面角的解题模型[对点训练]如图，四棱锥P-ABCD的底面ABCD为菱形，平面P AD⊥平面ABCD，P A＝PD＝5，AD＝6，∠DAB＝60°，E为AB的中点．(1)证明：AC⊥PE；(2)求二面角D-P A-B的余弦值．解：(1)证明：如图，取AD的中点O，连接OP，OE，BD，∵四边形ABCD为菱形，∴BD⊥AC，∵O，E分别为AD，AB的中点，∴OE∥BD，∴AC⊥OE.∵P A＝PD，O为AD的中点，∴PO⊥AD，又∵平面P AD⊥平面ABCD，平面P AD∩平面ABCD＝AD，∴PO⊥平面ABCD，∴PO⊥AC，∵OE∩OP＝O，∴AC⊥平面POE，∴AC⊥PE.(2)连接OB，∵四边形ABCD为菱形，∴AD＝AB，又∠DAB＝60°，∴△DAB为等边三角形，又O为AD的中点，∴OB⊥AD，∵PO⊥平面ABCD，OA⊂平面ABCD，OB⊂平面ABCD，∴PO⊥OA，PO⊥OB，∴OP，OA，OB两两垂直．以OA ，OB ，OP 所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系O -xyz ，则A (3,0,0)，B (0,33，0)，P (0，0,4)，OB ―→＝(0,33，0)为平面P AD 的一个法向量．设平面P AB 的法向量为n ＝(x ，y ，z )，又AP ―→＝(－3,0,4)，AB ―→＝(－3,33，0)，∴⎩⎪⎨⎪⎧AP ―→·n ＝0，AB ―→·n ＝0，即⎩⎪⎨⎪⎧－3x ＋4z ＝0，－3x ＋33y ＝0，取x ＝1，则y ＝33，z ＝34，n ＝⎝⎛⎭⎫1，33，34为平面P AB 的一个法向量，∴cos 〈OB ―→，n 〉＝OB ―→·n |OB ―→||n |＝333×1＋13＋916＝49191，结合图形可知二面角D -P A -B 的余弦值为49191.[典例感悟][典例] (2016·北京高考)如图，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，P A ⊥PD ，P A ＝PD ，AB ⊥AD ，AB ＝1，AD ＝2，AC ＝CD ＝ 5.(1)求证：PD ⊥平面P AB ；(2)求直线PB 与平面PCD 所成角的正弦值；(3)在棱P A 上是否存在点M ，使得BM ∥平面PCD ？若存在，求AMAP 的值；若不存在，说明理由．[解](1)证明：因为平面P AD⊥平面ABCD，平面P AD∩平面ABCD＝AD，AB⊥AD，AB⊂平面ABCD，所以AB⊥平面P AD.所以AB⊥PD.又因为P A⊥PD，P A∩AB＝A，所以PD⊥平面P AB.(2)取AD的中点O，连接PO，CO.因为P A＝PD，所以PO⊥AD.又因为PO⊂平面P AD，平面P AD⊥平面ABCD，所以PO ⊥平面ABCD . 因为CO ⊂平面ABCD ，所以PO ⊥CO .因为AC ＝CD ，所以CO ⊥AD . 如图所示，建立空间直角坐标系O -xyz .由题意得，A (0,1,0)，B (1,1,0)，C (2,0,0)，D (0，－1,0)，P (0,0,1)．则PD ―→＝(0，－1，－1)，PC ―→＝(2,0，－1)，PB ―→＝(1,1，－1)，设平面PCD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·PD ―→＝0，n ·PC ―→＝0，即⎩⎪⎨⎪⎧－y －z ＝0，2x －z ＝0.令z ＝2，则x ＝1，y ＝－2. 所以n ＝(1，－2,2)．又PB ―→＝(1,1，－1)，所以cos 〈n ，PB ―→〉＝n ·PB ―→| n ||PB ―→|＝－33.所以直线PB 与平面PCD 所成角的正弦值为33. (3)设M 是棱P A 上一点，则存在λ∈[0,1]，使得AM ―→＝λAP ―→.因此点M (0,1－λ，λ)，BM ―→＝(－1，－λ，λ)．因为BM ⊄平面PCD ，所以要使BM ∥平面PCD ，当且仅当BM ―→·n ＝0，即(－1，－λ，λ)·(1，－2,2)＝0.解得λ＝14.所以在棱P A 上存在点M 使得BM ∥平面BCD ，此时AM AP ＝14.[类题通法]利用空间向量求解探索性问题的策略(1)假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论．(2)在(1)的前提下进行逻辑推理，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标(或参数)是否有解，是否有规定范围内的解”等．若由此推导出矛盾，则否定假设；否则，给出肯定结论．[对点训练](2018·湖南五市十校联考)如图，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，AD ∥BC ，AD ⊥CD ，且AD ＝CD ＝22，BC ＝42，P A ＝2.(1)求证：AB ⊥PC;(2)在线段PD 上，是否存在一点M ，使得二面角M -AC -D 的大小为45°，如果存在，求BM 与平面MAC 所成角的正弦值，如果不存在，请说明理由．解：(1)证明：由已知得四边形ABCD 是直角梯形，由AD ＝CD ＝22，BC ＝42，可得△ABC 是等腰直角三角形，即AB ⊥AC ，因为P A ⊥平面ABCD ，所以P A ⊥AB ，又P A ∩AC ＝A ，所以AB ⊥平面P AC ，所以AB ⊥PC .(2)建立如图所示的空间直角坐标系，则A (0,0,0)，C (22，22，0)，D (0,22，0)，P (0,0,2)，B (22，－22，0)，PD ―→＝(0,2 2，－2)，AC ―→＝(22，22，0)，AP ―→＝(0,0,2)．设PM ―→＝t PD ―→ (0<t <1)，则PM ―→＝(0,22t ，－2t )，所以AM ―→＝AP ―→＋PM ―→＝(0,22t,2－2t )．设平面MAC 的法向量是n ＝(x ，y ，z )，则 ⎩⎪⎨⎪⎧n ·AC ―→＝0，n ·AM ―→＝0，即⎩⎪⎨⎪⎧22x ＋22y ＝0，22ty ＋(2－2t )z ＝0，则可取n ＝⎝ ⎛⎭⎪⎫1，－1，2t 1－t .又m ＝(0,0,1)是平面ACD 的一个法向量，所以|cos 〈m ，n 〉|＝|m ·n || m || n |＝⎪⎪⎪⎪⎪⎪2t t －12＋⎝ ⎛⎭⎪⎫2t t －12＝cos 45°＝22，解得t ＝12，即点M 是线段PD 的中点．此时平面MAC 的法向量n ＝(1，－1，2)，M (0，2，1)， BM ―→＝(－22，32，1)．设BM 与平面MAC 所成的角为θ，则sin θ＝|cos 〈n ，BM ―→〉|＝|n ·BM ―→||n ||BM ―→|＝269.所以存在PD 的中点M 使得二面角M -AC -D 的大小为45°，且BM 与平面MAC 所成角的正弦值为269.[解题通法点拨] 立体几何问题重在 “建”——建模、建系[循流程思维——入题快]立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深．解决这类题目的原则是建模、建系．建模——将问题转化为平行模型、垂直模型、平面化模型或角度、距离等的计算模型；建系——依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解．[按流程解题——快又准][典例] (2017·全国卷Ⅱ)如图，四棱锥P -ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝12AD ，∠BAD ＝∠ABC ＝90°，E 是PD 的中点．(1)证明：直线CE ∥平面P AB ；(2)点M 在棱PC 上，且直线BM 与底面ABCD 所成角为45°，求二面角M -AB -D 的余弦值．[解题示范](1)证明：取P A 的中点F ，连接EF ，BF .因为E 是PD 的中点，所以EF ∥AD ，EF ＝12AD .由∠BAD ＝∠ABC ＝90°，得BC ∥AD ，又BC ＝12AD ，所以EF 綊BC ，所以四边形BCEF 是平行四边形， CE ∥BF ，又BF ⊂平面P AB ，CE ⊄平面P AB ，故CE ∥平面P AB .❶(2)由已知得BA ⊥AD ，以A 为坐标原点，AB ―→的方向为x 轴正方向，|AB ―→|为单位长度，建立如图所示的空间直角坐标系A -xyz ，则A (0,0,0)，B (1，0,0)，C (1,1,0)，P (0，1，3)，PC ―→＝(1,0，－3)，AB ―→＝(1,0,0)．❷❶建模：证明线面平行的模型：⎭⎬⎫a ⊄αb ⊂αa ∥b ⇒a ∥α.❷建系：将线面角、二面角的求解问题转化为空间向量的计算问题．设M (x ，y ，z )(0<x <1)，则BM ―→＝(x －1，y ，z )，PM ―→＝(x ，y －1，z －3)．因为BM 与底面ABCD 所成的角为45°，而n ＝(0,0,1)是底面ABCD 的法向量，所以|cos 〈BM ―→，n 〉|＝sin 45°，|z |(x －1)2＋y 2＋z 2＝22，即(x －1)2＋y 2－z 2＝0.① 又M 在棱PC 上，设PM ―→＝λPC ―→，则x ＝λ，y ＝1，z ＝3－3λ.②由①②解得⎩⎨⎧x ＝1＋22，y ＝1，z ＝－62(舍去)，或⎩⎨⎧x ＝1－22，y ＝1，z ＝62，所以M ⎝⎛⎭⎫1－22，1，62，从而AM ―→＝⎝⎛⎭⎫1－22，1，62. 设m ＝(x 0，y 0，z 0)是平面ABM 的法向量，则⎩⎪⎨⎪⎧m ·AM ―→＝0，m ·AB ―→＝0，即⎩⎨⎧(2－2)x 0＋2y 0＋6z 0＝0，x 0＝0，所以可取m ＝(0，－6，2)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝105.由图知二面角M -AB -D 为锐角，因此二面角M -AB -D 的余弦值为105. [思维升华] 立体几何的内容在高考中的考查情况总体上比较稳定．在平时的学习中，要加强“一题两法(几何法与向量法)”的训练，切勿顾此失彼；要重视识图训练，能正确确定关键点或线的位置，将局部空间问题转化为平面模型；能依托于题中的垂直条件，建立适当的空间直角坐标系，将几何问题化归为代数问题的计算模型．[应用体验](2018·全国卷Ⅰ)如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF ⊥BF .(1)证明：平面PEF ⊥平面ABFD ； (2)求DP 与平面ABFD 所成角的正弦值．解：(1)证明：由已知可得BF ⊥PF ，BF ⊥EF ，又PF ∩EF ＝F ，所以BF ⊥平面PEF . 又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD .(2)如图，作PH ⊥EF ，垂足为H . 由(1)得，PH ⊥平面ABFD .以H 为坐标原点，HF ―→的方向为y 轴正方向，|BF ―→|为单位长，建立如图所示的空间直角坐标系H -xyz .由(1)可得，DE ⊥PE .又因为DP ＝2，DE ＝1，所以PE ＝ 3. 又PF ＝1，EF ＝2，所以PE ⊥PF . 所以PH ＝32，EH ＝32. 则H (0,0,0)，P ⎝⎛⎭⎫0，0，32，D ⎝⎛⎭⎫－1，－32，0， DP ―→＝⎝⎛⎭⎫1，32，32，HP ―→＝⎝⎛⎭⎫0，0，32.又HP ―→为平面ABFD 的法向量，设DP 与平面ABFD 所成角为θ，则sin θ＝|HP ―→·DP ―→||HP ―→||DP ―→|＝343＝34.所以DP 与平面ABFD 所成角的正弦值为34.[课时跟踪检测] A 卷——大题保分练1.(2018·洛阳模拟)如图，在四棱锥P -ABCD 中，E ，F 分别是PC ，PD 的中点，底面ABCD 是边长为2的正方形，P A ＝PD ＝2，且平面P AD ⊥平面ABCD .(1)求证：平面AEF ⊥平面PCD ；(2)求平面AEF 与平面ACE 所成锐二面角的余弦值．解：(1)证明：由题意知，P A ＝PD ＝AD ，F 为PD 的中点，可得AF ⊥PD ，∵平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，CD ⊂平面ABCD ，CD ⊥AD ， ∴CD ⊥平面P AD .又AF ⊂平面P AD ，∴CD ⊥AF ，又CD ∩PD ＝D ，∴AF ⊥平面PCD ，又AF ⊂平面AEF ， ∴平面AEF ⊥平面PCD .(2)取AD 的中点O ，BC 的中点G ，连接OP ，OG ，∵P A ＝PD ＝AD ，∴OP ⊥AD .∵平面P AD ⊥平面ABCD ，OP ⊂平面P AD ，∴OP ⊥平面ABCD . 分别以OA ，OG ，OP 所在直线为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，则A (1,0,0)，C (－1,2,0)，E ⎝⎛⎭⎫－12，1，32，F ⎝⎛⎭⎫－12，0，32，AF ―→＝⎝⎛⎭⎫－32，0，32，FE―→＝(0,1,0)．设平面AEF 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ m ·AF ―→＝0，m ·FE ―→＝0，即⎩⎪⎨⎪⎧－32x ＋32z ＝0，y ＝0，可取m ＝(1,0，3)，为平面AEF 的一个法向量．同理，可得平面ACE 的一个法向量为n ＝(3，3，1)． cos 〈m ，n 〉＝m ·n |m |·|n |＝1×3＋3×12×7＝217.∴平面AEF 与平面ACE 所成锐二面角的余弦值为217. 2.(2018·山西八校联考)如图，三棱柱ABC -A1B 1C 1中，∠ACB ＝90°，CC 1⊥底面ABC ，AC ＝BC ＝CC 1＝2，D ，E ，F 分别是棱AB ，BC ，B 1C 1的中点，G 是棱BB 1上的动点．(1)当BGBB 1为何值时，平面CDG ⊥平面A 1DE? (2)求平面A 1BF 与平面A 1DE 所成的锐二面角的余弦值．解：(1)当BG BB 1＝12，即G 为BB 1的中点时，平面CDG ⊥平面A 1DE .证明如下：因为点D ，E 分别是AB ，BC 的中点，所以DE ∥AC 且DE ＝12AC ，又AC ∥A 1C 1，AC ＝A 1C 1，所以DE ∥A 1C 1，DE ＝12A 1C 1，故D ，E ，C 1，A 1四点共面．如图，连接C1E 交GC 于H .在正方形CBB 1C 1中，tan ∠C 1EC ＝2，tan ∠BCG ＝12，故∠CHE ＝90°，即CG ⊥C 1E .因为A 1C 1⊥平面CBB 1C 1，CG ⊂平面CBB 1C 1，所以DE ⊥CG ，又C 1E ∩DE ＝E ，所以CG ⊥平面A 1DE ，故平面CDG ⊥平面A 1DE .(2)由(1)知，当G 为BB 1的中点时，平面A 1DE 的一个法向量为CG ―→.三棱柱ABC -A 1B 1C 1中，∠ACB ＝90°，CC 1⊥底面ABC ，所以以C 为原点，CA ，CB ，CC 1所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示．因为AC ＝BC ＝CC 1＝2，D ，E ，F 分别是棱AB ，BC ，B 1C 1的中点，所以C (0,0,0)，A 1(2,0,2)，D (1,1,0)，E (0,1,0)，B (0,2,0)，F (0,1,2)，G (0,2,1)，A 1B ―→＝(－2,2，－2)，A 1F ―→＝(－2,1,0)，CG ―→＝(0,2,1)．由CD 知CG ―→为平面A 1DE 的一个法向量．设平面A 1BF 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·A 1F ―→＝0，n ·A 1B ―→＝0，即⎩⎪⎨⎪⎧－2x ＋y ＝0，－2x ＋2y －2z ＝0，令x ＝1得n ＝(1,2,1)，为平面A 1BF 的一个法向量．设平面A 1BF 与平面A 1DE 所成的锐二面角为θ，则cos θ＝|CG ―→·n ||CG ―→|·|n |＝530＝306，所以平面A 1BF 与平面A 1DE 所成的锐二面角的余弦值为306. 3．如图①，在矩形ABCD 中，AB ＝4，AD ＝2，E 是CD 的中点，将△ADE 沿AE 折起，得到如图②所示的四棱锥D 1-ABCE ，其中平面D 1AE ⊥平面ABCE .(1)设F 为CD 1的中点，试在AB 上找一点M ，使得MF ∥平面D 1AE ；(2)求直线BD 1与平面CD 1E 所成的角的正弦值．解：(1)如图，取D1E 的中点，记为L ，连接AL ，FL ，则FL ∥EC ，又EC ∥AB ，∴FL ∥AB ，且FL ＝14AB ， ∴M ，F ，L ，A 四点共面，且平面D 1AE ∩平面AMFL ＝AL ，若MF ∥平面D 1AE ，则MF ∥AL ，∴四边形AMFL 为平行四边形，∴AM ＝FL ＝14AB .(2)取AE 的中点O ，过点O 作OG ⊥AB 于G ，OH ⊥BC 于H ，连接OD 1.∵AD 1＝D 1E ，∴D 1O ⊥AE ，∴D 1O ⊥平面ABCE ，D 1O ⊥OG ，D 1O⊥OH ，又易得OG ⊥OH ，故OG ，OH ，OD 1两两垂直，以O 为坐标原点，OG ，OH ，OD 1为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示．则B (1,3,0)，C (－1,3,0)，E (－1,1,0)，D 1(0,0，2)．故BD 1―→＝(－1，－3，2)，CD 1―→＝(1，－3，2)，CE ―→＝(0，－2,0)．设平面CD 1E 的一个法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ m ·CD 1―→＝0，m ·CE ―→＝0，即⎩⎪⎨⎪⎧x －3y ＋2z ＝0，－2y ＝0，取x ＝2，得m ＝(2，0，－1)．设直线BD 1与平面CD 1E 所成的角为θ，则sin θ＝|cos 〈m ，BD 1―→〉|＝|m ·BD 1―→||m ||BD 1―→|＝|－22|3×12＝23. 即直线BD 1与平面CD 1E 所成的角的正弦值为23.4.如图，在多面体ABCDEF 中，底面ABCD 是边长为2的菱形，∠BAD ＝60°，四边形BDEF 是矩形，平面BDEF ⊥平面ABCD ，BF ＝3，H是CF 的中点．(1)求证：AC ⊥平面BDEF ；(2)求直线DH 与平面BDEF 所成角的正弦值；(3)求二面角H -BD -C 的大小．解：(1)证明：∵四边形ABCD 是菱形，∴AC ⊥BD .又∵平面BDEF ⊥平面ABCD ，平面BDEF ∩平面ABCD ＝BD ，且AC ⊂平面ABCD ，∴AC ⊥平面BDEF .(2)设AC ∩BD ＝O ，取EF 的中点N ，连接ON ，∵四边形BDEF 是矩形，O ，N 分别为BD ，EF 的中点，∴ON ∥ED .∵ED ⊥平面ABCD ，∴ON ⊥平面ABCD .由AC ⊥BD ，得OB ，OC ，ON 两两垂直．∴以O 为原点，OB ，OC ，ON 所在直线分别为x 轴，y 轴，z 轴，建立如图所示空间直角坐标系．∵底面ABCD 是边长为2的菱形，∠BAD ＝60°，BF ＝3，∴A (0，－3，0)，B (1,0,0)，D (－1，0,0)，E (－1,0,3)，F (1,0,3)，C (0，3，0)，H ⎝⎛⎭⎫12，32，32. ∵AC ⊥平面BDEF ，∴平面BDEF 的法向量AC ―→＝(0,23，0)．设直线DH 与平面BDEF 所成角为α，∵DH ―→＝⎝⎛⎭⎫32，32，32， ∴sin α＝|cos 〈DH ―→，AC ―→〉|＝⎪⎪⎪⎪⎪⎪⎪⎪DH ―→·AC ―→|DH ―→||AC ―→|＝77， ∴直线DH 与平面BDEF 所成角的正弦值为77. (3)由(2)，得BH ―→＝⎝⎛⎭⎫－12，32，32，DB ―→＝(2,0,0)．设平面BDH 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧－x ＋3y ＋3z ＝0，2x ＝0，令z ＝1，得n ＝(0，－3，1)．由ED ⊥平面ABCD ，得平面BCD 的法向量为ED ―→＝(0,0，－3)，则cos 〈n ，ED ―→〉＝n ·ED ―→|n ||ED ―→|＝－12，由图可知二面角H -BD -C 为锐角，∴二面角H -BD -C 的大小为60°.B 卷——深化提能练1.(2019届高三·辽宁五校联考)如图，在四棱锥E -ABCD 中，底面ABCD为直角梯形，其中CD ∥AB ，BC ⊥AB ，侧面ABE ⊥平面ABCD ，且AB ＝AE ＝BE ＝2BC ＝2CD ＝2，动点F 在棱AE ，且EF ＝λF A .(1)试探究λ的值，使CE ∥平面BDF ，并给予证明；(2)当λ＝1时，求直线CE 与平面BDF 所成角的正弦值．解：(1)当λ＝12时，CE ∥平面BDF .证明如下：连接AC 交BD 于点G ，连接GF (图略)，∵CD ∥AB ，AB ＝2CD ，∴CG GA ＝CD AB ＝12， ∵EF ＝12F A ，∴EF F A ＝CG GA ＝12，∴GF ∥CE ，又CE ⊄平面BDF ，GF ⊂平面BDF ，∴CE ∥平面BDF .(2)如图，取AB 的中点O ，连接EO ，则EO ⊥AB ，∵平面ABE ⊥平面ABCD ，平面ABE ∩平面ABCD ＝AB ，∴EO ⊥平面ABCD ，连接DO ，∵BO ∥CD ，且BO ＝CD ＝1，∴四边形BODC 为平行四边形，∴BC ∥DO ，又BC ⊥AB ，∴AB ⊥OD ，则OD ，OA ，OE 两两垂直，以OD ，OA ，OE 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系O -xyz ，则O (0,0,0)，A (0,1,0)，B (0，－1,0)，D (1,0,0)，C (1，－1，0)，E (0,0，3)．当λ＝1时，有EF ―→＝F A ―→，∴F ⎝⎛⎭⎫0，12，32， ∴BD ―→＝(1,1,0)，CE ―→＝(－1,1，3)，BF ―→＝⎝⎛⎭⎫0，32，32. 设平面BDF 的法向量为n ＝(x ，y ，z )，则有⎩⎪⎨⎪⎧ n ·BD ―→＝0，n ·BF ―→＝0，即⎩⎪⎨⎪⎧ x ＋y ＝0，32y ＋32z ＝0，令z ＝3，得y ＝－1，x ＝1，则n ＝(1，－1，3)为平面BDF 的一个法向量，设直线CE 与平面BDF 所成的角为θ，则sin θ＝|cos 〈CE ―→，n 〉|＝15，故直线CE 与平面BDF 所成角的正弦值为15.2.(2018·山东潍坊模拟)如图，在四棱锥P -ABCD 中，底面四边形ABCD内接于圆O ，AC 是圆O 的一条直径，P A ⊥平面ABCD ，P A ＝AC ＝2，E是PC 的中点，∠DAC ＝∠AOB .(1)求证：BE ∥平面P AD ；(2)若二面角P -CD -A 的正切值为2，求直线PB 与平面PCD 所成角的正弦值．解：(1)证明：∵∠DAC ＝∠AOB ，∴AD ∥OB .∵E 为PC 的中点，O 为圆心，连接OE ，∴OE ∥P A ，又OB ∩OE ＝O ，P A ∩AD ＝A ，∴平面P AD ∥平面EOB ，∵BE ⊂平面EOB ，∴BE ∥平面P AD .(2)∵四边形ABCD 内接于圆O 且AC 为直径，∴AD ⊥CD ，又P A ⊥平面ABCD ，∴P A ⊥CD ，又P A ∩AD ＝A ，∴CD ⊥平面P AD ，∴CD ⊥PD ，∴∠PDA 是二面角P -CD -A 的平面角，∵tan ∠PDA ＝2，P A ＝2，∴AD ＝1，如图，以D 为坐标原点，DA所在的直线为x 轴，DC 所在的直线为y 轴，过点D 且垂直于平面ABCD的直线为z 轴建立空间直角坐标系D -xyz .P A ＝AC ＝2，AD ＝1，延长BO 交CD 于点F ，∵BO∥AD ，∴BF ⊥CD ，∴BF ＝BO ＋OF ，∴BF ＝1＋12＝32，又CD ＝3，∴DF ＝32，∴P (1,0,2)，B ⎝⎛⎭⎫32，32，0，C (0，3，0)，CP ―→＝(1，－3，2)，DC ―→＝(0，3，0)，设平面PCD 的法向量n ＝(x ，y ，z )，∵⎩⎪⎨⎪⎧ n ·CP ―→＝0，n ·DC ―→＝0.即⎩⎪⎨⎪⎧x －3y ＋2z ＝0，3y ＝0. 令z ＝1，则x ＝－2，y ＝0.∴n ＝(－2,0,1)是平面PCD 的一个法向量，又PB ―→＝⎝⎛⎭⎫12，32，－2， ∴|cos 〈PB ―→，n 〉|＝⎪⎪⎪⎪⎪⎪⎪⎪PB ―→·n |PB ―→||n |＝⎪⎪⎪⎪⎪⎪－1＋0－25×5＝35， ∴直线PB 与平面PCD 所成角的正弦值为35. 3.(2018·合肥一模)如图，已知平行四边形ABCD 与△EMN 所在的平面都与矩形BDEF 所在的平面垂直，且∠BAD ＝60°，AB ＝MN ＝2AD ＝2，EM ＝EN ，F 为MN 的中点．(1)求证：MN ∥AD ；(2)若直线AE 与平面ABCD 所成的角为60°，求二面角M -AB -C 的余弦值．解：(1)证明：在△ABD 中，∠BAD ＝60°，AB ＝2，AD ＝1，由余弦定理可得BD 2＝AB 2＋AD 2－2AB ·AD ·cos ∠BAD ＝22＋12－2×2×1×cos 60°＝3，所以BD ＝3，AD 2＋BD 2＝AB 2，所以AD ⊥BD .又平面ABCD ⊥平面BDEF ，平面ABCD ∩平面BDEF ＝BD ，所以AD ⊥平面BDEF .在△EMN 中，EM ＝EN ，F 为MN 的中点，所以MN ⊥EF ，又平面EMN ⊥平面BDEF ，平面EMN ∩平面BDEF ＝EF ，所以MN ⊥平面BDEF .所以MN ∥AD .(2)在矩形BDEF 中，ED ⊥BD ，又平面ABCD ⊥平面BDEF ，平面ABCD ∩平面BDEF ＝BD ，所以ED ⊥平面ABCD . 所以∠EAD 为直线AE 与平面ABCD 所成的角，故∠EAD ＝60°.在Rt △EAD 中，ED ＝AD tan ∠EAD ＝1×tan 60°＝ 3.如图，以D 为坐标原点，分别以DA ，DB ，DE 所在直线为x轴，y 轴，z 轴建立空间直角坐标系，则D (0,0,0)，A (1,0,0)，B (0，3，0)，E (0,0，3)，F (0，3，3)，M (1，3，3)，MA ―→＝(0，－3，－3)，AB ―→＝(－1，3，0)．因为DE ⊥平面ABCD ，所以DE ―→＝(0,0，3)为平面ABCD 的一个法向量．设平面MAB 的法向量为n ＝(x ，y ，z )，所以⎩⎪⎨⎪⎧ n ⊥MA ―→，n ⊥AB ―→，即⎩⎪⎨⎪⎧n ·MA ―→＝－3y －3z ＝0，n ·AB ―→＝－x ＋3y ＝0，整理得⎩⎪⎨⎪⎧y ＋z ＝0，x ＝3y ，令y ＝1，则x ＝3，z ＝－1，所以n ＝(3，1，－1)是平面MAB 的一个法向量．所以cos 〈DE ―→ ，n 〉＝DE ―→·n |DE ―→|×|n |＝－3×13×(3)2＋12＋(－1)2＝－55. 设二面角M -AB -C 的大小为θ，由图可知θ为钝角，所以cos θ＝cos 〈DE ―→，n 〉＝－55. 4．已知直角梯形ABCD 中，AB ∥CD ，AB ⊥AD ，CD ＝2，AD ＝2，AB ＝1，如图①所示，将△ABD 沿BD 折起到△PBD 的位置得三棱锥P -BCD ，如图②所示．(1)求证：BD ⊥PC ；(2)当平面PBD ⊥平面PBC 时，求二面角P -DC -B 的大小．解：(1)证明：在图①中，连接AC ，交BD 于点G ，因为∠CDA ＝∠DAB ＝90°，所以tan ∠CAD ＝CD AD ＝2，tan ∠DBA ＝AD AB＝2，所以∠CAD ＝∠DBA ，因为∠CAD ＋∠BAG ＝90°，所以∠DBA ＋∠BAG ＝90°，所以BD ⊥AC .所以将△ABD 沿BD 折起到△PBD 的位置后，仍有BD ⊥PG ，BD ⊥CG ，如图②所示，又PG ∩CG ＝G ，所以BD ⊥平面PCG ，又PC ⊂平面PCG ，所以BD ⊥PC .(2)因为平面PBD ⊥平面PBC ，PB ⊥PD ，平面PBD ∩平面PBC ＝PB ，PD ⊂平面PBD ，所以PD ⊥平面PBC ，因为PC ⊂平面PBC ，所以PD ⊥PC ，又BD ⊥PC ，BD ∩PD ＝D ，所以PC ⊥平面PBD ，所以BP ⊥CP . 以P 为坐标原点，PC ，PB ，PD 所在的直线分别为x 轴，y 轴，z 轴建立空间直角坐标系如图③所示，则P (0,0,0)，B (0,1,0)，C (2，0,0)，D (0,0，2)，BD ―→＝(0，－1，2)，BC ―→＝(2，－1,0)，易知平面PCD 的一个法向量为m ＝(0,1,0)，设n ＝(x ，y ，z )为平面BCD 的法向量，则⎩⎪⎨⎪⎧ BD ―→·n ＝0，BC ―→·n ＝0，即⎩⎪⎨⎪⎧－y ＋2z ＝0，2x －y ＝0，令x ＝1，则y ＝2，z ＝1，得n ＝(1，2，1)是平面BCD 的一个法向量．则cos 〈m ，n 〉＝m ·n |m |·|n |＝22，易知二面角P -DC -B 为锐角，所以二面角P -DC -B 的大小为45°.。

(完整版)2020年高考理科数学《立体几何》题型归纳与训练,推荐文档

2020年高考理科数学《立体几何》题型归纳与训练【题型归纳】题型一线面平行的证明例1如图，高为1的等腰梯形ABCD 中，AM ＝CD ＝AB ＝1.现将△AMD 沿MD 折起，使平面AMD ⊥13平面MBCD ，连接AB ，AC .试判断：在AB 边上是否存在点P ，使AD ∥平面MPC ?并说明理由【答案】当AP ＝AB 时，有AD ∥平面MPC .13理由如下：连接BD 交MC 于点N ，连接NP .在梯形MBCD 中，DC ∥MB ，＝＝，DNNB DCMB 12在△ADB 中，＝，∴AD ∥PN .APPB 12∵AD ⊄平面MPC ，PN ⊂平面MPC ，∴AD ∥平面MPC .【解析】线面平行，可以线线平行或者面面平行推出。

此类题的难点就是如何构造辅助线。

构造完辅助线，证明过程只须注意规范的符号语言描述即可。

本题用到的是线线平行推出面面平行。

【易错点】不能正确地分析DN 与BN 的比例关系，导致结果错误。

【思维点拨】此类题有两大类方法：1.构造线线平行，然后推出线面平行。

此类方法的辅助线的构造须要学生理解线面平行的判定定理与线面平行的性质之间的矛盾转化关系。

在此，我们需要借助倒推法进行分析。

首先，此类型题目大部分为证明题，结论必定是正确的，我们以此为前提可以得到线面平行。

再次由线面平行的性质可知，过已知直线的平面与已知平面的交线必定平行于该直线，而交线就是我们要找的线，从而做出辅助线。

从这个角度上看我们可以看出线线平行推线面平行的本质就是过已知直线做一个平面与已知平面相交即可。

如本题中即是过AD 做了一个平面ADB 与平面MPC 相交于线PN 。

最后我们只须严格使用正确的符号语言将证明过程反向写一遍即可。

即先证AD 平行于PN ，最后得到结论。

构造交线的方法我们可总结为如下三个图形。

一一一一一一一一一2.构造面面平行，然后推出线面平行。

此类方法辅助线的构造通常比较简单，但证明过程较繁琐，一般做为备选方案。

2019-2020年高考数学第七章立体几何专题演练文(含两年高考一年模拟)

2019-2020年高考数学第七章立体几何专题演练文（含两年高考一年模拟）考点21 空间几何体的结构、三视图、几何体的表面积与体积1．(xx·浙江)某几何体的三视图如图所示(单位：cm)，则该几何体的体积是( )A ．8 cm 3B ．12 cm 3 C.323 cm 3 D.403cm 3 2．(xx·陕西)一个几何体的三视图如图所示，则该几何体的表面积为( )A ．3πB ．4πC ．2π＋4D ．3π＋43．(xx·新课标全国Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A ．14斛B ．22斛C ．36斛D ．66斛4．(xx·重庆)某几何体的三视图如图所示，则该几何体的体积为( )A.13＋2π B.13π6C.7π3D.5π25.(xx·新课标全国Ⅰ)如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是( )A．三棱锥B．三棱柱C．四棱锥D．四棱柱6．(xx·陕西)已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为( )A.32π3B．4π C．2π D.4π37．(xx·江苏)现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为________．8．(xx·四川)在三棱柱ABC－A1B1C1中，∠BAC＝90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，设点M，N，P分别是AB，BC，B1C1的中点，则三棱锥P－A1MN的体积是________.考点21 空间几何体的结构、三视图、几何体的表面积与体积一年模拟试题精练1．(xx·北京朝阳区期末)一个四棱锥的三视图如图所示，则该四棱锥的侧面中，直角三角形的个数为( )A．1 B．2 C．3 D．42．(xx·成都市一诊)若一个几何体的正视图和侧视图是两个全等的正方形，则这个几何体的俯视图不可能是( )3．(xx·桂林市一调)已知底面为正方形的四棱锥，其一条侧棱垂直于底面，那么该四棱锥的三视图可能是下列各图中的( )4．(xx·厦门市质检)如图，在棱长为1的正方体ABCD－A1B1C1D1中，E是棱BC上的一点，则三棱锥D1－B1C1E的体积等于( )A.13B.512C.36D.16第4题图第5题图5．(xx·山西省三诊)如图是一个几何体的三视图，若该几何体的表面积为9π，则正视图中实数a的值等于( )A．1 B．2 C．3 D．46．(xx·厦门质检)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体最长的棱的长度等于( )A.34B.41C．5 2 D．2157．(xx·衡水中学期中)三棱锥P－ABC的四个顶点均在同一球面上，其中△ABC是正三角形，PA⊥平面ABC，PA＝2AB＝6，则该球的体积为( )A．163π B．323π C．48π D．643π8．(xx·武汉市调考)若一个几何体的三视图如图所示，则此几何体的体积为( )A.1112B．5 C.92D．49．(xx·眉山市一诊)一个棱锥的三视图如图，则此棱锥的全面积是( )A．4＋2 6 B．4＋ 6 C．4＋2 2 D．4＋ 2考点22 平行关系两年高考真题演练1．(xx·新课标全国Ⅱ)如图，长方体ABCD－A1B1C1D1中AB＝16，BC＝10，AA1＝8，点E，F分别在A1B1，D1C1上，A1E＝D1F＝4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求平面α把该长方体分成的两部分体积的比值．2．(xx·四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示．(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG与平面ACH的位置关系．并证明你的结论．(3)证明：直线DF⊥平面BEG.3．(xx·北京)如图，在三棱柱ABC－A1B1C1中，侧棱垂直于底面，AB⊥BC，AA1＝AC＝2，BC＝1，E，F 分别是A1C1，BC的中点．(1)求证：平面ABE⊥平面B1BCC1；(2)求证：C1F∥平面ABE；(3)求三棱锥E－ABC的体积．考点22 平行关系一年模拟试题精练1．(xx·宿迁市摸底)如图，在四棱锥P－ABCD中，底面ABCD是菱形，且PB＝PD.(1)求证：BD⊥PC；(2)若平面PBC与平面PAD的交线为l，求证：BC∥l.2．(xx·重庆一中检测)如图，已知DE⊥平面ACD，DE∥AB，△ACD是正三角形，AD＝DE＝2AB＝2，且F是CD 的中点．(1)求证：AF∥平面BCE；(2)求四棱锥C－ABED的全面积．3．(xx·桂林市一调)如图，四棱锥P－ABCD中，BC∥AD，BC＝1，AD＝3，AC⊥CD，且平面PCD⊥平面ABCD.(1)求证：AC⊥PD.(2)在线段PA 上，是否存在点E ，使BE ∥平面PCD ？若存在，求PE PA的值，若不存在，请说明理由．4．(xx·盐城模拟)如图所示，斜三棱柱ABC －A 1B 1C 1中，点D ，D 1分别为AC ，A 1C 1上的点．(1)当A 1D 1D 1C 1等于何值时，BC 1∥平面AB 1D 1? (2)若平面BC 1D ∥平面AB 1D 1，求ADDC 的值．考点23 垂直关系两年高考真题演练1．(xx·新课标全国Ⅰ)如图，四边形ABCD为菱形，G是AC与BD的交点，BE⊥平面ABCD.(1)证明：平面AEC⊥平面BED；(2)若∠ABC＝120°，AE⊥EC，三棱锥E－ACD的体积为63，求该三棱锥的侧面积．2．(xx·江苏)如图，在直三棱柱ABC－A1B1C1中，已知AC⊥BC，BC＝CC1.设AB1的中点为D，B1C∩BC1＝E.求证：(1)DE∥平面AA1C1C；(2)BC1⊥AB1.3．(xx·重庆)如图，四棱锥P －ABCD 中，底面是以O 为中心的菱形，PO ⊥底面ABCD ，AB ＝2，∠BAD ＝π3，M 为BC 上一点，且BM ＝12. (1)证明：BC ⊥平面POM ；(2)若MP ⊥AP ，求四棱锥P －ABMO 的体积．4．(xx·福建)如图，三棱锥A －BCD 中，AB ⊥平面BCD ，CD ⊥BD . (1)求证：CD ⊥平面ABD ；(2)若AB ＝BD ＝CD ＝1，M 为AD 中点，求三棱锥A －MBC 的体积．考点23 垂直关系一年模拟试题精练1．(xx·唐山一中检测)如图所示，△ABC和△BCE是边长为2的正三角形，且平面ABC ⊥平面BCE，AD⊥平面ABC，AD＝2 3.(1)证明：DE⊥BC；(2)求三棱锥D－ABE的体积．2．(xx·晋冀豫三省调研)如图，菱形ABCD的边长为6，∠BAD＝60°，AC∩BD＝O.将菱形ABCD沿对角线AC折起，得到三棱锥，点M是棱BC的中点，DM＝3 2.(1)求证：平面ABC⊥平面MDO.(2)求三棱锥M－ABD的体积．3．(xx·山西省三诊)如图，已知菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直，AB＝2AD＝2CD＝4，∠ABE＝60°，∠BAD＝∠CDA＝90°，点H是线段EF的中点．(1)求证：平面AHC⊥平面BCE；(2)求多面体ABCDEF的体积．4．(xx·北京西城区高三检测)如图，在四棱柱ABCD－A1B1C1D1中，A1A⊥底面ABCD，∠BAD＝90°，AD∥BC，且A1A＝AD ＝2BC＝2，AB＝1.点E在棱AB上，平面A1EC与棱C1D1相交于点F.(1)求证：A1F∥平面B1CE；(2)求证：AC⊥平面CDD1C1；(3)写出三棱锥B1－A1EF体积的取值范围．考点24 立体几何综合问题两年高考真题演练1．(xx·福建)若l ，m 是两条不同的直线，m 垂直于平面α，则“l ⊥m ”是“l ∥α”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件2．(xx·安徽)已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是( )A ．若α，β垂直于同一平面，则α与β平行B ．若m ，n 平行于同一平面，则m 与n 平行C ．若α，β不平行，则在α内不存在与β平行的直线D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面3．(xx·新课标全国Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点，若三棱锥O －ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π4．(xx·辽宁)已知m ，n 表示两条不同直线，α表示平面．下列说法正确的是( ) A ．若m ∥α，n ∥α，则m ∥n B ．若m ⊥α，n ⊂α，则m ⊥n C ．若m ⊥α，m ⊥n ，则n ∥α D ．若m ∥α，m ⊥n ，则n ⊥α 5．(xx·安徽)如图，三棱锥P ABC 中，PA ⊥平面ABC ，PA ＝1，AB ＝1，AC ＝2，∠BAC ＝60°. (1)求三棱锥P ABC 的体积；(2)证明：在线段PC 上存在点M ，使得AC ⊥BM ，并求PM MC的值．6．(xx·四川)在如图所示的多面体中，四边形ABB1A1和ACC1A1都为矩形．(1)若AC⊥BC，证明：直线BC⊥平面ACC1A1；(2)设D，E分别是线段BC，CC1的中点，在线段AB上是否存在一点M，使直线DE∥平面A1MC？请证明你的结论．考点24 立体几何综合问题一年模拟试题精练1．(xx·荆门市调研)若m，n是两条不重合的空间直线，α是平面，则下列命题中正确的是( )A．若m∥n，n⊂α，则m∥αB．若m∥n，n∥α，则m∥αC．若m∥n，n⊥α，则m⊥αD．若m⊥n，n⊥α，则m∥α2．(xx·眉山市一诊)下列说法错误的是( )A．两两相交且不过同一点的三条直线必在同一平面内B．过直线外一点有且只有一个平面与已知直线垂直C．如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直D．如果两条直线和一个平面所成的角相等，则这两条直线一定平行3．(xx·深圳五校一联)已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是( )A．若m∥α，n∥α，则m∥nB ．若m ∥α，m ∥β，则α∥βC ．若α⊥γ，β⊥γ，则α∥βD ．若m ⊥α，n ⊥α，则m ∥n4．(xx·汕头市质检)设l ，m 是两条不同直线，α，β是两个不同平面，则下列命题中正确的是( )A ．若l ∥α，α∩β＝m ，则l ∥mB ．若l ∥α，m ⊥l ，则m ⊥αC ．若l ∥α，m ∥α，则l ∥mD ．若l ⊥α，l ∥β，则α⊥β5．(xx·黄冈中学检测)设α、β是两个不同的平面，l 、m 为两条不同的直线，命题p ：若平面α∥β，l ⊂α，m ⊂β，则l ∥m ；命题q ：l ∥α，m ⊥l ，m ⊂β，则β⊥α，则下列命题为真命题的是( )A ．p 或qB ．p 且qC ．綈p 或qD ．p 且綈q6．(xx·山西省三诊)已知a ，b ，c 是三条不同的直线，命题“a ∥b 且a ⊥c ⇒b ⊥c ”是真命题，如果把a ，b ，c 中的两个或三个换成平面，在所得的命题中，真命题有( )A ．1个B ．2个C ．3个D ．4个7．(xx·山东省实验中学三诊)对于不重合的两个平面α与β，给定下列条件：①存在平面γ，使得α、β都垂直于γ；②存在平面γ，使得α、β都平行于γ；③α内有不共线的三点到β的距离相等；④存在异面直线l 、m ，使得l ∥α，l ∥β，m ∥α，m ∥β，其中，可以判定α与β平行的条件有( )A ．1个B ．2个C ．3个D ．4个 8．(xx·青岛模拟)如图所示，在棱长为1的正方体ABCD －A 1B 1C 1D 1中，点E ，F 分别是棱BC ，CC 1的中点，P 是侧面BCC 1B 1内一点，若A 1P ∥平面AEF ，则线段A 1P 长度的取值范围是( )A.⎣⎢⎡⎦⎥⎤1，52B.⎣⎢⎡⎦⎥⎤324，52 C.⎣⎢⎡⎦⎥⎤52，2 D ．[2，3]9．(xx·眉山市一诊)如图，圆O 为三棱锥P －ABC 的底面ABC 的外接圆，AC 是圆O 的直径，PA ⊥BC ，点M 是线段PA 的中点．(1)求证：BC ⊥PB ；(2)设PA ⊥AC ，PA ＝AC ＝2，AB ＝1，求三棱锥P －MBC 的体积； (3)在△ABC 内是否存在点N ，使得MN ∥平面PBC ？请证明你的结论．参考答案第七章立体几何考点21 空间几何体的结构、三视图、几何体的表面积与体积【两年高考真题演练】1．C [由三视图可知该几何体是由棱长为2 cm 的正方体与底面为边长为2 cm 正方形、高为2 cm 的四棱锥组成，V ＝V 正方体＋V 四棱锥＝8 cm 3＋83 cm 3＝323cm 3.故选C.]2．D [由三视图可知原几何体为半圆柱，底面半径为1，高为2，则表面积为：S ＝2×12π×12＋12×2π×1×2＋2×2＝π＋2π＋4＝4＋3π.]3．B [由题意知：米堆的底面半径为163(尺)，体积V ＝13×14πR 2·h ＝3209(立方尺)．所以堆放的米大约为3209×1.62≈22(斛)．]4．B [该几何体由一个圆柱和一个从轴截面截开的“半圆锥”组成，其体积为V ＝π×12×2＋12×13π×12×1＝2π＋π6＝136π.]5．B [由题知，该几何体的三视图为一个三角形，两个四边形，分析可知该几何体为三棱柱，故选B.]6．D [正四棱柱的外接球的球心为上下底面的中心连线的中点，所以球的半径r ＝⎝ ⎛⎭⎪⎫222＋⎝ ⎛⎭⎪⎫222＝1，球的体积V ＝4π3r 3＝4π3.故选D.] 7.7 [设新的底面半径为r ，由题意得13πr 2·4＋πr 2·8＝13π×52×4＋π×22×8，解得r ＝7.]8.124[由题意知还原后的几何体是一个直放的三棱柱，三棱柱的底面是直角边长为1的等腰直角三角形，高为1的直三棱柱，∵VP －A 1MN ＝VA 1－PMN ，又∵AA 1∥平面PMN ，∴VA 1－PMN ＝V A －PMN ， ∴V A －PMN ＝13×12×1×12×12＝124，故VP －A 1MN ＝124.]【一年模拟试题精练】1．D [满足条件的四棱锥的底面为矩形，且一条侧棱与底面垂直，如图所示，易知该四棱锥四个侧面均为直角三角形．]2．C [由题意知，俯视图的长度和宽度相等，故C 不可能．] 3．C [选项A ，B ，D 中的俯视图，正方形内的线应该为另一条对角线，当四棱锥的直观图为右图时，它的三视图是C.]4．D [VD 1－B 1C 1E ＝13S △B 1C 1E ·D 1C 1＝13×12×1×1×1＝16.]5．C [由三视图知该几何体是由一个圆锥和一个圆柱组成，由条件得：2πa ＋3π＝9π，解得a ＝3.]6.C [该多面体的直观图为底面为直角三角形，一条棱垂直于底边的三棱锥，其直观图如图所示，故该多面体最长的棱为CD ＝AD 2＋AC 2＝5 2.]7．B [设O 为球的球心，O 1为△ABC 外接圆的圆心，连接OO 1得OO 1＝12PA ＝3，AO 1＝23×32×3＝3，故R ＝OO 21＋AO 21＝2 3. 因此该球的体积为43πR 3＝323π.]8．D [由题意可知，该几何体为一直六棱柱，∴底面六边形的面积可以看成一个矩形与两个等腰直角三角形的面积和，即S ＝1×2＋12×2×1×2＝4， ∴V ＝Sh ＝4.]9．A [其直观图为三棱锥，如图所示AE ⊥面BCD ，BE ＝ED ＝1，EC ＝AE ＝2，AD ＝DC ＝AB ＝BC ＝5，AC ＝22，故其全面积为S △ABD ＋S △BCD ＋S △ABC ＋S △ADC ＝4＋2 6.]考点22 平行关系【两年高考真题演练】1．解 (1)交线围成的正方形EHGF 如图：(2)作EM ⊥AB ，垂足为M ，则AM ＝A 1E ＝4，EB 1＝12，EM ＝AA 1＝8. 因为EHGF 为正方形，所以EH ＝EF ＝BC ＝10.于是MH ＝EH 2－EM 2＝6，AH ＝10，HB ＝6. 因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为97(79也正确)．2．(1)解点F ，G ，H 的位置如图所示． (2)证明平面BEG ∥平面ACH ，证明如下：因为ABCD －EFGH 为正方体，所以BC ∥FG ，BC ＝FG ，又FG ∥EH ，FG ＝EH ，所以BC ∥EH ，BC ＝EH ，于是BCHE 为平行四边形，所以BE ∥CH ，又CH ⊂平面ACH ，BE ⊄平面ACH ，所以BE ∥平面ACH ，同理BG ∥平面ACH ，又BE ∩BG ＝B ，所以平面BEG ∥平面ACH . (3)证明连接FH ，因为ABCD －EFGH 为正方体，所以DH ⊥平面EFGH ，因为EG ⊂平面EFGH ，所以DH ⊥EG ，又EG ⊥FH ，EG ∩FH ＝O ，所以EG ⊥平面BFHD ，又DF ⊂平面BFHD ，所以DF ⊥EG ，同理DF ⊥BG ，又EG ∩BG ＝G ，所以DF ⊥平面BEG . 3.(1)证明在三棱柱ABC －A 1B 1C 1中，BB 1⊥底面ABC . 所以BB 1⊥AB .又因为AB ⊥BC ，且BC ∩BB 1＝B ，BC ，BB 1⊂面B 1BCC 1，所以AB ⊥平面B 1BCC 1. 又AB ⊂面ABE ，所以平面ABE ⊥平面B 1BCC 1.(2)证明取AB 中点G ，连接EG ，FG . 因为E ，F 分别是A 1C 1，BC 的中点，所以FG ∥AC ，且FG ＝12AC .因为AC ∥A 1C 1，且AC ＝A 1C 1，所以FG ∥EC 1，且FG ＝EC 1.所以四边形FGEC 1为平行四边形．所以C 1F ∥EG . 又因为EG ⊂平面ABE ，C 1F ⊄平面ABE ，所以C 1F ∥平面ABE .(3)解因为AA 1＝AC ＝2，BC ＝1，AB ⊥BC ，所以AB ＝AC 2－BC 2＝ 3. 所以三棱锥E －ABC 的体积V ＝13S △ABC ·AA 1＝13×12×3×1×2＝33. 【一年模拟试题精练】1．证明 (1)连接AC ，交BD 于点O ，连接PO . 因为四边形ABCD 为菱形，所以BD ⊥AC又因为PB ＝PD ，O 为BD 的中点，所以BD ⊥PO ，又因为AC ∩PO ＝O ，所以BD ⊥平面APC ，又因为PC ⊂平面APC ，所以BD ⊥PC . (2)因为四边形ABCD 为菱形，所以BC ∥AD ，因为AD ⊂平面PAD ，BC ⊄平面PAD . 所以BC ∥平面PAD ，又因为BC ⊂平面PBC ，平面PBC ∩平面PAD ＝l . 所以BC ∥l .2．(1)证明取CE 中点P ，连接FP ，BP ， ∵F 为CD 的中点，∴FP 綉12DE ，又AB 綉12DE ，∴AB 綉FP ，∴ABPF 为平行四边形，∴AF ∥BP ，又∵AF ⊄平面BCE ，BP ⊂平面BCE ，∴AF ∥平面BCE .(2)解 S ABED ＝3，S △ACD ＝3，S △CDE ＝2，S △ABC ＝1，S △BCE ＝6，S 全＝6＋3＋ 6. 3．(1)证明 ∵平面PCD ⊥平面ABCD ，平面PCD ∩平面ABCD ＝CD ，AC ⊥CD ，AC ⊂平面ABCD ，∴AC ⊥平面PCD ，∵PD ⊂平面PCD ，∴AC ⊥PD .(2)解线段PA 上，存在点E ，使BE ∥平面PCD ，∵AD ＝3，∴在△PAD 中，存在EF ∥AD (E ，F 分别在AP ，PD 上)，且使EF ＝1，又∵BC ∥AD ， ∴BC ∥EF ，且BC ＝EF ， ∴四边形BCFE 是平行四边形，∴BE ∥CF ，BE ⊄平面PCD ，CF ⊂平面PCD ， ∴BE ∥平面PCD ，∵EF ＝1，AD ＝3，∴EF AD ＝PE PA ＝13. 4．解 (1)连接A 1B ，A 1B ∩AB 1＝E ，连接D 1E ，若BC 1∥面AB 1D 1，则BC 1∥D 1E ，∵AE ＝B 1E ， ∴A 1D 1＝D 1C 1，故A 1D 1D 1C 1＝1. (2)∵面BC 1D ∥面AB 1D 1，面A 1BC 1∩面AB 1D 1＝D 1E ， ∴BC 1∥ED 1，又∵A 1E ＝EB ，∴A 1D 1＝D 1C 1，∵面BC 1D ∥面AB 1D 1，AD 1C ⊂面ACC 1A 1，DC 1⊂面ACC 1A ，∴AD 1∥DC 1，∴AD ＝D 1C 1，故AD ＝DC ，因此AD DC＝1.考点23 垂直关系【两年高考真题演练】1．(1)证明因为四边形ABCD 为菱形，所以AC ⊥BD . 因为BE ⊥平面ABCD ，所以AC ⊥BE . 故AC ⊥平面BED .又AC ⊂平面AEC ，所以平面AEC ⊥平面BED .(2)解设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，可得AG ＝GC ＝32x ，GB ＝GD ＝x 2. 因为AE ⊥EC ，所以在Rt △AEC 中，可得EG ＝32x . 由BE ⊥平面ABCD ，知△EBG 为直角三角形，可得BE ＝22x . 由已知得，三棱锥E －ACD 的体积V E －ACD ＝13×12AC ·GD ·BE ＝624x 3＝63.故x ＝2.从而可得AE ＝EC ＝ED ＝ 6.所以△EAC 的面积为3，△EAD 的面积与△ECD 的面积均为 5. 故三棱锥E －ACD 的侧面积为3＋2 5. 2.证明 (1)由题意知，E 为B 1C 的中点，又D 为AB 1的中点，因此DE ∥AC . 又因为DE ⊄平面AA 1C 1C ，AC ⊂平面AA 1C 1C ，所以DE ∥平面AA 1C 1C .(2)因为棱柱ABC －A 1B 1C 1是直三棱柱，所以CC 1⊥平面ABC .因为AC ⊂平面ABC ，所以AC ⊥CC 1.又因为AC ⊥BC ，CC 1⊂平面BCC 1B 1，BC ⊂平面BCC 1B 1，BC ∩CC 1＝C ，所以AC ⊥平面BCC 1B 1. 又因为BC 1⊂平面BCC 1B 1，所以BC 1⊥AC . 因为BC ＝CC 1，所以矩形BCC 1B 1是正方形，因此BC 1⊥B 1C .因为AC ，B 1C ⊂平面B 1AC ，AC ∩B 1C ＝C ，所以BC 1⊥平面B 1AC . 又因为AB 1⊂平面B 1AC ，所以BC 1⊥AB 1. 3.(1)证明如图，因为四边形ABCD 为菱形，O 为菱形中心，连接OB ，则AO ⊥OB .因∠BAD ＝π3，故OB ＝AB ·sin∠OAB ＝2sin π6＝1，又因BM ＝12，且∠OBM ＝π3，在△OBM 中，OM 2＝OB 2＋BM 2－2OB ·BM ·cos∠OBM＝12＋⎝ ⎛⎭⎪⎫122－2×1×12×cos π3＝34. 所以OB 2＝OM 2＋BM 2，故OM ⊥BM .又PO ⊥底面ABCD ，所以PO ⊥BC .从而BC 与平面POM 内两条相交直线OM ，PO 都垂直，所以BC ⊥平面POM .(2)解由(1)可得，OA ＝AB ·cos∠OAB ＝2×cos π6＝ 3.设PO ＝a ，由PO ⊥底面ABCD 知，△POA 为直角三角形，故PA 2＝PO 2＋OA 2＝a 2＋3.由△POM 也是直角三角形，故PM 2＝PO 2＋OM 2＝a 2＋34.连接AM ，在△ABM 中，AM 2＝AB 2＋BM 2－2AB ·BM ·cos ∠ABM ＝22＋(12)2－2×2×12×cos2π3＝214. 由已知MP ⊥AP ，故△APM 为直角三角形，则PA 2＋PM 2＝AM 2，即a 2＋3＋a 2＋34＝214，得a ＝32，a ＝－32(舍去)，即PO ＝32. 此时S 四边形ABMO ＝S △AOB ＋S △OMB ＝12·AO ·OB ＋12·BM ·OM ＝12×3×1＋12×12×32＝538.所以四棱锥P －ABMO 的体积V P －ABMO ＝13·S 四边形ABMO ·PO ＝13×538×32＝516.4．法一 (1)证明 ∵AB ⊥平面BCD ，CD ⊂平面BCD ， ∴AB ⊥CD .又∵CD ⊥BD ，AB ∩BD ＝B ，AB ⊂平面ABD ，BD ⊂平面ABD ， ∴CD ⊥平面ABD .(2)解由AB ⊥平面BCD ，得AB ⊥BD ， ∵AB ＝BD ＝1，∴S △ABD ＝12.∵M 是AD 的中点， ∴S △ABM ＝12S △ABD ＝14.由(1)知，CD ⊥平面ABD ， ∴三棱锥C －ABM 的高h ＝CD ＝1，因此三棱锥A －MBC 的体积V A －MBC ＝V C －ABM ＝13S △ABM ·h ＝112.法二 (1)同法一．(2)解由AB ⊥平面BCD 知，平面ABD ⊥平面BCD ，又平面ABD ∩平面BCD ＝BD ，如图，过点M 作MN ⊥BD 交BD 于点N ，则MN ⊥平面BCD ，且MN ＝12AB ＝12，又CD ⊥BD ，BD ＝CD ＝1， ∴S △BCD ＝12.∴三棱锥A －MBC 的体积V A －MBC ＝V A －BCD －V M －BCD＝13AB ·S △BCD －13MN ·S △BCD ＝112. 【一年模拟试题精练】 1．(1)证明取BC 的中点为F ，连接AF ，EF ，BD ， ∵△BCE 为正三角形，∴EF ⊥BC ，又平面ABC ⊥平面BCE ，且交线为BC ，∴EF ⊥平面ABC ，又AD ⊥平面ABC ，∴AD ∥EF ，∴D ，A ，F ，E 共面，又易知在正三角形ABC 中，AF ⊥BC ，AF ∩EF ＝F ， ∴BC ⊥平面DAFE ，又DE ⊂平面DAFE ，故DE ⊥BC .(2)解由(1)知EF ∥AD ，所以有V D －ABE ＝V E －DAB ＝V F －DAB ＝V D －ABF ，所以S △ABF ＝12BF ·AF ＝32，所以V D －ABF ＝13S △ABF ·AD ＝1，即V D －ABE ＝1.2．(1)证明 ∵∠BAD ＝60°，菱形的边长为6，∴OM ＝OD ＝3，∵DM ＝32，∴∠DOM ＝90°，OD ⊥OM ，又∵折叠前四边形ABCD 是菱形，∴OD ⊥AC . ∵OM ∩AC ＝O ，∴OD ⊥平面ABC . ∵OD ⊂平面MDO ，∴平面ABC ⊥平面MDO . (2)解 ∵V M －ABD ＝V D －ABM ，由(1)知OD ⊥平面ABC ， ∴OD ＝3为三棱锥D －ABM 的高．S △ABM ＝12BA ×BM ×sin 120°＝12×6×3×32＝932， ∴V ＝13S △ABM ×OD ＝932.3．(1)证明在菱形ABEF 中，因为∠ABE ＝60°，所以△AEF 是等边三角形，又H 是线段EF 的中点，所以AH ⊥EF ⇒AH ⊥AB ，因为平面ABEF ⊥平面ABCD ，所以AH ⊥平面ABCD ，所以AH ⊥BC ，在直角梯形ABCD 中，AB ＝2AD ＝2CD ＝4，∠BAD ＝∠CDA ＝90°，得到：AC ＝BC ＝22，从而AC 2＋BC 2＝AB 2，所以AC ⊥CB ；所以CB ⊥平面AHC ，又BC ⊂平面BCE ，所以平面AHC ⊥平面BCE .(2)解多面体ABCDFE 可拆分成一个四棱锥C －ABEF 和一个三棱锥D －AFC ，由题可知AD ⊥平面ABEF ，且CD ∥平面ABEF ，∴点C 到平面ABEF 的距离d ＝AD ＝2.∴V C －ABEF ＝13·AD ·S ABEF ＝13×2×2S △ABE ＝13×2×2×12×AB ·BE ·sin 60°＝1633，又V D －AFC ＝V F －ADC ，∵EF ∥平面ABCD ，∴点F 到平面ACD 的距离d ＝AH ＝23，S △ADC ＝12AD ·DC ＝12×2×2＝2，∴V D －AFC ＝13×AH ·S △ADC ＝433，∴多面体ABCDFE 的体积为1633＋433＝2033.4．(1)证明因为ABCD －A 1B 1C 1D 1是棱柱，所以平面ABCD ∥平面A 1B 1C 1D 1. 又因为平面ABCD ∩平面A 1ECF ＝EC ，平面A 1B 1C 1D 1∩平面A 1ECF ＝A 1F ，所以A 1F ∥CE .又A 1F ⊄平面B 1CE ，CE ⊂平面B 1CE ，所以A 1F ∥平面B 1CE . (2)证明在四边形ABCD 中，因为∠BAD ＝90°，AD ∥BC ，且AD ＝2BC ，AD ＝2，AB ＝1，所以AC 2＝12＋12＝2，CD 2＝12＋12＝2. 所以AC 2＋CD 2＝AD 2，所以∠ACD ＝90°，即AC ⊥CD . 因为A 1A ⊥平面ABCD ，AC ⊂平面ABCD ，所以A 1A ⊥AC .因为在四棱柱ABCD －A 1B 1C 1D 1中，A 1A ∥C 1C ，所以C 1C ⊥AC .又因为CD ，C 1C ⊂平面CDD 1C 1，CD ∩C 1C ＝C ，所以AC ⊥平面CDD 1C 1.(3)解三棱锥B 1－A 1EF 的体积的取值范围是⎣⎢⎡⎦⎥⎤13，23.考点24 立体几何综合问题【两年高考真题演练】1．B [m 垂直于平面α，当l ⊂α时，也满足l ⊥m ，但直线l 与平面α不平行，∴充分性不成立，反之，l ∥α，一定有l ⊥m ，必要性成立．故选B.]2．D [对于A ，α，β垂直于同一平面，α，β关系不确定，A 错；对于B ，m ，n 平行于同一平面，m ，n 关系不确定，可平行、相交、异面，故B 错；对于C ，α，β不平行，但α内能找出平行于β的直线，如α中平行于α，β交线的直线平行于β，故C 错；对于D ，若假设m ，n 垂直于同一平面，则m ∥n ，其逆否命题即为D 选项，故D 正确．]3．C [如图，要使三棱锥O －ABC 即C －OAB 的体积最大，当且仅当点C 到平面OAB 的距离，即三棱锥C －OAB 底面OAB 上的高最大，其最大值为球O 的半径R ，则V O －ABC 最大＝V C －OAB 最大＝13×12S △OAB ×R ＝13×12×R 2×R ＝16R 3＝36，所以R ＝6，得S 球O ＝4πR 2＝4π×62＝144π，选C.]4．B [对于选项A ，若m ∥α，n ∥α，则m 与n 可能相交、平行或异面，A 错误；显然选项B 正确；对于选项C ，若m ⊥α，m ⊥n ，则n ⊂α或n ∥α，C 错误；对于选项D ，若m ∥α，m ⊥n ，则n ∥α或n ⊂α或n 与α相交．D 错误．故选B.]5.(1)解由题设AB ＝1，AC ＝2，∠BAC ＝60°，可得S △ABC ＝12·AB ·AC ·sin 60°＝32. 由PA ⊥平面ABC ，可知PA 是三棱锥P ABC 的高，又PA ＝1. 所以三棱锥P ABC 的体积V ＝13·S △ABC ·PA ＝36. (2)证明在平面ABC 内，过点B 作BN ⊥AC ，垂足为N ，在平面PAC 内，过点N 作MN ∥PA 交PC 于点M ，连接BM .由PA ⊥平面ABC 知PA ⊥AC ，所以MN ⊥AC .由于BN ∩MN ＝N ，故AC ⊥平面MBN ，又BM ⊂平面MBN ，所以AC ⊥BM .在Rt △BAN 中，AN ＝AB ·cos∠BAC ＝12，从而NC ＝AC －AN ＝32，由MN ∥PA ，得PM MC ＝AN NC ＝13. 6．(1)证明因为四边形ABB 1A 1和ACC 1A 1都是矩形，所以AA 1⊥AB ，AA 1⊥AC .因为AB ，AC 为平面ABC 内两条相交直线，所以AA 1⊥平面ABC .因为直线BC ⊂平面ABC ，所以AA 1⊥BC .又由已知，AC ⊥BC ，AA 1，AC 为平面ACC 1A 1内两条相交直线，所以BC ⊥平面ACC 1A 1.(2)解取线段AB 的中点M ，连接A 1M ，MC ，A 1C ，AC 1，设O 为A 1C ，AC 1的交点．由已知可知，O 为AC 1的中点．连接MD ，OE ，则MD ，OE 分别为△ABC ，△ACC 1的中位线，所以，MD 綉12AC ， OE 綉12AC ，因此MD 綉OE .连接OM ，从而四边形MDEO 为平行四边形，则DE ∥MO .因为直线DE ⊄平面A 1MC ，MO ⊂平面A 1MC ，所以直线DE ∥平面A 1MC .即线段AB 上存在一点M (线段AB 的中点)，使直线DE ∥平面A 1MC .【一年模拟试题精练】1．C [选项A 、B 、D 均存在m ⊂α的情形，排除A 、B 、D ，故选C.]2．D [对于D ，一个等腰三角形的底放在桌面上，两个腰与桌面所成的角相等，但两腰所在直线平行．]3．D [对于选项A ：若m ∥α，n ∥α，则m ，n 平行、相交、异面都有可能；对于选项B ：若m ∥α，m ∥β，则α，β可能平行、可能相交；对于选项C ：若α⊥γ，β⊥γ，则α，β可能平行、可能相交；所以选项A 、B 、C 都不正确．]4．D [对于A ：l 与m 可能异面，排除A ；对于B ：m 与α可能平行或相交，排除B ；对于C ：l 与m 可能相交或异面，排除C ；故选D.]5．C [命题p ：l 和m 可能平行也可能异面，故p 为假命题；命题q ：α和β可能平行也可能相交，故q 为假命题，因此p 或q 为假，p 且q 为假，綈p 或q 为真，p 且綈q 为假．]6．C [根据题意，可构成四个命题：①面α∥面β，且面α⊥面γ，则面β⊥面γ；②直线a ∥面β，且a ⊥面γ，则面β⊥面γ；③面α∥面β，且面α⊥直线c ，则面β⊥直线c ；④面α∥直线b ，且面α⊥面γ，则直线b ⊥面γ，可知①②③为真命题，④中直线b 与平面γ位置关系不确定，为假命题．]7．B [对于①：正方体的一个角的三个平面就是反例，故①错误；对于②：平面平行判定定理的推论，故②正确；对于③：可能两平面相交，三点分别在两侧，故③错误；对于④：过P 上任一点P 可做m 的平行线m ′，则l 与m ′相交，满足平面平行的判定定理，故④正确．]8．B [取B 1C 1的中点M ，BB 1的中点N ，连接A 1M ，A 1N ，MN ，可以证明平面A 1MN ∥平面AEF ，所以点P 位于线段MN 上，因为A 1M ＝A 1N ＝1＋⎝ ⎛⎭⎪⎫122＝52，MN ＝⎝ ⎛⎭⎪⎫122＋⎝ ⎛⎭⎪⎫122＝22，所以当点P 位于M ，N 处时，A 1P 最大，当P 位于MN 的中点O 时，A 1P 最小，此时A 1O ＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫242＝324，所以A 1O ≤A 1P ≤A 1M ，即324≤A 1P ≤52，所以线段A 1P 长度的取值范围是⎣⎢⎡⎦⎥⎤324，52，选B.] 9．(1)证明如图，因为，AC 是圆O 的直径，所以BC ⊥AB ，因为，BC ⊥PA ，又PA 、AB ⊂平面PAB ，且PA ∩AB ＝A ，所以，BC ⊥平面PAB ，又PB ⊂平面PAB ，所以，BC ⊥PB ，(2)解如图，在Rt △ABC 中，AC ＝2，AB ＝1，所以，BC ＝3，因此，S △ABC ＝32，因为PA ⊥BC ，PA ⊥AC ，所以PA ⊥平面ABC ，所以，V P －MBC ＝V P －ABC －V M －ABC ＝13×32×2－13×32×1＝36. (3)解如图，取AB 的中点D ，连接OD 、MD 、OM ，则N 为线段OD (除端点O 、D 外)上任意一点即可，理由如下：因为，M、O、D分别是PA、AC、AB的中点，所以，MD∥PB，MO∥PC，因为，MD⊄平面PBC，PB⊂平面PBC，所以，MD∥平面PBC，同理可得，MO∥平面PBC，因为，MD、MO⊂平面MDO，MD∩MO＝M，所以，平面MDO∥平面PBC，因为，MN⊂平面MDO.故，MN∥平面PBC.。

2019-2020年高考数学大题综合练习(一)(含答案)

2019-2020年高考数学大题综合练习（一）1.在△ABC 中，已知2510,?510cosA sinB == （1）求证: △ABC 的内角B 是锐角;（2）若△ABC 的最短边的长等于5，求△ABC 的面积.【解析】（1）由于11010sin ≠=B ，则B 不是直角。

假设B 为钝角，由于1010sin =B ，则31tan -=B 。

又由552cos =A 求得21tan =A ，则71)(1tan tan 1tan tan )tan(21312131=--+-=-+=+B A B A B A ，则71)tan(tan -=--=B A C π,则角C 也是钝角，这与B 为钝角的假设相矛盾，于是假设不成立. 综上，ABC ∆的内角B 是锐角（2）由于552cos =A ，则21tan =A .由于1010sin =B 且B 为锐角，则31tan =B .于是，11tan tan 1tan tan )tan(tan 21312131-=⋅-+-=-+-=+-=B A B A B A C ，则︒>︒=90135C 10sin sin 5,sin sin 5==∴=∴BABC A BC B B 最小，据正弦定理得角252251021sin 21=⨯⨯⨯=⋅⋅=∴∆C CA CB S ABC2.如图，四棱锥S -ABCD 中，SD ⊥底面ABCD ，//AB DC ,AD DC ⊥,1AB AD ==，2DC SD ==，E 为棱SB 上的一点，平面EDC ⊥平面SBC . （1）证明：2SE EB =；（2）求二面角A DE C --的大小.【解析】以D 为坐标原点，射线DA ，DC ，DS 分别为x 轴，y 轴，z 轴，建立直角坐标系Dxyz ，设()1,0,0A =，则()1,1,0B ，()0,2,0C ，()0,0,2S .（1）证明：()0,2,2SC =-，()1,1,0BC =-，设平面SBC 的法向量为(),,n a b c =，由n SC ⊥，n BC ⊥，得到0n SC ⋅=，0n BC ⋅=，故0b c -=，0a b -+=，取1a b c ===，则()1,1,1n =，又设()0SE EB λλ=>，则2,,111E λλλλλ⎛⎫ ⎪+++⎝⎭，2,,111DE λλλλλ⎛⎫= ⎪+++⎝⎭,()0,2,0DC = 设平面CDE 的法向量为(),,m x y z =，由m DE ⊥，m DC ⊥，得到0m DE ⋅=，0m DC ⋅=，故20111x y zλλλλλ++=+++，20y =，令2x =，则()2,0,m λ=-，由平面DEC ⊥平面SBC ，得到m n ⊥，所以0m n ⋅=，20λ-=，2λ=，故2SE EB =. （2）解：由（1）知222,,333DE ⎛⎫=⎪⎝⎭，取DE 的中点F ，则111,,333F ⎛⎫= ⎪⎝⎭，211,,333FA ⎛⎫=-- ⎪⎝⎭，故0FA DE ⋅=，FA DE ⊥，又242,,333EC ⎛⎫=-- ⎪⎝⎭，故EC DE ⊥，因此向量FA 与EC 的夹角等于二面角A DE C --的平面角，于是 ()1cos ,2FA ECFA EC FA EC⋅==-，所以二面角A DE C --的大小为120.3.已知数列{a n }，{b n }满足12a =，121n n n a a a +=+，1n n b a =-，0n b ≠．（1）求证：数列1n b ⎧⎫⎨⎬⎩⎭是等差数列，并求数列{a n }的通项公式；（2）令12n nn c b =，求数列{c n }的前n 项和T n ．【解析】（1）∵1n n b a =-，∴1n n a b =+，由121n n n a a a +=+， ∴12(1)1(1)(1)n n n b b b ++=+++，化简得11n n n n b b b b ++-=， ∵0n b ≠，∴+1111n n n n n n b b b b b b ++-=，即+1111n nb b -=（*n N ∈），而111111121b a ===--， ∴数列1n b ⎧⎫⎨⎬⎩⎭是以1为首项，1为公差的等差数列． ∴11(1)1n n n b =+-⨯=，即1(*)n b n N n =∈，∴111n n a n n+=+=（*n N ∈）．（2）由（1）知，2n n n c =，∴1212222n n n T =+++…，∴2311122222n n n T +=+++…，两式相减得，1211111(1)111122211222222212n n n n n n n n n T +++-+=+++-=-=--…，故222n nn T +=-．4. 按照我国《机动车交通事故责任强制保险条例》规定，交强险是车主必须为机动车购买的险种，若普通7座以下私家车投保交强险第一年的费用（基准保费）统一为a 元，在下一年续保时，实行的是保费浮动机制，保费与上一、二、三个年度车辆发生道路交通事故的情况相关联，发生交通事故的次数越多，费率也就越高，具体浮动情況如表：交强险浮动因素和浮动费率比率表的该品牌同型号私家车在下一年续保时的情况，统计得到了下面的表格：（1）某家庭有一辆该品牌车且车龄刚满三年，记X 为该车在第四年续保时的费用，求X 的分布列；（2）某销售商专门销售这一品牌的二手车，且将下一年的交强险保费高于基准保费的车辆记为事故车.①若该销售商购进三辆车（车龄已满三年）该品牌二手车，求这三辆车中至少有2辆事故车的概率；②假设购进一辆事故车亏损4000元，一辆非事故车盈利800元.若该销售商一次购进100辆(车龄已满三年）该品牌二手车，求其获得利润的期望值.【解析】（1）由题意可知X 的可能取值为0.9,0.8,0.7,,1.1,1.3a a a a a a . 由统计数据可知：()10.94P X a ==，()10.88P X a ==，()10.78P X a ==，()14P X a ==， ()31.116P X a ==，()11.316P X a ==. 所以X 的分布列为:（2）①由统计数据可知任意一辆该品牌车龄已满三年的二手车为事故车的概率为4，三辆车中至少有2辆事故车的概率为321311351144432P C ⎡⎤⎛⎫⎛⎫=--+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦. ②设Y 为该销售商购进并销售一辆二手车的利润，Y 的可能取值为4000-，8000. 所以的分布列为：所以()1340008000500044E Y =-⨯+⨯=，所以该销售商一次购进100辆该品牌车龄已满三年的二手车获得利润的期望为()10050E Y ⨯=万元.5.在平面直角坐标系中，点F 1、F 2分别为双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点，双曲线C 的离心率为2，点3(1,)2在双曲线C 上.不在x 轴上的动点P 与动点Q 关于原点O 对称，且四边形12PF QF 的周长为（1）求动点P 的轨迹方程；（2）在动点P 的轨迹上有两个不同的点1122(,)(,)M x y N x y 、，线段MN 的中点为G ，已知点12(,)x x 在圆222x y +=上，求||||OG MN ⋅的最大值，并判断此时OMN ∆的形状.【解析】（1）设点1F 、2F 分别为(,0),(,0)(0)c c c -> 由已知2ca=，所以2c a =，224c a =，22223b c a a =-= 又因为点3(1,)2在双曲线C 上，所以229141a b-= 则222294b a a b -=，即2249334a a a -=，解得214a =，12a = 所以1c =连接PQ ，因为12,OF OF OP OQ ==，所以四边形12PF QF 为平行四边形因为四边形12PF QF的周长为所以21122PF PF F F +=>=所以动点P 的轨迹是以点1F 、2F 分别为左、右焦点，长轴长为可得动点P 的轨迹方程为：221(0)2x y y +=≠ （2）因为22221=+x x ,,12,1222222121=+=+y x y x 所以12221=+y y所以||||OG MN ⋅=212122212221212122212221222221y y x x y y x x y y x x y y x x +++++--+++==1212121232232213()222x x y y x x y y --+++≤= 等号当仅当21212121223223y y x x y y x x ++=--,即02121=+y y x x 所以ON OM ⊥,即OMN ∆为直角三角形6.已知常数0a >，函数2()ln(1)2xf x ax x =+-+. （1）讨论()f x 在区间(0,+∞)上的单调性；（2）若()f x 存在两个极值点1x ，2x ，且12()()0f x f x +>，求a 的取值范围.【解析】（1）22(2)2'()1(2)a x x f x ax x +-=-++224(1)(*)(1)(2)ax a ax x +-=++，当1a ≥时，'()0f x >，此时()f x 在区间(0,)+∞上单调递增. 当01a <<时，由'()0f x =得1x =2x =-舍去）. 当1(0,)x x ∈时，'()0f x <；当1(,)x x ∈+∞时，'()0f x >. 故()f x 在区间1(0,)x 上单调递减，在区间1(,)x +∞上单调递增. 综上所述，1a ≥时，()f x 在区间(0,)+∞上单调递增；01a <<时，()f x在区间0,⎛ ⎝上单调递减，在区间⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增. （2）由(*)式知，当1a ≥时，'()0f x >，此时()f x 不存在极值点，因而要使得()f x 有两个极值点，必有01a <<. 又()f x的极值点只可能是1x =2x =-，且由()f x 的定义域可知，1x a>-且2x ≠-，所以1a ->-，2-≠-，解得12a ≠. 此时，由(*)式易知，1x ，2x 分别是()f x 的极小值点和极大值点. 而121()()ln(1)f x f x ax +=+121222ln(1)22x xax x x -++-++ 21212ln[1()]a x x a x x =+++1212121244()2()4x x x x x x x x ++-+++24(1)ln(21)21a a a -=---22ln(21)221a a =-+--. 令21a t -=.由01a <<且12a ≠知，当102a <<时，10t -<<；当112a <<时，01t <<.记22()ln 2g t t t=+-. （i ）当10t -<<时，2()2ln()2g t t t =-+-，所以222222'()0t g t t t t-=-=<，因此，()g t 在区间(1,0)-上单调递减，从而()(1)40g t g <-=-<. 故当102a <<时，12()()0f x f x +<. （ii ）当01t <<时，2()2ln 2g t t t =+-，所以222222'()0t g t t t t-=-=<，因此，()g t 在区间(0,1)上单调递减，从而()(1)0g t g >=. 故当112a <<时，12()()0f x f x +>. 综上所述，满足条件的a 的取值范围为1,12⎛⎫⎪⎝⎭.。

2019-2020年高考数学大一轮复习第七章立体几何单元质量检测理新人教A版

一、选择题（每小题4分，共40分） 1.以下关于几何体的三视图的叙述中，正确的是（）A. 球的三视图总是三个全等的圆B. 正方体的三视图总是三个全等的正方形C. 水平放置的各面均为正三角形的四面体的三视图都是正三角形D. 水平放置的圆台的俯视图是一个圆解析：画几何体的三视图要考虑视角，但对于球无论选择怎样的视角，其三视图总是三个全等的圆.答案：A2.用与球心距离为1的平面去截球，所得的截面面积为n ，则球的体积为（）8 n A.3B 呼解析：S 圆=n r 2 = n ? r = 1,而截面圆圆心与球心的距离 ,r 2 + d 2= ,2.所以 V = 4 n R 3= 8 f 冗，故选 B. 答案：B 3.设a 、B 、Y 是三个互不重合的平面， m n 是两条不重合的直线，下列命题中正确的是（）A. 若 a 丄B, B 丄丫，贝V a 丄丫B. 若 m 〃a, n 〃B, a 丄B ，贝U ml nC. 若 a 丄 B , ml a ,贝y m/ BD. 若 a / B ,m? B , m//a ,贝U m // B解析：对于A ,若a 丄B , B 丄Y , a , 丫可以平行，也可以相交， A 错；对于B ,若m // a , n //B , a 丄B ，贝y m n 可以平行，可以相交，也可以异面， B 错；对于C ,若a 丄 B , ml a ,贝U m 可以在平面 B 内，C 错；易知D 正确.答案：D 4.一个C. 8 2 nD.32 nd = 1,所以球的半径为R =C.47D.23棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图所示，则该几何体的体积为（）22A. 7B.y解析：依题意可知该几何体的直观图如图所示，其体积为答案：D5.已知直四棱柱 ABC —ABCD 中，底面 ABC ［为正方形，AA = 2AB E 为AA 的中点,则异面直线BE 与CD 所成角的余弦值为解析:设 AA = 2AB= 2,则耳1,1,0) , E (1,0,1) , C (0,1,0) , D (0,0,2),••• BE = (0，- 1,1) , CD = (0，- 1,2), ...cos 〈匪 CD>= 土芍5 =噜答案：C3 1 1 232-2X3x 2X 1X 1X仁百A 迈101 B.5 3 D.5如图，以 D 为坐标原点建立如图所示空间直角坐标系.C.47D .23与BE 所成的角为（）A. n冗 C.T解析：连接AC, BD 交于点Q 连接OE 易得OE/ PA 所以所求角为/ BEO由所给条件易得 OB=¥ , OE=尹心#，BE= 2. 所以 cos / OEB= 2,所以/ OEB= 60°,选 C. 答案：CJF C///BE N\ AM7.如图为棱长是1的正方体的表面展开图，在原正方体中给出下列三个命题：①点M 到AB 的距离为 ¥；②三棱锥C — DNE 的体积是；；③AB 与EF 所成的角是n 2 6 2其中正确命题的个数是（）A . 0 B. 1 C. 2 D. 3解析:6.如图所示，正四棱锥P- ABCD 勺底面积为3,体积为-2, E 为侧棱PC 的中点,PA4A .35依题意可作出正方体的直观图如图，显然M 到AB 的距离为1M C=¥，•①正确；而V —DNE11 1=3X 2X 1X 1X仁6，•②正确；AB 与EF 所成的角等于AB 与MC 所成的角,即为正确.答案：D&正△ ABC 与正厶BCD 所在平面垂直，则二面角 L BD — C 的正弦值为（）B.F C-攀解析:取BC 中点0,连接AQDO 建立如图所示坐标系，设BC= 1,则A 0 , 0 ,今,B 0,为平面BCD 勺一个法向量，可进一步求出平面 ABD 的一个法向量 n = （1 , - 3, 1） , • cos〈n , OA =理• sin 〈n , OA =芈.5答案：C9.正三棱柱 ABC-ABC 的棱长都为2, E, F , G 为AB AA , AC 的中点，贝U BF 与平面n••12, 0，•••O A =B D = -2, 2, 0 .由于O A0, 0,NA,0, 0 . 0, 0,苑 0 , 1 ,A E aGEF所成角的正弦值为（）A.3 510.如图，在正四棱柱（底面是正方形的直四棱柱）ABC —ABCD 中，E 、 BG 的中点，则下列结论不成立的是（）A. EF 与BB 垂直B. EF 与BD 垂直C. EF 与CD 异面D. EF 与AC 异面解析：C. 70"D.10解析:如图，取AB 的中点E,建立如图所示空间直角坐标系 E — xyz .则E (0,0,0) B(1,0,2) ，A i ( — 1,0,2) , C (0,乖,2) , G -2 j••• BF= ( — 2,0，— 1) , EF= ( — 1,0,1) , FG= £，1 .设平面GEF 勺一个法向量为n = (x , y , z ),,H —1,0,1),「n • EF =— x + z = 0, 由 T 1 ■ 3n • FG= -x + 斗y + z = 0, L 2 2得#霍= ——3x.令x = 1，则n = （1 ,—寸3, 1）,设BF 与平面GEF 所成角为0，则sin 0 |cos 〈 n , BF >| n • B F | | = —= |n || 論 3 5.答案：AF 分别是AB 、连接BC, AC则BC交BG于F,且F为BC的中点，1又E为AB的中点，所以EF綊g AC而BB丄平面ABCD所以BB丄AC所以BB丄EF, A正确；又ACL BD所以EFL BD B正确；显然EF与CD异面，C正确；1由EF綊g AC AC// A C ,得EF// AQ ,故不成立的选项为 D.答案：D二、填空题（每小题4分，共16分）11 •已知某几何体的三视图如图所示，则该几何体的体积为____________ •解析：由三视图可知：该几何体是一个三棱锥,底面是底边长为 4 3 ,高为2的等腰三角形，棱锥的高为2,故体积为V= 3X 2X4 3X 2X 2=空孝.答案：竽312.已知球与棱长均为2的三棱锥各条棱都相切，则该球的表面积为_______________•解析：* 此R将该三棱锥放入正方体内，若球与三棱锥各棱均相切等价于球与正方体各面均相切，所以2R=叮2 , R= 2 ,则球的表面积为S= 4 n R= 4 n X ? = 2 n .答案：2n13.三棱锥S—ABC中，/ SBA=Z SCA F90°,A ABC是斜边AB= a的等腰直角三角形, 则以下结论中：①异面直线SB与AC所成的角为90°;②直线SBL平面ABC③平面SBCL平面SAC1④点C到平面SAB的距离是2a.其中正确结论的序号是 __________ .解析：由题意知ACL平面SBC故ACL SB SBL平面ABC平面SBCL平面SAC①②③正确；取AB 的中点E连接CE （如图）可证得CE L平面SAB故CE的长度即为C到平面SAB的距1离q a,④正确.答案：①②③④14.如图，在矩形ABCD中 , AB= 3 , BC= 1, EF// BC且AE= 2EB G为BC的中点，K为AF的中点•沿EF将矩形折成120°的二面角A—EF-B,此时KG的长为______________ .解析：如图，过K作KM L EF,垂足M为EF的中点，贝U向量Ml与三的夹角为120° ,〈运M FO =60°.又K G=亦MG=亦FC, ••• R G= R M+ F C+ 2kM- F C= 1 + 1 + 2X 1X 1X cos60°= 3.| K G = \：3.答案：3三、解答题（共4小题，共44分，解答应写出必要的文字说明、计算过程或证明步骤.15. （10分）一个几何体是由圆柱 ADDA 和三棱锥E — ABC 组合而成，点 A , B , C 在圆O 的圆周上，其正（主）视图，侧（左）视图的面积分别为 10和12,如图所示，其中EAL 平面ABC ABL AC ,AB= AC , AE= 2.(1) 求证：AC L BD(2) 求三棱锥E — BCD 勺体积.解：⑴因为EAL 平面ABC AC ?平面ABC 所以 EAL AC 即 ED L AC又因为 AC L AB, ABH ED= A ,所以AC L 平面EBD 因为BD ?平面EBD 所以ACL BD(2)因为点代B, C 在圆O 的圆周上，且 AB 丄AC 所以BC 为圆O 的直径.设圆 O 的半径为 r ,圆柱高为 h ,根据正(主)视图，侧(左)视图的面积可得, 12rh +-r x 2= 10 ,r2r = 2 , { 解得*1 h = 2.2rh +-X2 r x 2= 12. -i 2所以 BC = 4 , AB= AC= 2 2.以下给出求三棱锥 E- BCD 体积的两种方法：方法1:由(1)知，AC L 平面EBD1 所以 V E -BCD = VC- EBD = 3S EBD X CA3因为EAL 平面 ABC AB ?平面ABC 所以 EAL AB 即 ED L AB 其中 ED= EA^ DA= 2+ 2= 4 , 因为 ABL AC AB= AC= 2 2 ,所以 &EBD = 2"ED X AB= |x 4x2 2 = 4 2 , 所以 S E -BCD = 3x4 ,2X2 ,2=學3 3方法2：因为EA!平面 ABCEE A\A图1 1 1V E —BCD = V E — ABc + V D -ABC = 3S A ABC X EA^ —S A ABC X DA= q S x ABC X ED333Sx ABC = 2X AC< AB= 2 X2 2X2 2= 4, 1 16所以 V E —BCD = 3X 4X 4=—.16. （10分）如图，AB= AD / BAD= 90°, M N G 分别是BD BC AB 的中点，将等边△ BC ［沿BD 折叠成△ BC D 的位置，使得 ADL C B(1)求证：平面 GNM 平面 ADC .⑵求证：C A 丄平面ABD证明：(1)因为M N 分别是BD BC 的中点，所以MN/ DC .因为 MN 平面ADC ,DC ?平面ADC ，所以 M /平面 ADC .同理NG/平面 ADC .又因为 MN P NG= N, 所以平面GNM 平面ADC . ⑵因为/ BA = 90°,所以 AD L AB 又因为 AD L C B ,且 ABA C B = B, 所以AD L 平面C' AB因为C' A?平面C AB 所以AD L C A 因为△ BCD 是等边三角形，AB= AD不妨设 AB= 1，贝V BC = CD= BD= 2，可得 C' A = 1. 由勾股定理的逆定理，可得 AB L C' A. 因为ABA AD= A,所以C' A L 平面 ABD所以其中 ED= EA^ DA= 2+ 2= 4,因为A 吐 AC AB = AC = 2頁,所以17. (12分)如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直，AB// CD, ABL BC AB= 2CD= 2BC EAL EB⑴求证：ABL DEEA若不存在，请说明理(3)线段EA上是否存在点F,使EC//平面FBD若存在，求出(2)求直线EC与平面ABE所成角的正弦值;由.解:(1)证明：取AB的中点0,连接EQ D0 因为EB= EA 所以EO L AB因为四边形ABCD^直角梯形.AB= 2CD= 2BC AB丄BC所以四边形OBCD^正方形，所以ABL 0D 因为E6 D0= 0.所以ABL平面EOD所以ABL ED⑵因为平面ABEL平面ABCD且EO L AB 所以EOL平面ABCD所以EO L 0D由0B 0D 0E两两垂直，建立如图所示的空间直角坐标系0—xyz.因为三角形EAB为等腰直角三角形，所以0A= 0B= 0D= 0E设0B= 1,所以00,0,0) , A—1,0,0) , B(1,0,0) , C(1,1,0) , D(0,1,0),日0,0,1)所以E C= (1,1 , —1),平面ABE的一个法向量为6D= (0,1,0)设直线EC与平面ABE所成的角为0 ,〈弐比=LfC•复習，所以sin 0 = |cos即直线EC 与平面ABE 所成角的正弦值为EF 1⑶存在点F ,且EA = 3时，有EC//平面FBD证明如下：由 E F = 1EA = — 3, 0,— 1 ,F — 3, 0, 2，所以 FB = 3, 0, — 3 , BD=( —1,1,0)设平面FBD 勺法向量为v = (a , b , c ),取 a = 1，得 v = (1,1,2).因为 E C- v = (1,1 , — 1) • (1,1,2) = 0, 且EC ?平面FBD 所以EC//平面FBDEF 1即点F 满足寸-时，有EC//平面FBDEA —18. (12分)如图，AB 为圆O 的直径，点E , F 在圆O 上，AB// EF,矩形ABCD 所在的平面与圆O 所在的平面互相垂直.已知 AB= 2, EF = 1.(1) 求证：平面 DAFL 平面 BCF(2) 求直线AB 与平面CBF 所成角的大小；(3) 当AD 的长为何值时，平面 DFC 与平面FCB 所成的锐二面角的大小为 60°?解：(1)证明：•••平面 ABC D 平面 ABEF CBL AB 平面ABC B 平面 ABE = AB CBL 平面 ABEF •/ AF ?平面 ABEF 二 AF 丄 CB又AB 为圆O 的直径，••• AF 丄BF,又BF A CB= B,••• AF 丄平面CBF•/ AF ?平面ADF •平面DAFL 平面CBF (2)由(1)知AF 丄平面CBF• FB 为AB 在平面CBF 内的射影，因此，/ ABF 为直线AB 与平面CBF 所成的角.v • BD )= 0,则有v • FB= 0, £ 7厂 a + b = 0, 所以4 23a —3c = 0••• AB// EF, •••四边形ABEF为等腰梯形,过点F作FHL AB交AB于H已知AB= 2 , EF= 1,贝U AH=笃EF= g在Rt △ AFB中，根据射影定理得A F= AH- AB • AF= 1, sin / ABF= A F= 1, ABF= 30°.•直线AB与平面CBF所成角的大小为30°.⑶设EF中点为G以0为坐标原点，O A O G AD方向分别为x轴、y轴、z轴正方向建立空间直角坐标系(如图).设AD= t(t>0),则点D的坐标为(1,0 , t) , C( —1,0 , t),又A(1,0,0), B(—1,0,0), F 2 , -2 , 0,• 6D= (2,0,0),设平面DCF的法向量为m= (x , y , z),贝U m - 6D= 0 , m - F D= 0.2x= 0+ tz = 0,令z = 3 ,解得x= 0 , y = 2t,• m= (0,2 t, 3).由(1)可知AF丄平面CFB取平面CBF的一个法向量为n2= X F=—~2, 0 ,依题意, n1与n2的夹角为60°.• cos60°n1• n2即! = 一Qt| M • r)2|，2 4t2+ 3 -1，因此，当AD的长为-4时，平面DFC与平面FCB所成的锐二面角的大小为60°.新人教A 版一、选择题1 •圆台的一个底面周长是另一个底面周长的 3倍，母线长为3，圆台的侧面积为 84 n,则圆台较小底面的半径为（）A . 7 B. 6 C. 5D. 3解析：设圆台较小底面半径为 r ，则另一底面半径为 3r . 由 S = n （r + 3r ） • 3= 84 n ，解得 r = 7. 答案：A2 .设一个球的表面积为 S ，它的内接正方体的表面积为 9,则S 的值等于（）2A.—nnD. —解析：设球的半径为 R 其内接正方体的棱长为 a ,则易知R 2= |a 2,即a =则S = 4 n R n =亍6X 竽R j<3丿答案：D3•某几何体的三视图如图所示，则其表面积为（）A . 38+ nB . 38 + 2 n C. 40 + n D . 40 + 2n解析：由三视图可知，该组合体下方是一个长方体，上方是一个半圆柱，所以表面积为 12（4 X 2+ 4X 2+ 2X 2）一 2 + Q X2 n X 1 + n = 38 + 2 n .答案：B6 B.—n4. （xx •陕西卷）已知底面边长为1,侧棱长为，2的正四棱柱的各顶点均在同一个球面上，则该球的体积为（）得到，则切削掉部分的体积与原来毛坯体积的比值为（）17A.27 10解析：由三视图可知切削得到的零件是由两个圆柱组成的一个组合体，一个是底面半径为2,高为4的圆柱，一个是底面半径为 3,高为2的圆柱，于是零件的体积 V = n r^+n r ； h 2= n X2 X 4+n X3 X 2= 34 n ，而原来毛坯的体积 V = n r h = n X3 X 6= 54 n ，所以切A. 32 nB. 4 nC. 2 nD.解析：依题意可知正四棱柱体对角线的长度等于球的直径，可设球半径 R,贝 U 2R =12 + 12 + ：2 2= 2，解得 R= 1，所以 V == ~3~ 3 3答案：D5.把一个周长为12 cm 的长方形围成一个圆柱，当圆柱的体积最大时，该圆柱的底面周长与高之比为（）A . 1 B. C. 2D.71解析: 设底面周长为 x cm ,贝U 2n r = x ，即 r =，高为6- x ，故V = n右 2(6 -1 X )= 47(6X 2-X 3)，则 V 41-(12x — 3x 2)，由 V = 0 得 x = 4.易知当 x = 4 时,4 n圆柱的体积最大，此时圆柱的底面周长是4 cm ，圆柱的高为2 cm ，从而底面周长与高之比为1. 答案：C6. （xx •新课标全国卷n ）如右图，网格纸上正方形小格的边长为 1（表示1 cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为 3 cm ，高为6 cm 的圆柱体毛坯切削V — V 20 n 10削掉部分的体积与原来毛坯体积的比值之比= 亍547 = 27,故选C.答案：C 、填空题7•若一个圆锥的侧面展开图是面积为2n 的半圆面，则该圆锥的体积为 ___________解析：设圆锥底面半径为r ,母线长为I ，高为h ,V 圆锥=3 n XI 2X #3=n .答案：fn& （xx •江苏卷）设甲、乙两个圆柱的底面积分别为的侧面积相等，且|=4，则鲁的值是——-解析：设甲、乙两个圆柱的底面和咼分别为h 1, 「、 h 2；由题意知 2 n r 1h 1 — 2 nr h , h 1 「2 S n 2 r 1 9 r 1 V n r h2 r 1 h 1 2 r 1 「2 r 1 3一，2—，所以=…从血、，=— — 2 2— 2--- ---------2h 2 r 1 S 2r 2 4 r 2 2 V 2n r 2h 2r 2 h 2 r 2n r 2答案:39.已知三棱锥 O- ABC 中，/ BO = 90°, 0A ±平面 BOC 其中 AB= AC =J7, BC =“，O, A, B, C 四点均在球S 的表面上，则球 S 的表面积为 _____________ .解析：易知以O 点为顶点的三条棱两两垂直，则球 S 即为以O 为顶点，以 OA OB OC 为棱的长方体的外接球，所以2R =寸O A + O B + O C =±7 oA + O B+ O C =¥（R 为球 S 的半径），所以R= 4，表面积 S = 4 n R =—.三、解答题10.一个几何体的三视图如图所示•已知正视图是底边长为 1的平行四边形，侧视图是一个长为.3，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形.I = 2,|2= 2n ,S , S,体积分别为V , V 2.若它们答案:25 n正视图侧视图俯视图(1) 求该几何体的体积V；(2) 求该几何体的表面积S.解:(1) 由三视图可知，该几何体是一个平行六面体(如图)，其底面是边长为1的正方形，高为3.所以V= 1 X 1 X ‘寸3 =』3.(2) 由三视图可知，该平行六面体中，AD丄平面ABCD CDL平面BCCB，所以AA= 2, 侧面ABBA, CDDC 均为矩形，所以S= 2X (1 X 1 + 1 X 寸3 + 1X 2) = 6+ R3.11.如图，在直三棱柱ABC-ABC中，AB= AC= 5, BB = BC= 6, D, E分别是AA和BC 的中点.⑴求证：DE/平面ABC⑵求三棱锥E—BCD勺体积.解:⑴证明：如图，取BC的中点G连接AG EG因为E是BC的中点，所以EG BB,且EG由题意知，AA綊BB.而D是AA的中点，所以EG綊AD所以四边形EGA毘平行四边形.所以ED// AG又D曰平面ABC AC?平面ABC所以DE//平面ABC⑵因为AD/ BB,所以AD//平面BCE所以V E—BCD^ V—BCE= V A—BCE= V E—ABC.由⑴知，DE/平面ABC1 1 1所以V E—BC= VE—AB= 3A D-尹° AG= 6X3X 6X 4= 12.1. （xx •湖南卷）一块石材表示的几何体的三视图如下图所示. 将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（）由二视图可得原石材为如右图所示的直二棱柱 ABiCi —ABC 且AB= 8, BC= 6, BB = 12.若要得到半径最大的球，则此球与平面 A i B i BA BCCB , ACCA 相切，故此时球的半径与6 + 8一 io△ ABC 内切圆的半径相等，故半径 r == 2.故选B.答案：B2. （xx •湖北卷）《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也•又以高乘之，三十六成一.该术相当于给出了由圆锥的底面周长 L 与高h ,计算其体积 V 的近似公式 V它实际上是将圆锥体积公式中的圆周率36L 2h 相当于将圆锥体积公式中的n 近似取为（）22A . 1 解析:B . 225C.15750 D. 355 113n 近似取为3.2解析：借助圆锥的体积公式，底面圆的面积、周长公式求解.设圆锥的底面圆半径为L 11则圆锥的底面圆周长L = 2n「，所以圆锥底面圆的半径r =右，则圆锥的体积为V = 3Sh =3n r 2h = 1n L 2 1 2 2 2 1 2 2 2 25•-—2h = L h .又 V ~ L h ,所以 L h ~ L h ,解得 n 〜.4 n 12 n 75 12 n 75 8答案： B3•如图，在三棱锥 D-ABC 中，已知 BCL AD BC= 2, AD= 6, AB+ BD= AO CD= 10，则三棱锥D — ABC 的体积的最大值是 _________ •解析：由题意知，线段 AB+ BD 与线段AO CD 的长度是定值，因为棱 AD 与棱BC 相互垂直.设d 为AD 到BC 的距离.贝U V )-ABC = AD- BCX dx 卜扌=2d,2 3 当d 最大时，V D 」ABC 体积最大， •/ AB+ BD= AO CD= 10,•••当 AB= BD= AC= CD= 5 时，d 有最大值 4 — 1 =15.此时V = 2 15. 答案：2. 154.如图所示，从三棱锥P -ABC 勺顶点P 沿着三条侧棱 PA PB PC 剪开成平面图形得到 △ P 1P 2P 3,且 P 2P 1 = P 2P 3.题图D 答图⑴在三棱锥P—ABC中，求证：PA L BC⑵若P i P2= 26, P i F3= 20,求三棱锥P-ABC勺体积.解：(1) 证明：由题设知A, B, C分别是P1P3, P iR, P2P3的中点，且P2P i= P2P3.从而PB= PC AB= AC取BC的中点D,连AD, PD,则AD L BC PD L BC ADA PD= D,••• BC丄平面PAD•/ PA?平面PAD 故PAL BC(2) 由题设有1AB= AC=尹皆13 , PA= P i A= BC= 10 ,PB= PC= PiB= 13 ,• AD= PD=7AB_ BD= 12 ,在等腰三角形DPA中 ,底边PA上的高h =•- DPA= ^PA' h= 5号119.又BCL平面PADV P— ABC= V B—PD卄V—PDA1 1=~BD* S^DPA+ ~DC* S^ PDA3 310X5 , 119 =。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

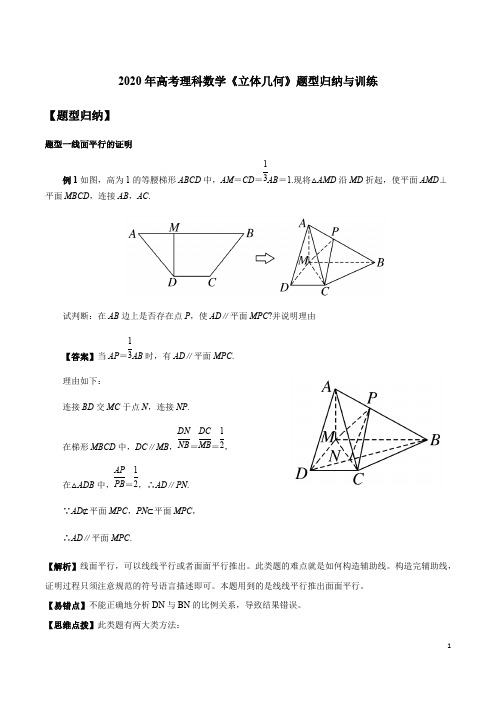
1 2019-2020年高考数学大题专题练习——立体几何（一） 1.如图所示，四棱锥PABCD中，底面ABCD为正方形，PD平面ABCD，2PDAB，点,,EFG分别为,,PCPDBC的中点. (1)求证：EFPA； (2)求二面角DFGE的余弦值.

2.如图所示，该几何体是由一个直角三棱柱ADEBCF和一个正四棱锥PABCD组合而成，AFAD，2AEAD. (1)证明：平面PAD平面ABFE；

(2)求正四棱锥PABCD的高h，使得二面角CAFP的余弦值是223. 2

3.四棱锥PABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是面积为23的菱形，ADC为锐角，M为PB的中点．（Ⅰ）求证：PD∥面ACM．（Ⅱ）求证：PACD．（Ⅲ）求三棱锥PABCD的体积．

4.如图，四棱锥SABCD满足SA面ABCD，90DABABC．SAABBCa，2ADa．（Ⅰ）求证：面SAB面SAD．（Ⅱ）求证：CD面SAC．

CBAD

MCBAPD 3 5.在四棱锥PABCD中，底面ABCD为矩形，测棱PD底面ABCD，PDDC，点E是

BC的中点，作EFPB交PB于F．

（Ⅰ）求证：平面PCD平面PBC．（Ⅱ）求证：PB平面EFD．

6.在直棱柱111

ABCABC中，已知ABAC，设1AB中点为D，1AC中点为E．

（Ⅰ）求证：DE∥平面11BCCB．（Ⅱ）求证：平面11ABBA平面11ACCA．

EDABC

C1B

DAB

P 4 7.在四棱锥PABCD中，PA平面ABCD，//ABCD，ABAD，PAPB，::2:2:1ABADCD.

（1）证明BDPC；（2）求二面角APCD的余弦值；（3）设点Q为线段PD上一点，且直线AQ平面PAC所

成角的正弦值为23，求PQPD的值.

8.在正方体1111ABCDABCD中，O是AC的中点，E是线段D1O上一点，且D1E＝λEO. （1）若λ=1，求异面直线DE与CD1所成角的余弦值；（2）若λ=2，求证：平面CDE⊥平面CD1O. 5

9.如图，在四棱锥PABCD中，底面ABCD是平行四边形，135BCD∠，侧面PAB⊥

底面ABCD，90BAP∠，2ABACPA，E，F分别为BC，AD的中点，点M在线段PD上．（Ⅰ）求证：EF⊥平面PAC．（Ⅱ）若M为PD的中点，求证：ME∥平面PAB．（Ⅲ）如果直线ME与平面PBC所成的角和直线ME与

平面ABCD所在的角相等，求PMPD的值．

10.如图，在三棱柱111ABCABC，1AA⊥底面ABC，ABAC⊥，1

ACABAA，E，F

分别是棱BC，1AA的中点，G为棱1CC上的一点，且1CF∥平面AEG．

（1）求1CGCC的值．（2）求证：1EGAC⊥．（3）求二面角1AAGE的余弦值．

ABC

MFECB

PD 6 11.如图，在四棱锥PABCD中，PB⊥底面ABCD，底面ABCD为梯形，ADBC∥，ADAB⊥，且3PBABAD，1BC．

（Ⅰ）若点F为PD上一点且13PFPD，证明：CF∥平面PAB．（Ⅱ）求二面角BPDA的大小．（Ⅲ）在线段PD上是否存在一点M，使得CMPA⊥若存在，求出PM的长；若不存在，说明

理由．

12.如图，在四棱锥EABCD中，平面EAD⊥平面ABCD，CDAB∥，BCCD⊥，EAED⊥，4AB，2BCCDEAED．

Ⅰ证明：BDAE⊥． Ⅱ求平面ADE和平面CDE所成角（锐角）的余弦值．

DAB

DBC

A 7

13.己知四棱锥PABCD中，PA平面ABCD，底面ABCD是菱形，且2PAAB．60ABC，BC、PD的中点分别为E，F．（Ⅰ）求证BCPE．（Ⅱ）求二面角FACD的余弦值．（Ⅲ）在线段AB上是否存在一点G，使得AF平行于平面PCG？若存在，指出G在AB上的位置并给予证明，若不存在，请说明理由．

14.如图，ABCD是边长为3的正方形，DE平面ABCD，AFDE∥，3DEAF，BE与平面ABCD所成角为60．

（Ⅰ）求证：AC平面BDE．（Ⅱ）求二面角FBED的余弦值．（Ⅲ）设点M线段BD上一个动点，试确定点M的位置，使得AM∥平面BEF，并证明你的结论．

FECBAD

DAB

EF 8

15.如图，PA面ABC，ABBC，22ABPABC，M为PB的中点．

（Ⅰ）求证：AM平面PBC．（Ⅱ）求二面角APCB的余弦值．（Ⅲ）在线段PC上是否存在点D，使得

BDAC，若存在，求出PDPC的值，若不存在，说明理由．

16.如图所示，在四棱锥P-ABCD中，AB⊥平面,//,PADABCDE是PB的中点, 2,5,3,2AHPDPAABADHD .

（1）证明：PH⊥平面ABCD；（2）若F是CD上的点，且23FCFD，求二面角BEFC的正弦值.

MDAB

P 9 17.如图，DC⊥平面ABC，//EBDC，

22ACBCEBDC，120ACB，Q

为AB的中点．（Ⅰ）证明：CQ⊥平面ABE；（Ⅱ）求多面体ACED的体积；（Ⅲ）求二面角A-DE-B的正切值．

18.如图1 ,在△ABC中，AB=BC=2, ∠B=90°,D为BC边上一点，以边AC为对角线做平行四边形ADCE，沿AC将△ACE折起，使得平面ACE ⊥平面ABC,如图2.

(1)在图 2中，设M为AC的中点，求证:BM丄AE； (2)在图2中，当DE最小时，求二面角A -DE-C的平面角. 10

19.如图所示，在已知三棱柱ABF-DCE中，90ADE，60ABC，

2ABADAF，平面ABCD⊥平面ADEF，点M

在线段BE上，点G是线段AD的中点．（1）试确定点M的位置，使得AF∥平面GMC；（2）求直线BG与平面GCE所成角的正弦值．

20.已知在四棱锥P-ABCD中，底面ABCD是菱形，AC=AB，PA⊥平面ABCD，E，F分别是AB，PD的中点. （Ⅰ）求证：AF∥平面PCE；（Ⅱ）若22ABAP，求平面PAD与平面PCE所成锐二面角的余弦值. 11

21.如图，五面体PABCD中，CD⊥平面PAD，ABCD为直角梯形，

,2BCDPDBCCD1,2ADAPPD.

（1）若E为AP的中点，求证：BE∥平面PCD；（2）求二面角P-AB-C的余弦值.

22.如图（1）所示，已知四边形SBCD是由Rt△SAB和直角梯形ABCD拼接而成的，其中90SABSDC.且点A为线段SD的中点，21ADDC，2AB.现将△SAB

沿AB进行翻折，使得二面角S-AB-C的大小为90°，得到图形如图（2）所示，连接SC，点E，F分别在线段SB，SC上. （Ⅰ）证明：BDAF；

（Ⅱ）若三棱锥B-AEC的体积为四棱锥S-ABCD体积的25，求点E到平面ABCD的距离. 12

23.四棱锥S-ABCD中， AD∥BC，,BCCD060SDASDC，

ADDC1122BCSD，E为SD的中点.

（1）求证：平面AEC⊥平面ABCD；（2）求BC与平面CDE所成角的余弦值.

24.已知三棱锥P-ABC，底面ABC是以B为直角顶点的等腰直角三角形，PA⊥AC，BA=BC=PA=2，二面角P-AC-B的大小为120°. （1）求直线PC与平面ABC所成角的大小；（2）求二面角P-BC-A的正切值.