高考物理压轴题电磁场汇编
高考物理压轴题-电磁场计算题

08全国如图所示,在坐标系xOy 中,过原点的直线OC 与x 轴正向的夹角φ=120°,在OC 右侧有一匀强电场。
在第二、三象限内有一匀强磁场,其上边界与电场边界重叠、右边界为y 轴、左边界为图中平行于y 轴的虚线,磁场的磁感应强度大小为B ,方向垂直纸面向里。
一带正电荷q 、质量为m 的粒子以某一速度自磁场左边界上的A 点射入磁场区域,并从O 点射出,粒子射出磁场的速度方向与x 轴的夹角θ=30°,大小为v ,粒子在磁场中的运动轨迹为纸面内的一段圆弧,且弧的半径为磁场左右边界间距的两倍。
粒子进入电场后,在电场力的作用下又由O 点返回磁场区域,经过一段时间后再次离开磁场。
已知粒子从A 点射入到第二次离开磁场所用的时间恰好等于粒子在磁场中做圆周运动的周期。
忽略重力的影响。
求 (1)粒子经过A 点时速度的方向和A 点到x 轴的距离; (2)匀强电场的大小和方向;(3)粒子从第二次离开磁场到再次进入电场时所用的时间。
(08宁夏)24.(17分)如图所示,在xOy 平面的第一象限有一匀强电场,电场的方向平行于y 轴向下;在x 轴和第四象限的射线OC 之间有一匀强磁场,磁感应强度的大小为B ,方向垂直于纸面向外。
有一质量为m ,带有电荷量+q 的质点由电场左侧平行于x 轴射入电场。
质点到达x 轴上A 点时,速度方向与x 轴的夹角ϕ,A 点与原点O 的距离为d 。
接着,质点进入磁场,并垂直于OC 飞离磁场。
不计重力影响。
若OC 与x 轴的夹角为ϕ,求: (1)粒子在磁场中运动速度的大小: (2)匀强电场的场强大小。
答:(1)ϕsin mqBdv =;(2)23sin cos qB d E m φφ=x y φ)θO C A v B × × × × × ×× × × × × × × × × × × × × × ×(07全国1)25.两屏幕荧光屏互相垂直放置,在两屏内分别取垂直于两屏交线的直线为x轴和y 轴,交点O 为原点,如图所示。
2024年高考物理真题分类汇编专题10 磁场

2024年高考物理真题分类汇编专题10磁场仅增大两极板间的距离,极板间的电压减小仅增大等离子体的喷入速率,极板间的电压增大仅增大喷入等离子体的正、负带电粒子数密度,极板间的电压增大图示左侧通电导线受到安培力向下 B.a、b两点的磁感应强度相同D.c、d两点的磁感应强度大小相等【解析】由左手定则可知,图示左侧通电导线受到安培力向下,选项A正确;错误;磁感线是闭合的曲线,则圆柱内的磁感应强度不为零,选项粒子射出圆形区域时的速度方向不一定沿该区域的半径方向方向射入圆形区域的最小时间间隔为7π3错误;粒子从A点射入到从C 根据几何关系可知边时速度方向与ad边夹角为45°,则粒子必垂直边时速度方向与ad边夹角为60°,则粒子必垂直射出,则粒子穿过ad边的速度方向与射出,则粒子穿过ad边时速度方向与【解析】根据几何关系可知,若粒子穿过ad边时速度方向与正确;粒子穿过ad边时速度方向与正确。
空间中存在竖直向下的匀强电场和垂直于纸面向里的匀强磁场,电场强度大小的带电油滴a,在纸面内做半径为时,瞬间分成两个小油滴Ⅰ、Ⅱ,二者带电量、质量均相同。
Ⅰ在的圆周运动,轨迹如图所示。
Ⅱ的轨迹未画出。
己知重力加速度大小为带负电,所带电量的大小为mg EgBR2r L π;(3)222022r v mEeL π(1)电子在匀强磁场中运动时,将其分解为沿x 轴的匀速直线运动和在轴的分速度大小为y v ,由电子在x 轴方向做匀速直线运动得最大,此时R r =,又02L m e v B π=,R =最大时,电子在电场中运动时沿y 轴正方向有最大位移m y ,根据匀变速直线运动规律有0m Bt ;(2)0038t U D B π=;0024U v Bt ππ=;(3)(1)根据带电粒子在右侧磁场中的运动轨迹结合左手定则可知,粒子带正电;粒子在磁场中运动的周02t =2mT qBπ=m q Bt π=(2)若金属板的板间距离为D ,则板长3D π粒子在板间运动时3Dπ=出电场时竖直速度为零,则竖直方向20012(0.5)2U qy t Dm=⨯2v qvB mr =22mv y r qB==0024U Bt ππ0038t U D Bπ=(3)带电粒子在电场和磁场中的运动轨迹如图,由(2)的计算可知金属板的板间距离0 qL;(2)32d Lπ=;(3)3qF xvω=⋅∆(1)对乙粒子,如图所示2001v qv B mr =1sin 30L r ︒=02mv B qL=。
高考物理带电粒子在磁场中的运动压轴难题知识归纳总结附答案解析
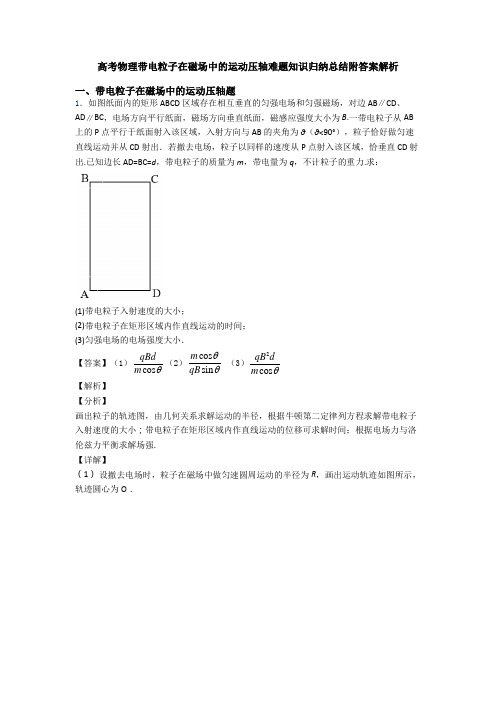
高考物理带电粒子在磁场中的运动压轴难题知识归纳总结附答案解析一、带电粒子在磁场中的运动压轴题1.如图纸面内的矩形 ABCD 区域存在相互垂直的匀强电场和匀强磁场,对边 AB ∥CD 、AD ∥BC ,电场方向平行纸面,磁场方向垂直纸面,磁感应强度大小为 B .一带电粒子从AB 上的 P 点平行于纸面射入该区域,入射方向与 AB 的夹角为 θ(θ<90°),粒子恰好做匀速直线运动并从 CD 射出.若撤去电场,粒子以同样的速度从P 点射入该区域,恰垂直 CD 射出.已知边长 AD=BC=d ,带电粒子的质量为 m ,带电量为 q ,不计粒子的重力.求:(1)带电粒子入射速度的大小;(2)带电粒子在矩形区域内作直线运动的时间; (3)匀强电场的电场强度大小.【答案】(1)cos qBd m θ(2)cos sin m qB θθ (3)2cos qB dm θ【解析】 【分析】画出粒子的轨迹图,由几何关系求解运动的半径,根据牛顿第二定律列方程求解带电粒子入射速度的大小;带电粒子在矩形区域内作直线运动的位移可求解时间;根据电场力与洛伦兹力平衡求解场强. 【详解】(1) 设撤去电场时,粒子在磁场中做匀速圆周运动的半径为R ,画出运动轨迹如图所示,轨迹圆心为O .由几何关系可知:cos d Rθ=洛伦兹力做向心力:200v qv B m R= 解得0cos qBdv m θ=(2)设带电粒子在矩形区域内作直线运动的位移为x ,有sin d xθ= 粒子作匀速运动:x=v 0t 联立解得cos sin m t qB θθ=(3)带电粒子在矩形区域内作直线运动时,电场力与洛伦兹力平衡:Eq=qv 0B解得2qB dE mcos θ=【点睛】此题关键是能根据粒子的运动情况画出粒子运动的轨迹图,结合几何关系求解半径等物理量;知道粒子作直线运动的条件是洛伦兹力等于电场力.2.如图所示,在平面直角坐标系xOy 的第二、第三象限内有一垂直纸面向里、磁感应强度为B 的匀强磁场区域△ABC ,A 点坐标为(0,3a ),C 点坐标为(0,﹣3a ),B 点坐标为(23a -,-3a ).在直角坐标系xOy 的第一象限内,加上方向沿y 轴正方向、场强大小为E=Bv 0的匀强电场,在x=3a 处垂直于x 轴放置一平面荧光屏,其与x 轴的交点为Q .粒子束以相同的速度v 0由O 、C 间的各位置垂直y 轴射入,已知从y 轴上y =﹣2a 的点射入磁场的粒子在磁场中的轨迹恰好经过O 点.忽略粒子间的相互作用,不计粒子的重力. (1)求粒子的比荷;(2)求粒子束射入电场的纵坐标范围;(3)从什么位置射入磁场的粒子打到荧光屏上距Q 点最远?求出最远距离.【答案】(1)0v Ba(2)0≤y≤2a (3)78y a =,94a【解析】 【详解】(1)由题意可知, 粒子在磁场中的轨迹半径为r =a 由牛顿第二定律得Bqv 0=m 2v r故粒子的比荷v q m Ba= (2)能进入电场中且离O 点上方最远的粒子在磁场中的运动轨迹恰好与AB 边相切,设粒子运动轨迹的圆心为O ′点,如图所示.由几何关系知O ′A =r ·ABBC=2a 则OO ′=OA -O ′A =a即粒子离开磁场进入电场时,离O 点上方最远距离为OD =y m =2a所以粒子束从y 轴射入电场的范围为0≤y ≤2a (3)假设粒子没有射出电场就打到荧光屏上,有3a =v 0·t 02019222qE y t a a m ==>,所以,粒子应射出电场后打到荧光屏上粒子在电场中做类平抛运动,设粒子在电场中的运动时间为t ,竖直方向位移为y ,水平方向位移为x ,则 水平方向有x =v 0·t竖直方向有212qE y t m=代入数据得x =2ay设粒子最终打在荧光屏上的点距Q 点为H ,粒子射出电场时与x 轴的夹角为θ,则002tan y x qE x v m v y v v aθ⋅===有H =(3a -x )·tan θ=(32)2a y y -当322a y y -=时,即y =98a 时,H 有最大值 由于98a <2a ,所以H 的最大值H max =94a ,粒子射入磁场的位置为y =98a -2a =-78a3.某控制带电粒子运动的仪器原理如图所示,区域PP′M′M 内有竖直向下的匀强电场,电场场强E =1.0×103V/m ,宽度d =0.05m ,长度L =0.40m ;区域MM′N′N 内有垂直纸面向里的匀强磁场,磁感应强度B =2.5×10-2T ,宽度D =0.05m ,比荷qm=1.0×108C/kg 的带正电的粒子以水平初速度v 0从P 点射入电场.边界MM′不影响粒子的运动,不计粒子重力.(1) 若v 0=8.0×105m/s ,求粒子从区域PP′N′N 射出的位置;(2) 若粒子第一次进入磁场后就从M′N′间垂直边界射出,求v 0的大小; (3) 若粒子从M′点射出,求v 0满足的条件.【答案】(1)0.0125m (2) 3.6×105m/s. (3) 第一种情况:v 0=54.00.8()10/21nm s n -⨯+ (其中n =0、1、2、3、4)第二种情况:v 0=53.20.8()10/21nm s n -⨯+ (其中n =0、1、2、3).【解析】 【详解】(1) 粒子以水平初速度从P 点射入电场后,在电场中做类平抛运动,假设粒子能够进入磁场,则竖直方向21··2Eq d t m= 得2mdt qE=代入数据解得t =1.0×10-6s 水平位移x =v 0t 代入数据解得x =0.80m因为x 大于L ,所以粒子不能进入磁场,而是从P′M′间射出,则运动时间t 0=0Lv =0.5×10-6s ,竖直位移201··2Eq y t m==0.0125m所以粒子从P′点下方0.0125m 处射出.(2) 由第一问可以求得粒子在电场中做类平抛运动的水平位移x =v 0 2mdqE粒子进入磁场时,垂直边界的速度 v 1=qE m ·t =2qEd m设粒子与磁场边界之间的夹角为α,则粒子进入磁场时的速度为v =1v sin α在磁场中由qvB =m 2v R得R =mv qB 粒子第一次进入磁场后,垂直边界M′N′射出磁场,必须满足x +Rsinα=L把x =v 02md qE 、R =mv qB 、v =1v sin α、12qEdv m =代入解得 v 0=L·2Eqmd-E B v 0=3.6×105m/s.(3) 由第二问解答的图可知粒子离MM′的最远距离Δy =R -Rcosα=R(1-cosα) 把R =mv qB 、v =1v sin α、12qEd v m=代入解得 12(1cos )12tan sin 2mEd mEd y B q B q ααα-∆==可以看出当α=90°时,Δy 有最大值,(α=90°即粒子从P 点射入电场的速度为零,直接在电场中加速后以v 1的速度垂直MM′进入磁场运动半个圆周回到电场)1max 212mv m qEd mEdy qB qB m B q∆===Δy max =0.04m ,Δy max 小于磁场宽度D ,所以不管粒子的水平射入速度是多少,粒子都不会从边界NN′射出磁场.若粒子速度较小,周期性运动的轨迹如下图所示:粒子要从M′点射出边界有两种情况, 第一种情况: L =n(2v 0t +2Rsinα)+v 0t 把2md t qE =R =mv qB 、v 1=vsinα、12qEdv m=代入解得 0221221L qE n E v n md n B=⋅++v 0= 4.00.821n n -⎛⎫⎪+⎝⎭×105m/s(其中n =0、1、2、3、4)第二种情况:L =n(2v 0t +2Rsinα)+v 0t +2Rsinα 把2md t qE =、R =mv qB 、v 1=vsinα、12qEd v m=02(1)21221L qE n E v n md n B+=⋅++v0=3.20.8 21nn-⎛⎫⎪+⎝⎭×105m/s(其中n=0、1、2、3).4.如图所示,半径r=0.06m的半圆形无场区的圆心在坐标原点O处,半径R=0.1m,磁感应强度大小B=0.075T的圆形有界磁场区的圆心坐标为(0,0.08m),平行金属板MN的极板长L=0.3m、间距d=0.1m,极板间所加电压U=6.4x102V,其中N极板收集到的粒子全部中和吸收.一位于O处的粒子源向第一、二象限均匀地发射速度为v的带正电粒子,经圆形磁场偏转后,从第一象限出射的粒子速度方向均沿x轴正方向,已知粒子在磁场中的运动半径R0=0.08m,若粒子重力不计、比荷qm=108C/kg、不计粒子间的相互作用力及电场的边缘效应.sin53°=0.8,cos53°=0.6.(1)求粒子的发射速度v的大小;(2)若粒子在O点入射方向与x轴负方向夹角为37°,求它打出磁场时的坐标:(3)N板收集到的粒子占所有发射粒子的比例η.【答案】(1)6×105m/s;(2)(0,0.18m);(3)29%【解析】【详解】(1)由洛伦兹力充当向心力,即qvB=m2vR可得:v=6×105m/s;(2)若粒子在O点入射方向与x轴负方向夹角为37°,作出速度方向的垂线与y轴交于一点Q,根据几何关系可得PQ=0.0637cos=0.08m,即Q为轨迹圆心的位置;Q到圆上y轴最高点的距离为0.18m-0.0637sin=0.08m,故粒子刚好从圆上y轴最高点离开;故它打出磁场时的坐标为(0,0.18m);(3)如上图所示,令恰能从下极板右端出射的粒子坐标为y ,由带电粒子在电场中偏转的规律得: y =12at 2…① a =qE m =qU md …② t =Lv…③ 由①②③解得:y =0.08m设此粒子射入时与x 轴的夹角为α,则由几何知识得:y =r sinα+R 0-R 0cosα 可知tanα=43,即α=53° 比例η=53180︒×100%=29%5.如图所示,坐标原点O 左侧2m 处有一粒子源,粒子源中,有带正电的粒子(比荷为qm=1.0×1010C/kg)由静止进人电压U= 800V 的加速电场,经加速后沿x 轴正方向运动,O 点右侧有以O 1点为圆心、r=0.20m 为半径的圆形区域,内部存在方向垂直纸面向里,磁感应强度大小为B=1.0×10-3T 的匀强磁场(图中未画出)圆的左端跟y 轴相切于直角坐标系原点O ,右端与一个足够大的荧光屏MN 相切于x 轴上的A 点,粒子重力不计。
2024全国高考真题物理汇编:电磁感应章节综合

2024全国高考真题物理汇编电磁感应章节综合一、单选题1.(2024甘肃高考真题)如图,相距为d 的固定平行光滑金属导轨与阻值为R 的电阻相连,处在磁感应强度大小为B 、方向垂直纸面向里的匀强磁场中长度为L 的导体棒ab 沿导轨向右做匀速直线运动,速度大小为v 。
则导体棒ab 所受的安培力为()A .22B d v R,方向向左B .22B d v R ,方向向右C .22B L v R ,方向向左D .22B L v R,方向向右2.(2024甘肃高考真题)工业上常利用感应电炉冶炼合金,装置如图所示。
当线圈中通有交变电流时,下列说法正确的是()A .金属中产生恒定感应电流B .金属中产生交变感应电流C .若线圈匝数增加,则金属中感应电流减小D .若线圈匝数增加,则金属中感应电流不变3.(2024广东高考真题)电磁俘能器可在汽车发动机振动时利用电磁感应发电实现能量回收,结构如图甲所示。
两对永磁铁可随发动机一起上下振动,每对永磁铁间有水平方向的匀强磁场,磁感应强度大小均为B .磁场中,边长为L 的正方形线圈竖直固定在减震装置上。
某时刻磁场分布与线圈位置如图乙所示,永磁铁振动时磁场分界线不会离开线圈。
关于图乙中的线圈。
下列说法正确的是()A .穿过线圈的磁通量为2BL B .永磁铁相对线圈上升越高,线圈中感应电动势越大C .永磁铁相对线圈上升越快,线圈中感应电动势越小D .永磁铁相对线圈下降时,线圈中感应电流的方向为顺时针方向4.(2024江苏高考真题)如图所示,在绝缘的水平面上,有闭合的两个线圈a 、b ,线圈a 处在匀强磁场中,现将线圈a 从磁场中匀速拉出,线圈a 、b 中产生的感应电流方向分别是()A .顺时针,顺时针B .顺时针,逆时针C .逆时针,顺时针D .逆时针,逆时针5.(2024湖北高考真题)《梦溪笔谈》中记录了一次罕见的雷击事件:房屋被雷击后,屋内的银饰、宝刀等金属熔化了,但是漆器、刀鞘等非金属却完好(原文为:有一木格,其中杂贮诸器,其漆器银扣者,银悉熔流在地,漆器曾不焦灼。
2020-2024北京高考真题物理汇编:压轴计算题(第20题)

2020-2024北京高考真题物理汇编压轴计算题(第20题)一、解答题1.(2022北京高考真题)指南针是利用地磁场指示方向的装置,它的广泛使用促进了人们对地磁场的认识。
现代科技可以实现对地磁场的精确测量。
(1)如图1所示,两同学把一根长约10m的电线两端用其他导线连接一个电压表,迅速摇动这根电线。
若电线中间位置的速度约10m/s,电压表的最大示数约2mV。
粗略估算该处地磁场磁感应强度的大小B;地(2)如图2所示,一矩形金属薄片,其长为a,宽为b,厚为c。
大小为I的恒定电流从电极P流入、从电极Q流出,当外加与薄片垂直的匀强磁场时,M、N两电极间产生的电压为U。
已知薄片单位体积中导电的电子数为n,电子的电荷量为e。
求磁感应强度的大小B;(3)假定(2)中的装置足够灵敏,可用来测量北京地区地磁场磁感应强度的大小和方向,请说明测量的思路。
2.(2023北京高考真题)螺旋星系中有大量的恒星和星际物质,主要分布在半径为R的球体内,球体外仅有极少的恒星。
球体内物质总质量为M,可认为均匀分布,球体内外的所有恒星都绕星系中心做匀速圆周运动,恒星到星系中心的距离为r,引力常量为G。
(1)求r R>区域的恒星做匀速圆周运动的速度大小v与r的关系;(2)根据电荷均匀分布的球壳内试探电荷所受库仑力的合力为零,利用库仑力与万有引力的表达式的相似性和相关力学知识,求r R≤区域的恒星做匀速圆周运动的速度大小v与r的关系;(3)科学家根据实测数据,得到此螺旋星系中不同位置的恒星做匀速圆周运动的速度大小v随r的变化关系图像,如图所示,根据在r R>)存>范围内的恒星速度大小几乎不变,科学家预言螺旋星系周围(r R在一种特殊物质,称之为暗物质。
暗物质与通常的物质有引力相互作用,并遵循万有引力定律,求r nR =内暗物质的质量M '。
3.(2020北京高考真题)某试验列车按照设定的直线运动模式,利用计算机控制制动装置,实现安全准确地进站停车。
高考物理压轴题集(磁场)

1如图12所示,PR 是一块长为L =4 m 的绝缘平板固定在水平地面上,整个空间有一个平行于PR 的匀强电场E ,在板的右半部分有一个垂直于纸面向外的匀强磁场B ,一个质量为m =0.1 kg ,带电量为q =0.5 C 的物体,从板的P 端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。
当物体碰到板R 端的挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在C 点,PC =L/4,物体与平板间的动摩擦因数为μ=0.4,取g=10m/s 2,求:(1)判断物体带电性质,正电荷还是负电荷? (2)物体与挡板碰撞前后的速度v 1和v 2 (3)磁感应强度B 的大小(4)电场强度E 的大小和方向2如图10所示,空间分布着有理想边界的匀强电场和匀强磁场,左侧匀强电场的场强大小为E 、方向水平向右,其宽度为L ;中间区域匀强磁场的磁感应强度大小为B 、方向垂直纸面向外;右侧匀强磁场的磁感应强度大小也为B 、方向垂直纸面向里。
一个带正电的粒子(质量m,电量q,不计重力)从电场左边缘a 点由静止开始运动,穿过中间磁场区域进入右侧磁场区域后,又回到了a 点,然后重复上述运动过程。
(图中虚线为电场与磁场、相反方向磁场间的分界面,并不表示有什么障碍物)。
(1)中间磁场区域的宽度d 为多大;(2)带电粒子在两个磁场区域中的运动时间之比;(3)带电粒子从a 点开始运动到第一次回到a 点时所用的时间t.3如图10所示,abcd 是一个正方形的盒子,在cd 边的中点有一小孔e ,盒子中存在着沿ad 方向的匀强电场,场强大小为E 。
一粒子源不断地从a 处的小孔沿ab 方向向盒内发射相同的带电粒子,粒子的初速度为v 0,经电场作用后恰好从e 处的小孔射出。
现撤去电场,在盒子中加一方向垂直于纸面的匀强磁场,磁感应强度大小为B (图中未画出),粒子仍恰好从e 孔射出。
2024届高考高效提分物理情景题压轴汇编-4电磁学(基础必刷)
2024届高考高效提分物理情景题压轴汇编-4电磁学(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题两个位于纸面内的点电荷产生电场的等势面如图中实线所示,相邻等势面间的电势差相等。
虚线MPN是一电子在电场中的运动轨迹,轨迹与某等势面相切于P点。
下列说法正确的是()A.两点电荷可能是异种点电荷B.A点的电场强度比B点的大C.A点的电势高于B点的电势D.电子在M点的加速度大于在P点的加速度第(2)题如图所示,空间存在水平向左的匀强电场,场强大小为E,一轻质绝缘弹簧置于光滑绝缘水平地面上,左端固定在墙面上,弹簧处于自然状态时右端位于B点。
一质量为m,电量为+Q的绝缘物体从A点由静止释放,与弹簧发生相互作用后,弹簧压缩至最远位置C,下列说法正确的是( )A.物体最终将停在B点B.物体反弹后不能回到A点C.从开始释放到运动至C点,物体电势能的减少量等于弹簧弹性势能增加量D.从开始释放到运动至C点过程中,物体的最大动能大于弹簧的最大弹性势能第(3)题如图甲所示,A、B是某点电荷电场中一条电场线上的两点,一个电子仅在静电力的作用下从A点运动到B点的图像如图乙所示。
下列说法正确的是( )A.该点电荷为正电荷B.电子在A点受到的电场力小于在B点受到的电场力C.A点的电势高于B点的电势D.电子在A点的电势能大于在B点的电势能第(4)题一辆智能电动玩具车在水平路面上由静止开始加速,其加速度a随时间t的变化关系如图所示,当玩具车加速后,牵引力的功率保持恒定。
已知玩具车的质量,行驶过程中受到恒定的阻力,则玩具车()A.从到的位移为2m B.从到的牵引力做功为4JC.从到的位移约为7m D.从到的牵引力做功为21J第(5)题小明某天在阳春东湖环湖刚好走了一圈,花了约1一个小时走完了3.5km,以下说法正确的是( )A.位移是3.5km B.路程是3.5kmC.平均速度是3.5km/h D.平均速率为0第(6)题下列说法不符合事实的是( )A.普朗克提出能量子的概念B.法拉第发现了电磁感应现象C.牛顿提出了万有引力定律,并测得了引力常量G的数值D.通电螺线管的磁场与条形磁铁的磁场相似,受此启发,安培提出了分子电流假说第(7)题如图所示,下列有关生活中的圆周运动实例分析,其中说法正确的是( )A.汽车通过凹形桥的最低点时,汽车处于失重状态B.在铁路的转弯处,通常要求外轨比内轨高,目的是利用轮缘与外轨的侧压力助火车转弯C.杂技演员在表演“水流星”节目时,盛水的杯子通过最高点而水不流出,水对杯底压力可以为零D.脱水桶的脱水原理是水滴受到的离心力大于它受到的向心力,从而沿切线方向甩出第(8)题无线蓝牙耳机开启了新的音频传输方式,摆脱了线材束缚。
高考物理电磁感应现象压轴难题培优题及答案
高考物理电磁感应现象压轴难题培优题及答案一、高中物理解题方法:电磁感应现象的两类情况1.如图所示,足够长的光滑平行金属导轨MN 、PQ 倾斜放置,两导轨间距离为L ,导轨平面与水平面间的夹角θ,所处的匀强磁场垂直于导轨平面向上,质量为m 的金属棒ab 垂直于导轨放置,导轨和金属棒接触良好,不计导轨和金属棒ab 的电阻,重力加速度为g .若在导轨的M 、P 两端连接阻值R 的电阻,将金属棒ab 由静止释放,则在下滑的过程中,金属棒ab 沿导轨下滑的稳定速度为v ,若在导轨M 、P 两端将电阻R 改接成电容为C 的电容器,仍将金属棒ab 由静止释放,金属棒ab 下滑时间t ,此过程中电容器没有被击穿,求:(1)匀强磁场的磁感应强度B 的大小为多少?(2)金属棒ab 下滑t 秒末的速度是多大?【答案】(1)2sin mgR B L v θ=2)sin sin t gvt v v CgR θθ=+ 【解析】试题分析:(1)若在M 、P 间接电阻R 时,金属棒先做变加速运动,当加速度为零时做匀速运动,达到稳定状态.则感应电动势E BLv =,感应电流E I R=,棒所受的安培力F BIL = 联立可得22B L v F R =,由平衡条件可得F mgsin θ=,解得2 mgRsin B L vθ (2)若在导轨 M 、P 两端将电阻R 改接成电容为C 的电容器,将金属棒ab 由静止释放,产生感应电动势,电容器充电,电路中有充电电流,ab 棒受到安培力.设棒下滑的速度大小为v ',经历的时间为t则电容器板间电压为 UE BLv ='= 此时电容器的带电量为Q CU = 设时间间隔△t 时间内流经棒的电荷量为Q 则电路中电流 Q C U CBL v i t t t ∆∆∆===∆∆∆,又v a t∆=∆,解得i CBLa = 根据牛顿第二定律得mgsin BiL ma θ-=,解得22mgsin gvsin a m B L C v CgRsin θθθ==++所以金属棒做初速度为0的匀加速直线运动,ts 末的速度gvtsin v at v CgRsin θθ'==+. 考点:导体切割磁感线时的感应电动势;功能关系;电磁感应中的能量转化【名师点睛】本题是电磁感应与电路、力学知识的综合,关键要会推导加速度的表达式,通过分析棒的受力情况,确定其运动情况.2.如图所示,光滑的水平平行金属导轨间距为 L ,导轨电阻忽略不计.空间存在垂直于导 轨平面竖直向上的匀强磁场,磁感应强度大小为 B ,轻质导体棒 ab 垂直导轨放置,导体棒 ab 的电阻为 r ,与导轨之间接触良好.两导轨之间接有定值电阻,其阻值为 R ,轻质导体棒中间系一轻细线,细 线通过定滑轮悬挂质量为 m 的物体,现从静止释放该物体,当物体速度达到最大时,下落的高度为 h , 在本问题情景中,物体下落过程中不着地,导轨足够长,忽略空气阻力和一切摩擦阻力,重力加速度 为 g .求:(1)物体下落过程的最大速度 v m ;(2)物体从静止开始下落至速度达到最大的过程中,电阻 R 上产生的电热 Q ;(3)物体从静止开始下落至速度达到最大时,所需的时间 t .【答案】(1)22()mg R r B L + (2) 3244()2mghR m g R R r R r B L+-+ (3) 2222()()m R r B L h B L mg R r +++ 【解析】【分析】在物体加速下落过程中,加速度逐渐减小,当加速度为0时,下落速度达到最大,由平衡条件、闭合电路欧姆定律和电磁感应定律求出物体下落过程的最大速度;在物体下落过程中,物体重力势能减少,动能增加,系统电热增加,根据能量守恒定律求出电阻R 上产生的电热;在系统加速过程中,分别对导体棒和物体分析,根据动量定理可得所需的时间;解:(1)在物体加速下落过程中,加速度逐渐减小,当加速度为0时,下落速度达到最大 对物体,由平衡条件可得mg=Fr对导体棒Fr=BIL对导体棒与导轨、电阻R 组成的回路,根据闭合电路欧姆定律E I R r =+ 根据电磁感应定律E=BLv m联立以上各式解得m 22()v mg R r B L += (2)在物体下落过程中,物体重力势能减少,动能增加,系统电热增加,根据能量守恒定律可得mgh=12mv m 2+Q 总 在此过程中任一时刻通过R 和r 两部分电阻的电流相等,则电功率之比正比于电阻之比,故整个过程中回路中的R 与r 两部分电阻产生的电热正比于电阻,所以Q R Q R r=+总 联立解得3244()Q 2mghR m g R R r R r B L+=-+ (3)在系统加速过程中,任一时刻速度设为v ,取一段时间微元Δt ,在此过程中分别对导体棒和物体分析,根据动量定理可得22T F 0B L v t R r ⎛⎫-∆= ⎪+⎝⎭ ()T m F m g t v -∆=∆ 整理可得22m m B L v g t t v R r∆-∆=∆+ 即22m m B L g t x v R r∆-∆=∆+ 全过程叠加求和22m m m B L gt h v R r-=+ 联方解得2222()t ()m R r B L h B L mg R r +=++3.电源是通过非静电力做功把其它形式的能转化为电势能的装置,在不同的电源中,非静电力做功的本领也不相同,物理学中用电动势E 来表明电源的这种特性。
高考物理带电粒子在磁场中的运动压轴难题知识点及练习题附答案
高考物理带电粒子在磁场中的运动压轴难题知识点及练习题附答案一、带电粒子在磁场中的运动压轴题1.如图所示,两条竖直长虚线所夹的区域被线段MN 分为上、下两部分,上部分的电场方向竖直向上,下部分的电场方向竖直向下,两电场均为匀强电场且电场强度大小相同。
挡板PQ 垂直MN 放置,挡板的中点置于N 点。
在挡板的右侧区域存在垂直纸面向外的匀强磁场。
在左侧虚线上紧靠M 的上方取点A ,一比荷qm=5×105C/kg 的带正电粒子,从A 点以v 0=2×103m/s 的速度沿平行MN 方向射入电场,该粒子恰好从P 点离开电场,经过磁场的作用后恰好从Q 点回到电场。
已知MN 、PQ 的长度均为L=0.5m ,不考虑重力对带电粒子的影响,不考虑相对论效应。
(1)求电场强度E 的大小; (2)求磁感应强度B 的大小;(3)在左侧虚线上M 点的下方取一点C ,且CM=0.5m ,带负电的粒子从C 点沿平行MN 方向射入电场,该带负电粒子与上述带正电粒子除电性相反外其他都相同。
若两带电粒子经过磁场后同时分别运动到Q 点和P 点,求两带电粒子在A 、C 两点射入电场的时间差。
【答案】(1) 16/N C (2) 21.610T -⨯ (3) 43.910s -⨯ 【解析】 【详解】(1)带正电的粒子在电场中做类平抛运动,有:L=v 0t2122L qE t m = 解得E=16N/C(2)设带正电的粒子从P 点射出电场时与虚线的夹角为θ,则:0tan v qE t mθ=可得θ=450粒子射入磁场时的速度大小为2v 0粒子在磁场中做匀速圆周运动:2v qvB m r=由几何关系可知2r L = 解得B=1.6×10-2T(3)两带电粒子在电场中都做类平抛运动,运动时间相同;两带电粒子在磁场中都做匀速圆周运动,带正电的粒子转过的圆心角为32π,带负电的粒子转过的圆心角为2π;两带电粒子在AC 两点进入电场的时间差就是两粒子在磁场中的时间差; 若带电粒子能在匀强磁场中做完整的圆周运动,则其运动一周的时间22r mT v qBππ==; 带正电的粒子在磁场中运动的时间为:4135.910s 4t T -==⨯; 带负电的粒子在磁场中运动的时间为:4212.010s 4t T -==⨯ 带电粒子在AC 两点射入电场的时间差为412 3.910t t t s -∆=-=⨯2.如图所示,在一直角坐标系xoy 平面内有圆形区域,圆心在x 轴负半轴上,P 、Q 是圆上的两点,坐标分别为P (-8L ,0),Q (-3L ,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
优秀学习资料 欢迎下载 24、在半径为R的半圆形区域中有一匀强磁场,磁场的方向垂直于纸面,磁感应强度为B。一质量为m,带有电量q的粒子以一定的速度沿垂直于半圆直径AD方向经P点(AP=d)射入磁场(不计重力影响)。 ⑴如果粒子恰好从A点射出磁场,求入射粒子的速度。 ⑵如果粒子经纸面内Q点从磁场中射出,出射方向与半圆在Q点切线方向的夹角为φ(如图)。求入射粒子的速度。
24、⑴由于粒子在P点垂直射入磁场,故圆弧轨道的圆心在AP上,AP是直径。 设入射粒子的速度为v1,由洛伦兹力的表达式和牛顿第二定律得:
211/2vmqBvd 解得:12qBdvm ⑵设O/是粒子在磁场中圆弧轨道的圆心,连接O/Q,设O/Q=R/。 由几何关系得: /OQO
//OORRd 由余弦定理得:2/22//()2cosOORRRR 解得:/(2)2(1cos)dRdRRd
设入射粒子的速度为v,由2/vmqvBR 解出:(2)2(1cos)qBdRdvmRd 24.(17分) 如图所示,在xOy平面的第一象限有一匀强电场,电场的方向平行于y轴向下;在x轴和第四象限的射线OC之间有一匀强磁场,磁感应强度的大小为B,方向垂直于纸面向外。有一质量为m,带有电荷量+q的质点由电场左侧平行于x轴射入电场。质点到达x轴上A点时,速度方向与x轴的夹角为φ,A点与原点O的距离为d。接着,质点进入磁场,并垂直于OC飞离磁场。不计重力影响。若OC与x轴的夹角也为φ,求:⑴质点在磁场中运动速度的大小;⑵匀强电场的场强大小。
24.质点在磁场中偏转90º,半径qBmvdrsin,得mqBdvsin;
R A O
P
D
Q φ
R A O
P D
Q φ
O/ R/
x O
y E
B A φ φ
C v 优秀学习资料 欢迎下载 由平抛规律,质点进入电场时v0=vcosφ,在电场中经历时间t=d/v0,在电场中竖直位移221tan2tmqEdh,由以上各式可得
cossin32mdqBE
25.(18分)如图所示,在第一象限有一匀强电场,场强大小为E,方向与y轴平行;在x轴下方有一匀强磁场,磁场方向与纸面垂直。一质量为m、电荷量为-q(q>0)的粒子以平行于x轴的速度从y轴上的P点处射入电场,在x轴上的Q点处进入磁场,并从坐标原点O离开磁场。粒子在磁场中的运动轨迹与y轴交于M点。已知OP=l,OQ=23l。不计重力。求:⑴M点与坐标原点O间的距离;⑵粒子从P点运动到M点所用的时间。
25.⑴MO=6l ⑵qEmlt212333、(20XX年宁夏卷)25.如图所示,在第一象限有一均强电场,场强大小为E,方向与y轴平行;在x轴下方有一均强磁场,磁场方向与纸面垂直。一质量为m、电荷量为-q(q>0)的粒子以平行于x轴的速度从y轴上的P点处射入电场,在x轴上的Q点处进入磁场,并从坐标原点O离开磁场。粒子在磁场中的运动轨迹与
y轴交于M点。已知OP=l,lOQ32。不计重力。求 (1)M点与坐标原点O间的距离; (2)粒子从P点运动到M点所用的时间。 【解析】(1)带电粒子在电场中做类平抛运动,在y轴负方向上做初速度为零的匀加速运动,
设加速度的大小为a;在x轴正方向上做匀速直线运动,设速度为0v,粒子从P点运动到Q
点所用的时间为1t,进入磁场时速度方向与x轴正方向的夹角为,则qEam ①
01
2yta ②
00
1
xvt ③
其中0023,xlyl。又有10tanatv ④ 联立②③④式,得30
φ O y E
B A φ
C
φ d h x
x y O P Q
M v0 优秀学习资料 欢迎下载 因为MOQ、、点在圆周上,=90MOQ,所以MQ为直径。从图中的几何关系可知。 23Rl ⑥ 6MOl ⑦
(2)设粒子在磁场中运动的速度为v,从Q到M点运动的时间为2t, 则有0 cosvv ⑧ 2Rtv ⑨ 带电粒子自P点出发到M点所用的时间为t为12+ ttt ⑩
联立①②③⑤⑥⑧⑨⑩式,并代入数据得32+ 12mltqE ⑾
25.(18分) 如图所示,在0≤x≤a、o≤y≤2a2a范围内有垂直手xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点0处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向
的夹角分布在0~090范围内。己知粒子在磁场中做圆周运动的半径介于a/2到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子从粒子源射出时的 (1)速度的大小: (2)速度方向与y轴正方向夹角的正弦。
【答案】(1)6(2)2aqBvm(2)6-6sin=10 命题点10:带电粒子在组合场中的运动——电场中的加速、偏转;磁场中的圆周运动 07—25.(18分)飞行时间质谱仪可以对气体分子进行分析。如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生不同价位的正离子,自a板小孔进入a、b间的加速电场,从b板小孔射出,沿中线方向进入M、N板间的偏转控制区,到达探测器。已知元电荷电量为e,a、b板间距为d,极板M、N的长度和间距均为L。不计离子重力及进入a板时的初速度。 ⑴当a、b间的电压为U1时,在M、N间加上适当的电压U2,使离子到达探测器。请导出离子的全部飞行时间与比荷K(K
P
S d L
L M N a
b
探测器 激光束 优秀学习资料 欢迎下载 =ne/m)的关系式。 ⑵去掉偏转电压U2,在M、N间区域加上垂直于纸面的匀强磁场,磁感应强度B,若进入a、b间所有离子质量均为m,要使所有的离子均能通过控制区从右侧飞出,a、b间的加速电压U1至少为多少?
25、解:⑴由动能定理:2112neUmv
n价正离子在a、b间的加速度:11neUamd
在a、b间运动的时间: 1112vmtaneUd 在MN间运动的时间:2Ltv 离子到达探测器的时间:t=t1+t2=122KULd ⑵假定n价正离子在磁场中向N板偏转,洛仑兹力充当向心力,设轨迹半径为R,由牛顿第二定律得:2vnevBmR 离子刚好从N板右侧边缘穿出时,由几何关系: R2=L2+(R-L/2)2
由以上各式得:2212532neLBUm
当n=1时U1取最小值22min2532eLBUm
08—25.(18分)【2010示例】 两块足够大的平行金属极板水平放置,极板间加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律分别如图1、图2所示(规定垂直纸面向里为磁感应强度的正方向)。在t=0时刻由负极板释放一个初速度为零的带负电的粒子(不计重力)。若电场强度E0、磁
感应强度B0、粒子的比荷qm均已知,且002mtqB,两板间距202010mEhqB。 (1)求粒子在0~t0时间内的位移大小与极板间距h的比值。 (2)求粒子在板板间做圆周运动的最大半径(用h表示)。 (3)若板间电场强度E随时间的变化仍如图1所示,磁场的变化改为如图3所示,试画出粒子在板间运动的轨迹优秀学习资料 欢迎下载 图(不必写计算过程)。 解法一:(1)设粒子在0~t0时间内运动的位移大小为21012sat① 0qEam②
又已知200200102,mEmthqBqB 联立①②式解得115sh③ (2)粒子在t0~2t0时间内只受洛伦兹力作用,且速度与磁场方向垂直,所以粒子做匀速圆周运动。设运动速度大小为v1,轨道半径为R1,周期为T,则10vat④ 2110
1
mvqvBR⑤ 联立④⑤式得15hR⑥
又02mTqB⑦ 即粒子在t0~2t0时间内恰好完成一个周期的圆周运动。在2t0~3t0时间内,粒子做初速度为v1的匀加速直线运动,设位移大小为2210012svtat⑧ 解得235sh⑨ 由于s1+s2<h,所以粒子在3t0~4t0时间内继续做匀速圆周运动,设速度大小为v2,半径为R2
210vvat⑩ 22202mvqvBR○11 解得225hR○12
由于s1+s2+R2<h,粒子恰好又完成一个周期的圆周运动。在4t0~5t0时间内,粒子运动到正极板(如图1所示)。因此粒子运动的最大半径225hR。 (3)粒子在板间运动的轨迹如图2所示。
09—25.(18分)如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l。第一、四象限有磁感应强度为B的匀强磁场,方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴向右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子。在0~3t0时间内两板间加上如图乙所示的电压(不考虑极边缘的影响)。已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、l、t0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)⑴求电压U0的大小。 ⑵求t0/2时刻进入两板间的带电粒子在磁场中做圆周运动的半径。 ⑶何时进入两板间的带电粒子在磁场中的运动时间最短?求此最短时间。 y
x O
B
P
Q v0 l l
图甲
UPQ
t O
U0
-U0
t0 2t
0 3t
0
图乙
