chap 2 线性规划的对偶理论
运筹学Chap线性规划对偶理论及其应用PPT学习教案

max 2u1 u2
u1 u2 5
s.t.6uu11
u2 2u2
0 21
u1
0
u2 0
第5页/共51页
模型对比(对称形式)
m a xZ 1 0x1 1 8x2
5 x1 2 x2 1 7 0
2 x1 x1
3 x2 5 x2
100 150
x1 , x2 0
又由于X *是原问题的最优解,故 cT X * cBT B1b
由此得到
c T X * bTY * 可见Y *是对偶问题的最优解。
第22页/共51页
3、互补松弛性
在线性规划问题的最优解中, 如果对应某一约束条件的对偶变量值为非零,
则该约束条件取严格等式;
反之如果约束条件取严格不等式,
x5 1
x j 0, j 1,,5
解: c (5,0,21,0,0)T ,b (2,1)T , A 1 1 6 1 0 1 1 2 0 1
第4页/共51页
其对偶问题为
写成分量形式,即
max 2
1
u1 u2
1 1
s.t.
6
1
0
1
5
1 2 0
u1 u2
0
21
0
1
0
(2)无界性
如果原问题(对偶问题)具有无界解, 则其对偶问题(原问题)无可行解。
(3)最优性
如果xˆ j ( j 1, 2, , n)是原问题的可行解
yˆi (i 1, 2, , m)是其对偶问题的可行解
n
m
且有 cj xˆ j bi yˆi
j 1
i 1
则xˆ j ( j 1, 2, , n)是原问题的最优解
运筹学基础-对偶线性规划(2)

用单纯形法同时求解原问题和对偶问题
原问题是:
maxZ=2x1 +x2 5x2 ≤15 6x1 + 2x2 ≤ 24 x1 + x2 ≤ 5 x1 , x2 ≥0
5x2 +x3 =15 6x1 + 2x2 +x4 = 24 x1 + x2 +x5 = 5 xi ≥0
原问题的标准型是:maxZ=2x1 +x2+0x3+0x4 +0x5
b
15 24 5 0
x1 0 6 1 2
比 值
-
24/6=4
5/1=5
检验数j
对偶问题剩余变量 y4、y5
对偶问题变量 y1、y2 、y3
检验数行的- (cj-zj)值是其对偶问题的一个基本解yi ;
原问题变量
0 2
原问题松驰变量
1 0 0 0 0 1/6 -1/6 -1/3 0 0 1 0
3
x3 x1
x2 1 检验数j= cj-zj
-1/4 -1/2
对偶问题剩余变量 y4、y5
对偶问题变量 y1、y2 、y3
此时得原问题最优解:X*=(7/2,3/2,15/2,0,0)T,Z*=17/2 则对偶问题最优解:Y*=(0,1/4,1/2,0,0)T,S*=17/2
又例:用单纯形法同时求解原问题和对偶问题
定理6(互补松弛定理)
在线性规划问题的最优解中,如果对应某一约束条件的 对偶变量值为非零,则该约束条件取严格等式;反之如果约 束条件取严格不等式,则其对应的对偶变量一定为零。
注:证明过程参见教材59页性质5证明
讨论:
互补松弛定理也称松紧定理,它描述了线性规划达到最
第02章 线性规划的对偶理论及灵敏度分析 《运筹学》PPT课件

x1, x2 ,, xn 0
对 称 形 式 的
的 定 义
minW b1y1 b2 y2 bm ym
对
s.t.
a11 a12
a1n
a21 a22
a2n
am1 y1 c1
am2
y2
c2
amn ym cn
偶 问 题
y1, y2 ,, ym 0
max Z CX
用5h设备A,2h设备B及1h调试可 生产一件家电Ⅱ,赢利1元
该公司希望用最小代价把美佳公司的全部资源收买过来,即:
min z 15y1 24y2 y3
问 题 的 导 出
例2-1
综上所述,
(LP2) min w 15y1 24y2 y3
6 y2 y3 2
s.t.5 y1 2 y2 y3 1
的
x1, x2,, xn 0
对
minW b1y1 b2 y2 bm ym
a11 y1 a21 y2 am1 ym c1
偶 问 题
a12y1
a22 y2
am2 ym
c2
a1n y1 a2n y2 amn ym cn y1, y2 ,, ym符号不限
对
例2-3
称
minZ 4x1 2x2 3x3
[B-1A,B-1I]=[B-1B,B-1N,B-1I]=[I,B-1N,B-1] •若初始矩阵中变量xj的系数向量为Pj,迭代后为 Pj′,则有Pj′=B-1Pj •当B为最优基时,表中应有
CN-CBB-1N≤0,-CBB-1≤0
例2-5
对
偶
参看例2-1中的原问题和对偶问题,并分别加上松 弛变量和剩余变量,如下:
23 3
第二章 线性规划问题的对偶理论与灵敏度分析总结
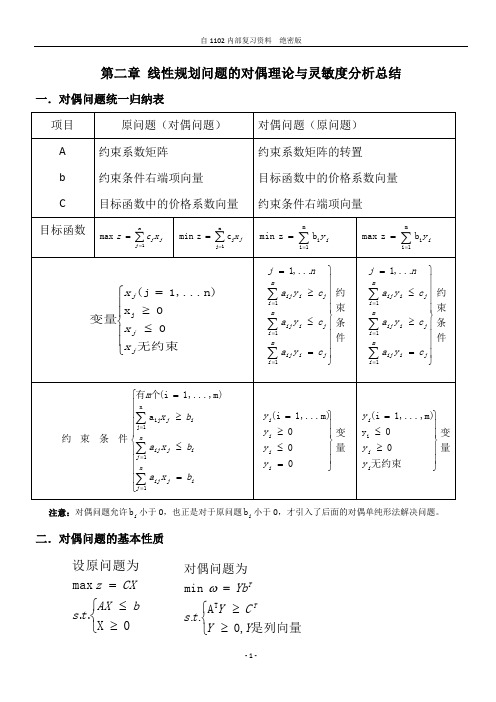
第二章 线性规划问题的对偶理论与灵敏度分析总结一.对偶问题统一归纳表注意:对偶问题允许i b 小于0,也正是对于原问题i b 小于0,才引入了后面的对偶单纯形法解决问题。
二.对偶问题的基本性质⎩⎨⎧≥≤=0X ..max 设原问题为b AX t s CXz⎩⎨⎧≥≥=是列向量,0A .. min 对偶问题为TY Y C Y t s Yb TTω1.对称定理:对偶问题的对偶是原问题2.弱对偶性定理:若Y X 和分别是原问题和对偶问题的可行解,则有b TY X C ≤推论(1)max 问题的任一可行解的目标是对偶问题最优目标值的一个下界。
min 问题的任一可行解的目标函数 值是原问题最优目标值的一个上界。
(2)若原问题可行且其目标函数值无界,则对偶问题无可行解。
反之对偶问题可行且其目标函数值无界,则原问题无可行解。
(3)若原问题有可行解而对偶问题无可行解,则原问题目标函数值无界;反之对偶问题有可行解而原问题无可行解,则对偶问题目标函数值无界。
3. 最优性定理:若Y X 和分别是原问题和对偶问题的可行解,并且b TY X C =,则X 是原问题最优解,Y 是其对偶问题的最优解4. 强对偶性:若原问题及其对偶问题均具有可行解,则两者均具有最优解,且它们最优解的目标函数值相等。
5.互不松弛性:若Y X 和分别是原问题和对偶问题的可行解,则它们分别是最优解的充要条件是:0ˆ,ˆˆ0ˆ1j 1=<=>∑∑==i i nj ij i nj j ij i y b xa b x a y则如果,则如果练习:判断下列说法是否正确:(1) 任何线性规划问题存在并具有惟一的对偶问题;(✓)(2) 根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解;(✗)(3) 设j ˆx ,i ˆy 分别为标准形式的原问题与对偶问题的可行解,*j x ,*i y 分别为其最优解,则恒有n n m m**j j j j i i i i j 1j 1i 1i 1ˆˆc x c x b y b y ====≤=≤∑∑∑∑;(✓) (5) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0>,说明在最优生产计划中第i 种资源已完全耗尽;(✓) (6) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0=,说明在最优生产计划中第i 种资源一定有剩余;(✗)简析:对(5)、(6),由互补松弛性质判断,具体详见课本P59三.对偶单纯形法(1). 对偶单纯形法应用前提: 1.检验数行全部非正2.变量取值有负数(2). 对偶单纯形法计算步骤:1.确定换出基变量 取{}i rb min b =,其对应变量r x 为换出基的变量。
运筹学第2章:线性规划的对偶理论

目
标函数求极小时取“≥”号
注:对称形式与线性规划标准型是两种不同的形 式,对称形式中约束条件的符号由目标函数决定
从以下方面比较(LP1)与(LP2):
原问题
对偶问题 约束系数矩阵的转 臵 目标函数中的价格 系数向量 约束条件的右端项 向量 Min w=Y’b A’Y≥C’ Y≥0
A
b C 目标函数 约束条件 决策变量
非基变量 基变量
XB
0 b Xs C j - zj B
XN
N
Xs
I
0
初始 单纯形表
非基变量
CB
CN
基变量
最终
单纯形表
CB
XB
XB B-1b Cj - zj
I 0
Xs B-1 N B-1 CN-CBB-1N -CBB-1
XN
若B-1b为最优解,则
CB CB ( B 1B) 0 C N CB B N 0 CB B 1 0
令 y 2 y 2 , y3 y3 y3 ,则
min 2 y1 y2 4 y3
2 y1 3 y2 y3 1 3 y y y 4 1 2 3 s.t. 5 y1 6 y2 y3 3 y1 0, y2 0, y3无约束
n j 1 m j j
C X Y b, 即 c j x j y i bi
j 1 i 1
__
__
n
m
c x ( a
j 1 m i 1 n i i i 1 i 1 j 1
n
m
ij
yi ) x j aij x j yi ( a ji yi c j )
例1
线性规划的对偶理论

线性规划的对偶理论线性规划的对偶理论⾸先我们指出对线性规划问题引⼊对偶问题的动机:有时解对偶问题会⽐解原问题更容易,同时便于后续进⾏灵敏度分析。
⽬录1 推导考虑线性规划问题max z=cx s.t.Ax≤b,x i≥0现假设x是⼀个可⾏解,则对于任意⼀个⾮负向量y≥0,有y T Ax≤y T b假设能找到y满⾜c≤y T A,那么对所有可⾏解x都有cx≤y T Ax≤y T b即y T b是原问题的⼀个上界,那么现在我们要找最⼩的⼀个,得到对偶问题min w=b T y s.t.A T y≥c T,y i≥0此时原问题的最优解和对偶问题的最优解⼀定满⾜max z=min w。
2 变换假设我们由⼀个最⼤化的问题,我们通过如下步骤将其转化为其对偶问题⽬标函数改为最⼩化x i≥0 对应约束条件≥,x i⽆约束对应约束条件=原约束条件≤对应y i≥0,原约束条件=对应y i⽆约束补充说明⼀点,从实际意义上来说,光看⼤于号⼩于号或许会有点奇怪,我们可以考虑变量⾃⾝约束或者⽅程约束条件对于⽬标函数优化的贡献“⽅向”。
设想⼀个系数全正的⽬标函数,那么≥0 的变量变换后始终是限制⽬标函数的,反之亦然。
3 性质对偶的对偶就是原问题CX≤Yb,其中X,Y是原问题、对偶问题的任意可⾏解具有⽆界解的问题的对偶是⽆解的问题当可⾏解X,Y满⾜CX=Yb时它们是最优解原问题有最优解则对偶问题有⽬标函数值相同的最优解互补松弛性:可⾏解X,Y是最优解当且仅当YX S=0 且Y S X=0原问题单纯形表的检验数⾏对应对偶问题的⼀个基本解4 影⼦价格我们观察到乘⼦Y=C B B−1到处都是,它究竟是什么?现考虑问题的最优基B,那么z∗=C B B−1b=Y∗b,对b求偏导数,得到∂z∗∂b=C−1=Y∗B B因此,Y∗实际上反映了某种资源的单位资源转化为利润的效率。
由于它是在⽬标函数的最优值中体现的,因此说Y∗包含了每种资源对⽬标函数的边际贡献。
第二章线性规划的对偶理论总结
解:首先将问题化为如下形式:
max z 2 x1 3x2 4 x3
s.t.
2 x1 3x2 5 x3 2 3 x1 x2 7 x3 3 x1 4 x2 6 x3 5 x j 0( j 1, 2,3)
再根据定义2.1, 写出其(D)问题:
max z cx
s.t.
Ax b x0
为了利用对称型问题的结论,先将问题等价地化为:
max z cx
s.t.
Ax
≤b ≤-b x≥0
Ax
再引入对偶向量(u,v),其中u为对应于第一组不等式约束 的对偶变量, v为对应于第二组不等式约束的对偶变量,按 对称型的结论,可写出其(D)问题为:
b min w (u, v) b
s.t.
A (u, v) c A u, v 0
即 s.t.
min w (u v)b
(u v) A c u, v 0
令y=u-v为m维行向量,则以上模型又可写成:
min w yb
s.t.
yA c y无符号限制
例2.3
s.t.
写出(P)问题的(D)问题.
max z 2x1 3x2 5x3 x4
4 x1 x2 3 x3 2 x4 5 3 x1 2 x2 7 x4 4 2 x1 3 x2 4 x3 x4 6 x1 0, x2 , x3 0, x4无符号限制
max z cx
考虑对称形式下
(P)问题:
(D)问题:
min w yb
max z cx
s.t.
s.t. Ax ≤ b x≥0
线性规划对偶理论PPT课件
max z c1 x1 c2 x2 cn xn
a11x1 a12x2
a21x1 a22x2
a1nxn ≤ b1 ≤ a2nxn b2
≤
am1x1 am2 x2
amn xn bm
x
j
≥
0
j 1, 2,
,n
min w b1 y1 b2 y2 bm ym
a11 y1 a21y 2
a12
y1
a
22
y
2
a1n y1 a2n y2 yi ≥ 0 i 1, 2,
am1y m ≥ c1 am2xm≥ c2
amn ym ≥ cn ,m
6
第6页/共45页
规范形式下对偶关系的一般形式
max z CX
AX ≤b
X
≥
0
min w Yb YA≥ C Y ≥ 0
7
第7页/共45页
【证】因为X°、Y°是可行解,故有AX°≤b, X°≥0及Y°A≥C, Y°≥0,将不等式 AX°≤b
两边左乘Y°,得Y0AX°≤Y0b
再将不等式Y°A≥C两边右乘X°,得C X°≤Y°AX°
故
C X°≤Y°AX≤Y°b
这一性质说明了两个线性规划互为对偶时,求最大值的线性 规划的任意目标值都不会大于求最小值的线性规划的任一目 标值,不能理解为原问题的目标值不超过对偶问题的目标值。
6
y2
8 y3 y3
≥ ≤
5 4
y1
5 y2
≤9
y1≤0, y2≥0, y3无约束
15
第15页/共45页
线性规划对偶问题的基本性质
下面介绍对偶基本性质时,一般假定是如下规范对偶关系。
设原问题是(记为LP): 对偶问题是(记为DP):
运筹学:第2章 线性规划的对偶理论
y1 y2
ym
2021/4/18
12
类似于前面的资源定价问题,每一个约束条件对 应一个“ 对偶变量”,它就相当于给各资源的单 位定价。于是我们有如下的对偶规划:
min W b1 y1 b2 y2 bm ym
a11 y1 a21 y2 am1 ym c1 a12y1 a22y2 am2ymc2 a1n y1 a2n y2 amn ym cn y1, y2 ,, ym 0
1/5
0
-4/5
1
1/5 -1/5
j
0
4
0
3
3
x3
x4
x5
x1
x2
2021/4/18
31
§4 影子价格
假设有原问题和对偶问题如下:
max Z CX
minW bTY
AX b
ATY CT
X 0
Y 0
1、 对偶变量 yi 可理解为对一个单位第 i 种资源
的估价,称为影子价格,但并非市场价格。
2、 对偶变量 yi 的值(即影子价格)表示第 i 种资
若
n
yˆi 0, 则 aij x j bi ;
j 1
n
若
aij x j bi , 则yˆi 0.
j 1
2021/4/18
25
证明 由弱对偶性知:
n
mn
m
c j xˆ j
aij xˆ j yˆi bi yˆi
j 1
i1 j1
i 1
又因在最优解中 应为等式,即有
n
m
c j xˆ j bi yˆi
可以先将原问题化成规范的原问题,再写出对偶 问题。
2021/4/18
4运筹学第二章线性规划的对偶理论-PPT精选文档44页
证:设原问题为: max z=CX;AX≤b;X≥0 则 对偶问题为:min ω=Yb;YA≥C;Y ≥0
因X(0)是原问题的可行解,所以AX(0)≤b
又因Y(0)是对偶问题的可行解,所以Y(0)A≥C
Y (0) A X(0) ≤ Y (0) b
Y (0) A X(0) ≥ CX (0)
因此, CX(0) ≤Y(0) A X(0) ≤ Y(0) b 结论成立。
20
军事运筹学
6﹒互补松弛性:若X(0)是原问题的可行解, Y(0)是对偶 问题的可行解,则YξX(0)=0和Y(0)Xξ=0 当且仅当X(0), Y(0)是最优解。
证: 设原问题和对偶问题的标准型是
max z=CX AX+xξ=b X≥0,Xξ ≥0
min ω =Yb YA-Yξ=C Y≥0,Yξ ≥0
6
军事运筹学
4.1 对偶问题的提出
min ω=8 y1+16y2 +12y3
y1+4y2
≥2
2 y1 +4y3≥3
与
y1 , y2 ,y3≥0 12
max z=2x1+3x2 x1+ 2x2 ≤8
4x1
≤16
4x2 ≤12
x1﹐x2 ≥0
有何关 系?
对愿模型设: A= 4 0 04
b=(8,16,12)T C=(2,3)
X=(x1,x2)T
Y=(y1,y2 ,y3 ) 则可得:
max z=CX AX≤b (5.1) 和
min ω =Yb YA ≥ C (5.2)
X≥0
Y≥0
我们把(5.2)式的问题称为(5.1)式问题的对偶线 性规划问题。
7
军事运筹学
