文档:物理光学作业参考答案4
人教版高中物理选修3-4光的反射和折射练习及答案.doc

高中物理学习材料唐玲收集整理光的反射和折射练习及答案光的直线传播1.下列现象中能说明光是沿直线传播的是(A) 小孔成像 (B) 日食、月食(C) 海市蜃楼 (D) 射击中的三点一线解:(ABD)“海市蜃楼”现象说明光在不均匀介质(密度不一样的各空气层)中会发生折射,以至于全反射现象。
(在后面将了解到全反射)沙漠中,在沙面上方较高处的空气层比贴近沙面的空气层受热少,密度较大。
这样,沙面上的空气形成了上密下疏的状况。
从远处景物—绿树射来的光线穿过着上密下疏的空气层时就要发生折射,入射角逐渐增大,当达到临界角时,就会发生全反射,应而看到湖水得倒影,见图:空气层高,温度高,(空气导热不好)密度小,折射率小空气层较接近海面,温度低,(水海面上的“海市蜃楼”的形成过程也是上述道理。
见上图。
2.关于日食和月食的说法正确的是(A) 日全食是在地球的本影中发生的(B) 日环食是在月球的伪本影中发生的(C) 月偏食是在地球的半影区中发生的(D) 月偏食是在地球的本影区中发生的解:(BD )日食不再说了,月蚀是怎么会事呢?月球本身不是光源,反射太阳光而被我们看见。
发生月蚀时,太阳、地球、月球几近排在一条直线上,太阳照射地球在地球后面留下影子,有半影区和本影区,当月球一部分进入半影区时,有一部分太阳光被挡住,但月球向着地球的一面仍能反射另一部分太阳光而被我们看见,此时月球比平常略暗;当月球一部分进入本影区,一部分在半影区,则进入本影的部分不反射任何太阳光,为全黑,如图所示。
因此,月偏食是在月球一部分进入本影区,一部分在半影区时发生的;当月球全部进入本影区时,发生月全食。
注意:关键是我们总是在地球上观察!3.如图所示,小球位于距墙MO 和地面NO 等远的一点A ,在球的右边紧靠小球有一点光源S. 当小球以速度v 水平抛出后,恰好落在墙角O 处,当小球在空中运动时,在墙上就有球的影子由上向下运动,其影子中心的运动是(A) 匀速直线运动(B) 初速度为零的匀加速直线运动,加速度小于g(C) 自由落体运动 (D) 变加速运动 解:(A )设光源(即小球初始位置)到墙的距离为d,小球的影子在位置1;当小球经过时间t 下落到某一位置时,光照着它在墙上留下的影子在位置2;1、2两个位置之间的距离可以这样求出:太阳 地球 月球 M AS v 1 23θ在三角形12A 中,S 12=d ·tan θ而由平抛运动的知识我们知道,tan θ=t v gt 0221=02v gt 因此,S 12=d ·tanθ=02v dgt也就是说,影子的位移与时间成正比!当然,它对应的运动应为匀速直线运动。
物理光学晶体光学答案

物理光学作业参考答案[15-1] 一束自然光以ο30角入射到玻璃-空气界面,玻璃的折射率54.1=n ,试计算(1)反射光的偏振度;(2)玻璃-空气界面的布儒斯特角;(3)以布儒斯特角入射时透射光的偏振度。
解:(1)入射自然光可以分解为振动方向互相垂直的s 波和p 波,它们强度相等,设以0I 表示。
已知:ο301=θ,所以折射角为:οο35.50)30sin 54.1(sin )sin (sin 1112=⨯==--θθn 根据菲涅耳公式,s 波的反射比为:12.0)35.5030sin()35.5030sin()sin()sin(222121=⎥⎦⎤⎢⎣⎡+-=⎥⎦⎤⎢⎣⎡+-=οοοοθθθθρs 4 因此,反射波中s 波的强度:00)(124.0I I I s R s ==ρ而p 波的反射比为:004.0881.5371.0)()(222121=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+-=θθθθρtg tg p 因此,反射波中p 波的强度: 00)(004.0I I I p R p==ρ于是反射光的偏振度: %94%8.93004.0124.0004.0124.00000≈=+-=I I I I P(2)玻璃-空气界面的布儒斯特角: ο3354.11111121====---tg n tg n n tgB θ (3)对于以布儒斯特角入射时的透射光,s 波的透射系数为: 4067.133cos 57sin 2cos sin 2)sin(cos sin 2122112===+=οοθθθθθθs t式中,ο331==B θθ,而οο57902=-=B θθ 所以,s 波的透射强度为:002021122)(834.04067.133cos 54.157cos 0.1)cos cos (I I I t n n Is T s=⨯==οοθθ 而p 波的透射系数为:5398.1)5733cos(4067.1)cos()cos()sin(cos sin 221212112=-=-=-+=οοθθθθθθθθs p t t所以,p 波的透射强度为: 002021122)(9998.05398.133cos 54.157cos 0.1)cos cos (I I I t n n Ip T p=⨯==οοθθ 所以,透射光的偏振度: %9834.09998.0834.09998.00000=+-=I I I I P[15-3]选用折射率为的硫化锌和折射率为的氟化镁作镀膜材料,制作用于氦氖激光()8.632nm =λ的偏振分光镜。
大学物理光学习题附答案
[
]
33.5649:在如图所示的夫琅禾费衍射装置中,将单缝宽
度 a 稍稍变窄,同时使会聚透镜 L 沿 y 轴正方向作微小平移(单缝与
屏幕位置不动),则屏幕 C 上的中央衍射条纹将
(A) 变宽,同时向上移动
(B) 变宽,同时向下移动
(C) 变宽,不移动
(D)
变窄,同时向上移动
(E) 变窄,不移动
[
]
34.5650:在如图所示的单缝夫琅禾费衍射装置中,设中央明
的部分
(A) 凸起,且高度为 / 4
(B) 凸起,且高度为 / 2
(C) 凹陷,且深度为 / 2
(D) 凹陷,且深度为 / 4 [
]
平玻璃
空气劈尖
工件
O
n=1.68
n=1.60 n=1.58
O
3507 图
14.3507:如图所示,平板玻璃和凸透镜构成牛顿环装置,全 部浸入 n=1.60 的液体中,凸透镜可沿 OO 移动,用波长=500 nm(1nm=109m)的单色光垂直入射。 从上向下观察,看到中心是一个暗斑,此时凸透镜顶点距平板玻璃 的距离最少是
(C) 向棱边方向平移,条纹间隔不变
(D) 向远离棱边的方向平移,条纹间隔不变
(E)
向远离棱边的方向平移,条纹间隔变小
[
]
19.5326:两块平玻璃构成空气劈形膜,左边为棱边,用单色
平行光垂直入射。若上面的平玻璃以棱边为轴,沿逆时针方向作微
小转动,则干涉条纹的
(A) 间隔变小,并向棱边方向平移
(B) 间隔变大,并向远离棱边方向平移
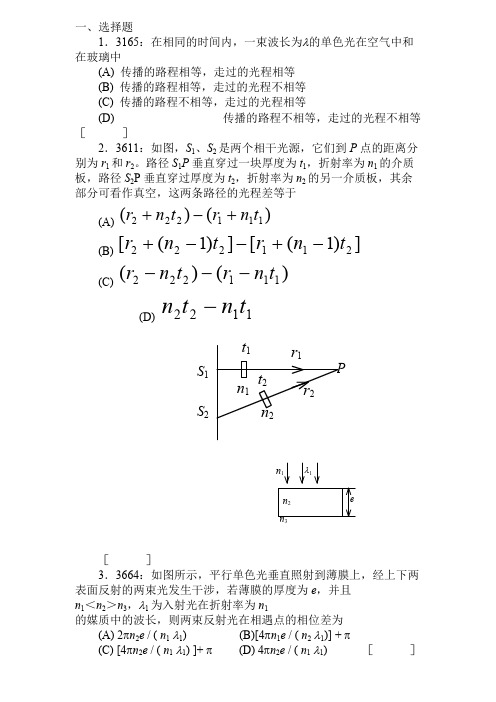
一、选择题 1.3165:在相同的时间内,一束波长为的单色光在空气中和
在玻璃中
工程光学物理光学参考答案

物理光学作业参考答案[13-1] 波长nm 500=λ的单色光垂直入射到边长3cm 的方孔,在光轴(它通过孔中心并垂直孔平面)附近离孔z 处观察衍射,试求出夫琅和费衍射区的大致范围。
解:夫琅和费衍射条件为:π<<+zy x k2)(max2121 即: m nm y x z 900109.0500)1015()1015()(122626max2121=⨯=⨯+⨯=+>>λ[13-3]平行光斜入射到单缝上,证明:(1)单缝夫琅和费衍射强度公式为20)sin (sin )]sin (sin sin[⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=i a i a I I θλπθλπ 式中,0I 是中央亮纹中心强度;a 是缝宽;θ是衍射角,i 是入射角(见图)。
证明:(1缝上任意点Q 的位矢:单逢上光场的复振幅为:因此,观察面上的夫琅和费衍射场为: (其中: ))cos ,0,(sin i i k k =)0,,(11y x r = 1sin 1)(~x i ik rk i Ae Ae x E ⋅⋅== )sin (sin )]sin (sin sin[)(~1)(~)2(1122)sin (sin )2(11sin 22sin )2(11221)2(11211211112111121i a i a ae z A dx e e z i A dx e e e z i A dx e x E e z i x E z x z ik a a x i ik z x z ik x ik a a x i ik z x z ik x z x ik a az x z ik --====+---+⋅--⋅+--+⎰⎰⎰θλπθλπλλλλθθθsin 1≈z x所以,观察面上的光强分布为:式中:(2)第一暗点位置:[13-4]在不透明细丝的夫琅和费衍射图样中,测得暗条纹的间距为1.5mm ,所用透镜的焦距为30mm ,光波波长为632.8nm 。
大学物理光学试题及答案

大学物理光学试题及答案一、选择题(每题2分,共20分)1. 光的干涉现象是由于光波的:A. 反射B. 折射C. 衍射D. 叠加答案:D2. 以下哪种现象不属于光的波动性质?A. 干涉B. 衍射C. 反射D. 偏振答案:C3. 光的偏振现象说明光是:A. 横波B. 纵波C. 非波D. 随机波答案:A4. 光的双缝干涉实验中,当缝间距增加时,干涉条纹的间距将:A. 增加B. 减少C. 不变D. 先增加后减少答案:A5. 光的折射定律是由哪位科学家提出的?A. 牛顿B. 爱因斯坦C. 胡克D. 斯涅尔答案:D6. 光的全反射现象发生时,光的入射角必须:A. 小于临界角B. 大于临界角C. 等于临界角D. 与临界角无关答案:B7. 光的衍射现象表明光具有:A. 粒子性B. 波动性C. 随机性D. 确定性答案:B8. 光的多普勒效应是指:A. 光的颜色变化B. 光的频率变化C. 光的强度变化D. 光的相位变化答案:B9. 光的波长越长,其频率:A. 越高B. 越低C. 不变D. 无法确定答案:B10. 光的色散现象是由于:A. 光的折射B. 光的反射C. 光的干涉D. 光的衍射答案:A二、填空题(每空1分,共20分)1. 光的干涉现象中,两束相干光波的相位差为________时,会产生干涉加强。
答案:0或π2. 光的偏振方向与光的传播方向垂直,说明光是________波。
答案:横3. 光的波长与频率的关系是________。
答案:成反比4. 在光的双缝干涉实验中,若两缝间距为d,屏幕到缝的距离为L,则干涉条纹间距为________。
答案:λL/d5. 光的全反射发生时,光从光密介质进入光疏介质,且入射角大于临界角,临界角的计算公式为________。
答案:sinC = 1/n6. 光的多普勒效应中,当光源向观察者移动时,观察到的光频率会________。
答案:增加7. 光的色散现象是由于不同波长的光在介质中的折射率不同,导致________。
新概念物理光学习题答案

新概念物理光学习题答案新概念物理光学习题答案光学作为物理学的一个重要分支,研究光的传播、反射、折射和干涉等现象。
在学习光学的过程中,我们常常会遇到一些习题,通过解答这些习题可以更好地理解光学的原理和应用。
本文将为大家提供一些新概念物理光学习题的答案,希望能够帮助大家更好地掌握光学知识。
1. 一束光从空气射入玻璃介质,发生折射现象。
如果入射角为30°,折射角为20°,求玻璃的折射率。
解答:根据折射定律,光线从空气射入玻璃介质时,入射角i和折射角r之间的关系为:n1*sin(i) = n2*sin(r)。
其中,n1为空气的折射率,近似为1;n2为玻璃的折射率,待求。
代入已知条件,得到:1*sin(30°) = n2*sin(20°)。
解方程可得,n2 ≈ 1.5。
所以,玻璃的折射率约为1.5。
2. 一束光从空气射入水中,发生折射现象。
已知水的折射率为1.33,求光线从水中射入空气时的折射角。
解答:同样利用折射定律,光线从水中射入空气时,入射角i和折射角r之间的关系为:n1*sin(i) = n2*sin(r)。
其中,n1为水的折射率,n2为空气的折射率。
代入已知条件,得到:1.33*sin(i) = 1*sin(r)。
由于光线从水中射入空气,空气的折射率近似为1。
解方程可得,sin(r) ≈ 1.33*sin(i)。
再利用反正弦函数,可求得折射角r的近似值。
所以,光线从水中射入空气时的折射角约为反正弦(1.33*sin(i))。
3. 一束光从空气射入玻璃球,球的折射率为1.5。
已知入射角为60°,求光线在球内的传播路径。
解答:当光线从空气射入玻璃球时,由于两种介质的折射率不同,光线会发生折射现象。
根据折射定律,入射角i和折射角r之间的关系为:n1*sin(i) =n2*sin(r)。
其中,n1为空气的折射率,n2为玻璃球的折射率。
代入已知条件,得到:1*sin(60°) = 1.5*sin(r)。
大学物理光学答案Word版
第十七章光的干涉一. 选择题1.在真空中波长为的单色光,在折射率为n的均匀透明介质中从月沿某一路径传播到氏若儿万两点的相位差为3 ,则路径初的长度为:(D )A. 1・ 5B. 1. onC. 3D. 1.5 /n解: △卩=二-nil = 3/r所以d= 1.52/n本题答案为D。
2.在杨氏双缝实验中, 若两缝之间的距离稍为加大,英他条件不变,则干涉条纹将(A)A. 变密B.变稀C.不变D.消失解:条纹间距= 所以/增大,Ar变小。
干涉条纹将变密。
本题答案为A。
3.在空气中做双缝干涉实验,屏幕E上的P处是明条纹。
若将缝S:盖住,并在S,、S:连线的垂直平分而上放一平面反射镜氐其它条件不变(如图),则此时(B )A.P处仍为明条纹B.P处为暗条纹C.P处位于明、暗条纹之间D.屏幕E上无干涉条纹解对于屏幕E上方的P点,从S,直接入射到屏幕E上和从出发5经平而反射镜M 反射后再入射到屏幕上的光相位差在均比原来增,因此原来是明条纹的将变为暗条纹,而原来的暗条纹将变为明条纹。
故本题答案为B。
4.在薄膜干涉实验中,观察到反射光的等倾干涉条纹的中心是亮斑,则此时透射光的等倾干涉条纹中心是(B )A.亮斑B.暗斑C.可能是亮斑,也可能是暗斑D.无法确泄解:反射光和透射光的等倾干涉条纹互补。
本题答案为&5.一束波长为的单色光由空气垂宜入射到折射率为刀的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜最小的厚度为(B )A. /4B. / (4n)C・ /2 D・/ (2n)6.在折射率为m =1.60的玻璃表而上涂以折射率沪1.38的MgF:透明薄膜,可以减少光的反射。
当波长为500. Onm的单色光垂直入射时,为了实现最小反射,此透明薄膜的最小厚度为(C )A. 5. OnmB. 30. OnmC. 90.6nmD. 250. Onm解:增透膜e min = A/4n = 90.6 nm本题答案为C。
物理第3-4讲光学作业
35. 如果两个偏振片堆叠在一起,且偏振化方向之间夹角为 45°,假设二者对 光无吸收,光强为 I0 的自然光垂直射在偏振片上,则出射光强为:【 】。
(A) I0 4
(B) 3I 0 8
(C) I0 2
(D) 3I 0 4
2008-36. 一束波长为 的单色光分别在空气和在玻璃中传播,则在相同的传播
2101-32. 在双缝干涉实验中,光的波长 600nm,双缝间距 2mm,双缝与屏的间距 为 300cm,则屏上形成的干涉图样的相邻条纹间距为:【 】。 (A)0.45mm (B)0.9mm (C)9mm (D)4.5mm
2010-33. 在双缝干涉实验中,若在两缝后(靠近屏一侧)各覆盖一块厚度均为 d ,
(A) D a
(B) D 2a
(C) 2D a
(D) D 4a
2013
2013-32. 两偏振片叠放在一起,欲使一束垂直入射的线偏振光经过这两个偏振 片后振动方向转过 90°,且使出射光强尽可能大,则入射光的振动方向与前后 二偏振片的偏振化方向夹角分别为:( )。 (A)45°和 90° (B)0°和 90° (C)30°和 90° (D)60°和 90°
A.2.24×10-3rad
B.1.12×10-4rad
C.2.24×10-4rad
D.1.12×10-3rad
2016-36.在光栅光谱中,假如所有偶数级次的主极大都恰好在每透光栅衍射的暗 纹方向上,因而时间上不出现,那么此光栅每个透光缝宽度 a 和相邻两缝间
6/7
不透光部分宽度 b 的关系为: A.a=2b C.a=b
已知通过此两偏振片后的光强为 I ,则入射至第二偏振片的线偏振光强度为:
A. I C. 3I
大学物理光学练习题及答案详解(word文档良心出品)
光学练习题一、 选择题11. 如图所示,用厚度为d 、折射率分别为n 1和n 2 (n 1<n 2)的两片透明介质分别盖住杨氏双缝实验中的上下两缝, 若入射光的波长为, 此时屏上原来的中央明纹处被第三级明纹所占据, 则该介质的厚度为 [ ] (A) λ3(B) 123n n -λ(C) λ2(D)122n n -λ17. 如图所示,在杨氏双缝实验中, 若用一片厚度为d 1的透光云母片将双缝装置中的上面一个缝挡住; 再用一片厚度为d 2的透光云母片将下面一个缝挡住, 两云母片的折射率均为n , d 1>d 2, 干涉条纹的变化情况是 [ ] (A) 条纹间距减小(B) 条纹间距增大 (C) 整个条纹向上移动(D) 整个条纹向下移动18. 如图所示,在杨氏双缝实验中, 若用一片能透光的云母片将双缝装置中的上面一个缝盖住, 干涉条纹的变化情况是 [ ] (A) 条纹间距增大(B) 整个干涉条纹将向上移动 (C) 条纹间距减小(D) 整个干涉条纹将向下移动26. 如图(a)所示,一光学平板玻璃A 与待测工件B 之间形成空气劈尖,用波长λ=500nm(1nm = 10-9m)弯曲部分的顶点恰好与其右边条纹的直线部分的切线相切.则工件的上表面缺陷是[ ] (A) 不平处为凸起纹,最大高度为500 nm(B) 不平处为凸起纹,最大高度为250 nm (C) 不平处为凹槽,最大深度为500 nm (D) 不平处为凹槽,最大深度为250 nm43. 光波的衍射现象没有声波显著, 这是由于[ ] (A) 光波是电磁波, 声波是机械波 (B) 光波传播速度比声波大(C) 光是有颜色的(D) 光的波长比声波小得多53. 在图所示的单缝夫琅禾费衍射实验中,将单缝K平移,则[ ] (A) 衍射条纹移动,条纹宽度不变(B) 衍射条纹移动,条纹宽度变动 (C) 衍射条纹中心不动,条纹变宽 (D) 衍射条纹不动,条纹宽度不变54. 在图所示的单缝夫琅禾费衍射实验中,将单缝宽度 a 稍稍变宽,同时使单缝沿x 轴正向作微小移动,则屏幕E 的中央衍射条纹将 [ ] (A) 变窄,同时上移(B) 变窄,同时下移 (C) 变窄,不移动 (D) 变宽,同时上移55. 在图所示的单缝夫琅禾费衍射实验中,将单缝宽度a 稍稍变窄,同时使汇聚透镜L 2沿x 轴正方向作微小移动,则屏幕E 上的中央衍射条纹将[ ] (A) 变宽,同时上移(B) 变宽,同时下移 (C) 变宽,不移动 (D) 变窄,同时上移56. 一衍射光栅由宽300 nm 、中心间距为900 nm 的缝构成, 当波长为600 nm 的光垂直照射时, 屏幕上最多能观察到的亮条纹数为[ ] (A) 2条 (B) 3条 (C) 4条 (D) 5条57. 白光垂直照射到每厘米有5000条刻痕的光栅上, 若在衍射角ϕ = 30°处能看到某一波长的光谱线, 则该光谱线所属的级次为 [ ] (A) 1 (B) 2 (C) 3 (D) 483. 如图所示,起偏器A 与检偏器B 的偏振化方向相互垂直,偏振片C 位于A 、B 中间且与A 、B 平行,其偏振化方向与A 的偏振化方向成30°夹角. 当强度为I 的自然光垂直射向A 片时,最后的出射光强为 [ ] (A) 0(B)2I (C)8I(D) 以上答案都不对84. 如图所示,一束光强为I 0的自然光相继通过三块偏振片P 1、P 2、P 3后,其出射光的强度为8I I =.已知P 1和P 3的偏振化方向相互垂直.若以入射光线为轴转动P 2, 问至少要转过多少角度才能出射光的光强度为零?[ ] (A) 30° (B) 45° (C) 60° (D) 90°IACI1P 32P86. 两偏振片堆叠在一起,一束自然光垂直入射其上时没有光线通过.当其中一偏振片慢慢转动时, 投射光强度发生的变化为 [ ] (A) 光强单调增加(B) 光强先增加,后又减小至零 (C) 光强先增加,后减小,再增加(D) 光强先增加,然后减小,再增加,再减小至零1. 在相同的时间内,一束波长为λ的单色光在空气和在玻璃中[ ] (A) 传播的路程相等,走过的光程相等 (B) 传播的路程相等,走过的光程不相等 (C) 传播的路程不相等,走过的光程相等 (D) 传播的路程不相等,走过的光程不相2. 真空中波长为的单色光, 在折射率为n 的均匀透明介质中从a 点沿某一路径传到b点.若a 、b 两点的相位差为π3,则此路径的长度为[ ] (A)n23λ (B)nλ3 (C)λ23 (D)λn 23 3. 相干光波的条件是振动频率相同、相位相同或相位差恒定以及[ ] (A) 传播方向相同 (B) 振幅相同 (C) 振动方向相同 (D) 位置相同4. 如图所示,有两个几何形状完全相同的劈形膜:一个由空气中的玻璃形成玻璃劈形膜; 一个由玻璃中的空气形成空劈形膜.当用相同的单色光分别垂直照射它们时, 从入射光方向观察到干涉条纹间距较大的是[ ] (A) 玻璃劈形膜(B) 空气劈形膜(C) 两劈形膜干涉条纹间距相同 (D) 已知条件不够, 难以判定5. 用波长可以连续改变的单色光垂直照射一劈形膜, 如果波长逐渐变小, 干涉条纹的变化情况为[ ](A) 明纹间距逐渐减小, 并背离劈棱移动 (B) 明纹间距逐渐变小, 并向劈棱移动 (C) 明纹间距逐渐变大, 并向劈棱移动 (D) 明纹间距逐渐变大, 并背向劈棱移动 6. 牛顿环实验中, 透射光的干涉情况是[ ] (A) 中心暗斑, 条纹为内密外疏的同心圆环 (B) 中心暗斑, 条纹为内疏外密的同心圆环 (C) 中心亮斑, 条纹为内密外疏的同心圆环 (D) 中心亮斑, 条纹为内疏外密的同心圆环7. 若用波长为的单色光照射迈克耳孙干涉仪, 并在迈克耳孙干涉仪的一条光路中放入一厚度为l 、折射率为n 的透明薄片, 则可观察到某处的干涉条纹移动的条数为[ ](A)λln )1(4- (B)λln(C)λln )1(2- (D)λln )1(-8. 如图12-1-44所示,波长为 的单色光垂直入射在缝宽为a 的单缝上, 缝后紧靠着焦距为f 的薄凸透镜, 屏置于透镜的焦平面上,出现的中央明纹宽度为[ ] (A) na f λ(B) na f λ (C)naf λ2(D)anf λ2 9. 在一光栅衍射实验中,若衍射光栅单位长度上的刻痕数越多, 则在入射光波长一定的情况下, 光栅的[ ] (A) 光栅常数越小(B) 衍射图样中亮纹亮度越小 (C) 衍射图样中亮纹间距越小(D) 同级亮纹的衍射角越小10. 一束平行光垂直入射在一衍射光栅上, 当光栅常数)(b a +为下列哪种情况时(a 为每条缝的宽度, b 为不透光部分宽度) , k = 3, 6, 9, …等级次的主极大均不出现.[ ] (A) a b a 2=+ (B) a b a 3=+ (C) a b a 4=+(D) a b a 6=+11. 自然光以 60的入射角照射到不知其折射率的某一透明介质表面时,反射光为线偏振光,则[ ](A) 折射光为线偏振光,折射角为 30 (B) 折射光为部分线偏振光,折射角为 30 (C) 折射光为线偏振光,折射角不能确定 (D) 折射光为部分线偏振光,折射角不能确定 12. 关于光的干涉,下面说法中唯一正确的是[ ](A) 在杨氏双缝干涉图样中, 相邻的明条纹与暗条纹间对应的光程差为2λ (B) 在劈形膜的等厚干涉图样中, 相邻的明条纹与暗条纹间对应的厚度差为2λ (C) 当空气劈形膜的下表面往下平移2λ时, 劈形膜上下表面两束反射光的光程差将增加2λ (D) 牛顿干涉圆环属于分波振面法干涉二、 填空题1. 如图12-2-1所示,折射率为2n 、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为1n 和3n ,已知321n n n ><,若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下表面反射的光束(用①与②示意)的光程差是2. 真空中波长 = 400 nm 的紫光在折射率为 n =1.5 的介质中从A 点传到B 点时, 光振动的相位改变了5, 该光从A 到B 所走的光程为 .4. 如图所示,在双缝干涉实验中SS 1=SS 2,用波长为λ的光照射双缝S 1和S 2,通过空气后在屏幕E 上形成干涉条纹.已知P 点处为第三级明条纹,则S 1和S 2到P 点的光程差为 ____________.若将整个装置放于某种透明液体中,P 点为第四级明条纹,则该液体的折射率n = ____________.5. 两条狭缝相距2 mm, 离屏300 cm, 用600 nm 的光照射时, 干涉条纹的相邻明纹间距为___________mm.6. 将一块很薄的云母片(n = 1.58)覆盖在杨氏双缝实验中的一条缝上,这时屏幕上的中央明纹中心被原来的第7级明纹中心占据.如果入射光的波长λ = 550 nm, 则该云母片的厚度为___________.9. 如图所示,在玻璃(折射率n 3 = 1.60)表面镀一层MgF 2(折射n 2=1.38)薄膜作为增透膜.为了使波长为500 nm 的光从空气(折射率n 1=1.00)正入射时尽可能减少反射,MgF 2膜的最小厚度应是 . 10. 用白光垂直照射厚度e = 350 nm 的薄膜,若膜的折射率n 2 = 1.4 , 薄膜上面的介质折射率为n 1,薄膜下面的介质折射率为n 3,且n 1 < n 2 < n 3.则透射光中可看到的加强光的波长为 .14. 波长为λ的平行单色光垂直地照射到劈尖薄膜上,劈尖薄膜的折射率为n ,第二级明纹与第五条明纹所对应的薄膜厚度之差是 _____________. 15. 两玻璃片中夹满水(水的折射率34=n )形成一劈形膜, 用波长为λ的单色光垂直照射其上, 若要使某一条纹从明变为暗, 则需将上面一片玻璃向上平移 .22. 若在迈克耳孙干涉仪的可动反射镜M 移动0.620mm 的过程中,观察到干涉条纹移动了2300条,则所用光波的波长为 .23. 在迈克耳孙干涉仪的一条光路中,放入一折射率为n ,厚度为d 的透明介质薄片,放入后,这条光路的光程改变了 .25. 如果单缝夫琅禾费衍射的第一级暗纹发生在衍射角为30=ϕ的方位上,所用的单色光波长为nm 500=λ,则单缝宽度为 .26. 一束平行光束垂直照射宽度为1.0 mm 的单缝上,在缝后放一焦距为2.0 mm 的汇聚透镜.已知位于透镜焦平面处的中央明纹的宽度为2.0 mm ,则入射光波长约为 . 29 用半波带法讨论单缝衍射暗条纹中心的条件时,与中央明条纹旁第三个暗条纹中心相对应的半波带的数目是__________.30. 平行单色光垂直入射于单缝上,观察夫琅禾费衍射.若屏上P 点处为第三级暗纹,则单缝处波面相应地可划分为___________ 个半波带.若将单缝宽度缩小一半,P 点处将是_________级________纹.36. 一衍射光栅, 狭缝宽为a , 缝间不透明部分宽为b .当波长为600 nm 的光垂直照射时, 在某一衍射角 ϕ 处出现第二级主极大.若换为400 nm 的光垂直入射时, 则在上述衍射角 ϕ 处出现缺级, b 至少是a 的 倍.38. 已知衍射光栅主极大公式(a +b ) sin ϕ=±k λ,k =0, 1, 2, ….在k =2的方向上第一条缝与第六条缝对应点发出的两条衍射光的光程差∆=_____________.40. 当自然光以58︒角从空气射入到玻璃板表面上时, 若反射光为线偏振光, 则透射光的折射角为_________.41. 一束自然光入射到空气和玻璃的分界面上, 当入射角为60︒时反射光为完全偏振光, 则此玻璃的折射率为_________.44. 一束由自然光和线偏振光组成的混合光,让它垂直通过一偏振片.若以此入射光束轴旋转偏振片,测得透射光强度的最大值是最小值的7倍;那么入射光束自然光和线偏振光的光强比为_____________.三、 计算题8. 用白光垂直照射置于空气中的厚度为0.50 μm 的玻璃片.玻璃片的折射率为1.50.在可见光范围内(400 nm ~ 760 nm)哪些波长的反射光有最大限度的增强? 13. 图12-3-13所示为一牛顿环装置,设平凸透镜中心恰好与平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm .(1) 求入射光的波长;(2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.18. 在某个单缝衍射实验中,光源发出的光含有两种波长1λ和2λ,并垂直入射于单缝上.假如1λ的第一级衍射极小与2λ的第二级衍射极小相重合,试问:(1) 这两种波长之间有何关系?(2) 在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合?19. 某种单色平行光垂直地入射在一单缝上, 单缝的宽度a = 0.15 mm .缝后放一个焦距f = 400 mm 的凸透镜,在透镜的焦平面上,测得中央明条纹两侧的两个第三级暗条纹之间的距离为8.0 mm ,求入射光的波长.30. 一衍射光栅,每厘米有200条透光缝,每条透光缝宽为a = 2⨯10-3 cm ,在光栅后方一焦距f = 1 m 的凸透镜.现以nm 600=λ的单色平行光垂直照射光柵,求:(1) 透光缝a 的单缝衍射中央明区条纹宽度; (2) 在透光缝a 的单缝衍射中央明纹区内主极大条数.31. 波长λ = 600nm 的单色光垂直入射到一光柵上,测得第二级主级大的衍射角为30o ,且第三级是缺级.(1) 光栅常量(a +b )等于多少?(2) 透光缝可能的最小宽度a 等于多少?(3) 在选定了上述(a +b )和a 之后,求在屏幕上可能呈现的全部主极大的级次.36 两个偏振片叠在一起,欲使一束垂直入射的线偏振光经过这两个偏振片之后振动方向转过了90°,且使出射光强尽可能大,那么入射光振动方向和两偏振片的偏振化方向之间的夹角应如何选择?这种情况下的最大出射光强与入射光强的比值是多少?。
物理光学梁铨廷版习题答案
第一章光的电磁理论1.1在真空中传播的平面电磁波,其电场表示为Ex=0,Ey=0,Ez=,(各量均用国际单位),求电磁波的频率、波长、周期和初相位。
解:由Ex=0,Ey=0,Ez=,则频率υ===0.5×1014Hz,周期T=1/υ=2×10-14s,初相位φ0=+π/2(z=0,t=0),振幅A=100V/m,波长λ=cT=3×108×2×10-14=6×10-6m。
1.2.一个平面电磁波可以表示为Ex=0,Ey=,Ez=0,求:(1)该电磁波的振幅,频率,波长和原点的初相位是多少?(2)波的传播和电矢量的振动取哪个方向?(3)与电场相联系的磁场B的表达式如何写?解:(1)振幅A=2V/m,频率υ=Hz,波长λ==,原点的初相位φ0=+π/2;(2)传播沿z轴,振动方向沿y 轴;(3)由B=,可得By=Bz=0,Bx=1.3.一个线偏振光在玻璃中传播时可以表示为Ey=0,Ez=0,Ex=,试求:(1)光的频率;(2)波长;(3)玻璃的折射率。
解:(1)υ===5×1014Hz;(2)λ=;(3)相速度v=0.65c,所以折射率n=1.4写出:(1)在yoz平面内沿与y 轴成θ角的方向传播的平面波的复振幅;(2)发散球面波和汇聚球面波的复振幅。
解:(1)由,可得;(2)同理:发散球面波,汇聚球面波。
1.5一平面简谐电磁波在真空中沿正x方向传播。
其频率为Hz,电场振幅为14.14V/m,如果该电磁波的振动面与xy平面呈45º,试写出E,B 表达式。
解:,其中===,同理:。
,其中=。
1.6一个沿k方向传播的平面波表示为E=,试求k 方向的单位矢。
解:,又,∴=。
1.9证明当入射角=45º时,光波在任何两种介质分界面上的反射都有。
证明:====1.10证明光束在布儒斯特角下入射到平行平面玻璃片的上表面时,下表面的入射角也是布儒斯特角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理光学作业参考答案[15-1] 一束自然光以30角入射到玻璃-空气界面,玻璃的折射率54.1=n ,试计算(1)反射光的偏振度;(2)玻璃-空气界面的布儒斯特角;(3)以布儒斯特角入射时透射光的偏振度。
解:(1)入射自然光可以分解为振动方向互相垂直的s 波和p 波,它们强度相等,设以0I 表示。
已知: 301=θ,所以折射角为:35.50)30sin 54.1(sin )sin (sin 1112=⨯==--θθn根据菲涅耳公式,s 波的反射比为:12.0)35.5030sin()35.5030sin()sin()sin(222121=⎥⎦⎤⎢⎣⎡+-=⎥⎦⎤⎢⎣⎡+-= θθϑθρs 4 因此,反射波中s 波的强度:00)(124.0I I I s R s ==ρ而p 波的反射比为:004.0881.5371.0)()(222121=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+-=θθθθρtg tg p 因此,反射波中p 波的强度: 00)(004.0I I I p R p==ρ于是反射光的偏振度: %94%8.93004.0124.0004.0124.00000≈=+-=I I I I P(2)玻璃-空气界面的布儒斯特角:3354.11111121====---tg n tg n n tg B θ (3)对于以布儒斯特角入射时的透射光,s 波的透射系数为: 4067.133cos 57sin 2cos sin 2)sin(cos sin 2122112===+=θθθθθθs t式中,331==B θθ,而57902=-=B θθ 所以,s 波的透射强度为:002021122)(834.04067.133cos 54.157cos 0.1)cos cos (I I I t n n Is T s=⨯==θθ 而p 波的透射系数为:5398.1)5733cos(4067.1)cos()cos()sin(cos sin 221212112=-=-=-+=θθθθθθθθs p t t所以,p 波的透射强度为: 002021122)(9998.05398.133cos 54.157cos 0.1)cos cos (I I I t n n Ip T p=⨯==θθ 所以,透射光的偏振度: %9834.09998.0834.09998.00000=+-=I I I I P[15-3]选用折射率为2.38的硫化锌和折射率为1.38的氟化镁作镀膜材料,制作用于氦氖激光()8.632nm =λ的偏振分光镜。
试问(1)分光棱镜的折射率应为多少?(2)膜层的厚度分别应为多少?解:偏振分光镜材料的选取应使光线在相邻材料界面上的入射角等于布儒斯特角,从而使反射光成为线偏振光;膜层厚度的选取应使膜层上下表面反射的光满足干涉加强的条件。
因此:(1)H θ应为布儒斯特角,即1065.3038.238.111===--tg n n tg H L H θ 由题意知 45=i θ,故由折射定律,得:69.145sin 1065.30sin 38.2sin sin =⨯==i H H G n n θθ(2)在硫化锌膜和氟化镁膜分别满足条件:λλθλλθ=+=+2cos 22cos 2L L L H H H d n d n而:8659.07071.038.169.145sin sin 5021.07071.038.269.145sin sin =⨯===⨯==L G L H G H n n n n θθ所以,5002.0sin 1cos 8648.0sin 1cos 22=-==-=L L H H θθθθ于是得到:nmnmn d nmnmn d L L L HH H 2295002.038.148.632cos 4778648.038.248.632cos 4=⨯⨯===⨯⨯==θλθλ[15-5]方解石晶片的厚度d=0.013mm ,晶片的光轴与表面成60角,当波长nm 8.632=λ的氦氖激光垂直入射到晶片时,求(1)晶片内o 、e 光线的夹角;(2)o 光和e 光的振动方向;(3)o 、e 光通过晶片后的相位差。
解:当波长nm 8.632=λ时方解石的主折射率查表知:486.1,658.1==e o n n(1) o 光遵守折射定律,因此它将不偏折地通过晶片。
此外,由惠更斯作图法,可知e光波法线的方向与o 光相同,故'221221'423571.3530486.1658.1306090==⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡==-=--tg tg tg n n tg e o θθθ 由此得到o 光与e 光的夹角:'''425304235 =-=-=θθα(2) 由于o 光和e 光都在图面内(见图),所以图面是o 光和e 光的共同主平面。
o 光的振动方向垂直于图面,以黑点表示。
e 光的振动方向在图面内,以线条表示。
(3) e 光波法线方向与光轴成30时的折射率为: 6095.130sin 30cos 2222"=+=oeeo e n n n n n因此,o 、e 光通过晶片后的相位差: ππλπδ2013.0)6095.1658.1(108.6322)(26"≈⨯-⨯=-=-d n n e o[15-6] 一束汞绿光以60角入射到KDP(磷酸二氢钾)晶体表面,晶体的470.1,512.1==e o n n ,若光轴与晶面表面平行且垂直于入射面,试求晶体中o 光与e 光的夹角。
解:本题所设情况如下图所示。
这时,e 波波面与图面(入射面)的截线跟o 波波面的截线类似,都是圆形。
从图中容易看出,对于任意的入射角1θ,其正弦与e 光折射角e 2θ的正弦之比都为e ee e n V C t V t C R BD ADAE AD BD==⋅⋅===21sin sin θθ式中R 是e 波面的圆截线的半径。
由于c /V e 是一常数,所以在本题的特殊情况下,光线遵守普通的折射定律,它的折射方向可按上式计算。
当601=θ时,e 光的折射角: '111263647.160sin sin sin sin=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=--e en θθ 而o 光的折射角:'11125634512.160sin sin sin sin=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=--o on θθ因此晶体中o 光与e 光的夹角:'''221015634636 =-=-=o e θθα[15-7]如下图所示,一块单轴晶片的光轴垂直于表面,晶片的两个主折射率分别为o n 和e n ,证明当平面波以1θ入射到晶片时,晶体中非常光线的折射角'e θ可由下式给出 1221'sin sin θθθ-=ee o e n n n tg证明:如图,e 光波法线与光轴的夹角为e θ,由折射定律有:e e n n θθθsin sin sin "111==式中,e 光相应的折射率为: eee oeo e n n n n n θθ2222"cos sin +=由以上两式,解得 1221sin sin θθθ-=eo e e n n n tg而e 光线与光轴的夹角'e θ:122112212222'sin sin sin sin θθθθθθ-=-⋅==e e o e o e e o e e o en n n n n n n n tg n n tg得证。
[15-13] 石英晶体制成的塞拿蒙棱镜,每块的顶角是20(见图)。
光束正入射于棱镜,求从棱镜出射的o 光线与e 光线之间的夹角。
[注:此题条件不充分] 解:设入射光为钠黄光(波长为589.3nm),则石英的主折射率为:55335.1,54424.1==e o n n 。
光束通过第一块棱镜时,是沿光轴方向传播的,因此o 光和e 光不分开,传播速度也相等,o 光振动方向垂直于纸面,e 光振动方向平行于纸面。
振动方向垂直于纸面的这一支光束进入第二块棱镜后仍然是o 光,其传播方向不变。
而振动方向平行于纸面的这一支光束进入第二块棱镜后虽然仍为e 光,但其传播速度与在第一块棱镜时不同,因而在界面上发生折射,可由折射定律近似计算:88.1955335.120sin 54424.1sin sin sin 1112=⎥⎦⎤⎢⎣⎡⨯=⎥⎦⎤⎢⎣⎡=--e o en n θθ在棱镜后表面折射时,有:[][][]"'12111'1311186.0)88.1920sin(55335.1sin )sin(sin sin sin =≈-⨯=-==---e e e e e n n θθϕϕ此即从棱镜出射的o 光线与e 光线之间的夹角。
[15-14] 一束线偏振的钠黄光(nm 3.589=λ)垂直通过一块厚度为mm 210618.1-⨯的石英晶片。
晶片折射率为55335.1,54424.1==e o n n ,光轴沿x 轴方向(见图),试对于以下三种情况,决定出射光的偏振态:(1)入射线偏振光的振动方向与X 轴成45角; (2)入射线偏振光的振动方向与X 轴成—45 角; (3)入射线偏振光的振动方向与X 轴成30 角。
解:建立图中坐标系,晶片光轴平行于x 轴,且是慢轴,其产生的相位延迟:可见,晶片的作用相当于1/4波片。
该晶片的琼斯矩阵为: ⎥⎦⎤-⎢⎣⎡=i G 001(1)入射线偏振光的振动方向与x 轴成45°角,其琼斯矢量为:出射光为:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤-⎢⎣⎡==i i GE E 11100112 这是右旋圆偏振光。
(2)入射线偏振光的振动方向与x 轴成-45°角,其琼斯矢量为:出射光为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤-⎢⎣⎡==i i GE E 11100112 这是左旋圆偏振光。
(3)入射线偏振光的振动方向与x 轴成30°角,其琼斯矢量为:出射光为:⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤-⎢⎣⎡==30130cos 30sin 30cos 30sin 30cos 00112itg i i GE E 这是右旋椭圆偏振光。
[15-15] 设计一个产生椭圆偏振光的装置,使椭圆的长轴方向在竖直方向,且长短轴之比为2:1。
详细说明各元件的位置与方位。
解:为产生椭圆偏振光,首先让一束平行自然光垂直通过一起偏器,然后通过一1/4波片。
设椭圆的长轴方向沿Y 轴(竖直方向)正方向,椭圆的短轴方向沿X 轴正方向,波片的快轴沿Y 轴,波片的慢轴沿X 轴正方向,起偏器的透光轴与X 轴成β角,则自波片出射的椭圆偏振光的琼斯矢量为:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤-⎢⎣⎡=ββββββitg i i E 1cos sin cos sin cos 0012该椭圆偏振光的长短轴之比为:121212===βtg a a A A210618.155335.154424.110589.62d n n 226-e o ππλπδ≈⨯⨯-⨯=-=-⎥⎦⎤⎢⎣⎡=111E ⎥⎦⎤⎢⎣⎡-=111E ⎥⎥⎦⎤⎢⎢⎣⎡= 30sin 30cos 1E因此,起偏器的透光轴与X 轴的夹角应为:"'162663435.632 ===-tg β[15-16] 通过检偏器观察一束椭圆偏振光,其强度随着检偏器的旋转而改变。
