2018届湖北省襄阳市高三1月调研统一测试数学(文)试题(图片版,无答案)
2018-2019学年湖北省高三(上)元月调研数学试卷(理科)(解析版)
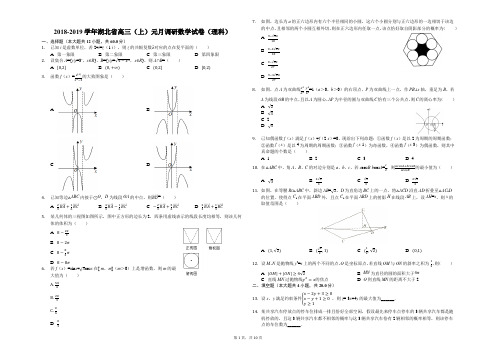
2018-2019学年湖北省高三(上)元月调研数学试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知i是虚数单位,若2+i=z(1-i),则z的共轭复数z−对应的点在复平面的()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.设集合A={y|y=3x,x∈R},B={y|y=√4−x2,x∈R},则A∩B=()A. [0,2]B. (0,+∞)C. (0,2]D. [0,2)3.函数f(x)=e|x|x2−3的大致图象是()A. B.C. D.4.已知等边△ABC内接于⊙O,D为线段OA的中点,则BD⃗⃗⃗⃗⃗⃗ =()A. 23BA⃗⃗⃗⃗⃗ +16BC⃗⃗⃗⃗⃗ B. 43BA⃗⃗⃗⃗⃗ −16BC⃗⃗⃗⃗⃗ C. −23BA⃗⃗⃗⃗⃗ +56BC⃗⃗⃗⃗⃗ D. 23BA⃗⃗⃗⃗⃗ +13BC⃗⃗⃗⃗⃗5.某几何体的三视图如图所示,图中正方形的边长为2,四条用虚线表示的线段长度均相等,则该几何体的体积为()A. 8−2π3B. 8−2πC. 8−83πD. 8−8π6.若f(x)=sin x+√3cos x在[-m,m](m>0)上是增函数,则m的最大值为()A.5π6B.2π3C.π6D. π37.如图,边长为a的正六边形内有六个半径相同的小圆,这六个小圆分别与正六边形的一边相切于该边的中点,且相邻的两个小圆互相外切,则在正六边形内任取一点,该点恰好取自阴影部分的概率为()A. 9−√3π18B. 9−4√3π18C. 9−√3π27D. 9−4√3π278.如图,点A为双曲线x2a2-y2b2=1(a>0,b>0)的右顶点,P为双曲线上一点,作PB⊥x轴,垂足为B,若A为线段OB的中点,且以A为圆心,AP为半径的圆与双曲线C恰有三个公共点,则C的离心率为()A. √2B. √3C. 2D. √59.已知偶函数f(x)满足f(x)+f(2-x)=0,现给出下列命题:①函数f(x)是以2为周期的周期函数;②函数f(x)是以4为周期的周期函数;③函数f(x-1)为奇函数,④函数f(x-3)为偶函数,则其中真命题的个数是()A. 1B. 2C. 3D. 410.在△ABC中,角A、B、C的对边分别是a、b、c,若a cos B-b cos A=c2,则acosA+bcosBacosB的最小值为()A. √3B. 4√33C. √33D. 2√3311.如图,在等腰Rt△ABC中,斜边AB=√2,D为直角边BC上的一点,将△ACD沿直AD折叠至△AC1D的位置,使得点C1在平面ABD外,且点C1在平面ABD上的射影H在线段AB上,设AH=x,则x的取值范围是()A. (1,√2)B. (√22,1) C. (12,√2) D. (0,1)12.设M,N是抛物线y2=x上的两个不同的点,O是坐标原点,若直线OM与ON的斜率之积为-12,则()A. |OM|+|ON|≥4√2B. MN为直径的圆的面积大于4πC. 直线MN过抛物线y2=x的焦点D. O到直线MN的距离不大于2二、填空题(本大题共4小题,共20.0分)13.设x,y满足约束条件{x−2y+3≥0x−y+1≥0y≥1,则z=-3x+4y的最大值为______.14.某共享汽车停放点的停车位排成一排且恰好全部空闲,假设最先来停车点停车的3辆共享汽车都是随机停放的,且这3辆共享汽车都不相邻的概率与这3辆共享汽车恰有2辆相邻的概率相等,则该停车点的车位数为______.15.《数书九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白.与著名的海伦公式完全等价,由此可以看出我国古代具有很高的数学水平,其求法是“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实,一为从偶,开平方得积”,若把这段文字写成公式,即S=√14[c2a2−(c2+a2−b 22)2],已知△ABC满足(sin A-sin B)(sin A+sin B)=sin A sin C-sin2C,且AB=2BC=2√2,则用以上给出的公式求得△ABC的面积为______.16.设函数f(x)=ax22e-ln|ax|(a>0),若函数f(x)有4个零点,则a的取值范围为______.三、解答题(本大题共7小题,共82.0分)17.已知等比数列{a n}为递增数列,且a52=a10,2(a n+a n+2)=5a n+1,数列{b n}的前n项和为S n,b1=1,b n≠0,b n b n+1=4S n-1.(1)求数列{a n}和{b n}的通项公式;(2)设c n=a n b n,求数列{c n}的前n项和T n.18.如图,在四棱锥P-ABCD中,AB⊥PC,AD∥BC,AD⊥CD,且PC=BC=2AD=2CD=2√2,PA=2.(1)PA⊥平面ABCD;(2)在线段PD上,是否存在一点M,使得二面角M-AC-D的大小为60°?如果存在,求PMPD的值;如果不存在,请说明理由.19.为发挥体育在核心素养时代的独特育人价值,越来越多的中学已将某些体育项目纳入到学生的必修课程,甚至关系到是否能拿到毕业证.某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究性学习小组随机从该校高一年级学生中抽取了100人进行调查,其中男生60人,且抽取的男生中对游泳有兴趣的占56,而抽取的女生中有15人表示对游泳没有兴趣.(1)试完成下面的2×2列联表,并判断能否有99%的把握认为“对游泳是否有兴趣与性别有关”?有兴趣没兴趣合计男生______ ______ ______女生______ ______ ______合计______ ______ ______()已知在被抽取的女生中有名高一()班的学生,其中名对游泳有兴趣,现在从这6名学生中随机抽取3人,求至少有2人对游泳有兴趣的概率.(3)该研究性学习小组在调查中发现,对游泳有兴趣的学生中有部分曾在市级和市级以上游泳比赛中获奖,如下表所示.若从高一(8)班和高一(9)班获奖学生中各随机选取2人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为ξ,求随机变量ξ的分布列及数学期望.班级一(1)一(2)一(3)一(4)一(5)一(6)一(7)一(8)一(9)一(10)…市级比赛获奖人数2233443342…市级以上比赛获奖人数2210233212…P(K2≥k0)0.5000.4000.2500.1500.1000.0500.0250.0100.0050.001k00.4550.708 1.323 2.072 2.706 3.841 5.024 6.6357.87910.828K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)20.已知椭圆Γ:x2a2+y2b2=1(a>b>0)的右焦点为F(1,0),上顶点为A.过F且垂直于x轴的直线l交椭圆F于B、C两点,若S△FOAS△COB=√22(1)求椭圆Γ的方程;(2)动直线m与椭圆Γ有且只有一个公共点,且分别交直线1和直线x=2于M、N两点,试求|MF||NF|的值21.已知函数f(x)=ax lnx-x2-ax+a2+1(a∈R).(1)试讨论函数f(x)的导函数f′(x)的零点个数;(2)若对任意的:x∈[1,+∞),关于x的不等式f(x)≤f′(x)+2恒成立,求实数a的取值范围.22. 在直角坐标系xOy 中,曲线C :{y =2sinαx=2+2cosα(a 为参数),直线l :{y =tsinβx=−1+tcosβ(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系.(1)求曲线C 与直线l 的极坐标方程(极径用p 表示,极角用θ表示);(2)若直线l 与曲线C 相交,交点为A 、B ,直线l 与x 轴也相交,交点为Q ,求|QA |+|QB |的取值范围23. 已知函数f (x )=|2x +1|-|x -2|.(1)画出函数f (x )的图象;(2)若关于x 的不等式x +2m +1≥f (x )有解,求实数m 的取值范围.答案和解析1.【答案】D【解析】解:由2+i=z(1-i),得z=,∴,则z的共轭复数z对应的点的坐标为(),在复平面的第四象限.故选:D.把已知等式变形,再由复数代数形式的乘除运算化简,求出z的坐标得答案.本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.2.【答案】C【解析】解:由y=3x,x∈R,得y>0,即A=(0,+∞),由y=,x∈R,得:0≤y≤2,即B=[0,2],即A∩B=(0,2],故选:C.分别求y=3x,x∈R,y=,x∈R的值域,得:A=(0,+∞),B=[0,2],再求交集即可.本题考查了求函数值域及交集的运算,属简单题.3.【答案】A【解析】解:f(-x)===f(x),则函数f(x)为偶函数,故排除CD,当x=1时,f(1)=<0,故排除B,故选:A.先判断函数偶函数,再求出f(1)即可判断本题考查了函数图形的识别,关键掌握函数的奇偶性,和函数值,属于基础题4.【答案】A【解析】解:如图所示设BC中点为E,则=+=+=+(+)=-+•=+.故选:A.根据题意画出图形,结合图形,利用平面向量的线性运算写出用、的表达式即可.本题考查了平面向量的线性表示与应用问题,是基础题.5.【答案】A【解析】解:根据几何体的三视图:该几何体是由一个边长为2正方体挖去一个底面半径为1,高为2的圆锥构成的不规则的几何体.所以:v=,=.故选:A.直接利用三视图,整理出几何体的构成,进一步利用几何体的体积公式求出结果.本题考查的知识要点:三视图的应用,几何体的体积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型.6.【答案】C【解析】解:若f(x)=sinx+cosx=2(sinx+cosx)=2sin(x+)在[-m,m](m>0)上是增函数,∴-m+≥-,且m+≤.求得m≤,且m≤,∴m≤,故m的最大值为,故选:C.利用辅助角公式,化简函数的解析式,再根据正弦函数的单调性,求得m的最大值.本题主要考查辅助角公式,正弦函数的单调性,属于中档题.7.【答案】C【解析】解:如图所示,边长为a的正六边形,则OA=OB=AB=a,设小圆的圆心为O',则O'C⊥OA,∴OC=a,∴O'C=a,OO'=a,∴OD=a,∴S阴影=12[×a•a-π•(a)2]=(-)a2,S正六边形=a2,∴点恰好取自阴影部分的概率P===,故选:C.分别求出正六边形和阴影部分的面积,作商即可.本题考查了几何概型问题,考查特殊图形面积的求法,是一道常规题.8.【答案】A【解析】解:由题意可得A(a,0),A为线段OB的中点,可得B(2a,0),令x=2a,代入双曲线的方程可得y=±b,可设P(2a,-b),由题意结合图形可得圆A经过双曲线的左顶点(-a,0),即|AP|=2a,即有2a=,可得a=b,e===,故选:A.设A的坐标(a,0),求得B的坐标,考虑x=2a,代入双曲线的方程可得P的坐标,再由圆A经过双曲线的左顶点,结合两点的距离公式可得a=b,进而得到双曲线的离心率.本题考查双曲线的方程和性质,主要是离心率的求法,考查方程思想和运算能力,属于中档题.9.【答案】B【解析】解:偶函数f(x)满足f(x)+f(2-x)=0,即有f(-x)=f(x)=-f(2-x),即为f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),可得f(x)的最小正周期为4,故①错误;②正确;由f(x+2)=-f(x),可得f(x+1)=-f(x-1),又f(-x-1)=f(x+1),即有f(-x-1)=-f(x-1),故f(x-1)为奇函数,故③正确;由f(-x-3)=f(x+3),若f(x-3)为偶函数,即有f(-x-3)=f(x-3),可得f(x+3)=f(x-3),即f(x+6)=f(x),可得6为f(x)的周期,这与4为最小正周期矛盾,故④错误.故选:B.由偶函数的定义和条件,将x换为x+2,可得f(x+4)=f(x),可得周期为4,即可判断①②的正确性;再由奇函数、偶函数的定义,将x换为-x,化简变形即可判断③④的正确性.本题考查抽象函数的周期性和奇偶性的判断,注意运用定义法,考查化简变形能力和运算能力,属于中档题.10.【答案】D【解析】解:∵acosB-bcosA=,∴由正弦定理化简得:sinAcosB-sinBcosA=sinC=sin(A+B)=sinAcosB+cosAsinB,整理得:sinAcosB=3cosAsinB,∴cosAcosB>0,∴tanA=3tanB;∴则=+=+≥2=2=2=.∴可得的最小值为.故选:D.由题意利用正弦定理化简已知等式,利用同角三角函数间基本关系可求tanA=3tanB,进而利用正弦定理,基本不等式化简所求即可求解.本题主要考查了正弦定理,同角三角函数间基本关系,基本不等式在解三角形中的综合应用,考查了转化思想,属于中档题.11.【答案】B【解析】解:∵在等腰Rt△ABC中,斜边AB=,D为直角边BC上的一点,∴AC=BC=1,∠ACB=90°,将△ACD沿直AD折叠至△AC1D的位置,使得点C1在平面ABD外,且点C1在平面ABD上的射影H在线段AB上,设AH=x,∴AC1=AC=1,CD=C1D∈(0,1),∠AC1D=90°,CH⊥平面ABC,∴AH<AC1=1,故排除选项A和选项C;当CD=1时,B与D重合,AH=,当CD<1时,AH >=,∵D为直角边BC上的一点,∴CD∈(0,1),∴x的取值范围是(,1).故选:B.推导出AC=BC=1,∠ACB=90°,AC1=AC=1,CD=C1D∈(0,1),∠AC1D=90°,CH⊥平面ABC,从而AH<AC1=1,当CD=1时,B与D重合,AH=,当CD<1时,AH >=,由此能求出x的取值范围.本题考查线段长的取值范围的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.12.【答案】D【解析】解:当直线MN的斜率不存在时,设M (,y0),N (,-y0),由斜率之积为,可得,即,∴MN的直线方程为x=2;当直线的斜率存在时,设直线方程为y=kx+m,联立,可得ky2-y+m=0.设M(x1,y1),N(x2,y2),则,,∴,即m=-2k.∴直线方程为y=kx-2k=k(x-2).则直线MN过定点(2,0).则O到直线MN的距离不大于2.故选:D.由已知分类求得MN所在直线过定点(2,0),结合选项得答案.本题考查抛物线的简单性质,考查直线与篇文章位置关系的应用,是中档题.13.【答案】5【解析】解:作出x,y满足约束条件,所示的平面区域,如图:作直线-3x+4y=0,然后把直线L向可行域平移,结合图形可知,平移到点A时z最大,由可得A(1,2),此时z=5.故答案为:5.先画出约束条件的可行域,利用目标函数z=-3x+4y的几何意义,求解目标函数的最大值.本题主要考查了线性规划的简单应用,解题的关键是:明确目标函数的几何意义.14.【答案】10【解析】解:设停车位有n个,这3辆共享汽车都不相邻的种数:相当于先将(n-3)个停车位排放好,再将这3辆共享汽车,插入到所成(n-2)个间隔中,故有A n-23种,恰有2辆相邻的种数:先把其中2辆捆绑在一起看做一个复合元素,再和另一个插入到,将(n-3)个停车位排放好所成(n-2)个间隔中,故有A32A n-22种,因为这3辆共享汽车都不相邻的概率与这3辆共享汽车恰有2辆相邻的概率相等,∴A n-23=A32A n-22,解得n=10,故答案为:10.设停车位有n个,求出这3辆共享汽车都不相邻的种数和恰有2辆相邻的种数,可得A n-23=A32A n-22,解得即可本题考查了排列组合中的相邻问题和不相邻问题,考查了运算能力和转化能力,属于中档题15.【答案】√3【解析】解:∵AB=2BC=2,∴由题意可得:c=2a=2,a=,∵(sinA-sinB)(sinA+sinB)=sinAsinC-sin2C,∴由正弦定理可得:(a-b)(a+b)=ac-c2,可得:a2+c2-b2=ac,∴S===ac==.故答案为:.由题意可得:c=2a=2,a=,利用正弦定理化简已知等式可得a2+c2-b2=ac,根据题意利用三角形的面积公式即可计算得解.本题主要考查了正弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.16.【答案】(1,+∞)【解析】解:函数f(x)的定义域为{x|x≠0},f(-x)=-f(x),则f(x)是偶函数,若函数f(x)有4个零点,等价为当x>0时,f(x)有2个零点,当x>0时,f(x)=-lnax,则f′(x)=-=-=,当x→+∞,f(x)→+∞,当x→0,f(x)→+∞,则由f′(x)>0得x>,此时f(x)为增函数,由f′(x)<0得0<x<,此时f(x)为减函数,即当x<,f(x)取得极小值f(),要使当x>0时,f(x)有2个零点,则极小值f()<0,即极小值f()=-ln(a•)=-ln=-lnae<0,得lnae>1,则ae>e,即a>1,即实数a的取值范围是(1,+∞),故答案为:(1,+∞)先判断函数是偶函数,则条件等价为当x>0时,f(x)有2个零点,求函数的导数,研究函数的单调性,求出函数的极小值,让极小值小于0,即可.本题主要考查函数与方程的应用,结合偶函数的性质转化为当当x>0时,f(x)有2个零点,求函数的导数,利用导数研究的极小值是解决本题的关键.17.【答案】解:(1)设公比为q等比数列{a n}为递增数列,且a52=a10,首项为a1,则:a1q4⋅a1⋅q4=a1⋅q9,解得:a1=q,2(a n+a n+2)=5a n+1,所以:2q2-5q+2=0,解得:q=2或12,由于数列为单调递增数列,故:q=2,所以:a n=a1⋅q n−1=2n,数列{b n}的前n项和为S n,b1=1,b n≠0,b n b n+1=4S n-1①.当n≥2时,b n-1b n=4S n-1-1②,整理得:b n -b n -1=2(常数),对n 分偶数和奇数进行分类讨论, 整理得:b n =2n -1故:c n =a n b n =(2n -1)•2n ,则:T n =1⋅21+3⋅22+⋯+(2n −1)⋅2n ①, 2T n =1⋅22+3⋅23+⋯+(2n −1)⋅2n+1②, ①-②得:-T n =2⋅2(2n −1)2−1−(2n −1)⋅2n+1−2,解得:T n =(2n −3)⋅2n+1+6.【解析】(1)直接利用递推关系式求出数列的通项公式.(2)利用(1)的结论,进一步利用乘公比错位相减法求出数列的和.本题考查的知识要点:数列的通项公式的求法及应用,乘公比错位相减法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于基础题型.18.【答案】证明:(1)∵在四棱锥P -ABCD 中,AB ⊥PC ,AD ∥BC ,AD ⊥CD ,且PC =BC =2AD =2CD =2√2,PA =2. ∴AB =AC =√AD 2+CD 2=2,∴AB 2+AC 2=BC 2,PA 2+AC 2=PC 2, ∴AB ⊥AC ,AP ⊥AC ,∵AB ⊥PC ,∴AB ⊥平面PAC ,∴PA ⊥AB , ∵AB ∩AC =A ,∴PA ⊥平面ABCD .解:(2)以A 为原点,AB 为x 轴,AC 为y 轴,AP 为z 轴, 建立空间直角坐标系,设在线段PD 上,存在一点M (a ,b ,c ),使得二面角M -AC -D 的大小为60°,且PMPD =λ,(0≤λ≤1), A (0,0,0),C (0,2,0),P (0,0,2), D (-1,1,0),PM ⃗⃗⃗⃗⃗⃗ =(a ,b ,c -2),PD ⃗⃗⃗⃗⃗ =(-1,1,-2),∴{a =−λb =λc =2−2λ,∴M (-λ,λ,2-2λ), ∴AC ⃗⃗⃗⃗⃗ =(0,2,0),AM ⃗⃗⃗⃗⃗⃗ =(-λ,λ,2-2λ),设平面ACM 的法向量m⃗⃗⃗ =(x ,y ,z ), 则{m ⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =2y =0m ⃗⃗⃗ ⋅AM ⃗⃗⃗⃗⃗⃗ =−λx +λy +(2−2λ)z =0,取x =1,得m ⃗⃗⃗ =(1,0,λ2−2λ),平面ACD 的法向量n⃗ =(0,0,1), ∵二面角M -AC -D 的大小为60°, ∴cos60°=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=|λ2−2λ|√1+(λ2−2λ)2,解得λ=4−2√3.∴在线段PD 上,存在一点M ,使得二面角M -AC -D 的大小为60°,PMPD =4-2√3. 【解析】(1)推导出AB ⊥AC ,AP ⊥AC ,AB ⊥PC ,从而AB ⊥平面PAC ,进而PA ⊥AB ,由此能证明PA ⊥平面ABCD .(2)以A 为原点,AB 为x 轴,AC 为y 轴,AP 为z 轴,建立空间直角坐标系,利用向量法能求出在线段PD 上,存在一点M ,使得二面角M-AC-D 的大小为60°,=4-2.本题考查线面垂直的证明,考查满足二面角的点是否存在的判断与求法,考查空间中线线、线面、面面间的位置关系,考查运算求解能力,考查数形结合思想,是中档题. 19.【答案】50 10 60 25 15 40 75 25 100【解析】解:(1)由题意能得到如下的列联表: 有兴趣 没兴趣 合计 男生 50 10 60 女生 25 15 40 合计 7525100∴K 2==≈5.556<6.635.∴没有99%的把握认为“对游泳是否有兴趣与性别有关”.(2)记事件A i 表示“从这6名学生中随机抽取的3人中恰好有i 人有兴趣,i=0,1,2,3”, 则A 2+A 3表示“从这6名学生中随机抽取的3人中到少有2人有兴趣”,且A 2,A 3互斥, ∴现在从这6名学生中随机抽取3人,至少有2人对游泳有兴趣的概率: P (A 2+A 3)=P (A 2)+P (A 3)==.(3)由题意可知ξ的所有可能取值为0,1,2,3, P (ξ=0)==,P (ξ=1)==, P (ξ=2)==,P (ξ=3)==,∴ξ的分布列是: ξ 0 1 2 3 P∴E (ξ)==.(1)完成列联表求出K 2≈5.556<6.635.从而没有99%的把握认为“对游泳是否有兴趣与性别有关”.(2)记事件A i 表示“从这6名学生中随机抽取的3人中恰好有i 人有兴趣,i=0,1,2,3”,则A 2+A 3表示“从这6名学生中随机抽取的3人中到少有2人有兴趣”,且A 2,A 3互斥,由此能求出现在从这6名学生中随机抽取3人,至少有2人对游泳有兴趣的概率.(3)由题意可知ξ的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和E (ξ).本题考查独立检验的应用,考查概率、离散型随机变量概率分布列、数学期望的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,考查函数与方程能力,是中档题.20.【答案】解:(1)易知,|BC|=2b2a,S △FOAS △COB =b2b 2a=a2b =√22,∴a =√2b ,c =√a 2−b 2=b ,所以,b =1,a =√2,因此,椭圆Γ的方程为x 22+y 2=1;(2)设直线m 与椭圆Γ的切点为点P (x 0,y 0),则直线m 的方程为x 0x 2+y 0y =1,且有x 022+y 02=1,可得y 02=1−x 022,直线m 与直线l :x =1交于点M(1,2−x 02y 0),直线m 交直线x =2于点N(2,1−x 0y 0).所以,|MF|=|2−x 02y 0|,|NF|=√(2−1)2+(1−x0y 0)2=√1+x 02−2x 0+1y 02=√x 02−2x 0+1+1−x 022y 02=√x 022−2x 0+2y 02=√12(x 02−4x 0+4)y 02=√22⋅|2−x 0y 0|,因此,|MF||NF|=|2−x 02y 0|√22|2−x 0y 0|=√22. 【解析】(1)由通径公式得出,结合已知条件得出,再由c=1,可求出a 、b 的值,从而得出椭圆的方程;(2)设切点为(x 0,y 0),从而可写出切线m 的方程为,进而求出点M 、N 的坐标,将切点坐标代入椭圆方程得出x 0与y 0之间的关系,最后利用两点间的距离公式可求出答案. 本题考查直线与椭圆的综合,考查计算能力与推理能力,属于中等题. 21.【答案】解:(1)f ′(x )=a (ln x +1)-2x -a =a ln x -2x ,(x >0),a =0时,函数f ′(x )=-2x 无零点. a ≠0时,由a ln x -2x =0,化为:2a=lnxx =g (x ),x >0.g ′(x )=1−lnx x 2.可得函数g (x )在x =e 时取得极大值即最大值,g (e )=1e . 画出图象可得:2a >1e 即0<a <2e 时,函数f ′(x )无零点. 2a =1e 或2a<0时,即a =2e 或a <0时,函数f ′(x )只有一个零点. 0<2a <1e ,即a >2e 时,函数f ′(x )有两个零点.综上可得:0≤a <2e 时,函数f ′(x )无零点. a =2e 或a <0时,函数f ′(x )只有一个零点. a >2e 时,函数f ′(x )有两个零点.(2)对任意的:x ∈[1,+∞),关于x 的不等式f (x )≤f ′(x )+2恒成立, 化为:h (x )=ax lnx-x 2-ax +a 2-a ln x +2x -1≤0恒成立,x ∈[1,+∞), 则h (1)=a 2-a ≤0,解得0≤a ≤1. h ′(x )=a ln x -2x -ax +2,h ′(1)=-a ≤0.h ″(x )=−2x 2+ax+ax 2,令u (x )=-2x 2+ax +a =-2(x −a2)2+a(2−a)2≤u (1)=2(a -1)≤0,x ∈[1,+∞),∴函数h ′(x ),在x ∈[1,+∞)上单调递减,∴h ′(x )≤h ′(1)=-a ≤0. ∴函数h (x ),在x ∈[1,+∞)上单调递减,∴h (x )≤h (1)=a 2-a ≤0. ∴实数a 的取值范围是[0,1]. 【解析】(1)求出函数的导数,分类讨论得到单调性和极值,结合图象从而判断导函数的零点个数. (2)对任意的:x ∈[1,+∞),关于x 的不等式f (x )≤f′(x )+2恒成立,化为:h (x )=axlnx-x 2-ax+a 2-alnx+2x-1≤0恒成立,x ∈[1,+∞),可得h (1)=a 2-a≤0,解得0≤a≤1.研究函数的单调性和最值即可.本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、数形结合方法,考查了推理能力与计算能力,属于难题.22.【答案】解:(1)曲线C :{y =2sinαx=2+2cosα(a 为参数),转换为直角坐标方程为:(x -2)2+y 2=4, 转换为极坐标方程为:ρ=4cosθ. 直线l :{y =tsinβx=−1+tcosβ(t 为参数),转换为直角坐标方程为:y =tanβ(x +1),转换为极坐标方程为:ρsinθ=tanβ(ρcosθ+1).(2)直线l 与曲线C 相交,交点为A 、B ,直线l 与x 轴也相交,交点为Q , 则:Q (-1,0).故:直线的参数方程为:{y =tsinβx=−1+tcosβ(t 为参数), 被直线的参数方程代入圆的方程(x -2)2+y 2=4,得到:t 2-6cosβt +5=0(t 1和t 2为A 、B 对应的参数), 故:t 1+t 2=6cosβ,所以:|QA |+|QB |=|t 1+t 2|=|6cosβ|, 由于-1≤cosβ≤1, 故:0≤|6cosβ|≤6,所以:|QA |+|QB |的取值范围为[0,6]. 【解析】(1)直接利用转换关系式,把参数方程直角坐标方程和极坐标方程之间进行转换.(2)利用(1)的结论,进一步利用一元二次方程根和系数关系的应用求出关系式,最后利用三角函数的值域求出结果.本题考查的知识要点:参数方程直角坐标方程和极坐标方程之间的转换,一元二次方程根和系数关系的应用,三角函数关系式的恒等变变换,主要考查学生的运算能力和转化能力,属于基础题型.23.【答案】解:(1)f (x )=|2x +1|-|x -2|={−x −3,x ≤−123x −1,−12<x <2x +3,x ≥2,画出y =f (x )的图象,如右图:(2)关于x 的不等式x +2m +1≥f (x )有解, 即为2m +1≥f (x )-x , 由x ≥2时,y =f (x )-x =3;当-12<x <2时,y =f (x )-x =2x -1∈(-2,3); 当x ≤-12时,y =f (x )-x =-2x -3∈[-2,+∞), 可得y =f (x )-x 的最小值为-2, 则2m +1≥-2, 解得m ≥-32. 【解析】(1)写出f (x )的分段函数式,画出图象;(2)由题意可得2m+1≥f (x )-x 的最小值,对x 讨论去绝对值,结合一次函数的单调性可得最小值,即可得到所求范围.本题考查绝对值不等式的解法和不等式有解的条件,注意运用分类讨论思想方法和分离参数法,考查单调性的运用:求最值,属于中档题.。
湖北剩州市2018届高三数学1月月考试题文201801080183

湖北省荆州市 2018届高三数学 1月月考试题 文满分:150分第Ⅰ卷(选择题 共 60分)一、选择题:本大题共 12小题,每小题 5分,共 60分.在每小题给出的四个选项中,只有 一项符合题目要求.11.已知集合,,则=()U {y | y log x , x1} P {y | y , x 2}C P2Ux1 1,0,+A . 0B .C ,+2 21D .,0,+2a 3(a2a 3)i22.若复数( 为虚数单位)为纯虚数,则实数 的值是()zi aiA . 3B . 3或1C .3或-1D .1 3. 从1, 2,3, 4,5中任取三个数,则这三个数能构成三角形的概率为( )1 32 1 A .B .C .D .5105214. 在 等 比 数 列中是 函 数 的 极 值 点 , 则 =aa 1,a 5 f x x 3 x 2 xlog a( ) 5 16 1 n2 33( )A . 2B . 4C . 2或4D . 2或无意义5. 已知函数 f (x )2 s in(x )(0,| | )的最小正周期是 ,若将其图象向右平移2个单位后得到的图象关于 轴对称,则函数的图象()yf (x ) 35A .关于直线对称 B .关于直线对称 C .关于点对称 D .关于点x x ( ,0)121212 5 ( ,0)对称12x26. 在椭圆中任取一点,则所取的点能使直线与圆y21P(x,y)y y0k(x x0)002x y22x2y21221(a b0)恒有公共点的概率为()(注:椭圆的面积公式为a bab)11221 A.B.C.D.2222x2y27.已知实数x,y满足约束条件2x y4,若a x,y,b3,1,设z表示向量a在b4x y1方向上的投影,则z的取值范围是()3161,6A.B.C.,6,2101013 6D .,2 10 10x y228.过双曲线a b 的一个焦点F 的直线与双曲线相交于 A , B 两点,当 2210,abAB x 轴时,称线段 AB 为双曲线的通径.若 AB 的最小值恰为通径长,则此双曲线的离心率的范围为( )A .1, 2B .1, 2C .1,D .2,9. 执行如下左图所示的程序框图,输出的 a ()A . 20B .14C .10D . 710. 如上右图是某几何体的三视图,则该几何体的内切球的表面积为( )A .B . 2C . 4D .1811. 已 知 偶 函 数 f (x ) 满 足 f (1 x ) f (1 x ) 且 当 x 0,1时f(x )=x , 则 函 数2g x f x x x ,( ) ( ) cos在上的零点个为( ) A .4B .5C .6D .812. 已知下列命题: ①命题“ ,”的否定是:“,”; xR sin x1 x R sin x 1②若样本数据 的平均值和方差分别为和则数据的平x 1, x 2 ,, x16 1.443x -8, 3x -8,,3x -8 n12n均值和标准差分别为 40 ,3.6 ; ③两个事件不是互斥事件的必要不充分条件是两个事件不是对立事件;④在 22列联表中,若比值 a c 相差越大,则两个分类变量有关系的可能性就越大.a b c d与⑤已知 α、β 为两个平面,且,l 为直线.则命题:“若l则l / / ”的逆命题和否命题均为假命题. 1⑥设定点 F 1(0,1) 、 2 (0,1) ,动点 满足条件 PFPFa a 为正常数 ,则 P 的F P()12a轨迹是椭圆. 其中真命题的个数为( ) A .5 B .4 C .3 D .2第Ⅱ卷(非选择题 共 90分) 二、填空题:本大题共 4小题,每小题 5分,共 20分.213. 已知平面向量 a (2,1),b (2,).且 ab(a 2b ) ,则.14.已 知 数 列a为 等 差 数 列 , D 为ABC 的 边 BC 上 任 意 一 点 , 且 满 足nAD a AB aACaa,则的最大值为.140342017201815. 抛物线 y 22pxp的焦点为 F ,M 为抛物线上一点,若 OFM 的外接圆与抛物线的准线相切(O 为坐标原点),且外接圆的面积为9 ,则 p.x x 3 x 4 x 341 f (x ) f (x ) R16.“求方程 的解”有如下解题思路:设 ,则 在5555上 单 调 递 减 , 且 f (2) 1, 所 以 原 方 程 有 唯 一 解 x 2 .类 比 上 述 解 题 思 路 , 不 等 式x 6 (x 2) (x 2)3 x 2的解集是 .三、解答题:本大题共 6小题,共 70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分 12分)在如图四边形 DCAB 中, a ,b ,c 为的 ABC 内角 A , B ,C 的对边,且sin B sin C cos B cos C 2满足.Dsin Acos ACθ(Ⅰ)证明:b ,a ,c 成等差数列; 3 1 (Ⅱ)已知求四边形 的面积.b c , cos CDB , DC 2, DB 4. DCAB54AB图 17图 图18.(本小题满分 12分)如图,在直三棱柱 中,ABC A B C1 1 1AB BC 2, AC 2 2, AC 2 3, M , NAC BB分别是 和的中点.11(Ⅰ)求证:;MN P 平面A B C1 1B 1C 11(Ⅱ)若 AB 上一点 P 满足V,求 B P 与 MN 所成角的余弦值.N B PM161A 1NB CMA图18图图19.(本小题满分12分)某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示:(Ⅰ)试估计平均收益率;(Ⅱ)根据经验若每份保单的保费在20元的基础上每增加x元,对应的销量y(万份)与x(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组x与y的对应数据:图图图图3.02.5 2.0x25354045 55(元)1.5 1.0销量y(万份)7.3 6.3 6.0 5.9 4.30.500.10.20.30.40.5图19图图0.6图图图3(ⅰ)根据数据计算出销量y(万份)与x(元)的回归方程为;y b x ay b x a y x(ⅱ)若把回归方程当作与的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.nnx y nx y(x x)(y y)i ii i参考公示:i1i1b,a y b xn n2 ()x x2x2nxi ii 1i1:x y1(0)12220.(本小题满分12分)已知椭圆的离心率为,且椭圆过点C a b Ca b22231,l C F C M,N,直线过椭圆的右焦点且与椭圆交于两点.2(Ⅰ)求椭圆C的标准方程;(Ⅱ)已知点P4,0,求证:若圆与直线相切,则圆与直线x2y2r2r PM PN:(0)也相切.21.(本小题满分12分)已知函数f(x)(x a)(m a R),g(x)2e x8.(Ⅰ)当g(x)在x0处的切线与直线mx2y10垂直时,方程f(x)g(x)有两相异实数根,求a的取值范围;(Ⅱ)若幂函数h(x)(m23m3)x m的图象关于y轴对称,求使不等式g(x)f(x)0在0,a上恒成立的的取值范围.22.(本小题满分 10分)选修 4-4:参数方程与极坐标系cosx t在直角坐标系 xoy 中,曲线C :(t 为参数且t0),其中 0 ,在以O 为1y t sin极点, x 轴正半轴为极轴的极坐标系中,曲线C 2 : 2 s in ,C 3 : 2 3 cos .(Ⅰ)求与交点的直角坐标;CC235(Ⅱ)若与相交于点 ,与相交于点 ,求当 时 的值.CCA C CB AB12136423.(本小题满分10分)选修4-5:不等式选讲已知x R,不等式x1x2t成立.(Ⅰ)求实数t的取值范围;(Ⅱ)在(Ⅰ)的条件下,对于实数m,n满足m1,n1且不等式log m g log n t恒成立,33求m n的最小值.5数学(文科)试题参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12答案 C D B A D B D A C B C A113. 114. 15. 16.4,1(2,)417. 解析:(Ⅰ)由题设有sin B cos A sin C cos A 2s in A cos B sin A cos C sin A即sin B cos A cos B sin A sin C cos A cos C sin A 2s in A sin(A B)sin(A C)2s in A由三角形内角和定理有sin B sin C 2s in A由正弦定理有b c 2ab,a,c成等差数列(Ⅱ) 在BDC中,由余弦定理有BC2=CD2BD22CD g BD g cos CDB 16即BC 4 3Q b c 2a,bc54, 即则为.a c 4c 5b 3ABC RtS 6ABC5由于sin CDB 1cos2CDB 151sin15S CD g BD g CBDCDB42S S S 615DCAB CDB ABC18. 解析:(Ⅰ)证明:Q直三棱柱ABC A B C中,AB BC 2,AC 22111AB BC AC AB BC AC 2311222 222,又,,A A AC AC1取的中点,连接, 为中点,且。
湖北省襄阳市普通高中2016届高三1月调研统一测试数学(文)试题(图片版-word答案)

2016年1月襄阳市普通高中调研统一测试高三数学(文史类)参考答案及评分标准说明1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分。
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅。
当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数的一半,如果有较严重的概念性错误,就不给分。
3.解答题中右端所标注的分数,表示考生正确做到这一步应得的该题分数。
一.选择题:BCCDC DCADA BC二.填空题:13.47 14.644π+ 15.1216.3三.解答题:17.(1)解:在△ABC 中,依题意有:222b c a bc +=+2分 ∴2221cos 22b c a A bc +-==4分 又(0)A π∈,,∴3A π=6分(2)解:由3a A π==及正弦定理得:2sin sin sin bcaB C A === ∴222sin 2sin 2sin 2sin()2sin()33b B c C B ππθθ====-=-,8分故22sin 2sin()3y a b c πθθ=+++-即)6y πθ=+10分 由203πθ<<得:5666πππθ<+<∴当62ππθ+=,即3πθ=时,max y =.12分18.(1)证:∵PD ⊥CD ,平面PCD ⊥平面ABCD ,平面PCD 与平面ABCD 相交于CD ∴PD ⊥平面ABCD ,∴PD ⊥BC2分在△ABD 中,∠A = 90°,AB = AD = 2,∴BD =ADB = 45°在△ABD 中,∠BDC = 45°,BD =DC = 4∴222cos 452BD DC BC BC BD DC +-︒=⇒=⋅由BD 2 + BC 2 = 16 = DC 2知BD ⊥BC4分 ∵PD ⊥BC ,BD 、PD 相交于D ,∴BC ⊥平面PBD6分 (2)解:过E 作EF ∥PD 交DC 于F ,由(1)知EF ⊥平面ABCD由CE = 2PE 得:23EF CE PD PC ==,∴43EF =8分 112339P BDE P BCD E BCD BCD BCD BCD V V V PD S EF S S ---=-=⋅-⋅=V V V10分1142422BCD S CD AD =⋅=⨯⨯=V ∴89P BDE V -= 12分 19.(1)解:由a 3 + a 4 = 3(a 1 + a 2)得:a 1 + 2d + a 1 +3d = 3(a 1 + a 1 + d ) ⇒ 2a 1 = d ① 2分 由a 2n -1 = 2a n 得:a 1 + (2n -1)d -1 = 2[a 1 + (n -1)d ] ⇒ a 1 = d -1 ② 由①②得:a 1 = 1,d = 2,∴a n = 2n -1 4分(2)解:当n ≥2时,1111112()222n n n n n n n n a a n b S S m m ----++-=-=---= 6分 ∴1221221(1)()24n n n n n c b n ---==-⨯ 8分 012111110()1()2()(1)()4444n n T n -=⨯+⨯+⨯++-⨯L 12311111110()1()2()(2)()(1)()444444n n n T n n -=⨯+⨯+⨯++-⨯+-⨯L 10分 两式相减得:123111()311111144()()()()(1)()(1)()1444444414n n n n n T n n --=++++--⨯=--⨯-L 1311()334n n +=-⋅ ∴14311()994n n n T -+=-⋅ 12分20.(1)解:由已知222222252511142c e a a b c a b a b ⎧==⎪⎧=⎪⎪⎪+=⇒⎨⎨⎪⎪=+=⎩⎪⎪⎩ ∴椭圆C 的方程为2224155y x += 2分 (2)解:由221324155y kx y x ⎧=-⎪⎪⎨⎪+=⎪⎩得:229(24)12430k x kx +--= ① 4分设A (x 1,y 1),B (x 2,y 2),则x 1、x 2是方程①的两根 ∴12122212439(24)9(24)k x x x x k k +==-++, 6分 设P (0,p ),则1122()()PA x y p PB x y p =-=-u u u r u u u r ,,, 22121212121212112()()()()333p PA PB x x y y p y y p x x kx kx pk x x p ⋅=+-++=+---+++u u u r u u u r 2222(1845)3624399(24)p k p p k -++-=+ 8分若PA PB ⊥u u u r u u u r ,则0PA PB ⋅=u u u r u u u r即222(1845)3624390p k p p -++-=对任意k ∈R 恒成立10分∴22184503624390p p p ⎧-=⎨+-=⎩此方程组无解,∴不存在定点满足条件12分21.(1)解:()ln 1ag x x x +-,21()ag x x x '=-2分 g (x )在点(2,g (2))处的切线与直线x + 2y -1 = 0平行 ∴11(2)4242a g a '=-=-⇒=4分 (2)证:由(1)()ln 1b x h x x x -=-+得:2221(1)(1)2(1)1()(1)(1)b x b x x b x h x x x x x +--+-+'=-=++∵h (x ) 在定义域上是增函数,∴()0h x '>在(0,+∞)上恒成立∴22(1)10x b x +-+>,即2212x x b x ++<恒成立6分∵2211112222x x xx x ++=++=≥ 当且仅当11222xx x ==,时,等号成立∴b ≤2,即b 的取值范围是(-∞,2]8分 (3)证:不妨设m > n > 0,则1mn > 要证ln ln ||2m n m n m n --<+,即证ln ln 2m n m nm n --<+,即2(1)ln 1mmn m n n -<+10分 设2(1)()ln (1)1x h x x x x -=->+由(2)知h (x )在(1,+∞)上递增,∴h (x ) > h (1) = 0 故2(1)ln 01m m n m n n -->+,∴ln ln||2m n m nm n --<+成立12分22.(1)证:∵OA = OC ,∴∠OAC = ∠OCA2分 ∵CD 是圆的切线,∴OC ⊥CD4分 ∵AD ⊥CD ,∴AD ∥OC ,∴∠DAC = ∠OCA故∠DAC = ∠OAC ,即AC 平分∠BAD6分 (2)解:由(1)得:»»BC CE =,∴BC = CE8分 连结CE ,则∠DCE = ∠DAC = ∠OAC ,∴△CDE ∽△ACD ,△ACD ∽△ABC ∴CE DE CE AB BC AB ==,故2ABDEBC CE ⋅==10分23.(1)解:由3444sin x cox y θθ=+⎧⎨=+⎩消去θ得:22(3)(4)16x y -+-=2分 即226890x y x y +--+=将cos sin x y ρϕρϕ==,代入得极坐标方程为26cos 8sin 90ρρϕρϕ--+=4分 (2)解:由4sin ρθ=得C 2的普通方程为:2240x y y +-=6分 由2222689040x y x y x y y ⎧+--+=⎨+-=⎩得:6490x y +-=8分 ∴C 1、C 2的交点所在直线方程为6490x y +-=∴其极坐标方程为:6cos 4sin 90ρθρθ+-=10分24.(1)解:| x + 1 | + | x + 2 |-5≥0当x ≤-2时,得x ≤-4,当-2 < x <-1时,得x ≤4,当x ≥-1时,得x ≥1 2分 ∴A = { x | x ≤-4或x ≥1}4分 (2)证:B A R I ð = { x |-1< x < 1},∴a 、b ∈{ x |-1< x < 1}6分 要证|||1|24a b ab+<+,只需证224()(4)a b ab +<+8分 ∵222222224()(4)4416(4)(4)a b ab a b a b b a +-+=+--=--∵a 、b ∈{ x |-1< x < 1},∴22(4)(4)0b a --<∴224()(4)a b ab +<+ ∴|||1|24a b ab+<+成立10分。
2018年最新 湖北省襄樊市高三调研测试数学(理科) 精品

湖北省襄樊市高三调研测试数学(理工农医类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分,考试时间120分钟。
注意事项:1.请考生将自己的学校、班级、姓名、考号填写在答题卷内密封栏中,将考号最后两位填在答题卷右下方座位号内,同时请认真阅读答题卷上的注意事项。
2.第Ⅰ卷每小题选出正确答案后用2B 铅笔把答题卡上对应题目的答案代号涂黑,如需改动,必须用橡皮擦干净后,再选涂其它答案。
第Ⅱ卷用黑色签字笔直接答在答题卷每题对应的答题区域内,答在试题卷上无效。
3.考试结束后,监考人员将试题卷、答题卡和答题卷一并收回。
试题卷 第 Ⅰ 卷 (选择题,共50分)一.选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.“两条直线没有公共点”是“这两条直线异面”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件2.函数xxx f -=1)(的反函数为)(1x f -,若0)(1<-x f ,则x 的取值范围是A .(-∞,0)B .(-1,1)C .(1,+∞)D .(-∞,-1)3.若命题P :x ∈A ∩B ,则命题非P 是 A .x ∈A ∪BB .x ∉A ∪BC .x ∉A 或x ∉BD .x ∉A 且x ∉B4.已知l 、m 为两条不重合的直线,α、β为两个不重合的平面,则下列条件中可以判断平面α与平面β平行的是 A .βα////l l , B .βα⊥⊥l l ,C .βα//l l ,⊂D .ββα////m l m l ,,、⊂ 5.定义运算bc ad dc b a -=,则符合条件i ziz 2411+=-的复数z 为A .3-iB .1+3iC .3+iD .1-3i6.首项为2,公比为3的等比数列,从第m 项到第n 项)(n m <的和为720,则 A .m =2,n =6B .m =2,n =7C .m =3,n =6D .m =3,n =97.设f (x )是定义在实数集R 上以2为周期的奇函数,已知)10(,∈x 时, )1(l o g )(1x x f -=,则f (x )在(1,2)上A .是减函数,且f (x )>0B .是增函数,且f (x )>0C .是减函数,且f (x )<0D .是增函数,且f (x )<08.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线)(x f y =,另一种是平均价格曲线)(x g y =(如f (2) = 3是指开始买卖后二个小时的即时价格为3元;g (2) = 3表示二个小时内的平均价格为3元),下图给出的四个图像中,实线表示)(x f y =,虚线表示)(x g y =,其中可能正确的是9.路灯距地平面为8 m ,一个身高为1.6 m 的人以1.4m/s 的速率从路灯在地面上射影点C ,沿某直线离开路灯,那么人影长度的变化速率v 为A .227 m/sB .247m/s C .207 m/sD .237m/s 10.将一个四棱锥V -ABCD 的每个顶点染上一种颜色,并使每一条棱的两端异色,若只有4 种颜色可供使用,则不同的染色方法种数为 A .64 B .72 C .36 D .48第 Ⅱ 卷(非选择题,共100分)二.填空题(本大题共5小题,每小题5分,共25分。
湖北省武汉市武昌区2018届高三元月调研考试数学(文)试题+Word版含答案【KS5U+高考】

武昌区2018届高三年级元月调研考试文科数学本试卷共5页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.2.答题前,考生务必将自己的姓名、准考证号填写在本试卷答题卡相应位置上.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合A ={﹣1,0,1,2,3},B ={x |x 2﹣3x <0},则A ∩B = A .}1{- B .}2,1{ C .}3,2,1{ D .}3,1,0{-2.已知复数z 满足i 1||+=+z z ,则=zA .i -B .iC .i -1D .i 1+3. 奇函数)(x f 在()-∞+∞,单调递增,若1)1(=f ,则满足1)2(1≤-≤-x f 的x 的取值范围是A .]2,2[-B .]1,1[-C .]4,0[D .]3,1[4.设实数y x ,满足条件⎪⎩⎪⎨⎧≤++≥+≥+-,01,01,01y x y y x 那么y x -2的最大值为A .3-B .2-C .1D .25.执行如图所示的程序框图,如果输入的a 依次为2,2,5时, 输出的s 为17,那么在框中,可以填入 A. n k >? B. n k <? C. n k ≤? D. n k ≥?6.函数)cos()(ϕω+=x A x f 的部分图像如图所示,给出以下结论: ①)(x f 的周期为2; ②)(x f 的一条对称轴为21-=x ; ③)(x f 在)432,412(+-k k ,Z ∈k 上是减函数;④)(x f 的最大值为A .则正确结论的个数为A .1B .2C .3D .47.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为开始 输入ax =2,n =2,k =0,s =0输出s 结束是 否s =sx +a k =k +1A .121 B .49 C .29D .38. 在ABC ∆中,a ,b ,c 分别是角A ,B ,C 的对边,且c a C b +=2cos 2,则=B A .6π B .4π C .3π D .3π2 9.已知点P 在双曲线)0,0(12222>>=-b a by a x 上,x PF ⊥轴(其中F 为双曲线的焦点),点P到该双曲线的两条渐近线的距离之比为31,则该双曲线的离心率为A.332 B.3 C.552 D. 510.已知底面半径为1,高为3的圆锥的顶点和底面圆周都在球O 的球面上,则此球的表面积为A. 27π323 B. π4 C. 3π16 D. π1211.过抛物线C :x y 42=的焦点F 的直线l 与抛物线C 交于P ,Q 两点,与其准线交于点M ,且3=,则=||FP A .32 B .34 C .31D .1 12.已知函数kx xxx f -=ln )(在区间]e ,e [41上有两个不同的零点,则实数k 的取值范围为 A .)e 21,e 41[B .)e21,e 41( C .]e 41,e 1[2 D .]e 1,e 1[2 第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生必须做答.第22题~第23题为选考题,考生根据要求做答.二、填空题:本题共4小题,每小题5分,共20分。
湖北省襄阳市普通高中2018届高三上学期1月调研统一测试 理科综合 图片版含答案

2018年1月襄阳市高中调研统一测试高三物理参考答案14. D 15. B 16. B 17.C 18.B 19. AD 20. BD 21. BC22. D =1.21cm (2分) V B =t D (2分) 2g )(2D L +=2)(tD (2分) 23. (1)2 (2分) (3)Er R R R R E r R R R I g g ++++++=01011))((1 (3分) (4)2.08(2.07~2.09) (2分) (5)= (2分)24.解:以O 点为坐标原点,沿水平方向建立x 轴,竖直方向建立y 轴。
当小球A 以v 0的速度做平抛运动时,有:t v x 0= (1分)221gt y = (1分) 联立得小球A 的平抛轨迹方程为:2022v gx y = (1分) 在M 点,x =y ,所以gv y M 202= (1分) 小球A 自O 点沿该轨道无初速下滑到M 点,有:M M m g y mv =221 (2分) 可得:022v gy v M M == (2分)小球A 由轨道经M 点的速度方向与平抛经M 点时的速度方向相同,则有:My M Mx gy v v v v v v v 22002200+=+= (3分) 联立解得:0552v v Mx =(1分) 25.解:(1)在乙恰好能通过最高点的情况下,设乙达到最高点的速度为v D ,乙离开D 点到达水平轨道的时间为t ,乙的落点到B 点的距离为x ,则: qE mg Rv m D +=2 (1分) 2)(212t mqE mg R += (1分) t v x D = (1分)联立解得:x =0.4m (1分)(2)设碰撞后甲、乙的速度分别为v 甲、v 乙,根据动量守恒和机械能守恒有:乙甲mv mv mv +=0 (1分)2220212121乙甲mv mv mv += (1分) 联立可得:0v v =乙 (1分) 由动能定理得:22212122乙mv mv R qE R mg D -=⋅-⋅- (2分)联立解得:m/s 5.2)(50=+=mR qE mg v (1分) (3)设甲的质量为M ,碰撞后甲、乙的速度分别为v M 、v m ,根据动量守恒和机械能守恒有:m M mv Mv Mv +=0 (1分) 2220212121m M mv Mv Mv += (1分) 联立得:02v mM M v m += (1分) 由题意知:m M ≥ 可得:002v v v m <≤ (1分)设乙球过D 点的速度为v D /,由动能定理得:22/212122m D mv mv R qE R mg -=⋅-⋅- (2分) 联立解得:m/s 8m/s 2/<≤D v (1分)设乙在水平轨道上的落点到B 点的距离为x /,则有:t v x D //= (1分)可得:m 8.0m 4.0/<≤x (1分)33.(1)BDE(2)解:(i)当气缸内气体与大气达到平衡时,其压强由P =1.2P 0下降到P 0,温度由T =2.4T 0变为T 0,体积由V 变为V 1,由理想气体状态方程得:10T V P T PV = (2分) 解得:V V T P PT V 21001== (1分) (ii) 在活塞下降过程中,活塞对气体做功为:)(10V V P W -= (2分)在这一过程中,气体内能减少量为:)(01T T U -=∆α (2分)由热力学第一定律得,气缸内气体放出的热量为:U W Q ∆+= (2分)联立解得:0021T V P Q α+=(1分) 34.(1)ABE(2)解:(i) n 1=sin β1sin θ, (1分) n 2=sin β2sin θ(1分) 代入数据得β1=45°,β2=60° (2分) 故彩色光带的宽度为R R R d )331()90tan()90tan(21-=-︒--︒=ββ (3分) (ii)当复色光恰好全部发生全反射时,211sin 1==n C (2分) 即入射角θ=C =45° (1分)2018年1月襄阳市普通高中高三元月调考理综化学参考答案及评分标准7-13 选择题:CADCD CD26(14分)(1) 水浴 (2分);维持反应速率,并减少HNO 3的挥发及分解,减少副反应的发生 (2分,答对两点即给2分)(2) 吸收HNO 3被还原生成的氮氧化物,防止污染空气 (2分)(3) 加快过滤速度,减少过滤过程中产品的变质,得到较干燥的产品(2分,答对两点即给2分)(4) 除去残留的HNO 3,减小己二酸的损失 (2分)(5) 58.9 (2分)(6) (2分)27 (14分)(1) Al 2O 3 + 2NaOH = 2NaAlO 2 + H 2O (2分)(2) 溶解Li 2O 、Fe 2O 3、并将Co 3O 4转化为Co 2+,防止在后续除杂中将Co 3+沉淀而造成损失 (2分)(3) 3.2≤pH <7.15 (2分) LiF 、Fe(OH)3 (2分,少答或错答均不给分)(4) 取少量滤液B 于试管中,向其中滴加KSCN 溶液,观察溶液是否变红,若变红,则有Fe 3+,反之则无Fe 3+ (2分,其他合理答案也给分)(5) CoC 2O 4 △ CoO+CO↑+CO 2↑ (2分,缺少条件扣1分,气体符号未打扣1分,两个未打只扣1分) ; Co 3O 4(2分)28(15分)(1)CH 4(g)+H 2O(g)=CO(g)+3H 2(g) △H= + 206 kJ/mol (2分)(2) ①0.016mol/(L·min) (1分)②C (2分)③小于 (1分); 大于 (1分); 1.6384 mol 2/L 2 (保留小数点后1位、2位或3位均可,未带单位不扣分) (2分)(3) c(NH 4+)>c(HS —)>c(OH —)>c(H +)>c(S 2—) (2分)(4) ①有副反应发生 (1分)②< (1分);平衡后,升高温度,甲醚的产率降低; (2分)35【化学—选修3物质结构与性质】(15分)(1) 28 (1分); [Ar]3d 104s 24p 3 (2分)(2) 5 (2分)(3) AsCl 3 + 3H 2O ==== H 3AsO 3 + 3HCl (2分)(4) sp 3杂化 (1分)【注:Cl -形成配位键,孤电子对数为2,σ键数为2,Cl 的杂化方式为sp 3】(5) NH 3>HCl ;NH 3存在分子间氢键,HCl 分子间只存在范德华力,氢键作用力比范德华力强,NH 3的熔沸点高于HCl (2分)(6) X-射线衍射 (1分) a. NiAs 或AsNi ; (2分) b.2122110b a 232⨯⨯⨯⨯+A N M M )( (2分)36【化学—选修5有机化学基础】(15分)(1) 碳碳双键、羧基(各1分,共2分) ;苯乙炔(1分)(2) (2分);消去反应(1分) (3) C (2分)(4) (2分)(5)(2分)(6) 17 (2分)2018年1月高三统考理科综合生物参考答案1—6 BACDA B29.(10分)(1)蓝紫光和红光类囊体的薄膜上(或基粒)(2)光照强度突变型水稻由于叶绿素含量低,吸收的光能少,光反应强度低,故暗反应强度也低,导致其CO2吸收速率低(3分)(3)突变型突变型的气孔导度大,进入叶片的CO2多,而胞间CO2浓度与野生型相近,说明突变型的光合速率较高,能较快地消耗CO2(3分)30.(9分)(1)大脑皮层(高级中枢)分级外正内负(2)神经和体液(激素)共同(3)下丘脑甲状腺激素乳酸(4)淋巴细胞(2分)31.(10分)(1)实验组(1分)样方法(1分)(2)生物性别比例出生率(3)生物种群的繁衍32.(10分)(1)正反交(2分)(2)S(rr)(2分)5(2分)(3)注:4分,只写出雄性不育植株的杂交过程也可。
【优质文档】2018届襄阳市高考理科数学模拟试卷及答案-word范文 (7页)
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! == 2018届襄阳市高考理科数学模拟试卷及答案要想准确地把握高考理科数学的考点,那就是多做一些高考理科数学的模拟试卷,以下是小编为你整理的2018届襄阳市高考理科数学模拟试卷,希望能帮到你。
2018届襄阳市高考理科数学模拟试卷题目一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的).1. 设集合,,则 ( )A. B. C. D.2. 已知复数在复平面上对应的点在直线上,复数 ( 是虚数单位),则( )A. B. C. D.3. 若,则的值为( )A. B. C. D.4. 在内随机取出两个数,则这两个数满足的概率为( )A. B. C. D.5. 若圆与直线交于不同的两点,则实数的取值范围为( )A. B. C. D.6. 70年代中期,美国各所名牌大学校园内,人们都像发疯一般,夜以继日,废寝忘食地玩一个数学游戏.这个游戏十分简单:任意写出一个自然数,并且按照以下的规律进行变换:如果是个奇数,则下一步变成 ;如果是个偶数,则下一步变成 .不单单是学生,甚至连教师、研究员、教授与学究都纷纷加入.为什么这个游戏的魅力经久不衰?因为人们发现,无论是怎样一个数字,最终都无法逃脱回到谷底 .准确地说,是无法逃出落入底部的循环,永远也逃不出这样的宿命.这就是著名的“冰雹猜想”.按照这种运算,自然数经过十步运算得到的数为 ( )A. B. C. D.7. 在中,,,分别为内角,,的对边,且,则的值为( )A. B. C. D.8. 某几何体的三视图如图所示,若该几何体的体积为,则图中的值为( )A. B. C. D.9. 运行如下程序框图,如果输入的,则输出属于( )A. B. C. D.10. 已知向量,,,若与的夹角为60°,且,则实数的值为( )A. B. C. 6 D. 411. 如图,在四边形中,,, .现沿对角线折起,使得平面平面,且三棱锥的体积为,此时点,,,在同一个球面上,则该球的体积是( )A. B. C. D.12. 已知函数存在极值,若这些极值的和大于,则实数的取值范围为( )A. B. C. D.第Ⅱ卷本试卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分)13. 若,其中,则的值为 .14. 已知函数,若,实数满足约束条件,则目标函数的最大值为 .15. 过点的直线交抛物线于两点,若抛物线的焦点为,则面积的最小值为 .16. 以下四个命题:①已知随机变量,若,则的值为 ;②设,则“ ”是“ ”的充分不必要条件;③函数的零点个数为1;④命题,,则为 .其中真命题的序号为 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17. (本小题满分12分)已知数列为公差不为0的等差数列,满足,且成等比数列.(1)求的通项公式;(2)若数列满足,且,求数列的前项和 .18. (本小题满分12分)已知在四棱锥中,平面 , , 是边长为的等边三角形,,为的中点.(1)求证: ;(2)若直线与平面所成角的正切值为,求二面角的大小.19. (本小题满分12分)近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的名顾客进行统计,其中岁以下占,采用微信支付的占,岁以上采用微信支付的占 .(1)请完成下面列联表:岁以下岁以上合计使用微信支付未使用微信支付合计并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”?(2)采用分层抽样的方法从名顾客中抽取人参与抽奖活动,一等奖两名,记“ 岁以下”得一等奖的人数为,求的分布列及数学期望.参考公式: , .参考数据:20. (本小题满分12分)已知椭圆的两个焦点为,,是椭圆上一点,若, .(1)求椭圆的方程;(2)点是椭圆上任意一点,分别是椭圆的左、右顶点,直线与直线分别交于两点,试证:以为直径的圆交轴于定点,并求该定点的坐标.21. (本小题满分12分)已知函数 .(1)如果对于任意的,恒成立,求实数的取值范围;(2)若,过点作函数的图象的所有切线,令各切点的横坐标按从小到大构成数列,求数列的所有项之和.请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22. (本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系中,点,以原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为 .直线的参数方程为为参数 .(Ⅰ)写出曲线的直角坐标方程和直线的普通方程;(Ⅱ)设直线与曲线的两个交点分别为,求的值.23. (本小题满分10分)选修4-5:不等式选讲已知函数 .(Ⅰ)解不等式 ;(Ⅱ)若关于的不等式在上的解集为,求实数的取值范围.2018届襄阳市高考理科数学模拟试卷答案1 2 3 4 5 6C D A B C C7 8 9 10 11 12B C A A A B13. 14. 15. 16.②③17.【解析】(1)设等差数列的公差为 ( ),由成等比数列可知 ,又,解得,∴ .………………4分(2)由,得,当时,,………………………8分对上式也成立,∴ ,∴ ,∴ .………12分18. 【解析】(1)因为是等边三角形,为的中点,所以 .又因为平面 ,,可得平面,因为平面,所以 ;(4分)(2)如图,以点为坐标原点,所在直线分别为轴,过且与直线平行的直线为轴,建立空间直角坐标系.因为平面,所以为直线与平面所成的角.(6分)由题意得,即,故,,,于是,,,,设平面与平面的法向量分别为,,则由得,令,得,所以 .同理求得, (10分)所以,则二面角的大小为 .(12分)19.【解析】(1)由已知可得,岁以下的有人,使用微信支付的有人,岁以上使用微信支付的有人.所以列联表为:岁以下岁以上合计使用微信支付 40 10 50未使用微信支付 20 30 50合计 60 40 100由列联表中的数据计算可得的观测值为,由于,所以有的把握认为“使用微信支付与年龄有关”. .....5分(2)采用分层抽样的方法从名顾客中抽取人,则从“ 岁以下”的人中抽取人,从“ 岁以上”的人中抽取人,的所有可能取值为,又,,,故分布列如下:数学期望 . .....12分20.【解析】(1)由,得,即,由勾股定理,得,且,解得,根据椭圆的定义,可得,即,所以,所以椭圆的方程为 ......4分(2)由(1)得,,设,则直线的方程为,它与直线的交点的坐标为,直线的方程为,它与直线的交点的坐标为,再设以为直径的圆交轴于点,则,从而,即,即,解得 .故以为直径的圆交轴于定点,该定点的坐标为或 . ..........12分21.【解析】(1)令,要使恒成立,只需当时,,,令,则对恒成立,在上是增函数,则,..........2分①当时,恒成立,在上为增函数,,满足题意;②当时,在上有实根 , 在上是增函数,则当时,,不符合题意;③当时,恒成立,在上为减函数,不符合题意,,即 . ..........5分(2) ,,设切点坐标为,则切线斜率为,从而切线方程为,,即,令,,这两个函数的图象关于点对称,则它们交点的横坐标关于对称,从而所作的所有切线的切点的横坐标构成数列的项也关于成对出现,又在内共有1008对,每对和为,∴数列的所有项之和为 . .....12分22.【解析】(1)曲线的直角坐标方程为,直线的普通方程为.……5分(2)点在直线上,将直线的参数方程代入曲线的直角坐标方程,得,,设两根为,,,,故与异号,,,.………………10分23.【解析】(1)不等式可化为,当时,,解得,即 ;当时,,解得,即 ;当时,,解得,即,综上所述,不等式的解集为或.……………5分(2)由不等式可得,,∴ ,即,解得或,故实数的取值范围是或.…10分。
2018届湖北省襄阳高三数学三模试卷(理科)Word版含解析
2018届湖北省襄阳高三三模试卷(理科数学)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的).1.设集合A={x|log2(x+1)<2},B={y|y=},则(∁R A)∩B=()A.(0,3)B. C.,y∈内随机取出两个数,则这两个数满足x﹣y﹣3>0的概率为()A.B.C.D.5.若圆x2+y2﹣12x+16=0与直线y=kx交于不同的两点,则实数k的取值范围为()A.(﹣,)B.(﹣,)C.(﹣,)D.(﹣,)6.70年代中期,美国各所名牌大学校园内,人们都像发疯一般,夜以继日,废寝忘食地玩一个数学游戏.这个游戏十分简单:任意写出一个自然数N,并且按照以下的规律进行变换:如果是个奇数,则下一步变成3N+1;如果是个偶数,则下一步变成.不单单是学生,甚至连教师、研究员、教授与学究都纷纷加入.为什么这个游戏的魅力经久不衰?因为人们发现,无论N是怎样一个数字,最终都无法逃脱回到谷底1.准确地说,是无法逃出落入底部的4﹣2﹣1循环,永远也逃不出这样的宿命.这就是著名的“冰雹猜想”.按照这种运算,自然数27经过十步运算得到的数为()A.142 B.71 C.214 D.1077.在△ABC中,a,b,c分别为内角A,B,C的对边,且a2=3b2+3c2﹣2bcsinA,则C的值为()A.B.C.D.8.某几何体的三视图如图所示,若该几何体的体积为,则图中x的值为()A.3 B.1 C.2 D.9.运行如下程序框图,如果输入的t∈,则输出S属于()A. C. D.10.已知向量||=3,||=2, =m+n,若与的夹角为60°,且⊥,则实数的值为()A.B.C.6 D.411.如图,在四边形ABCD中,AB=BC=2,∠ABC=90°,DA=DC=.现沿对角线AC折起,使得平面DAC⊥平面ABC,此时点A,B,C,D在同一个球面上,则该球的体积是()A.B.C.D.12π12.已知函数f(x)=ax﹣x2﹣lnx存在极值,若这些极值的和大于5+ln2,则实数a的取值范围为()A.(﹣∞,4)B.(4,+∞)C.(﹣∞,2)D.(2,+∞)二、填空题(本大题共4小题,每小题5分,共20分)13.若(1+x)(a﹣x)6=a0+a1x+a2x2+…+a7x7,其中a=(sinx﹣cosx)dx,则a0+a1+a2+…+a6的值为.14.已知函数f(x)=,若f=a,实数x,y满足约束条件,则目标函数z=的最大值为.15.过点P(2,0)的直线交抛物线y2=4x于A,B两点,若抛物线的焦点为F,则△ABF面积的最小值为.16.以下四个命题:①已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为;②设a、b∈R,则“log2a>log2b”是“2a﹣b>1”的充分不必要条件;③函数f(x)=﹣()x的零点个数为1;④命题p:∀n∈N,3n≥n2+1,则¬p为∀n∈N,3n≤n2+1.其中真命题的序号为.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.已知数列{a n}为公差不为0的等差数列,满足a1=5,且a2,a9,a30成等比数列.(1)求{a n}的通项公式;(2)若数列{b n}满足﹣=a n(n∈N*),且b1=,求数列{b n}的前n项和T n.18.已知在四棱锥C﹣ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点.(1)求证:CM⊥EM;(2)若直线DM与平面ABC所成角的正切值为2,求二面角B﹣CD﹣E的大小.19.近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的100名顾客进行统计,其中40岁以下占,采用微信支付的占,40岁以上采用微信支付的占.(Ⅰ)请完成下面2×2列联表:并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”?(Ⅱ)若以频率代替概率,采用随机抽样的方法从“40岁以下”的人中抽取2人,从“40岁以上”的人中抽取1人,了解使用微信支付的情况,问至少有一人使用微信支付的概率为多少?参考公式:,n=a+b+c+d.参考数据:20.已知椭圆的两个焦点为F1(﹣,0),F2(,0),M是椭圆上一点,若•=0,||•||=8.(1)求椭圆的方程;(2)点P是椭圆上任意一点,A1、A2分别是椭圆的左、右顶点,直线PA1,PA2与直线x=分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.21.已知函数f(x)=e x(sinx+cosx).(1)如果对于任意的x∈,f(x)≥kx+e x cosx恒成立,求实数k的取值范围;(2)若x∈,过点M(,0)作函数f(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{x n},求数列{x n}的所有项之和.请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.在直角坐标系xOy中,点P(0,),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.直线l的参数方程为为参数).(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求+的值.23.已知函数f(x)=|x﹣2|﹣|x+1|.(Ⅰ)解不等式f(x)+x>0;(Ⅱ)若关于x的不等式f(x)≤a2﹣2a在R上的解集为R,求实数a的取值范围.2018届湖北省襄阳高三数学三模试卷(理科)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的).1.设集合A={x|log2(x+1)<2},B={y|y=},则(∁R A)∩B=()A.(0,3)B. C.,y∈内随机取出两个数,则这两个数满足x﹣y﹣3>0的概率为()A.B.C.D.【考点】CB:古典概型及其概率计算公式.【分析】基本事件满足的可行域为:,设事件A表示“这两个数满足x﹣y﹣3>0”作出可行域,利用几何概型能求出这两个数满足x﹣y﹣3>0的概率.【解答】解:在x∈,y∈内随机取出两个数,∴基本事件满足的可行域为:,设事件A表示“这两个数满足x﹣y﹣3>0”作出可行域如右图,则这两个数满足x﹣y﹣3>0的概率:P(A)==.故选:B.5.若圆x2+y2﹣12x+16=0与直线y=kx交于不同的两点,则实数k的取值范围为()A .(﹣,)B .(﹣,)C .(﹣,)D .(﹣,)【考点】J9:直线与圆的位置关系.【分析】求出圆的圆心与半径,利用点到直线的距离公式列出不等式求解即可.【解答】解:圆x 2+y 2﹣12x+16=0的圆心(6,0),半径为2,圆x 2+y 2﹣12x+16=0与直线y=kx 交于不同的两点,可得<2,解得k ∈(﹣,).故选:C .6.70年代中期,美国各所名牌大学校园内,人们都像发疯一般,夜以继日,废寝忘食地玩一个数学游戏.这个游戏十分简单:任意写出一个自然数N ,并且按照以下的规律进行变换:如果是个奇数,则下一步变成3N+1;如果是个偶数,则下一步变成.不单单是学生,甚至连教师、研究员、教授与学究都纷纷加入.为什么这个游戏的魅力经久不衰?因为人们发现,无论N 是怎样一个数字,最终都无法逃脱回到谷底1.准确地说,是无法逃出落入底部的4﹣2﹣1循环,永远也逃不出这样的宿命.这就是著名的“冰雹猜想”.按照这种运算,自然数27经过十步运算得到的数为( ) A .142 B .71 C .214 D .107 【考点】F1:归纳推理.【分析】根据要求一步一步的推即可得到答案【解答】解:27→82→41→124→62→31→94→47→142→71→214, 故选:C7.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且a 2=3b 2+3c 2﹣2bcsinA ,则C 的值为( )A .B .C .D .【考点】HR :余弦定理.【分析】利用余弦定理与不等式结合的思想求解a ,b ,c 的关系.即可求解C 的值.【解答】解:根据a 2=3b 2+3c 2﹣2bcsinA ,…①余弦定理a 2=b 2+c 2﹣2bccosA ,…②由①﹣②可得:2b2+2c2=2bcsinA﹣2bccosA化简:b2+c2=bcsinA﹣bccosA⇔b2+c2=2bcsin(A﹣),∵b2+c2≥2bc,∴sin(A﹣)=1,∴A=,此时b2+c2=2bc,故得b=c,即B=C,∴C==.故选:B.8.某几何体的三视图如图所示,若该几何体的体积为,则图中x的值为()A.3 B.1 C.2 D.【考点】L!:由三视图求面积、体积.【分析】如图所示,该几何体为三棱柱ABC﹣A1B1C1,去掉一个三棱锥A﹣CDC1后剩下的几何体.其中AB⊥BC,侧面ABB1A1是正方形,D为BC的中点,BC=4.【解答】解:如图所示,该几何体为三棱柱ABC﹣A1B1C1,去掉一个三棱锥A﹣CDC1后剩下的几何体.其中AB⊥BC,侧面ABB1A1是正方形,D为BC的中点,BC=4.∴该几何体的体积为=﹣•x,解得x=2.故选:C.9.运行如下程序框图,如果输入的t∈,则输出S属于()A. C. D.【考点】EF:程序框图.【分析】根据程序框图的功能进行求解即可.【解答】解:本程序为条件结果对应的表达式为S=,则当输入的t∈,则当t∈时,s=t2﹣4t=(t﹣2)2﹣4∈,综上s∈=a,实数x,y满足约束条件,则目标函数z=的最大值为8 .【考点】7C:简单线性规划.【分析】根据分段函数的表达式,求出a的值,作出不等式组对应的平面区域,利用分式函数的性质结合直线斜率的公式进行求解即可.【解答】解:f(﹣2)==4,则a=f=f(4)=4﹣2=2,则约束条件为,作出不等式组对应的平面区域如图:z===3+4•,设k=,则k的几何意义是区域内的点到定点D(﹣2,﹣1)的斜率,则z=3+4k,由图象知AD的斜率最大,由得,即A(2,4),此时k==,则z=3+4×=3+4=8,即目标函数z=的最大值为8,故答案为:815.过点P(2,0)的直线交抛物线y2=4x于A,B两点,若抛物线的焦点为F,则△ABF面积的最小值为2.【考点】K8:抛物线的简单性质.【分析】方法一:分类讨论,当直线l的斜率不存在时,求得A和B点坐标,根据三角形的面积公式,即可求得△ABF面积,当直线斜率存在时,设直线l的方程,利用韦达定理及弦长公式即可求得△ABF面积的取值范围,综上即可求得△ABF面积的最小值;方法二:设直线AB:x=my+2,代入椭圆方程,利用韦达定理及弦长公式即可求得三角形的面积的最小值.【解答】解:方法一:抛物线y2=4x焦点F(1,0),当直线l的斜率不存在时,此时将x=2代入抛物线C:y2=4x中,得y2=8,解得y=±2,则点A,B的坐标为(2,2),(2,﹣2),∴△ABF面积S=×1×丨AB丨=2,当直线的存在,且不为0,设直线AB:y=k(x﹣2).A(x1,y1),B(x2,y2)(y1>0,y2<0),联立,消去y,得k2x2﹣(4k2+4)x+4k2=0,且△=32k2+16>0,则由韦达定理,x1+x2=,x1x2=4,y1+y2=,y1y2=﹣8,∴△ABF面积S=×丨PF丨×丨y1﹣y2丨=×1×=×>2,综上可知:则△ABF面积的最小值2,故答案为:2.方法二:抛物线y2=4x焦点F(1,0),设直线AB:x=my+2,A(x1,y1),B(x2,y2)(y1>0,y2<0),,整理得:y2﹣4my﹣8=0,则y1+y2=4m,y1y2=﹣8,∴△ABF面积S=×丨PF丨×丨y1﹣y2丨=×1×≥×4=2,当m=0时,取最小值,最小值为2,∴△ABF面积的最小值2,故答案为:2.16.以下四个命题:①已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为;②设a、b∈R,则“log2a>log2b”是“2a﹣b>1”的充分不必要条件;③函数f(x)=﹣()x的零点个数为1;④命题p:∀n∈N,3n≥n2+1,则¬p为∀n∈N,3n≤n2+1.其中真命题的序号为②③.【考点】2K:命题的真假判断与应用.【分析】由曲线关于y轴对称,由概率分布特点,即可判断①;运用对数函数和指数函数的单调性,结合充分必要条件的定义,即可判断②;画出y=和y=()x的图象,即可判断③;由全称命题的否定为特称命题,即可判断④.【解答】解:①已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)=(1﹣P(|X|<2))=,故①错;②设a、b∈R,log2a>log2b⇔a>b>0⇒a﹣b>0⇒2a﹣b>1,由于a﹣b>0,a,b不一定大于0,则“log2a>log2b”是“2a﹣b>1”的充分不必要条件,故②对;③由y=和y=()x的图象,可得它们只有一个交点,即函数f(x)=﹣()x的零点个数为1,故③对;④命题p:∀n∈N,3n≥n2+1,则¬p为∃n∈N,3n<n2+1.故④错.故答案为:②③.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.已知数列{a n}为公差不为0的等差数列,满足a1=5,且a2,a9,a30成等比数列.(1)求{a n}的通项公式;(2)若数列{b n}满足﹣=a n(n∈N*),且b1=,求数列{b n}的前n项和T n.【考点】8H:数列递推式;8E:数列的求和.【分析】(1)设等差数列{a n}的公差为d(d≠0),由a2,a9,a30成等比数列可知,又a1=5,解得d即可得出.(2)由数列{b n}满足﹣=a n(n∈N*),可得: =a n﹣1(n≥2).且b1=,当n≥2时, =++…+=3+a1+a2+…+a n﹣1,利用等差数列的求和公式即可得出=n(n+2).可得b n==,再利用裂项求和方法即可得出.【解答】解:(1)设等差数列{a n}的公差为d(d≠0),由a2,a9,a30成等比数列可知,又a1=5,解得d=2,∴a n=2n+3.(2)由数列{b n}满足﹣=a n(n∈N*),可得: =a n﹣1(n≥2).且b1=,当n≥2时, =++…+=3+a1+a2+…+a n﹣1=3+=n(n+2).对b1=上式也成立,∴ =n(n+2).∴b n==,∴T n=++…++==.18.已知在四棱锥C﹣ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点.(1)求证:CM⊥EM;(2)若直线DM与平面ABC所成角的正切值为2,求二面角B﹣CD﹣E的大小.【考点】MI:直线与平面所成的角;LX:直线与平面垂直的性质;MT:二面角的平面角及求法.【分析】(1)推导出CM⊥AB,DB⊥CM,从而CM⊥平面ABDE,由此能证明CM⊥EM.(2)以点M为坐标原点,MC,MB所在直线分别为x,y轴,过M且与直线BD平行的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣CD﹣E的大小.【解答】证明:(1)∵△ABC是等边三角形,M为AB的中点,∴CM⊥AB.又∵DB⊥平面ABC,∴DB⊥CM,∴CM⊥平面ABDE,∵EM⊂平面ABDE,∴CM⊥EM.解:(2)如图,以点M为坐标原点,MC,MB所在直线分别为x,y轴,过M且与直线BD平行的直线为z轴,建立空间直角坐标系.∵DB⊥平面ABC,∴∠DMB为直线DM与平面ABC所成的角.由题意得tan,即BD=2,故B(0,1,0),C(),D(0,1,2),E(0,﹣1,1),∴=(),=(0,0,2),=(﹣),=(﹣),设平面BCD与平面CDE的法向量分别为=(x,y,z),=(a,b,c),则,令x=1,得=(1,,0).同理求得=(1,﹣,),∴cos<>==0,∴二面角B﹣CD﹣E的大小为90°.19.近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的100名顾客进行统计,其中40岁以下占,采用微信支付的占,40岁以上采用微信支付的占.(Ⅰ)请完成下面2×2列联表:并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”?(Ⅱ)若以频率代替概率,采用随机抽样的方法从“40岁以下”的人中抽取2人,从“40岁以上”的人中抽取1人,了解使用微信支付的情况,问至少有一人使用微信支付的概率为多少?参考公式:,n=a+b+c+d.参考数据:【考点】BL:独立性检验.【分析】(Ⅰ)由40岁以下的有100×=60人,使用微信支付的有60×=40人,40岁以上使用微信支付有40×=10人.即可完成2×2列联表,根据2×2列联表求得观测值K2与参考值对比即可求得答案;(Ⅱ)分别求得“40岁以下”的人中抽取2人,这两人使用微信支付的概率,从“40岁以上”的人中抽取1人,这个人使用微信支付的概率,根据独立事件的概率公式,即可求得答案.【解答】解:(Ⅰ)由已知可得,40岁以下的有100×=60人,使用微信支付的有60×=40人,40岁以上使用微信支付有40×=10人.∴2×2列联表为:由列联表中的数据计算可得K2的观测值为k==,由于>10.828,∴有99.9%的把握认为“使用微信支付与年龄有关”;…(Ⅱ)若以频率代替概率,采用随机抽样的方法从“40岁以下”的人中抽取2人,这两人使用微信支付分别记为A,B,则P(A)=P(B)=,从“40岁以上”的人中抽取1人,这个人使用微信支付记为C,则P(C)=,显然A,B,C相互独立,则至少有一人使用微信支付的概率为P=1﹣P()=1﹣××=.故至少有一人使用微信支付的概率为.…20.已知椭圆的两个焦点为F1(﹣,0),F2(,0),M是椭圆上一点,若•=0,||•||=8.(1)求椭圆的方程;(2)点P是椭圆上任意一点,A1、A2分别是椭圆的左、右顶点,直线PA1,PA2与直线x=分别交于E,F两点,试证:以EF为直径的圆交x轴于定点,并求该定点的坐标.【考点】KL:直线与椭圆的位置关系;9R:平面向量数量积的运算;K4:椭圆的简单性质.【分析】(1)由题意可设椭圆的标准方程为: +=1(a>b>0),由•=0,可得⊥,设||=m,||=n.又||•||=8.可得m2+n2=,m+n=2a,mn=8,a2=b2+5.解出即可得出.(2)由(1)得A1(﹣3,0),A2(3,0),设P(x0,y0),则直线PA1的方程为y=(x+3),它与直线x=的交点的坐标为E,直线PA2的方程为:y=(x﹣3),它与直线x=的交点的坐标为F.再设以EF为直径的圆交x轴于点Q(m,0),则QE⊥QF,可得k QE•k QF=﹣1,又=9.即可得出.【解答】解:(1)由题意可设椭圆的标准方程为: +=1(a>b>0),由•=0,∴⊥,设||=m,||=n.又||•||=8.∴m2+n2=,m+n=2a,mn=8,a2=b2+5.解得:a=3,b=2.∴椭圆的方程为=1.(2)由(1)得A1(﹣3,0),A2(3,0),设P(x0,y0),则直线PA1的方程为y=(x+3),它与直线x=的交点的坐标为E,直线PA2的方程为:y=(x﹣3),它与直线x=的交点的坐标为F.再设以EF为直径的圆交x轴于点Q(m,0),则QE⊥QF,从而k QE•k QF=﹣1,即××=﹣,即=﹣,又=9.∴=1,解得m=±1.故以EF为直径的圆交x轴于定点,该定点的坐标为.21.已知函数f(x)=e x(sinx+cosx).(1)如果对于任意的x∈,f(x)≥kx+e x cosx恒成立,求实数k的取值范围;(2)若x∈,过点M(,0)作函数f(x)的图象的所有切线,令各切点的横坐标按从小到大构成数列{x n},求数列{x n}的所有项之和.【考点】6H:利用导数研究曲线上某点切线方程;6K:导数在最大值、最小值问题中的应用.【分析】(1)由题意可得任意的x∈,f(x)≥kx+e x cosx恒成立,只需当x∈时,g(x)min≥0,求出g′(x),令h(x)=e x(sinx+cosx),求出导数,可得h(x)的单调性,及值域,讨论k≤1时,1<k<e时,当k≥e时,由单调性确定最小值,即可得到所求k的范围;(2)求出f(x)的导数,设切点坐标为(x0,e x0(sinx0+cosx0)),可得切线的斜率和方程,代入M(,0),可得tanx0=2(x0﹣),令y1=tanx,y2=2(x﹣),这两个函数的图象关于点(,0)对称,即可得到所求数列{x n}的所有项之和.【解答】解:(1)函数f(x)=e x(sinx+cosx),可得g(x)=f(x)﹣kx﹣e x cosx=e x sinx﹣kx,要使任意的x∈,f(x)≥kx+e x cosx恒成立,只需当x∈时,g(x)min≥0,g′(x)=e x(sinx+cosx)﹣k,令h(x)=e x(sinx+cosx),则h′(x)=2e x cosx≥0对x∈时恒成立,∴h(x)在x∈上是增函数,则h(x)∈,①当k≤1时,g′(x)≥0恒成立,g(x)在x∈上为增函数,∴g(x)min≥g(0)=0,∴k≤1满足题意;②当1<k<e时,g′(x)=0在x∈上有实根x0,h(x)在x∈上是增函数,则当x∈上为减函数,∴g(x)<g(0)=0不符合题意,∴k≤1,即k∈(﹣∞,1];(2)函数f(x)=e x(sinx+cosx),∴f′(x)=2e x cosx,设切点坐标为(x0,e x0(sinx0+cosx0)),则切线斜率为f′(x0)=2e x0cosx0,从而切线方程为y﹣e x0(sinx0+cosx0)=2e x0cosx0(x﹣x0),∴﹣e x0(sinx0+cosx0)=2e x0cosx0(﹣x0),即tanx0=2(x0﹣),令y1=tanx,y2=2(x﹣),这两个函数的图象关于点(,0)对称,则它们交点的横坐标关于x=对称,从而所作的所有切线的切点的横坐标构成数列{x n}的项也关于x=成对出现,又在内共有1008对,每对和为π,∴数列{x n}的所有项之和为1008π.请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.在直角坐标系xOy中,点P(0,),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为.直线l的参数方程为为参数).(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求+的值.【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.【分析】(Ⅰ)由曲线C的极坐标方程能求出曲线C的直角坐标方程;直线l的参数方程消去t,能求出直线l的普通方程.(Ⅱ)点P(0,)在直线l:上,将直线l的参数方程代入曲线C的直角坐标方程,得5t2+12t﹣4=0,设两根为t1,t2,则,,由此能求出+.【解答】解:(Ⅰ)∵曲线C的极坐标方程为,∴曲线C的直角坐标方程为,∵直线l的参数方程为为参数),∴消去t得直线l的普通方程为.…(Ⅱ)点P(0,)在直线l:上,将直线l的参数方程代入曲线C的直角坐标方程,得2(﹣)2+()2=4,∴5t2+12t﹣4=0,设两根为t1,t2,则,,故t1与t2异号,∴|PA|+|PB|=|t1﹣t2|==,|PA|•|PB|=|t1•t2|=﹣t1t2=,∴+==.…23.已知函数f(x)=|x﹣2|﹣|x+1|.(Ⅰ)解不等式f(x)+x>0;(Ⅱ)若关于x的不等式f(x)≤a2﹣2a在R上的解集为R,求实数a的取值范围.【考点】R5:绝对值不等式的解法.【分析】(Ⅰ)通过讨论x的范围求出各个区间上的不等式的解集,取并集即可;(Ⅱ)根据绝对值的性质,得到关于a的不等式,解出即可.【解答】解:(Ⅰ)不等式f(x)+x>0可化为|x﹣2|+x>|x+1|,当x<﹣1时,﹣(x﹣2)+x>﹣(x+1),解得x>﹣3,即﹣3<x<﹣1;当﹣1≤x≤2时,﹣(x﹣2)+x>x+1,解得x<1,即﹣1≤x<1;当x>2时,x﹣2+x>x+1,解得:x>3,即x>3,综上所述,不等式f(x)+x>0的解集为{x|﹣3<x<1或x>3}.…(Ⅱ)由不等式f(x)≤a2﹣2a,可得|x﹣2|﹣|x+1|≤a2﹣2a,∵|x﹣2|﹣|x+1|≤|x﹣2﹣x﹣1|=3,∴a2﹣2a≥3,即a2﹣2a﹣3≥0,解得a≤﹣1或a≥3,故实数a的取值范围是a≤﹣1或a≥3.…。
2018年襄阳市普通高中调研统一考试
2018年襄阳市普通高中调研统一考试高二数学(理工类)第Ⅰ卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知复数z 满足1iz i i++=(i 为虚数单位),则z =A. 12i -+B. 12i --C. 12i +D.12i -2. .双曲线()222104x y a a -=>的一个焦点与抛物线2y =的焦点重合,则双曲线的渐近线方程是 A. 14y x =± B. 12y x =± C. 2y x =± D.4y x =±3. 一动圆与定圆()22:21F x y ++=相外切,且与直线:1l x =相切,则动圆圆心的轨迹方程为A. 24y x =B. 22y x =C. 24y x =-D. 28y x =- 4.下列说法错误的是A. 命题“若2320x x -+=,则1x =”的逆否命题是“若1x ≠,则2320x x -+≠” B.若p q ∧为假命题,则,p q 均为假命题C.“1x =”是“2320x x -+=”的充分不必要条件D.若命题:,p x R ∃∈使得210x x ++<,则:,p x R ⌝∀∈都有210x x ++≥5. 直线l 与椭圆22:184x y C +=相交于A,B 两点,若直线l 的方程为210x y -+=,则线段AB 的中点坐标是A. 11,32⎛⎫-- ⎪⎝⎭B. 11,33⎛⎫- ⎪⎝⎭C. ()1,1D. 11,33⎛⎫- ⎪⎝⎭6.广告投入对商品的销售额有较大影响.某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如下表:(单位:万元)由上表可得回归直线方程为ˆˆ10.2y x a =+,据此模型,预测广告费为10万元时的销售额约为A. 111.2B. 108.8C. 101.2D.118.27.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:参照上表,得到的结论是A. 有99%的把握认为“爱好该项运动与性别有关”B.有99%的把握认为“爱好该项运动与性别无关”C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”8. 双曲线()2222:10,0x y C a b a b-=>>的离心率为2则双曲线C 的焦距等于A. 9. 已知函数()sin f x x x =-,则不等式()()1220f x f x ++->的解集是A. 1,3⎛⎫-∞- ⎪⎝⎭B. 1,3⎛⎫-+∞ ⎪⎝⎭C. ()3,+∞D. (),3-∞10.抛物线2:12C y x =的准线与轴交于点P ,A 是抛物线C 上的一点,F 是抛物线C 的焦点,若AP AF =,则点A 的横坐标为A. 4B. 3C. 11.已知()2168ln 2f x x x x =-+在[],1m m +上不是单调函数,则实数m 的取值范围是A. ()1,2B. ()3,4C. (][)1,23,4 D. ()()1,23,412. 关于函数()2ln f x x x=+,下列说法错误的是 A. 2x =是()f x 的最小值点B. 函数()y f x x =-有且只有1个零点C. 存在正实数k ,使得()f x kx >恒成立D.对任意两个不相等的正实数12,x x ,若()()12f x f x =,则124x x +> 二、填空题:本大题共4小题,每小题5分,共20分.13.曲线3ln 2y x x =++在点P 处的切线方程为410x y --=,则点P 的坐标为 .14.若椭圆22164x y +=的两个焦点为12,F F ,P 是椭圆上的一点,若12PF PF ⊥,则12PF F ∆的面积为 .15.已知函数()32693,0ln ,0x x x x f x a x x ⎧+++≤=⎨>⎩在[]2,2-上的最小值为-1,则实数a 的取值范围为 .16. 我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不能割,则与圆合体而无所失矣”它体现了一种无限与有限转化过程.比如在表达式1111x +++中“”即代表无限次重复,但原式却是个定值,它可以通过方程()110x x x +=>求得x =,类似上述过程,则= .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.(本题满分12分) 已知()322 2.f x x ax a x =+-+(1)当1a =时,求曲线()y f x =在点()()1,1f 处的切线方程; (2)当0a >时,求函数()f x 的单调区间.18.(本题满分12分)已知命题()21:,2102p x R x m x ∃∈+-+≤,命题:q “曲线222:128x y C m m +=+表示焦点在x 轴上的椭圆”,命题:s “曲线22:11x y C m t m t +=---表示双曲线” (1)若“p q ∧”是真命题,求m 的取值范围; (2)若q 是s 的必要不充分条件,求t 的取值范围.19.(本题满分12分)如图,在长方体1111ABCD A BC D -中,,AC BD 相交于点O ,2AB BC ==异面直线DB 与1D C . (1)求此长方体的体积;(2)求截面1D AC 和底面ABCD 所成锐二面角的余弦值;(3)在棱1BB 上找一点P ,使得DP ⊥平面1D AC .20.(本题满分12分)已知ABC ∆的两个顶点,A B 的坐标分别为()()0,1,0,1-,且边,AC BC 所在直线的斜率之积等于()0.m m ≠(1)求顶点C 的轨迹E 的方程,并判断轨迹E 的曲线类型; (2)当12m =-时,过点()1,0F 的直线l 交曲线E 于M,N 两点,设点N 关于x 轴的对称点为Q (,M Q 不重合),求证:直线MQ 与x 轴的交点为定点,并求出该定点的坐标.21.(本题满分12分)记{}max ,m n 表示,m n 中的最大值,如{max =(){}()22221max 1,2ln ,max ln ,24.2f x x x g x x x x a x a a ⎧⎫⎛⎫=-=+-+-++⎨⎬ ⎪⎝⎭⎩⎭(1)设()()()21312h x f x x x ⎛⎫=--- ⎪⎝⎭,求函数()h x 在(]0,1上的零点个数;(2)试探究是否存在实数()2,a ∈-+∞,使得()342g x x a <+对()2,x a ∈++∞恒成立?若存在,求a 的取值范围;若不存在,说明理由.22.(本题满分10分)已知双曲线22:14x C y -=,P 是C 上的任意一点.(1)求证:点P 到C 的两条渐近线的距离之积是一个常数; (2)设点A 的坐标为()5,0,求PA 的最小值.2018襄阳市普通高中调研统一测试高二数学(理工类)参考答案及评分标准一.选择题:CCDBD AABCB DC 二.填空题:13.(1,3) 14.4 15.10ln 2a -<≤ 16.3 三.解答题:17.(Ⅰ)解:当a = 1时,322()2f x x x x =+-+,∴2()321f x x x '=+- 2分 ∴切线斜率为(1)4k f '==又f (1) = 3,∴切点坐标为(1,3)4分 ∴所求切线方程为34(1)y x -=-,即410x y --= 6分(Ⅱ)解:22()32()(3)f x x ax a x a x a '=+-=+- 由()0f x '=,得x =-a 或3a x = 8分∵a > 0,∴3aa >- ∴当x a <-或3a x >时,()0f x '>,当3aa x -<<时,()0f x '<10分因此,函数f (x )的单调递减区间为()3aa -,,单调递增区间为()a -∞-,和()3a +∞,.12分18.(Ⅰ)解:若p 为真,则21(1)4202m ∆=--⨯⨯≥ 1分 解得:m ≤-1或m ≥32分 若q 为真,则228280m m m ⎧>+⎨+>⎩3分 解得:-4 < m < -2或m > 4 4分 若“p 且q ”是真命题,则43424m m m m -⎧⎨-<<->⎩或或≤≥6分解得:42m -<<-或m > 4∴m 的取值范围是{ m |42m -<<-或m > 4}7分 (Ⅱ)解:若s 为真,则()(1)0m t m t ---<,即t < m < t + 1 8分∵由q 是s 的必要不充分条件∴{|1}{|424}m t m t m m m <<+-<<->或Ü 9分 即412t t -⎧⎨+-⎩≥≤或t ≥411分解得:43t --≤≤或t ≥4∴t 的取值范围是{ t |43t --≤≤或t ≥4} 12分 19.方法一(Ⅰ)解:以DA 、DC 、1DD 为x 轴、y 轴、z 轴建立空间直角坐标系D -xyz 则A (2,0,0),B (2,2,0),C (0,2,0), D 1(0,0,h ) 3分 ∴(220)DB =,,,1(02)D C h =-,,1cos DB D C <>=,=,解得:h = 4 故V = 2×2×4 = 164分(Ⅱ)解:易知1DD 是平面ABCD 的一个法向量1(220)(204)AC AD =-=-,,,,,设平面D 1AC 的法向量为m = (x ,y ,z ) 则10(220)()0(204)()00AC x y z x y z AD ⎧⋅=-⋅=⎪⎧⇒⎨⎨-⋅=⋅=⎩⎪⎩,,,,,,,,m m ,即020x y x z -=⎧⎨-=⎩ 令z = 1,则x = y = 2平面D 1AC 的法向量为m = (2,2,1)6分1(004)(221)1cos 433DD ⋅<>==⨯,,,,,m∴所求二面角的余弦值为13.8分(Ⅲ)解:设P (2,2,z ),则(22)DP z =,, 若PD ⊥平面D 1AC ,则(220)(22)0(204)(22)0z z -⋅=⎧⎨-⋅=⎩,,,,,,,,10分解得z = 1∴当BP = 1时,PD ⊥平面D 1AC . 12分方法二(Ⅰ)解:连结A 1B ,则A 1B ∥D 1C ,∴∠A 1DB 是异面直线DB 与D 1C 所成的角 2分设DD 1 = h,则由余弦定理得:2224(4)2h h +=++-⨯ 解得:h = 4,∴故V = 2×2×4 = 164分(Ⅱ)解:连结D 1O∵ABCD 是正方形,∴AC ⊥BD又D 1D ⊥平面ABCD ,AC 在平面ABCD 内,∴AC ⊥D 1D 5分 因此AC ⊥平面BDD 1,而D 1O 在平面BDD 1内,∴AC ⊥D 1O 6分 ∴∠D 1OD 是所求二面角的平面角7分111cos 3ODD OD D O∠===. 8分(Ⅲ)解:∵AC ⊥平面D 1DB ,∴AC ⊥PD 要PD ⊥平面D 1AC ,只需PD ⊥D 1O 10分这时,△D 1DO ∽△DBP,∴1PB =⇒=∴当BP = 1时,PD ⊥平面D 1AC . 12分20.(Ⅰ)解:设C (x ,y ),由已知11y y m x x+-⨯=,即221(0)mx y x -+=≠ 2分当1m <-时,轨迹E 表示焦点在y 轴,且除去(0,1),(0,)两点的椭圆;当1m =-时,轨迹E 表示以点(0,0)为圆心,以1为半径,且除去(0,1),(0,1-)两点的圆; 当10m -<<,轨迹E 表示焦点在x 轴,且除去(0,1),(0,1-)两点的椭圆; 当m > 0时,轨迹E 表示焦点在y 轴,且除去(0,1),(0,1-)两点的双曲线. 5分(Ⅱ)证:设M (x 1,y 1),N (x 2,y 2),Q (x 2,-y 2) (x 1·x 2≠0).当12m =-时,轨迹E 的方程为221(0)2x y x +=≠依题意可知直线l 的斜率存在且不为零,则可设直线l 的方程为1x ty =+联立22112x ty x y =+⎧⎪⎨+=⎪⎩,整理得(t 2 + 2)y 2 + 2ty -1 = 0 7分所以1212222122t y y y y t t --+==++, 8分又因为M 、Q 不重合,则x 1≠x 2,且y 1≠-y 2 故直线MQ 的方程为121112()y y y y x x x x +-=--9分令y = 0,得21211211211121212212()()2211122t y x x ty y y ty y t x x ty y y y y y y t -⋅--+=+=+++=+=++++ 11分故直线MQ 与x 轴的交点为定点,且定点坐标为(2,0). 12分21.(Ⅰ)解:设2()12ln F x x x =--,则22(1)(1)()2(0)x x F x x x x x+-'=-=> 由2(1)(1)0(0)x x x x+-=>得:x = 1∴当x > 1时,()0F x '>,函数F (x )递增;当0 < x < 1时,()0F x '<,函数F (x )递减∴min ()(1)0F x F ==,即F (x )≥0,∴212ln x x -≥ 因此2()1f x x =-2分∴2221111()13()(1)(1)(3)222h x x x x x x x =----=--+- 由h (x ) = 0得:2(1)(6111)0x x x --+=∴1231(01](01]x x x ===,,,, ∴h (x ) = 0在(0,1]上有两个根,即h (x )在(0,1]上零点的个数为2.4分(Ⅱ)解:假设存在实数(2)a ∈-+∞,,使得3()42g x x a <+对(2)x a ∈++∞,恒成立,则 2223ln 4213()24422x x x a x a x a a x a ⎧+<+⎪⎨⎪-+-++<+⎩即21ln 42(2)()0x x a x x a ⎧-<⎪⎨⎪+->⎩对(2)x a ∈++∞,恒成立 5分(1)若1ln 42x x a -<对(2)x a ∈++∞,恒成立 设1()ln 2H x x x =- ,则112()(0)22xH x x x x-'=-=>易知,当0 < x < 2时,()0H x '>,函数H (x ) 递增 当x > 2时,()0H x '<,函数H (x ) 递减∴max ()(2)ln 21H x H ==-6分当022a <+<,即20a -<<时,4ln 21a >-,∴ln 214a -> ∵a < 0,∴ln 21(0)4a -∈, 7分当22a +≥ ,即a ≥0时,H (x )在(2)a ++∞,上递减 ∴1()(2)ln(2)12H x H a a a <+=+-- 令1()ln(2)12G a a a =+--,则11()0222(2)a G a a a -'=-=++≤ ∴()(0)ln 21G a G =-≤∴(2)()ln 210H a G a +=-<≤∴a ≥0合题意.故ln 214a ->时,1ln 42x x a -<对(2)x a ∈++∞,恒成立. 9分(2)若2(2)()0x x a +->对(2)x a ∈++∞,恒成立 ∵242x a +>+>,∴等价20x a ->对(2)x a ∈++∞,恒成立 故22a a +≥,解得:12a -≤≤11分由(1)、(2)得:ln 2124a -<≤ 12分22.(Ⅰ)解:设P (x 0,y 0),P 到双曲线的两条渐近线的距离记为d 1、d 2双曲线的两条渐近线方程为2020x y x y -=+=, 2分 ∴2212001|4|5d d x y =-4分又点P 在双曲线C 上,∴220044x y -=,故1245d d =6分(Ⅱ)解:22200||(5)(0)PA x y =-+-∵220044x y -=,∴22220005||(5)1(4)444x PA x x =-+-=-+ 8分 ∵点P 在双曲线C 上,∴| x 0 |≥2故当04x =时,| PA |2有最小值4,| PA |有最小值2.。
湖北省襄阳市2018届高三1月调研统一测试语文试题(附答案)
湖北省襄阳市2018届高三1月调研统一测试语文试题一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
人的一生,绝大部分时间都是在家庭中度过的。
家庭不仅为人的生存发展提供基本物质保障,而且也为人的精神生活提供重要环境。
人生的幸福很大程度上可归结为家庭的幸福。
因此,家庭是生命的摇篮、情感的港湾、文明的载体。
中华文化强调人伦之道,重视家庭成员之间的和谐,在几千年的发展进程中形成了一系列具有鲜明民族特色的家庭伦理道德规范,如尊老爱幼、父慈子孝、夫勤妇俭等,这些家庭伦理道德规范对维护家庭关系、家庭模式和社会稳定都具有重要作用。
《礼记》说:“父子笃,兄弟睦,夫妇和,家之肥也。
”所谓“肥”,即健康、和谐、融洽之意。
在我国先贤看来,每个家庭成员都有自己的角色,每个角色都有自己的责任,所有角色互相配合才能成为团结协作的整体。
当然,家庭之中难免会有矛盾,这就需要协调。
协调得好,大家都心情舒畅,同心协力发展事业、发家致富,培养子女健康成长,这就是“家和万事兴”。
家庭关系的重要协调和保障机制之一是孝道。
“百善孝为先”。
孝道的基本内容是父慈子孝,它在社会道德生活中具有重要地位,得到普遍奉行。
由孝道形成的浓厚的家族亲情,对家庭稳定乃至社会稳定有着极为重要的作用。
孔子认为,“子生三年,然后免于父母之怀”,把“孝”的准则诉诸报恩的情理。
饮水思源、知恩图报,这是中华民族的传统美德。
懂得报恩是一个有教养的人的必备品质,古今中外概莫能外。
中华文化的特别之处在于,它不像宗教那样通过教堂而主要通过家庭来培育这种品质。
“立爱自亲始”“孝弟也者,其为仁之本与”,强调从报父母养育之恩开始,再推广到报师长教导之恩、朋友知遇之恩、国家培养之恩等。
亲情之爱犹如投进湖里的石子,荡开的层层涟漪由近及远。
传统的孝道还要求子孙继承祖辈的志向、理想及其崇高事业,弘扬祖辈进取的精神和坚忍的意志。
这是家族乃至民族后继有人、兴旺发达的重要精神纽带。
