中学考试数学专题复习——四边形中地折叠、剪切、旋转与动点最值问题
初中数学《菱形中折叠、动点、旋转、最值、新定义》题型及答案解析

解题技巧专题:菱形中折叠、动点、旋转、最值、新定义型问题目录【考点一利用菱形的性质与判定解决折叠问题】 1【考点二利用菱形的性质与判定解决动点与函数图象问题】 5【考点三利用菱形的性质与判定解决旋转问题】 10【考点四利用菱形的性质与判定解决最值问题】 16【考点五利用菱形的性质与判定解决新定义型问题】 21【典型例题】【考点一利用菱形的性质与判定解决折叠问题】1.(2024九年级下·江苏南京·专题练习)如图,在菱形ABCD中,点E,F分别在AB,BC上,沿EF翻折后,点B落在边CD上的G处,若EG⊥CD,BE=4,DG=3,则AE的长为.【变式训练】2.(2024·广东东莞·二模)如图,将菱形纸片ABCD折叠,使点B落在AD边的点F处,折痕为CE,若∠D= 80°,则∠BCF的度数是.3.(23-24八年级下·江苏无锡·期中)如图,在菱形ABCD中,AB=8,∠A=120°,M是CD上,DM=3,N是点AB上一动点,四边形CMNB沿直线MN翻折,点C对应点为E,当AE最小时,AN=.4.(23-24八年级下·河北邢台·期中)如图,在菱形纸片ABCD中,∠A=60°.(1)∠C=°.(2)点E在BC边上,将菱形纸片ABCD沿DE折叠,点C对应点为点C ,且DC 是AB的垂直平分线,则∠DEC的大小为°.5.(2024·云南曲靖·二模)如图,已知在△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E为AC上一点,连接BE,交CD于点G,△BFE是△BCE沿BE折叠所得,且点C的对应点F恰好落在AB上,连接FG.(1)求证:四边形CEFG为菱形;(2)若AC=8,BC=6,求DG的长.【考点二利用菱形的性质与判定解决动点与函数图象问题】6.(2024·北京朝阳·二模)如图1,在菱形ABCD 中,∠B =60°,P 是菱形内部一点,动点M 从顶点B 出发,沿线段BP 运动到点P ,再沿线段P A 运动到顶点A ,停止运动.设点M 运动的路程为x ,MA MC=y ,表示y 与x 的函数关系的图象如图2所示,则菱形ABCD 的边长是()A.43B.4C.23D.2【变式训练】7.(2024·广东深圳·三模)如图(1),点P 为菱形ABCD 对角线AC 上一动点,点E 为边CD 上一定点,连接PB ,PE ,BE .图(2)是点P 从点A 匀速运动到点C 时,△PBE 的面积y 随AP 的长度x 变化的关系图象(当点P 在BE 上时,令y =0),则菱形ABCD 的边长为()A.5B.6C.23D.258.(23-24九年级下·山东淄博·期中)如图1,点P 从菱形ABCD 的顶点A 出发,沿A →C →B 以1cm/s 的速度匀速运动到点B ,点P 运动时△P AD 的面积y cm 2 随时间x (s )变化的关系如图2,则a 的值为()A.254B.253C.9D.1929.(2024·甘肃·中考真题)如图1,动点P 从菱形ABCD 的点A 出发,沿边AB →BC 匀速运动,运动到点C 时停止.设点P 的运动路程为x ,PO 的长为y ,y 与x 的函数图象如图2所示,当点P 运动到BC 中点时,PO 的长为()A.2B.3C.5D.2210.(23-24八年级下·江苏苏州·阶段练习)在菱形ABCD 中,∠ABC =60°,P 是直线BD 上一动点,以AP 为边向右侧作等边△APE ,(A 、P ,E 按逆时针排列),点E 的位置随点P 的位置变化而变化.(1)如图1,当点P 在线段BD 上,且点E 在菱形ABCD 内部或边上时,连接CE ,则BP 与CE 的数量关系是,BC 与CE 的位置关系是;(2)①如图2,当点P 在线段BD 上,且点E 在菱形ABCD 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;②在①的条件下,连接BE ,若AB =2,∠APD =75°,直接写出BE 的长;(3)当点P 在直线BD 上时,其他条件不变,连接BE .若AB =23,BE =219,请直接写出△APE 的面积.【考点三利用菱形的性质与判定解决旋转问题】11.(2024·河南·三模)如图,菱形OABC 的顶点O (0,0),A (-1,0),∠B =60°,若菱形OABC 绕点O 顺时针旋转90°后得到菱形OA 1B 1C 1,依此方式,绕点O 连续旋转2024次得到菱形OA 2024B 2024C 2024,那么点C 2024的坐标是()A.32,12B.12,-32C.-32,-12D.-12,32【变式训练】12.(2024九年级·全国·竞赛)在菱形ABCD 中,∠ABC =120°,边长为2cm ,现将菱形ABCD 绕其外一点O影部分的面积为cm2.13.如图①,菱形ABCD和菱形AEFG有公共顶点A,点E,G分别落在边AB,AD上,连接DF,BF.(1)求证:DF=BF;(2)将菱形AEFG绕点A按逆时针方向旋转.设旋转角∠BAE=α0°≤α≤180°,且AB=6,AE= 3,∠DAB=∠GAE=60°.①如图②,当α=90°时,则线段DF的长度是多少?②连接BD,当△DFB为直角三角形时,则旋转角α的度数为多少度?14.(23-24八年级下·湖北武汉·期中)在菱形ABCD和菱形BEFG中,∠ABC=∠EBG=60°,AB=6,BE=2.(1)如图1,若点E、G分别在边AB、BC上,点F在菱形ABCD内部,连接DF,直接写出DF的长度为;(2)如图2,把菱形BEFG绕点B顺时针旋转α°(0<α<360),连接DF、CG,判断DF与CG的数量关系,并给出证明;(3)如图3,①把菱形BEFG继续绕点B顺时针旋转,连接GD,O为DG的中点,连接CO、EO,试探究CO与EO的关系;②直接写出菱形BEFG绕B点旋转过程中CO的取值范围.【考点四利用菱形的性质与判定解决最值问题】15.(23-24八年级下·重庆沙坪坝·期中)如图,菱形ABCD的周长为8,∠DAC=30°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是.【变式训练】16.(2024九年级下·全国·专题练习)如图,在菱形ABCD中,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠B=45°,BC=23,则GH的最小值是.17.(23-24八年级下·安徽合肥·期末)菱形ABCD中,∠B=60°,E是BC中点,连接AE,DE,点F是DE上一动点,G为AF中点,连接CG.(1)∠BAE=;(2)若AB=2,则CG的最小值为.18.(2024八年级下·全国·专题练习)如图,菱形ABCD中,AB=4,∠ABC=60°,点P为AD边上任意一点(不包括端点),连结AC,过点P作PQ∥AC,交边CD于点Q,点R线段AC上的一点.(1)若点R为菱形ABCD对角线的交点,PQ为△ACD的中位线,求PR+QR的值;(2)当PR+QR的值最小时,请确定点R的位置,并求出PR+QR的最小值;(3)当PR+QR的值最小,且PR+QR+PQ的值最小时,在备用图中作出此时点P,Q的位置,写作法并写出PR+QR+PQ的最小值.【考点五利用菱形的性质与判定解决新定义型问题】19.(22-23八年级下·江苏苏州·期末)定义:如果三角形有两个内角的差为90°,那么称这样的三角形为“准直角三角形”.(1)已知△ABC是“准直角三角形”,∠C>90°,若∠A=40°,则∠B=°.(2)如图,在菱形ABCD中,∠B>90°,AB=5,连接AC,若△ABC正好为一个准直角三角形,求菱形ABCD的面积.【变式训练】20.(23-24九年级下·山东威海·期中)【理解新定义】若一个四边形具备一组对角互补和一组邻边相等,则称该四边形为“补等四边形”.如正方形和筝形,它们都具备这样的特征,所以称为补等四边形.【解决新问题】(1)如图Ⅰ,点E,F分别在菱形ABCD的边CD,AD上,CE=DF,∠A=60°.四边形BEDF是否为补等四边形?(填“是”或“否”)(2)如图Ⅱ,在△ABC中,∠B>90°.∠ACB的平分线和边AB的中垂线交于点D,中垂线交边AC于点G,连接DA,DB.四边形ADBC是否为补等四边形?若是,进行证明;若不是,说明理由.21.(22-23八年级下·浙江宁波·期末)我们定义:以已知菱形的对角线为边且有一条边与已知菱形的一条边共线的新菱形称为已知菱形的伴随菱形.如图1,在菱形ABCD中,连接AC,在AD的延长线上取点E 使得AC=AE,以CA、AE为边作菱形CAEF,我们称菱形CAEF是菱形ABCD的“伴随菱形”.(1)如图2,在菱形ABCD中,连接AC,在BC的延长线上作CA=CF,作∠ACF的平分线CE交AD的延长线于点E,连接FE.求证:四边形AEPC为菱形ABCD的“伴随菱形”.(2)①如图3,菱形AEFC为菱形ABCD的“伴随菱形”,过C作CH垂直AE于点H,对角线AC、BD相交于点O.连接EO若EO=2CH,试判断ED与BD的数量关系并加以证明.②在①的条件下请直接写出CHED的值.22.(22-23八年级下·安徽合肥·期末)定义:在三角形中,若有两条中线互相垂直,则称该三角形为中垂三角形.(1)如图(a),△ABC是中垂三角形,BD,AE分别是AC,BC边上的中线,且BD⊥AE于点O,若∠BAE=45°,求证:△ABC是等腰三角形.(2)如图(b),在中垂三角形ABC中,AE,BD分别是边BC,AC上的中线,且AE⊥BD于点O,求证:AC2+BC2=5AB2.(3)如图(c),四边形ABCD是菱形,对角线AC,BD交于点O,点M,N分别是OA,OD的中点,连接BM,CN并延长,交于点E.求证:△BCE是中垂三角形;解题技巧专题:菱形中折叠、动点、旋转、最值、新定义型问题目录【考点一利用菱形的性质与判定解决折叠问题】 1【考点二利用菱形的性质与判定解决动点与函数图象问题】 5【考点三利用菱形的性质与判定解决旋转问题】 10【考点四利用菱形的性质与判定解决最值问题】 16【考点五利用菱形的性质与判定解决新定义型问题】 21【典型例题】【考点一利用菱形的性质与判定解决折叠问题】1.(2024九年级下·江苏南京·专题练习)如图,在菱形ABCD 中,点E ,F 分别在AB ,BC 上,沿EF 翻折后,点B 落在边CD 上的G 处,若EG ⊥CD ,BE =4,DG =3,则AE 的长为.【答案】914【分析】此题重点考查菱形的性质、轴对称的性质、平行四边形的判定与性质、勾股定理等知识,正确地作出所需要的辅助线是解题的关键.作BH ⊥CD 交DC 的延长线于点H ,因为EG ⊥CD ,所以BH ∥EG ,由四边形ABCD 是菱形,得AB ∥CD ,AB =BC =CD ,则四边形BEGH 是平行四边形,所以GH =BE =4,由折叠得GE =BE =4,则BH =GE =4,所以DH =DG +GH =3+4=7,由勾股定理得42+7-AB 2=AB 2,求得AB =6514,所以AE =AB -BE =6514-4=914,于是得到问题的答案.【详解】解:作BH ⊥CD 交DC 的延长线于点H ,则∠H =90°,∵EG ⊥CD ,∴BH ∥EG ,∵四边形ABCD 是菱形,∴AB ∥CD ,AB =BC =CD ,∴BE ∥GH ,∴四边形BEGH 是平行四边形,∴GH =BE =4,由折叠得GE =BE =4,∵DG =3,∴DH =DG +GH =3+4=7,∵BH 2+CH 2=BC 2,CH =7-CD =7-AB ,∴42+7-AB 2=AB 2,解得AB =6514,∴AE =AB -BE =6514-4=914,故答案为:914.【变式训练】2.(2024·广东东莞·二模)如图,将菱形纸片ABCD 折叠,使点B 落在AD 边的点F 处,折痕为CE ,若∠D =80°,则∠BCF 的度数是.【答案】80°/80度【分析】此题考查了菱形的性质,折叠的性质,等边对等角和平行线的性质,首先根据平行的性质得到BC =CD ,由折叠得BC =CF ,然后求出CF =CD ,然后根据等边对等角和平行线的性质求解即可.【详解】∵四边形ABCD 是菱形∴BC =CD由折叠可得,BC =CF∴CF =CD∴∠CFD =∠D =80°∵四边形ABCD 是菱形∴AD ∥BC∴∠BCF =∠DFC =80°.故答案为:80°.3.(23-24八年级下·江苏无锡·期中)如图,在菱形ABCD 中,AB =8,∠A =120°,M 是CD 上,DM =3,N 是点AB 上一动点,四边形CMNB 沿直线MN 翻折,点C 对应点为E ,当AE 最小时,AN =.【答案】7【分析】本题考查了菱形的性质,折叠的性质,勾股定理等知识,解决本题的关键是确定点E在AM上时,AE的值最小.作AH⊥CD于H,如图,根据菱形的性质可求得AH=32AD=83,DH=CH=8,在Rt△AHM中,利用勾股定理计算出AM=7,再根据两点间线段最短得到当点E在AM上时,AE的值最小,然后证明AN=AM即可.【详解】解:作AH⊥CD于H,如图,∵菱形ABCD的边AB=8,∠A=120°,∴AD=AB=CD=8,AB∥CD,∴∠D=180°-∠BAD=60°,∴∠DAH=30°,∴DH=12AD=4,AH=AD2-DH2=43,∵DM=3,∴HM=1,MC=CD-DM=5,在Rt△AHM中,AM=AH2+HM2=7,∵四边形CMNB沿直线MN翻折,点C对应点为E,,∴ME=MC=10,∵AE+ME≥AM,∴AE≥AM-ME,∴当点E在AM上时,AE的值最小,由折叠的性质得∠AMN=∠CMN,而AB∥CD,∴∠ANM=∠CMN,∴∠AMN=∠ANM,∴AN=AM=7.故答案为:7.4.(23-24八年级下·河北邢台·期中)如图,在菱形纸片ABCD中,∠A=60°.(1)∠C=°.(2)点E在BC边上,将菱形纸片ABCD沿DE折叠,点C对应点为点C ,且DC 是AB的垂直平分线,则∠DEC的大小为°.【答案】6075【分析】本题考查菱形的性质,垂直平分线的定义.(1)直接根据菱形的对角相等即可求解;(2)如图,由垂直平分线的定义得到∠1=90°,从而∠ADC =30°,由菱形的性质得到∠CDC =∠1=90°,从而由折叠有∠CDE=∠C DE=12∠CDC =45°,因此∠ADE=75°,再根据菱形的对边平行即可求解.【详解】解:(1)∵四边形ABCD是菱形,∴∠C=∠A=60°.故答案为:60(2)如图,∵C D 是AB 的垂直平分线,∴∠1=90°,∴∠ADC =90°-∠A =90°-60°=30°,∵在菱形ABCD 中,AB ∥CD ,∴∠CDC =∠1=90°,由折叠可得∠CDE =∠C DE =12∠CDC =12×90°=45°,∴∠ADE =∠ADC +∠C DE =30°+45°=75°,∵在菱形ABCD 中,AD ∥BC ,∴∠DEC =∠ADE =75°.故答案为:755.(2024·云南曲靖·二模)如图,已知在△ABC 中,∠ACB =90°,过点C 作CD ⊥AB 于点D ,点E 为AC 上一点,连接BE ,交CD 于点G ,△BFE 是△BCE 沿BE 折叠所得,且点C 的对应点F 恰好落在AB 上,连接FG .(1)求证:四边形CEFG 为菱形;(2)若AC =8,BC =6,求DG 的长.【答案】(1)见解析(2)GD =1.8.【分析】(1)推出CG =EF ,CG ∥EF ,进而推出四边形CEFG 是平行四边形,并根据EC =EF 证得四边形CEFG 是菱形;(2)首先利用勾股定理求出AB ,设CG =x ,然后用x 表示出AE 和EF ,再在Rt △AEF 中,利用勾股定理构建方程,求出x ,进一步计算即可求解.【详解】(1)证明:∵CD ⊥AB ,△BFE 是△BCE 沿BE 折叠所得,∴∠BFE =∠BCE =90°,∠CEG =∠FEG ,EC =EF ,∴CD ∥EF ,∴∠CGE =∠FEG ,∴∠CGE =∠CEG ,∴CE =CG ,∴CG =EF ,∵CG ∥EF ,∴四边形CEFG 是平行四边形,∵EC =EF ,∴平行四边形CEFG 是菱形;(2)解:∵AC =8,BC =6,∠ACB =90°,22∵四边形CEFG 是菱形,∴EF =FG =CE =CG =x ,∴AE =8-x ,∵△BFE 是△BCE 沿BE 折叠所得,∴BF =BC =6,∴AF =AB -BF =10-6=4,∵在Rt △AEF 中,EF 2+AF 2=AE 2,∴x 2+42=8-x 2,解得:x =3,即CG =3.∵CD ⊥AB ,∴S △ABC =12AC ×BC =12AB ×CD ,∴CD =4.8,∴GD =4.8-3=1.8.【点睛】本题考查了平行线的性质,角平分线的性质,等腰三角形的判定,平行四边形的判定,菱形的判定和性质以及勾股定理的应用,灵活运用各性质进行推理论证是解题的关键.【考点二利用菱形的性质与判定解决动点与函数图象问题】6.(2024·北京朝阳·二模)如图1,在菱形ABCD 中,∠B =60°,P 是菱形内部一点,动点M 从顶点B 出发,沿线段BP 运动到点P ,再沿线段P A 运动到顶点A ,停止运动.设点M 运动的路程为x ,MA MC=y ,表示y 与x 的函数关系的图象如图2所示,则菱形ABCD 的边长是()A.43B.4C.23D.2【答案】C【分析】首先根据题意作图,然后由图象判断出点P 在对角线BD 上,BP =4,BP +AP =6,设AO =x ,则AB =2AO =2x ,利用勾股定理求解即可.【详解】如图所示,由图象可得,当x 从0到4时,MA MC=y =1∴MA =MC∵四边形ABCD 是菱形∴点P 在对角线BD 上∴由图象可得,BP =4,BP +AP =6∵在菱形ABCD 中,∠B =60°,∴∠ABD =30°,AC ⊥BD∴设AO =x ,则AB =2AO =2x∴PO =BP -BO =4-3x∴BO =AB 2-AO 2=3x∴在Rt △APO 中,AP 2=AO 2+PO 2∴22=x 2+4-3x 2解得x =3,负值舍去∴AB =2x =23∴菱形ABCD 的边长是23.故选:C .【点睛】此题考查了动点函数图象问题,菱形的性质,勾股定理,含30°角直角三角形的性质等知识,解题的关键是根据图象正确分析出点P 在对角线BD 上.【变式训练】7.(2024·广东深圳·三模)如图(1),点P 为菱形ABCD 对角线AC 上一动点,点E 为边CD 上一定点,连接PB ,PE ,BE .图(2)是点P 从点A 匀速运动到点C 时,△PBE 的面积y 随AP 的长度x 变化的关系图象(当点P 在BE 上时,令y =0),则菱形ABCD 的边长为()A.5B.6C.23D.25【答案】A 【分析】根据图象可知,当x =0时,即点P 与点A 重合,此时S △ABE =12,进而求出菱形的面积,当x =8时,此时点P 与点C 重合,即AC =8,连接BD ,利用菱形的性质,求出边长,即可得出结果.本题考查菱形的性质和动点的函数图象.熟练掌握菱形的性质,从函数图象中有效的获取信息,是解题的关键.【详解】解:由图象可知:当x =0时,即点P 与点A 重合,此时S △ABE =12,∴S 菱形ABCD =2S △ABE =24,当x =8时,此时点P 与点C 重合,即AC =8,连接BD ,交AC 于点O ,则:BD ⊥AC ,OA =OC =4,OB =OD ,∴S 菱形ABCD =12AC ⋅BD =24,∴BD =6,∴OB =OD =3,∴AB =OA 2+OB 2=5,∴菱形ABCD 的边长为5;故选A .8.(23-24九年级下·山东淄博·期中)如图1,点P 从菱形ABCD 的顶点A 出发,沿A →C →B 以1cm/s 的速度匀速运动到点B ,点P 运动时△P AD 的面积y cm 2 随时间x (s )变化的关系如图2,则a 的值为()A.254B.253C.9D.192【答案】B【分析】本题主要考查了菱形的性质,勾股定理,动点问题的函数图象,过点C 作CE ⊥AD ,根据函数图象求出菱形的边长为a ,再根据图像的三角形的面积可得CE =8,再利用菱形的性质和勾股定理列方程可求a 即可.【详解】解:如图所示,过点C 作CE ⊥AD 于E ,∵在菱形ABCD 中,AD ∥BC ,AD =BC ,∴当点P 在边BC 上运动时,y 的值不变,∴AD =BC =10+a -10=a ,即菱形的边长是a ,∴12⋅AD ⋅CE =4a ,即CE =8.当点P 在AC 上运动时,y 逐渐增大,∴AC =10,∴AE =AC 2-CE 2=102-82=6.在Rt △DCE 中,DC =a ,DE =a -6,CE =8,∴a 2=82+a -6 2,解得a =253.故选:B .9.(2024·甘肃·中考真题)如图1,动点P 从菱形ABCD 的点A 出发,沿边AB →BC 匀速运动,运动到点C 时停止.设点P 的运动路程为x ,PO 的长为y ,y 与x 的函数图象如图2所示,当点P 运动到BC 中点时,PO 的长为()A.2B.3C.5D.22【答案】C 【分析】结合图象,得到当x =0时,PO =AO =4,当点P 运动到点B 时,PO =BO =2,根据菱形的性质,得∠AOB =∠BOC =90°,继而得到AB =BC =OA 2+OB 2=25,当点P 运动到BC 中点时,PO 的长为12BC=5,解得即可.本题考查了菱形的性质,图象信息题,勾股定理,直角三角形的性质,熟练掌握菱形的性质,勾股定理,直角三角形的性质是解题的关键.【详解】结合图象,得到当x=0时,PO=AO=4,当点P运动到点B时,PO=BO=2,根据菱形的性质,得∠AOB=∠BOC=90°,故AB=BC=OA2+OB2=25,当点P运动到BC中点时,PO的长为12BC=5,故选C.10.(23-24八年级下·江苏苏州·阶段练习)在菱形ABCD中,∠ABC=60°,P是直线BD上一动点,以AP为边向右侧作等边△APE,(A、P,E按逆时针排列),点E的位置随点P的位置变化而变化.(1)如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是,BC与CE的位置关系是;(2)①如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;②在①的条件下,连接BE,若AB=2,∠APD=75°,直接写出BE的长;(3)当点P在直线BD上时,其他条件不变,连接BE.若AB=23,BE=219,请直接写出△APE的面积.【答案】(1)BP=CE,CE⊥BC;(2)①仍然成立,见解析;②20-83(3)73或313【分析】(1)连接AC,根据菱形的性质和等边三角形的性质证明△BAP≌△CAE即可证得结论;(2)①(1)中的结论成立,用(1)中的方法证明△BAP≌△CAE即可;②根据已知得出DP=AD,进而根据①可得BP=CE,根据CE⊥BC,勾股定理,即可求解;(3)分两种情形:当点P在BD的延长线上时或点P在线段DB的延长线上时,连接AC交BD于点O,由∠BCE=90°,根据勾股定理求出CE的长即得到BP的长,再求AO、PO、PD的长及等边三角形APE的边长可得结论.【详解】(1)解:如图1,连接AC,延长CE交AD于点H,∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠BAC=60°;∴AP=AE,∠P AE=60°,∴∠BAP=∠CAE=60°-∠P AC,∴△BAP≌△CAE SAS,∴BP=CE;∵四边形ABCD是菱形,∴∠ABP=1∠ABC=30°,2∴∠ABP=∠ACE=30°,∵∠ACB=60°,∴∠BCE=60°+30°=90°,∴CE⊥BC;故答案为:BP=CE,CE⊥BC;(2)(1)中的结论:BP=CE,CE⊥AD仍然成立,理由如下:如图2中,连接AC,设CE与AD交于H,∵菱形ABCD,∠ABC=60°,∴△ABC和△ACD都是等边三角形,∴AB=AC,∠BAD=120°,∠BAP=120°+∠DAP,∵△APE是等边三角形,∴AP=AE,∠P AE=60°,∴∠CAE=60°+60°+∠DAP=120°+∠DAP,∴∠BAP=∠CAE,∴△ABP≌△ACE SAS,∴BP=CE,∠ACE=∠ABD=30°,∴∠DCE=30°,∵∠ADC=60°,∴∠DCE+∠ADC=90°,∴∠CHD=90°,∴CE⊥AD;∴(1)中的结论:BP=CE,CE⊥AD仍然成立;②如图所示,∵△ABP≌△ACE SAS,∴CE=BP,∵∠APD=75°,∠ADB=30°∴∠DAP=75°=∠APD,∴DA=DP=2,∵BD=2BO=23AO=3AB=23∴BP=CE=BD-DP=23-2∵CE⊥AD,AD∥BC∴CE⊥BC∴BE=BC2+CE2=22+23-22=20-83故答案为:20-83.(3)如图3中,当点P在BD的延长线上时,连接AC交BD于点O,连接CE,BE,作EF⊥AP于F,∵四边形ABCD是菱形,∵∠ABC =60°,AB =23,∴∠ABO =30°,∴AO =12AB =3,OB =3AO =3,∴BD =6,由(2)知CE ⊥AD ,∵AD ∥BC ,∴CE ⊥BC ,∵BE =219,BC =AB =23,∴CE =(219)2-(23)2=8,由(2)知BP =CE =8,∴DP =2,∴OP =5,∴AP =OA 2+OP 2=(3)2+52=27,∵△APE 是等边三角形,∴S △AEP =34×27 2=73,如图4中,当点P 在DB 的延长线上时,同法可得AP =OA 2+OP 2=(3)2+112=231,∴S △AEP =34×231 2=313.【点睛】此题考查菱形的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理等知识点,解题的关键是正确地作出解题所需要的辅助线,将菱形的性质与三角形全等的条件联系起来.【考点三利用菱形的性质与判定解决旋转问题】11.(2024·河南·三模)如图,菱形OABC 的顶点O (0,0),A (-1,0),∠B =60°,若菱形OABC 绕点O 顺时针旋转90°后得到菱形OA 1B 1C 1,依此方式,绕点O 连续旋转2024次得到菱形OA 2024B 2024C 2024,那么点C 2024的坐标是()A.32,12B.12,-32C.-32,-12D.-12,32【答案】D 【分析】本题考查了旋转的性质、菱形的性质,含30°直角三角形的性质,勾股定理,坐标与图形,根据题意得到旋转的规律是解题的关键.根据题意得到点C 2024与点C 重合,在菱形中算出C 点坐标,即可解答.【详解】解:作CD ⊥OA 于D ,则∠CDO =90°,∵四边形OABC 是菱形,O 0,0 ,A -1,0 ,∴∠AOC =∠B =60°,OC =OA =1∴∠OCD =30°∴OD =12OC =12,CD =3OD =32∴点C 的坐标为-12,32,若菱形绕点O 顺时针旋转90°后得到菱形OA 1B 1C 1,依此方式,绕点O 连续旋转2024次得到菱形OA 2024B 2024C 2024,则菱形OABC 绕点O 连续旋转2024次,旋转4次为一周,旋转2024次为2024÷4=506(周),∴绕点O 连续旋转2024次得到菱形OA 2024B 2024C 2024与菱形OABC 重合,∴点C 2024与C 重合,∴点C 2024的坐标为-12,32,故选:D .【变式训练】12.(2024九年级·全国·竞赛)在菱形ABCD 中,∠ABC =120°,边长为2cm ,现将菱形ABCD 绕其外一点O按顺时针方向分别旋转90°、180°、270°后,得到如图的图形,每相邻两个菱形有一个顶点重合,则图中阴影部分的面积为cm 2.【答案】12-43【分析】连接AC 、OB ,交点为点E ,则OB 为AC 的中垂线,S △AOD =12×AE ×OD =12×3×3-1 =3-32cm 2 ,计算即可.【详解】如图,连接AC 、OB ,交点为点E ,则OB 为AC 的中垂线,∴点D 在OB 上,由已知条件易得BE =DE =12AB =1cm ,AE =OE =3cm ,∴OD =3-1cm ,∴S =1×AE ×OD =1×3×3-1 =3-3cm 2 ,∴所求面积为8×3-32=12-43cm2.故答案为:12-43.13.如图①,菱形ABCD和菱形AEFG有公共顶点A,点E,G分别落在边AB,AD上,连接DF,BF.(1)求证:DF=BF;(2)将菱形AEFG绕点A按逆时针方向旋转.设旋转角∠BAE=α0°≤α≤180°,且AB=6,AE= 3,∠DAB=∠GAE=60°.①如图②,当α=90°时,则线段DF的长度是多少?②连接BD,当△DFB为直角三角形时,则旋转角α的度数为多少度?【答案】(1)证明见解析(2)①33;②30°或90°【分析】(1)连接AF,根据菱形的性质,可得到△GAF≅△EAF,从而得到∠GAF=∠EAF,进而得到△DAF ≅△BAF,即可求证;(2)①连接AF,EG,BD,AC,BD与AC交于点O,AF交EG于点P,根据旋转的性质和菱形的性质可得AF∥OD,△ABD和△AEG是等边三角形,从而得到AF=OD,进而得到四边形AODF是平行四边形,即可求解;②分两种情况讨论:∠BDF=90°和∠BFD=90°,利用矩形的性质、等边三角形的判定与性质求解即可得.【详解】(1)证明:连接AF,∵四边形AEFG是菱形,∴AE=EF=FG=GA,在△GAF和△EAF中,AG=AEGF=EFAF=AF,∴△GAF≅△EAF SSS,∵四边形ABCD 是菱形,∴AD =AB ,在△DAF 和△BAF 中,AD =AB∠DAF =∠BAF AF =AF,∴△DAF ≅△BAF SAS ,∴DF =BF .(2)解:①如图,连接AF ,EG ,BD ,AC ,BD 与AC 交于点O ,AF 交EG 于点P ,由(1)得当菱形AEFG 没有旋转时,AC 平分∠BAD ,AF 平分∠EAG ,∴此时点A 、F 、C 三点共线,∴当菱形AEFG 绕点A 按逆时针方向旋转时,∠FAC =α,∴当α=90°时,∠FAC =∠BAE =90°,在菱形ABCD 中,AB =AD ,OD =12BD ,OA =12AC ,BD ⊥AC ,∠DAO =12∠BAD =30°,∴∠AOD =90°∴∠DOA +∠FAC =180°,∴AF ∥OD ,在菱形AEFG 中,∠EAF =12∠EAG =30°,AE =AG ,AP =12AF ,PE =12EG ,∵∠DAB =∠GAE =60°.∴△ABD 和△AEG 是等边三角形,∴BD =AB =6,EG =AE =3,∴OD =3,EP =32,∴AP =AE 2-EP 2=32,OA =AD 2-OD 2=33∴AF =3,∴AF =OD ,∴四边形AODF 是平行四边形,∴DF =OA =33;②由①得四边形AODF 是平行四边形,∵∠FAC =90°,∴四边形AODF 是矩形,∴∠BDF =90°,即△DFB 为直角三角形,∴此时旋转角α的度数为90°;如图,当点F 在AD 上时,由①得AF =3,∴AF=DF,∵△ABD为等边三角形,∴BF⊥AD,即∠BFD=90°,∴此时△DFB为直角三角形,∵∠EAF=1∠EAG=30°,2∴∠BAE=∠BAD-∠EAF=30°,即此时旋转角α的度数为30°;综上所述,当△DFB为直角三角形时,旋转角α的度数为30°或90°.【点睛】本题主要考查了菱形的性质,图形旋转的性质,等边三角形的判定和性质,勾股定理等知识,熟练掌握菱形的性质,图形旋转的性质,等边三角形的判定和性质,勾股定理等知识,并利用分类讨论思想解答是解题的关键.14.(23-24八年级下·湖北武汉·期中)在菱形ABCD和菱形BEFG中,∠ABC=∠EBG=60°,AB=6,BE=2.(1)如图1,若点E、G分别在边AB、BC上,点F在菱形ABCD内部,连接DF,直接写出DF的长度为;(2)如图2,把菱形BEFG绕点B顺时针旋转α°(0<α<360),连接DF、CG,判断DF与CG的数量关系,并给出证明;(3)如图3,①把菱形BEFG继续绕点B顺时针旋转,连接GD,O为DG的中点,连接CO、EO,试探究CO与EO的关系;②直接写出菱形BEFG绕B点旋转过程中CO的取值范围.【答案】(1)43(2)FD=3CG,证明见解析(3)OE=3OC,2≤OC≤4【分析】(1)连接AC,EG,BF,DB,AC,BD交于点O,EG,BF交于点H,根据菱形的性质,证明B,F,D三点共线,求出BD,BF的长,用BD-BF即可求出DF的长度;(2)过点D作DM∥FG,过点G作GM∥DF,过点C作CN⊥MG,得到四边形DMGF为平行四边形,证明△CDM≌△CBG,得到CM=CG,∠DCM=∠BCG,进而求出∠MCG=∠BCG+∠BCM=∠DCM+∠BCM=∠DCB=120°,利用等腰三角形的性质结合30度角的直角三角形的性质,即可得出结论;(3)①延长CO至点H,使OC=OH,连接AC,AH,HE,HG,延长BA,交CH于点Q,先证明△DOC≌△GOH,推出四边形AHGB为平行四边形,再证明△HAC≌△EBC,推出△CHE为等边三角形,利用等边三角形的性质和含30度角的直角三角形的性质,即可得出结论;②三角形的三边关系,求出CE的范围,进而求出OC的范围即可.【详解】(1)解:连接AC,EG,BF,DB,AC,BD交于点O,EG,BF交于点H,∵菱形ABCD ,菱形EBGF ,∴∠ABD =∠CBF =12∠ABC =30°,∠EBF =∠GBF =12∠EBG =30°,AC ⊥BD ,EG ⊥BF ,BD =2OB ,BF =2HB ,∵点E 、G 分别在边AB 、BC 上,∴∠ABD =∠ABF =30°,∴B ,F ,D 三点共线,∵BE =2,∠EBF =30°,∴HE =12BE =1,BH =3HE =3,∴BF =2BH =23,同理:BD =2OB =23OA =2×32AB =63,∴DF =BD -BF =43;故答案为:43;(2)FD =3CG ,证明如下:过点D 作DM ∥FG ,过点G 作GM ∥DF ,过点C 作CN ⊥MG ,则:四边形DMGF 为平行四边形,∴DF =MG ,DM =GF ,∵菱形ABCD ,菱形EBGF ,∠ABC =∠EBG =60°,∴AD ∥BC ,BE ∥GF ,∠ADB =∠ABC =∠EBG =60°,CD =BC ,BG =GF =DM∴BE ∥DM ,∠1=∠2,∠DCB =180°-∠ADC =120°,∴∠3=∠DMN ,∵∠1=∠ADM +∠DMN ,∠2=∠3+∠CBE∴∠ADM =∠CBE ,∴∠CDA +∠ADM =∠CBE +∠EBG ,即:∠CDM =∠CBG ,又∵CD =BC ,BG =DM ,∴△CDM ≌△CBG ,∴CM =CG ,∠DCM =∠BCG ,∴∠MCG =∠BCG +∠BCM =∠DCM +∠BCM =∠DCB =120°,∴∠CMG =∠CGM =12180°-120° =30°,∵CN ⊥MG ,∴DF =MG =2NG ,CN =12CG ,∴NG=CG2-CN2=3CG,2∴DF=3CG;(3)①延长CO至点H,使OC=OH,连接AC,AH,HE,HG,延长BA,交CH于点Q,∵O是DG的中点,∴OD=OG,又∵∠DOC=∠HOG,∴△DOC≌△GOH,∴GH=CD,∠OCD=∠OHG,∴CD∥HG,∵菱形ABCD,∴AB∥CD,AD∥BC,AB=BC=CD=DA,∠ADC=∠ABC=60°,∴AB∥HG,GH=CD=AB,△ABC为等边三角形,∴四边形AHGB为平行四边形,∠BAC=∠ACB=60°,AC=AB=BC,∴AH∥BG,AH=BG,∠CAQ=180°-∠CAB=120°,∴∠HAQ=∠ABG,∵BG=BE,∴AH=BE,∵∠CBE=∠ABC+∠ABG+∠EBG=120°+∠ABG,∠HAC=∠HAQ+∠CAQ=∠HAQ+120°,∴∠CBE=∠HAC,又∵AH=BE,AC=BC,∴△HAC≌△EBC,∴CH=CE,∠HCA=∠ECB,∴∠HCE=∠HCA+∠ACE=∠BCE+∠ACE=∠ACB=60°,∴△CHE为等边三角形,∵OC=OH,∠HEC=60°,∴OE⊥OC,∠CEO=30°,∴OC=1CE,2∴OE=3OC;②∵BC=AB=6,BE=2,∴BC-BE≤CE≤BC+BE,即:4≤CE≤8,∵OC=1CE,2∴2≤OC≤4.【点睛】本题考查菱形的性质,平行四边形的判定和性质,等腰三角形的判定和性质,等边三角形的判定和性质,含30度角的直角三角形,勾股定理,三角形的三边关系等知识点,综合性强,难度大,属于压轴题,熟练掌握相关知识点,添加辅助线构造特殊图形和全等三角形,是解题的关键.【考点四利用菱形的性质与判定解决最值问题】15.(23-24八年级下·重庆沙坪坝·期中)如图,菱形ABCD的周长为8,∠DAC=30°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是.【答案】3【分析】此题考查轴对称确定最短路线问题,菱形的性质,等边三角形的判定与性质连接BD ,DE ,根据菱形的性质可得,△ABD 是等边三角形,再证明△ADP ≌△ABP ,可得PD =PB ,从而得到PE +PB 的最小值为DE 的长,再由E 是AB 的中点,可得DE ⊥AB ,AE =12AB =1,然后根据勾股定理可得DE =3,即可求解.【详解】解:如图,连接BD ,DE ,∵四边形ABCD 是菱形,周长为8,∠DAC =30°,∴∠DAB =2∠DAC =60°,∠DAP =∠BAP ,AB =AD =2,∴△ABD 是等边三角形,在△ADP 和△ABP 中,∵AP =AP ,∠DAP =∠BAP ,AB =AD ,∴△ADP ≌△ABP ,∴PD =PB ,∴PE +PB =PE +PD ≥DE ,即PE +PB 的最小值为DE 的长,∵E 是AB 的中点,∴DE ⊥AB ,AE =12AB =1,∴DE =AD 2-AE 2=3,即PE +PB 的最小值为3.故答案为:3.【变式训练】16.(2024九年级下·全国·专题练习)如图,在菱形ABCD 中,E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH .若∠B =45°,BC =23,则GH 的最小值是.【答案】62【分析】连接AF ,利用三角形中位线定理,可知GH =12AF ,当AF ⊥BC 时,AF 最小,求出AF 最小值即可求出.【详解】解:连接AF ,如图,∵四边形ABCD 是菱形,∵G ,H 分别为AE ,EF 的中点,∴GH 是△AEF 的中位线,∴GH =12AF ,当AF ⊥BC 时,则∠AFB =90°,AF 最小,GH 得到最小值,∵∠B =45°,∴△ABF 是等腰直角三角形,∴AF 2+BF 2=AB 2,即2AF 2=AB 2,∴AF =6,∴GH =62,故答案为:62.【点睛】本题考查了菱形的性质、三角形的中位线定理、等腰直角三角形的判定与性质、垂线段最短等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.17.(23-24八年级下·安徽合肥·期末)菱形ABCD 中,∠B =60°,E 是BC 中点,连接AE ,DE ,点F 是DE 上一动点,G 为AF 中点,连接CG .(1)∠BAE =;(2)若AB =2,则CG 的最小值为.【答案】30°2217【分析】(1)连接AC ,证明△ABC 为等边三角形,三线合一,即可得出结果;(2)取AD 的中点I ,AE 的中点H ,连接HG ,IG ,CH ,CI ,根据三角形的中位线定理,推出点G 在IH 上运动,当CG ⊥HG 时,CG 最小,进行求解即可.【详解】解:(1)连接AC ,∵菱形ABCD ,∴AB =BC ,∵∠B =60°,∴△ABC 为等边三角形,∴∠BAC =60°,∵E 是BC 中点,∴AE 平分∠BAC ,∴∠BAE =12∠BAC =30°;故答案为:30°;(2)取AD 的中点I ,AE 的中点H ,连接HG ,IG ,CH ,CI则:IG ∥DF ,HG ∥DF ,∴I ,G ,H 三点共线,。
中考数学复习:专题7-2 中考折叠问题的归类解析

专题02 中考折叠问题的归类解析【专题综述】折叠问题在近年来各地的中考试卷中频频出现,解决这一类问题主要抓住两点:折叠前后重合的角相等,重合的边也相等.【方法解读】一、折叠与平行例1:如图,在四边形ABCD中,∠A=100°,∠C=70°.将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=___.【来源】2013-2014学年江苏省宜兴市和桥学区七年级下学期期中考试数学试卷(带解析)【答案】95°在△BMN中,∠B=180°-(∠BMN+∠BNM)=180°-(50°+35°)=180°-85°=95°.考点:1.平行线的性质;2.三角形内角和定理;3.翻折变换(折叠问题).【解读】根据两直线平行,同位角相等求出∠BMF,∠BNF,再根据翻折的性质求出∠BMN和∠BNM,然后利用三角形的内角和定理列式计算即可得解.【举一反三】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.(1)求证:EDB EBD∠=∠;(2)判断AF与BD是否平行,并说明理由.【来源】2015中考真题分项汇编第1期专题4 图形的变换【答案】【解析】试题解析:(1)由折叠可知:∠CDB =∠EDB∵四边形ABCD是平行四边形∴DC∥AB∴∠CDB =∠EBD∴∠EDB=∠EBD(2) ∵∠EDB=∠EBD∴DE=BE由折叠可知:DC=DF∵四边形ABCD是平行四边形∴DC=AB∴AE=EF∴∠EAF=∠EFA△BED中, ∠EDB+∠EBD+∠DEB=180°即2∠EDB+∠DEB=180°同理△AEF中,2∠EFA+∠AEF=180°∵∠DEB=∠AEF∴∠EDB= ∠EFA∴AF∥BD考点:折叠变换,平行四边形的性质,等腰三角形的性质与判定,三角形的内角和二、折叠与全等例2:如图,在□ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在点B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G。
2020初中数学中考专题复习——四边形中的线段最值问题专项训练5(附答案详解)
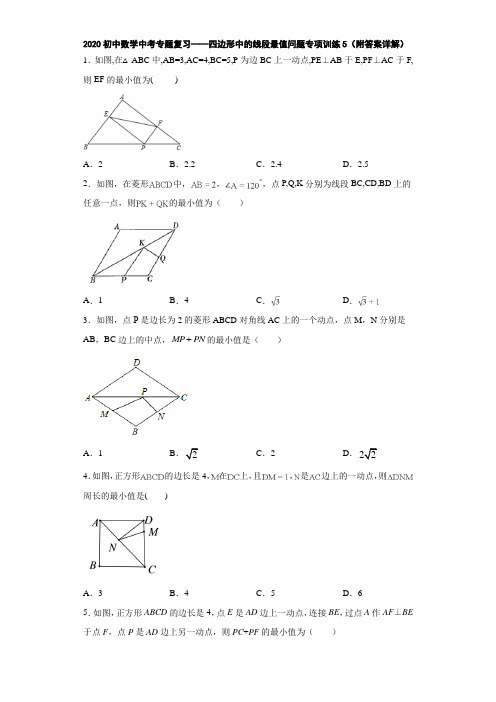
1.C
参考答案
【解析】
【分析】
根据三个角都是直角的四边形是矩形,得四边形 AEPF 是矩形,根据矩形的对角线相等,得
EF=AP,则 EF 的最小值即为 AP 的最小值,根据垂线段最短,知:AP 的最小值即等于直角
三角形 ABC 斜边上的高.
【详解】
连接 AP,
∵在△ ABC 中,AB=3,AC=4,BC=5, ∴AB2+AC2=BC2, 即∠BAC=90°, 又∵PE⊥AB 于 E,PF⊥AC 于 F, ∴四边形 AEPF 是矩形, ∴EF=AP, ∵AP 的最小值即为直角三角形 ABC 斜边上的高,即 2.4, ∴EF 的最小值为 2.4, 故选:C. 【点睛】 本题考查了矩形的性质和判定,勾股定理的逆定理,直角三角形的性质的应用,要能够把要 求的线段的最小值转化为便于求的最小值得线段是解此题的关键. 2.C 【解析】 【分析】 根据轴对称确定最短路线问题,作点 P 关于 BD 的对称点 P',连接 与 BD 的交点即为所求的 点 K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知 ⊥CD 时
的最小值,求解即可.
【详解】
解::如图,∵
,
,,
∴点 P'到 CD 的距离为 2× = ,
∴ 故选 C.
的最小值为 .
【点睛】 本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最 短路线的方法是解题的关键. 3.C 【解析】 【分析】 先作点 M 关于 AC 的对称点 M′,连接 M′N 交 AC 于 P,此时 MP+NP 有最小值.然后证明 四边形 ABNM′为平行四边形,即可求出 MP+NP=M′N=AB=2. 【详解】 解:如图,作点 M 关于 AC 的对称点 M′,连接 M′N 交 AC 于 P,此时 MP+NP 有最小值, 最小值为 M′N 的长. ∵菱形 ABCD 关于 AC 对称,M 是 AB 边上的中点, ∴M′是 AD 的中点, 又∵N 是 BC 边上的中点, ∴AM′∥BN,AM′=BN, ∴四边形 ABNM′是平行四边形, ∴M′N=AB=2, ∴MP+NP=M′N=2,即 MP+NP 的最小值为 2, 故选:C.
中考数学复习《四边形的最值问题》专项测试卷(带答案)

中考数学复习《四边形的最值问题》专项测试卷(带答案)学校:___________班级:___________姓名:___________考号:___________一、单选题1.如图,正方形ABCD 中4AB =,点E ,F 分别在边AB ,BC 上,点P 在对角线AC 上EF AC ∥,PE PF m +=下列结论错误..的是( )A .若2BE =,则m 的最小值为4B .若m 的最小值为4,则2BE =C .若0.5BE ,则m 的最小值为5D .若m 的最小值为5,则0.5BE2.如图,已知矩形ABCD ,AB=8,BC=12,点M 为矩形内一点,点E 为BC 边上任意一点,则MA MD ME ++的最小值为( )A .642+B .4413+C .863+D .203.如图,在ABC 中345AB AC BC ===,,,P 为边BC 上一动点,且PE AB ⊥于点E ,PF AC ⊥于点F ,则线段EF 的最小值为( )A .2B .2.2C .2.4D .2.54.如图,ABC 和ABE 是等腰三角形2AB BC BE ===,120ABC ∠= D 为AE 的中点,线段CD 的最大值为( )A .2 B1 C .1 D 15.如图是一个轴对称的房型图案.测得矩形BCDE 中3BC =,CD=8,ABE 中5AB =,现用一个半径为r 的圆形纸片将其完全覆盖,则r 的最小值是( )A .133B .256CD 6.如图,菱形ABCD 的对角线相交于点O ,AC=12,DB=16,点P 为边BC 上一点,且P 不与点B 、C 重合.过P 作PE AC ⊥于E ,PF BD ⊥于F ,连EF ,则EF 的最小值等于( ).A .3.6B .4.8C .5D .67.如图,在Rt ABC △中90C ∠=︒,BC=3,AC=4,M 为斜边AB 上一动点,过M 作MD AC ⊥于点D ,过M 作ME CB ⊥于点E ,则线段DE 的最小值为( )A .125B .5C .245D .2.58.如图,菱形ABCD 中点M 为BC 的中点,点N 为对角线AC 上一个动点,连接BN 、MN ,若5MN BN +=,则AB 的最大值为( )A .53B 53C 103D .3二、填空题9.如图,在矩形ABCD 中2AD = 3AB = 点P 为BC 边上一点 则12AP PC +的最小值等于 .10.如图 在ABC 中AB AC = 8BC = 30ACB ∠=︒ D 为边AC 上一动点(C 点除外) 以BD 为一边作正方形BDEF 连接CE 则CDE 面积的最大值为 .11.如图 在平面直角坐标系中点()20A -, ()01B , ()03C ,将线段AB 沿x 轴向右平移得到A B '' 连接A C ' B C ' 则A C B C ''+的最小值为 .12.如图 在边长为2的正方形ABCD 中E F 分别是边AB BC 上的动点(可与端点重合) M N 分别是ED EF 的中点 则MN 的最大值为 .13.如图 平行四边形ABCD 的面积为28 7AB = 45BAD ∠=︒.E 为对角线BD 上任意一点 连接AE得ABE 和ADE ;已知ABE CDF △≌△ ADE CBG ≌△△ 则五边形CFDBG 的对角线GF 的最小值为 .三、解答题14.已知正方形ABCD 和正方形EFGH 按图1所示叠放在一起 其中4AB = 2EF = 点O 为AB 和EF 的中点.(1)图2中正方形EFUV 为图1中正方形EFGH 关于直线AB 的轴对称图形 求点D 和点U 的连结线段DU 的长度;(2)将图1中的正方形EFGH 绕点O 旋转 如图3所示 求运动过程中点D 和点G 之间距离的最大值和最小值.15.在矩形ABCD 中E 是CD 上一个动点 连接AE(1)如图1 若AB AE = 5AB = 3AD = 求EC 的长;(2)如图2 点P 是AE 中点 将直线AE 绕点P 顺时针旋转α︒后 恰好经过点B 交AD 于点F 连接EF 若DEF EAB α=∠+∠.求证:2FB FP FE =+.(3)如图3 若点P 是AE 上一点 直线AE 绕P 点顺时针旋转90° 恰好经过点D .若5AB = 3AD = 连接PC 请直接写出....PC 的最小值.16.已知:将ABCD 沿对角线AC 折叠 DAC 折到FAC 位置.(1)证明BE EF =;(2)如果6AC cm = B 、D 两点间距离为8cm 请在对角线AC 上找一点O 使得OB OF +的值最小 并求最小值;(3)探索:线段AF 与BC 满足什么关系时 点D 、C 、F 在同一条直线上 请给出证明.17.如图1 菱形ABCD 中B α∠= 2BC = E 是边BC 上一动点(不与点,B C 重合) 连接DE点C 关于直线DE 的对称点为C ' 连接AC '并延长交直线DE 于点,P F 是AC '的中点 连接,DC DF '.(1)填空:DC '=______ APD ∠=______(用含α的代数式表示);(2)如图2 当90α=︒ 题干中其余条件均不变 连接BP .求证:BP =.(3)(2)的条件下 连接AC .①若动点E 运动到边BC 的中点处时 ACC '△的面积为______.①在动点E 的整个运动过程中ACC '△面积的最大值为______.18.综合与实践课上 老师让同学们以“矩形与垂直”为主题开展数学活动.(1)操作判断如图1 正方形纸片ABCD 在边BC 上任意取一点E 连接AE 过点B 作BF AE ⊥于点G 与边CD 交于点F .根据以上操作 请直接写出图1中线段AE 与线段BF 的关系.(2)迁移探究小华将正方形纸片换成矩形纸片 继续探究 过程如下:如图2 在矩形纸片ABCD 中::=AB AD m n 在边BC 上任意取一点E 连接AE 过点B 作BF AE ⊥于点G 与边CD 交于点F 请求出线段AE 与BF 的关系 并说明理由.(3)拓展应用如图3 已知正方形纸片ABCD 的边长为2 动点E 由点A 向终点D 做匀速运动 动点F 由点D 向终点C 做匀速运动 动点E 、F 同时开始运动 且速度相同 连接AF 、BE 交于点G 连接GD 则线段GD 长度的最小值为______.(直接写出答案不必说明理由)参考答案:1.D2.C3.C4.B5.A6.B7.A8.C9.5 210.611121314.(1)解:延长FG 交CD 于点P①90GFB B C ∠=∠=∠=︒①四边形BFPC 是矩形①4PF BC ==①1PC BF OB OF ==-=①3DP CD PC =-=①DU == (2)解:连接OG①2FG = 1OF =①OG =①点G 在以点O 为圆心 OG 长为半径的圆上 ①当点G 在线段OD 上时 DG 取得最小值; 当点G 在DO 延长线上时 DG 取得最大值;①2OA = 4=AD ①222425OD +=如图1DG 最小值为2555如图2DG 取得最大值为5535= 15.(1)解:①矩形ABCD①CD AB = 90D ①2222534DE AE AD -=-=①1EC DC DE =-=;(2)过A 作AM EF ∥交PB 于M 点①PAM PEF ∠=∠①P 是AE 中点①AP EP =在EPF 与APM △中PEF PAM EP APEPF APM ∠=∠⎧⎪=⎨⎪∠=∠⎩①(ASA)EPF APM △≌△;①EF AM = PF MP①矩形ABCD①AB CD ∥①DEP BAP ∠=∠①DEP PEF PAB PAM ∠-∠=∠-∠即DEF MAB ∠=∠ ①旋转角APF DEF EAB α=∠=∠+∠ PAB 中有APF EAB PBA ∠=∠+∠①DEF PBA ∠=∠ MAB PBA ∠=∠①MB AM =①MB EF =①2FB FM MB FP PM EF FP FE =+=++=+; (3)解:直线AE 绕P 点顺时针旋转90° 恰好经过点D ①90APD ∠=︒取AD 的中点O 连接,OP OC则:1322OP OD AD ===①矩形ABCD①90ADC ∠=︒ 5CD AB == ①22109OC CD OD =+=①10932PC OC OP ≥-=-①PC 1093-.16.(1)解:证明:如图1中四边形ABCD 是平行四边形AD BC AD BC ∴=∥,DAC ACB ∴∠=∠ DAC 翻折得到FACAD AF DAC FAC ∴=∠=∠,ACB FAC ∴∠=∠AE CE ∴=,AD BC AD AF ==BC AF ∴=BE EF ∴=;(2)连接BD 交AC 于点O 连接OF点F 与D 关于AC 对称OD OF ∴=∴当点O 为AC 与BD 交点时 OB OF +的值最小 最小值为线段BD 的长 即最小值为8cm ;(3)当线段AF 与BC 互相平分时 点D 、C 、F 在同一条直线上. 理由:AF 与BC 互相平分 AF BC =EA EB EC EF ∴===,EAC ECA ECF F ∴∠=∠∠=∠180EAC ECA ECF F ∠+∠+∠+∠=︒90ECA ECF ∴∠+∠=︒即90ACF ∠=︒ DAC 翻折得到FAC90ACF ACD ∴∠=∠=︒∴点D 、C 、F 在同一条直线上.17.(1)解:四边形ABCD 是菱形ADC B α∠=∠= 2AD CD AB ===C '是C 关于DE 的对称点CD ∴沿DE 翻折后可得到C D '2C D CD '∴== 12CDP C DP CDC ''∠=∠=∠AD C D '∴= F 是AC '的中点12C DF ADC ''∴∠=∠ DF AC '⊥ 即90DFC '=︒∠FDP C DF C DP ∴∠=∠+'∠'1122ADC CDC ''=∠+∠12ADC =∠ 12α= ①190902APD DFP α=︒-=︒-∠∠. 故答案:2 1902α︒-. (2)证明:如图 过A 作GA PA ⊥ 交PD 的延长线于G90GAP ∴∠=︒四边形ABCD 是菱形 90B∴四边形ABCD 是正方形90ADC BAD ∴∠=∠=︒ AB AD =由(1)得:19090452DPF ∴∠=︒-⨯︒=︒45G DPF ∴∠=∠=︒AG AP ∴=在Rt AGP △中2PG AP =2DP DG ∴+=;90DAG DAP ∠+∠=︒90BAP DAP ∠+∠=︒BAP DAG ∴∠=∠在BAP △和DAG 中AB ADBAP DAGAG AP=⎧⎪∠=∠⎨⎪=⎩∴BAP DAG ≌(SAS )BP DG ∴=BP DP ∴+.在Rt DFP △中DP =①)BP AF FP =+①BP =(3)解:①如图 连接BD 交AC 于O连接PC由(2)得:45APB G ∠=∠=︒90BPD BPA DPF ∴∠=∠+∠=︒90BPD BCD ∴∠=∠=︒∴B 、P 、C 、D 四点共圆 O 为圆心四边形ABCD 是正方形OA OC ∴=A ∴在O 上90APC ∴∠=︒ E 是BC 的中点112CE BE CD ∴===2222125DE CE CD ∴++BEP DEC ∠=∠ 90BPE DCE ∠=∠=︒BPE DCE ∴∽BEBP PEDE DC CE ∴==215BP PE==25BP ∴= 5PE =25DG BP ∴==52552=410AP ∴=由(2)得:45FPD FDP ∠=∠=︒ ∴22PD DF FP ==65PD PE DE =+=310DF FP ∴==在Rt AFD △中2210AF AD DF =-=10C F '∴210C P FP C F ''∴=-=由(1)折叠得:210CP C P '==12ACC SAC CP ''∴=⋅12=45=. ①如图 过C '作C M AC '⊥ 交AC 于M C '的运动轨迹是以D 为圆心 2C D '=为半径的AC AC 与BD 交于Q12ACC S AC C M ''∴=⋅2AC ==12ACC S M M '''∴=⨯=∴当C M '取最大时 ACC S '△最大如图 当C '与Q 重合时 即C M QO'=C M '最大BD AC ==12DM BD ∴==2C M C D DM ''∴=-=22ACC S '∴==故ACC '△面积的最大值为22. 18.(1)解:①四边形ABCD 是正方形 90,,ABC BCD AB BC ∴∠=∠=︒= 又,AE BF ⊥90,AGB ∴∠=︒90,BAE ABG ABG FBC ∴∠+∠=∠+∠=︒ ,BAE FBC ∴∠=∠在ABE 和BCF △中,,,BAE FBC AB BC ABE BCF ∠=∠=∠=∠ (),ABE BCF ASA ∴≌;AE BF ∴=(2)AE m BF n=.理由如下: ①四边形ABCD 是矩形90,,ABC BCF AD BC ∴∠=∠=︒= 又,AE BF ⊥90,AGB ∴∠=︒90,BAE ABG ABG FBC ∴∠+∠=∠+∠=︒ ,BAE FBC ∴∠=∠,ABE BCF ∴∽,AE AB BF BC∴= ,AB AB m AD BC n== AE m BF n∴=; (3)如图 取AB 的中点M 连接,DM GM 由题意知 AE DF =由(1)可得Rt ABE Rt DAF ≌ 同理可得:90AGB ∠=︒①M 是AB 的中点 2AB =①1AM MB MG ===在Rt ADM中MD在MGD中≥-=GD MD MG1,①GD11.。
中考数学二轮专题复习图形变换——折叠问题【含答案】

二轮复习:图形变换(一)—折叠图形变换历来是中考必考点之一。
考试大纲要求:会运用图形变换的相关知识进行简单的作图与计算,并能解决相关动态需求数学问题,并能进行图案设计。
图形变换一般包括,折叠、平移、旋转、对称、位似和图形的探究。
在图形变换的考题中,最多题型是折叠、旋转。
在解决折叠问题时,应注意折叠前后相对应的边相等、角相等。
下面着重从三个方面进行讲述:三角形折折叠、特殊平行四边形折叠和在平面直角坐标系内的图形折叠三大类进行。
(一)三角形的折叠:题型1、一般三角形的折叠:1、如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°﹣α﹣β2、(2019•江西)如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE=°.3、如图,在△ABC中,AB=10,∠B=60°,点D、E分别在AB、BC上,且BD=BE=4,将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内),连接AB′,则AB′的长为___.题型2、等腰或等边三角形的折叠:4、如图,在△ABC 中,AB =AC ,BC =24,tanC =2,如果将△ABC 沿直线l 翻折后,点B 落在边AC 的中点E 处,直线l 与边BC 交于点D ,那么BD 的长为_____.5、如图,D 是等边△ABC 边AB 上的点,AD=2,DB=4.现将△ABC 折叠,使得点C 与点D 重合,折痕为EF ,且点E 、F 分别在边AC 和BC 上,则CF CE=_______.(利用相似三角形周长的比等于相似比△AED 相似△DBF)题型3、直角三角形的折叠:6、如图,在Rt △ABC 中,∠ACB=90°,BC=6,CD 是斜边AB 上的中线,将△BCD 沿直线CD 翻折至△ECD 的位置,连接AE .若DE ∥AC ,计算AE 的长度等于.7、如图,在等腰直角三角形ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是(二)特殊平行四边形的折叠:题型1、矩形折叠:1、(求角).如图,将矩形沿对角线折叠,点落在处,交于点,已知,则的度为A. B. C. D.2、(求三角函数值)如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,如果AB:AD=2:3,那么tan∠EFC值是.3、(求边长)如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE 折叠,使点B落在矩形内点F处,连接CF,则CF的长为4、(求折痕长)如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为5、(求边的比)如下图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为。
四边形动点最值专题(包含答案)

设Q是AB的中点,连接DQ,
∵∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,
∵AB=AC=4,P为AC中点,
∴AQ=AP,
在△AQD和△APF中,
AQ=AP
∠QAD=∠PAF,
AD=AF
∴△AQD≌△APF(SAS),
∴QD=PF,
∵点D在直线BC上运动,
A. B. C. D.
9.如图,矩形ABCD中,AB=8,BC=4,把矩形ABCD沿过点A的直线AE折叠,点D落在矩形ABCD内部的点D′处,则CD′的最小值是()
A.4B. C. D.
10.如图,菱形 的顶点 、 在 轴上( 在 的左侧),顶点 、 在 轴上方,对角线 的长是 ,点 为 的中点,点 在菱形 的边上运动.当点 到 所在直线的距离取得最大值时,点 恰好落在 的中点处,则菱形 的边长等于()
【详解】
连接PC,
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=∠C=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,
即当CP⊥AB时,PC最小,
∵AC=8,BC=6,
∴AB=10,
∴PC的最小值为: =4.8.
∴线段EF长的最小值为4.8.
故选:C.
【点睛】
本题主要考查的是矩形的判定与性质,关键是根据矩形的性质和三角形的面积公式解答.
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故选:D.
【点睛】
本题考查了轴对称-最短路线问题,平行四边形的性质和判定,菱形的性质,勾股定理的应用,解此题的关键是能根据轴对称找出P的位置.
2024年中考数学总复习第一部分考点精讲第五单元四边形微专题几何最值问题
情形1 异侧线段和的最小值问题 问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得PA +PB的值最小. 解决思路:连接AB交直线l于点P.
微专题 几何最值问题
情形2 同侧线段和的最小值问题 问题:两定点A,B位于直线l同侧,在直线l上找一点P,使得PA +PB的值最小.
解决思路:作点B关于直线l的对称点B′,连接AB′,与直线l交于 点P.
例2题图
微专题 几何最值问题
类型三 一动两定(“胡不归问题 ”)
方法解读
问题:如图,点A为直线l上一定点,点B为直线l外一定点,点P 为直线l上一动点,要使kAP+BP(0<k<1)的值最小.
解决思路:一找:找带有系数k的线段AP;
微专题 几何最值问题
二构:构造以线段AP为斜边的直角三角形; ①以定点A为顶点作∠NAP,使sin ∠NAP=k; ②过动点P作垂线,构造Rt△APE; 三转化:化折为直,将kAP转化为PE; 四求解:使得kAP+BP=PE+BP,利用“垂线段最短”转化为求 BF的长.
微专题 几何最值问题
例4 (人教八上P62第2题改编)如图,等边△ABC的边长为4, AD是BC边上的中线,点F是AD上的动点,点E是AB边上一点, 且AE=2,则EF+CF的最小值为___2__3___.
例4题图
微专题 几何最值问题
例5 (北师八下P13第2题改编)如图,在等腰Rt△ABC中,AB= BC=2,点D是AB的中点,点E为AC边上一动点,则DE+BE的 最小值为____5____.
解决思路:作点B关于直线l的对称点B′,连接AB′并延长,与直 线l交于点P.
微专题 几何最值问题
例6 如图,在△ABC中,AB=3,EF是BC的垂直平分线,点P 是EF上的动点,则|PA-PB|的最大值为____3____.
中考数学专题复习《四边形中最值问题的分类讨论、存在性问题》测试卷(带答案)
第 1 页 共 17 页 中考数学专题复习《四边形中最值问题的分类讨论 存在性问题》测试卷(带答案) 学校:___________班级:___________姓名:___________考号:___________ 一 单选题 1.如图 在RtABC△中 90B 6AB 8BC 点D在BC上 以AC为对角线的
所有平行四边形ADCE中 DE的最小值是( )
A.4 B.6 C.8 D.10 2.如图.菱形ABCD的对角线
,ACBD
相交于点O P为AB边上一动点(不与点A B重
合).PEOA于点,EPFOB于点F 若8,60ABBAD 则线段EF长度的最小值为( )
A.23 B.
22 C.43 D.42
3.如图 已知矩形ABCD 8AB 12BC 点M为矩形内一点 点E为BC边上任意
一点 则MAMDME的最小值为( )
A.
642 B.4413 C.863 D.20
4.如图1 矩形ABCD中 点E为AB的中点 动点P从点A出发 沿折线ADDC匀速运
动 到达点C时停止运动 连接AP PE 设AP为x PE为y 且y关于x的函数图象 第 2 页 共 17 页
如图2所示 则AP的最大值为( ) A.5 B.
21 C.4 D.17
5.如图 在平行四边形ABCD中 120C 24ADAB 点H G分别是边CDBC、
上的动点.连接AHHG、 点E为AH的中点 点F为GH的中点 连接EF.则EF的最大值与最小值的差为( )
A.1 B.31 C.
3
2 D.23
6.如图 正方形ABCD的边长为12 点E F分别为AB BC上动点(E F均不与端点
重合) 且7AECF P是对角线AC上的一个动点 则PEPF的最小值是( )
A.12 B.13 C.189 D.
122
7.如图 在矩形ABCD中 6AB 63BC 点P在线段BC上运动(含
,BC
两点) 连
备战2020年中考数学二轮专项——四边形、动点、最值问题(中考真题汇编)(含解析)
备战2020年中考数学二轮专项——四边形、动点、最值问题(中考真题汇编)1.(2019威海中考第24题12分)如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.(1)求证:CE=EF;(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;(3)求△BEF面积的最大值.【解答】(1)证明:过E作MN∥AB,交AD于M,交BC于N,∵四边形ABCD是正方形,∴AD∥BC,AB⊥AD,∴MN⊥AD,MN⊥BC,∴∠AME=∠FNE=90°=∠NFE+∠FEN,∵AE⊥EF,∴∠AEF=∠AEM+∠FEN=90°,∴∠AEM=∠NFE,∵∠DBC=45°,∠BNE=90°,∴BN=EN=AM,∴△AEM≌△EFN(AAS),∴AE=EF,∵四边形ABCD是正方形,∴AD=CD,∠ADE=∠CDE,∵DE=DE,∴△ADE≌△CDE(SAS),∴AE=CE=EF;(2)解:在Rt△BCD中,由勾股定理得:BD==10,∴0≤x≤5,由题意得:BE=2x,∴BN=EN=x,由(1)知:△AEM≌△EFN,∴ME=FN,∵AB=MN=10,∴ME=FN=10﹣x,∴BF=FN﹣BN=10﹣x﹣x=10﹣2x,∴y===﹣2x2+5x(0≤x≤5);(3)解:y=﹣2x2+5x=﹣2(x﹣)2+,∵﹣2<0,∴当x =时,y 有最大值是;即△BEF 面积的最大值是.2.(2019山西中考 第22题 11分)综合与实践动手操作:第一步:如图1,正方形纸片ABCD 沿对角线AC 所在直线折叠,展开铺平.在沿过点C 的直线折叠,使点B ,点D 都落在对角线AC 上.此时,点B 与点D 重合,记为点N ,且点E ,点N ,点F 三点在同一直线上,折痕分别为CE ,CF.如图2.第二步:再沿AC 所在的直线折叠,△ACE 与△ACF 重合,得到图3第三步:在图3的基础上继续折叠,使点C 与点F 重合,如图4,展开铺平,连接EF ,FG ,GM ,ME ,如图5,图中的虚线为折痕.问题解决:(1)在图5中,∠BEC 的度数是 ,BEAE 的值是 ; (2)在图5中,请判断四边形EMGF 的形状,并说明理由;(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形: .【解析】解:(1)67.5°2(2)四边形EMGF 是矩形理由如下:∵四边形ABCD是正方形,∴∠B=∠BCD=∠D=90°由折叠可知:∠1=∠2=∠3=∠4,CM=CG,∠BEC=∠NEC=∠NFC=∠DFC=67.5°由折叠可知:MH、GH分别垂直平分EC,FC,∴MC=ME,GC=GF∴∠5=∠1=22.5°,∠6=∠4=22.5°,∴∠MEF∠GFE=90°∵∠MCG=90°,CM=CG.∴∠CMG=45°又∵∠BME=∠1+∠5=45°,∴∠EMG=180°-∠CMG-∠BME=90°∴四边形EMGF是矩形.(1)菱形FGCH或菱形EMCH(一个即可),如下图所示3.(2019潍坊中考第24题13分)如图1,菱形ABCD的顶点A,D在直线上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l 于点N,连接MN.(1)当MN∥B′D′时,求α的大小.(2)如图2,对角线B′D′交AC于点H,交直线l与点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.解:(1)∵四边形AB′C′D′是菱形,∴AB′=B′C′=C′D′=AD′,∵∠B′AD′=∠B′C′D′=60°,∴△AB′D′,△B′C′D′是等边三角形,∵MN∥B′C′,∴∠C′MN=∠C′B′D′=60°,∠CNM=∠C′D′B′=60°,∴△C′MN是等边三角形,∴C′M=C′N,∴MB′=ND′,∵∠AB′M=∠AD′N=120°,AB′=AD′,∴△AB′M≌△AD′N(SAS),∴∠B′AM=∠D′AN,∵∠CAD=∠BAD=30°,∠DAD′=15°,∴α=15°.(2)∵∠C′B′D′=60°,∴∠EB′G=120°,∵∠EAG=60°,∴∠EAG+∠EB′G=180°,∴四边形EAGB′四点共圆,∴∠AEB′=∠AGD′,∵∠EAB′=∠GAD′,AB′=AD′,∴△AEB′≌△AGD′(AAS),∴EB′=GD′,AE=AG,∵AH=AH,∠HAE=∠HAG,∴△AHE≌△AHG(SAS),∴EH=GH,∵△EHB′的周长为2,∴EH+EB′+HB′=B′H+HG+GD′=B′D′=2,∴AB′=AB=2,∴菱形ABCD的周长为8.4.(2019济宁中考第22题11分)如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G.(1)求线段CE的长;(2)如图2,M,N分别是线段AG,DG上的动点(与端点不重合),且∠DMN=∠DAM,设AM=x,DN =y.①写出y关于x的函数解析式,并求出y的最小值;②是否存在这样的点M,使△DMN是等腰三角形?若存在,请求出x的值;若不存在,请说明理由.【解答】解:(1)如图1中,∵四边形ABCD是矩形,∴AD=BC=10,AB=CD=8,∴∠B=∠BCD=90°,由翻折可知:AD=AF=10.DE=EF,设EC=x,则DE=EF=8﹣x.在Rt△ABF中,BF==6,∴CF=BC﹣BF=10﹣6=4,在Rt△EFC中,则有:(8﹣x)2=x2+42,∴x=3,∴EC=3.(2)①如图2中,∵AD∥CG,∴=,∴=,∴CG=6,∴BG=BC+CG=16,在Rt△ABG中,AG==8,在Rt△DCG中,DG==10,∵AD=DG=10,∴∠DAG=∠AGD,∵∠DMG=∠DMN+∠NMG=∠DAM+∠ADM,∠DMN=∠DAM,∴∠ADM=∠NMG,∴△ADM∽△GMN,∴=,∴=,∴y=x2﹣x+10.当x=4时,y有最小值,最小值=2.②存在.有两种情形:如图3﹣1中,当MN=MD时,∵∠MDN=∠GMD,∠DMN=∠DGM,∴△DMN∽△DGM,∴=,∵MN=DM,∴DG=GM=10,∴x=AM=8﹣10.如图3﹣2中,当MN=DN时,作MH⊥DG于H.∵MN=DN,∴∠MDN=∠DMN,∵∠DMN=∠DGM,∴∠MDG=∠MGD,∴MD=MG,∵BH⊥DG,∴DH=GH=5,由△GHM∽△GBA,可得=,∴=,∴MG=,∴x=AM=8﹣=.综上所述,满足条件的x的值为8﹣10或.5.(2019临沂中考第25题11分)如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.解:过点H作HN⊥BM于N,则∠HNC=90°,∵四边形ABCD为正方形,∴AD=AB=BC,∠D=∠DAB=∠B=∠DCB=∠DCM=90°,①∵将△ADE沿AE所在的直线折叠得到△AFE,∴△ADE≌△AFE,∴∠D=∠AFE=∠AFG=90°,AD=AF,∠DAE=∠FAE,∴AF=AB,又∵AG=AG,∴Rt△ABG≌Rt△AFG(HL),∴∠BAG=∠FAG,∠AGB=∠AGF,∴AG是∠BAF的平分线,GA是∠BGF的平分线;②由①知,∠DAE=∠FAE,∠BAG=∠FAG,又∵∠BAD=90°,∴∠GAF+∠EAF=×90°=45°,即∠GAH=45°,∵GH⊥AG,∴∠GHA=90°﹣∠GAH=45°,∴△AGH为等腰直角三角形,∴AG=GH,∵∠AGB+∠BAG=90°,∠AGB+∠HGN=90°,∴∠BAG=∠NGH,又∵∠B=∠HNG=90°,AG=GH,∴△ABG≌△GNH(AAS),∴BG=NH,AB=GN,∴BC=GN,∵BC﹣CG=GN﹣CG,∴BG=CN,∴CN=HN,∵∠DCM=90°,∴∠NCH=∠NHC=×90°=45°,∴∠DCH=∠DCM﹣∠NCH=45°,∴∠DCH=∠NCH,∴CH是∠DCN的平分线;③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,由①知,∠AGB=∠AGF,∴∠HGN=∠EGH,∴GH是∠EGM的平分线;综上所述,AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCN的平分线,GH是∠EGM的平分线.6、(2019益阳中考第26题12分)如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.(1)当∠OAD=30°时,求点C的坐标;(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为时,求OA的长;(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.解:(1)如图1,过点C作CE⊥y轴于点E,∵矩形ABCD中,CD⊥AD,∴∠CDE+∠ADO=90°,又∵∠OAD+∠ADO=90°,∴∠CDE=∠OAD=30°,∴在Rt△CED中,CE=CD=2,DE==2,在Rt△OAD中,∠OAD=30°,∴OD=AD=3,∴点C的坐标为(2,3+2);(2)∵M为AD的中点,∴DM=3,S△DCM=6,又S四边形OMCD=,∴S△ODM=,∴S△OAD=9,设OA=x、OD=y,则x2+y2=36,xy=9,∴x2+y2=2xy,即x=y,将x=y代入x2+y2=36得x2=18,解得x=3(负值舍去),∴OA=3;(3)OC的最大值为8,如图2,M为AD的中点,∴OM=3,CM==5,∴OC≤OM+CM=8,当O、M、C三点在同一直线时,OC有最大值8,连接OC,则此时OC与AD的交点为M,过点O作ON⊥AD,垂足为N,∵∠CDM=∠ONM=90°,∠CMD=∠OMN,∴△CMD∽△OMN,∴==,即==,解得MN=,ON=,∴AN=AM﹣MN=,在Rt△OAN中,OA==,∴cos∠OAD==.7.(2019南充中考 第24题 10分)如图,在正方形ABCD 中,点E 是AB 边上的一点,以DE 为边作正方形DEFG ,DF 与BC 交于点M ,延长EM 交GF 于点H ,EF 与GB 交于点N ,连接CG.(1)求证:CD ⊥CG ;(2)若tan ∠MEN=31,求EM MN 的值;(3)已知正方形ABCD 的边长为1,点E 在运动过程中,EM 的长能否为21?请说明理由.(1)证明:在正方形ABCD ,DEFG 中,DA=DC ,DE=DG ,∠ADC=∠EDG=∠A=90°(1分)∴∠ADC-∠EDC=∠EDG-∠EDC ,即∠ADE=∠CDG ,∴△ADE ≌△CDG (SAS )(2分)∴∠DCG=∠A=90°,∴CD ⊥CG (3分)(2)解:∵CD ⊥CG ,DC ⊥BC ,∴G 、C 、M 三点共线∵四边形DEFG 是正方形,∴DG=DE ,∠EDM=∠GDM=45°,又∵DM=DM∴△EDM ≌△GDM ,∴∠DME=∠DMG (4分)又∠DMG=∠NMF ,∴∠DME=∠NMF ,又∵∠EDM=∠NFM=45°∴△DME ∽△FMN ,∴DMFM ME MN =(5分) 又∵DE ∥HF ,∴DM FM ED HF =,又∵ED=EF ,∴EF HF ME MN =(6分) 在Rt △EFH 中,tan ∠HEF=31=EF HF ,∴31=ME MN (7分) (3)设AE=x ,则BE=1-x ,CG=x ,设CM=y ,则BM=1-y ,EM=GM=x+y (8分)在Rt △BEM 中,222EM BM BE =+,∴222)()1()1(y x y x +=-+-, 解得11+-=x x y (9分)∴112++=+=x x y x EM ,若21=EM ,则21112=++x x ,化简得:0122=+-x x ,△=-7<0,∴方程无解,故EM 长不可能为21. 8、(2019岳阳中考 第23题 10分)操作体验:如图,在矩形ABCD 中,点E 、F 分别在边AD 、BC 上,将矩形ABCD 沿直线EF 折叠,使点D 恰好与点B 重合,点C 落在点C ′处.点P 为直线EF 上一动点(不与E 、F 重合),过点P 分别作直线BE 、BF 的垂线,垂足分别为点M 和N ,以PM 、PN 为邻边构造平行四边形PMQN .(1)如图1,求证:BE =BF ;(2)特例感知:如图2,若DE =5,CF =2,当点P 在线段EF 上运动时,求平行四边形PMQN 的周长;(3)类比探究:若DE =a ,CF =b .①如图3,当点P 在线段EF 的延长线上运动时,试用含a 、b 的式子表示QM 与QN 之间的数量关系,并证明; ②如图4,当点P 在线段FE 的延长线上运动时,请直接用含a 、b 的式子表示QM 与QN 之间的数量关系.(不要求写证明过程)【解答】(1)证明:如图1中,∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠DEF =∠EFB ,由翻折可知:∠DEF =∠BEF ,∴∠BEF =∠EFB ,∴BE =BF .(2)解:如图2中,连接BP ,作EH ⊥BC 于H ,则四边形ABHE 是矩形,EH =AB .∵DE=EB=BF=5,CF=2,∴AD=BC=7,AE=2,在Rt△ABE中,∵∠A=90°,BE=5,AE=2,∴AB==,∵S△BEF=S△PBE+S△PBF,PM⊥BE,PN⊥BF,∴•BF•EH=•BE•PM+•BF•PN,∵BE=BF,∴PM+PN=EH=,∵四边形PMQN是平行四边形,∴四边形PMQN的周长=2(PM+PN)=2.(3)①证明:如图3中,连接BP,作EH⊥BC于H.∵ED=EB=BF=a,CF=b,∴AD=BC=a+b,∴AE=AD﹣DE=b,∴EH=AB=,∵S△EBP﹣S△BFP=S△EBF,∴BE•PM﹣•BF•PN=•BF•EH,∵BE=BF,∴PM﹣PN=EH=,∵四边形PMQN是平行四边形,∴QN﹣QM=(PM﹣PN)=.②如图4,当点P在线段FE的延长线上运动时,同法可证:QM﹣QN=PN﹣PM=.9.(2019益阳中考第23题10分)如图,在Rt△ABC中,M是斜边AB的中点,以CM为直径作圆O交AC 于点N,延长MN至D,使ND=MN,连接AD、CD,CD交圆O于点E.(1)判断四边形AMCD的形状,并说明理由;(2)求证:ND=NE;(3)若DE=2,EC=3,求BC的长.(1)解:四边形AMCD是菱形,理由如下:∵M是Rt△ABC中AB的中点,∴CM=AM,∵CM为⊙O的直径,∴∠CNM=90°,∴MD⊥AC,∴AN=CN,∵ND=MN,∴四边形AMCD是菱形.(2)∵四边形CENM为⊙O的内接四边形,∴∠CEN+∠CMN=180°,∵∠CEN+∠DEN=180°,∴∠CMN=∠DEN,∵四边形AMCD是菱形,∴CD=CM,∴∠CDM=∠CMN,∴∠DEN=∠CDM,∴ND=NE.(3)∵∠CMN=∠DEN,∠MDC=∠EDN,∴△MDC∽△EDN,∴,设DN=x,则MD=2x,由此得,解得:x=或x=﹣(不合题意,舍去),∴,∵MN为△ABC的中位线,∴BC=2MN,∴BC=2.10、(2019十堰中考第24题10分)如图1,△ABC中,CA=CB,∠ACB=α,D为△ABC内一点,将△CAD绕点C按逆时针方向旋转角α得到△CBE,点A,D的对应点分别为点B,E,且A,D,E三点在同一直线上.(1)填空:∠CDE=(用含α的代数式表示);(2)如图2,若α=60°,请补全图形,再过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论;(3)若α=90°,AC=5,且点G满足∠AGB=90°,BG=6,直接写出点C到AG的距离.【解答】解:(1)∵将△CAD绕点C按逆时针方向旋转角α得到△CBE∴△ACD≌△BCE,∠DCE=α∴CD=CE∴∠CDE=故答案为:(2)AE=BE+CF理由如下:如图,∵将△CAD绕点C按逆时针方向旋转角60°得到△CBE∴△ACD≌△BCE∴AD=BE,CD=CE,∠DCE=60°∴△CDE是等边三角形,且CF⊥DE∴DF=EF=∵AE=AD+DF+EF∴AE=BE+CF(3)如图,当点G在AB上方时,过点C作CE⊥AG于点E,∵∠ACB=90°,AC=BC=5,∴∠CAB=∠ABC=45°,AB=10∵∠ACB=90°=∠AGB∴点C,点G,点B,点A四点共圆∴∠AGC=∠ABC=45°,且CE⊥AG∴∠AGC=∠ECG=45°∴CE=GE∵AB=10,GB=6,∠AGB=90°∴AG==8∵AC2=AE2+CE2,∴(5)2=(8﹣CE)2+CE2,∴CE=7(不合题意舍去),CE=1若点G在AB的下方,过点C作CF⊥AG,同理可得:CF=7∴点C到AG的距离为1或7.11、(2019贵港中考第26题)已知:△ABC是等腰直角三角形,∠BAC=90°,将△ABC绕点C顺时针方向旋转得到△A′B′C,记旋转角为α,当90°<α<180°时,作A′D⊥AC,垂足为D,A′D与B′C交于点E.(1)如图1,当∠CA′D=15°时,作∠A′EC的平分线EF交BC于点F.①写出旋转角α的度数;②求证:EA′+EC=EF;(2)如图2,在(1)的条件下,设P是直线A′D上的一个动点,连接PA,PF,若AB=,求线段PA+PF的最小值.(结果保留根号)【答案】(1)①解:旋转角为105°.理由:如图1中,∵A′D⊥AC,∴∠A′DC=90°,∵∠CA′D=15°,∴∠A′CD=75°,∴∠ACA′=105°,∴旋转角为105°.②证明:连接A′F,设EF交CA′于点O.在EF时截取EM=EC,连接CM.∵∠CED=∠A′CE+∠CA′E=45°+15°=60°,∴∠CEA′=120°,∵FE平分∠CEA′,∴∠CEF=∠FEA′=60°,∵∠FCO=180°-45°-75°=60°,∴∠FCO=∠A′EO,∵∠FOC=∠A′OE,∴△FOC∽△A′OE,∴=,∴=,∵∠COE=∠FOA′,∴△COE∽△FOA′,∴∠FA′O=∠OEC=60°,∴△A′OF是等边三角形,∴CF=CA′=A′F,∵EM=EC,∠CEM=60°,∴△CEM是等边三角形,∠ECM=60°,CM=CE,∵∠FCA′=∠MCE=60°,∴∠FCM=∠A′CE,∴△FCM≌△A′CE(SAS),∴FM=A′E,∴CE+A′E=EM+FM=EF.(2)解:如图2中,连接A′F,PB′,AB′,作B′M⊥AC交AC的延长线于M.由②可知,∠EA′F=′EA′B′=75°,A′E=A′E,A′F=A′B′,∴△A′EF≌△A′EB′,∴EF=EB′,∴B′,F关于A′E对称,∴PF=PB′,∴PA+PF=PA+PB′≥AB′,在Rt△CB′M中,CB′=BC=AB=2,∠MCB′=30°,∴B′M=CB′=1,CM=,∴AB′===.∴PA+PF的最小值为.。
中考数学专项复习折叠类
矩形ABCD沿中心对称轴折叠,则∠A与∠C、∠B与∠D分别相等。
三角形折叠的性质
对应边相等
三角形ABC沿中心对称轴折叠,则AB与BC、AC与CA、AH与HC分别相等。
对应角相等
三角形ABC沿中心对称轴折叠,则∠A与∠B、∠B与∠C、∠A与∠C分别相等。
菱形折叠的性质
对应边相等
菱形ABCD沿中心对称轴折叠,则AB与BC、AD与CD、AC与 BD分别相等。
THANKS
谢谢您的观看
折叠问题的基本类型
1 2
直线型折叠
将一个矩形或正方形沿一条直线折叠,求折痕 的长度。
圆心型折叠
将一个圆沿着圆心对称的两个点折叠,求折痕 的长度。
3
旋转式折叠
将一个矩形或正方形绕着一个顶点旋转一定角 度后折叠,求折痕的长度。
折叠问题的基本解法
利用全等三角形
在折叠前后的两个图形中,通过全 等三角形对应边相等的关系,求得 折痕的长度。
在代数中的应用
因式分解
在代数中,折叠问题常常与因式分解有关,如利用平方差公式进行因式分解等。
方程
折叠问题在方程中也有应用,如利用换元法解方程等。
在三角函数中的应用
角度折叠
在三角函数中,折叠问题常常涉及到角度的倍数关系,如一 个角折半后等于多少度等。
图形折叠
在三角函数中,折叠问题还涉及到图形的折叠,如一个直角 三角形沿一条直角边折叠后得到一个正方形等。
对应角相等
菱形ABCD沿中心对称轴折叠Βιβλιοθήκη 则∠A与∠B、∠C与∠D分别相 等。
03
折叠问题的应用
在几何中的应用
平面几何
折叠问题常常用于平面几何中,如三角形、四边形等图形的折叠,涉及角度 、边长、面积等概念的考察。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用文档 文案大全 C D E B A 图②
中考数学专题复习——四边形中的折叠、剪切、旋转与动点最值问题
一、折叠、剪切类问题 1、折叠后求度数 (1)将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为( ) A.600 B.750 C.900 D.950
(2)如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( ) A.50° B.55° C.60° D.65°
(3)用一条宽相等的足够长的纸条,打一个结,如图①所示,然后轻轻拉紧、压平就可以得到如图②所示的正五边形ABCDE,其中∠BAC=____________度.
2、折叠后求长度 (1)将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,
∠BAE=30°,AB=3,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( ).
A、3 B、2 C、3 D、32
(2)如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且EDBC,则CE的长是( )
(A)10315 (B)1053
(C)535 (D)20103
图① A B C
D
E F 实用文档 文案大全 (3)如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是( ) A.3cm B.4cm C.5cm D.6cm
(4)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是___________厘米.
(5)如图,是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=
(6)如图(1),把一个长为m、宽为n的长方形(mn)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
A.2mn B.mn C.2m
D.2n
3、折叠后求面积 (1)如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( ) A.4 B.6 C.8 D.10
(2)如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿左图中的虚线剪开,拼成如下右图的一座“小别墅”,则图中阴影部分的面积是( )
N M F
E
D
C B
A
m n n
n (2) (1) 实用文档
文案大全 A.2 B.4 C.8 D.10
(3)如图a,ABCD是一矩形纸片,AB=6cm,AD=8cm,E是AD上一点,且AE=6cm。操作:①将AB向AE折过去,使AB与AE重合,得折痕AF,如图b;②将△AFB以BF为折痕向右折过去,得图c。则△GFC的面积是( )
A.1cm2 B.2 cm2 C.3 cm2 D.4 cm2 (4)点E、F分别在一张长方形纸条ABCD的边AD、BC上,将这张纸条沿着直线EF对折后如图,BF与DE交于点G,如果∠BGD=30°,长方形纸条的宽AB=2cm,那么这张纸条对折后的重叠部分△GEF的面积=______ cm2
(5)如图,红丝带是关注艾滋病防治问题的国际性标志.将宽为1cm的红丝带交叉成60°角重叠在一起,则重叠四边形的面积为_______2.cm
(6)如图,一个四边形花坛ABCD,被两条线段MN、EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1、S2、S3、S4,若MN∥AB∥DC、EF∥DA∥CB,请你写出一个关于S1、S2、S3、S4的等量关系________________________________. 4、折叠、剪切后得图形 (1)将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
A.矩形 B.三角形 C.梯形 D.菱形
E A A A B B B C C C G D D D F F F 图a 图b 图c 实用文档
文案大全 (2)在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是( )
A. B. C. D. (3)小强拿了张正方形的纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )
(4)将一圆形纸片对折后再对折,得到图1,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( )
(5)如图1所示,把一个正方形三次对折后沿虚线剪下,则所得的图形是( )
(6)如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,AD=BC. 将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平面四边形,则能拼出互不全等的四边形的个数是( ) A. 1 B. 2 C. 3 D. 4
ABCD
图3图1 实用文档
文案大全 (7)如图7所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是( )
5、折叠后得结论 (1)亲爱的同学们,在我们的生活中处处有数学的身影.请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于_______°.”
(2)从边长为a的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( ) A.a2–b2 =(a+b)(a-b) B.(a–b)2 = a2–2ab+b2
C.(a+b)2 = a2 +2ab+ b2 D.a2 + ab = a (a+b)
(3)如图,一张矩形报纸ABCD的长AB=a cm,宽BC=b cm,E、F分别是AB、CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a∶b等于( ).
A.1:2 B.2:1 C.1:3 D.3:1
6、折叠和剪切的应用 (1)如图,有一个边长为5的正方形纸片ABCD,要将其剪拼
成边长分别为ab,的两个小正方形,使得2225ab.①ab,的值可以是________(写出一组即可);②请你设计一种具有一般性的裁剪方法,在图中画出裁剪线,并拼接成两个小正方形,同时说明该裁剪方法具有一般性: _____________________________________________________________ _____________________________________________________________
(1) (2) A. B. C. D. D C
B A 实用文档
文案大全 _____________________________________________________________ (2)如图,已四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到:__________(用“能”或“不能”填空)。若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由。 ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ ____________________________________________________ (3)如图,已知五边形ABCDE中,AB//ED,∠A=∠B=90°, 则可以将该五边形ABCDE分成面积相等的两部分的直线 有__________条,满足条件的直线可以这样趋确定: ____________________________________________________ ____________________________________________________ ____________________________________________________
(4)如图,有一个边长为a的正六边形纸片ABCDEF.①六边形ABCDEF的外接圆半径与内切圆半径之比为_____________;②请你设计一种用剪刀只剪两刀将其拼为一个矩形(在图中画出裁剪线),叙述裁剪过程并简要说明得到的矩形是否是正方形: __________________________________________________ __________________________________________________ __________________________________________________ __________________________________________________ __________________________________________________
(5)如图,有一个长:宽=2:1的长方形纸片ABCD.①含有30°、60°的直角三角形最短边与最长边之比为___________;②请你设计一种折叠一次使这张纸片出现30°和60°(在图中画出折叠线和折叠后图线),叙述折叠过程并简要说明理由: __________________________________________________ __________________________________________________ __________________________________________________ __________________________________________________
(6)如图,有一个长方体的底面边长分别是1cm和3cm,高为6cm.①现用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么细线最短需要________cm;②若从点A经过开始经过3个侧面缠绕n圈到达点B,此时细线最短需要____________________cm.③若有一个长方体的边长为a的正方形,高为b,那么细线从点A到点C的最短距离: __________________________________________________________ __________________________________________________________
