BP神经网络与模糊控制在检测系统中的应用 (现代测试技术论文)
BP神经网络研究综述【文献综述】

文献综述电气工程及自动化BP神经网络研究综述摘要:现代信息化技术的发展,神经网络的应用范围越来越广,尤其基于BP算法的神经网络在预测以及识别方面有很多优势。
本文对前人有关BP神经网络用于识别和预测方面的应用进行归纳和总结,并且提出几点思考方向以作为以后研究此类问题的思路。
关键词:神经网络;数字字母识别;神经网络的脑式智能信息处理特征与能力使其应用领域日益扩大,潜力日趋明显。
作为一种新型智能信息处理系统,其应用贯穿信息的获取、传输、接收与加工各个环节。
具有大家所熟悉的模式识别功能,静态识别例如有手写字的识别等,动态识别有语音识别等,现在市场上这些产品已经有很多。
本文查阅了中国期刊网几年来的相关文献包括相关英文文献,就是对前人在BP神经网络上的应用成果进行分析说明,综述如下:(一)B P神经网络的基本原理BP网络是一种按误差逆向传播算法训练的多层前馈网络它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阀值,使网络的误差平方最小。
BP网络能学习和存贮大量的输入- 输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程.BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer),如图上图。
其基本思想是通过调节网络的权值和阈值使网络输出层的误差平方和达到最小,也就是使输出值尽可能接近期望值。
(二)对BP网络算法的应用领域的优势和其它神经网络相比,BP神经网络具有模式顺向传播,误差逆向传播,记忆训练,学习收敛的特点,主要用于:(1)函数逼近:用输入向量和相应的输出向量训练一个网络以逼近一个函数;(2)模式识别:用一个待定的输出向量将它与输入向量联系起来;(3)数据压缩:减少输出向量维数以便于传输或存储;(4)分类:把输入向量所定义的合适方式进行分类;]9[BP网络实质上实现了一个从输入到输出的映射功能,,而数学理论已证明它具有实现任何复杂非线性映射的功能。
BP神经网络与模糊控制在隧道施工中的预测与应用

文 。 李怀 国 ( 贵州省 交通规划勘察设计研 究院 贵 阳)
函
工 进 度的 需 要 ,为 隧 道 的施 工 提供 准 确 可 靠 的地 质 资料 ;O 位移 监 测 ,包括 周 边 3 收 敛和 拱 顶 下沉 位 移 监 测 ,拱 顶 下沉 测 线 布 置 ,测 线 布 置和 数 量 与地 质 条件 、开 挖 方 法 、位 移 速度 有 关 。 根据 设 计 文件 提 供 的 信 息 ,确 定采 用 下 图所 示 测 线布 置 。 项 糊 控 制 技 术 对 隧 道 的 掘 进 过 程 进 行 施 工 控 目开 展后 再 依情 况 调 整 。 周边 收 敛一 般 地 制 。 通 过 对 比 , 发 现 用 本 文 的 方 法 进 行 预 段应 采用 2~3条测 线 ,但拱脚 处必须 有一 测 与 实际 情 况 基本 吻合 ,研 究成 果 为 隧道 条 水 平 测 线 。若 位 移 值 较 大 或 偏 压 显 著 , 掘 进过 程 中的施 工控 制 和 预测 预 报提 供 了 可 同时 进 行 绝 对 位移 量测 。 新 的 思路 。 四 、隧 道 施 工 前 期 的 数据 分析 关键 词 :隧道 ;拱 顶 下沉 ;1P神 经 网 3 根 据 现场 施 工 条件 及 地 质 条件 ,该 工 络 ; 模 糊 逻 辑 控 制 程 采 用新 奥 法施 工 ,对 地 质条 件 复杂 、稳 引 言 定 性极 差 的 岩 层地 段 进 行重 点监 测 ,选 择 B P 神 经 网络 是 使用 最 为广 泛 的人 工 此 范 围 内的 断 面 z K 2 + 8 3 0 、 l 6 6+8 40、 ZK 21 6+8 50、 ZK21 +86 6 0、 神 经 网络 之一 ,它具 有 较 强的 非 线性 动 态 ZK2l 处 理能 力 ,无 需 知道 变 形 与 力学 参数 之 间 Z K 2 16+ 8 7 0 重 点进 行 研 究 。断 面 的 关 系 ,可 实现 高 度非 线性 映 射 ,其较 强 Z 1 + K2 6 8 0处拱顶下沉 的时 间曲线 比较典 3 的 学 习 、存储 和 计算 能 力 ,特 别 是 较强 的 型 ,拱 顶 测 点随 着 时 间 的增 长 ,累计 拱 顶 容 错 特 性 ,适 用 于 从 实 例 样 本 中提 取 特 下 沉量 逐 渐 增大 ( 顶 向下 沉 降位 移 值 小 拱 征 ,获 取 知识 ,从而 较 好 地表 达 位移 和 力 干 零 ,本 文 将神 经 网 络 与模 糊控 制 器 技 术 学 参数 间 的隐 式非 线 性 映射 关 系 ,人工 神 结 合起 来 ,通过 模 拟 训 练 ,得 到 理想 的 神 经 网络 近 年来 在土 建 方 面应 用 较 多 ,其 主 经 网络 参 数 和模 糊 逻辑 准则 ,然 后用 于 位 要优 点 是 无须 建 立输 入 值 与输 出值 之 间 具 移 预 测 和 施 工监 控 。 体 的数 学 力学 关 系式 ,只 需通 过 对 样本 值 五 、神 经 网 络 计 算 原 理 的 训练 和 学 习得 到 网络 的 最佳 连接 权 值 和 BP 神 经 网络 模型是 当前应 用最广 泛 闽值 ,并 通过 新 的样 本 值对 上 述模 型进 行 也 是发 展 最 成熟 的 一 种 网络 模 型 ,通 常 由 检验 ,若 检验 合格 ,便 成 功得 到 了 预期 的 输 入 层 、输 出 层和 隐 含 层构 成 。 层与 层 之 人 工神 经 网络 模 型 ,并 可 以用 来 进行 下 一 间 的神 经 采 用全 互 连 的连 接 方式 ,通 过 相 步 的 预测 预 报 。 应 的网络 权 系数 w 相互 联 系,每 层内 的神 二 、工 程 概 况 经 元之 问没 有连 接 。 网 络结 点 作 用 函数 有 全长 59公里的攀 田高速 公路 ,北接 西 很 多 ,本文 采 用较 常用 的 S 型逻 辑非 线性 昌至 攀 枝 花 高 速 公路 ,南 接 云 南 省 永 仁 函数 。 ( 川滇界 )至 元谋高 速公 路 ,被誉 为 “ 南方 通 过训 练 和 学 习 , 可确 定 网络 的 连接 丝 绸 之路 ”贸 易通 道 ,为 交 通部 规 划 的 8 权 值和 阈 值 等参 数 ,这样 ,也 就 确定 了输 条西 部 大通 道 之一 的 甘肃 兰州 至 云 南 入 向量 与输 出 向量 的映 射 关 系 然后 ,将 磨憨 口岸 公路 的核心路段 ,总投资 2 8亿 新 的输 入 输 出样 本 值代 入 上述 神 经 网络 6. 元人民币 。其中全长 2 8米的望江 岭隧道 模 型进 行 验证 。验 证 合格 的 神 经 网络 模 型 84 洞身 最大埋 深约 3 ,为 全线 最长 的一 即 为 所 需 。 0m 2 条 隧 道 ,是 四 川 与 云 南 接 壤 处 的 最 大 隧 六 、控 制 器 的 实 时 控 制 道 ,该 隧道 下穿 l 8国道 ,全线 范 围内地 0 人 工神 经 网 络 与模 糊 控制 理 论 的结 合 质 条件 极其 复 杂 :软 质 岩受 地 质 卸荷 影 响 延 伸 了传 统 模糊 控 制理 论 和 神 经 网络 技术 较重 、陡倾 状 裂 隙岩 体破 碎 、岩 层稳 定 性 的 功能 ,使 得模 糊 控 制理 论 的应 用 范 围得 极差 等 复 杂的 地 质地 貌特 征 ,施 工难 度 最 到 拓展 ,本 文应 用 模糊 逻 辑 控制 理 论 进行 为艰 巨 ,被列 入重 点 控制 性 工 程进 行 科技 实 际隧 道 工程 的 施 工控 制 。 将总 位 移 值 和 攻关。 位移 变化 量 ( 后 两次 总位 移差 值 ) 为输 前 作 三 、 隧道 施 工 过 程 中 的监 测 项 目 入 变量 ,通过 模 糊 控制 器可 推得 相 应 的施 隧道 掘 进过 程 中 的监 测项 目主 要有 以 工控 制 方案 ,从 而 达 到控 制 隧洞 变 形 的 目 下几 项 :C l隧道 初 期 支护 背后 回填质 量 的 。隶 属 度 函数 的 确定 是 模 糊控 制 器 处理 监 测 ,针对 I 、I I类围岩的 初期 支护背后 问题的关键步骤 ,本文采用 MATLAB6.1 I I 回填 质量 ,采 用地 质 雷达 技 术 按三 条纵 线 模糊 逻 辑 工具 箱 提 供的 中间 对称 型 隶 属度 进行 背后 空 洞情 况 检 测 , 同时 采用 该 技 术 函 数 : 按每 5 m 一 个断面 ( 0 布置 7个 点 )检测 喷 射 混凝 土 厚度 及其 背 后空 洞情 况 ;o 按 2 u ( Ik l a 。,b (> , > 为正 照施 工设 计 条 件和 国 家及 交通 部 现 行 的物 探 、勘查 等 技 术标 准 、规 范 进 行地 质超 前 偶数 ) () 7 预 报 工作 ,探 明隧 道 掌子 面 前 方是 否有 断 本 文以 大 量的 隧 道 监测 资 料 和施 工 经 层、 暗河及煤 层等不 良地 质 ,满 足隧道施 验 为依 据 ,并 重 点 总结 了隧 道前 期 的监 测
基于BP算法的模糊神经网络控制系统的仿真实现

基于BP算法的模糊神经网络控制系统的仿真实现随着计算机和控制技术的不断发展,控制系统的设计也越来越受到关注。
基于BP算法的模糊神经网络控制系统是一种新型的控制方法,可以有效解决传统控制方法难以解决的问题。
在本篇文章中,我们将介绍基于BP算法的模糊神经网络控制系统的仿真实现。
1. BP算法简介BP算法是一种常见的人工神经网络训练算法,它是一种迭代算法,通过不断调整权值来实现网络的训练。
BP算法的基本思想是利用梯度下降求出网络误差函数的最小值。
在模糊神经网络中,BP算法可以用于训练输入输出关系的映射。
通过训练可以得到网络的权值和阈值,使得网络能够更好地拟合输入输出映射。
2. 模糊神经网络控制系统模糊神经网络控制系统是一种强大的控制方法,它将模糊控制和神经网络控制相结合,能够有效地处理模糊性问题和非线性问题。
模糊神经网络控制系统将模糊控制器和神经网络控制器相结合,用模糊控制器处理模糊性问题,用神经网络控制器处理非线性问题。
3. 仿真实现在仿真实现中,我们以飞行控制系统为例,设计了一个基于BP算法的模糊神经网络控制系统,该系统包含一个模糊控制器和一个BP神经网络控制器。
模糊控制器将输入的误差和误差变化率转化为模糊量,然后根据模糊规则得到输出控制量。
BP神经网络控制器通过训练得到输入输出映射,进而对输出控制量进行优化。
我们通过MATLAB软件进行仿真,将仿真结果与经典控制方法进行对比,发现基于BP算法的模糊神经网络控制系统具有更好的控制性能和更强的鲁棒性。
在控制飞行器的姿态过程中,基于BP算法的模糊神经网络控制系统具有更快的响应速度和更小的稳态误差。
4. 总结基于BP算法的模糊神经网络控制系统是一种强大的控制方法,能够有效地解决传统控制方法难以解决的问题。
在仿真实现中,我们设计了一个基于BP算法的模糊神经网络控制系统,得到了良好的控制效果,这也表明了该方法的可行性和优越性。
在实际应用中,我们需要对系统进行优化和调试,以达到更好的控制效果。
bp神经网络的应用综述

bp神经网络的应用综述近年来,人工神经网络(ANN)作为一种神经网络形式在不断发展,因其计算能力强,对现实世界较好地识别和适应能力,已得到越来越广泛的应用,其中,BP神经网络是最典型的人工神经网络之一。
BP神经网络是指以马尔可夫随机过程为基础的反向传播算法,具有自组织学习、泛化、模糊推理的特点,具有非常广泛的应用场景。
它可以用来解决实际问题。
首先,BP神经网络可以用来解决分类问题。
它可以根据给定的输入向量和输出向量,训练模型以分类相关的输入特征。
这种模型可以用来解决工业控制问题、专家系统任务等。
例如,BP神经网络可以用来识别照片中的面孔,帮助改进自动门的判断等。
此外,BP神经网络还可以用于计算机视觉,即以计算机图像识别的形式进行图像处理。
通常,计算机视觉技术需要两个步骤,即识别和分析。
在识别步骤中,BP神经网络可以被用来识别图片中的特征,例如物体的形状、大小、颜色等;在分析步骤中,BP神经网络可以用来分析和判断图片中的特征是否满足要求。
此外,BP神经网络还可以用于机器人技术。
它可以用来识别机器人环境中的物体,从而帮助机器人做出正确的动作。
例如,利用BP神经网络,机器人可以识别障碍物并做出正确的行动。
最后,BP神经网络还可以用于未来的驾驶辅助系统中。
这种系统可以利用各种传感器和摄像机,搜集周围环境的信息,经过BP神经网络分析,判断当前环境的安全程度,及时采取措施,以达到更好的安全驾驶作用。
综上所述,BP神经网络具有自组织学习、泛化、模糊推理的特点,拥有非常广泛的应用场景,可以用于分类问题、计算机视觉、机器人技术和驾驶辅助系统等。
然而,BP神经网络也存在一些问题,例如训练时间长,需要大量的训练数据,容易受到噪声攻击等。
因此,研究人员正在积极改进BP神经网络,使其能够更好地解决各种问题。
BP神经网络和模糊时间序列组合预测模型及其应用

Co mp st r d ci n mo e fBP n u a e wo k n o i p e ito d l0 e r ln t r s a d e
f z i e s re nd is a uz y tm e isa t ppl a in i to c
0 引 言
人工 神经网络具有很强的非线性映射 能力 , 通过 各神经
元 的 自学 能力实现样 本数 据的输 入与输 出间 的非线性关 系 , 它 已广 泛应 用于矿产开发 、 农业 病虫 害预测及农 产 品品质检 测等领域 , 并且取 得 了较好 的 预测 效果 。在 实 际应用 中 , P B 神经 网络及其改 进形 式是经常被采用的神经 网络模型 。 模 糊理论本身具有语 义变量 蕴含特性 , 以减少 在处理 可 具体 问题 时可能出现不 确定性 的 困扰 。因此 , 目前模糊 理论 已经 被广泛地用预测方法 与模型领域 。1 9 9 3年 S n og等人 ” 提 出了模 糊时间序列模 型; 着他们 又提 出了一个新 的模糊 接
基于神经网络的模糊控制系统设计与实现

基于神经网络的模糊控制系统设计与实现随着科技的不断发展,应用人工智能技术来解决问题已经成为趋势。
其中,神经网络和模糊控制系统是两个比较常用的技术,二者结合起来也是很有前途的。
一、神经网络神经网络是模拟人类神经系统的一种计算模型。
它由许多简单的神经元组成,这些神经元之间通过连接进行信息传递,从而实现了模式识别、分类、回归等功能。
通俗地说,就是让计算机模拟人脑的思维方式。
神经网络有很多种结构和算法,其中比较常用的是多层感知机(Multi-layer Perceptron,MLP)。
MLP是一种前向反馈神经网络,由输入层、隐藏层和输出层组成,如图1所示。
图1 MLP网络结构示意图其中,输入层和输出层很好理解,而隐藏层则是用来处理输入与输出之间的关系,其中每个神经元计算的结果会被传递给下一层。
MLP是一种有监督学习算法,即需要给定训练集和对应的目标输出,通过反向传播算法来训练神经网络,不断调整权重和偏置,从而减小预测输出与真实输出之间的误差。
在训练完成以后,神经网络可以用来进行预测,从而实现分类、预测等任务。
二、模糊控制系统模糊控制系统是一种基于模糊数学理论的控制系统。
不同于传统控制系统中的明确的控制规则和精确的数学模型,模糊控制系统通过模糊集合、模糊逻辑来处理模糊信息,从而实现控制目标。
通俗地说,就是将现实世界中的模糊概念映射到数学空间中,通过对模糊概念的描述和处理来实现控制。
例如,温度控制系统可以被描述为“当室内温度较低时,加热器应该加热;当室内温度较高时,加热器应该停止加热”这样一个模糊规则库,从而实现对室内温度的控制。
模糊控制系统有很多算法和方法,其中最常用的是基于 Mamdani 模型的模糊控制系统。
Mamdani 模型将输入变量和输出变量用模糊集合来描述,通过一系列的 IF-THEN 规则来实现模糊控制,具体结构如图2所示。
图2 Mamdani 模糊控制系统结构示意图其中,输入变量被映射到它们各自的模糊集合上,每个输入变量都有自己的隶属函数来描述模糊集合的特征。
BP神经网络在质量控制中的应用
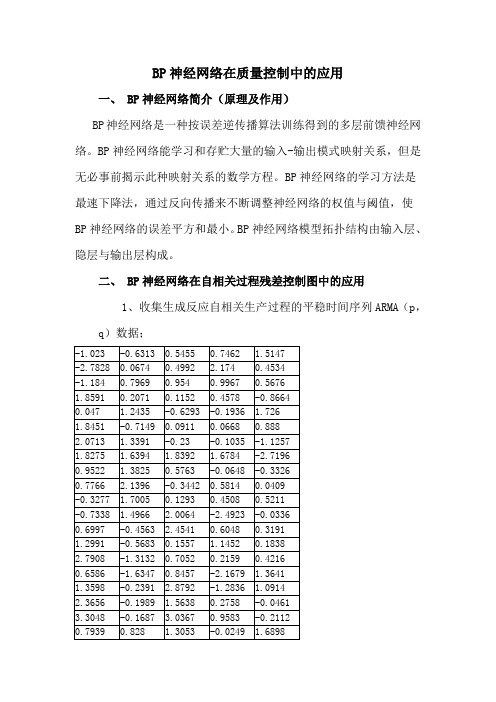
BP神经网络在质量控制中的应用一、 BP神经网络简介(原理及作用)BP神经网络是一种按误差逆传播算法训练得到的多层前馈神经网络。
BP神经网络能学习和存贮大量的输入-输出模式映射关系,但是无必事前揭示此种映射关系的数学方程。
BP神经网络的学习方法是最速下降法,通过反向传播来不断调整神经网络的权值与阈值,使BP神经网络的误差平方和最小。
BP神经网络模型拓扑结构由输入层、隐层与输出层构成。
二、 BP神经网络在自相关过程残差控制图中的应用1、收集生成反应自相关生产过程的平稳时间序列ARMA(p,q)数据;-1.023 -0.6313 0.5455 0.7462 1.5147-2.7828 0.0674 0.4992 2.174 0.4534-1.184 0.7969 0.954 0.9967 0.56761.8591 0.2071 0.1152 0.4578 -0.86640.047 1.2435 -0.6293 -0.1936 1.7261.8451 -0.7149 0.0911 0.0668 0.8882.0713 1.3391 -0.23 -0.1035 -1.12571.8275 1.6394 1.8392 1.6784 -2.71960.9522 1.3825 0.5763 -0.0648 -0.33260.7766 2.1396 -0.3442 0.5814 0.0409-0.3277 1.7005 0.1293 0.4508 0.5211-0.7338 1.4966 2.0064 -2.4923 -0.03360.6997 -0.4563 2.4541 0.6048 0.31911.2991 -0.5683 0.1557 1.1452 0.18382.7908 -1.3132 0.7052 0.2159 0.42160.6586 -1.6347 0.8457 -2.1679 1.36411.3598 -0.23912.8792 -1.2836 1.09142.3656 -0.1989 1.5638 0.2758 -0.04613.3048 -0.1687 3.0367 0.9583 -0.21120.7939 0.828 1.3053 -0.0249 1.68982、用自相关或偏自相函数判断其自相性;自相关函数: C3滞后 ACF T LBQ1 0.402804 4.03 16.722 0.101053 0.88 17.783 0.013824 0.12 17.804 0.103236 0.89 18.935 0.010944 0.09 18.946 -0.085554 -0.73 19.747 -0.119216 -1.01 21.308 -0.077815 -0.66 21.979 0.039590 0.33 22.1410 0.144187 1.21 24.5011 0.266638 2.20 32.6512 0.101412 0.80 33.8413 -0.102219 -0.80 35.0714 -0.114110 -0.89 36.6115 -0.036642 -0.28 36.7716 -0.124414 -0.96 38.6517 -0.236740 -1.81 45.5418 -0.194370 -1.44 50.2419 -0.169470 -1.23 53.8520 -0.181176 -1.30 58.0421 -0.021112 -0.15 58.1022 0.031273 0.22 58.2323 -0.005770 -0.04 58.2324 -0.084652 -0.60 59.1925 -0.050194 -0.35 59.53C3 的自相关自相关函数拖尾偏自相关函数: C3滞后 PACF T1 0.402804 4.032 -0.073050 -0.733 -0.000516 -0.014 0.125802 1.265 -0.095023 -0.956 -0.075121 -0.757 -0.049732 -0.508 -0.025613 -0.269 0.100444 1.0010 0.129852 1.3011 0.212013 2.1212 -0.101057 -1.0113 -0.190027 -1.9014 -0.053501 -0.5415 -0.030070 -0.3016 -0.105012 -1.0517 -0.069409 -0.6918 0.014053 0.1419 -0.126045 -1.2620 -0.185761 -1.8621 0.090942 0.9122 -0.042419 -0.4223 -0.023667 -0.2424 0.012443 0.1225 -0.001695 -0.02C3 的偏自相关偏自相关拖尾3、用神经网络建立过程的时间序列模型并计算出残差序列程序如下:clear all;clc;x=randn(100,1);y=zeros(100,1);a(1)=0.2;a(2)=0.6;b=0.3;y(1)=a(1)+x(1);for n=2:100y(n)=a(1)+a(2)*y(n-1)+x(n)-b*x(n-1);endyfor j=1:100y(j)=(y(j)-min(y))/(max(y)-min(y)); %归一化处理endfor i=1:97P(:,i)=[y(i),y(i+1),y(i+2)]endT=y(4:100)T=T'net=newff([0 1;0 1;0 1],[5,1],{'tansig','logsig'},'traingd'); net.trainParam.epochs=15000;net.trainParam.goal=0.01;net.trainParam.lr=0.1;net=train(net,P,T);figure(1);title('原时间序列“+”与预测时间序列“*”')plot(1:length(T),T,'+-',1:length(t1),t1,'-*')e=T-t1e=e'figure(2);%title('残差时间序列')plot(1:length(T),e,'+-')figure(3);title('残差直方图')histfit(e)0.2366 -0.1103 -0.1347 0.0955 -0.2325-0.2022 0.0982 -0.2208 -0.0528 0.4290.1373 -0.3146 0.0455 0.0304 -0.0720.0421 0.141 -0.1098 -0.033 -0.26720.1186 -0.0118 0.2591 0.3786 -0.528-0.0244 0.0773 -0.1636 -0.1394 -0.3301-0.0334 0.2119 -0.2117 0.1149 -0.2868-0.1985 0.106 0.0163 0.0122 0.1711-0.1802 0.102 0.2793 -0.5816 -0.19590.1525 -0.2415 0.2005 0.3676 0.00480.0551 -0.1765 -0.1366 0.0093 -0.34290.2826 -0.2238 -0.0147 0.0284 0.082-0.1092 -0.1699 -0.0041 -0.499 0.42020.0545 0.091 0.3523 -0.0172 -0.06470.1789 -0.0488 0.038 -0.0458 -0.54320.3439 -0.0845 0.3745 0.1863 -0.3494-0.0301 0.1056 0.1167 -0.0359 0.3699-0.2519 -0.059 0.0907 0.3310.061 -0.0509 0.3782 -0.04710.0566 0.0478 0.1333 0.1134、用minitab软件作残差序列的均值-极差控制图三、BP神经网络在过程运行状态监测中的应用,程序如下:clear all;clc;p=load('p.txt')p=p't=load('t.txt');t=t'net=newff(minmax(p),[13,5],{'tansig','purelin'},'trainlm');net.trainParam.epochs=1500;net.trainParam.goal=0.01;net.trainParam.lr=0.1;net=train(net,p,t);t1=sim(net,p)t1=sim(net,p)IW=net.IW{1,1}LW=net.LW{2,1}b1=net.b{1,1}b2=net.b{2,1}[max_t1,index]=max(abs(t1))a=index[max_t,index]=max(t)b=indexc=a-bIW =0.0640 -0.5101 0.2478 -0.4403 -0.8649 0.18960.0006 -0.1196 0.0979 -0.0657 -0.2098 0.0668-0.0053 0.0410 -0.0702 0.8421 0.3494 -0.09370.0094 -0.1322 -0.5518 0.1521 -0.1917 0.27660.0013 0.0185 -0.2406 -0.7263 -0.0901 0.0174-0.0009 -0.0356 0.8021 0.3594 -0.2108 -0.0675 -0.0024 0.0267 0.1138 -1.5195 0.2918 -0.04690.0044 -0.0443 -0.0628 0.2705 -0.4481 0.0552-0.0037 0.0238 1.1816 0.1243 -1.0187 -0.2500-0.0052 0.0371 0.0803 0.1021 0.3516 -0.0855-0.0055 0.0768 0.0038 -1.2757 0.7139 -0.04330.0068 -0.0272 0.3743 -0.1718 0.3354 -0.35750.0344 -0.2047 -0.0930 0.2048 -0.2176 -0.1199LW =Columns 1 through 90.1376 0.0869 -0.1398 0.4112 -0.2075 0.0110 -0.0962 0.5371 0.0239-0.1376 0.0611 1.3396 -0.5504 0.4445 0.9519 0.4120 0.0603 0.00970.3503 -0.1868 -0.9021 0.1470 0.3105 -1.0563 0.8960 -1.0719 -1.51000.0572 0.1904 -0.3101 -1.2424 0.1771 0.1718 -1.0742 -0.32351.5496-0.1858 -0.5161 -0.0474 -0.1411 -0.3059 0.0009 0.0243 -0.2128 -0.0040Columns 10 through 130.4351 0.2808 -0.3877 0.2027-1.4555 0.0508 0.3579 0.10241.9025 -2.3776 -1.2106 -0.3322-1.4560 1.7723 -0.5082 0.2653-0.0842 -0.0927 -0.3173 0.7161b1 =0.99525.36374.57663.265113.45791.44588.72311.8922-5.27307.5620-8.57463.43124.1175b2 =0.7094-0.0903-0.0619-0.0755-0.5540四、总结。
基于BP神经网络与模糊控制的小麦灌溉系统

基于BP神经网络与模糊控制的小麦灌溉系统目录1. 小麦灌溉系统概述 (3)1.1 内容综述 (4)1.1.1 研究背景与意义 (5)1.1.2 研究现状与不足 (7)1.1.3 研究目的与方法 (8)1.2 小麦灌溉的重要性 (9)1.2.1 合理灌溉对小麦生长的影响 (9)1.2.2 水资源合理利用的现实挑战 (10)1.3 灌溉技术综述 (12)1.3.1 传统的灌溉系统与技术 (13)1.3.2 智能化大规模灌溉系统的需求 (15)2. 模糊控制理论基础 (16)2.1 模糊集与隶属函数 (17)2.1.1 模糊集的基本概念 (18)2.1.2 隶属函数的定义与应用 (19)2.2 模糊推理与决策 (21)2.2.1 模糊推理的规则与结构 (22)2.2.2 模糊决策与控制的朋友技巧 (23)2.3 模糊控制系统的设计原理 (24)2.3.1 设计步骤及注意事项 (25)2.3.2 应用案例分析 (27)3. BP神经网络理论 (28)3.1 神经网络基本原理 (29)3.1.1 前向传播与后向传播 (31)3.1.2 网络结构与学习算法 (31)3.2 BP算法的优化 (33)3.2.1 初始权值的选择 (34)3.2.2 误差反向传播的优化 (35)3.3 BP神经网络在小麦灌溉中的应用优势 (35)3.3.1 自适应学习与泛化能力 (37)3.3.2 实时与在线控制的能力 (38)4. 基于BP神经网络与模糊控制的小麦灌溉系统的设计与实现 (39)4.1 系统总体架构设计 (40)4.1.1 感知层组成与功能 (41)4.1.2 决策层结构与工作原理 (42)4.2 具体实现步骤 (43)4.2.1 确定输入输出参数 (44)4.2.2 定义模糊集的规则 (46)4.2.3 网络训练与规则库更新 (46)4.3 系统的优化与性能评估 (47)4.3.1 系统性能指标的设定 (49)4.3.2 系统优化与调参策略 (49)4.3.3 实际应用案例分析与结果对比 (50)5. 讨论与展望 (51)5.1 基于BP神经网络与模糊控制的小麦灌溉系统优劣分析 (52)5.1.1 系统优势 (54)5.1.2 局限性与挑战 (55)5.2 未来发展方向 (56)5.2.1 技术的进一步优化与改进 (57)5.2.2 更大的应用范围与区域 (59)5.2.3 跨学科的综合研究与应用探索 (60)1. 小麦灌溉系统概述小麦作为全球主要的粮食作物之一,其生长状况直接影响到粮食产量和质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BP 神经网络与模糊控制在火灾探测系统中的应用1 Bp 神经网络1.1 Bp 神经网络的概述BP (Back Propagation )网络是是一种按误差逆向传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。
BP 网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。
它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。
BP 神经网络模型拓扑结构包括输入层、隐含层和输出层。
输入层各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,负责信息变换,根据信息变化能力的需求,中间层可以设计为单隐含层或者多隐含层结构;最后一个隐含层传递到输出层各神经元的信息,经进一步处理后,完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。
当实际输出与期望输出不符时,进入误差的反向传播阶段。
误差通过输出层,按误差梯度下降的方式修正各层权值,向隐含层、输入层逐层反传。
周而复始的信息正向传播和误差反向传播过程,是各层权值不断调整的过程,也是神经网络学习训练的过程,此过程一直进行到网络输出的误差减少到可以接受的程度,或者预先设定的学习次数为止。
1.2 Bp 神经网络的结构及算法BP 网络可以有多层,但为叙述简捷以三层为例导出计算公式。
设BP 网络为三层网络,输入神经元以i 编号,隐蔽层神经元以j 编号,输出层神经元以k 编号,示意图如图1-1所示,其具体形式在下面给出,隐蔽层第j 个神经元的输入为:∑=ii ji j o w net ,第j 个神经元的输出为)(j j net g o =,输出层第k 个神经元的输入为∑=j kj k o w net ,相应的输出为)(k k net g o =,式中g 为sigmoid 型函数,g(x)=)(11)(Θ+-+=x ex g ,式中ʘ为阈值或偏置值。
ʘ˃0则使sigmoid 曲线沿横坐标左移,反之则右移。
因此,各神经元的输出应为∑Θ+-+=i j i ji j o w o )))(ex p(1(1、∑Θ+-+=jk j kj k o w o )))(exp(1(1图1-1 神经网络结构图BP 网络学习过程中的误差反向传播过程是通过使一个目标函数(实际输出与希望输出之间的误差平方和)最小化来完成的,可以利用梯度下降法导出计算公式。
在学习过程中,设第k 个输出神经元的希望输出为pk t ,而网络输出为pk o ,则系统平均误差为∑∑-=p kpk pk o t p E 2)(21,为了表示方便,省去下标p ,平均误差可写成∑-=kk k o t E 2)(21,式中平均误差E 也称为目标函数。
根据梯度下降法,权值的变化项∆kj w 与ƏE/Əkj w 成正比,即∆kj w =-ƞ ƏE/Əkj w ,由上述各公式可得:∆kj w =-ƞ ƏE/Əkj w = j k k k k kjk k k k o o o o t w net net o o E )1()()(--=∂∂∂∂∂∂-ηη,记j k k k k k o o o o t )1()(--=δ,对于隐含层神经元,也可写成∆ji w =-ƞ ƏE/Əji w =i j j jji j j j j o o o o E w net net o o E )1()(-∂∂-=∂∂∂∂∂∂-ηη,)1(j j j j o o o E -∂∂-=δ,由于ƏE/Əj o 不能直接计算,而是以参数的形式表示,即-ƏE/Əj o =-∑∑∑∑∑=∂∂-=∂∂∂∂-=∂∂∂∂kkj k kj k k j j j kj k k j k k k w w net E o o w net E o net net E δ)())(()(,则导出各个权重系数的调整量为∆kj w j k k k k o o o o t )1()(--=η,∆ji w =i j o ηδ,式中ƞ称为学习效率,)]1([j j kkj k j o o w -=∑δδ,)1()(k k k k k o o o t --=δBP 网络的学习算法的具体步骤如下:从训练本集中取某一样本,把它的输入信息输入到网络中由网络正向计算出各层节点的输出计算网络的实际输出与期望输出的误差从输入层起始反向计算到第一个隐层,按一定原则向减小误差方向调整网络的各个联接权值对训练样本集中的每一个样本重复以上步骤,直到对整个训练样本集的误差达到要求为止。
1.3 BP 网络的优缺点多层前向BP 网络的优点:1)网络实质上实现了一个从输入到输出的映射功能,而数学理论已证明它具有实现任何复杂非线性映射的功能。
这使得它特别适合于求解内部机制复杂的问题;2)网络能通过学习带正确答案的实例集自动提取“合理的”求解规则,即具有自学习能力;3)网络具有一定的推广、概括能力。
虽然BP网络得到了广泛的应用,但自身也存在一些缺陷和不足,主要包括以下几个方面的问题。
1)由于学习速率是固定的,因此网络的收敛速度慢,需要较长的训练时间。
对于一些复杂问题,BP算法需要的训练时间可能非常长,这主要是由于学习速率太小造成的,可采用变化的学习速率或自适应的学习速率加以改进。
2)BP算法可以使权值收敛到某个值,但并不保证其为误差平面的全局最小值,这是因为采用梯度下降法可能产生一个局部最小值。
对于这个问题,可以采用附加动量法来解决。
3)网络隐含层的层数和单元数的选择尚无理论上的指导,一般是根据经验或者通过反复实验确定。
因此,网络往往存在很大的冗余性,在一定程度上也增加了网络学习的负担。
4)网络的学习和记忆具有不稳定性。
也就是说,如果增加了学习样本,训练好的网络就需要从头开始训练,对于以前的权值和阈值是没有记忆的。
但是可以将预测、分类或聚类做的比较好的权值保存。
1.4 概述神经网络在检测系统中的应用在检测系统中,利用神经网络的高度并行运算能力,可以实时实现难以用数字计算机技术实现的最优信号处理算法;利用神经网络分布式信息处理和并行处理的特点,可以避开模式识别方法中建模与特征提取的过程,对复杂多部件系统进行故障诊断与分类;利用神经网络高度的非线性描述能力,还可以对传感器的线性特性进行高精度的拟合等等。
2. 模糊控制2.1 模糊控制的概述模糊控制是以模糊集合论、模糊语言变量及模糊推理为基础的一种计算机数字控制。
它基于被控系统的物理特性,模拟人的思维方式和人的控制经验来实现的一种智能控制。
经典控制理论对那些复杂、不能精确建立数字模型的被控对象经常是无能为力的,所以很多人一直在思考,对于这一类被控过程,能否让计算机模拟人的思维方式,接受人的操作规则去进行控制呢?回答是可能的,模糊控制正式源于这种朴素的思想。
2.2 模糊控制的结构与算法模糊控制系统的原理框图如图2-1所示。
图2-1 模糊控制原理框图可以看出其结构与一般计算机数字控制系统基本类似。
只是其控制器为模糊控制器。
模糊控制系统由以下几部分组成:输入输出接口、执行机构、检测装置、被控对象及模糊控制器。
模糊控制器是模糊控制系统的核心,也是模糊控制系统区别于其他自动控制系统的主要标志,下面对模糊控制器三个主要阶段做简要的介绍:2.2.1 输入模糊化模糊化是把系统输入的精确量转化为模糊控制器中所需的模糊量的过程,为了完成输入的模糊化,我们必须知道输入精确值对模糊集的隶属函数(这里不作说明)。
模糊集的个数可根据被控对象的不同而不同,例如,可分成正大,正中,正小,零,负小,负中,负大七种。
隶属函数的形状可根据实际情况而定,要求不高的一般可取三角形或梯形。
2.2.2 模糊推理决策模糊控制器的主要工作是依据语言规则进行模糊推理决策。
因此在进行模糊规则推理之前,先要指定好语言控制规则。
实际上控制规则是根据操作者或专家的经验知识来确定的,它们也可以在试验过程中不断进行修正和完善。
规则的形式很像计算机程序设计语言常用到的条件语句“IF …THEN …”。
模糊控制规则随着模糊控制器的输入输出维数的不同采用不同的形式。
1)单输入单输出型:其控制规则为 IF X=A, THEN Y=B2) 多输入单输出型:其控制规则为 IF X 1=A 1,AND(OR) X 2=A 2,…AND(OR)X N =A N ,THEN Y=B3) 多输入多输出型:IF X 1=A 1, AND(OR) X 2=A 2,…AND(OR)X N =A N ,THEN Y=B 1,AND(OR)Y2=B 2,…AND(OR)Y N =B N这里的AND 和OR 在模糊推理中相应于“交”“并”运算2.2.3逆模糊化输出逆模糊化就是将语言表达的模糊量恢复到精确的数值,也就是根据输出模糊子集的隶属度计算出确定的数值。
下面介绍三种主要的方法1)最大隶属度法:这种方法就是选取模糊子集隶属度最大的元素作为控制量。
如果最大点有几个,则取它们的平均值。
例如有两个模糊子集分别为26.018.002.013.021.01+++-+-=U ,28.0110115.022.01+++-+-=U ,在U1中,元素1的隶属度最大,则取u=1为输出量;而在U2中,元素0和1的隶属度都为最大,则取u=(0+1)/2=0.5作为输出量。
选择最大隶属度方法简单易行,算法实时性好,但它利用的信息量较少,会引起一定的不确定性。
2)加权平均法:此法又称重心法,有两种形式。
第一种是普通加权平均法,其控制量的精确值u 由下式决定:∑∑===n i in i i iu u u u 11)()(μμ.第二种是算术加权平均法,其控制量的精确值u 由下式求出: ∑∑===n i in i ii ku k u 11,其中k 的选择可根据实际情况来决定。
3)取中位法:为了充分利用所有信息,求出将模糊集隶属函数曲线与横坐标之间的面积平分为两等的数,用此数作为逆模糊化的结果。
模糊控制的算法步骤1)根据当前采样得到的系统的输出值,计算所选择的系统的输入变量2)将输入变量的精确值变为模糊量,即模糊化处理3)根据输入模糊变量及模糊控制规则,按模糊推理合成规则计算控制模糊量,即进行推理决策4)由上述得到的控制模糊量计算精确的控制量,即模糊化处理2.3 概述模糊控制在检测系统中的应用模糊数学模仿人脑逻辑思维的特点进行分析判断,具有对不确定性,不完全模糊信息的处理能力,能获取并融合多源信息。
对于涉及人的自身知识和经验测量问题,传统的检测难以进行,而模糊检测则显示出其独特的优越性。
传统的测量通过试验和计算直接给出被测量的数值描述,但在工程实际中会存在不确定性和复杂性,一些重要的信息难以通过传感器直接测出或通过函数关系间接求出,而只能根据人们的先验知识并经过人脑的推理过程才能得出正确的结论。
