信号分析与处理答案(第二版)
随机信号分析与处理(第2版)

随机信号分析与处理(第2版)概述本文档介绍了随机信号分析与处理(第2版)的主要内容。
随机信号是一种在时间上或空间上具有随机性质的信号,在诸多领域中都有广泛的应用,如通信、图像处理、控制系统等。
随机信号的分析和处理对于了解其性质、提取有用信息以及设计有效的处理算法都是必不可少的。
主要内容第一章:随机信号的基本概念本章介绍了随机信号的基本概念和特性,包括随机信号的定义、概率密度函数、均值、方差等。
通过对随机信号的特性分析,可以为后续的分析和处理提供基础。
第二章:随机过程本章讨论了随机过程的定义和性质。
随机过程是一类具有随机性质的信号集合,其在时间上的取值不确定,但具有统计规律性。
通过对随机过程的分析,可以了解其演化规律和统计性质。
本章介绍了随机信号的表示与分解方法。
随机信号可以通过不同的数学模型进行表示,如傅里叶级数、傅里叶变换、小波变换等。
通过将随机信号进行分解,可以提取出其中的有用信息。
第四章:随机信号的功率谱密度本章研究了随机信号的功率谱密度。
功率谱密度描述了随机信号在频率域上的分布,通过分析功率谱密度可以获得随机信号的频率特性和频谱信息。
第五章:随机信号的相关与协方差本章讨论了随机信号的相关与协方差。
相关是用来描述随机信号之间的依赖关系,协方差是用来描述随机信号之间的线性关系。
通过分析随机信号的相关与协方差,可以研究信号之间的相关性和相关结构。
本章介绍了随机信号的滤波和平均处理方法。
滤波是用来抑制或增强随机信号中的某些频率分量,平均则是通过对多次采样的随机信号进行求平均来减小随机性。
第七章:随机信号的参数估计本章研究了随机信号的参数估计方法。
参数估计是通过对随机信号进行采样和分析,通过估计参数来了解信号的统计性质和特征。
第八章:随机信号的检测和估计本章讨论了随机信号的检测和估计方法。
检测是用来判断随机信号的存在或不存在,估计是通过对随机信号的采样和分析来估计信号的参数。
第九章:随机信号的最优滤波本章研究了随机信号的最优滤波方法,最优滤波是通过优化设计滤波器来最小化系统误差或最大化输出信噪比。
数字信号处理答案 第二版 刘顺兰6

zk = e
j
2π k N
, k = 0,1,2L, N − 1 。
后一项极点有两个,在: p1 = e
j
2π N
和 p2 = e
−j
2π N
(与前一项的零点抵消) ,零点也
⎛ 2π ⎞ 有两个: z1 = 0 (与前一项的极点抵消) , z2 = cos⎜ ⎟ ⎝ N ⎠
系统级联后,有零极点抵消。为:
H e jω = H ( z ) z = e jω
( )
③画出幅频图 H (e jω ) (略) ④由于级联后系统没有非零的极点 (或因 h (n) 是有限长) , 所以判断系统是 FIR 的。
±j ⎞ ⎟ ;Pole: z = re N ⎠ 2π
1⎛ j N ② h( n) = ⎜ re 2⎜ ⎝
2π
2π ⎞ 1⎛ −j ⎟ u (n) + ⎜ re N ⎟ 2⎜ ⎠ ⎝
n
⎞ 2π ⎞ ⎟ u (n) = r n cos⎛ n ⎟u (n) ⎜ ⎟ ⎝ N ⎠ ⎠
n
H ( e jω ) = H ( z ) z = e j ω =
当 ω = 0 ,或 ω = π 时, H (e jω ) > 2. 补充作业 2:
①求级联后系统的零极点,并画出零极点图。 ②求 h(n) , H (e jω ) ③画出幅频图 H (e jω ) ④判断系统是 IIR 还是 FIR? 解: (本题的零极点图以 N=8 为例) 梳妆滤波器与二阶谐振器级联后的系统函数为:
《数字信号处理》2010-2011-1 作业-6 教材《数字信号处理》 (第二版)刘顺兰
1. 补充作业 1 实用的二阶谐振器,参数作如下修正:
ห้องสมุดไป่ตู้
信号分析与处理 杨西侠 第2章习题答案

2-1 画出下列各时间函数的波形图,注意它们的区别1)x 1(t) = sin Ω t ·u(t )2)x 2(t) = sin[ Ω ( t – t 0 ) ]·u(t )3)x 3(t) = sin Ω t ·u ( t – t 0 )-14)x2(t) = sin[ ( t – t0) ]·u( t – t0)2-2 已知波形图如图2-76所示,试画出经下列各种运算后的波形图(1)x ( t-2 )(2)x ( t+2 )(3)x (2t)(4)x ( t/2 )(5)x (-t)(6)x (-t-2)(7)x ( -t/2-2 )(8)dx/dt2-3 应用脉冲函数的抽样特性,求下列表达式的函数值(1)⎰+∞∞--)(0t t x δ(t) dt = x(-t 0) (2)⎰+∞∞--)(0t t x δ(t) dt = x(t 0) (3)⎰+∞∞--)(0t t δ u(t -20t ) dt = u(2t )(4)⎰+∞∞--)(0t t δ u(t – 2t 0) dt = u(-t 0) (5)()⎰+∞∞--+t etδ(t+2) dt = e 2-2(6)()⎰+∞∞-+t t sin δ(t-6π) dt =6π+21(7) ()()[]⎰+∞∞-Ω---dt t t t e tj 0δδ=()⎰+∞∞-Ω-dt t etj δ–⎰+∞∞-Ω--dt t t e t j )(0δ= 1-0t j eΩ- = 1 – cos Ωt 0 + jsin Ωt 02-4 求下列各函数x 1(t)与x 2(t) 之卷积,x 1(t)* x 2(t) (1) x 1(t) = u(t), x 2(t) = e -at · u(t) ( a>0 ) x 1(t)* x 2(t) =⎰+∞∞---ττττd t ue u a )()( =⎰-ta d e 0ττ = )1(1ate a--x 1(t)* x 2(t) =ττδτδτπd t t u t )]1()1([)]()4[cos(---+-+Ω⎰+∞∞-= cos[Ω(t+1)+4π]u(t+1) – cos[Ω(t-1)+4π]u(t-1)(3) x 1(t) = u(t) – u(t-1) , x 2(t) = u(t) – u(t-2) x 1(t)* x 2(t) =⎰+∞∞-+-----τττττd t u t u u u )]1()()][2()([当 t <0时,x 1(t)* x 2(t) = 0 当 0<t <1时,x 1(t)* x 2(t) =0td τ⎰ = t 当 1<t <2时,x 1(t)* x 2(t) =21d τ⎰= 1当 2<t<3时,x 1(t)* x 2(t) = 12t d τ-⎰=3-t 当 3<t 时,x 1(t)* x 2(t) = 0(4) x 1(t) = u(t-1) , x 2(t) = sin t · u(t) x 1(t)* x 2(t) =⎰+∞∞---ττττd t u u )1( )( )sin(=⎰⎰∞==01-t 01-t 0| cos - d sin 1)d --u(t sin ττττττ= 1- cos(t-1)2-5 已知周期函数x(t)前1/4周期的波形如图2-77所示,根据下列各种情况的要求画出x(t)在一个周期( 0<t<T )的波形(1) x(t)是偶函数,只含有偶次谐波分量f(t) = f(-t), f(t) = f(t ±T/2)(2) x(t)是偶函数,只含有奇次谐波分量 f(t) = f(-t), f(t) = -f(t ±T/2)(3) x(t)是偶函数,含有偶次和奇次谐波分量f(t) = f(-t)(4) x(t)是奇函数,只含有奇次谐波分量f(t) = -f(-t), f(t) = -f(t±T/2)(5) x(t)是奇函数,只含有偶次谐波分量f(t) = -f(-t), f(t) = f(t±T/2)(6) x(t)是奇函数,含有偶次和奇次谐波分量f(t) = -f(-t)2-6 利用信号x(t)的对称性,定性判断图2-78所示各周期信号的傅里叶级数中所含有的频率分量(a)这是一个非奇、非偶、非奇偶谐波函数,且正负半波不对称,所以含有直流、正弦等所有谐波分量,因为去除直流后为奇函数。
信号分析与处理习题答案(P155)

信号分析与处理习题答案(P155)3、绘图程序:%sinusoidal sequence n=0:29;x=sin(16*pi/5*n+pi/4); stem(n,x);xlabel('n');ylabel('x(n)');title('Sinusoidal sequence'); grid;55825162=∴===N N m序列为周期序列为有理数πππω4、绘图程序:%delta sequencen=[-5 -4 -3 -2 -1 0 1 2 3 4 5]; x=[0 5 0 0 2 0 -4 0 3 0 0]; stem(n,x);xlabel('n');ylabel('x(n)');title('delta sequence'); grid;8、根据DTFT 性质, (1)时域尺度变换特性:连续时间傅里叶变换的尺度变换表示为:⎪⎭⎫ ⎝⎛↔a X a at x ω1)( 然而,在离散时间的情况下,若a 不是整数,x[an]就不是一个序列。
另一方面,如果a 是一个整数,例如a=2,那么x[2n]仅包含x[n]的偶数样点。
因此,离散时间中的时域尺度变换与上式有些不同。
令m 为一正整数,则序列的傅里叶变换为⎩⎨⎧≠===km n kmn k x m n x n x m 0][]/[][)(()a b{})(][][][][)()()()(Ω====∑∑∑∞-∞=Ω-∞-∞=Ω-∞-∞=Ω-m X ek x ekm xen xn x F n km j n kmj m n nj m m所以)(0]/[][)(Ω↔⎩⎨⎧≠==m X km n km n m n x n x m⎪⎭⎫⎝⎛Ω↔a X an x )( (3)时域位移:)(][00Ω↔-Ω-X en n x n j)()1()()()2()(22Ω-=Ω-Ω↔--Ω-Ω-X e X eX n x n x j j10.(2)根据P109式3-26)())(()(1)()()(00101000Ω=Ω+=ΩΩ=∑∑-=Ω--=Ωk X qN k X en x Nk X e k X n x N k njk N k njk根据题意,序列x(n)的基本周期为N=8,Ω0=2π/N=π/4 根据欧拉公式,nj nj njnjee een 002121214cos 44Ω-Ω-+=⎪⎪⎭⎫ ⎝⎛+=πππ则x(n)的傅里叶系数为X(1)=1/2,X(-1)= X(-1+8)= X(7)=1/2,其他系数等于0。
信号分析与处理 杨西侠 第2章习题答案
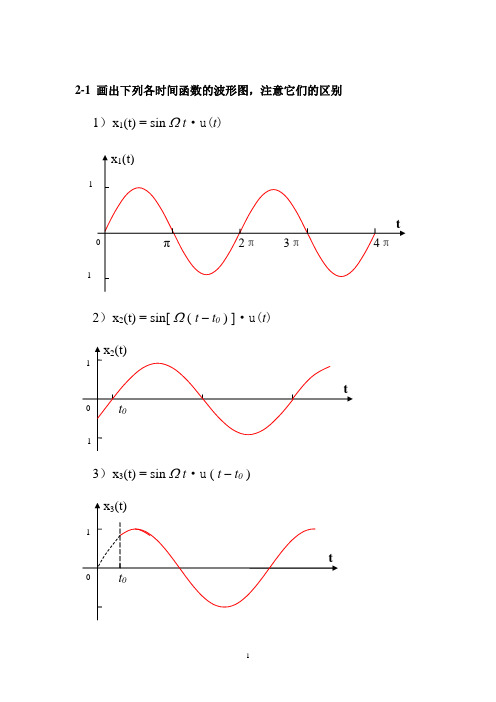
2-1 画出下列各时间函数的波形图,注意它们的区别1)x 1(t) = sin Ω t ·u(t )2)x 2(t) = sin[ Ω ( t – t 0 ) ]·u(t )3)x 3(t) = sin Ω t ·u ( t – t 0 )-14)x2(t) = sin[ ( t – t0) ]·u( t – t0)2-2 已知波形图如图2-76所示,试画出经下列各种运算后的波形图(1)x ( t-2 )(2)x ( t+2 )(3)x (2t)(4)x ( t/2 )(5)x (-t)(6)x (-t-2)(7)x ( -t/2-2 )(8)dx/dt2-3 应用脉冲函数的抽样特性,求下列表达式的函数值(1)⎰+∞∞--)(0t t x δ(t) dt = x(-t 0) (2)⎰+∞∞--)(0t t x δ(t) dt = x(t 0) (3)⎰+∞∞--)(0t t δ u(t -20t ) dt = u(2t )(4)⎰+∞∞--)(0t t δ u(t – 2t 0) dt = u(-t 0) (5)()⎰+∞∞--+t etδ(t+2) dt = e 2-2(6)()⎰+∞∞-+t t sin δ(t-6π) dt =6π+21(7) ()()[]⎰+∞∞-Ω---dt t t t e tj 0δδ=()⎰+∞∞-Ω-dt t etj δ–⎰+∞∞-Ω--dt t t e t j )(0δ= 1-0t j eΩ- = 1 – cos Ωt 0 + jsin Ωt 02-4 求下列各函数x 1(t)与x 2(t) 之卷积,x 1(t)* x 2(t) (1) x 1(t) = u(t), x 2(t) = e -at · u(t) ( a>0 ) x 1(t)* x 2(t) =⎰+∞∞---ττττd t ue u a )()( =⎰-ta d e 0ττ = )1(1ate a--x 1(t)* x 2(t) =ττδτδτπd t t u t )]1()1([)]()4[cos(---+-+Ω⎰+∞∞-= cos[Ω(t+1)+4π]u(t+1) – cos[Ω(t-1)+4π]u(t-1)(3) x 1(t) = u(t) – u(t-1) , x 2(t) = u(t) – u(t-2) x 1(t)* x 2(t) =⎰+∞∞-+-----τττττd t u t u u u )]1()()][2()([当 t <0时,x 1(t)* x 2(t) = 0 当 0<t <1时,x 1(t)* x 2(t) =0td τ⎰ = t 当 1<t <2时,x 1(t)* x 2(t) =21d τ⎰= 1当 2<t<3时,x 1(t)* x 2(t) = 12t d τ-⎰=3-t 当 3<t 时,x 1(t)* x 2(t) = 0(4) x 1(t) = u(t-1) , x 2(t) = sin t · u(t) x 1(t)* x 2(t) =⎰+∞∞---ττττd t u u )1( )( )sin(=⎰⎰∞==01-t 01-t 0| cos - d sin 1)d --u(t sin ττττττ= 1- cos(t-1)2-5 已知周期函数x(t)前1/4周期的波形如图2-77所示,根据下列各种情况的要求画出x(t)在一个周期( 0<t<T )的波形(1) x(t)是偶函数,只含有偶次谐波分量f(t) = f(-t), f(t) = f(t ±T/2)(2) x(t)是偶函数,只含有奇次谐波分量 f(t) = f(-t), f(t) = -f(t ±T/2)(3) x(t)是偶函数,含有偶次和奇次谐波分量f(t) = f(-t)(4) x(t)是奇函数,只含有奇次谐波分量f(t) = -f(-t), f(t) = -f(t±T/2)(5) x(t)是奇函数,只含有偶次谐波分量f(t) = -f(-t), f(t) = f(t±T/2)(6) x(t)是奇函数,含有偶次和奇次谐波分量f(t) = -f(-t)2-6 利用信号x(t)的对称性,定性判断图2-78所示各周期信号的傅里叶级数中所含有的频率分量(a)这是一个非奇、非偶、非奇偶谐波函数,且正负半波不对称,所以含有直流、正弦等所有谐波分量,因为去除直流后为奇函数。
《信号与系统(第2版》【附录+习题答案】

附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
数字信号处理_吴镇扬_第二版_第五章习题答案

5.7 (1)由于h2(n)是h1(n)圆周移位的序列,根据DFT的 2π 性质有: −j 4k − jπ k
H 2 (k ) = e
8
H 1 (k ) = e
H 1 (k )
~ ~ H1 ( k ) = H 2 ( k ) 成立 所以
(2)由于h1 (n ) 和h2 (n ) 均为偶对称序列,以其构成的低通滤波器
(3)若采用海明窗设计,则
⎡ ⎛ 2πn ⎞⎤ wHam ( n) = ⎢0.54 − 0.46 cos ⎜ ⎟ ⎥ RN ( n ) ⎝ N − 1 ⎠⎦ ⎣ 2 h( n) = sin[(n − α )ωc ]cos[(n − α )ω0 ]wHam (n) N 为奇数时, (n − α )π
h( n N 为偶数时, ) =
0 −ωc
e − jωα e jω nd ω
可见h(n)关于(N-1)/2偶对称,即 h( n) = h( N − 1 − n)
(1)当 N 为奇数时,为第一类滤波器。 (2)当N为偶数时,为第二类滤波器
⎧hd ( n) h( n) = hd ( n) ⋅ R(n ) = ⎨ ⎩0 0 ≤ n ≤ N −1
解:由经验公式可知若 不小于 At 40dB , 则
β = 0.5842 At - 21)0.4 + 0.07886(At - 21) ≈ 3.3953 ( At − 8 40 − 8 N= = ≈ 22.28 2.286∆ω 2.286× 0.2π ωc + ωr ωc′ = = 0.2π 2 ′ ⎧ωc ′ ⎪ π Sa[ωc (n − α )] n ≠ α ′ 1 ωc − jωα jωn ⎪ hd (n) = ∫ ′ e e dω = ⎨ ′ 2π −ωc ωc ⎪ n =α ⎪ ⎩ π
信号分析与处理答案及考点提要
令y(n) = x1(n) + jx2(n)
3.解:(1)直接-I型结构:
(2)直接-II型结构:
(3)级联型结构:
(4)并联型结构
4.解:
(1)求阶数 。
带入 的计算公式得:
,所以取 =5
(2)求归一化系统函数 。由阶数 =5直接查表可得到5阶巴特沃斯归一化低通滤波器系统函数 为:
(3)去归一化,由归一化系统函数 得到实际滤波器系统函数 。
Y(k) = DFT[y(n)],k = 0,1,…, N-1
则X1(k) = DFT[x1(n)] = Yep(k) = 0.5[Y(k)+Y*(N-k)]
X2(k) = DFT[jx2(n)] = Yop(k) = 0.5[Y(k)-Y*(N-k)]
2N点得DFT[x(n)] = X(k)可由X1(k)和X2(k)得到
提示:幅度谱中,在 处:幅值为2;在 处,幅值为1;在 处,幅值为-3!!(一定要画成负的)……另外注意幅度谱是偶函数,所以左右两边关于y轴对称;
画相位谱前,需要把f(t)变换成余弦函数的形式,如上式所示。然后在 处:相位为0;在 处,相位为30度;在 处,相位为-45度(一定要画成负的!)……另外注意相位谱是奇函数,所以左右两边关于原点对称。
利用FFT计算:复乘次数为 ,复加次数为 ;
(1)直接DFT计算:
复乘所需时间
复加所需时间
所以总时间FFT计算: Nhomakorabea复乘所需时间
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章习题参考解答
2.1 求下列系统的阶跃响应和冲激响应。
(1)
解 当激励为时,响应为,即:
由于方程简单,可利用迭代法求解:
, ,
…,
由此可归纳出的表达式:
利用阶跃响应和冲激响应的关系,可以求得阶跃响应:
(2)
解 (a)求冲激响应
,当时,。
特征方程 ,解得特征根为。所以:
…(.1)
通过原方程迭代知,,,代入式(.1)中得:
解得, 代入式(.1):
…(.2)
可验证满足式(.2),所以:
(b)求阶跃响应
通解为
特解形式为 ,,代入原方程有 , 即
完全解为
通过原方程迭代之,,由此可得
解得,。所以阶跃响应为:
(3)
解
(4)
解
当t>0时,原方程变为:。
…(.1)
…(.2)
将(.1)、式代入原方程,比较两边的系数得:
阶跃响应:
2.2 求下列离散序列的卷积和。
(1)
解 用表格法求解
(2)
解 用表格法求解
(3) 和 如题图所示
解 用表格法求解
(4)
解
(5)
解
(6)
解 参见右图。
当时:
当时:
当时:
当时:
当时:
(7) ,
解 参见右图:
当时:
当时:
当时:
当时:
当时:
(8) ,
解 参见右图
当时:
当时:
当时:
当时:
(9)
,
解
(10) ,
解
或写作:
2.3 求下列连续信号的卷积。
(1) ,
解 参见右图:
当时:
当时:
当时:
当时:
当时:
当时:
(2) 和 如图所示
解 当时:
当时:
当时:
当时:
当时:
(3) ,
解
(4) ,
解
(5) ,
解 参见右图。当时:
当时:
当时:
当时:
(6) ,
解
(7) ,
解
(8) ,
解
(9) ,
解
2.4 试求题图2.4示系统的总冲激响应表达式。
解
2.5 已知系统的微分方程及初始状态如下,试求系统的零输入响应。
(1) ;
解 ,,
(2) ; ,
解 ,,
,,可定出
(3) ; ,
解 ,
,,可定出
2.6 某一阶电路如题图2.6所示,电路达到稳定状态后,开关S于时闭合,试求输出响应。
解 由于电容器二端的电压在t=0时不会发生突变,所以。
根据电路可以立出t>0时的微分方程:
, 整理得
齐次解:
非齐次特解:设 代入原方程可定出B=2
,
则:
2.7 积分电路如题图2.7所示,已知激励信号为,试求零状态响应。
解 根据电路可建立微分方程:
当时:
由可定出 ,
根据系统的时不变性知,当时:
当 时:
2.8 求下列离散系统的零输入响应。
(1) ; ,
解
由,, 可定出 ,
(2) ; ,
解
由,, 可定出
.
(3) ; ,,
解 特征方程,,
由
可定出
2.9 求下列离散系统的完全响应。
(1) ;
解 齐次方程通解:
非齐次方程特解: 代入原方程得:
由 可定出
(2) ; ,
解 齐次方程通解:
非齐次方程特解: 代入原方程定出
由 可定出
2.10 试判断下列系统的稳定性和因果性。
(1)
解 因果的;稳定的。
(2)
解 因为冲激响应不满足绝对可和条件,所以是不稳定的;非因果的。
(3)
解 稳定的,非因果的。
(4)
解 不稳定的,因果的。
(5)
解 不稳定的,因果的。
(6) (为实数)
解 时: 不稳定的,因果的;
时: 稳定的,因果的;
时:
不稳定的,因果的。
(7)
解 不稳定的,非因果的。
(8)
解 稳定的,非因果的。
2.11 用方框图表示下列系统。
(1)
(2)
(3)
*2.12 根据系统的差分方程求系统的单位脉冲响应。
(1)
解
当时: ,
由原方程知当时:,由此可定出
(2)
解
当时: 齐次方程的通解为,
由原方程迭代求解可得为:
由此可以定出
*2.13 根据系统的微分方程求系统的单位冲激响应。
(1)
解
当时:,,代入原方程可确定
(2)
解
当时:
代入原方程,比较两边系数得:
*2.14 试求下列系统的零输入响应、零状态响应、强迫响应、自由响应。
(1) ;,,
解 (a)求强迫响应: 假设特解为:
代入原方程,可定出; 则强迫响应
(a)求自由响应:
利用冲激平衡法可知:
可定出;所以
完全解形式:,由定出
即完全响应为:
所以自由响应为:
(b)求强迫响应: 假设特解为:
代入原方程,可定出; 则强迫响应
(c)求零输入响应:
由 可定出
(d)求零状态响应
零状态响应=自由响应+强迫响应-零输入响应
=
综上所求,有:
(2) ;,,
解法一 用z变换求解。方程两边进行z变换,则有:
解法二:时域解法。
求强迫响应:
当时: 即为常值序列,
设特解为,代入原方程可定出
当时:仅在激励作用下,由原方程知,即:
特解在时均满足方程。
求自由响应:
完全解:
由经迭代得:
由可定出完全解中系数为:
则自由响应分量为:
零输入响应:
由 可以定出:
零状态响应:
*2.15 试证明线性时不变系统具有如下性质:
(1) 若系统对激励的响应为,则系统对激励的响应为;
(2) 若系统对激励的响应为,则系统对激励的响应为。
证(1) 已知,根据系统的线性试不变性有:
;令,则有:
证(2) 已知,根据系统的线性试不变性有:
令 则 ,
所以
证毕。
*2.16 考察题图2.16(a)所示系统,其中开平方运算取正根。
(1) 求出和之间的关系;
(2) 该系统是线性系统吗,是时不变系统吗?
(3) 若输入信号是题图2.16(b)所示的矩形脉冲(时间单位:秒),求响应。
解 (1)
由系统
框图可
得
(2) 由输入一输出关系可以看出,该系统不满足可加性,故系统是非线性的。
又因为当输入为时,输出为),故系统是时不变的。
(3) 由输入一输出关系,可以求得输出为图示波形。
*2.17 一个线性系统对的响应为,
(1) 该系统是否为时不变系统?
(2) 该系统是否是因果系统?
(3) 若 a);b),求该系统对每个输入的响应。
解 (1) 当时,输入为输出为
当时,输入为输出为
显然 ,是时变系统。
(2) 当时,如
显然,响应出现于激励之前,所以是非因果系统。
(3) 因为不是LTI系统,所以输出响应不能用来计算。对于线性时变系统,输出响
应可求解如
下:
任意信号仍可分解为冲激函数的和,即有:
因为(这里是的二元函数)
由于系统为线性的,故有:
对于此例有,
当时:
(注意:)
即
当时:
第三章习题参考解答
3.1 求下列信号展开成傅里叶级数,并画出响应相应的幅频特性曲线。
解 (a)
解 (b)
解 (c)
解 (d)
3.2 求题图3.2所示信号的傅里叶变换。
解 (a)
解 (b) 设,
由傅氏变换的微积分性质知:
