常用截面惯性矩与截面系数的计算
抗弯截面系数

截面抵抗矩(1):截面抵抗矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。
主要用来计算弯矩作用下截面最外边的正应力。
工程实际中最常见的弯曲问题是横力弯曲,横截面上不仅有正应力,而且还有切应力。
由于切应力的作用,横截面发生翘曲,平面假设不再成立。
但进一步的理论分析证明,对于跨长与截面高度比 l/h>5的长梁利用公式δ=My/I 来计算其横力弯曲的正应力,所得结果误差甚微,足够满足工程实际需要。
其中W=I/y,W称为抗弯截面系数(又称为截面抵抗矩)。
由于横力弯曲时,梁的弯矩随截面位置变化,Mmax所在截面称为危险截面,最大弯曲正应力发生在弯矩最大的截面上,且离中心轴最远处,该处为危险点。
中和轴的确定1)找出达到极限弯矩时截面的中和轴。
中和轴分为弹性中和轴和塑性中和轴。
弹性状态下的中和轴:整个截面关于经此轴线的截面面积矩为0。
横截面在此轴线弯曲正应力为0。
(中和轴初始定义即为构件弯曲后某一截面的长度没有改变即为没有正应力或者说轴力)(和形心的定义一致,一般情况下中和轴即为形心的一条轴线)截面面积矩:指弹性状态下截面各微元面积与各微元至中和轴距离乘积的积分。
单位mm。
指弹性状态下中和轴一侧截面的面积矩,主要用于计算截面上任意点的剪切应力值。
塑性状态下的中和轴:塑性中和轴为构件截面面积平分线,该中和轴两边的面积相等。
2)弹性状态下截面抵抗矩:如本文开头定义。
其意义在于在弹性状态下计算某一构件断面位置最不利位置的最大应力,该位置应力满足则此位置截面满足计算要求;塑性状态下截面塑性抵抗矩:分别求两侧面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵抗矩。
常用截面抗弯系数公式矩形截面抵抗矩W=bh^2/6圆形截面的抵抗矩W=πd^3/32圆环截面抵抗矩:W=π(D^4-d^4)/(32D)。
常见截面面积、形心和惯性矩抗弯系数公式常见图形的面积、形心和惯性矩表2—2.1序号图形面积形心位置惯性矩(形心轴)123 456。
实心空心及圆环形惯性矩与抗弯截面系数

实心空心及圆环形惯性矩与抗弯截
面系数
部门: xxx
时间: xxx
整理范文,仅供参考,可下载自行编辑
梁的强度条件
1. 纯弯曲梁的最大弯曲正应力:
(1> 等截面直梁,中性轴为横截面对称轴
Wz ——抗弯截面系数
(2> 中性轴不是横截面对称轴,且材料拉压强度不相等
(3> 利用正应力的强度条件可以对梁进行三种不同形式的强度计算:
(a> 校核强度
(b> 选择截面尺寸或型钢号
(c> 确定许可荷载
2. 横力弯曲的梁
注意:
(1> 一般的梁,其强度主要受到按正应力的强度条件控制,所以在选择梁的截面尺寸或确定许可荷载时,都先按正应力强度条件进行计算,然后按切应力强度条件校核。
b5E2RGbCAP
(2> 在弯矩为最大的横截面上距中性轴最远点处有最大正应力;在剪力为最大的横截面的中性轴上各点处有最大切应力。
p1EanqFDPw 轴惯性矩及抗弯截面系数
(1> 实心矩形的惯性矩及抗弯截面系数
(2> 空心矩形的惯性矩及抗弯截面系数
(3> 实心圆截面的惯性矩及抗弯截面系数
(4> 空心圆截面的惯性矩
三角形
bh
惯性矩IIx1bh^3/4
Ixbh^3/36
Ix2bh^3/16
抗弯截面系数W
Wx1bh^2/24
Wx2bh^2/12
申明:
所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
矩形管抗弯截面系数公式

矩形管抗弯截面系数公式哎呀,你问这个问题可真是让我犯了难。
不过,既然是矩形管抗弯截面系数公式,那我就得好好给你讲讲,不能让你失望哦!咱们来聊聊矩形管。
矩形管就是那种长长的,方方正正的管子,你知道吧?它可是我们生活中常见的一种东西。
比如,我们家里的水管、电线管,还有建筑工地上用的脚手架管,都是矩形管。
那么,这个矩形管抗弯截面系数公式究竟是干什么用的呢?简单来说,它就是为了计算矩形管在受到弯曲力作用时,抵抗变形的能力。
听起来挺高深的吧?其实,只要你仔细听我说,一定能明白。
我们要了解什么是抗弯截面系数。
抗弯截面系数就是一个值,用来表示矩形管在受到弯曲力作用时,抵抗变形的能力。
这个系数越大,说明矩形管抵抗变形的能力越强。
而这个系数又是如何计算出来的呢?这就要说到矩形管抗弯截面系数公式了。
这个公式其实很简单,就分为三个部分:第一部分是计算矩形管的惯性矩;第二部分是计算矩形管的截面积;第三部分是将惯性矩除以截面积,得到的就是抗弯截面系数。
好了,我给你讲完了公式,现在轮到你来试试了。
不过,别着急,我先给你举个例子。
假设我们有一个矩形管,它的长度是1米,宽度是0.5米,厚度是0.1米。
那么,我们可以按照以下步骤来计算它的抗弯截面系数:第一步,计算惯性矩。
惯性矩是一个衡量物体抵抗转动能力的物理量。
对于矩形管来说,它的惯性矩等于它的截面积乘以长度的四倍。
所以,这个矩形管的惯性矩为:0.5 * 1 * 4 = 2平方米。
第二步,计算截面积。
对于矩形管来说,它的截面积等于它的宽度乘以厚度。
所以,这个矩形管的截面积为:0.5 * 0.1 = 0.05平方米。
第三步,计算抗弯截面系数。
将惯性矩除以截面积,得到的抗弯截面系数为:2 / 0.05 = 40。
所以,这个矩形管的抗弯截面系数为40。
这只是一个简单的例子。
实际上,矩形管的尺寸和材料可能会有所不同,所以我们需要根据具体情况来计算抗弯截面系数。
不过,只要你掌握了这个公式,就再也不用担心不知道怎么计算矩形管的抗弯截面系数了!矩形管抗弯截面系数公式虽然看起来有点复杂,但其实它就是一个简单的数学问题。
任意截面抗弯截面系数简易计算方法

任意截面抗弯截面系数简易计算方法
本文为“自动机算范例模板“系列原创文档之一。
本文档主要介绍:
如何利用SolidWorks 软件快速计算抗弯截面系数(旧称截面模量)的方法。
理论依据
根据材料力学,抗弯截面系数W X 与截面惯性矩I X 的关系公式如下: 的距离离中性为,其中轴X最远点截面上W max max
y y I X X
计算范例
以图中的型材为例:
在SolidWorks 中点选“评估”→点选需要测量的截面→“剖面属性”。
如下图,在弹出的“截面属性”对话框里,可以找到对应红圈内输出坐标系X 轴的截面惯性矩Lxx (即Ix )和对应Y 轴的截面惯性矩Lyy (即Iy )。
(注:在SolidWorks2018里,截面惯性矩the area moment of inertia 被翻译成了区域惯性矩)
由上图可以看到X 轴的截面惯性矩Ix=Lxx=16818.34mm
4 抗弯截面系数3max mm 22.11211534.16818W ===y I X X 当然熟悉其他三维建模软件的朋友,也可以通过类似的测量方法获得截面惯性矩。
计算结果的评估
找到铝型材的官方数据来验证我们的计算方法是否可靠,铝型材的官方数据如下图。
可以看到截面惯性矩为:3322.112112.1mm cm ,说明本文的计算方法是可靠的。
弯矩截面系数

弯矩截面系数,也被称为截面抵抗矩,是用于衡量结构截面对弯曲荷载的抗性能力的指标。
它是通过计算结构截面的惯性矩和截面模量得到的。
简单来说,弯矩截面系数描述了结构截面抵御弯曲力矩的能力。
弯矩截面系数通常用符号W表示,它的计算公式为:
W = I / y
其中,I是截面的惯性矩,y是截面的极其坐标。
对于一个给定的截面形状,惯性矩I是固定的,因此弯矩截面系数W主要受截面的几何形状和尺寸参数的影响。
一般来说,较大的弯矩截面系数表示截面对弯曲荷载的抗性能力较高,而较小的弯矩截面系数则意味着截面的抗性能力较低。
工程设计中常用弯矩截面系数来评估结构截面的弯曲性能,以确保结构在受到弯曲荷载时具有足够的抵抗能力。
各种截面下极惯性矩
y
dA
y2dA z2dA I z I y
o
A
A
z
y
图形对任一对相互垂直的坐标系的惯性矩之和恒等于此图形对该两轴交点的极惯性矩。
四、惯性半径(Radius of gyration of the area)
iy
Iy A
iz
Iz A
I y I yi
I z I zi
I yz I yizi
(1)两平行轴中,必须有一轴为形心轴,截面对任意两平行轴 的惯性矩间的关系,应通过平行的形心轴惯性矩来换算;
(2)截面图形对所有平行轴的惯性矩中,以对通过形心轴的惯 性矩最小.
6、惯性矩与极惯性矩的关系:
z
I p
2dA
A
( y2 z2 )dA
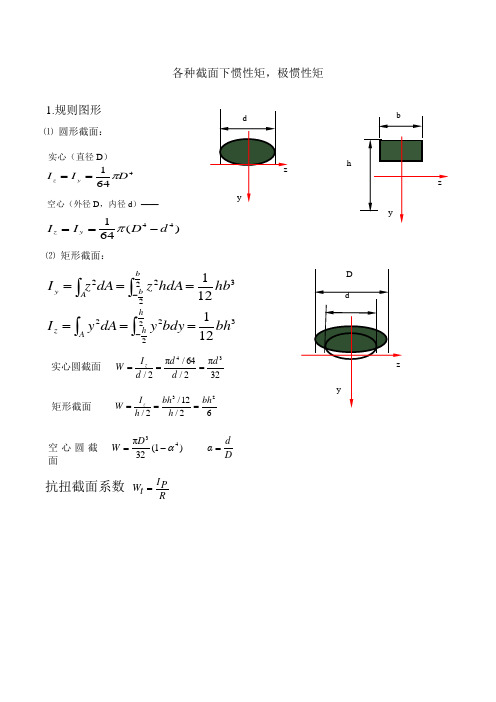
各种截面下惯性矩,极惯性矩
1.规则图形
d
⑴ 圆形截面:
实心(直径 D)
Iz
Iy
1 D4
64
空心(外径 D,内径 d)——
Iz
Iy
1 (D4
64
d 4)
⑵ 矩形截面:
z y
I y
z2dA
A
b
2 b
2
z 2 hdA
1 12
hb3
Iz
y2dA
A
h
2 h
2
y 2bdy
1 bh3 12
实心圆截面 W I z πd 4 / 64 πd 3 d / 2 d / 2 32
矩形截面
W I z bh3 /12 bh2 h/2 h/2 6
空 心 圆 截 W πD3 (1 4 )
面
32
抗扭截面系数
Wt
抗弯截面系数

截面抵抗矩(1):截面抵抗矩(W)就是截面对其形心轴惯性矩与截面上最远点至形心轴距离的比值。
主要用来计算弯矩作用下截面最外边的正应力。
工程实际中最常见的弯曲问题是横力弯曲,横截面上不仅有正应力,而且还有切应力。
由于切应力的作用,横截面发生翘曲,平面假设不再成立。
但进一步的理论分析证明,对于跨长与截面高度比 l/h>5 的长梁利用公式δ=My/I 来计算其横力弯曲的正应力,所得结果误差甚微,足够满足工程实际需要。
其中W=I /y,W称为抗弯截面系数(又称为截面抵抗矩)。
由于横力弯曲时,梁的弯矩随截面位置变化,Mmax所在截面称为危险截面,最大弯曲正应力发生在弯矩最大的截面上,且离中心轴最远处,该处为危险点。
中和轴的确定1)找出达到极限弯矩时截面的中和轴。
中和轴分为弹性中和轴和塑性中和轴。
弹性状态下的中和轴:整个截面关于经此轴线的截面面积矩为0。
横截面在此轴线弯曲正应力为0。
(中和轴初始定义即为构件弯曲后某一截面的长度没有改变即为没有正应力或者说轴力)(和形心的定义一致,一般情况下中和轴即为形心的一条轴线)截面面积矩:指弹性状态下截面各微元面积与各微元至中和轴距离乘积的积分。
单位mm。
指弹性状态下中和轴一侧截面的面积矩,主要用于计算截面上任意点的剪切应力值。
塑性状态下的中和轴:塑性中和轴为构件截面面积平分线,该中和轴两边的面积相等。
2)弹性状态下截面抵抗矩:如本文开头定义。
其意义在于在弹性状态下计算某一构件断面位置最不利位置的最大应力,该位置应力满足则此位置截面满足计算要求;塑性状态下截面塑性抵抗矩:分别求两侧面积对中和轴的面积矩,面积矩之和即为塑性截面模量,也称为塑性抵抗矩。
常用截面抗弯系数公式矩形截面抵抗矩W=bh^2/6圆形截面的抵抗矩W=πd^3/32圆环截面抵抗矩:W=π(D^4-d^4)/(32D)。
常见截面面积、形心和惯性矩抗弯系数公式常见图形的面积、形心和惯性矩表2—2.1序号图形面积形心位置惯性矩(形心轴)1234 5 6。
结构力学公式大全

结构力学公式大全之欧侯瑞魂创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它暗示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边沿到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用截面惯性矩与截面系数的计算
截面惯性矩和截面系数是在工程设计和结构分析中经常使用的参数。
在设计任何结构时,了解截面的惯性矩和截面系数是非常重要的,因为它
们可以帮助工程师确定结构的强度、刚度和稳定性。
截面惯性矩(Moment of inertia)是描述截面对于弯曲的抵抗能力
的一个重要参数。
它表示了截面沿着垂直轴的转动惯性,即截面对于旋转
的抵抗程度。
截面惯性矩的计算可以使用不同的方法,具体取决于截面的
形状和材料。
对于简单形状的截面,如矩形、圆形和等边三角形,可以直接使用公
式来计算惯性矩。
例如,矩形截面(宽度为b,高度为h)的惯性矩可以
通过以下公式计算:
I=(b*h^3)/12
其中^表示乘方运算。
对于复杂形状的截面,可以将其分解为更简单的几何形状,并计算每
个部分的惯性矩。
然后,可以使用平行轴定理将它们合并为整个截面的惯
性矩。
平行轴定理可以使用以下公式表示:
I_total = Σ(I_individual) + A * d^2
其中I_total是整个截面的惯性矩,I_individual是每个部分的惯
性矩,A是每个部分的面积,d是每个部分到整个截面的质心的距离。
截面系数(Section modulus)是用于描述截面对弯曲应力的抵抗能
力的参数。
它表示了截面的特定尺寸和形状对于弯曲应力的敏感程度。
截
面系数的计算通常涉及到截面的惯性矩和截面的最外边缘到中性轴的距离。
对于矩形截面来说,截面系数可以通过以下公式计算:
S=(b*h^2)/6
对于其他形状的截面,可以通过将其分解为简单的几何形状,并计算
每个部分的截面系数,然后将它们合并为整个截面的截面系数。
使用平行
轴定理,可以将每个部分的截面系数合并为整个截面的截面系数。
在实际的工程设计中,截面惯性矩和截面系数经常用于计算截面的抗
弯刚度和承载能力。
在结构设计中,通常使用截面系数来考虑不同形状和
尺寸的截面的性能,以满足设计要求和规范。
总结起来,截面惯性矩和截面系数是结构设计和分析中常用的重要参数。
它们可以用于计算截面的弯曲刚度和抗弯能力。
对于简单形状的截面,可以直接使用公式计算惯性矩和截面系数。
对于复杂形状的截面,可以通
过分解截面为简单形状,并使用平行轴定理来计算整个截面的惯性矩和截
面系数。
这些参数在工程设计中的应用非常广泛,可以帮助工程师确定结
构的性能和稳定性。
