T型截面形心及惯性矩系数
惯性矩、静矩,形心坐标公式
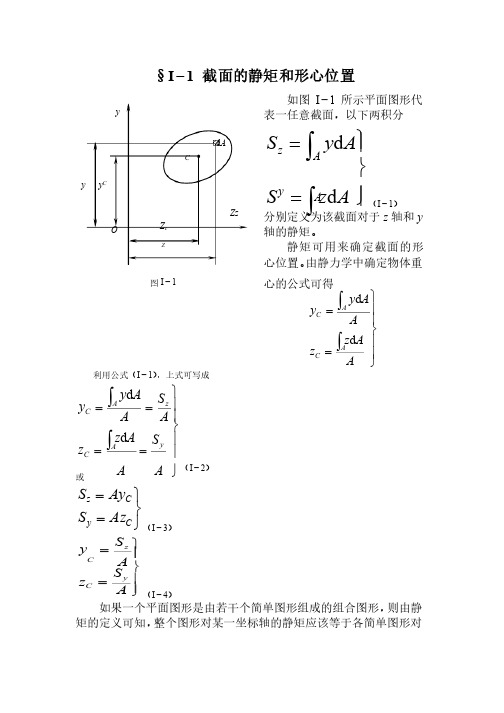
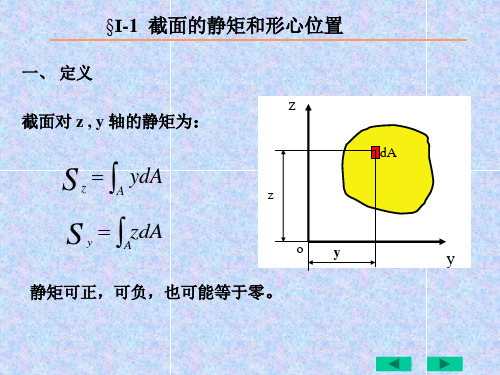
§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面,以下两积分表一任意截面,以下两积分ïþïýü==òòA z S A y S A y Az d d (I −1)分别定义为该截面对于z 轴和y 轴的静矩。
轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得心的公式可得ïïþïïýü==òòA A z z A A y y AC ACd d利用公式(I −1),上式可写成,上式可写成ïïþïïýü====òòA S A A z z A SA Ay y y A C z A C d d (I −2) 或þýü==C y C z Az S Ay S (I −3)ïïþïýü==A S z A S y y C z C(I −4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对d A C Zz y y y C Z c O 图I −1 Z 同一坐标轴的静矩的代数和。
即:同一坐标轴的静矩的代数和。
即:ïïþïïýü==åå==ni ci i y ni ci i z z A S y A S 11(I −5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为ïïïïïþïïïïýü==åååå====ni ini c iic ni ini c i i c AzA z A y A y 1111(I −6)例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
材料力学第六章 截面的几何性质惯性矩
IP
2dA
A
(y2
A
z2 )dA
IZ
Iy.
返回 下一张 上一张 小结
第三节 惯性矩和惯性积的 y1dA (y a)2 dA A
y2dA 2a ydA a2 dA
I z1 z a2 A; y1 y b2 A;
2dA
A
(y2
A
z2 )dA
IZ
Iy.
Izy
z y dA;
A
五、平行移轴公式:
I z1 z a2 A; y1 y b2 A;
I z1y1 I zy abA;
返回 下一张 上一张 小结
六、主惯性轴和主惯性矩: 主惯性轴(主轴)—使 I zoyo 0 的这对正交坐标轴; 主惯性矩(主惯矩)—截面对主惯性轴的惯性矩; 形心主惯性轴(形心主轴)—通过形心的主惯性轴; 形心主惯性矩(形心主惯矩)—截面对形心主轴的惯性矩。
I z1y1 I zy abA;
注意: y、z轴必须是形心轴。
二、转轴公式:
Iz1
A y12dA
( y cos z sin)2 dA;
A
I z1
Iz
Iy 2
Iz
Iy 2
cos 2
I zy
sin 2;
I y1
Iz
2
Iy
Iz
2
Iy
cos 2
I zy
sin 2;
I z1y1
Iz
Iy 2
三、惯性积:
定义:平面图形内, 微面积dA与其两个坐 标z、y的乘积zydA在整个图形内的积分称为 该图形对z、y轴的惯性积。
Izy
z y dA;
A
特点: ①惯性积是截面对某两个正交
惯性矩的计算方法

第1节静矩和形心4.1静矩和形心任何受力构件的承载能力不仅与材料性能和加载方式有关.而口与构件截面的几何形状和尺寸有关.如:计算杆的拉伸与压缩变形时用到截面而积A ,计算圆轴扭转变形时用到横截面的极惯性矩I?等.A、1?等是从不同角度反映了截而的几何特性,因此称它们为截而图形的几何性质.4.1静矩和形心设有一任意截而图形如图4 一1所示,其面积为A .选収直角坐标系yoz ,在坐标为(y,z)处取一微小而积dA ,定义微而积dA乘以到y轴的距离z ,沿整个截面的积分,为图形对y轴的静矩S?,其数学表达式(4 -la )同理,图形对z轴的静矩为□4-1图41截面静矩与坐标轴的选取有关•它随坐标轴y、z的不同而不同.所以静矩的数值可能足正,也可能足负或定零.静矩的虽纲为长度的三次方.确定截面图形的形心位置(图4-1中C点):A (4-2b)第1页共30页式中T、"为截而图形形心的坐标值.若把式(4-2)改写成心"•儿,為"•乙(4 3)性质:・若截面图形的静矩等于零,则此坐标轴必定通过截面的形心.・若坐标轴通过截而形心,则截而对此轴的静矩必为零.・山于截而图形的对称轴必定通过截而形心,故图形对其对称轴的静矩恒为零。
4 )工程实际中,有些构件的截面形状比较复杂,将这些复杂的截面形状看成是山若干简单图形(如矩形、圆形等)组合g而成的.对于这样的组合截而图形,计算静矩(S»‘ r)与形心坐标(y*、z ')时,可用以下公式1-1 2-1式中A— y i , z i分别表示第,个简单图形的面积及其形心坐标值,n为组成组合图形的简单图形个数.即:组合图形对某一轴的静矩等于组成它的简单图形对同一轴的静矩的代数和.组合图形的形心坐标值等于组合图形对相应坐标轴的静矩除以组合图形的面积.组合截面图形有时还可以认为是山一种简单图形减去另一种简单图形所组成的.例4J己知T形截面尺寸如图4-2所示,试确定此截面的形心坐标值.i-1 i-1 (4-5)图4-2解:(1)选参考轴为y 轴,z 轴为对称轴,(2)将图形分成I 、口两个矩形,则= 20 x 100加朋 S 右=(10 + 140)^^34 = 2Q X 14%/,22 二注型(3)代入公式(4・5)20x100x150+20x140x70 20x100 + 20x140此=°4.2惯性矩、惯性积和惯性半径设任一截面图形(图4-3),其而积为A ・选取直角坐标系yoz ,在坐标为(y 、z)处取一微小面积dA ,定义此微2面积dA 乘以到坐标原点o 的距离的平方Q ,沿整个截面积分,为截而图形的极惯性矩I?.做而积dA 乘以到坐标轴y 的2距离的平方2 ,沿整个截而积分为截面图形对y 轴的惯性矩I 》•极惯性矩、惯性矩常简称极惯矩、惯矩.j.l ~2Z4数学表达式为打=f p^dA极惯性矩“俎(4-6)对y轴惯性矩图4-3山图4-3看到“ =y +Z 9所以有打=\A^dA= £cy2 +/)曲二必+加必即;? (4-8)式(4-8)说明截面对任一对正交轴的惯性矩之和恒等于它对该两轴交点的极惯性矩。
惯性矩、静矩,形心坐标公式
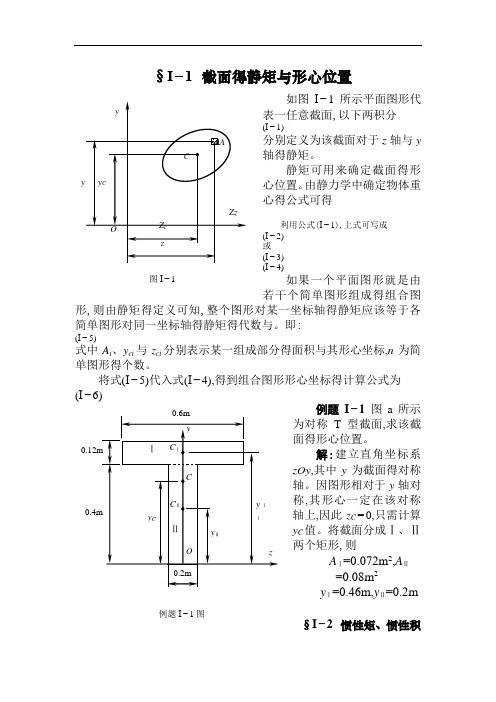
§I−1 截面得静矩与形心位置如图I −1所示平面图形代表一任意截面,以下两积分(I −1)分别定义为该截面对于z 轴与y 轴得静矩。
静矩可用来确定截面得形心位置。
由静力学中确定物体重心得公式可得利用公式(I −1),上式可写成 (I −2) 或 (I −3) (I −4)如果一个平面图形就是由若干个简单图形组成得组合图形,则由静矩得定义可知,整个图形对某一坐标轴得静矩应该等于各简单图形对同一坐标轴得静矩得代数与。
即:(I −5)式中A i 、y ci 与z ci 分别表示某一组成部分得面积与其形心坐标,n 为简单图形得个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标得计算公式为 (I −6)例题I −1 图a 所示为对称T 型截面,求该截面得形心位置。
解:建立直角坐标系zOy ,其中y 为截面得对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m,y Ⅱ=0.2m§I −2 惯性矩、惯性积例题I −1图图I −1与极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
现在图形内取微面积d A ,d A 得形心在坐标系zOy 中得坐标为y 与z ,到坐标原点得距离为ρ。
现定义y 2d A 与z 2d A 为微面积d A 对z 轴与y 轴得惯性矩,ρ2d A 为微面积d A 对坐标原点得极惯性矩,而以下三个积分(I −7)分别定义为该截面对于z 轴与y 轴得惯性矩以及对坐标原点得极惯性矩。
由图(I −2)可见,,所以有(I −8) 即任意截面对一点得极惯性矩,等于截面对以该点为原点得两任意正交坐标轴得惯性矩之与。
另外,微面积d A 与它到两轴距离得乘积zy d A 称为微面积d A 对y 、z 轴得惯性积,而积分(I −9)定义为该截面对于y 、z 轴得惯性积。
截面的静矩和形心位置和惯性矩的计算
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
惯性积。
组合截面的惯性矩,惯性积
n
I x I xi i1
n
I y I yi i1
n
I xy I xyi i 1
例 3 -1 求梯形截面对其形心轴 yc 的惯性矩。
解:将截面分成两个矩形截面。
截面的形心必在对称轴 zc 上。 取过矩形 2 的形心且平行 于底边的轴作为参考轴, 记作 y 轴 。
97.3 104 mm4
2 I xy
tg2 0 (
Ix
) 1.093 Iy
Ix Iy 2α 0 在第三象限 2α 0 227.60
0
113.80
形心主惯性轴 x0 , y0 分别由 x 轴和 y 轴绕 C点 逆时针转 113.80 得出。
形心主惯形矩为
I x0 I x I y 1
形心主惯性矩—— 截面对形心主惯性轴的惯性矩。
主惯性轴的位置:设 为主惯性轴与原坐标轴 之间的夹角,
则有 由此
I I x I y 2 sin 2 0 xy cos 2 0 0
tg 20
2I xy
Ix Iy
求出后,主惯性轴的位置就确定出来了。
主惯性矩的计算公式
I x0
I y0
Ix
y 0
截面对 y ,z 轴的惯性矩分别为
惯性矩、静矩、截面抵抗矩计算

惯性矩和对Y轴的惯性矩。
y
解:
100
1)求出A1和A2分别对自身形心 2
轴的惯性矩
0
I x1
b1h13 12
100 203 12
66.67 103
100
A1 •Ⅱ•ຫໍສະໝຸດ A2Ⅰx1
xc a2 30 x
Ix2
b2h23 12
20 100 3 12
16.67 105
2 0
2)求对整个截面形心X轴的惯性矩
截面对x轴的惯性矩:
I x y2dA
量纲:L4 y
A
截面对y轴的惯性矩: I y x2dA
A
注意:
1)同一截面对不同的轴惯性 矩不同;
2)惯性矩永远为正值;
x
dA
y r
x
3)惯性矩的单位为m4;
2、惯性半径(回转半径)
截面对x轴的惯性半径: ix I x / A 截面对y轴的惯性半径: iy I y / A
二、常见截面的惯性矩和惯性半径
形心轴:通过截面形心的坐标轴 ➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性矩。
y
对x轴的惯性矩
x
Ix
1 12
bh3
h 对y轴的惯性矩:
b
Iy
1 12
hb3
➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性半径。
y
对x轴的惯性半径
x
h
ix
Ix A
1/12bh3 h
截面的几何性质
知识点:截面惯性矩和静矩的计算 一、截面惯性矩的定义及计算 二、常见截面的惯性矩和惯性半径 三、组合截面的概念 四、惯性矩的平行移轴公式 五、静矩的概念及公式 六、常见截面的静矩
各种截面下极惯性矩
y
dA
y2dA z2dA I z I y
o
A
A
z
y
图形对任一对相互垂直的坐标系的惯性矩之和恒等于此图形对该两轴交点的极惯性矩。
四、惯性半径(Radius of gyration of the area)
iy
Iy A
iz
Iz A
I y I yi
I z I zi
I yz I yizi
(1)两平行轴中,必须有一轴为形心轴,截面对任意两平行轴 的惯性矩间的关系,应通过平行的形心轴惯性矩来换算;
(2)截面图形对所有平行轴的惯性矩中,以对通过形心轴的惯 性矩最小.
6、惯性矩与极惯性矩的关系:
z
I p
2dA
A
( y2 z2 )dA
各种截面下惯性矩,极惯性矩
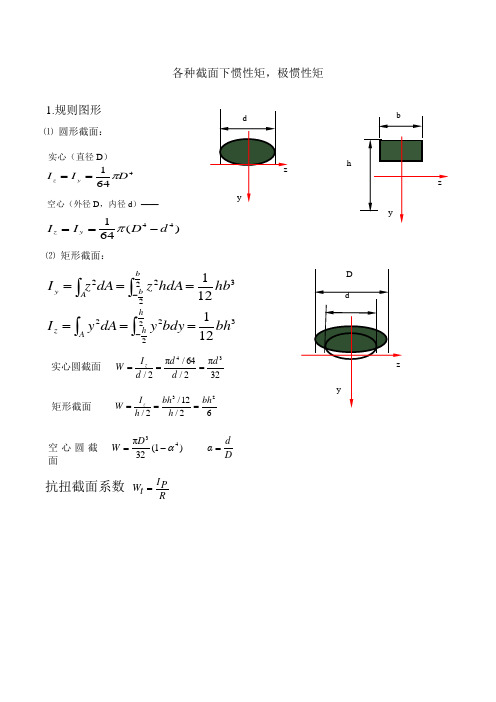
1.规则图形
d
⑴ 圆形截面:
实心(直径 D)
Iz
Iy
1 D4
64
空心(外径 D,内径 d)——
Iz
Iy
1 (D4
64
d 4)
⑵ 矩形截面:
z y
I y
z2dA
A
b
2 b
2
z 2 hdA
1 12
hb3
Iz
y2dA
A
h
2 h
2
y 2bdy
1 bh3 12
实心圆截面 W I z πd 4 / 64 πd 3 d / 2 d / 2 32
矩形截面
W I z bh3 /12 bh2 h/2 h/2 6
空 心 圆 截 W πD3 (1 4 )
面
32
抗扭截面系数
Wt
各种截面下极惯性矩

面
32
抗扭截面系数
Wt
IP R
α d D
b
h z
y
D d
z y
2.组合图形
W 称为抗弯截面系数
I y I yC a2 A I z I zC b2 A
I yz I yC zC abA
I y I yi
I z I zi
I yz I yizi
(1)两平行轴中,必须有一轴为形心轴,截面对任意两平行轴 的惯性矩间的关系,应通过平行的形心轴惯性矩来换算;
(2)截面图形对所有平行轴的惯性矩中,以对通过形心轴的惯 性矩最小.
6、惯性矩与极惯性矩的关系:
z
I p
2dA
A
( y2 z2 )dA
A
y
dA
y2dA z2dA I z I y
o
A
A
z
y
图形对任一对相互垂直的坐标系的惯性矩之和恒等于此图形对该两轴交点的极惯性矩。
四、惯性半径(Radius of gyration of the area)
iy
Iy A
iz
Iz A
组合图形1两平行轴中必须有一轴为形心轴截面对任意两平行轴的惯性矩间的关系应通过平行的形心轴惯性矩来换算
各种截面下惯性矩,极惯性矩
1.规则图形
d
⑴ 圆形截面:
实心(直径 D)
Iz
Iy
1 D4
64
空心(外径 D,内径 d)——
Iz
Iy
1 (D4
64
d 4)
⑵ 矩形截面:
z y
I y
z2dA
A
b
2 b
2
z 2 hdA
1 12
