第九章题目
【3套试题】人教版七年级数学下第九章不等式与不等式组复习检测试题(有答案)

人教版七年级数学下第九章不等式与不等式组复习检测试题(有答案)人教版七年级数学下册第九章不等式与不等式组单元测试题复习检测试卷(有答案)一、选择题1.下列式子:①-2<0;②2x+3y<0;③x=3;④x+y中,是不等式的个数有A. 1个B. 2个C. 3个 D . 4个2.若m>n,则下列不等式中一定成立的是()A. m+2<n+3B. 2m<3nC. a-m<a-nD. ma2>na23.数a、b在数轴上的位置如图所示,则下列不等式成立的是()A. a>bB. ab>0C. a+b>0D. a+b<04.若关于x的一元一次不等式组的解集是x<5,则m的取值范围是()A. m≥5B. m>5C. m≤5D. m<55.某商品的标价比成本价高m%,根据市场需要,该商品需降价n%出售,为了不亏本,n应满足()A. n≤mB. n≤C. n≤D. n≤6.某种记事本零售价每本6元,凡一次性购买两本以上给予优惠,优惠方式有两种,第一种:“两本按原价,其余按七折优惠”;第二种:全部按原价的八折优惠,若想在购买相同数量的情况下,要使第一种办法比第二种办法得到的优惠多,最少要购买记事本()A. 5本B. 6本C. 7本D. 8本7.不等式组的解集在数轴上表示正确的是()A. B.C. D.8.不等式组的解集是()A. x>4B. x≤3C. 3≤x<4D. 无解9.如果不等式组只有一个整数解,那么a的范围是()A. 3<a≤4B. 3≤a<4C. 4≤a<5D. 4<a≤510. 现有三种不同的物体:“甲、乙、丙”,用天平称了两次,情况如图所示,那么“甲、乙、丙”这三种物体按质量从大到小的顺序排列为A. 丙甲乙B. 丙乙甲C. 乙甲丙D. 乙丙甲二、填空题1.不等式组:的解集是2.某采石场爆破时,点燃导火线的甲工人要在爆破前转移到400m以外的安全区域甲工人在转移过程中,前40m只能步行,之后骑自行车。
鲁教新版九年级化学第九章《到实验室去》探究金属的化学性质基础题(word有答案)

鲁教新版九年级化学第九章《到实验室去》探究金属的化学性质基础题(word有答案)基础题一.选择题〔共16 小题〕1.某研讨性学习小组设计以下实验方案,验证铁、铜、银三种金属的活动性顺序,每种方案所需试剂如下〔反响所得产物可用作试剂进一步反响〕,其中不可行的方案是〔〕A.铜、硝酸银溶液、氯化亚铁溶液B.银、铜、氯化亚铁溶液C.铁、银、氯化铜溶液D.铁、硝酸银溶液、氯化铜溶液2.如下图:将铁钉置于水中,那么铁钉三个不同部位,最先生锈的是〔〕A.a 处B.b 处C.c 处D.以上都有能够3.有M、N、R 三种金属,将M 和N 浸入稀盐酸中,N 溶解,M 不溶解;将M 浸入R 的硫酸盐溶液中,在M 的外表有R 析出,那么M、N、R 的金属活动性由强到弱可陈列为〔〕A.R>M>N B.N>R>M C.R>N>M D.N>M>R4.有X、Y、Z 三种金属,将Y 放入XSO4 溶液时,溶液质量不时添加;把X 放入ZNO3 溶液时,溶液质量不时增加,那么以下契合X、Y、Z 顺序陈列的是〔〕A.Zn、Fe、Cu B.Fe、Mg、Cu C.Al、Fe、Ag D.Cu、Zn、Ag5.以下四个实验中只需求完成三个就可以证明Fe、Cu、Ag 三种金属的活动性顺序.其中不用停止的是〔〕A.将铁片放入稀盐酸B.将铜片放入稀盐酸C.将铁片放入硝酸银溶液D.将铜片放入硝酸银溶液6.为验证镁、铁、铜三种金属的活动性顺序,可选用的一组物质是〔〕A.铜、氯化亚铁溶液、氯化镁溶液B.铁、铜、氯化镁溶液C.镁、氯化铜溶液、硫酸亚铁溶液D.铁、硫酸铜溶液、氯化镁溶液7.有A、B、C 三种金属,把A、C 区分放入稀硫酸中,C 有反响,A 无反响;A能从B 的化合物溶液中置换出B.这三种金属活动性由强到弱的顺序是〔〕A..C>A>B B..A>B>C C..B>A>C D..C>B>A8.A、B、C、D 四种金属,区分投入稀盐酸中,A、B、D 反响,气体放出,C 无清楚现象,再把A、D 投入B 盐溶液中,A 外表有B 析出,而D 没有,那么四种金属的活动性顺序是〔〕A.A>B>D>C B.B>D>A>C C.D>A>B>C D.D>B>A>C9.某化学兴味小组设计了验证Fe、Cu、Ag 的金属活动性顺序的多种方案,每种方案所需的试剂如下:①Fe、Ag、CuSO4 溶液;②Cu、FeCl2 溶液、AgNO3 溶液;③Fe、Cu、稀盐酸、AgNO3溶液;④Fe、Cu、AgNO3 溶液;⑤Cu、Ag、FeSO4 溶液,你以为可行的方案是A.①②③④ B.①②③⑤ C.只要①②⑤D.只要①②③10.把金属X 放人CuCl2 溶液中有白色物质析出,放入MgCl2 溶液中无现象。
五年中考,三年模拟数学七年级下册第九章练习电子版的试卷。

五年中考,三年模拟数学七年级下册第九章练习电子版的试卷。
一、选择题.本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求1、若集合M=(r|VE<4),N=(x |3x>1),则MON =()A.[r|0<r<2)B.(x<r<2)C.[r|3 <r<16)D.(x1<r<16)2、若i(1-=)=1,则.+3=()A.-2B.-1C.1D.23、在AABC中,点D在边AB上,BD =2DA、记CA=m,CD=n、则CB=()A.3m-2nB.-2m +3nC.3m + 2nD.2m +3n4、南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库,已知该水库水位为海拔148、5 m时,相应水面的面积为140、0km2;水位为海拔157、5 m时,相应水面的面积为180、0km2、将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148、5m上升到157、5m时,增加的水量约为(V7= 2、65)()A.1、0 x 100 m3B.1、2 x 100 m3C.1、4 x 109 m3D.1、6 x 109 m35,从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为()A.1/6B.1/3C.1/2D.2/36、记函数f(z)= sin(wr+)+b(w> 0)的最小正周期为T、若〈T<x,且y=f(z)的图像关于点(、2)中心对称,则f()=A.1B.3/2C.2/5D.3二、选择题.本题共4小题,每小题5分,共20分,每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分7、已知正方体ABCD-asic,Di,则()A.直线bcg与DA1所成的角为90°B.直线BC;与CA1所成的角为90°C.直线BC]与平面BB,DiD所成的角为45D.直线BC]与平面ABCD所成的角为45°8、已知函数f(r)=r3-r+1,则()A.f(r)有两个极值点B.f(r)有三个零点C.点(0,1)是曲线y=f(x)的对称中心D.直线y=2r是曲线y=f(z)的切线9、已知0为坐标原点,点A(1,1)在抛物线C:r=2py(p>0)上,过点B(0,-1)的直线交C于P,Q两点,则()A.C的准线为y=-1B.直线AB与C相切C.OPI-JOQ > |OAD.BPI-|BQI > |BA210、已知函数f(z)及其导函数J"(z)的定义域均为R,记g(z)= f'(r)、若f(;-2r),9(2+r)均为偶函数,则()A.f(0)=09B.g(-1)=g(2)C.f(-1)= f(4)D.g(-1)= g(2)三、填空题.本题共4小题,每小题5分,共20分11、(1-)(z+ y)*的展开式中ry的系数为()(用数字作答)、12、写出与圆r2+y2=1和(x-3)2+(y-4)2=16都相切的一条直线的方程15、若曲线y=(r+a)e有两条过坐标原点的切线,则a的取值范围是13、已知椭圆C.+=1(a>b>0),C的上顶点为A、两个焦点为Fi,Fz,离心率为过F.且垂直于AF2的直线与C交于D,E两点,DE=6,则AADE的周长是四、解答题.本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤14、(10分)记S,为数列(an的前n项和,已知a1=1,)是公差为.的等差数列(1)求(an)的通项公式;(2)证明:=+-++<215、(12分)已知函数/(r)=e'-ar 和g(r)= ax-jnr有相同的最小值(1)求a;(2)证明.存在直线y=6,其与两条曲线y=f(r)和y= g(r)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列16、(12 分)cos A记AABC的内角A、B、C的对边分别为a、b、c,已知1+ sin A(1)若C=,求B;(2)求的最小值。
人教版第九章 压强单元达标提优专项训练试题
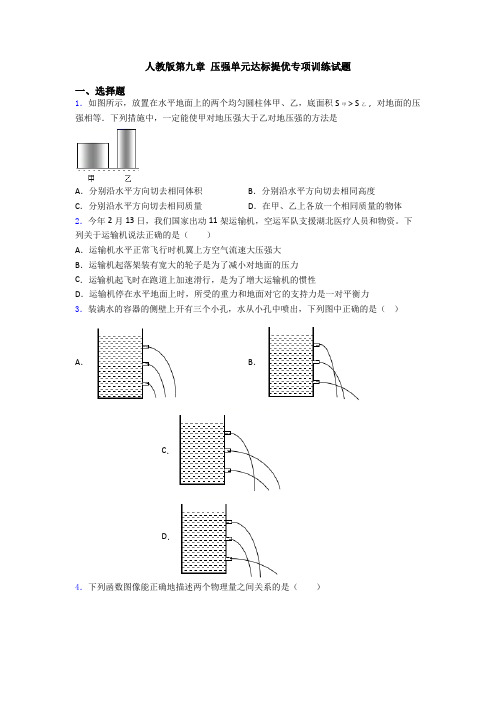
人教版第九章压强单元达标提优专项训练试题一、选择题1.如图所示,放置在水平地面上的两个均匀圆柱体甲、乙,底面积S甲>S乙,对地面的压强相等.下列措施中,一定能使甲对地压强大于乙对地压强的方法是A.分别沿水平方向切去相同体积B.分别沿水平方向切去相同高度C.分别沿水平方向切去相同质量D.在甲、乙上各放一个相同质量的物体2.今年2月13日,我们国家出动11架运输机,空运军队支援湖北医疗人员和物资。
下列关于运输机说法正确的是()A.运输机水平正常飞行时机翼上方空气流速大压强大B.运输机起落架装有宽大的轮子是为了减小对地面的压力C.运输机起飞时在跑道上加速滑行,是为了增大运输机的惯性D.运输机停在水平地面上时,所受的重力和地面对它的支持力是一对平衡力3.装满水的容器的侧壁上开有三个小孔,水从小孔中喷出,下列图中正确的是()A.B.C.D.4.下列函数图像能正确地描述两个物理量之间关系的是()A.弹性限度内弹簧所受拉力与伸长关系B.粗糙程度不变时,滑动摩擦力与压力关系C.压力一定时,物体受到压强与受力面积关系D.液体密度不变时,液体压强与深度关系5.一薄壁正方体容器放在台秤上,当在容器中装满水时,台秤的示数为12 N。
容器底部受到水的压强为1×103 Pa;当在容器中装满另一种液体时,容器底部受到的压力是8N;将液体倒掉,然后将一个实心正方体物块放入容器中,物块正好填满容器,此时台秤受到的压强为2.9×103 Pa。
则下列说法正确的是(g=10 N/kg)()A.容器的底面积为120 cm2B.物块的密度为2.9×103 kg/m3C.液体对容器底部的压强为0.4×103 Pa D.薄壁正方体容器的重力为2N6.高压锅是应用液体沸点随着气压增大而升高的原理设计的,下表中列出了水的沸点跟气压的关系.图中高压锅盖出气孔的横截面积为10mm2,限压阀的质量为40g,大气压值取1.0×105Pa.请你通过计算并对照下表来判断,用该高压锅烧水,水温最高可以达到气压/×1051.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8帕水的沸点100104108111114116118119120 /℃A .120℃B .118℃C .114℃D .104℃7.图中的两个容器中盛有同种相同质量的液体,容器底部受到液体的压强分别为P A 、P B , 容器底部受到液体的压力分别为F A 、F B ,则( )A .P A =PB B .P A >P BC .F A =F BD .F A >F B8.如图甲是我校某生毕业后收到的可乐定制礼物,该生打开瓶盖喝了些后将其置于桌面上,此时液体对瓶子底部的压强为p 甲,液体对瓶子底部的压力为F 甲。
高中数学第九章统计考点题型与解题方法(带答案)

高中数学第九章统计考点题型与解题方法单选题1、某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是()A.收入最高值与收入最低值的比是3︰1B.结余最高的月份是7月C.1至2月份的收入的变化率与4至5月份的收入的变化率相同D.前6个月的平均收入为40万元答案:D分析:根据统计图对选项逐一分析,由此确定说法错误的选项.最高收入90万元,最低收入30万元,所以A正确.结余最高的为7月,结余60万元,所以B正确.根据两点连线的斜率可知,1至2月份的收入的变化率与4至5月份的收入的变化率相同,所以C正确.前6个月的平均收入为40+60+30+30+50+60=45万元,所以D选项错误.6故选:D2、在样本的频率分布直方图中,一共有n(n≥4,n∈Z)个小矩形,第4个小矩形的面积等于其余(n−1)个,则第4个小矩形对应的频率为()小矩形面积和的37A.0.3B.0.4C.0.5D.0.7答案:A(1−x),解方程可分析:设第4个小矩形对应的频率为x,然后根据频率分布直方图的性质和题意可得x=37得结果设第4个小矩形对应的频率为x,则其余(n−1)个小矩形对应的频率为1−x,(1−x),解得x=0.3.所以x=37故选:A.3、下列调查中,适合普查的是()A.一批手机电池的使用寿命B.中国公民保护环境的意识C.你所在学校的男女同学的人数D.了解全国人民对建设高铁的意见答案:C分析:根据抽样调查和普查的特点即可判断.由题调查一批手机电池的使用寿命,中国公民保护环境的意识,了解全国人民对建设高铁的意见适合用抽样调查,调查所在学校的男女同学的人数适合普查.故选:C.4、m个数据的平均数为a,中位数为b,方差为c.若将这m个数据均扩大到原来的2倍得到一组新数据,则下列关于这组新数据的说法正确的是()A.平均数为a B.中位数为2b C.标准差为√2c D.方差为2c答案:B分析:m个x1,x2,⋯,x n数据的平均数为a,中位数为b,方差为c.若将这m个数据均扩大到原来的2倍得到一组新数据2x1,2x2,⋯,2x n,根据平均数、中位数、方差、标准差的定义进行判断即可.m个x1,x2,⋯,x n数据的平均数为a,中位数为b,方差为c.若将这m个数据均扩大到原来的2倍得到一组新数据2x1,2x2,⋯,2x n,则由于平均数为所有数之和除以m,故平均数变为2a,故A错;中位数为这组数从小到大排列后中间的那个数或中间两数和的平均数,由于每个数都变为原来2倍,所以中位数也变为原来的2倍,即2b,故B对;方差描述的是这组数的波动情况,x1,x2,⋯,x n的方差为c,则2x1,2x2,⋯,2x n的方差为22c=4c,标准差为√22c=2c,故C,D错;故选:B小提示:熟悉平均数、中位数、方差、标准差的概念,特别是一组数据扩大某个倍数或增加某个数值的情况下,平均数、中位数、方差、标准差的变化.5、抽样统计甲射击运动员10次的训练成绩分别为86,85,88,86,90,89,88,87,85,92,则这10次成绩的80%分位数为()A.88.5B.89C.91D.89.5答案:D分析:将数据从小到大排列,计算10×80%=8,得到答案.甲射击运动员10次的训练成绩从小到大分别为:85,85,86,86,87,88,88,89,90,92.10×80%=8,这10次成绩的80%分位数为:89+90=89.5.2故选:D.6、某汽车制造厂分别从A,B两类轮胎中各随机抽取了6个进行测试,下面列出了每一个轮胎行驶的最远里程(单位:103km).A类轮胎:94,96,99,99,105,107.B类轮胎:95,95,98,99,104,109.根据以上数据,下列说法正确的是()A.A类轮胎行驶的最远里程的众数小于B类轮胎行驶的最远里程的众数B.A类轮胎行驶的最远里程的极差等于B类轮胎行驶的最远里程的极差C.A类轮胎行驶的最远里程的平均数大于B类轮胎行驶的最远里程的平均数D.A类轮胎的性能更加稳定答案:D分析:根据众数、极差、平均数和方差的定义以及计算公式即可求解.解:对A:A类轮胎行驶的最远里程的众数为99,B类轮胎行驶的最远里程的众数为95,选项A错误;对B:A类轮胎行驶的最远里程的极差为13,B类轮胎行驶的最远里程的极差为14,选项B错误.对C :A 类轮胎行驶的最远里程的平均数为100+−6−4−1−1+5+76=100,B 类轮胎行驶的最远里程的平均数为100+−5−5−2−1+4+96=100,选项C 错误.对D :A 类轮胎行驶的最远里程的方差为(94−100)2+(96−100)2+(99−100)2×2+(105−100)2+(107−100)26=643,B 类轮胎行驶的最远里程的方差为(95−100)2×2+(98−100)2+(99−100)2+(104−100)2+(109−100)26=763>643,故A 类轮胎的性能更加稳定,选项D 正确. 故选:D.7、关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请全校m 名同学每人随机写下一个都小于1的正实数对(x,y );再统计两数能与1构成钝角三角形三边的数对(x,y )的个数a ;最后再根据统计数a 估计π的值,那么可以估计π的值约为( ) A .4am B .a+2mC .a+2m mD .4a+2m m答案:D解析:由试验结果知m 对0~1之间的均匀随机数x,y ,满足{0<x <10<y <1,面积为1,再计算构成钝角三角形三边的数对(x,y),满足条件的面积,由几何概型概率计算公式,得出所取的点在圆内的概率是圆的面积比正方形的面积,即可估计π的值.解:根据题意知,m 名同学取m 对都小于1的正实数对(x,y ),即{0<x <10<y <1,对应区域为边长为1的正方形,其面积为1,若两个正实数x,y 能与1构成钝角三角形三边,则有{x 2+y 2<1x +y >10<x <10<y <1,其面积S =π4−12;则有am=π4−12,解得π=4a+2m m故选:D .小提示:本题考查线性规划可行域问题及随机模拟法求圆周率的几何概型应用问题. 线性规划可行域是一个封闭的图形,可以直接解出可行域的面积;求解与面积有关的几何概型时,关键是弄清某事件对应的面积,必要时可根据题意构造两个变量,把变量看成点的坐标,找到试验全部结果构成的平面图形,以便求解.8、数据x1,x2,x3,…,x m的平均数为x,数据y1,y2,y3,…,y n的平均数为y,则数据x1,x2,x3,…,x m,y1,y2,y3,…,y n的平均数为()A.xn +ymB.xm+ynC.nx+mym+n D.mx+nym+n答案:D分析:利用平均数的计算公式计算.由题意得:x1+x2+x3+⋯+x m=mx,y1+y2+y3+⋯+y n=ny,所以x1+x2+x3+⋯+x m+y1+y2+y3+⋯+y nm+n =mx+nym+n故选:D多选题9、2020年突如其来的新冠肺炎疫情对房地产市场造成明显的冲击,如图为某市2020年国庆节7天假期的楼房认购量与成交量的折线图,某同学根据折线图对这7天的认购量(单位:套)与成交量(单位:套)作出如下判断,则判断正确的是()A.日成交量的中位数是16B.日成交量超过平均成交量的只有1天C.10月7日认购量量的增长率大于10月7日成交量的增长率D.日认购量的方差大于日成交量的方差答案:BD解析:根据拆线图判断各数据特征后判断各选项.由拆线图日成交量的中位数是26,A错;日成交量均值为13+8+32+16+26+38+1667≈42.7,大于均值的只有一天,B正确;10月7日认购量量的增长率为y1=276−112112≈1.464,成交量的增长率为y2=166−3838≈3.368,显然C错;日认购量的均值为223+105+91+107+100+112+2767≈144.857,由各数据与均值的差可以看出日认购量的方差大于日成交量的方差,D正确.故选:BD.小提示:关键点点睛:本题考查统计图表,考查拆线图的识别.解题关键是由拆线图得出各数据,然后求得各数据特征.如中位数,均值,增长率,方差,解题中还要善于估值,如本题中的方差,从而大致比较出大小.10、如图是国家统计局发布的2020年12月至2021年12月的全国居民消费价格涨跌幅,其中同比=本期数−去年同期数去年同期数×100%,环比=本期数−上期数上期数×100%.则下列说法正确的是()A.2020年12月至2021年12月全国居民消费价格环比的极差为1.5% B.2020年12月至2021年12月全国居民消费价格同比的中位数为0.9% C.这13个月中,2021年6月全国居民消费价格最低D.2021年比2020年全国居民消费平均价格增长大于1.0%答案:AB分析:计算出2020年12月至2021年12月全国居民消费价格环比的极差,可判断A选项;利用中位数的定义可判断B选项;根据涨幅可判断C选项;利用平均数公式可判断D选项.2020年12月至2021年12月全国居民消费价格环比的最大值为1.0%,最小值为−0.5%,所以其极差为1.5%,A项正确;2020年12月至2021年12月全国居民消费价格同比(单位:%)从小到大依次为−0.3、−0.2、0.2、0.4、0.7、0.8、0.9、1.0、1.1、1.3、1.5、1.5、2.3,其中位数为0.9%,B项正确;从环比来看,假设2020年全国居民消费平均价格为1,经计算可得2020年12月全国居民消费平均价格,C 项错误;2021年比2020年全国居民消费价格平均增长为1 12(−0.3−0.2+0.4+0.9+1.3+1.1+1.0+0.8+0.7+1.5+2.3+1.5)=1112<1.0,D项错误.故选:AB.11、如图所示的两个扇形统计图分别统计了某地2010年和2020年小学生参加课外兴趣班的情况,已知2020年当地小学生参加课外兴趣班的总人数是2010年当地小学生参加课外兴趣班的总人数的4倍,则下列说法正确的是()A.2020年参加音乐兴趣班的小学生人数是2010年参加音乐兴趣班的小学生人数的4倍B.这10年间,参加编程兴趣班的小学生人数变化最大C.2020年参加美术兴趣班的小学生人数少于2010年参加美术兴趣班的小学生人数D.相对于2010年,2020年参加不同课外兴趣班的小学生人数更平均答案:ABD分析:设2010年参加课外兴趣班的小学生总人数为a,则2020年参加课外兴趣班的小学生总人数是4a,根据扇形统计图中的比例计算,并逐项检验,即可得到结果.设2010年参加课外兴趣班的小学生总人数为a,则2020年参加课外兴趣班的小学生总人数是4a;由统计图可知,2010年参加音乐兴趣班的小学生人数是a×21%=0.21a,2020年参加音乐兴趣班的小学生人数是4a×21%=0.84a,故A正确.这10年间参加编程兴趣班的小学生人数变化量为4a×32%−a×5%=1.23a,这10年间参加语言表演的小学生人数变化量为4a×20%−a×14%=0.66a,这10年间参加音乐的小学生人数变化量为4a×21%−a×21%=0.63a,这10年间参加美术的小学生人数变化量为4a×27%−a×60%=0.48a,所以这10年间参加编程兴趣班的小学生人数变化量最大,故B正确.2020年参加美术兴趣班的小学生人数为4a×27%=1.08a,2010年参加美术兴趣班的小学生人数为a×60%=0.6a,1.08a>0.6a,故C不正确,根据扇形统计图中的比例分布,可知D正确.故选:ABD12、某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述正确的有()A.各月的平均最低气温都在0℃以上B.七月的平均温差比一月的平均温差大C.三月和十一月的平均最高气温基本相同D.平均最高气温高于20℃的月份有5个答案:ABC分析:根据雷达图提供的数据判断各选项可得.对于选项A,由图易知各月的平均最低气温都在0℃以上,A正确;对于选项B,七月的平均最高气温点与平均最低气温点间的距离大于一月的平均最高气温点与平均最低气温点间的距离,所以七月的平均温差比一月的平均温差大,B正确;对于选项C,三月和十一月的平均最高气温均为10℃,所以C正确;对于选项D,平均最高气温高于20℃的月份有七月、八月,共2个月份,故D错误.故选:ABC.13、PM2.5是衡量空气质量的重要指标,下图是某地7月1日到10日的PM2.5日均值(单位:ug/m3)的折线图,则下列关于这10天中PM2.5日均值的说法正确的是A.众数为30B.中位数是31C.平均数小于中位数D.后4天的方差小于前4天的方差答案:AD分析:根据折线图,由众数,中位数,平均数,方差等概念及公式,逐项判断,即可得出结果.众数即是出现次数最多的数字,由折线图可得,众数为30,即A正确;中位数即是处在中间位置的数字,将折线图中数字由小到大依次排序,得到:17,25,30,30,31,32,34,38,42,126;处在中间位置的数字是:31,32,因此中位数为31.5,即B错;由折线图可得,平均数为:17+25+30+30+31+32+34+38+42+12610=40.5>31.5,故C错;前4天的平均数为:38+25+17+304=27.5,后4天的平均数为42+31+32+304=33.75前4天方差为:s12=(38−27.5)2+(25−27.5)2+(17−27.5)2+(30−27.5)24=58.25,后4天方差为:s22=(42−33.75)2+(31−33.75)2+(32−33.75)2+(30−33.75)24=23.1875,所以后4天的方差小于前4天的方差,故D正确.故选:AD.小提示:本题主要考查由折线图计算众数、中位数、平均数、方差等,属于基础题型.填空题14、某次数学考试中20个人的成绩如下:101,103,107,110,112,113,116,123,124,125,125,125,126,128,134,135,137,139,144,148,若这组数据的众数为a,中位数为b,极差为c,则a+b+ c=___________.答案:297分析:根据众数、中位数和极差的定义逐个求解再求和即可由题意,a=125,b=125,c=148−101=47,故a+b+c=125+125+47=297所以答案是:29715、某学校组织学生参加数学测试,成绩的频率分布直方图如下,数据的分组依次是[20,40),[40,60),[60,80),[80,100],则可估计这次数学测试成绩的第40百分位数是_________.答案:65分析:利用百分位数的定义求解.解:成绩在[20,60)的频率是(0.005+0.01)×20=0.3,成绩在[20,80)的频率为0.3+0.02×20=0.7,所以第40百分位数一定在[60,80)内,×20=65,所以这次数学测试成绩的第40百分位数是60+0.4−0.30.4所以答案是:6516、若一组数据x1,x2,x3,⋯,x n的平均数是30,另一组数据x1+y1,x2+y2,x3+y3,⋯,x n+y n的平均数是70,则第三组数据4y1+1,4y2+1,4y3+1,⋯,4y n+1的平均数是___________.答案:161分析:根据数据平均数计算公式可得.数据x1+y1,x2+y2,x3+y3,⋯,x n+y n共有n个,其平均数为1 n ∑(x i+y i)ni=1=1n∑x ini=1+1n∑y ini=1=30+y=70.因此y=40故数据4y1+1,4y2+1,4y3+1,⋯,4y n+1的平均数是4×40+1=161.所以答案是:161解答题17、某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:s12和s22.(1)求x,y,s12,s22;(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果y−x≥2√s12+s2210,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).答案:(1)x=10,y=10.3,s12=0.036,s22=0.04;(2)新设备生产产品的该项指标的均值较旧设备有显著提高.分析:(1)根据平均数和方差的计算方法,计算出平均数和方差.(2)根据题目所给判断依据,结合(1)的结论进行判断.(1)x=9.8+10.3+10+10.2+9.9+9.8+10+10.1+10.2+9.710=10,y=10.1+10.4+10.1+10+10.1+10.3+10.6+10.5+10.4+10.510=10.3,s12=0.22+0.32+0+0.22+0.12+0.22+0+0.12+0.22+0.3210=0.036,s22=0.22+0.12+0.22+0.32+0.22+0+0.32+0.22+0.12+0.2210=0.04.(2)依题意,y−x=0.3=2×0.15=2√0.152=2√0.0225,2√0.036+0.0410=2√0.0076,y−x≥2√s12+s2210,所以新设备生产产品的该项指标的均值较旧设备有显著提高.18、“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分为100分(90分及以上为认知程度高).现从参赛者中抽取了x人,按年龄分成5组,第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45],得到如图所示的频率分布直方图,已知第一组有6人.(1)求x;(2)求抽取的x人的年龄的中位数(结果保留整数);(3)从该市大学生、军人、医务人员、工人、个体户五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.①分别求5个年龄组和5个职业组成绩的平均数和方差;②以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度,并谈谈你的感想.答案:(1)总体是该中学高三年级400名学生的视力;样本是所抽取的50名学生的视力.(2)答案见解析.分析:(1)根据总体与样本的定义直接写出;(2)根据抽签法与随机数法的抽样过程写出即可.解:(1)总体是该中学高三年级400名学生的视力;样本是所抽取的50名学生的视力.(2)选择①.利用抽签法步骤如下,第一步:将这50名学生编号,编号为1,2,3, (50)第二步:将50个号码分别写在纸条上,并揉成团,制成号签.第三步:将得到的号签放在一个不透明的容器中,搅拌均匀.第四步:从容器中逐一抽取6个号签,并记录上面的号码.对应上面6个号码的学生就是抽取的学生.选择②.利用随机数法步骤如下,第一步:将这50名学生编号,编号为01,02,03, (50)第二步:用计算机产生1~50范围内的整数随机数,把产生的随机数作为抽中的编号.第三步:重复第二步的过程,直到抽足6个号码.对应上面6个号码的学生就是抽取的学生.=0.05,即可求解.解析:(1)根据频率分布直方图求出第一组的频率,再由6x(2)设中位数为a,根据0.01×5+0.07×5+(a-30)×0.06=0.5,求解即可.(3)①求出平均数,再根据方差的式子即可求解;②比较平均数与方差即可得出结论.=0.05,∴x=120.(1)根据频率分布直方图得第一组的频率为0.01×5=0.05,∴6x(2)设中位数为a,则0.01×5+0.07×5+(a-30)×0.06=0.5,∴a=95≈32,则中位数为32.3(3)①5个年龄组成绩的平均数为x1=1×(93+96+97+94+90)=94,5×[(-1)2+22+32+02+(-4)2]=6.方差为s12=15×(93+98+94+95+90)=94,5个职业组成绩的平均数为x2=15×[(-1)2+42+02+12+(-4)2]=6.8.方差为s22=15②从平均数来看两组的认知程度相同,从方差来看年龄组的认知程度更稳定(感想合理即可).当今,青少年视力水平的下降已引起全社会的关注.为了了解某中学高三年级400名学生的视力情况,从中抽取了50名学生进行视力检测.(1)在这个问题中,总体、样本各是什么?(2)在①抽签法,②随机数法这两个条件中任选一个填入下面的横线上,并解答.为深入了解这50名学生的视力情况,从中随机抽取6人,请写出利用___9___抽取该样本的过程.。
第九章非流动负债 题目带答案

第九章非流动负债一、单项选择题(一)要求:下列各小题的4个备选答案中,只有1个是正确的,请您将正确答案的字母序号填入每小题后面的“()”内。
(二)题目:1、下列账户中,用于生产周转的长期借款的利息,应借记的账户是( A )。
A、财务费用B、管理费用C、销售费用D、长期借款2、借款费用准则中的“专门借款”是指( A )。
A、为购建或者生产符合资本化条件的资产而专门借入的款项B、发行债券借款C、技术改造借款D、生产周转借款3、下列项目中,不属于借款费用的项目是( B )。
A、借款过程中发生的承诺费B、发行公司债券发生的折价C、外币借款发生的汇兑损失D、发行公司债券溢价的摊销【解析】发行公司债券发生的折价或溢价不属于借款费用,债券折价或溢价的摊销属于借款费用。
4、下列各项中,不属于或有事项的特征的是( B )。
A、由未来事项来决定B、可以确认为资产或负债C、结果具有不确定性D、由过去的交易或事项形成5、下列有关“预计负债”账户的表述中,不正确的是:该账户的( C )。
A、贷方登记按规定的预计项目和金额确认的预计负债B、借方登记预计负债发生并实际偿付的金额C、期末借方余额,反映已预计但尚未实际发生并偿付的债务D、明细账应按预计负债项目设置,如产品质量保证、亏损合同、固定资产弃置义务等6、下列符合资本化条件的资产所发生的借款费用在予以资本化时,要与资产支出相挂钩的是( C )。
A.专门借款利息B.专门借款的溢价摊销C.一般借款利息D.外币专门借款的汇兑差额7、在确定借款费用资本化金额时,资本化期间与专门借款有关的利息收入应( D )。
A、计入营业外收入B、计入当期的财务费用C、计入投资收益D、冲减借款费用资本化的金额8、下列在建工程连续超过3个月中断的原因中,不应暂停借款费用资本化的是(D )。
A.由于资金周转困难而造成B.由于劳务纠纷而造成C.由于发生安全事故而造成D.由于可预测的气候影响而造成9、债券折价发行是由于( A )。
开封市物理八年级第九章 压强单元专项综合训练
开封市物理八年级第九章压强单元专项综合训练一、选择题1.两个正方体甲乙放在水平地面上,它们对水平面的压强相等,沿水平方向切去不同厚度,使剩余的厚度相同,剩余的压力相同,则甲乙切去的质量Δm甲、Δm乙和甲乙的密度满足的关系是()A.ρ甲>ρ乙,Δm甲>Δm乙B.ρ甲<ρ乙,Δm甲>Δm乙C.ρ甲<ρ乙,Δm甲<Δm乙D.ρ甲>ρ乙,Δm甲<Δm乙2.如图所示,放置在水平地面上的两个均匀圆柱体甲、乙,底面积S甲>S乙,对地面的压强相等.下列措施中,一定能使甲对地压强大于乙对地压强的方法是A.分别沿水平方向切去相同体积B.分别沿水平方向切去相同高度C.分别沿水平方向切去相同质量D.在甲、乙上各放一个相同质量的物体3.下列各组连线配对中,完全正确的是()A.生产运输工具与制造原理:推土机安装履带——增大受力面积减小压力;潜水艇原理——利用“空心法”;飞机能上升——流速大的地方压强小B.物理量及单位:压强——P;速度——m/s;力——NC.物理学家及其主要贡献:汤姆生——发现中子;牛顿——发现万有引力定律;托勒玫——提出“日心说”D.物理量及测量工具:力——测力计;大气压——气压计;液体体积——量筒4.如图所示,两个底面积不同的圆柱形容器甲和乙,容器足够高,分别盛有水和酒精(ρ>ρ酒精),且两种液体对容器底部的压强相等。
一定能使水对容器底部的压强大于酒精对水容器底部压强的方法是()A.倒入相同质量的水和酒精B.倒入相同体积的水和酒C.抽出相同质量的水和酒精D.抽出相同体积的水和酒精5.如图所示,实心正方体物体甲、乙放在水平地面上.沿水平方向切去不同的厚度,使二者剩余部分的体积相同、剩余部分对地面压强相同.则切去部分的质量△m甲、△m乙和切去前甲、乙对地面的压强p甲、p乙的关系是()A.△m甲>△m乙p甲>p乙B.△m甲>△m乙p甲<p乙C.△m甲<△m乙p甲>p乙D.△m甲<△m乙p甲<p乙6.如图甲所示,密闭的容器中装有一定量的水,静止在水平桌面上,水对容器底的压力为F甲,容器对桌面的压强为p甲;若把该容器倒放在该桌面上,如图乙所示,水对容器底的压力为F乙,容器对桌面的压强为p乙,则()A.F甲<F乙p甲>p乙B.F甲=F乙p甲=p乙C.F甲>F乙p甲<p乙D.无法确定7.如图所示的四个实验均与大气压有关,下列关于实验结果的预测,说法正确的是()A.将自制气压计随电梯从一楼上升至十楼,气压计细玻璃管中的液面会下降B.将空的易拉罐放在火上加热,用橡皮泥封住开口处,冷却一会儿,易拉罐会变瘪C.将玻璃杯中装满水,用硬纸片盖住,倒置杯子,纸片不掉;杯子倾斜,纸片会掉下来D.将装满水的试管用薄片盖住管口,倒置在水中,拿掉薄片,管中的水会从管口流出8.如图,甲、乙是放在水平地面上的两个质量均匀的长方体,它们的密度之比ρ甲:ρ乙=4:5,底面积之比S甲:S乙=5:8,对水平地面的压强之比p甲:p乙=6:5,下列有关甲、乙的说法正确的是①甲、乙的质量之比是3:4②甲、乙的体积之比是15:16③将甲、乙分别沿水平方向切去相同的体积后,剩余部分对地面的压强可能相等④将甲、乙分别沿水平方向切去相同的高度后,剩余部分对地面的压强可能相等A.①③④B.③④C.①②③D.②③④9.如图所示,两个完全相同的圆柱形容器内分别盛有不同的的液体A和B,已知甲容器内液体的质量小于乙容器内液体的质量.下列措施中,有可能使两容器内液体对容器底部的压强相等的是(无液体溢出)A.分别倒入相同质量的液体A、BB.分别倒入相同体积的液体A、BC.分别抽出相同质量的液体A、BD.分别抽出相同体积的液体A、B10.如图是表示甲、乙两种物质“质量与体积关系”的图象. 用这两种物质分别做成A、B两个质量相等的实心正方体. 把它们放在水平地面上,A、B两物体对水平地面的压强之比p A:p BA.1:1 B.2:1C.4:1 D.8:1二、填空题11.如图甲所示,一个底面积为200 cm2且足够深的薄壁柱形平底容器放置于水平桌面上,现用一弹簧将边长为10 cm的正方体实心物体M(不吸水)固定连接在容器底部的中心位置。
(整理)统计学原理第九章相关与回归习题答案
第九章相关与回归一.判断题部分题目1:负相关指的是因素标志与结果标志的数量变动方向是下降的。
()答案:×题目2:相关系数为+1时,说明两变量完全相关;相关系数为-1时,说明两个变量不相关。
()答案:√题目3:只有当相关系数接近+1时,才能说明两变量之间存在高度相关关系。
()答案:×题目4:若变量x的值增加时,变量y的值也增加,说明x与y之间存在正相关关系;若变量x的值减少时,y变量的值也减少,说明x与y之间存在负相关关系。
()答案:×题目5:回归系数和相关系数都可以用来判断现象之间相关的密切程度。
()答案:×题目6:根据建立的直线回归方程,不能判断出两个变量之间相关的密切程度。
()答案:√题目7:回归系数既可以用来判断两个变量相关的方向,也可以用来说明两个变量相关的密切程度。
()答案:×题目8:在任何相关条件下,都可以用相关系数说明变量之间相关的密切程度。
()答案:×题目9:产品产量随生产用固定资产价值的减少而减少,说明两个变量之间存在正相关关系。
()答案:√题目10:计算相关系数的两个变量,要求一个是随机变量,另一个是可控制的量。
()答案:×题目11:完全相关即是函数关系,其相关系数为±1。
()答案:√题目12:估计标准误是说明回归方程代表性大小的统计分析指标,指标数值越大,说明回归方程的代表性越高。
()答案×二.单项选择题部分题目1:当自变量的数值确定后,因变量的数值也随之完全确定,这种关系属于()。
A.相关关系B.函数关系C.回归关系D.随机关系答案:B题目2:现象之间的相互关系可以归纳为两种类型,即()。
A.相关关系和函数关系B.相关关系和因果关系C.相关关系和随机关系D.函数关系和因果关系答案:A题目3:在相关分析中,要求相关的两变量()。
A.都是随机的B.都不是随机变量C.因变量是随机变量D.自变量是随机变量答案:A题目4:测定变量之间相关密切程度的指标是()。
第九章习题及答案
第九章习题及答案第九章作业1、某企业现⾦收⽀状况⽐较稳定,预计全年(按360天计算)需要现⾦元,现⾦与有价证券的转换成本为每次400元,有价证券的年利率为10%,要求计算:(1)最佳现⾦持有量(Q)(2)最低现⾦管理相关总成本(TC)其中;转换成本持有机会成本(3)有价证券交易次数(4)有价证券交易间隔期2、假设某企业预测的年度赊销额为元,应收账款平均收账天数为60天,变动成本率为60%,资⾦成本率为10%,要求计算:(1)应收账款平均余额(2)维持赊销业务所需资⾦所需要的资⾦(3)应收账款机会成本3、某企业预测的2002年度赊销额为2400万元,其信⽤条件是:n/30,变动成本率为65%,资⾦成本率(或有价证券利息率)为20%。
假设企业收账政策不变,固定成本总额不变。
该企业准备了三个信⽤条件的备选⽅案:A、维持n/30的信⽤条件;B、将信⽤条件放宽到n/60;C、将信⽤条件放宽到n/90。
为各种备选⽅案估计的赊销⽔平,坏账百分⽐和收账费⽤等有关数据见下表1。
根据以上资料,计算如下表2中指标并作出决策。
表2 信⽤条件分析评价表单位:万元4、仍按题3,如果企业选择了B⽅案,但为了加速应收账款的回收,决定将赊销条件改为“2/10,1/20,n/60”(D⽅案),估计约有60%的客户(按赊销额计算)会利⽤2%的折扣;15%的客户将利⽤1%的折扣。
坏账损失率降为2%,收账费⽤降为30万元。
根据上资料,计算如下有关指标:(1)应收账款平均收帐期。
(2)应收账款平均余额(3)维持赊销业务所需要的资⾦(4)应收账款机会成本(5)坏账损失(6)现⾦折扣并根据以上资料编制表3并作出决策。
表3 单位:万元5、假设某企业应收账款原收账政策和拟改变的收账政策如表4所⽰。
假设资⾦成本率为20%,根据表4中的资料,计算两种⽅案的收账总成本如表5所⽰,试作出应否改变收账政策。
表4 收账政策备选⽅案资料表5 收账政策分析评价表⾦额单位:万元6、某企业每年需耗⽤甲材料720千克,该材料的单位采购成本20元,单位储存成本4元,平均每次进货费⽤40元,要求计算:经济订货批量Q相关总成本T C年最优订货次数N平均采购成本7、某企业甲材料的年需要量为4000千克,每千克标准价为20元。
初中数学冀教版七年级下第九章测试题及答案
第九章三角形一、选择题(第1~10小题各3分,第11~16小题各2分,共42分)1.不一定在三角形内部的线段是()A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形的中位线2.如图所示,三角形被遮住的两个角不可能是 ()A.一个锐角,一个钝角B.两个锐角C.一个锐角,一个直角D.两个钝角3.下列说法中错误的是()A.任意三角形的内角和都是180°B.三角形按边进行分类可分为不等边三角形和等腰三角形C.三角形的中线、角平分线、高都是线段D.三角形的一个外角大于任何一个内角4.如图所示,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中错误的是()A.△ABC中,AD是BC边上的高B.△GBC中,CF是BG边上的高C.△ABC中,GC是BC边上的高D.△GBC中,GC是BC边上的高5.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个图中,能表示它们之间关系的是()6.如图所示,一块试验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DC→CA→AB→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体()A.转过90°B.转过180°C.转过270°D.转过360°7.下列条件:①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;③∠A=90°-∠B;④∠A=∠B-∠C.其中能确定△ABC是直角三角形的条件有()A.1个B.2个C.3个D.4个(第6题图)(第8题图)8.如图所示,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为()A.30°B.40°C.50°D.60°9.若△ABC中,2(∠A+∠C)=3∠B,则∠B的外角度数为()A.36°B.72°C.108°D.144°10.把14 cm长的铁丝截成三段,围成不是等边三角形的三角形,并且使三边均为整数,那么()A.有1种截法B.有2种截法C.有3种截法D.有4种截法11.如图所示,在△ABC中,点D,E,F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD等于()A.80°B.75°C.70°D.65°(第11题图)(第12题图)12.在△ABC中,AD,CE分别是△ABC的高,且AD=2,CE=4,则AB∶BC等于()A.3∶4B.4∶3C.1∶2D.2∶113.如图所示,∠B+∠C+∠D+∠E-∠A等于()A.360°B.300°C.180°D.240°14.如图所示,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC等于()A.118°B.119°C.120°D.121°(第14题图)(第15题图)15.如图所示,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2,3,4,6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为()A.6B.7C.8D.1016.如图所示,△ABC的面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,CB1=CB,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…,按此规律,要使得到的三角形的面积超过2014,操作的次数最少是()A.7B.6C.5D.4二、填空题(第17~18小题各3分,第19小题4分,共10分)17.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为.18.已知a,b,c是三角形的三条边,则|a+b-c|-|c-a-b|的化简结果为.19.如图所示,将纸片△ABC沿DE折叠,点A落在点A'处,已知∠1+∠2=100°,则∠A的大小等于度.三、解答题(共68分)20.(9分)一副三角板叠在一起按如图所示的方式放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.已知∠ADF=100°,求∠DMB的度数.21.(9分)(1)如图(1)所示,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C.△ABC中,∠A=30°,则∠ABC+∠ACB=度,∠XBC+∠XCB=度;(2)如图(2)所示,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.22.(9分)如图所示,武汉有三个车站A,B,C成三角形,一辆公共汽车从B站前往C站.(1)当汽车运动到点D点时,刚好BD=CD,连接线段AD,AD这条线段是什么线段?这样的线段在△ABC中有几条呢?此时有面积相等的三角形吗?(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段呢?在△ABC中,这样的线段又有几条呢?(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?这样的线段在△ABC中有几条?(第22题图)(第23题图)23.(9分)(1)如图所示,有两根竹竿AB,DB靠在墙角上,并与墙角FCE形成一定的角度,测得∠CAB,∠CDB的度数分别为α,β.用含有α,β的代数式表示∠DBF和∠ABD的度数.(2)小明、小芳和小兵三位同学同时测量△ABC的三边长,小明说:“三角形的周长是11”,小芳说:“有一条边长为4”,小兵说:“三条边的长度是三个不同的整数”.三边的长度分别是多少?24.(10分)如图所示,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=26°,求∠BED的度数;(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?25.(10分)如图所示,点P是△ABC内部一点,连接BP,并延长交AC于点D.(1)试探究∠1,∠2,∠A从大到小的排列顺序;(2)试探究线段AB+BC+CA与线段2BD的大小关系;(3)试探究线段AB+AC与线段PB+PC的大小关系.(第25题图)(第26题图)26.(12分)如图所示,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:(1)∠BAE的度数;(2)∠DAE的度数;(3)如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,是否能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.参考答案:1.C(解析:三角形的角平分线、中线、中位线都在三角形的内部,只有高可能在外部或者与三角形的边重合.)2.D(解析:根据三角形内角和定理,可知三角形三个内角的和为180°,所以三角形被遮住的两个角不可能是两个钝角.)3.D(解析:分别根据三角形外角的性质、三角形的分类及三角形的内角和定理对各选项进行逐一分析即可.A,B,C都正确.D.三角形的一个外角大于任何一个和它不相邻的内角,故本选项错误.)4.C(解析:根据三角形的高的定义对各选项分析判断后利用排除法求解.)5.A (解析:根据各类三角形的概念可知A 可以表示它们之间的包含关系.)6.D(解析:管理员正面朝前行走,转过的角的度数和正好为三角形的外角和360°.)7.D(解析:①因为∠A +∠B =∠C ,则2∠C =180°,∠C =90°,所以△ABC 是直角三角形;②因为∠A ∶∠B ∶∠C =1∶2∶3,设∠A =x ,则x +2x +3x =180°,x =30°,∠C =30°×3=90°,所以△ABC 是直角三角形;③因为∠A =90°-∠B ,所以∠A +∠B =90°,则∠C =180°-90°=90°,所以△ABC 是直角三角形;④因为∠A =∠B -∠C ,所以∠C +∠A =∠B ,又∠A +∠B +∠C =180°,2∠B =180°,解得∠B =90°,△ABC 是直角三角形.能确定△ABC 是直角三角形的有①②③④,共4个.)8.B(解析:因为△ABC 中,∠A =100°,∠B =40°,所以∠C =180°-∠A -∠B =180°-100°-40°=40°.)9.C(解析:因为∠A +∠B +∠C =180°,所以2(∠A +∠B +∠C )=360°,因为2(∠A +∠C )=3∠B ,所以∠B =72°,所以∠B 的外角度数是180°-∠B =108°.)10.D (解析:根据三角形的三边关系,两边之和大于第三边,最短的边长是1时,不成立;当最短的边长是2时,三边长是2,6,6;当最短的边长是3时,三边长是3,5,6;当最短的边长是4时,三边长是4,4,6和4,5,5.最短的边长一定不能大于4.综上可知有2,6,6;3,5,6;4,4,6和4,5,5,共4种截法.)11.B(解析:先由平行线的性质可得∠BFE =∠C =60°,∠CFD =∠B =45°,再根据平角定义求得答案.因为EF ∥AC ,所以∠BFE =∠C =60°.因为DF ∥AB ,∠CFD =∠B =45°,所以∠EFD =180°-∠BFE -∠CFD =180°-60°-45°=75°.)12.C(解析:因为AD ,CE 分别是△ABC 的高,所以S △ABC =12AB ·CE =12BC ·AD ,因为AD =2,CE =4,所以AB ∶BC =AD ∶CE =2∶4=1∶2.)13.C(解析:根据三角形的外角的性质,得∠B +∠C =∠CGE =180°-∠1,∠D +∠E =∠DFG =180°-∠2,两式相加再减去∠A ,根据三角形的内角和是180°可求解.因为∠B +∠C =∠CGE =180°-∠1,∠D +∠E =∠DFG =180°-∠2,所以∠B +∠C +∠D +∠E -∠A =360°-(∠1+∠2+∠A )=180°.) 14.C(解析:因为∠ABC =42°,∠A =60°,所以∠ACB =78°,因为BE 是∠ABC 的平分线,所以∠EBC =12∠ABC =12×42°=21°,同理得∠DCB =39°,在△FBC 中,∠BFC =180°-∠EBC -∠DCB =180°-21°-39°=120°.)15.B (解析:若两个螺丝的距离最大,则此时这个木框的形状为三角形,可根据三根木条的长来判断有几种三角形的组合,然后分别找出这些三角形的最长边即可.已知4根木条的四边长分别为2,3,4,6:①选2+3,4,6作为三角形,则三边长为5,4,6;5-4<6<5+4,能构成三角形,此时两个螺丝间的最大距离为6;②选3+4,6,2作为三角形,则三边长为2,7,6;6-2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;③选4+6,2,3作为三角形,则三边长为10,2,3;2+3<10,不能构成三角形,此种情况不成立;④选6+2,3,4作为三角形,则三边长为8,3,4;而3+4<8,不能构成三角形,此种情况不成立.综上所述,任意两个螺丝间的距离的最大值为7.)16.D(解析:△ABC 与△A 1BB 1底相等(AB =A 1B ),其高的比为1∶2(BB 1=2BC ),故面积比为1∶2,因为△ABC 的面积为1,所以S △A 1B 1B =2.同理可得,S △C 1B 1C =2,S △AA 1C 1=2,所以S △A 1B 1C 1=S △C 1B 1C +S △AA 1C 1+S △A 1B 1B +S △ABC =2+2+2+1=7;同理可得△A 2B 2C 2的面积=7×△A 1B 1C 1的面积=49,第三次操作后的面积为7×49=343,第四次操作后的面积为7×343=2401.故按此规律,要使得到的三角形的面积超过2014,最少经过4次操作.)17.30°(解析:根据题目给予的定义,得α=100°⇒2β=100°⇒β=50°,进一步求出最小内角是180°-100°-50°=30°.)18.0(解析:根据三角形三边满足的条件是两边和大于第三边,根据此来确定绝对值内的式子的正负,从而化简计算即可.因为a ,b ,c 是三角形的三边长,所以a +b -c >0,c -a -b <0,所以原式=a +b -c +c -a -b =0.)19.50(解析:连接AA',易得AD =A'D ,AE =A'E ,故∠1+∠2=2(∠DAA'+∠EAA')=2∠BAC =100°.故∠BAC =50°.)20.解:因为∠ADF =100°,∠FDE =30°,∠ADF +∠FDE +∠MDB =180°,所以∠MDB =180°-100°-30°=50°,因为∠B =45°,∠B +∠DMB +∠MDB =180°,所以∠DMB =180°-50°-45°=85°. 21.解:(1)150 90 (2)不变化.理由如下:∠ABX +∠ACX =∠ABC -∠XBC +∠ACB -∠XCB =(∠ABC +∠ACB )-(∠XBC +∠XCB )=150°-90°=60°.22.解:(1)AD 是△ABC 中BC 边上的中线,△ABC 中有三条中线,此时△ABD 与△ADC 的面积相等. (2)AE 是△ABC 中∠BAC 的平分线,△ABC 中角平分线有三条. (3)AF 是△ABC 中BC 边上的高线,△ABC 中有三条高线.23.解:(1)∠DBF =90°+β,∠ABF =90°+α,所以∠ABD =∠ABF -∠DBF =α-β. (2)因为三角形的周长是11,有一条边长为4,所以另两边的和为7,因为三条边的长度是三个不同的整数,所以另两边长可能为1与6,1+4=5<6,不符合三角形三边关系,舍去,另两边长可能为2与5,2+4=6>5,符合三角形三边关系,另两边长可能为3与4,4=4,不符合题意,舍去.所以另两边长为2与5,所以三边的长度应该是2,4,5.24.解:(1)∠BED =∠ABE +∠BAD =15°+26°=41°. (2)因为AD 为△ABC 的中线,BE 为△ABD 的中线,所以S △BDE =12×12S △ABC =14×40=10,设△BDE 中BD 边上的高为h ,则12×5h =10,解得h =4,即△BDE 中BD 边上的高为4.25.解:(1)因为∠2是△ABD 的外角,所以∠2>∠A ,因为∠1是△PDC 的外角,所以∠1>∠2,所以∠1>∠2>∠A. (2)在△ABD 中,AB +AD >BD ,① 在△BCD 中,BC +CD >BD ,② ①+②得AB +AD +BC +CD >2BD ,即AB +BC +CA >2BD. (3)在△ABD 中,AB +AD >BP +PD ,在△PDC 中,PD +CD >PC ,两式相加得AB +AD +PD +DC >BP +PD +PC ,即AB +AC >PB +PC.26.解:(1)因为∠B +∠C +∠BAC =180°,所以∠BAC =180°-∠B -∠C =180°-70°-30°=80°,因为AE 平分∠BAC ,所以∠BAE =12∠BAC =40°. (2)因为AD ⊥BC ,所以∠ADE =90°,而∠ADE =∠B +∠BAD ,所以∠BAD =90°-∠B =90°-70°=20°,所以∠DAE =∠BAE -∠BAD =40°-20°=20°. (3)能.理由如下:因为∠B +∠C +∠BAC =180°,所以∠BAC =180°-∠B -∠C ,因为AE 平分∠BAC ,所以∠BAE =12∠BAC =12(180°-∠B -∠C )=90°-12(∠B +∠C ),因为AD ⊥BC ,所以∠ADE =90°,而∠ADE =∠B +∠BAD ,所以∠BAD =90°-∠B ,所以∠DAE =∠BAE -∠BAD =90°-12(∠B +∠C )-(90°-∠B )=12(∠B -∠C ),因为∠B -∠C =40°,所以∠DAE =12×40°=20°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
美国
1.美国人口超过 亿, 人是美国的土著居民。
2、主要是 种人,占80%,其次为 种人和亚洲的 种
人。在 、 和 有华人聚居的唐人街。
3.各国移民移入美国后,经过长时期的融合,形成统一的 民族。
4. 美国领土构成:本土48个州、 州、 州。
主体
部分位于 阿拉斯加州北部位于 带,夏威夷州主要位于
带,
属于 洲。
5. 美国处于 洋和 洋之间,阿拉斯加北临
洋,所以美国是濒临三大洋,地跨 温度带的国家。美国还地
跨 洲和 洲两大洲。
6.美国地形分三部分,呈现南北纵列分布,西部 ,中部 ,
东部 。具体地说,西部是 山脉,中部是
平原,东部是 山脉。与美国相似,地形分西中东三部分的还
有 。
7.左图为美国地形图,读图填空:
⑴美国本土西临A 洋,东临
C 洋,南临B 湾。北面的邻国
是D ,南邻E 。
⑵美国的地形区:F 山,属于
纵贯南北美洲的 山系;
G 平原,H 山脉。
⑶美国与加拿大的界湖是 湖,
其中有世界上最大的淡水湖① 。
⑷世界第四长河② 河,长度
仅次于非洲的 河,南美洲
的 河,中国的 。
⑸美国最大的城市,也是联合国总部所在地
③ ,首都④ ,
南部最大城市⑤ ,中部最大城市
⑥ ,西部城市⑦ ,⑧ 东南的硅谷是美国最早、
规模最大的 产业中心。
⑹③④⑥所在的工业区是 工业区,⑤所在的工业区是 工业
区,⑦⑧所在的工业区是 工业区。
8. 美国的农业生产实现了 和
。美国的农业产品的生
产量和出口量居世界前列。
9.读右边美国农业带图,填空:
农业带:② ③ ④ ⑤
⑥ ⑦
影响④农业带的主要因素:这里是 带,地势 ,土壤 ,春
夏 较高,适合 的生长。
影响⑤农业带的主要因素:这里位
置 ,气候 ,适宜 的
生长。而且,这里 和 分
布密集,因此 业非常发达。
10.美国是世界第一 强国,
也是世界最大的 消耗国
和 排放国。
11. 北美地区通用的主要语言
是 ,拉丁美洲国家通用的主要语
言是_ 语
12. 美国的人口居世界第________位,居________、________之后。
13.下列国家中,北极圈和北回归线都穿过的国家是( )
A.加拿大 B.中国 C.美国 D.俄罗斯
巴西
1.巴西
是拉丁美洲 最大、 最多的国家,人口超过一亿。 人是巴
西土著居民。
2.在巴西, 种人占一半多,其次是 种人。
拉丁美洲是一个有大
量 种人的社会。
3. 巴西的世界之最:最大的平原 平原;最大的高原是 高原;
世界最大的河流 河,其上覆盖着地球面积最大的
目前世界上最大的水电站是巴西和巴拉圭合建的 水电站;
产量居世界第一位的热带经济作物 、 、 。
4. 巴西主体位于 带,是世界上国土广大的热带国家,以 气候
和 气候为主
。
5. 巴西 矿储量大、质地优良,产量和出口量都居世界前列。主要分布
在
6. 1992年6月,联合国环境与发展大会在巴西的 召开,通过了
以 发展为核心的 。
7. 热带雨林掠夺式开发的后果:① .
② ③ 。
8. 巴西的城市主要分布在 沿海地区, 是巴西最大
的城市和工业中心,也是世界特大城市之一。第二大城
市 ,首都 。
9.巴西人口的分布与 非常相似,都分布在
地区,原因是:这里地形平坦,土壤肥沃;对外交通便利;气候温暖湿润;
开发历史悠久。
巴西与澳大利亚相似的地方还有:都有丰富的优质的 矿。
10.巴西把首都从沿海的里约热内卢迁到内陆的巴西利亚,原因是:
①加强对 的开发和管理。
②缩小 地区城市的规模,避免出现 问题。
11.读右图填空:
河流① ,平原②
高原③ ,水电站④
城市⑤ ⑥ ⑦
纬线的名称:A B
濒临的大洋C
12. 广大的亚马孙平原地区人口_ ,这是
因为这里气候湿热, 密布,不适
于人类居住。
13. 有关巴西地理位置的叙述,正确的是
( )
A.巴西和美国所处的位置差不多,西面濒临太
平洋,东面濒临大西洋
B.巴西是拉丁美洲面积最大的国家,其国土全
部位于南半球
C.巴西东临大西洋,北、西、南与众多国家为
邻,是个海陆兼备的国家
D.巴西就西半球的位置来看,位于西半球,且是西半球面积最大的国家
14. 巴西人热衷的民间娱乐活动有: 、 、
15.热带雨林有哪些经济效益和环境效益,对全球气候有没有影响?
16.巴西的重工业为什么多集中在圣保罗、里约热内卢等地区?
