[数学]2016-2017年重庆市六校联考高一(上)数学期末试卷带解析word
重庆市第一中学2016-2017学年高一下学期期末考试数学试题+Word版含答案

2017年重庆一中高2019级高一下学而去期末考试数学试题卷第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、圆224x y +=与圆226890x y x y +-++=的位置关系为A .内切B .相交C .外切D .相离2、若,a b R ∈且1ab =,则下列不等式恒成立的是A .2a b +≥B .222a b +>C .2b a a b +≥D .112a b+≥ 3、为了解重庆一中1800名高一学生的身体生长的状况,用系统抽样法抽取60名同学进行检验,将学生从11800进行编号,若已知第1组抽取的号码为10,则第3组用简单随机抽样抽取的号码为A .60B .70C .80D .904、下表是韩老师1-4月份用电量(单位:十度)的一组数据:由散点图可知,用电量y 与月份x 间有较好的线性相关关系,其线性回归直线方程是ˆ0.7yx a =-+,则a =A .10.5B .5.25C .5.2D .5.155、已知等比数列{}n a 的前项和为n S ,且1234,2,a a a 依次成等差数列,若11a =,则5S =A .16B .31C .32D .636、若圆的方程为2260x y x +-=,则过点(1,2)的所有弦中,最短的弦长为A .12B .1C .2D .4 7、已知在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若2cos cos b A a B c +=,则c =A .1B .2C .3D .48、右边程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值,执行如图所示的程序框图,若输入01231,1,2,3,a a a a ====4504,5,1a a x ===-,则输出y 的值为A .15B .3C .3-D .15-9、若关于x 的不等式ax b <的解集为(2,)-+∞,则关于的不等式230ax bx a +->的解集为A .(,3)(1,)-∞--+∞B .(,1)(3,)-∞-+∞C .(3,1)-D .(1,3)-10、已知实数[0,1],[0,2]m n ∈∈,则关于x 的一元二次方程224420x mx n n +-+=有实根的概率是A .14π-B .4πC .32π-D .12π- 11、若平面区域200340x x y x y -≤⎧⎪+≥⎨⎪-+≥⎩夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是A...4 D12、(原创),已知,在直角梯形ABCD 中,//,,,223BC AD BC CD BAD AB BC π⊥∠===,动点P 在以C 为圆心且与直线BD 相切的圆上运动,若AP AB AD αβ=+,则αβ+的取值范围是A .[0,1]B .[0,2]C .[1,2]D .(,1][2,)-∞+∞第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..13、已知n S 为等差数列{}n a 的前n 项和,若6104a a +=,则15S =14、若向量(1,2),(3,),//()a b m a a b =-=+,则实数m =15、右图茎叶图表示的是甲乙两人在5次总和测评中的成绩,其中一个数字被无损,则乙的平均成绩超过甲的概率为16、(原创)已知实数,x y 满足2240x y xy ++-=,则33x y -的取值范围为三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤17、(本小题满分10分)已知两直线1:(3)453l m x y m ++=-和2:2(5)80l x m y ++-=.(1)若12//l l ,求实数m 的值;(2)当1m =时,若31l l ⊥,且3l 过点(1,4),求直线3l 的方程.18、(原创)(本小题满分12分)数列{}n a满足11()n a a n N ++=∈. (1)求证:数列{}2n a 是等差数列,并求出{}n a 的通项公式; (2)若12n n n b a a +=+,求数列{}n b 的前n 项和. 19、(原创)(本小题满分12分)十二届全国人大常委会第十八次会议于2015年12月27日通过关于修改人口与计划生育法的决定,“全面二孩”从2016年元旦开始实施,沙坪坝区妇联为了解该去市民不同年龄层对“全面二孩”政策的态度,随机抽取了M 名二胎妈妈对其年龄进行调查,得到如下所示的频率分布表和频率分布直方图:(1)求表中p 的值和频率分布直方图中a 的值;(2)拟用分层抽样的方法从年龄在[)20,25和[)35,40的二胎妈妈中共抽取6人召开一个座谈会,现从这6人中选2人,求这两人在不同年龄组的概率.20、(本小题满分12分)在ABC ∆中,030,B AC ∠==(1)若045A ∠=,求AB 的长;(2)求ABC ∆的面积的最大值.21、(原创)(本小题满分12分)已知直线:2230()l x my m m R +--=∈.(1)判断直线l 与圆224690x y x y +--+=的位置关系,并说明理由;(2)求实数m 的取值范围,使得总能找到一个同事满足下列条件的圆与直线l 相切:①面积为π;②其某条直径的两端点分别在两个坐标轴上.22、(原创)(本小题满分12分)已知平面上的曲线l 及点P ,在l 上任取一点Q ,线段PQ 长度的最小值称为点P 到曲线l 的距离,记作(,)d P l .(1)求点(3,4)P 到曲线22:4l x y +=的距离(,)d P l ; (2)设曲线222221,(11):(1)1(12)(1)1(21)y x l x y x x y x ⎧=-<<⎪-+=≤≤⎨⎪++=-≤≤-⎩,求点集{|2(,)3}S P d P l =<≤所表示图形的面积;(3)设曲线1:0(11)l y x =-≤≤,曲线222:1l x y +=,求出到两条曲线12,l l 距离相等的点的集合12{|(,)(,)}P d P l d P l Ω==.。
重庆市重庆一中2016-2017学年高二上学期期末考试试卷-数学(文)-Word版含答案

(本小题满分 12 分)设函数 f ( x) x3 12 x c 的图象经过原点. 19(原创) (1)求 c 的值及函数 f ( x) 的单调区间; (2)求函数 f ( x)在 -1,3 上的最大值和最小值.
20 . ( 本 小 题 满 分 12 分 ) 如 图 1 , 在 直 角 梯 形 ABCD 中 , ADC 90 , CD∥AB ,
1 AD CD AB 2 ,点 E 为 AC 的中点.将 △ADC 沿 AC 折起,使平面 ADC 平面 2
ABC ,得到几何体 D ABC 如图 2 所示.
3.已知 p, q 是两个命题, 若“p q” 是假命题,则( A. p假q假
2 2
B. p真q真
2 2
C. p假q真
D. p真q假 ) D.相离
4.圆 ( x 2) y 4 与圆 ( x 2) ( y 1) 9 的位置关系为( A.内切 5.抛物线 x A. y 1
8.已知双曲线 C :
x2 y 2 1(a 0, b 0) 的离心率为 2,则双曲线 C 的渐近线方程为( ) a 2 b2
B. y
3 x
A. y x
3 x 3
C. y 3 x
D. y
2 x 2
)
9.若函数 f ( x) x e ax 在区间 [0, ) 上单调递增,则实数 a 的取值范围是( A. [0,1) B. (0,1] C. [1, ) D. (,1]
(1)在 CD 上找一点 F ,使 AD∥ 平面 EFB ; (2)求点 C 到平面 ABD 的距离.
【精品】2016-2017年辽宁省抚顺市六校联合体高一(上)期末数学试卷带解析
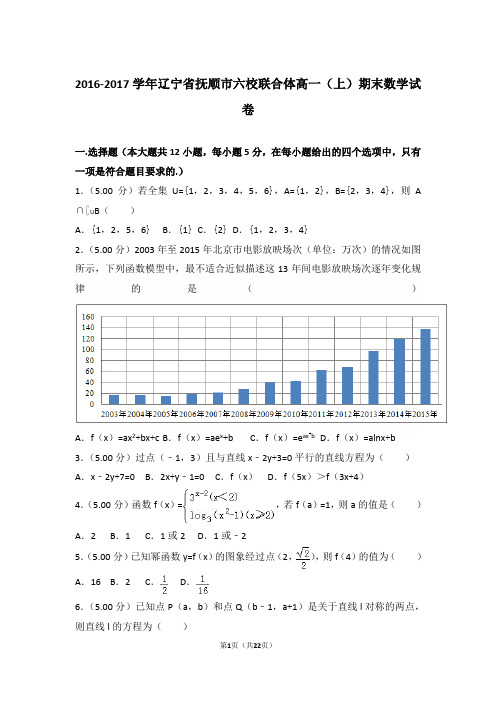
2016-2017学年辽宁省抚顺市六校联合体高一(上)期末数学试卷一.选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5.00分)若全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A ∩∁U B()A.{1,2,5,6}B.{1}C.{2}D.{1,2,3,4}2.(5.00分)2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是()A.f(x)=ax2+bx+c B.f(x)=ae x+b C.f(x)=e ax+b D.f(x)=alnx+b 3.(5.00分)过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为()A.x﹣2y+7=0 B.2x+y﹣1=0 C.f(x)D.f(5x)>f(3x+4)4.(5.00分)函数f(x)=,若f(a)=1,则a的值是()A.2 B.1 C.1或2 D.1或﹣25.(5.00分)已知幂函数y=f(x)的图象经过点(2,),则f(4)的值为()A.16 B.2 C.D.6.(5.00分)已知点P(a,b)和点Q(b﹣1,a+1)是关于直线l对称的两点,则直线l的方程为()A.x+y=0 B.x﹣y=0 C.x﹣y+1=0 D.x+y﹣1=07.(5.00分)设a=log410,b=log23,c=20.5,则()A.a>c>b B.b>c>a C.a>b>c D.c>b>a8.(5.00分)设α,β是两个不同的平面,m,n是两条不同的直线,给出下列四个论断①m∥n;②α∥β③m⊥α;④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,则一共可以写出真命题的个数为()A.1 B.2 C.3 D.49.(5.00分)一个几何体的三视图如图所示(单位:cm),那么此几何体的表面积(单位:cm2)是()A.102 B.128 C.144 D.18410.(5.00分)已知函数y=f(x)(x∈R)是奇函数且当x∈(0,+∞)时是减函数,若f(1)=0,则函数y=f(x2﹣2x)的零点共有()A.4个 B.6个 C.3个 D.5个11.(5.00分)利用“长方体ABCD﹣A1B1C1D1中,四面体A1BC1D”的特点,求得四面体PMNR(其中PM=NR=,PN=MR=,MN=PR=)的外接球的表面积为()A.14πB.16πC.13πD.15π12.(5.00分)对于函数f(x),若在其定义域内存在两个实数a,b(a<b),当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“Kobe函数”.若函数f(x)=k+是“Kobe函数”,则实数k的取值范围是()A.[﹣1,0]B.[1,+∞)C.D.二.填空题(本大题共4道小题,每道小题5分,满分20分.)13.(5.00分)已知集合A={x|x2﹣2x+a>0},且1∉A,则实数a的取值范围是.14.(5.00分)在△ABC中,AB=2,BC=1,∠ABC=120°若将△ABC绕直线BC旋转一周,则所形的旋转体的体积是.15.(5.00分)直线和x轴,y轴分别交于点A,B,以线段AB为一边在第一象限内作等边△ABC,则点C的坐标为.16.(5.00分)下列四个命题中,正确的是(写出所有正确命题的序号)①函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];②设集合A={﹣1,0,1},B={﹣1,1},则在A到B的所有映射中,偶函数共有4个;③不存在实数a,使函数的值域为(0,1]④函数在[2,+∞)上是减函数,则﹣4<a≤4.三.解答题(本大题共6道小题,满分70分,解答应写出文字说明,证明过程或演算步骤.)17.(10.00分)如图,在平行四边形OABC中,过点C(1,3)做CD⊥AB,垂足为点D,试求CD所在直线的一般式方程.18.(12.00分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(保留画图痕迹,不用说明画法和理由)(Ⅱ)求平面α把该长方体分成的两部分中较小部分的体积.19.(12.00分)已知集合A=(﹣∞,﹣1)∪(3,+∞),B={x|x2﹣4x+a=0,a ∈R}.(Ⅰ)若A∩B≠∅,求a的取值范围;(Ⅱ)若A∩B=B,求a的取值范围.20.(12.00分)为了绿化城市,准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR ⊥CD,经测量BC=70m,CD=80m,DE=100m,AE=60m问应如何设计才能使草坪的占地面积最大?并求出最大面积(精确到1m2).21.(12.00分)如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF ⊥PC垂足为F.(Ⅰ)设平面AEF∩PD=G,求证:PC⊥AG;(Ⅱ)设PA=,M是线段PC的中点,求证:DM∥平面AEC.22.(12.00分)已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有>0.(Ⅰ)证明f(x)在[﹣1,1]上是增函数;(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0(Ⅲ)若f(x)≤t2﹣2at+1对∀x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t 的取值范围.2016-2017学年辽宁省抚顺市六校联合体高一(上)期末数学试卷参考答案与试题解析一.选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5.00分)若全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A ∩∁U B()A.{1,2,5,6}B.{1}C.{2}D.{1,2,3,4}【分析】先求出C U B,由此利用交集定义能求出A∩∁U B.【解答】解:∵全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},∴C U B={1,5,6},∴A∩∁U B={1}.故选:B.2.(5.00分)2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是()A.f(x)=ax2+bx+c B.f(x)=ae x+b C.f(x)=e ax+b D.f(x)=alnx+b【分析】由图象可得:这13年间电影放映场次逐年变化规律的是随着x的增大,f(x)逐渐增大,图象逐渐上升.根据函数的单调性与图象的特征即可判断出结论.【解答】解:由图象可得:这13年间电影放映场次逐年变化规律的是随着x的增大,f(x)逐渐增大,图象逐渐上升.对于A.f(x)=ax2+bx+c,取a>0,<0,可得满足条件的函数;对于B.取a>0,b>0,可得满足条件的函数;对于C.取a>0,b>0,可得满足条件的函数;对于D.a>0时,为“上凸函数”,不符合图象的特征;a<0时,为单调递减函数,不符合图象的特征.故选:D.3.(5.00分)过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为()A.x﹣2y+7=0 B.2x+y﹣1=0 C.f(x)D.f(5x)>f(3x+4)【分析】设过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为x﹣2y+m=0,把点(﹣1,3)代入直线方程,求出m值即得直线l的方程.【解答】解:设过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为x﹣2y+m=0,把点(﹣1,3)代入直线方程得﹣1﹣2×3+m=0,m=7,故所求的直线方程为x﹣2y+7=0,故选:A.4.(5.00分)函数f(x)=,若f(a)=1,则a的值是()A.2 B.1 C.1或2 D.1或﹣2【分析】根据分段函数,直接解方程即可得到结论.【解答】解:若a<2,则由f(a)=1得,3a﹣2=1,即a﹣2=0,∴a=2.此时不成立.若a≥2,则由f(a)=1得,log=1,得a2﹣1=3,即a2=4,∴a=2,故选:A.5.(5.00分)已知幂函数y=f(x)的图象经过点(2,),则f(4)的值为()A.16 B.2 C.D.【分析】求出幂函数的解析式,然后求解函数值即可.【解答】解:设幂函数为y=xα,∵幂函数y=f(x)的图象经过点(2,),∴=2α,解得α=.y=x.f(4)==.故选:C.6.(5.00分)已知点P(a,b)和点Q(b﹣1,a+1)是关于直线l对称的两点,则直线l的方程为()A.x+y=0 B.x﹣y=0 C.x﹣y+1=0 D.x+y﹣1=0【分析】由题意可得直线l为线段PQ的中垂线,求得PQ的中点为(,),求出PQ的斜率可得直线l的斜率,由点斜式求得直线l的方程,化简可得结果.【解答】解:∵点P(a,b)与Q(b﹣1,a+1)(a≠b﹣1)关于直线l对称,∴直线l为线段PQ的中垂线,PQ的中点为(,),PQ的斜率为=﹣1,∴直线l的斜率为1,即直线l的方程为y﹣1×(x﹣),化简可得x﹣y+1=0.故选:C.7.(5.00分)设a=log410,b=log23,c=20.5,则()A.a>c>b B.b>c>a C.a>b>c D.c>b>a【分析】利用指数函数、对数函数的单调性求解.【解答】解:∵a=log 410=>b=log23>=1.5,c=20.5=,∴a>b>c.故选:C.8.(5.00分)设α,β是两个不同的平面,m,n是两条不同的直线,给出下列四个论断①m∥n;②α∥β③m⊥α;④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,则一共可以写出真命题的个数为()A.1 B.2 C.3 D.4【分析】根据线面垂直、线线垂直、面面垂直的判定与性质,分别探究,即可得到答案.【解答】解:同垂直于一个平面的两条直线互相平行,同垂直于两个平行平面的两条直线也互相平行.故②③④⇒①同理,①②③⇒④,①②④⇒③,①③④⇒②为真命题故选:D.9.(5.00分)一个几何体的三视图如图所示(单位:cm),那么此几何体的表面积(单位:cm2)是()A.102 B.128 C.144 D.184【分析】由三视图知几何体为正四棱锥,且底面正方形的边长为8,斜高为5,代入公式计算可得答案.【解答】解:由三视图知几何体为正四棱锥,且底面正方形的边长为8,斜高为5,其直观图如图:∴几何体的表面积S=82+4××8×5=144.故选:C.10.(5.00分)已知函数y=f(x)(x∈R)是奇函数且当x∈(0,+∞)时是减函数,若f(1)=0,则函数y=f(x2﹣2x)的零点共有()A.4个 B.6个 C.3个 D.5个【分析】根据题意,由奇函数的性质可得f(0)=0,结合函数的奇偶性与单调性可得函数在(0,+∞)与(﹣∞,0)上各有一个零点,则y=f(x)共有3个零点,依次为﹣1、0、1,对于y=f(x2﹣2x),依次令x2﹣2x=﹣1、0、1,解可得x 的值,即可得函数(x2﹣2x)的零点数目,即可得答案.【解答】解:根据题意,函数y=f(x)是定义域为R的奇函数,则f(0)=0,当x∈(0,+∞)时是减函数,且f(1)=0,则函数在(0,+∞)上只有一个零点,若函数y=f(x)是奇函数且当x∈(0,+∞)时是减函数,则f(x)在(﹣∞,0)为减函数,又由f(1)=0,则f(﹣1)=﹣f(1)=0,则函数在(﹣∞,0)上只有一个零点,故函数y=f(x)共有3个零点,依次为﹣1、0、1,对于y=f(x2﹣2x),当x2﹣2x=﹣1,解可得x=1,当x2﹣2x=0,解可得x=0或2,当x2﹣2x=1,解可得x=1+或1﹣,故y=f(x2﹣2x)的零点共有5个;故选:D.11.(5.00分)利用“长方体ABCD﹣A1B1C1D1中,四面体A1BC1D”的特点,求得四面体PMNR(其中PM=NR=,PN=MR=,MN=PR=)的外接球的表面积为()A.14πB.16πC.13πD.15π【分析】构造长方体,使得面上的对角线长分别为,,,则长方体的对角线长等于四面体PMNR外接球的直径,即可求出四面体PMNR外接球的表面积.【解答】解:由题意,构造长方体,使得面上的对角线长分别为,,,则长方体的对角线长等于四面体PMNR外接球的直径.设长方体的棱长分别为x,y,z,则x2+y2=10,y2+z2=13,x2+z2=5,∴x2+y2+z2=14∴三棱锥O﹣ABC外接球的直径为,∴三棱锥S﹣ABC外接球的表面积为π•14=14π,故选:A.12.(5.00分)对于函数f(x),若在其定义域内存在两个实数a,b(a<b),当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“Kobe函数”.若函数f(x)=k+是“Kobe函数”,则实数k的取值范围是()A.[﹣1,0]B.[1,+∞)C.D.【分析】根据新定义,当x∈[a,b]时,f(x)的值域也是[a,b],可知函数f (x)是增函数,其图象与y=x有两个不同的交点.即可求解.【解答】解:由题意,当x∈[a,b]时,f(x)的值域也是[a,b],可知函数f (x)是增函数,其图象与y=x有两个不同的交点,可得:x=k+,必有两个不相等的实数根.即:x﹣k=,∵,即x≥1,∴1﹣k≥0,可得k≤1.那么:(x﹣k)2=x﹣1有两个不相等的实数根.其判别式△>0,即(2k+1)2﹣4k2﹣4>0,解得:k,∴实数k的取值范围是(,1].故选:D.二.填空题(本大题共4道小题,每道小题5分,满分20分.)13.(5.00分)已知集合A={x|x2﹣2x+a>0},且1∉A,则实数a的取值范围是(﹣∞,1] .【分析】本题考查的是集合元素的分布以及集合与集合间的运算问题.在解答时可先根据1∉A,读出集合A在实数集当中没有元素1,又集合A中的元素是由一元二次不等式构成的解集,故问题可转化为一元二次不等式没有实数1.由12﹣2+a≤0解得a的范围即可..【解答】解:根据1∉A,可知,集合A在实数集当中没有元素1,又集合A中的元素是由一元二次不等式构成的解集,故问题可转化为一元二次不等式没有实数1.由12﹣2+a≤0解得a≤1.故答案为:(﹣∞,1].14.(5.00分)在△ABC中,AB=2,BC=1,∠ABC=120°若将△ABC绕直线BC旋转一周,则所形的旋转体的体积是π.【分析】大圆锥的体积减去小圆锥的体积就是旋转体的体积,结合题意计算可得答案.【解答】解:依题意可知,旋转体是一个大圆锥去掉一个小圆锥,所以OA=,OB=1,所以旋转体的体积:=π,故答案为:π.15.(5.00分)直线和x轴,y轴分别交于点A,B,以线段AB为一边在第一象限内作等边△ABC,则点C的坐标为.【分析】由题意,A(,0),B(0,1),则|AB|=2,AC⊥x轴,即可求出点C 的坐标.【解答】解:由题意,A(,0),B(0,1),则|AB|=2,AC⊥x轴,∴点C的坐标为.故答案为.16.(5.00分)下列四个命题中,正确的是②③④(写出所有正确命题的序号)①函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];②设集合A={﹣1,0,1},B={﹣1,1},则在A到B的所有映射中,偶函数共有4个;③不存在实数a,使函数的值域为(0,1]④函数在[2,+∞)上是减函数,则﹣4<a≤4.【分析】①,函数f(x)的定义域为[0,2],0≤2x≤2,则函数f(2x)的定义域为[0,1];②,依题意可知依题意可知f(﹣1)=f(1),进而分值域中有1、2个元素进行讨论.当值域中只有一个元素时,此时满足题意的映射有2种,当值域中有两个元素时,此时满足题意的映射有2个;③,若存在实数a,使函数的值域为(0,1]时,ax2+2ax+3的值域为(﹣∞,0],即,a∈∅;④,令t=x2﹣ax+3a,则由函数f(x)=g(t)=log t 在区间[2,+∞)上为减函数,可得函数t在区间[2,+∞)上为增函数且t(2)>0,解得a.【解答】解:对于①,函数f(x)的定义域为[0,2],0≤2x≤2,则函数f(2x)的定义域为[0,1],故错;对于②,依题意可知f(﹣1)=f(1),进而分值域中有1、2个元素进行讨论.当值域中只有一个元素时,此时满足题意的映射有2种,当值域中有两个元素时,此时满足题意的映射有2个,共有4个,故正确;对于③,若存在实数a,使函数的值域为(0,1]时,ax2+2ax+3的值域为(﹣∞,0],即,a∈∅,故正确;对于④,函数在[2,+∞)上是减函数,则令t=x2﹣ax+3a,则由函数f(x)=g(t)=在区间[2,+∞)上为减函数,可得函数t在区间[2,+∞)上为增函数且t(2)>0,解得﹣4<a≤4,故正确.故答案为:②③④三.解答题(本大题共6道小题,满分70分,解答应写出文字说明,证明过程或演算步骤.)17.(10.00分)如图,在平行四边形OABC中,过点C(1,3)做CD⊥AB,垂足为点D,试求CD所在直线的一般式方程.【分析】根据原点坐标和已知的C点坐标,求出直线OC的斜率;根据平行四边形的两条对边平行得到AB平行于OC,又CD垂直与AB,所以CD垂直与OC,由(1)求出的直线OC的斜率,根据两直线垂直时斜率乘积为﹣1,求出CD所在直线的斜率,然后根据求出的斜率和点C的坐标写出直线CD的方程即可.【解答】解:因为点O(0,0),点C(1,3),所以OC所在直线的斜率为.(2分),在平行四边形OABC中,AB∥OC,因为CD⊥AB,所以CD⊥OC.所以CD所在直线的斜率为.(6分)所以CD所在直线方程为,即x+3y﹣10=0.(10分)18.(12.00分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(保留画图痕迹,不用说明画法和理由)(Ⅱ)求平面α把该长方体分成的两部分中较小部分的体积.【分析】(Ⅰ)在面ABCD中做HG平行于BC,连接EH,FG,则EFGH就是所求正方形.(Ⅱ)由图形可以看出左半部分体积小,由此能求出平面α把该长方体分成的两部分中较小部分的体积.【解答】解:(Ⅰ)交线围成的正方形EHGF,如图,在面ABCD中做HG平行于BC,连接EH,FG且HB=GC=6,则EF平行且等于HG,所以四边形EFGH是平行四边形,EF平行于A1D1,所以EF垂直面A1AB1B,所以EF垂直于EH,且由题意得EH=FG=10,所以EFGH是正方形.(6分)(Ⅱ)由图形可以看出左半部分体积小…(2分),所以平面α把该长方体分成的两部分中较小部分的体积:…(6分)19.(12.00分)已知集合A=(﹣∞,﹣1)∪(3,+∞),B={x|x2﹣4x+a=0,a ∈R}.(Ⅰ)若A∩B≠∅,求a的取值范围;(Ⅱ)若A∩B=B,求a的取值范围.【分析】构造函数令f(x)=x2﹣4x+a=(x﹣2)2+a﹣4,则对称轴为x=2,(Ⅰ)由题意得B≠∅,并有A∩B≠∅,即可求出a的范围,(Ⅱ)A∩B=B,则B⊆A,分类讨论,即可求出a的范围.【解答】解:令f(x)=x2﹣4x+a=(x﹣2)2+a﹣4,则对称轴为x=2,(Ⅰ)由题意得B≠∅,∴△=16﹣4a≥0,解得a≤4…①∵A∩B≠∅,又∵A=(﹣∞,﹣1)∪(3,+∞),∴f(3)<0,解得a<3…②,由①②得,实数a的取值范围为(﹣∞,3).(Ⅱ)∵A∩B=B,∴B⊆A,当△=16﹣4a<0,即a>4时,B=∅,这时满足A∩B=B,当△=16﹣4a≥0时,B≠∅,此时a≤4…③,∵B⊆A,∴f(﹣1)<0,解得a<﹣5…④,由③④,得a<﹣5.综上所述,得实数a的取值范围为(﹣∞,﹣5)∪[4,+∞).20.(12.00分)为了绿化城市,准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR ⊥CD,经测量BC=70m,CD=80m,DE=100m,AE=60m问应如何设计才能使草坪的占地面积最大?并求出最大面积(精确到1m2).【分析】如图,先以BC边所在直线为x轴,,以AE边所在直线为y轴建立平面直角坐标系,求得直线AB的方程,再设出Q坐标,由矩形面积公式建立模型,然后根据函数的类型选择适当的方法求其最值.【解答】解:如图,以BC边所在直线为x轴,,以AE边所在直线为y轴建立平面直角坐标系,则A(0,20),B(30,0).所以直线AB的方程为:+=1,(4分)即设,则矩形PQRD的面积为(0≤x≤30)(8分)化简,得(0≤x≤30)配方,(0≤x≤30)(12分)易得当x=5,y=时,S最大,其最大值为Smax≈6017m2(14分)21.(12.00分)如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF ⊥PC垂足为F.(Ⅰ)设平面AEF∩PD=G,求证:PC⊥AG;(Ⅱ)设PA=,M是线段PC的中点,求证:DM∥平面AEC.【分析】(Ⅰ)证明BC⊥平面ABP,可得AE⊥BC,再证明AE⊥平面PBC,PC⊥平面AEFG,即可证明:PC⊥AG;(Ⅱ)取PE中点N,连结MN,ND,BD,AC,设BD∩AC=O,连结EO,证明平面MND∥平面AEC,即可证明:DM∥平面AEC.【解答】证明:(Ⅰ)∵PA⊥平面ABCD,BC⊂平面ABCD,∴BC⊥PA;又∵BC⊥AB,PA∩AB=A,∴BC⊥平面ABP;而AE⊂平面ABP,∴AE⊥BC,又∵AE⊥PB,PB∩BC=B,∴AE⊥平面PBC;∵PC⊂平面PBC,∴PC⊥AE,又∵PC⊥EF,EF∩AE=E,∴PC⊥平面AEFG,∵AG⊂平面AEFG,∴PC⊥AG…(6分)(Ⅱ)∵,∴PE=2,BE=1,即PE=2EB,取PE中点N,连结MN,ND,BD,AC,设BD∩AC=O,连结EO,则在△PEC中,PN=NE,PM=MC,∴MN∥EC,同理ND∥EO,∵MN∩ND=N,∴平面MND∥平面AEC,又∵DM⊂平面DMN,∴DM∥平面AEC…(12分)22.(12.00分)已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有>0.(Ⅰ)证明f(x)在[﹣1,1]上是增函数;(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0(Ⅲ)若f(x)≤t2﹣2at+1对∀x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t 的取值范围.【分析】(Ⅰ)任取﹣1≤x1<x2≤1,则,由已知,可比较f(x1)与f(x2)的大小,由单调性的定义可作出判断;(Ⅱ)利用函数的奇偶性可把不等式化为f(x2﹣1)<f(3x﹣3),在由单调性得x2﹣1<3x﹣3,还要考虑定义域;(Ⅲ)要使f(x)≤t2﹣2at+1对∀x∈[﹣1,1]恒成立,只要f(x)max≤t2﹣2at+1,由f(x)在[﹣1,1]上是增函数易求f(x)max,再利用关于a的一次函数性质可得不等式组,保证对a∈[﹣1,1]恒成立;【解答】解:(Ⅰ)任取﹣1≤x1<x2≤1,则,∵﹣1≤x1<x2≤1,∴x1+(﹣x2)≠0,由已知,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴f(x)在[﹣1,1]上是增函数;(Ⅱ)∵f(x)是定义在[﹣1,1]上的奇函数,且在[﹣1,1]上是增函数,∴不等式化为f(x2﹣1)<f(3x﹣3),∴,解得;(Ⅲ)由(Ⅰ)知f(x)在[﹣1,1]上是增函数,∴f(x)在[﹣1,1]上的最大值为f(1)=1,要使f(x)≤t2﹣2at+1对∀x∈[﹣1,1]恒成立,只要t2﹣2at+1≥1⇒t2﹣2at≥0,设g(a)=t2﹣2at,对∀a∈[﹣1,1],g(a)≥0恒成立,∴,∴t≥2或t≤﹣2或t=0.赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC.(1)如图,当∠APB=90°时,若AC=5,PC=,求BC的长;(2)当∠APB=90°时,若AB=APBC的面积是36,求△ACB的周长.P2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
2016-2017学年抚顺市六校联合体高一上期末数学试卷(有答案)

2016-2017学年辽宁省抚顺市六校联合体高一(上)期末数学试卷一.选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)若全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A∩∁U B()A.{1,2,5,6}B.{1}C.{2}D.{1,2,3,4}2.(5分)2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是()A.f(x)=ax2+bx+c B.f(x)=ae x+b C.f(x)=e ax+b D.f(x)=alnx+b3.(5分)过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为()A.x﹣2y+7=0 B.2x+y﹣1=0 C.f(x)D.f(5x)>f(3x+4)4.(5分)函数f(x)=,若f(a)=1,则a的值是()A.2 B.1 C.1或2 D.1或﹣25.(5分)已知幂函数y=f(x)的图象经过点(2,),则f(4)的值为()A.16 B.2 C.D.6.(5分)已知点P(a,b)和点Q(b﹣1,a+1)是关于直线l对称的两点,则直线l的方程为()A.x+y=0 B.x﹣y=0 C.x﹣y+1=0 D.x+y﹣1=07.(5分)设a=log410,b=log23,c=20.5,则()A.a>c>b B.b>c>a C.a>b>c D.c>b>a8.(5分)设α,β是两个不同的平面,m,n是两条不同的直线,给出下列四个论断①m∥n;②α∥β③m⊥α;④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,则一共可以写出真命题的个数为()A.1 B.2 C.3 D.49.(5分)一个几何体的三视图如图所示(单位:cm),那么此几何体的表面积(单位:cm2)是()A.102 B.128 C.144 D.18410.(5分)已知函数y=f(x)(x∈R)是奇函数且当x∈(0,+∞)时是减函数,若f(1)=0,则函数y=f(x2﹣2x)的零点共有()A.4个 B.6个 C.3个 D.5个11.(5分)利用“长方体ABCD﹣A1B1C1D1中,四面体A1BC1D”的特点,求得四面体PMNR(其中PM=NR=,PN=MR=,MN=PR=)的外接球的表面积为()A.14πB.16πC.13πD.15π12.(5分)对于函数f(x),若在其定义域内存在两个实数a,b(a<b),当x∈[a,b]时,f (x)的值域也是[a,b],则称函数f(x)为“Kobe函数”.若函数f(x)=k+是“Kobe函数”,则实数k的取值范围是()A.[﹣1,0]B.[1,+∞)C.D.二.填空题(本大题共4道小题,每道小题5分,满分20分.)13.(5分)已知集合A={x|x2﹣2x+a>0},且1∉A,则实数a的取值范围是.14.(5分)在△ABC中,AB=2,BC=1,∠ABC=120°若将△ABC绕直线BC旋转一周,则所形的旋转体的体积是.15.(5分)直线和x轴,y轴分别交于点A,B,以线段AB为一边在第一象限内作等边△ABC,则点C的坐标为.16.(5分)下列四个命题中,正确的是(写出所有正确命题的序号)①函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];②设集合A={﹣1,0,1},B={﹣1,1},则在A到B的所有映射中,偶函数共有4个;③不存在实数a,使函数的值域为(0,1]④函数在[2,+∞)上是减函数,则﹣4<a≤4.三.解答题(本大题共6道小题,满分70分,解答应写出文字说明,证明过程或演算步骤.)17.(10分)如图,在平行四边形OABC中,过点C(1,3)做CD⊥AB,垂足为点D,试求CD 所在直线的一般式方程.18.(12分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(保留画图痕迹,不用说明画法和理由)(Ⅱ)求平面α把该长方体分成的两部分中较小部分的体积.19.(12分)已知集合A=(﹣∞,﹣1)∪(3,+∞),B={x|x2﹣4x+a=0,a∈R}.(Ⅰ)若A∩B≠∅,求a的取值范围;(Ⅱ)若A∩B=B,求a的取值范围.20.(12分)为了绿化城市,准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR⊥CD,经测量BC=70m,CD=80m,DE=100m,AE=60m问应如何设计才能使草坪的占地面积最大?并求出最大面积(精确到1m2).21.(12分)如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.(Ⅰ)设平面AEF∩PD=G,求证:PC⊥AG;(Ⅱ)设PA=,M是线段PC的中点,求证:DM∥平面AEC.22.(12分)已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有>0.(Ⅰ)证明f(x)在[﹣1,1]上是增函数;(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0(Ⅲ)若f(x)≤t2﹣2at+1对∀x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.2016-2017学年辽宁省抚顺市六校联合体高一(上)期末数学试卷参考答案与试题解析一.选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)若全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A∩∁U B()A.{1,2,5,6}B.{1}C.{2}D.{1,2,3,4}【解答】解:∵全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},∴C U B={1,5,6},∴A∩∁U B={1}.故选:B.2.(5分)2003年至2015年北京市电影放映场次(单位:万次)的情况如图所示,下列函数模型中,最不适合近似描述这13年间电影放映场次逐年变化规律的是()A.f(x)=ax2+bx+c B.f(x)=ae x+b C.f(x)=e ax+b D.f(x)=alnx+b【解答】解:由图象可得:这13年间电影放映场次逐年变化规律的是随着x的增大,f(x)逐渐增大,图象逐渐上升.对于A.f(x)=ax2+bx+c,取a>0,<0,可得满足条件的函数;对于B.取a>0,b>0,可得满足条件的函数;对于C.取a>0,b>0,可得满足条件的函数;对于D.a>0时,为“上凸函数”,不符合图象的特征;a<0时,为单调递减函数,不符合图象的特征.故选:D.3.(5分)过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为()A.x﹣2y+7=0 B.2x+y﹣1=0 C.f(x)D.f(5x)>f(3x+4)【解答】解:设过点(﹣1,3)且与直线x﹣2y+3=0平行的直线方程为x﹣2y+m=0,把点(﹣1,3)代入直线方程得﹣1﹣2×3+m=0,m=7,故所求的直线方程为x﹣2y+7=0,故选A.4.(5分)函数f(x)=,若f(a)=1,则a的值是()A.2 B.1 C.1或2 D.1或﹣2【解答】解:若a<2,则由f(a)=1得,3a﹣2=1,即a﹣2=0,∴a=2.此时不成立.若a≥2,则由f(a)=1得,log=1,得a2﹣1=3,即a2=4,∴a=2,故选:A.5.(5分)已知幂函数y=f(x)的图象经过点(2,),则f(4)的值为()A.16 B.2 C.D.【解答】解:设幂函数为y=xα,∵幂函数y=f(x)的图象经过点(2,),∴=2α,解得α=.y=x.f(4)==.故选:C.6.(5分)已知点P(a,b)和点Q(b﹣1,a+1)是关于直线l对称的两点,则直线l的方程为()A.x+y=0 B.x﹣y=0 C.x﹣y+1=0 D.x+y﹣1=0【解答】解:∵点P(a,b)与Q(b﹣1,a+1)(a≠b﹣1)关于直线l对称,∴直线l为线段PQ的中垂线,PQ的中点为(,),PQ的斜率为=﹣1,∴直线l的斜率为1,即直线l的方程为y﹣1×(x﹣),化简可得x﹣y+1=0.故选:C.7.(5分)设a=log410,b=log23,c=20.5,则()A.a>c>b B.b>c>a C.a>b>c D.c>b>a【解答】解:∵a=log 410=>b=log23>=1.5,c=20.5=,∴a>b>c.故选:C.8.(5分)设α,β是两个不同的平面,m,n是两条不同的直线,给出下列四个论断①m∥n;②α∥β③m⊥α;④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,则一共可以写出真命题的个数为()A.1 B.2 C.3 D.4【解答】解:同垂直于一个平面的两条直线互相平行,同垂直于两个平行平面的两条直线也互相平行.故②③④⇒①同理,①②③⇒④,①②④⇒③,①③④⇒②为真命题故选D.9.(5分)一个几何体的三视图如图所示(单位:cm),那么此几何体的表面积(单位:cm2)是()A.102 B.128 C.144 D.184【解答】解:由三视图知几何体为正四棱锥,且底面正方形的边长为8,斜高为5,其直观图如图:∴几何体的表面积S=82+4××8×5=144.故选C.10.(5分)已知函数y=f(x)(x∈R)是奇函数且当x∈(0,+∞)时是减函数,若f(1)=0,则函数y=f(x2﹣2x)的零点共有()A.4个 B.6个 C.3个 D.5个【解答】解:根据题意,函数y=f(x)是定义域为R的奇函数,则f(0)=0,当x∈(0,+∞)时是减函数,且f(1)=0,则函数在(0,+∞)上只有一个零点,若函数y=f(x)是奇函数且当x∈(0,+∞)时是减函数,则f(x)在(﹣∞,0)为减函数,又由f(1)=0,则f(﹣1)=﹣f(1)=0,则函数在(﹣∞,0)上只有一个零点,故函数y=f(x)共有3个零点,依次为﹣1、0、1,对于y=f(x2﹣2x),当x2﹣2x=﹣1,解可得x=1,当x2﹣2x=0,解可得x=0或2,当x2﹣2x=1,解可得x=1+或1﹣,故y=f(x2﹣2x)的零点共有5个;故选:D.11.(5分)利用“长方体ABCD﹣A1B1C1D1中,四面体A1BC1D”的特点,求得四面体PMNR(其中PM=NR=,PN=MR=,MN=PR=)的外接球的表面积为()A.14πB.16πC.13πD.15π【解答】解:由题意,构造长方体,使得面上的对角线长分别为,,,则长方体的对角线长等于四面体PMNR外接球的直径.设长方体的棱长分别为x,y,z,则x2+y2=10,y2+z2=13,x2+z2=5,∴x2+y2+z2=14∴三棱锥O﹣ABC外接球的直径为,∴三棱锥S﹣ABC外接球的表面积为π•14=14π,故选A.12.(5分)对于函数f(x),若在其定义域内存在两个实数a,b(a<b),当x∈[a,b]时,f (x)的值域也是[a,b],则称函数f(x)为“Kobe函数”.若函数f(x)=k+是“Kobe函数”,则实数k的取值范围是()A.[﹣1,0]B.[1,+∞)C.D.【解答】解:由题意,当x∈[a,b]时,f(x)的值域也是[a,b],可知函数f(x)是增函数,其图象与y=x有两个不同的交点,可得:x=k+,必有两个不相等的实数根.即:x﹣k=,∵,即x≥1,∴1﹣k≥0,可得k≤1.那么:(x﹣k)2=x﹣1有两个不相等的实数根.其判别式△>0,即(2k+1)2﹣4k2﹣4>0,解得:k,∴实数k的取值范围是(,1].故选D.二.填空题(本大题共4道小题,每道小题5分,满分20分.)13.(5分)已知集合A={x|x2﹣2x+a>0},且1∉A,则实数a的取值范围是(﹣∞,1] .【解答】解:根据1∉A,可知,集合A在实数集当中没有元素1,又集合A中的元素是由一元二次不等式构成的解集,故问题可转化为一元二次不等式没有实数1.由12﹣2+a≤0解得a≤1.故答案为:(﹣∞,1].14.(5分)在△ABC中,AB=2,BC=1,∠ABC=120°若将△ABC绕直线BC旋转一周,则所形的旋转体的体积是π.【解答】解:依题意可知,旋转体是一个大圆锥去掉一个小圆锥,所以OA=,OB=1,所以旋转体的体积:=π,故答案为:π.15.(5分)直线和x轴,y轴分别交于点A,B,以线段AB为一边在第一象限内作等边△ABC,则点C的坐标为.【解答】解:由题意,A(,0),B(0,1),则|AB|=2,AC⊥x轴,∴点C的坐标为.故答案为.16.(5分)下列四个命题中,正确的是②③④(写出所有正确命题的序号)①函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];②设集合A={﹣1,0,1},B={﹣1,1},则在A到B的所有映射中,偶函数共有4个;③不存在实数a,使函数的值域为(0,1]④函数在[2,+∞)上是减函数,则﹣4<a≤4.【解答】解:对于①,函数f(x)的定义域为[0,2],0≤2x≤2,则函数f(2x)的定义域为[0,1],故错;对于②,依题意可知f(﹣1)=f(1),进而分值域中有1、2个元素进行讨论.当值域中只有一个元素时,此时满足题意的映射有2种,当值域中有两个元素时,此时满足题意的映射有2个,共有4个,故正确;对于③,若存在实数a,使函数的值域为(0,1]时,ax2+2ax+3的值域为(﹣∞,0],即,a∈∅,故正确;对于④,函数在[2,+∞)上是减函数,则令t=x2﹣ax+3a,则由函数f (x)=g(t)=在区间[2,+∞)上为减函数,可得函数t在区间[2,+∞)上为增函数且t(2)>0,解得﹣4<a≤4,故正确.故答案为:②③④三.解答题(本大题共6道小题,满分70分,解答应写出文字说明,证明过程或演算步骤.)17.(10分)如图,在平行四边形OABC中,过点C(1,3)做CD⊥AB,垂足为点D,试求CD 所在直线的一般式方程.【解答】解:因为点O(0,0),点C(1,3),所以OC所在直线的斜率为.(2分),在平行四边形OABC中,AB∥OC,因为CD⊥AB,所以CD⊥OC.所以CD所在直线的斜率为.(6分)所以CD所在直线方程为,即x+3y﹣10=0.(10分)18.(12分)如图,长方体ABCD﹣A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(Ⅰ)在图中画出这个正方形(保留画图痕迹,不用说明画法和理由)(Ⅱ)求平面α把该长方体分成的两部分中较小部分的体积.【解答】解:(Ⅰ)交线围成的正方形EHGF,如图,在面ABCD中做HG平行于BC,连接EH,FG且HB=GC=6,则EF平行且等于HG,所以四边形EFGH是平行四边形,EF平行于A1D1,所以EF垂直面A1AB1B,所以EF垂直于EH,且由题意得EH=FG=10,所以EFGH是正方形.(6分)(Ⅱ)由图形可以看出左半部分体积小…(2分),所以平面α把该长方体分成的两部分中较小部分的体积:…(6分)19.(12分)已知集合A=(﹣∞,﹣1)∪(3,+∞),B={x|x2﹣4x+a=0,a∈R}.(Ⅰ)若A∩B≠∅,求a的取值范围;(Ⅱ)若A∩B=B,求a的取值范围.【解答】解:令f(x)=x2﹣4x+a=(x﹣2)2+a﹣4,则对称轴为x=2,(Ⅰ)由题意得B≠∅,∴△=16﹣4a≥0,解得a≤4…①∵A∩B≠∅,又∵A=(﹣∞,﹣1)∪(3,+∞),∴f(3)<0,解得a<3…②,由①②得,实数a的取值范围为(﹣∞,3).(Ⅱ)∵A∩B=B,∴B⊆A,当△=16﹣4a<0,即a>4时,B=∅,这时满足A∩B=B,当△=16﹣4a≥0时,B≠∅,此时a≤4…③,∵B⊆A,∴f(﹣1)<0,解得a<﹣5…④,由③④,得a<﹣5.综上所述,得实数a的取值范围为(﹣∞,﹣5)∪[4,+∞).20.(12分)为了绿化城市,准备在如图所示的区域ABCDE内修建一个矩形PQRD的草坪,其中∠AED=∠EDC=∠DCB=90°,点Q在AB上,且PQ∥CD,QR⊥CD,经测量BC=70m,CD=80m,DE=100m,AE=60m问应如何设计才能使草坪的占地面积最大?并求出最大面积(精确到1m2).【解答】解:如图,以BC边所在直线为x轴,,以AE边所在直线为y轴建立平面直角坐标系,则A(0,20),B(30,0).所以直线AB的方程为:+=1,(4分)即设,则矩形PQRD的面积为(0≤x≤30)(8分)化简,得(0≤x≤30)配方,(0≤x≤30)(12分)易得当x=5,y=时,S最大,其最大值为Smax≈6017m2(14分)21.(12分)如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.(Ⅰ)设平面AEF∩PD=G,求证:PC⊥AG;(Ⅱ)设PA=,M是线段PC的中点,求证:DM∥平面AEC.【解答】证明:(Ⅰ)∵PA⊥平面ABCD,BC⊂平面ABCD,∴BC⊥PA;又∵BC⊥AB,PA∩AB=A,∴BC⊥平面ABP;而AE⊂平面ABP,∴AE⊥BC,又∵AE⊥PB,PB∩BC=B,∴AE⊥平面PBC;∵PC⊂平面PBC,∴PC⊥AE,又∵PC⊥EF,EF∩AE=E,∴PC⊥平面AEFG,∵AG⊂平面AEFG,∴PC⊥AG…(6分)(Ⅱ)∵,∴PE=2,BE=1,即PE=2EB,取PE中点N,连结MN,ND,BD,AC,设BD∩AC=O,连结EO,则在△PEC中,PN=NE,PM=MC,∴MN∥EC,同理ND∥EO,∵MN∩ND=N,∴平面MND∥平面AEC,又∵DM⊂平面DMN,∴DM∥平面AEC…(12分)22.(12分)已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有>0.(Ⅰ)证明f(x)在[﹣1,1]上是增函数;(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0(Ⅲ)若f(x)≤t2﹣2at+1对∀x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.【解答】解:(Ⅰ)任取﹣1≤x1<x2≤1,则,∵﹣1≤x1<x2≤1,∴x1+(﹣x2)≠0,由已知,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴f(x)在[﹣1,1]上是增函数;(Ⅱ)∵f(x)是定义在[﹣1,1]上的奇函数,且在[﹣1,1]上是增函数,∴不等式化为f(x2﹣1)<f(3x﹣3),∴,解得;(Ⅲ)由(Ⅰ)知f(x)在[﹣1,1]上是增函数,∴f(x)在[﹣1,1]上的最大值为f(1)=1,要使f(x)≤t2﹣2at+1对∀x∈[﹣1,1]恒成立,只要t2﹣2at+1≥1⇒t2﹣2at≥0,设g(a)=t2﹣2at,对∀a∈[﹣1,1],g(a)≥0恒成立,∴,∴t≥2或t≤﹣2或t=0.。
湖南省六校联盟2016-2017学年高一上学期期末联考数学

数学试题一、选择题:本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}2|23,|50A x x B x Z x x =-<<=∈-<,则AB =( )A .{}1,2B .{}23,C .{}12,3,D .{}2,3,4 2. ,,m n l 为不重合的直线,,,αβγ为不重合的平面,则下列说法正确的是( ) A .,m l n l ⊥⊥,则//m n B .,αγβγ⊥⊥,则αβ⊥ C .//,//m n αα,则//m n D .//,//αγβγ,则//αβ3. 已知ABC ∆在斜二测画法下的平面直观图A B C '''∆,A B C '''∆是边长为a 的正三角形,那么在原ABC ∆的面积为( )A 2B 2C 2D .2 4.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50π C. 125π D .都不对5.在空间直角坐标系中,点()1,3,5P -关于xOy 面对称的点的坐标是 ( ) A .()1,3,5-- B .()1,3,5- C. ()1,3,5 D .()1,3,5--6.过点()1,2A 且与原点距离最大的直线方程为 ( )A .240x y +-=B .370x y +-= C. 250x y +-= D .350x y +-=7. 若20.320.3,log 0.3,2a b c ===,则,,a b c 的大小关系是( )A .a c b <<B .a b c << C. b a c << D .b c a << 8.若函数()()0,1xxf x ka aa a -=->≠在(),-∞+∞上既是奇函数又是增函数,则函数()()log a g x x k =+的图象是( )A .B . C.D .9.在平面直角坐标系xOy 中,以()1,1C 为圆心的圆与x 轴和y 轴分别相切于,A B 两点,点,N M 分别在线段,OA OB 上,若MN 与圆C 相切,则MN 的最小值为( )A .1B .2-2+ D.210.定义在R 上的奇函数()f x ,当0x ≥时,()()[)[)12log 1,0,113,1,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩,则关于x 的函数()()()01F x f x a a =-<<的所有零点之和为 ( ) A .21a- B .21a-- C. 12a -- D .12a -11.如图,在正四棱柱1111ABCD A B C D -中,11,2AB AA ==,点P 是平面1111A B C D 内的一个动点,则三棱锥P ABC -的正视图与俯视图的面积之比的最大值为 ( )A . 1B . 2 C.12 D .1412. 若函数()f x 是R 上的单调函数,且对任意实数x ,都有()21213x f f x ⎡⎤+=⎢⎥+⎣⎦,则()2log 3f =( )A .1B .45 C. 12D .0 二、填空题(本大题共4小题,每小题4分,共16分,将答案填在答题纸上)13.已知函数()2log ,03,0xx x f x x >⎧=⎨≤⎩,则14f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦.14.圆2240x y x +-=在点(P 处的切线方程为: .15.已知偶函数()f x 在区间[)0,+∞上单调递增,则满足()()213f x f -<的x 取值集合是 .16.在直角坐标系内,已知()3,2A 是圆C 上一点,折叠该圆两次使点A 分别与圆上不相同的两点(异于点A )重合,两次的折痕方程分别为10x y -+=和70x y +-=,若圆C 上存在点P ,使090MPN ∠=,其中,M N 的坐标分别为()(),0,,0m m -,则实数m 的取值集合为 .三、解答题 (本大题共6小题,共56分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分8分)已知集合{}1|121,|3819x A x m x m B x ⎧⎫=-≤≤+=≤≤⎨⎬⎩⎭. (1)当2m =时,求AB ;(2)若B A ⊆,求实数m 的取值范围. 18. (本小题满分8分)已知圆()22:19C x y -+=内有一点()2,2P ,过点P 作直线l 交圆C 于A B 、两点.(1)当l 经过圆心C 时,求直线l 的方程; (2)当直线l 的倾斜角为45°时,求弦AB 的长. 19. (本小题满分8分) 已知函数()()b f x ax c a b c x =++、、是常数是奇函数,且满足()()5171,224f f ==. (1)求,,a b c 的值;(2)试判断函数()f x 在区间10,2⎛⎫⎪⎝⎭上的单调性并用定义证明. 20. (本小题满分10分)如图,在四棱锥P ABCD -中,侧面PAD ⊥底面ABCD ,侧棱PA PD ==,底面ABCD 为直角梯形,其中//,,222,BC AD AB AD AD AB BC O ⊥===为AD 中点.(1)求证:PO ⊥平面ABCD ;(2)求异面直线PB 与CD 所成角的余弦值;(3)线段AD 上是否存在Q ,使得它到平面PCD ?若存在,求出AQ QD的值;若不存在,请说明理由. 21. (本小题满分10分)已知圆22:2O x y +=,直线:2l y kx =-.(1)若直线l 与圆O 交于不同的两点,A B ,当2AOB π∠=时,求k 的值;(2)若1,2k P =是直线l 上的动点,过P 作圆O 的两条切线PC PD 、,切点为C D 、,探究:直线CD 是否过定点?若过定点则求出该定点,若不存在则说明理由;(3)若EF GH 、为圆22:2O x y +=的两条相互垂直的弦,垂足为M ⎛ ⎝,求四边形EGFH 的面积的最大值. 22. (本小题满分12分)设函数()y f x =的定义域为D ,值域为A ,如果存在函数()x g t =,使得函数()y f g t =⎡⎤⎣⎦的值域仍是A ,那么称()x g t =是函数()y f x =的一个等值域变换.(1)判断下列函数()x g t =是不是函数()y f x =的一个等值域变换?说明你的理由; ①()()21log ,0,,0f x x x x g t t t t=>==+>; ②()()21,,2,tf x x x x R xg t t R =-+∈==∈.(2)设()2log f x x =的定义域为[]2,8x ∈,已知()2231mt t nx g t t -+==+是()y f x =的一个等值域变换,且函数()y f g t =⎡⎤⎣⎦的定义域为R ,求实数m n 、的值.试卷答案一、选择题1-5: ADCBC 6-10: CCCDD 11、12:BC二、填空题13.1914. 40x +-= 15. {}|12x x -<< 16. []3,7三、解答题17.(1){}|25AB x x =-≤≤ (4分);(2)3m ≥ (4分)解:当2m =时,{}|15A x x =-≤≤,由B 中不等式变形得24333x -≤≤,解得24x -≤≤,即{}|24B x x =-≤≤.∴m 的取值范围为{}|3m m ≥.18.(1)220x y --=;(4分)(2(4分)试题解析:(1)已知圆()22:19C x y -+=的圆心为()1,0C ,因直线过点,P C ,所以直线l 的斜率为2,直线l 的方程为()21y x =-,即220x y --=.(2)当直线l 的倾斜角为45°时,斜率为1,直线l 的方程为22y x -=-,即0x y -=, 圆心C 到直线l,圆的半径为3,弦AB19.(1)12,,02a b c ===(4分)(2)证明见解析(4分) 解:(1)∵()f x 为奇函数,∴()()f x f x -=-,∴b bax c ax c x x--+=---,∴0c =,又()()5171,224f f ==,∴5217224a b b a ⎧+=⎪⎪⎨⎪+=⎪⎩,∴12,,02a b c ===.(2)由(1)可知()122f x x x =+.函数()f x 在区间10,2⎛⎫⎪⎝⎭上为减函数. 证明如下:任取12102x x <<<,则()()()()1212121212121212411112222222x x f x f x x x x x x x x x x x x x ⎛⎫--=+--=--=- ⎪⎝⎭. ∵12102x x <<<,∴1212120,20,410x x x x x x -<>-<. ∴()()()()12120f x f x f x f x ->⇒>,∴()f x 在102⎛⎫ ⎪⎝⎭,上为减函数.20.(1)证明见解析;(3分)(23分);(3)存在,13AQ QD =.(4分) 试题解析:(1)证明:在PAD ∆中,PA PD O =为AD 中点,所以PO AD ⊥. 又侧面PAD ⊥底面ABCD ,平面PAD 平面,ABCD AD PO =⊂平面PAD ,所以PO ⊥平面ABCD .(2)解:连接BO ,在直角梯形ABCD 中,//,22BC AD AD AB BC ==,有//OD BC 且OD BC =,所以四边形OBCD 是平行四边形,所以//DC OB . 由(1)知,PO OB POB ⊥∠为锐角, 所以POB ∠是异面直线PB 与CD 所成的角,因为222AD AB BC ===,在Rt AOB ∆中,1,1AB AO ==,所以OB =,在Rt POA ∆中,因为1AP AO ==,所以1OP =,在Rt PBO ∆中,PB =cos PBO ∠=,所以异面直线PB 与CD(3)解:假设存在点Q .设QD x =,则12DQC S x ∆=,由(2)得CD OB ==在POC Rt ∆中,PC =所以2,PCDPC CD DP S ∆====,由P DQC Q PCD V V --=得32x =,所以存在点Q 满足题意,此时13AQ QD =. 21.(1)k =(3分);(2)见解析(3分);(3)52(4分) 解析:(1)∵2AOB π∠=,∴点O 到l的距离d =,2k =⇒.(2)由题意可知:,,,O P C D 四点共圆且在以OP 为直径的圆上,设1,22P t t ⎛⎫- ⎪⎝⎭.其方程为:()1202x x t y y t ⎛⎫-+-+= ⎪⎝⎭, 即221202x tx y t y ⎛⎫-+--=⎪⎝⎭, 又C D 、在圆22:2O x y +=上, ∴1:2202CD l tx t y ⎛⎫+--=⎪⎝⎭,即2202y x t y ⎛⎫+--= ⎪⎝⎭,由02220y x y ⎧+=⎪⎨⎪+=⎩,得121x y ⎧=⎪⎨⎪=-⎩ ∴直线CD 过定点112⎛⎫- ⎪⎝⎭,.(3)设圆心O 到直线EF GH 、的距离分别为12,d d .则2221232d d OM+==,∴EF ===1522S EF GH ====≤, 当且仅当2234d =,即12d d ===”∴四边形EGFH 的面积的最大值为52. 22.(1)①不是等值域变换,②是等值域变换;(5分)(2)55m n ==(7分) 解:(1)①不是等值域变换,②()221331244f x x x x ⎛⎫=-+=-+≥ ⎪⎝⎭,即()f x 的值域为3,4⎡⎫+∞⎪⎢⎣⎭,当t R ∈时,()21332244t f g t ⎛⎫=-+≥⎡⎤ ⎪⎣⎦⎝⎭,即()y f g t =⎡⎤⎣⎦的值域仍为3,4⎡⎫+∞⎪⎢⎣⎭,所以()x g t =是()f x 的一个等值域变换,故①不是等值域变换,②是等值域变换;(2)()2log f x x =定义域为[]2,8,因为()x g t =是()f x 的一个等值域变换,且函数()y f g t =⎡⎤⎣⎦的定义域为R ,∴()223,1mt t nx g t t R t -+==∈+的值域为[]2,8, ()()22222328213811mt t n t mt t n t t -+≤≤⇔+≤-+≤++, ∴恒有()()()()12289422094880m m n m n <<⎧⎪∆=---=⎨⎪∆=---=⎩,解得55m n ⎧=-⎪⎪⎨⎪=+⎪⎩。
广东省六校2016-2017学年高一上学期期中联考数学试题 Word版含解析

2016-2017学年上学期期中六校联考高一数学一、选择题:本大题共12小题,每小题5分,共60分.1. 已知全集,集合,,则().A. B. C. D.【答案】C【解析】试题分析:由题意得,所以,故选C.考点:集合的运算.2. 下图分别为集合到集合的对应,其中,是从到的映射的是().A. ()()B. ()()()C. ()()()D. ()()()()【答案】A【解析】()()中的每一元素满足在中有唯一确定的元素和它们相对应,故()是映射,()中元素在中有两个元素和它对应,不满意映射定义,故()不是映射,()中元素在中有两个元素和它对应,且元素无元素和它对应,故()不是映射.故选.3. 函数的零点所在的区间是().A. B. C. D.【答案】B【解析】试题分析:解:∵函数f(x)=2x+3x是R上的连续函数,且单调递增,f(-1)=2-1+3×(-1)=-<0,f(0)=20+0=1>0,∴f(-1)f(0)<0.∴f(x)=2x+3x的零点所在的一个区间为(-1,0),故答案为(-1,0).选B.考点:函数零点点评:本题主要考查函数零点的概念与零点定理的应用,属于容易题。
视频4. 下列所示的图形中,可以作为函数的图像是().A. B. C. D.【答案】D【解析】作直线与曲线相交,由函数的概念可知,定义域中任意一个自变量对应唯一的函数值,∴是的函数,那么直线移动中始终与曲线只有一个交点,于是可排除,,,.只有符合.故选.5. 已知,,,则,,的大小关系是().A. B. C. D.【答案】A故选A.6. 已知函数的值域为,则().A. B. C. D.【答案】C【解析】,由题意,得,,,,∴,.故选.7. 已知函数,若,则().A. B. C. D.【答案】A【解析】,,所以.故选.8. 若集合,则().A. B. C. D.【答案】B【解析】,解得,即,所以为.故选.9. 若函数在上单调递增,则实数的取值范围是().A. B. C. D.【答案】D【解析】因为在上单调递增,所以,解得,.故选.点睛:本题考查分段函数的单调性,解决本题的关键是熟悉指数函数,一次函数的单调性,确定了两端函数在区间上单调以外,仍需考虑分界点两侧的单调性,需要列出分界点出的不等关系.10. 对于任意实数,符号表示的整数部分,即是不超过的最大整数,例如;;即函数叫做“取整部分”,它在数学本身和生产实践中有广泛应用,那么的值为().A. B. C. D.【答案】C【解析】由于,有个,,有个,,有个,∴.故选C.11. 已知函数是定义在区间上的偶函数,当,是减函数,如果不等式成立,则实数的取值范围是().A. B. C. D.【答案】A考点:函数的奇偶性与单调性.12. 用表示,,三个数中的最大值,设,,则取得最小值时所在的区间为().A. B. C. D.【答案】B【解析】分别作出,,在的图象,函数,的图象为如图中的实线部分.由图象可得的最低点为,即为和的交点,设的横坐标为,,在递增,,,由函数的零点存在定理可得,.故选.点睛:本题利用数形结合思想很好的解释了题中新函数表示,,三个数中的最大值的意义.函数取最小值,涉及到两函数的交点的求解,但是和联立不好求解,于是可以利用零点存在定理可以找到零点的所在的区间.二、填空题:本大题共4小题,每小题5分,共20分.13. 函数的定义域是__________.【答案】【解析】,解得.故答案为:.点睛:常见基本初等函数定义域的基本要求(1)分式函数中分母不等于零.(2)偶次根式函数的被开方式大于或等于0.(3)一次函数、二次函数的定义域均为R.(4)y=x0的定义域是{x|x≠0}.(5)y=a x(a>0且a≠1),y=sin x,y=cos x的定义域均为R.(6)y=log a x(a>0且a≠1)的定义域为(0,+∞).14. 已知幂函数的图像经过点,则函数的解析式为__________.【答案】【解析】幂函数的图象经过点,所以,解得:,所以函数.故答案为:.15. 若,,那么__________.【答案】15【解析】令,解得,当时,,所以.故答案为:15.16. 设函数是定义在上的偶函数,且对任意恒有,已知当,,则下列命题:①是函数的周期;②函数在上递减,在上递增;③函数的最大值是,最小值时是;④当,.其中,正确的命题的序号是__________.【答案】①②④【解析】∵对任意的恒有,∴则的周期为,故①正确;∵函数是定义在上的偶函数,当时,,∴函数在上是增函数,函数在上是减函数,所以在上递减,在上是增函数,故②正确;∴函数的最大值是,最小值为,故③不正确;设,则,,故④正确.故答案为:①②④.三、解答题:本大题共6个小题,满分70分.解答须写出说明.证明过程和演算步骤.17. 计算下列各式的值:().().【答案】(1);(2)3.【解析】试题分析:(1)由已知利用指数性质、运算法则求解.(2)由已知利用对数性质、运算法则求解.试题解析:()原式(或写成).()原式.18. 已知集合,.()当时,求.()若,求实数的取值集合.【答案】(1);(2).【解析】试题分析:(1)根据两个集合的交集的定义求出A∩B.(2)根据B⊆A,分B=∅时和B≠∅时两种情况,分别求得m的范围,再取并集,即得所求.试题解析:(),当时,,.()当时,,所以满足题意;当时,由题意,解得.综上知:实数的取集合.19. 已知函数为奇函数,当,.()求当时,函数的解析式.()设,作出的图像,并由图指出的单调区间和值域.【答案】(1);(2)单调增区间为,单调减区间,值域为.【解析】试题分析:(1)由奇函数可得当时,,则,即可得解;(2)根据分段函数的解析式得到图象,由图像可得单调区间和值域.试题解析:()当时,,则,∵为奇函数,∴,∴,∴当时,函数的解析式为.()由图得单调增区间为,单调减区间,值域为.20. 已知函数.()判断并证明函数的奇偶性.()判断并用定义法证明函数的单调性,并求不等式的解集.【答案】(1)奇函数;(2).【解析】试题分析:(1)的定义域为,关于原点对称,进而验证可得函数为奇函数;(2)任取,,且,判断的正负可得单调性,从而根据函数单调性解不等式即可.试题解析:()是奇函数,证明如下:的定义域为,关于原点对称,,∴,所以为奇函数.()在上为增函数.证明:任取,,且,则,∵,,且,∴,,,∴即,∴在上为增函数,∵在上为增函数且,∴,∴,即的解集为.点睛:本题主要考查函数函数单调性的证明与应用,属于中档题.利用定义法判断函数的单调性的一般步骤是:(1)在已知区间上任取;(2)作差;(3)判断的符号(往往先分解因式,再判断各因式的符号),可得在已知区间上是增函数,可得在已知区间上是减函数.21. 某创业投资公司拟开发某种新能源产品,估计能获得万元到万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金(单位:万元)随投资收益(单位:万元)的增加而增加,且奖金不超过万元,同时奖金不超过收益的.()请分析函数是否符合公司要求的奖励函数模型,并说明原因.()若该公司采用函数模型作为奖励函数模型,试确定最小正整数的值.【答案】(1);(2)328.【解析】试题分析:(1)题意要求且,当时,验证此式,发现不合要求;故不符合要求.(2)对函数,通过单调性得出的最大值,由最大值得一个范围,又由恒成立,又得一个范围,两者的交集就是我们所求的答案.试题解析:(1)对于函数模型当时,为增函数,, 所以恒成立,但当时,, 即不恒成立,故函数模型不符合公司要求(2)对于函数模型, 即当,即时递增,为使对于恒成立, 即要,即,为使对于恒成立, 即要,即恒成立, 即恒成立,又, 故只需即可,所以综上,, 故最小的正整数的值为.22. 已知函数,.()当时,求在区间上的最大值和最小值.()解关于的不等式.()当时,若存在,使得,求实数的取值范围.【答案】(1)最大值为4,最小值为-5;(2)见解析;(3).【解析】试题分析:(1)时,函数在上是减函数,在上是增函数,从而得最值;(2)不等式,即,进而讨论解不等式即可;(3)时,为开口向下的抛物线,抛物线的对称轴为,只需即可.试题解析:()时,函数在上是减函数,在上是增函数,所以当时,有最大值,且,当时,有最小值,且.()不等式,即,当时,解得,当时,的两根为和,当时,,不等式的解集为:或,当时,,所以当时,,不等式的解集为:,当时,不等式的解集为:,当时,,不等式的解集为:,综上所述:当时,,不等式的解集为:或;当时,不等式的解集为:;当时,,不等式的解集为:;当时,不等式的解集为:;当时,不等式的解集为:.()时,为开口向下的抛物线,抛物线的对称轴为,若存在,使得,则,即,解得或,综上所述:的取值范围是.点睛:函数的存在性问题可转化为函数的最值问题处理,存“在,使得成立,等价于”,“在,使得成立,等价于”,当的最值不存在时,可用函数值域的端点值代替,但要注意等号能否取得。
2016-2017学年安徽省高一上学期期末考试数学联考试题word版含答案
2016-2017学年安徽省高一上学期期末联考考试数学试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知锐角α终边上一点A 的坐标为(2sin3,-2cos3),则角α的弧度数为 ( )A .3B .π-3C . 3-2π D .2π-3 2.将函数y =sin(x -π3)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移π3个单位,得到图象的解析式是( ) A .y =sin(2x +π3)B .y =sin(12x -π2)C .y =sin(12x -π6)D .y =sin(2x -π6)3.函数y =x +sin|x |,x ∈[-π, π]的大致图象是( )4.已知扇形的面积为2,扇形圆心角的弧度是4,则扇形的周长为( ) A.6 B. 12 5.已知当6x π=时,函数sin cos y x a x =+取最大值,则函数sin cos y a x x =-图象的一条对称轴为( ) A .3x π=-B .3x π=C .6x π=-D .6x π=6.函数f (x )=tan(2x -π3)的单调递增区间是 ( )A .[k π2-π12,k π2+5π12](k ∈Z) B .(k π2-π12,k π2+5π12)(k ∈Z) C .(k π+π6,k π+2π3)(k ∈Z)D .[k π-π12,k π+5π12](k ∈Z)7.化简=-+)4tan()4(sin 42cos 2απαπα( )A.αcosB.αsinC.1D.218.已知cos α=13,cos(α+β)=-13,且α,β∈⎝ ⎛⎭⎪⎫0,π2,则cos(α-β)的值等于( )A .-12B.12 C .-13D.23279.已知△ABC 的三个顶点A 、B 、C 及平面内一点P 满足PA PB PC AB ++=,则点P 与△ABC 的关系是 ( ) A. P 在△ABC 的内部 B. P 在△ABC 的外部C. P 是AB 边上的一个三等分点D. P 是AC 边上的一个三等分点10.若偶函数()f x 在区间[]1,0-上是减函数,,αβ是锐角三角形的两个内角,且αβ≠,则下列不等式中正确的是 ( )A .(cos )(cos )f f αβ> B.(sin )(cos )f f αβ< C.(cos )(sin )f f αβ< D.(sin )(sin )f f αβ>11.设D 为△ABC 的边AB 的中点,P 为△ABC 内一点,且满足25AP AD BC =+,则APD ABCSS =△△( ) A.35 B. 25 C. 15 D. 31012.如图,在OAB ∆中,点P 是线段OB 及AB 、AO 的延长线所围成的阴影区域内(含边界)的任意一点,且OP xOA yOB =+u u u r u u r u u u r,则在直角坐标平面上,实数对(),x y 所表示的区域在直线3y x -=的右下侧部分的面积是( ) A .72B .92C .4D .不能求二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)13.已知D 为三角形ABC 边BC 的中点,点P 满足PA →+BP →+CP →=0,AP →=λPD →,则实数λ的值为________. 14.sin 250°1+sin10°=________.15.已知函数f (x )=sin(ωx +φ+π6)(ω>0,0<φ≤π2)的部分图象如图所示,则φ的值为________.16.设、为平面向量,若存在不全为零的实数λ,μ使得λ+μ=0,则称、线性相关,下面的命题中,、、均为已知平面M 上的向量. ①若 =2,则、线性相关;②若、为非零向量,且 ⊥,则、 线性相关; ③若、 线性相关,、 线性相关,则、 线性相关; ④向量、 线性相关的充要条件是、 共线.上述命题中正确的是 (写出所有正确命题的编号)三、解答题(本大题共6小题,17题每小题10分,18-22题每小题12分,共70分,解答应写出文字说明、证明过程或演算步骤)17.设D 、E 、F 分别是ABC ∆的边BC 、CA 、AB 上的点,且AB AF 21=BC BD 31=,CA CE 41=,若记=,=,试用,表示、、。
数学---天津市六校联考2016-2017学年高一(上)期中试卷(解析版)
天津市六校联考2016-2017学年高一(上)期中数学试卷一.选择题(本大题共8小题,每题4分共32分)1.(4分)已知集合A={0,1},B={﹣1,0,a+3},且A⊆B,则a等于()A.1 B.0 C.﹣2 D.﹣32.(4分)设全集U=R,A={x∈N|1≤x≤5},B=x∈R|x2﹣x﹣2=0},则图中阴影表示的集合为()A.{﹣1} B.{2} C.{3,4,5} D.{3,4}3.(4分)函数f(x)=+lg(x﹣1)+(x﹣3)0的定义域为()A.{x|1<x≤4}B.{x|1<x≤4且x≠3}C.{x|1≤x≤4且x≠3}D.{x|x≥4}4.(4分)已知a=log0.60.5,b=ln0.5,c=0.60.5.则()A.a>b>c B.a>c>b C.c>a>b D.c>b>a5.(4分)设函数f(x)=ln(1﹣x)﹣ln(1+x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数6.(4分)函数y=2x-1+x﹣1的零点为x0,则x0∈()A.(﹣1,0)B.(0,)C.(,1)D.(1,)7.(4分)已知f(x)=log(x2﹣2x)的单调递增区间是()A.(1,+∞)B.(2,+∞)C.(﹣∞,0)D.(﹣∞,1)8.(4分)已知函数f(x)=,若存在x1∈(0,+∞),x2∈(﹣∞,0],使得f(x1)=f(x2),则x1的最小值为()A.log23 B.log32 C.1 D.2二.填空题(本大题共6小题,每题4分共24分)9.(4分)已知集合A={1,2a},B={a,b},若A∩B={},则A∪B为.10.(4分)设函数f(x)=,则f(2)=.11.(4分)已知定义域为[a﹣4,2a﹣2]的奇函数f(x)=2016x3﹣5x+b+2,则f(a)+f(b)的值为.12.(4分)若幂函数在(0,+∞)上是增函数,则m=.13.(4分)已知函数f(x)=log a x+b(a>0,a≠1)的定义域、值域都是[1,2],则a+b=.14.(4分)已知函数f(x)是定义在R上的奇函数,若f(x)=,则关于x的方程f(x)+a=0(0<a<1)的所有根之和为.三.解答题(本大题共5题)15.(12分)已知:函数f(x)=+lg(3x﹣9)的定义域为A,集合B={x|x﹣a<0,a∈R},(1)求:集合A;(2)求:A∩B≠∅,求a的取值范围.16.(12分)设集合A={x|(x﹣2m+1)(x﹣m+2)<0},B={x|1≤x+1≤4}.(1)若m=1,求A∩B;(2)若A∩B=A,求实数m的取值集合.17.(13分)已知函数f(x)=+bx(其中a,b为常数)的图象经过(1,3)、(2,3)两点.(I)求a,b的值,判断并证明函数f(x)的奇偶性;(II)证明:函数f(x)在区间[,+∞)上单调递增.18.(13分)已知函数f(x)=(a>0且a≠1)(1)若a=2,解不等式f(x)≤5;(2)若函数f(x)的值域是[4,+∞),求实数a的取值范围.19.(14分)已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有>0.(Ⅰ)证明f(x)在[﹣1,1]上是增函数;(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0(Ⅲ)若f(x)≤t2﹣2at+1对∀x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.参考答案一.选择题(本大题共8小题,每题4分共32分)1.C【解析】∵集合A={0,1},B={﹣1,0,a+3},且A⊆B,∴a+3=1∴a=﹣2故选C【点评】本题考查集合关系中的参数取值问题,解题的关键是由集合之间的关系得出参数所满足的方程或不等式,从而解同参数的取值范围,集合中参数的取值范围问题,是集合知识综合运用题,需要运用集合中的相关知识综合判断,正确转化,考查了推理判断能力及转化的思想2.A【解析】阴影部分为B∩(C R A),而A={x∈N|1≤x≤5},B={x∈R|x2﹣x﹣2=0}={﹣1,2},∴B∩(C R A)={x|x=﹣1},故选A.【点评】本题考查集合的基本运算和韦恩图,真确理解韦恩图表达的集合是解决本题的关键.3.B【解析】要使f(x)有意义,则:;解得1<x≤4,且x≠3;∴f(x)的定义域为{x|1<x≤4,且x≠3}.故选B.【点评】考查函数定义域的概念及求法,以及对数函数的定义域,并清楚x0中的x≠0.4.B【解析】log0.60.5>1,ln0.5<0,0<0.60.5<1,即a>1,b<0,0<c<1,故a>c>b,故选:B【点评】本题主要考查函数值的大小比较,利用指数函数和对数函数的单调性是解决本题的关键.5.B【解析】∵函数f(x)=ln(1﹣x)﹣ln(1+x)=ln,由,求得﹣1<x<1,可得它的定义域为(﹣1,1).再根据f(﹣x)=ln=﹣ln=﹣f(x),可得它为奇函数.在(0,1)上,ln(1﹣x)是减函数,﹣ln(1+x)是减函数,故函数f(x)=ln(1﹣x)﹣ln(1+x)是减函数,故选:B.【点评】本题主要考查函数的奇偶性、单调性的判断和证明,属于中档题.6.B【解析】设f(x)=2x﹣1+x﹣1,∵,,即,∴函数的零点.故选B.【点评】本题考查函数零点的存在性.掌握零点存在性定理并能运用是关键.属于基础题.7.C【解析】令t=x2﹣2x>0,求得x<0,或x>2,故函数的定义域为(﹣∞,0)∪(2,+∞),且f(x)=log(x2﹣2x)=g(t)=log t.根据复合函数的单调性,本题即求函数t=x2﹣2x在定义域内的减区间.再利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间为(﹣∞,0),故选:C.【点评】本题主要考查复合函数的单调性,二次函数的性质,体现了转化的数学思想,属于中档题.8.B【解析】x≤0,f(x)≥1∵存在x1∈(0,+∞),x2∈(﹣∞,0],使得f(x1)=f(x2),∴﹣1≥1,∴≥2,∴x1≥log32,∴x1的最小值为log32.故选:B.【点评】本题考查分段函数,考查函数的值域,考查学生分析解决问题的能力,正确转化是关键.二.填空题(本大题共6小题,每题4分共24分)9.{﹣2,1,}【解析】集合A={1,2a},B={a,b},若A∩B={},则2a=,即有a=﹣2,b=.则A∪B={﹣2,1,}.故答案为:{﹣2,1,}.【点评】本题考查集合的运算,主要是交集和并集的运算,考查运算能力,属于基础题.10.19【解析】函数f(x)=,∵2<6,∴f(2)=f(2+3)=f(5);又5<6,∴f(5)=f(5+3)=f(8);8>6,∴f(8)=3×8﹣5=19.所以得f(2)=19.故答案为:19.【点评】本题考查了对函数的定义域和解析式的理解和带值计算能力.属于基础题.11.0【解析】根据奇函数f(x)=2016x3﹣5x+b+2得定义域为[a﹣4,2a﹣2],可得a﹣4+(2a﹣2)=0,求得a=2,故条件为奇函数f(x)=2016x3﹣5x+b+2得定义域为[﹣2,2],∴f(0)=b+2=0,求得b=﹣2,∴f(x)=2016x3﹣5x,∴f(a)+f(b)=f(2)+f(﹣2)=f(2)﹣f(2)=0,故答案为:0.【点评】本题主要考查奇函数的定义和性质,属于基础题.12.﹣1【解析】∵幂函数在(0,+∞)上是增函数,∴,解得m=﹣1.故答案为﹣1.【点评】熟练掌握幂函数的定义和单调性是解题的关键.13.或3【解析】当0<a<1时,易知函数f(x)为减函数,由题意有解得:a=,b=2,符合题意,此时a+b=;当a>1时,易知函数为增函数,由题意有,解得:a=2,b=1,符合题意,此时a+b=3.综上可得:a+b的值为或3.故答案为:或3.【点评】本题考查对数函数的性质以及分类讨论的思想方法.分类讨论函数的单调性是正确解决本题关键.属于易错题.14.1﹣2a【解析】∵f(x)为定义在R上的奇函数∴f(﹣x)=﹣f(x),∵当x≥0时,f(x)=,∴当x<0时,f(x)=作出图象:∵关于x的方程f(x)+a=0(0<a<1)的根转化为f(x)的图象与y=﹣a(0<a<1)图象的交点问题.从图象上依次零点为:x1,x2,x3,x4,x5,根据对称性得到零点的值满足x1+x2=﹣6,x4+x5=6,x3满足:log(1﹣x3)=﹣a,解得:故得x1+x2+x3+x4+x5=1﹣2a故答案为:1﹣2a.【点评】本题考查了分段函数性质,图象以及应用,考查了函数的零点与函数的交点问题,属于中档题.三.解答题(本大题共5题)15.解(1)∵f(x)=+lg(3x﹣9)∴4﹣x≥0且3x﹣9>0,即x≤4且x>2,则A={x|2<x≤4}(2)B={x|x﹣a<0,a∈R}={x|x<a},由A∩B≠∅,因此a>2,所以实数a的取值范围是(2,+∞).【点评】本题主要考查了函数的定义域及其求法,以及并集及运算和子集的概念,属于基础题.16.解集合B={x|0≤x≤3}.…(1分)(1)若m=1,则A={x|﹣1<x<1},则A∩B={x|0≤x<1}.…(4分)(2)当A=∅即m=﹣1时,A∩B=A;当A≠∅即m≠﹣1时,(ⅰ)当m<﹣1时,A=(2m﹣1,m﹣2),要使得A∩B=A,A⊆B,只要,所以m的值不存在.(ii)当m>﹣1时,A=(m﹣2,2m﹣1),要使得A∩B=A,A⊆B,只要,∴m=2.综上所述,m的取值集合是{﹣1,2}.【点评】本题考查集合的运算与关系,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.17.解(Ⅰ)∵函数f(x)的图象经过(1,3)、(2,3)两点∴,得a=2,b=1,∴函数解析,定义域为:(﹣∞,0)∪(0,+∞),关于原点对称,又∵,∴函数f(x)是奇函数;(II)设任意的,且x1<x2,∵=∵,∴x2﹣x1>0,且2﹣x1x2<0,所以f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴函数f(x)在区间上单调递增.【点评】本题考查函数的奇偶性和单调性.判断奇偶性注意定义域要关于原点对称,这是必要条件;证明单调性问题关键是第二步作差,正确变形是关键.18.解(1)∵函数f(x)=(a>0且a≠1),∴a=2时,,∵f(x)≤5,∴当x≤2时,﹣x+6≤5,解得x≥1,∴1≤x≤2;当x>2时,3+log2x≤5,解得x≤4,∴2<x≤4.综上,不等式f(x)<5的解集为{x|1≤x≤4}.…(7分)(2)∵函数f(x)=(a>0且a≠1)的值域是[4,+∞),∴当x≤2时,f(x)=﹣x+6≥4,解得x≤2,∴x=2时,f(x)=﹣x+6=4;当x>2时,f(x)=3+log a x≥4,∴log a x≥1,当0<a<1时,x≤a,由x>2,得a≥2,无解;当a>1时,x≥a,由x>2,得a≤2,∴1<a≤2.∴实数a的取值范围是(1,2].…(14分)【点评】本题考查不等式的解法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意分段函数的定义、对数的性质及运算法则、不等式性质的合理运用.19.解(Ⅰ)任取﹣1≤x1<x2≤1,则,∵﹣1≤x1<x2≤1,∴x1+(﹣x2)≠0,由已知,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴f(x)在[﹣1,1]上是增函数;(Ⅱ)∵f(x)是定义在[﹣1,1]上的奇函数,且在[﹣1,1]上是增函数,∴不等式化为f(x2﹣1)<f(3x﹣3),∴,解得;(Ⅲ)由(Ⅰ)知f(x)在[﹣1,1]上是增函数,∴f(x)在[﹣1,1]上的最大值为f(1)=1,要使f(x)≤t2﹣2at+1对∀x∈[﹣1,1]恒成立,只要t2﹣2at+1≥1⇒t2﹣2at≥0,设g(a)=t2﹣2at,对∀a∈[﹣1,1],g(a)≥0恒成立,∴,∴t≥2或t≤﹣2或t=0.【点评】本题考查抽象函数的单调性、奇偶性,考查抽象不等式的求解,可从恒成立问题,考查转化思想,考查学生灵活运用知识解决问题的能力.。
数学---天津市六校联考2016-2017学年高一第一学期试题(解析版)
天津市六校联考2016-2017学年高一第一学期数学试题一.选择题1.已知集合A={0,1},B={﹣1,0,a+3},且A⊆B,则a等于()A.1 B.0 C.﹣2 D.﹣32.设全集U=R,A={x∈N|1≤x≤5},B=x∈R|x2﹣x﹣2=0},则图中阴影表示的集合为()A.{﹣1} B.{2} C.{3,4,5} D.{3,4}3.函数f(x)=+lg(x﹣1)+(x﹣3)0的定义域为()A.{x|1<x≤4}B.{x|1<x≤4且x≠3}C.{x|1≤x≤4且x≠3}D.{x|x≥4}4.已知a=log0.60.5,b=ln0.5,c=0.60.5.则()A.a>b>c B.a>c>b C.c>a>b D.c>b>a5.设函数f(x)=ln(1﹣x)﹣ln(1+x),则f(x)是()A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数6.函数y=2x﹣1+x﹣1的零点为x0,则x0∈()A.(﹣1,0)B.(0,)C.(,1)D.(1,)7.已知f(x)=log(x2﹣2x)的单调递增区间是()A.(1,+∞)B.(2,+∞)C.(﹣∞,0)D.(﹣∞,1)8.已知函数f(x)=,若存在x1∈(0,+∞),x2∈(﹣∞,0],使得f(x1)=f(x2),则x1的最小值为()A.log23 B.log32 C.1 D.2二.填空题9.已知集合A={1,2a},B={a,b},若A∩B={},则A∪B为.10.设函数f(x)=,则f(2)=.11.已知定义域为[a﹣4,2a﹣2]的奇函数f(x)=2016x3﹣5x+b+2,则f(a)+f(b)的值为.12.若幂函数在(0,+∞)上是增函数,则m=.13.已知函数f(x)=log a x+b(a>0,a≠1)的定义域、值域都是[1,2],则a+b=.14.已知函数f(x)是定义在R上的奇函数,若f(x)=,则关于x的方程f(x)+a=0(0<a<1)的所有根之和为.三.解答题15.已知:函数f(x)=+lg(3x﹣9)的定义域为A,集合B={x|x﹣a<0,a∈R},(1)求:集合A;(2)求:A∩B≠∅,求a的取值范围.16.设集合A={x|(x﹣2m+1)(x﹣m+2)<0},B={x|1≤x+1≤4}.(1)若m=1,求A∩B;(2)若A∩B=A,求实数m的取值集合.17.已知函数f(x)=+bx(其中a,b为常数)的图象经过(1,3)、(2,3)两点.(I)求a,b的值,判断并证明函数f(x)的奇偶性;(II)证明:函数f(x)在区间[,+∞)上单调递增.18.已知函数f(x)=(a>0且a≠1)(1)若a=2,解不等式f(x)≤5;(2)若函数f(x)的值域是[4,+∞),求实数a的取值范围.19.已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有>0.(Ⅰ)证明f(x)在[﹣1,1]上是增函数;(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0(Ⅲ)若f(x)≤t2﹣2at+1对∀x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.参考答案一.选择题1.C【考点】集合关系中的参数取值问题.【分析】由题设条件A={0,1},B={﹣1,0,a+3},且A⊆B,根据集合的包含关系知,应有a+3=1,由此解出a的值选出正确选项【解答】解:∵集合A={0,1},B={﹣1,0,a+3},且A⊆B,∴a+3=1∴a=﹣2故选C2.A【考点】Venn图表达集合的关系及运算.【分析】阴影部分为B∩(C R A),所以只需解出集合B,在进行集合运算即可.【解答】解:阴影部分为B∩(C R A),而A={x∈N|1≤x≤5},B={x∈R|x2﹣x﹣2=0}={﹣1,2},∴B∩(C R A)={x|x=﹣1},故选A.3.B【考点】函数的定义域及其求法.【分析】为使函数f(x)有意义,便可得出关于x的不等式组,解出x的范围,即得出f(x)的定义域.【解答】解:要使f(x)有意义,则:;解得1<x≤4,且x≠3;∴f(x)的定义域为{x|1<x≤4,且x≠3}.故选B.4.B【考点】对数值大小的比较.【分析】根据指数函数和对数函数的性质即可得到结论.【解答】解:log 0.60.5>1,ln 0.5<0,0<0.60.5<1,即a >1,b <0,0<c <1,故a >c >b ,故选:B5.B【考点】函数奇偶性的性质;函数单调性的判断与证明.【分析】由函数的解析式求得函数的定义域关于原点对称,再根据在(0,1)上,ln (1﹣x )和﹣ln (1+x )都是减函数可得f (x )是减函数,从而得出结论.【解答】解:∵函数f (x )=ln (1﹣x )﹣ln (1+x )=ln,由,求得﹣1<x <1,可得它的定义域为(﹣1,1).再根据f (﹣x )=ln =﹣ln =﹣f (x ),可得它为奇函数. 在(0,1)上,ln (1﹣x )是减函数,﹣ln (1+x )是减函数,故函数f (x )=ln (1﹣x )﹣ln (1+x )是减函数,故选:B .6.B【考点】函数零点的判定定理.【分析】根据函数零点的存在性定理,判断在区间两个端点的函数值是否异号即可.【解答】解:设f (x )=2x ﹣1+x ﹣1,∵,,即, ∴函数的零点.故选B .7.C 【考点】复合函数的单调性.【分析】令t=x2﹣2x>0,求得函数的定义域,且f(x)=g(t)=log t,根据复合函数的单调性,本题即求函数t=x2﹣2x在定义域内的减区间,利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间.【解答】解:令t=x2﹣2x>0,求得x<0,或x>2,故函数的定义域为(﹣∞,0)∪(2,+∞),且f(x)=log(x2﹣2x)=g(t)=log t.根据复合函数的单调性,本题即求函数t=x2﹣2x在定义域内的减区间.再利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间为(﹣∞,0),故选:C.8.B【考点】分段函数的应用.【分析】x≤0,f(x)≥1,存在x1∈(0,+∞),x2∈(﹣∞,0],使得f(x1)=f(x2),可得﹣1≥1,求出x1的范围,即可求出x1的最小值.【解答】解:x≤0,f(x)≥1∵存在x1∈(0,+∞),x2∈(﹣∞,0],使得f(x1)=f(x2),∴﹣1≥1,∴≥2,∴x1≥log32,∴x1的最小值为log32.故选:B.二.填空题(本大题共6小题,每题4分共24分)9.{﹣2,1,}【考点】并集及其运算.【分析】由A∩B={},可得∈A,∈B,进而得到a,b的值,再由并集的定义可得所求.【解答】解:集合A={1,2a},B={a,b},若A∩B={},则2a=,即有a=﹣2,b=.则A∪B={﹣2,1,}.故答案为:{﹣2,1,}.10.19【考点】函数的值.【分析】根据定义域范围代值计算即可.【解答】解:函数f(x)=,∵2<6,∴f(2)=f(2+3)=f(5);又5<6,∴f(5)=f(5+3)=f(8);8>6,∴f(8)=3×8﹣5=19.所以得f(2)=19.故答案为:19.11.0【考点】函数奇偶性的性质.【分析】根据定义域关于原点对称,求得a=2,再根据f(x)为奇函数,求得b=﹣2,再利用奇函数的性质求得f(a)+f(b)的值.【解答】解:根据奇函数f(x)=2016x3﹣5x+b+2得定义域为[a﹣4,2a﹣2],可得a﹣4+(2a ﹣2)=0,求得a=2,故条件为奇函数f(x)=2016x3﹣5x+b+2得定义域为[﹣2,2],∴f(0)=b+2=0,求得b=﹣2,∴f(x)=2016x3﹣5x,∴f(a)+f(b)=f(2)+f(﹣2)=f(2)﹣f(2)=0,故答案为:0.12.﹣1【考点】幂函数的概念、解析式、定义域、值域;幂函数图象及其与指数的关系.【分析】利用幂函数的定义和单调性即可得出.【解答】解:∵幂函数在(0,+∞)上是增函数,∴,解得m=﹣1.故答案为﹣1.13.或3【考点】对数函数的图象与性质.【分析】分类讨论a的取值范围,得到函数单调性,代入数据即可求解.【解答】解:当0<a<1时,易知函数f(x)为减函数,由题意有解得:a=,b=2,符合题意,此时a+b=;当a>1时,易知函数为增函数,由题意有,解得:a=2,b=1,符合题意,此时a+b=3.综上可得:a+b的值为或3.故答案为:或3.14.1﹣2a【考点】根的存在性及根的个数判断;函数奇偶性的性质.【分析】利用奇函数性质作出函数的图象,依次标出零点,根据对称性得到零点的值满足x1+x2,x4+x5的值,运用对数求解x3满足:log2(x3+1)=﹣a,可出x3,可求解有根之和.【解答】解:∵f(x)为定义在R上的奇函数∴f(﹣x)=﹣f(x),∵当x≥0时,f(x)=,∴当x<0时,f(x)=作出图象:∵关于x的方程f(x)+a=0(0<a<1)的根转化为f(x)的图象与y=﹣a(0<a<1)图象的交点问题.从图象上依次零点为:x1,x2,x3,x4,x5,根据对称性得到零点的值满足x1+x2=﹣6,x4+x5=6,x3满足:log(1﹣x3)=﹣a,解得:故得x1+x2+x3+x4+x5=1﹣2a故答案为:1﹣2a.三.解答题(本大题共5题)15.【考点】对数函数的定义域;集合关系中的参数取值问题.【分析】(1)被开方数大于等于0,对数的真数大于0,可求出集合A.(2)由A∩B≠∅,可知A与B有公共元素,可解出实数a的取值范围.【解答】解(1)∵f(x)=+lg(3x﹣9)∴4﹣x≥0且3x﹣9>0,即x≤4且x>2,则A={x|2<x≤4}(2)B={x|x﹣a<0,a∈R}={x|x<a},由A∩B≠∅,因此a>2,所以实数a的取值范围是(2,+∞).16.【考点】集合的包含关系判断及应用.【分析】(1)化简集合A,B,即可求A∩B;(2)若A∩B=A,A⊆B,分类讨论求实数m的取值集合.【解答】解:集合B={x|0≤x≤3}.…(1)若m=1,则A={x|﹣1<x<1},则A∩B={x|0≤x<1}.…(2)当A=∅即m=﹣1时,A∩B=A;当A≠∅即m≠﹣1时,(ⅰ)当m<﹣1时,A=(2m﹣1,m﹣2),要使得A∩B=A,A⊆B,只要,所以m的值不存在.(ii)当m>﹣1时,A=(m﹣2,2m﹣1),要使得A∩B=A,A⊆B,只要,∴m=2.综上所述,m的取值集合是{﹣1,2}.17.【考点】函数单调性的判断与证明;函数奇偶性的判断.【分析】(Ⅰ)把点的坐标代入解析式即可求出a,b,用奇偶性的定义判断即可;(Ⅱ)利用函数单调性的定义证明即可.【解答】解:(Ⅰ)∵函数f(x)的图象经过(1,3)、(2,3)两点∴,得a=2,b=1,∴函数解析,定义域为:(﹣∞,0)∪(0,+∞),关于原点对称,又∵,∴函数f(x)是奇函数;(II)设任意的,且x1<x2,∵=∵,∴x2﹣x1>0,且2﹣x1x2<0,所以f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴函数f(x)在区间上单调递增.18.【考点】分段函数的应用.【分析】(1)a=2时,当x≤2时,﹣x+6≤5;当x>2时,3+log2x≤5.由此能求出不等式f(x)<5的解集.(2)当x≤2时,f(x)=﹣x+6≥4,解得x=2时,f(x)=﹣x+6=4;当x>2时,f(x)=3+log a x≥4,得log a x≥1,由此能求出实数a的取值范围.【解答】解:(1)∵函数f(x)=(a>0且a≠1),∴a=2时,,∵f(x)≤5,∴当x≤2时,﹣x+6≤5,解得x≥1,∴1≤x≤2;当x>2时,3+log2x≤5,解得x≤4,∴2<x≤4.综上,不等式f(x)<5的解集为{x|1≤x≤4}.…(2)∵函数f(x)=(a>0且a≠1)的值域是[4,+∞),∴当x≤2时,f(x)=﹣x+6≥4,解得x≤2,∴x=2时,f(x)=﹣x+6=4;当x>2时,f(x)=3+log a x≥4,∴log a x≥1,当0<a<1时,x≤a,由x>2,得a≥2,无解;当a>1时,x≥a,由x>2,得a≤2,∴1<a≤2.∴实数a的取值范围是(1,2].…19.【考点】奇偶性与单调性的综合;函数单调性的判断与证明;函数奇偶性的判断.【分析】(Ⅰ)任取﹣1≤x1<x2≤1,则,由已知,可比较f(x1)与f(x2)的大小,由单调性的定义可作出判断;(Ⅱ)利用函数的奇偶性可把不等式化为f(x2﹣1)<f(3x﹣3),在由单调性得x2﹣1<3x﹣3,还要考虑定义域;(Ⅲ)要使f(x)≤t2﹣2at+1对∀x∈[﹣1,1]恒成立,只要f(x)max≤t2﹣2at+1,由f(x)在[﹣1,1]上是增函数易求f(x)max,再利用关于a的一次函数性质可得不等式组,保证对a∈[﹣1,1]恒成立;【解答】解:(Ⅰ)任取﹣1≤x1<x2≤1,则,∵﹣1≤x1<x2≤1,∴x1+(﹣x2)≠0,由已知,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),∴f(x)在[﹣1,1]上是增函数;(Ⅱ)∵f(x)是定义在[﹣1,1]上的奇函数,且在[﹣1,1]上是增函数,∴不等式化为f(x2﹣1)<f(3x﹣3),∴,解得;(Ⅲ)由(Ⅰ)知f(x)在[﹣1,1]上是增函数,∴f(x)在[﹣1,1]上的最大值为f(1)=1,要使f(x)≤t2﹣2at+1对∀x∈[﹣1,1]恒成立,只要t2﹣2at+1≥1⇒t2﹣2at≥0,设g(a)=t2﹣2at,对∀a∈[﹣1,1],g(a)≥0恒成立,∴,∴t≥2或t≤﹣2或t=0.。
【优质文档】2016-2017学年辽宁省抚顺市六校联合体高一(上)期末数学试卷
9.(5 分)一个几何体的三视图如图所示(单位: cm),那么此几何体的表面积
(单位: cm2)是(
)
A.102 B.128 C.144 D.184
10.( 5 分)已知函数 y=f( x)(x∈R)是奇函数且当 x∈( 0,+∞)时是减函数,
若 f( 1) =0,则函数 y=f(x2﹣ 2x)的零点共有(
A.16 B.2 C. D.
6.(5 分)已知点 P( a, b)和点 Q( b﹣ 1, a+1)是关于直线 l 对称的两点,则
直线 l 的方程为( )
第 1 页(共 18 页)
《创新设计》图书
A.x+y=0 B.x﹣y=0 C.x﹣y+1=0 D.x+y﹣ 1=0
7.(5 分)设 a=log410,b=log23, c=20.5,则(
21.( 12 分)如图, PA垂直于矩形 ABCD所在平面, AE⊥PB,垂足为 E, EF⊥PC 垂足为 F. (Ⅰ)设平面 AEF∩PD=G,求证: PC⊥ AG;
(Ⅱ)设 PA=
,M 是线段 PC的中点,求证: DM∥平面 AEC.
22.( 12 分)已知 f( x)是定义在 [ ﹣ 1, 1] 上的奇函数,且 f(1)=1,若 m,n
2.(5 分) 2003 年至 2015 年北京市电影放映场次(单位:万次)的情况如图所
示,下列函数模型中,最不适合近似描述这 13 年间电影放映场次逐年变化规律
的
是
(
)
A.f (x)=ax2+bx+c B. f(x)=aex+b C.f (x) =eax+b D. f(x)=alnx+b 【解答】 解:由图象可得:这 13 年间电影放映场次逐年变化规律的是随着 x 的 增大, f(x)逐渐增大,图象逐渐上升. 对于 A.f (x)=ax2+bx+c,取 a>0, <0,可得满足条件的函数;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年重庆市六校联考高一(上)期末数学试卷 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的. 1.(5.00分)=( )
A. B. C. D. 2.(5.00分)已知集合M={1,2},N={2,3,4},若P=M∪N,则P的子集个数为( ) A.14 B.15 C.16 D.32
3.(5.00分)已知函数f(x)=,若f(﹣1)=f(1),则实数a的值为( ) A.1 B.2 C.0 D.﹣1 4.(5.00分)若函数f(x)=ax2﹣bx+1(a≠0)是定义在R上的偶函数,则函数g(x)=ax3+bx2+x(x∈R)是( ) A.奇函数 B.偶函数 C.非奇非偶函数 D.既是奇函数又是偶函数
5.(5.00分)设a=log2,b=()3,c=3,则( ) A.c<b<a B.a<b<c C.c<a<b D.b<a<c 6.(5.00分)已知tan(α﹣β)=,tan(﹣β)=,则tan(α﹣)等于( )
A. B. C. D. 7.(5.00分)方程x﹣logx=3和x﹣logx=3的根分别为α,β,则有( )
A.α<β B.α>β C.α=β D.无法确定α与β大小 8.(5.00分)函数f(x)=2sin(2x+)的图象为M,则下列结论中正确的是( )
A.图象M关于直线x=﹣对称 2
B.由y=2sin2x的图象向左平移得到M C.图象M关于点(﹣,0)对称 D.f(x)在区间(﹣,)上递增 9.(5.00分)函数y=sin2(x﹣)的图象沿x轴向右平移m个单位(m>0),所得图象关于y轴对称,则m的最小值为( ) A.π B. C. D. 10.(5.00分)已知f(x)是定义在R上的偶函数,且在区间(﹣∞,0)上单调递减,若实数a满足f(3|2a+1|)>f(﹣),则a的取值范围是( ) A.(﹣∞,﹣)∪(﹣,+∞) B.(﹣∞,﹣)
C.(﹣,+∞) D.(﹣,﹣) 11.(5.00分)已知α∈[,],β∈[﹣,0],且(α﹣)3﹣sinα﹣2=0,8β3+2cos2β+1=0,则sin(+β)的值为( ) A.0 B. C. D.1
12.(5.00分)若区间[x1,x2]的 长 度 定 义 为|x2﹣x1|,函数f(x)=(m∈R,m≠0)的定义域和值域都是[a,b],则区间[a,b]的最大长度为( ) A. B. C. D.3
二、填空题:本大题共4小题,每小题5分,共20分.把答案填写在答题卡相应位置上. 13.(5.00分)计算:log3+lg4+lg25+(﹣)0= . 14.(5.00分)已知扇形的面积为4cm2,扇形的圆心角为2弧度,则扇形的弧长为 . 15.(5.00分)若α∈(0,π),且cos2α=sin(+α),则sin2α的值为 . 3
16.(5.00分)已知正实数x,y,且x2+y2=1,若f(x,y)=,则f(x,y)的值域为 .
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10.00分)已知全集U=R,函数的定义域为集合A,集合B={x|5≤x<7} (1)求集合A; (2)求(∁UB)∩A. 18.(12.00分)在平面直角坐标系xOy中,若角α的始边为x轴的非负半轴,其终边经过点P(2,4). (1)求tanα的值;
(2)求的值. 19.(12.00分)已知二次函数f(x)=mx2+4x+1,且满足f(﹣1)=f(3). (1)求函数f(x)的解析式; (2)若函数f(x)的定义域为(﹣2,2),求f(x)的值域. 20.(12.00分)已知函数f(x)=sin2ωx+2cosωxsinωx+sin(ωx+)sin(ωx
﹣)(ω>0),且f(x)的最小正周期为π. (1)求ω的值; (2)求函数f(x)在区间(0,π)上的单调增区间. 21.(12.00分)已知函数f(x)=log2()﹣x(m为常数)是奇函数.
(1)判断函数f(x)在x∈(,+∞)上的单调性,并用定义法证明你的结论; (2)若对于区间[2,5]上的任意x值,使得不等式f(x)≤2x+m恒成立,求实数m的取值范围. 22.(12.00分)已知函数f(x)=a(|sinx|+|cosx|)﹣sin2x﹣1,若f()= 4
﹣. (1)求a的值,并写出函数f(x)的最小正周期(不需证明); (2)是否存在正整数k,使得函数f(x)在区间[0,kπ]内恰有2017个零点?若存在,求出k的值,若不存在,请说明理由. 5 2016-2017学年重庆市六校联考高一(上)期末数学试卷 参考答案与试题解析
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的. 1.(5.00分)=( )
A. B. C. D. 【分析】根据诱导公式可知cos=cos(π+),进而求得答案. 【解答】解:cos=cos(π+)=﹣cos=﹣ 故选:D.
2.(5.00分)已知集合M={1,2},N={2,3,4},若P=M∪N,则P的子集个数为( ) A.14 B.15 C.16 D.32 【分析】根据并集的定义写出P=M∪N,再计算P的子集个数. 【解答】解:集合M={1,2},N={2,3,4}, 则P=M∪N={1,2,3,4}, ∴P的子集有24=16个. 故选:C.
3.(5.00分)已知函数f(x)=,若f(﹣1)=f(1),则实数a的值为( ) A.1 B.2 C.0 D.﹣1 【分析】由已知得f(﹣1)=1﹣(﹣1)=2,f(1)=a,再由f(﹣1)=f(1),能求出a的值.
【解答】解:∵函数f(x)=,f(﹣1)=f(1), 6
∴f(﹣1)=1﹣(﹣1)=2,f(1)=a, ∵f(﹣1)=f(1),∴a=2. 故选:B.
4.(5.00分)若函数f(x)=ax2﹣bx+1(a≠0)是定义在R上的偶函数,则函数g(x)=ax3+bx2+x(x∈R)是( ) A.奇函数 B.偶函数 C.非奇非偶函数 D.既是奇函数又是偶函数 【分析】由f(x)为偶函数容易得出b=0,从而得出g(x)=ax3+x,这样判断g(x)的奇偶性即可. 【解答】解:f(x)为偶函数,则b=0; ∴g(x)=ax3+x; ∴g(﹣x)=a(﹣x)3﹣x=﹣(ax3+x)=﹣g(x); ∴g(x)是奇函数. 故选:A.
5.(5.00分)设a=log2,b=()3,c=3,则( ) A.c<b<a B.a<b<c C.c<a<b D.b<a<c 【分析】利用指数函数与对数函数的单调性即可得出.
【解答】解:a=log2<0,b=()3∈(0,1),c=3>1. ∴c>b>a. 故选:B.
6.(5.00分)已知tan(α﹣β)=,tan(﹣β)=,则tan(α﹣)等于( ) A. B. C. D. 【分析】由已知利用两角和的正切函数公式即可计算得解. 7
【解答】解:∵tan(α﹣β)=,tan(﹣β)=, ∴tan(α﹣)=tan[(α﹣β)﹣(﹣
β)]===. 故选:C. 7.(5.00分)方程x﹣logx=3和x﹣logx=3的根分别为α,β,则有( ) A.α<β B.α>β C.α=β D.无法确定α与β大小 【分析】方程x﹣logx=3和x﹣logx=3,分别化为:log2x=3﹣x,log3x=3﹣x.作
出函数图象:y=log2x,y=3﹣x,y=log3x.即可得出大小关系. 【解答】解:方程x﹣logx=3和x﹣logx=3,
分别化为:log2x=3﹣x,log3x=3﹣x. 作出函数图象:y=log2x,y=3﹣x,y=log3x. 则α<β. 故选:A.
8.(5.00分)函数f(x)=2sin(2x+)的图象为M,则下列结论中正确的是( ) A.图象M关于直线x=﹣对称 B.由y=2sin2x的图象向左平移得到M 8
C.图象M关于点(﹣,0)对称 D.f(x)在区间(﹣,)上递增 【分析】利用正弦函数的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,逐一判断各个选项是否正确,从而得出结论. 【解答】解:∵函数f(x)=2sin(2x+)的图象为M,令x=﹣,可得f(x)=0,
可得图象M关于点(﹣,0)对称,故图象M不关于直线x=﹣对称,故C正确且A不正确; 把y=2sin2x的图象向左平移得到函数y=2sin2(x+)=2sin(2x+)的图象,故B不正确; 在区间(﹣,)上,2x+∈(0,π),函数f(x)=2sin(2x+)在区间(﹣
,)上没有单调性,故D错误, 故选:C.
9.(5.00分)函数y=sin2(x﹣)的图象沿x轴向右平移m个单位(m>0),所得图象关于y轴对称,则m的最小值为( ) A.π B. C. D. 【分析】利用三角函数的恒等变换化简函数的解析式,再利用y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,求得m的最小值.
【解答】解:函数y=sin2(x﹣)==的图象沿x轴向右平移m个单位(m>0), 可得y=的图象,
再根据所得图象关于y轴对称,可得2m=(2k+1)•,k∈Z, 即m═(2k+1)•,则m的最小值为, 故选:D.
