电磁场大作业
电磁场的典型练习题及解答

电磁场的典型练习题及解答电磁学是物理学中的重要分支,研究电荷和电流所产生的电场和磁场的相互作用规律。
在学习电磁学的过程中,练习题是检验我们对理论知识掌握的有效方法。
本文将介绍一些典型的电磁场练习题,并给出详细的解答,帮助读者加深对电磁场的理解。
1. 题目:一根无限长直导线产生的电场强度已知一根无限长直导线,导线上带有均匀分布的电荷线密度λ。
求导线距离d处的电场强度E。
解答:根据库仑定律可知,电场强度E与电荷线密度λ成正比,与距离d 成反比。
所以可以得出结论:电场强度E和d满足反比关系。
2. 题目:两个点电荷的叠加效应已知两个点电荷q1和q2,分别位于坐标原点和坐标轴上一点P(x,0)。
求点P处的电场强度E。
解答:根据叠加原理,点P处的电场强度E等于点电荷q1和q2分别在点P处产生的电场强度之和。
由库仑定律可知,点电荷产生的电场强度与电荷量成正比,与距离的平方成反比。
根据该性质,可以分别求出点电荷q1和q2在点P处产生的电场强度,再将两者相加得到点P处的总电场强度。
3. 题目:平行板电容器的电场强度已知一对平行板电容器,两平行板间距离为d,电容器的电容为C。
求平行板电容器中的电场强度E。
解答:根据平行板电容器的结构特点,可知平行板电容器中的电场强度E对于两平行板之间的距离d是均匀的,且大小与电容C的倒数成正比。
所以可以得出结论:电场强度E和d满足正比关系,与电容C成正比。
4. 题目:磁场的洛伦兹力已知带电粒子以速度v在磁场B中运动,其电荷量为q。
求带电粒子所受的洛伦兹力F。
解答:根据洛伦兹力的定义,带电粒子所受的洛伦兹力F等于其电荷量q与速度v以及磁场B的矢量积。
通过对矢量积的计算,可以得到带电粒子所受的洛伦兹力F的大小和方向。
5. 题目:安培环路定理的应用已知一安培环路中有多个电流元素,它们的电流分别为I1,I2,I3...In。
求安培环路中的磁场强度B。
解答:根据安培环路定理,安培环路中的磁场强度B与电流元素的电流之和成正比。
大作业参考答案-电磁感应

电磁感应一、选择题⒈ D ; ⒉ B ;⒊ C ; ⒋ BD ; ⒌ C ; 6.E ; 7.B ; 8.A ; 9.A二、填空题⒈ < 。
⒉ 洛伦兹力,B x v ; 感生电场力; 变化的磁场。
⒊ S iR / 。
⒋ θω222/1B S i n L ; C A → 。
⒌ 0 ;dt dB l 4 ; dtdB l 2- 。
⒍ )ln (20d l d d l I +-πωμ; A O → 。
⒎ 1/16。
⒏ 1.6x106 J/m 3; 4.425 J/m 3; 磁场更易于存储能量。
9. ⎰⎰⎰∙∂∂=∙S S d t D l d H ;⎰⎰⎰∙∂∂-=∙SS d t B l d E ; 0=∙⎰⎰SS d B ; ∑⎰⎰=∙0q S d D S 。
三、问答题1. 答:(1) 起源不同:静止电荷激发静电场,而变化的磁场激发涡旋电场。
(2)性质不同:静电场是有源无旋、保守力场,而涡旋电场是无源有旋、非保守力场。
2. 答: (1) 传导电流源于自由电荷的定向移动,而位移电流本质上是变化的电场。
(2)传导电流通过导体时产生焦耳热,而位移电流则无热效应。
(3)传导电流只能在导体中存在,而位移电流可以在导体、电介质、真空中存在。
四、计算题1 解:(1) 因磁场分布为:r Iπμ2B 0=,则000ln 2200r lr Ix xdr r I S d B d l r r m m +==∙==⎰⎰⎰+πμπμφφ 。
(2)0m ln 2d d r lr Iv t i +-=-=πμφε00ln 2r lr R Iv R I i i +-==πμε(3)Rv r l r I dr r Ir l r R Iv Bdr I dF F l r r i 20000000)ln 2(2ln 200+=⋅⋅+===⎰⎰⎰+πμπμπμ方向垂直于导线向上。
2 解: t 时刻,磁通量为θθφc o s c o s ⋅⋅==l v t kt BS m则电动势为k l x k v t l t i -=-=-=θφεc o s 2d d m负号说明电动势方向沿顺时针3 解:(1)取顺时针方向为正绕线,则3ln 2ln 2200πμπμπμφφIac b Ia adr r I Sd B d b c m m ===∙==⎰⎰⎰则3ln 20πμφaI M m ==(2)3ln 2d d 0t m e at IM λλπμε-=-=电动势方向为顺时针。
《电磁场与电磁波》大作业A 答案

内外的电场强度及电位分布。
解:采用球坐标系分析本题(只涉及了一个变量半径r ,并未涉及其他角度变量)。
在r<a 的区域,高斯面是一个与这个球体相同球心,以r 为半径的球面,所包围的电荷是343r πρ ,因此22304443ii r r i S d r E r E r ρπππε===⎰E S e e (r e 表示方向沿径向向外,下面省略了中间过程)所以3i rρε=r E e (V m )在r>a 的区域,高斯面是一个与这个球体相同球心,以r 为半径的球面,所包围的电荷是343a πρ ,230443o r E a ρππε=3203o a rρε=rE e (V m ) 求解电势:由于电荷分布在有限区域,可选无穷远点为参考点。
则 在r<a 时2200(V)26a i i o rraa r dr E dr E dr ρρϕεε∞∞=⋅=+=-⎰⎰⎰E在r>a 时30(V)3o o ra dr r ρϕε∞=⋅=⎰E8、单匝矩形线圈置于时变场0sin y B t ω=B e 中,如图所示。
初始时刻,线圈平面的法向单位矢量n 与y 轴成0α角。
求:a) 线圈静止时的感应电动势;b) 线圈以速度ω绕x 轴旋转时的感应电动势。
答:a) 线圈静止时,穿过线圈的磁通为()()000sin sin cos y Sd t ab B ab t B Φωωα⋅⋅===⎰B Se n由式(2.59),故感应电动势为()00cos cos d abB t dt Φωωαε=-=-b) 线圈以角速度ω绕x 轴旋转时,法向单位矢量n 的方向随时间变化。
在t 时刻,n 与y 轴的夹角0t ααω=+,所以()()()000sin sin cos y Sd B t ab B ab t t Φωωαω⋅⋅===+⎰B Se n故感应电动势为()0cos 2d abB t dt Φωαωε=-=-+9、一个半径为a 的导体球的电位为U ,设无穷远处为零电位。
电磁场作业答案

第一章1-41-51-61-71-91-101-111-121-15 1-16思考与练习1-4 已知两个矢量场求:矢量场并证明在空间各点,的场矢量都与的场矢量垂直。
解:依题意==根据矢量垂直的定义,若与垂直必有故=所以,在空间各点,总是与垂直。
1-5已知,求在柱坐标和球坐标中的表达式。
解:①若位于原点,则有在柱坐标系中==3cos+4sin==5==0其中在球坐标系中:=其中其中②若位于处,由柱坐标与直角坐标间的变换关系坐标单位向量为此点的坐标单位向量得:其中其中: 均为处的,即: 同理球坐标系中其中其中均为处的,即1-6已知= , , 2,求:,,解:,,分别为在,,上的投影。
,,,,,的单位矢量为:1-7球坐标中点的表示为(,,),已知(5,,),(4,,)。
求:,之间的距离及的单位矢量。
解:为求得两点间的距离,应先将换成直角坐标:同理:两点间的距离为=的单位矢量为===1-9已知标量场(1)指出过点(1,1,1)的等值面的形状。
(2)求出这个等值面在该点的发线方向。
(3)求出在该点沿方向的导数解:(1)等值面方程为:为椭圆双曲面。
(2)由梯度性质可知,梯度的方向与等值面垂直所以的方向即为法线方向(3)根据方向导数的计算式,可知即为在方向的方向导数1-10 广义正交坐标系中证明:解:设广义坐标系的坐标变量为坐标单位矢量为长度系数为则有:将上式中U,V对调,则有1-11已知,求在(x=1,y=0,z=1)点处的值。
指出与z轴的夹角。
解:的梯度为:在(1,0,1)处,所以与 z轴的夹角为:而所以夹角为。
1-12已知平面矢量场,求沿下列路径由P1(1,2)到P2(2,4)的路径积分值;1)由P1到P2的直线,2)(1,2)(2,2)(2,4)的折线;解:路径积分为:对路径1,有y=2x,所以dy=2dx代入上式中,有。
对于路径2,,在段,y=2,dy=0,在段,x=2,dx=01-15计算解:1-16证明,其中,,分别表示对(x,y,z)和的坐标矢量运算。
电磁场作业答案

2.6 在圆柱坐标系中电荷分布为ρ={①r/a ,r ≤a ②0,r >a ,r 为场点到z 轴的距离,a 为常数。
求电场强度。
解:电场强度只有沿r 方向分量,选取长度为l 的圆柱sd 2r qE S rlE πε⋅==⎰⎰ (1)r a ≤时3223r lr q dV rldr a aπρπ===⎰⎰⎰⎰代入(1)得: 23r r E a ε=r a >时2223ar la q dV rldr a πρπ===⎰⎰⎰⎰代入(1)得: 23r a E r ε=2.7在直角坐标系中电荷分布为ρ(x ,y ,z )={①ρ0 ∣x ∣≤a ②0 ∣x ∣>a 求电场强度。
解:电场与y ,z 均无关,电场强度只有沿x 方向分量,()0x E E x ρε∂∇⋅==∂ (1) r a ≤时0ρρ=代入(1)得: 00x xE C ρε=+ 0x →时x E 为有限值所以0C =00x xE ρε=r a >时0ρ=代入(1)得: 'r E C = 在x a =处r E 连续,所以'00aC ρε=00r aE ρε=2.16已知电场强度为E=3x+4y-5z ,试求点(0,0,0)与点(1,2,1)之间的电压 解:6bbbbx y z aaaaU E dl E dx E dy E dz =⋅=++=⎰⎰⎰⎰2.26两同心导体球壳半径分别为a 、b ,两导体之间有两层介质,介电常数分别为ε1、ε2,介质界面半径为c ,内外导体球壳电位分别为V 和0,求两导体球壳之间的电场和球壳上的电荷面密度,以及介质分界面上的束缚电荷面密度。
解:两球壳之间电介质不带电电位分布满足拉普拉斯方程20ϕ∇=选取球坐标则有:22210r r r r ϕϕ∂∂⎛⎫∇== ⎪∂∂⎝⎭'111C C r ϕ=-+ '222C C rϕ=-+ 代入边界条件'2220r bC C b ϕ=∣=-+= '111r aC C V aϕ=∣=-+= 12n r c n r c D D ==∣=∣12r c r c ϕϕ==∣=∣由上式可得:1122211111()()1111()()VC a c c b VC a c c bεεεε=--+-=--+-12122221,()1111()(),()1111()()VE a r c r a c c bVE c r b r a c c bεεεε=<<-+-=<<-+-在介质与导体分界面上的电荷密度s n D ρ=()11212222211111()()()1111()()s s Vr a a a c c bVr b b a c c b ερεεερεε==-+-==-+-介质分界面上没有自由电荷感应电荷面密度为:()21012s n n n n P P E E ρε=-=-()02122111()11111111()()()()Vr c c a c c ba c c bερεεεε==--+--+-2.32同轴圆柱形电容器内、外半径分别为a 、b ,导体之间一半填充介电常数为ε1的介质,另一半填充介电常数为ε2的介质,如图所示,当电压为V 时,求电容器中的电场和电荷分布。
高等电磁场作业

高等电磁场作业(总24页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--1-1、证明:令M A =⨯∇ ϕ,N B =⨯∇ϕ。
所以B A B M B M B M M B A B ⨯∇⋅⨯∇+⨯⋅∇=⨯∇⋅+⨯⋅∇=⨯∇⋅=⨯∇⨯∇⋅)()(ϕϕ,A B A N A N A N N A B A ⨯∇⋅⨯∇+⨯⋅∇=⨯∇⋅+⨯⋅∇=⨯∇⋅=⨯∇⨯∇⋅)()(ϕϕ, 又因为B A ⨯∇⋅⨯∇)( ϕ=A B ⨯∇⋅⨯∇)(ϕ 所以原式=dsA B B A ds A B B A ds A N B M dv A N B M S Ssv⋅⨯∇⨯-⨯∇⨯=⋅⨯⨯∇-⨯⨯∇=⋅⨯-⨯=⨯⋅∇-⨯⋅∇⎰⎰⎰⎰)]()([][][][ϕϕϕ证毕1-2、证明:)()()()(z z y y x x z z y y x x z z y y x x g f g f g f zdz g f g f g f y d y g f g f g f x d x g f ++∂+++∂+++∂=⋅∇ []⎣⎦[]zz df g z df g z df g y y df g y df g y df g x x df g x df g x df g g gg z df z df z df y df y df y df x df x df x df z y x g g g z y x z y x z df z df zdf y df y df y df x df x df x df z y x g f z z y y x x z z y y x x z z y y x x z y x z y x z yx z y x z y x z y x z y x z y x)()()(∂+∂+∂+∂+∂+∂+∂+∂+∂=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⋅⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂=⋅∇同理可得zydg f y dg f y dg f y y dg f y dg f y dg f x x dg f x dg f x dg f f g z z y y x x z z y y x x z z y y x x)()()(∂+∂+∂+∂+∂+∂+∂+∂+∂=⋅∇由dx df g dx dg f dx g f d x x x x x x +=)( 并依次类推相加可得)(g f ⋅∇=g f ⋅∇+f g ⋅∇ 证毕讨论Maxwell 方程中四个边界条件的独立性。
面向新世纪课程教材大学物理大作业答案——电磁感应与电磁场答案
i
O′
r dr
b
R2
R1
1
3.解: (1) dΦ = B ⋅ dS = BLdx =
v
v
μ0 I
2π x b μ I IL μ b Φ = ∫ 0 Ldx = 0 ln a 2π x a 2π
Ldx
dx I L a b x
感应电动势为:
μ L b dI dΦ = − 0 ln ⋅ dt 2 π a dt dI Q I = I 0 e -4t = −4 I 0 e − 4 t dt 2 μ 0 LI 0 b −4 t ∴ εi = ln e a π ε i > 0 ,方向为顺时针 μ0 LI b ln Φ a = μ 0 L ln b (2) M = = 2π I I 2π a εi = −
2.解: (1)
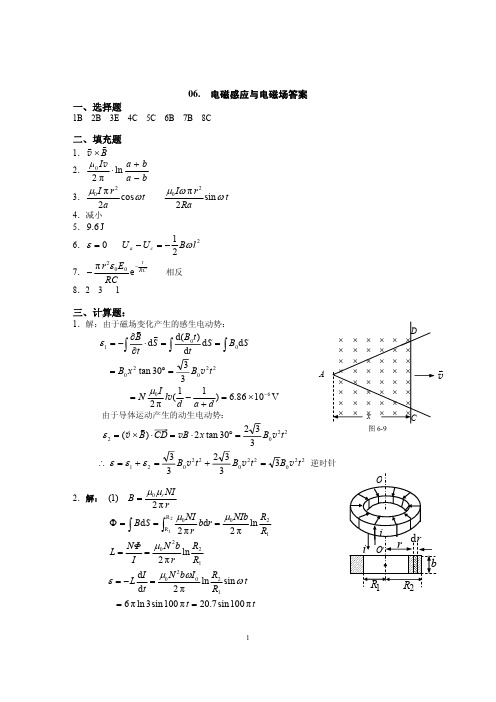
图 6-9
B=
μ0 μ r NI
2πr
R2 R1
2
O
Φ = ∫ BdS = ∫
μ0 NI
2πr
bdr =
μ0 NIb
2π
ln
R2 R1
i
NΦ μ 0 N b R 2 L= = ln I 2πr R1
dI μ N 2 bωI 0 R2 ε = −L = 0 ln sin ω t R1 dt 2π = 6 π ln 3 sin 100 π t = 20.7 sin 100 π t
由于导体运动产生的动生电动势:
A
× × × × × × × ×
× × × × × × × ×
× × × × × × × × x
× × × × × × × ×
× × × × × × × ×
× × × × × × × ×
D
电磁场作业题解读

《电磁场》作业题第一章作业:1、一均匀带电圆环,半径为R ,所带电量为q (设q>0),求圆环轴线上任一点P 的场强;解:本题答案见第二讲课件例题2、求均匀带电球面的电场分布,已知球面半径为R ,所带总电量为q (设q>0); 解:本题答案见第四讲课件例题3、求无限大均匀带电平面的电场分布。
已知面密度为 。
解:本题答案见第四讲课件例题x4、求下图中电荷q 受到的力。
解:本题答案见第九讲课件例题5、无限长两根导线,已知:h ,a ,求两导线间单位长度电容0C 。
解:本题答案见第十一讲课件例题6、两个形状相同的球形电容器,一个电容器介质为空气,另一电容器介质为硫磺,将空气电容器充电到12V ,与另一电容器并联后,电压降为3V ,求硫磺的相对介电系数r 。
解:本题答案见第十二讲课件例题第二章作业:1、同心电缆,内半径为1r ,外半径为2r ,内外导体之间的电压为U ,中间媒质的电导率为γ,计算单位长度的泄露电流。
解:本题答案见第十三讲课件例题2、直径为d ,长度为2L 的接地体,深埋在地中,求接地电阻j R ,设大地的电导率为γ。
解:本题答案见第十四讲课件例题(注:本题可以不做)第三章作业:1、真空中ω匝线圈,半径为R ,已知d ,求轴心处P 点的磁感应强度。
解:本题答案见第十五讲课件例题2L x2、已经电流环半径为R ,电流为I ,求轴心x 点处的标量磁位。
解:本题答案见第十七讲课件例题(注:本题可以不做)3、矩形铁磁物质如图所示,中间有空气隙,判断磁场能量主要存在于铁磁物质中还是空气隙中,磁动势主要落在哪一段,忽略边缘效应。
解:本题答案见第十八讲课件例题x《电磁场》模拟试卷一1、半径R=5cm 、ε=2ε0的无限长介质圆柱体,柱体内有均匀体电荷ρ=10-5 c/m 3,其周围介质为空气。
试求:⑴ 柱体内外电场强度分布;⑵ 圆柱体轴心的电位(以圆柱体表面为参考点)。
解:本题答案见第四讲课件例题(有改动)2、已知620a cm d cm ==,,导线间电压380U V =,不考虑地面影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WORD格式“可編辑••专业资料
-完整版学习资料分享
电磁场大作业实验报告
一、 实验目的
利用matlab完成平面电磁波在不同介质分界而上任意角度的入射、反射、折射仿頁•实验
二、 实验要求
动态演示平面电磁波的传播情况
媒介介电常数和入射角可任意设程
考虑金属导体和空气分界而平面电磁波的入射、反射情况
三、 实验原理
当正弦平而波以任意入射角向分界而斜入射时,电场强度E和磁场强度H在分界而上不仅有切 线
分量,而且还有法向分量。而边界条件只和切线分量有关。切线分量又和波的极化有关。
当平而波斜入射到分界而上时,入射方向与分界而的法线方向组成的而为入射而,因此入射波 的电
场E’和磁场H:组成的平面一左垂直于入射而,如下图所示。
可将此介质分为三段:入射前空间、介质(分界而)、岀介质空间,通过对三部分介电常数之 比、
导电率之比、磁导率之比的调整来任意仿真介质性质及介质层数等。苴中入射角、分界面宽度、 入射场
强、沿轴距离可调(取分界面z二Om)。可通过改变轴的采样点调整绘图精度,最后完成沿z 轴电场强
度E (或磁场强度H)的动态表示、绘岀整个域内E的强度图。
1.
电磁波斜入射到不同介质分界面上的反射和折射
如图1所示,平行极化的均匀平而波以角度8入射到良介质表而时,入射波、反射波和折射
波可用下列式子表示为
WORD格式••可编辑••专业资料
利用分界而上(z二0)电场和磁场切向分量连续的边界条件,可得斯耐尔反射上律:
0 = 0r
和斯耐尔折射定律:
sin 0
并计算岀平行极化波的反射系数7?和折射系数Tr.
_ 〃] COS &一〃
2 COS 0"
K” = ------------------ - ------- -
〃]COS& + 〃
2 COS&"
T _ 2〃2cos&
77] cos 0 + /j2 cos
。"
类似地,可求出垂宜极化波的反射系数和折射系数:
-完整版学习资料分享
入射波:
反射波:
折射波:
式中,
图1・平行极化波的斜入射示意图
E+ = E^(ax cos0-az sin
〜比-加聞“皿列
F
+
= a
^-/fcj(Asin^+ccos^>
5
= R曲f cos6r-az sin
歹比一川皿匸心®
El = T忒g cos歹-冬sin ey
曲
//l = U T”Em f-htgn少+zcos&・)
〃
2
! = k? = ejg
sin 0
n
时
“I = “2 =
WORD格式••可编辑••专业资料
-完整版学习资料分享一
77] COS 0 - 1]x COS&"
COS 0 + /J} COS0"
_ cos 0
“2 COS& + 〃] COS0ff
(2)
•对垂直入射情形,8H 反射系数和折射系数变为
T 一 2
仏
"U + 〃2
3.
电磁波斜入射到良导体表而的反射
良导体的特性近似于理想导体,电磁波投射到良导体表而时,可认为发生全反射,此时,
四、实验截图
下图为垂直入射时的波形演示
WORD格式••可编辑••专业资料
-完整版学习资料分享一
折射液形
1
0
WORD格式••可编辑••专业资料
-完整版学习资料分享一
介质1中的合成波
