快速超薄铸轧机铸轧辊变形热力耦合模型

合集下载

多孔介质模型镁合金流变铸轧LBM模拟

多孔介质模型镁合金流变铸轧LBM模拟张莹;马强;陈杨华;倪泽联【摘要】A thermal-fluid coupling numerical model was built to analyze the process of high solid fraction semi-solid slurry seepage according to the lattice-Boltzmann method of REV scale porous medium. The model was applied to simulate the Poiseuille flow with various porosity and the pure diffusion solidification. The simulation results of LBM is consistent with the simulation of finite difference, and it′s correctness has been verified. The seepage cooling and the thermal-fluid coupling process of slurry between the flat was analyzed under differential pressure. The simulation results show that the slurry flow velocity decreases as temperature decreases. The RE number of slurry seepage gets higher as the solidification latent heat is raising at the same time. The proposed model has been utilized to tentatively explore the heat-flow field distribution in the process of AZ91D magnesium alloy semi-solid casting and rolling.%根据REV尺度多孔介质格子-Boltzmann方法基本理论，建立求解高固相率半固态浆料渗流过程的热流耦合数值模型．应用模型对变孔隙率Poiseuille流动及纯扩散凝固进行模拟．LBM模拟结果与有限差分模拟吻合．分析了压差作用下浆料在平板间渗流冷却与热流耦合过程．模拟结果表明浆料渗流速度随温度降低而减慢，相同时刻下凝固潜热较大的浆料渗流Re数高．利用提出的模型初步探索了AZ91D镁合金半固态流变铸轧过程的热流场分布．【期刊名称】《材料科学与工艺》【年(卷),期】2014(000)002【总页数】6页(P117-122)【关键词】格子-Boltzmann;多孔介质;半固态;热流耦合【作者】张莹;马强;陈杨华;倪泽联【作者单位】南昌大学机电工程学院，南昌330031;南昌大学机电工程学院，南昌330031;南昌大学机电工程学院，南昌330031;南昌大学机电工程学院，南昌330031【正文语种】中文【中图分类】O359作为半固态金属凝固过程的最后阶段，高固相率浆料内的传输行为很大程度上影响了材料凝固的最终质量．目前，有部分学者通过多孔介质模型去研究了高固相率半固态浆料的挤压成形过程中的应力和两相分离行为并取得成功［1－2］，但是基于多孔介质模型对半固态对流凝固过程的热流场分析尚没有相关的文献报道．从孔隙尺度上说，研究液态合金在固相晶粒组织间的流动传热传质过程，分析晶粒生长环境，是获得晶粒组织形态，控制凝固质量的基础［3］．从表征体元（REV）尺度上说，研究浆料的固相率和渗透率、物性参数对热流场的影响，揭示固相率的半固态浆料热流场分布规律，对发展半固态铸造成型工艺有着十分重要的意义．在多孔介质数值模拟的方法中，Lattice⁃Boltzmann方法（LBM）无需直接求解复杂的偏微分方程，处理边界条件容易，计算并行好等特点在孔隙尺度［4］和REV尺度［5］都得到了很好的应用，并且也成功的用于处理多孔介质中的相变问题［6］．本文以变孔隙率多孔介质流动传热模型，利用LBM为计算工具，探索高固相率半固态浆料的传热和流动耦合作用关系．1．1 变孔隙率多孔介质流动传热宏观方程组在半固态浆料传热过程中，随着浆料固相率的增加，孔隙率也相应的降低，而固相率是温度的函数，因此可以建立孔隙率与温度的函数关系．根据不可压缩多孔介质的广义N－S方程，在忽略粘性耗散热并且考虑相变时得到u，T，p为液相的流速温度和压强等宏观物理量，ρ，υ为液相的密度、运动黏度和比热容等物性参数在本文中均视为常数．Q为相变潜热源项，ε，f为介质孔隙率和固相率，满足ε＋f＝1．σ，α为有效比热容和有效热扩散率，可以由固相和液相两者热物性参数加权得到cp，kp，cs，ks分别为液相和固相的比热容和导热系数．REV尺度研究多孔介质内的流动问题时，固相的骨架与占据骨架间空隙的流体相互作用是通过流体所受的阻力来表现的．多孔介质的外力项包括Darcy阻力，Brinkman黏性力和非线性的Forchheimaer阻力，根据文献［5］可以表示为G为流体所受的体积力，νs为流体黏性系数，Fε为多孔介质的形状函数，K为渗透率，其表达式根据Ergun关联式［7］得到，具体表达形式如公式（5）所示．其中dp为颗粒物直径．固相率与温度的关系受到合金物性和凝固条件的影响十分复杂加上热力学数据不完善，在平衡假设下常采用Scheil［8］方程求解：TM为纯金属的熔点，TL为合金液相线温度．k溶质分配系数，当k＝0时方程变为线性方程．通过求导代换把潜热项合并入有效比热容项中：1．2 格子Boltzmann速度分布函数演化方程根据郭照立等人提出的GLBE［9］模型，广义N－S动量方程所对应的演化方程为式中：fi（x，t）为粒子速度分布函数；（x，t）平衡态分布函数，ei为离散速度，i为离散速度方向．松弛时间平衡态分布方程和外力项的表达式为式中：cs为格子声速，ωi为权系数．相应的宏观变量的表达式可以定义为速度量的具体求解方法可参考文献［10］计算步骤获得．1．3 格子Boltzmann温度分布函数演化方程对于能量方程，可以改写成标准无源项对流扩散方程形式：针对本文的宏观方程，式中根据文献［11］可以得到变化将对流扩散方程改写为由文献［12］得到对应的演化方程为式中C为平衡态的二阶矩：类似动量方程可以写出松弛时间和温度宏观表达式：在本文中采用固相率与温度为线性关系简化，则α′是与温度无关的常数，τg为常数．本文计算中的速度边界条件采用非平衡态反弹格式［13］，热边界条件则仿照非平衡态外推格式［14］写出．2．1 数值验证文献11对上述GLBE模型模拟平板间均质多孔介质Poiseuille流动的数值验证，结合本文研究的具体对象，将变孔隙率条件下GLBE模型对速度场模拟与有限差分解做了对比验证．Poi⁃seuille流动的控制方程为定义流场的Dracy数为Da＝K/H2．雷诺数为Re＝HU0/ν，H为两板间的距离其中数值验证中设置孔隙率ε沿y方向以三种不同孔隙分布，设y∗＝y/Hy，三种条件下ε与y∗的函数关系式分别为模拟条件为Re＝100，由图1可知，在三种情况下GLBE的模拟结果与有限差分解的模拟结果基本一致，通过（a）和（b）条件的模拟表明随着多孔介质孔隙率的线性增大速度非线性的增加，这体现了强制对流非线性阻力项的作用．模拟区域中没有对流作用时，其凝固传热变为纯扩散问题．本文将一维非稳态纯扩散方程的有限差分方法（FDM）和热LBM对半固态凝固过程模拟做了对比分析．模拟设定冷边界TS＝0．88，热边界温度TH＝1．0，半固态合计的凝固温度区间为0．90～0．95，初始状态T0＝1．0，表示凝固潜热与显热之比的斯蒂芬数以及表示无量纲时间的傅里叶数为：Ste＝cpL/ΔT，Fo＝ατ/L2，ΔT为固液相的温差，L为特征长度．定义固相率为0．5的界面为合金的凝固前沿位置．图2可以看出LBM对半固态凝固过程模拟结果与有限差分解的吻合良好．Ste数越小潜热的作用越大，凝固的过程需要释放潜热大，凝固过程较慢，因此在同一Fo数时温度较高．相应的Ste数小的合金的凝固过程也会相对慢一些（如图3所示），图3中还可以得到在凝固过程初始时场内平均温度等于热边界温度，与冷边界温差较大，因此在定温条件下冷边界热流大，凝固过程较快．随着凝固过程进行，凝固前沿向热端推进，模拟区域内的平均温度降低，冷边界热流量不断减少，热边界的热流量增大，致使凝固速度逐渐减慢．2．2 压差作用下平板间半固态浆料渗流过程模拟对有些不伴随浆料较大塑性变形的铸造工艺，如液芯轻压下、半固态连铸、机械振动、充型铸造过程，可以近似认为固相骨架没有遭到破坏，半固态的液相在重力或压力作用下发生轻微的液固分离现象，此时可近似认为是半固态浆料在未凝固多孔固相骨架内的渗流过程．本节通过LBM模拟研究了半固态浆料在外部压差作用下在两平板间流动传热过程，探索多孔介质模型在此类热流场模拟中的可行性．平板间距离为H、板长L、L/H＝8，两板有恒定温度TS＝0．92，并保持静止．半固态浆料中的固相假设与平板无相对位移，即速度为0．液相在两端有一定压差作用下流动，液固相间产生一定的速度差．定义义表征板长两端压差关系欧拉数为Eu＝Δp/（ρu02），u0流动初始时刻平均速度．液相入口段温度恒定并等于初始温度T0＝0．97，半固态合金的凝固区间为0．9～1．0，定义无量纲温度θ＝（TTS）/（T0－TS）．图4为Ste＝0．5．Eu＝3×106时不同时刻x/L＝0．5时平板内H方向无量纲温度分布，可以看到随着时间推移，平板间的流体在流动过程中不断被冷却，温度逐步降低．随着相应的固相率增加，液相的合金不断的凝固构成多孔介质骨架的一部分，多孔介质的孔隙率降低．图5反映了不同Fo数时x/L＝0．5时平板内H方向Re数的变化，随着半固态区间的温度降低，两平板间的液相流速也不断降低，这是由于凝固，孔隙率的减少液相流动阻力增大的结果．并且Re数的降低速度比温度降低程度更为迅速，分析其原因为在对流条件下孔隙率的降低对流动阻力有非线性作用，即前文所提到的Forchheimaer力作用，在Fo＝0．5时，流场中心的Re数基本和边界区域Re数差距已经很小．通过计算流场内不同时刻流速和温度的平均值就可以得到半固态浆料渗流过程平均Re数和无量纲温度随时间变化的趋势，图6为Eu＝3× 106时不同Ste数下无量纲温度θ随Fo数的变化规律，由图可见，初始温度相同半固态浆料由于Ste数不同形成不同的冷却曲线．同一时刻Ste数高的合金温度较低，这与数值验证部分所说明的潜热大的半固态合金温度下降较慢是一致的．图7为Eu＝3×106时Re 数随Fo数变化趋势，图7表明随着浆料Ste的增大同计算区域内的同一时刻平均Re数也随之降低，这是由于合金的凝固潜热影响温度场，也造成固相率增加速度的差异，Ste数小较难凝固的半固态合金下相同时间时孔隙率也较高，从而在相同压差下流动阻力小，流场内的液相流动速度也相对高一些．从两图对比也可以看出因为非线性力的作用温度曲线的曲率较速度曲线的曲率要小一些．在薄带连续铸轧技术是一种近些年发展迅速的短流程板带成形技术，双辊薄带连续铸轧技术是众多该类成形技术中极具前途的一种［15］．半固态合金铸轧工艺如图8所示，制备好的半固态浆料通过铸嘴送入一对反向等角速度旋转的轧辊中，由于轧辊中有强制水冷，使得浆料在轧辊缝隙内迅速凝固形成薄带．整个过程在极短的时间内连续完成，温度场的分布和热流的传递直接决定了镁合金的凝固质量．本节以镁合金AZ91D半固态铸轧成形过程为对象，探索利用本文中提出的LBM方法和多孔介质模型来描述在半固态浆料在双棍间的热流耦合凝固过程．3．1 模拟参数的选取与无量纲化根据文献［16］列出的实际工艺参数本节采用的模拟几何参数和速度边界为：轧辊直径：d＝210 mm，辊缝宽度d0＝4 mm，轧辊速度um＝0．6 m/min，进口温度825～855 K．为了完成LBM模拟需要对实际的物理参数进行无量纲转，根据文献［16］，模拟涉及的AZ91D物性参数如表1所示．定义Re数为Re＝um·d0/ν，Pr数为Pr＝ρcpν/λ，重新定义无量纲温度θ＝（TTL）/（TH－TL），将表1中数据带入计算得到，Re＝20，Pr＝0．052，Ste＝350．87，Eu＝0，入口处无量纲温度θ0＝0．656～0．896．3．2 液固相间相互作用力确定与2．2节的分析不同，半固态浆料的连续铸轧过程中，合金已经凝固的部分和未完全凝固的固相骨架在轧辊的带动下向出口方向运动．为了描述这种固相运动过程中的多孔介质传热流动过程，假设多孔介质的固相部分满足无滑移条件，即固相部分与轧辊边具有相同的线速度um，定义液相与固相的相对速度为ur＝u－um．相应的公式（4）修改为由公式可以看出ur＞0时，固相骨架对液相的流动表现出阻力作用，而ur＜0时固相对液相的流动具有推动作用，并设定轧辊壁面具有一定的过冷度θs＝－0．2．3．3 模拟结果与分析作为LBM在材料凝固成形过程中的初步探索，本文仅不同的入口温度下AZ91D合金连铸铸轧热流场进行模拟，以验证研究方法的可行性．图9为不同浇铸入口温度下达到稳态是的半固态浆料固相率分布，从图中可看到随着浇铸温度的提高，合金在出口处的固相率逐渐减低．无量纲温度θ0＝0．656时，浆料还未到辊缝出口处变完全凝固为固相，此时固相板带在轧辊的压力作用下容易开裂，造成不合格产品，θ0＝0．816时浆料还未完全凝固就在轧辊推动下从辊缝送出，导致铸轧失败．而在本文所采取的冷却边界条件下，无量纲θ0＝0．736时浆料在辊缝处恰好完全凝固，是最理想的工艺条件．图10为θ0＝0．736是半固态镁合金在铸轧区域内速度绝对值分布情况．可以看到在出入口压力相等的情况下，半固态浆料一边被轧辊凝固一边在轧辊的作用下向出口方向运动．在最贴近轧辊的薄层内已经完全凝固的浆料在无滑移条件下与轧辊保持相同速度．而入口处因为固相率低固相骨架对液相的推动作用较弱，流动区域最宽，所以速度最小．随着凝固的进行固相率不断升高，并且双辊宽度逐渐缩小，半固态浆料的速度不断升高，直至进入辊缝位置是速度和轧辊速度保持一致，在完全凝固成板带后送出铸轧区域．本文通过将孔隙率与温度耦合，得到模拟半固态相变现象的变孔隙率LBM模型．将相变源项并入非稳态项避免了求解有源项的对流扩散方程，得到求解半固态相变传热问题的热LBM方程．对平板间外部压差作用下高固相率浆料的渗流冷却过程和板带铸轧成型过程进行热流耦合模拟，具体结论如下：1）所提出提出热流耦合LBM模型的相关模拟结果与有限差分解一致，验证了模型的正确性．2）半固态浆料平板间渗流过程中，半固态浆料液相流动速度随冷却时间增加而降低．浆料的相变潜热越大，传热降温过程越慢，相同压差作用下流场Re数越高．Re数随温度的变化趋势表现出非线性．3）利用多孔介质模型和LBM方法在通过无量纲处理后，对AZ91D镁合金半固态连续铸轧过程的温度场分布和流场分布进行了初步的模拟初步探索．得到了不同浇铸温度时铸轧区域内的固相率分布变化，和一定冷却条件下的最佳浇铸温度，分析了铸轧区域内的速度分布．【相关文献】［1］KHOSRAVANIA，AASHURI H，DAVAMI P．Liquid segregation behavior ofsemi⁃solid AZ91 alloy during back extrusion test［J］．Journal of Alloys and Com⁃pounds，2009，477：822－827．［2］SUN Z，LOG R E，BERNACKIM．3D finite element model of semi⁃solid permeability in an equiaxed granu⁃lar structure［J］．Computational Materials Science，2010，49：158－170．［3］ZHU M F，LEE S Y，HONG C P．Modified cellular automatonmodel for the prediction of dendritic growth with melt convection［J］．Phys Rev E，2004，69（6）：061610．［4］RAULM．Numerical simulations of surface reaction in porousmedia with lattice Boltzmann［J］．Chemical En⁃gineering Science，2012，69：628－643．［5］RONG Fumei，GUO Zhaoli，CHAI Zhenhua，et al．A Lattice Boltzmann Model for axsymmetriy thermal flows through Porousmedia［J］．International Jounal of Heat and Mass Transfer，2010，53：5519－5527．［6］杲东彦，陈振乾．格子Boltzmann方法模拟高Darcy数多孔介质内融化传热过程［J］．化工学报，2011，62（2）：321－328．GAO Dongyan，CHEN Zhenqian．Lattice Boltzmann method for heat transfer of melting in porous media with high Darcy number ［J］．Journal of Chemical In⁃dustry and Engineering（China），2011，62（2）：321－328．［7］ERGUN S．Flow through packed columns［J］．Chem．Eng．Prog．．1952，48：89－94．［8］FLEMINGSM C．Behavior ofmetal alloys in the semi⁃solid state［J］．Metal．Tras，1991，22B：269－293．［9］GUO Z L，ZHAO T S．Lattice Boltzmannmodel for in⁃compressible flows through porous media［J］．Phys Rev．E，2002，66，036304．［10］GUO Z L，ZHAO T S．A latticce Boltzmann model for convection heat transfer in porousmedia［J］．Numer Heat Trans Par t B，2005，47：157－177．［11］XIANG Xiugiao，WANG Zhenghua，Shi Baochang．Modified lattice Boltzmann scheme for nonlinear con⁃vection diffusion equations［J］．Communications in Nonlinear Science and Numerical Simulation，2012，17（6）：2415－2425．［12］SHIB C，GUO Z L．Lattice Boltzmannmodel for non⁃linear convection diffusion equations［J］．P hys Rev E，2009，79：016701．［13］ZOU Q S，HE X Y．On pressure and velocity boundary conditions for the lattice Boltzmann BGK model［J］．Physics of Fluids，1995，7（12）：2928－2930．［14］TANG G H，TAO W Q，HE Y．LThermal boundary condition for the thermal lattice Boltzmann equation［J］．Phys Rev．E，2005/72（1）：016703－1－6．［15］HENDRIEKSC．Strip Casting Technology⁃revolution in the Steel in dustly ［C］．MPT intemational，1995，18（3）：42－46．［16］谢水生，杨浩强，黄国杰，等．半固态镁合金连续铸轧过程的数值模拟［J］．塑性过程学报，2007，14（1）：80－84．XIE Shuisheng，YANG Haoqiang，HUANG Guojie，et al．Numerical simulation of semi⁃solid Magnesium alloy in continuous casting process ［J］．Journal of Plasticity Engineering，2007，14（1）：80－84．。

连铸结晶器内热一力耦合数值模拟及研究

报一
‰
Ｎｕｅｉａｉｕａｉｎａｄｒｓａｃｆｔｅｍａ－ｏｃｏｐｉｇｍｒｃｌｓｍｌｔｏｎｅｅｒｈｏｈｒｌｆｒｅｃｕｌｎｉｏｄｄｒｎｏｔｎｏｓｃｓｉｎｍｌｕｉｇｃｎｉｕｕａｔｎｇ
ｓｏｈａｏｒｃｎｔｏｆｔｍｐｒｔｒｒｐｒｔｆｂｌｅｎｍｏｌｎｕｘｈｓａｖｒｎｌｕｔｎｉｎｆｃｎｅｔｅｅｈｏｍａｉｎｈｗｓｔｔｐｒｐｅｏｒｌｏｅｅａｕｅｄｏａｅｏｉｌｔｉｕｄａｄｆａｅｙｉｐｒａｔｓｇｉａｃｏｐｒｖｎｔｔｅｆｒｔｌｉｏｏ＂ｈａ１ｌｇｍａｃｉｇ（ａｋｔｔｅｅｉＹｓａｔｈｎ：ｃ．ｒ
１１工艺参数．
连铸过程工艺参数选择见表１所示．
￥收稿日期：０２—０２２１６— ７
作者简介：王章岭（９６一）男，１８，山东菏泽人，硕上
王章岭，：等连铸结晶器内热一力耦合数值模拟及研究表１连铸工艺参数
ｏｈｅｓｒｎｉｇａｔｅｓｄｓｒｂｕｉｎｎｄｉｅｒｎａｎｇｓｅｄ．ｅｒｓｔｈｗｈｔｗｈｅｒｗｉｇｓｅｄｉｒａｅｔｅｓｎｅｐｏｔｆｔｈｉｋｎｎｄｓｒｓｉｔｉｔｏｉｆｅｔｄｒｗｉｐｅＴｈｅｕｌｓｓｏｔａ，ｔｎｄａｎｐｅｎｃｅｓｓ，ｈａｌｓ— ｔｏｎｔｕｌｆｔｅｓａ）ｓｒＨｅｔｍｐｒｔｅｊｃｅｓｓ．ｎｈｅｔｉｋｎｓｆｔｅｓｌｄｆｅｈｌｍｏｌ）ｅｍｅｈｉｎｉｇ．ｈｅｓｍｅｉｎｉｈｅｍｏｄｏｈｌｔｕ￣ｅｅｅａｕｒｎｒａｅａｄｔｈｃｅｓｏｈｏｉｉｄｓｅｌｕｄ１ｏｓｔｎｎＡｔｔａｉｅ

【CN109829219A】连轧机轧辊变速能量流模型和连轧机能量流模型建模方法【专利】

( 19 )中华人民共和国国家知识产权局
( 12 )发明专利申请
(21)申请号 201910058743 .7
(22)申请日 2019 .01 .22
(71)申请人中国地质大学（武汉）地址 430000 湖北省武汉市洪山区鲁磨路 388号
(72)发明人杨杰肖亭张文颖苏兆杰陈霖边汝霖缪钟毅
4 .如权利要求3所述的连轧机能量流模型建模方法，其特征在于：Pf1的计算公式为：
2
CN 109829219 A
权利要求书
2/2 页
其中F为单个轧辊的轧制力，d1为轴颈直径，d1＝2R ,f为摩擦系数，所述轧辊具有相同的摩擦系数，n1是总功率系数。
5 .如权利要求4所述的连轧机能量流模型建模方法，其特征在于：Pf2的计算公式为：
其中 ,轧辊的端部为轴颈，轧辊通过轴颈可转动的固定于轴承中，i整数，Pgi为第i个轧辊的密度，Lgi为第i个轧辊的长度，Rgi为第i个轧辊的半径，Lji为第i个轧辊的轴颈的长度， Rji为第i个轧辊的轴颈半径，αi为第i个轧辊变速时的角加速度，ni为第i个轧辊的转速；
A2：计算连轧机中所有轧辊变速消耗的轧辊动能和Pg，得到连轧机轧辊变速能量流模。 2 .一种连轧机能量流模型建模方法，其特征在于，包括如下步骤： B1 ：对酸洗-连轧产线中的连轧机构建连轧机电功率模型，该连轧机电功率模型包括连轧机的输入功率P，P的计算公式为 P＝Pz+Pg+Pf1+Pf2 其中，Pz为连轧机轧制工艺所需功率，Pg为连轧机中所有轧辊变速消耗的轧辊动能和， Pf1为连轧机中所有轴颈与轴承摩擦损失的功率，Pf2为连轧机中所有轧辊与带钢摩擦损失的功率；连轧机中单个的轧辊变速消耗的轧辊动能为Pgi，

连续铸造复合轧辊辊芯预热的数值模拟

连续铸造复合轧辊辊芯预热的数值模拟冯明杰;王恩刚;王俊刚;赫冀成【期刊名称】《东北大学学报（自然科学版）》【年(卷),期】2007(028)010【摘要】建立了连续铸造复合轧辊辊芯预热的数学模型,并对辊芯预热温度的分布情况进行了数值模拟,分析了拉坯速度及陶瓷隔热管对辊芯预热温度分布的影响.结果表明,辊芯到达线圈下端面时,辊芯表面与中心具有最大的断面温差,离开线圈一定距离后,由于表面的散热作用,中心温度会超过表面温度;较大的拉坯速度不利于提高辊芯的预热质量;在拉坯速度较小的情况下,安装陶瓷隔热管将会对辊芯表面起到较好的保温作用,而在拉坯速度较大时,保温效果不明显.【总页数】5页(P1401-1405)【作者】冯明杰;王恩刚;王俊刚;赫冀成【作者单位】东北大学,材料电磁过程研究教育部重点实验室,辽宁,沈阳,110004;东北大学,材料电磁过程研究教育部重点实验室,辽宁,沈阳,110004;东北大学,材料电磁过程研究教育部重点实验室,辽宁,沈阳,110004;东北大学,材料电磁过程研究教育部重点实验室,辽宁,沈阳,110004【正文语种】中文【中图分类】TF777.7【相关文献】1.连续铸造复合轧辊结晶器流场的数值模拟 [J], 冯明杰;王恩刚;邓安元;赫冀成2.辊芯温度对Fe-Cr-B/45#钢轧辊复合界面显微组织影响 [J], 杨文成;丁家伟;耿德英;丁刚;郭长庆3.复合轧辊球墨铸铁辊芯铸模底箱优化设计及生产验证 [J], 万敏;杨秀霞;王晋涛;郭修磊;孙格平4.数值模拟轧辊复合层连续铸造 [J], 杨大可;袁鹤清;陈乃琪;吴春京;沈定钊5.轧辊复合层连续铸造法计算机数值模拟 [J], 吴春京;沈定钊;杨大可;袁鹤清;陈乃琪因版权原因，仅展示原文概要，查看原文内容请购买。

基于ProCAST的卧式离心铸造轧辊的充型模拟

基于ProCAST的卧式离心铸造轧辊的充型模拟摘要：本文建立了复合轧辊卧式离心铸造在充型过程中金属液流动的三维模型，采用专业的铸造软件ProCAST求解得到重力和离心力作用下的流场分布，并讨论了金属液自由液面呈偏心分布的原因，分析结果对离心铸造过程中流场的认识和工艺优化设计具有参考意义。

关键词：ProCAST 卧式离心铸造充型模拟1 前言ProCAST是一款基于强大的有限元分析的铸造过程模拟软件，它能够预测严重畸变和残余应力，并能用于半固态成形，离心铸造，消失模铸造、连续铸造等特殊工艺。

利用ProCAST对离心铸造过程进行模拟，它能够针对离心铸造过程进行流动、传热、应力耦合作出分析。

ProCAST几乎可以模拟分析任何铸造生产过程中可能出现的问题，为铸造工程师提供新的途径来研究铸造过程，使有机会看到型腔内所发生的一切，从而产生新的设计方案。

2 模型建立及运算金属液在重力作用下浇入旋转着的铸型后，由于金属液与铸型之间的摩擦力及金属液内部的粘滞力和高速旋转产生的离心力使金属液在铸型内形成中空轧辊。

（1）利用ProE三维软件作为前处理软件创建模型，创建装配模型，输出ProCAST可接受的模型或网格格式的文件，通过标准格式文件，如IGES、STL 等可以和ProCAST实现数据交换。

（2）MeshCAST对输入的IGES文件进行修复，然后生成面网格，最终产生四面体网格，生成xx.mesh文件，文件中包含节点数量、单元数量、材料数量等信息。

建立的用于模拟轧辊的卧式离心铸造的模型如图1所示，图中不同颜色反应了模型是由两部分构成：铸型和铸件。

同时显示有两种材料、110940个节点、580647个单元以及模型的长宽高等信息。

此模型中，铸型外径200mm，铸件外径180mm、高度250mm。

图 1 物理网格模型（3）PreCAST为四面体网格文件分配材料、设定界面条件、边界条件、初始条件以及模拟参数。

铸型和铸件材料分别在材料数据库中选取，先试验性的以AlSi12CuNi为铸件材料，H13为铸型材料计算，从结果可以看出ProCAST对卧式离心铸造成型的模拟是否完好，再变换成实际中生产轧辊使用的材料进行模拟，这样能节省处理材料数据的时间。

入口温度分布对连续铸轧坯表面热带形成的影响

ＡｂｔａｔＢａｅｎｔｅｆｎｔｌｍｅｔａａｙｉｓｆｗａｅＭＳＡＲＣ，ｈ一ｉｎｉｎｄｎｍｉｓｒｃ：ｓｄｏｈｉｅｅｅｎｎｌｓｓｏｔｒｉＣＭｔｅ３ｄｍｅｓｏｙａｃｔｅｍａ — ｅｈｎｃｌｃｕｌｄｍａｈｍａｉａｄｐｙｉａｍｏｅｉｅｔｂｉｈｄＢａｅｏｈｒｌｍｃａｉａｏｐｅｔｅｔｃｎｈｓｃｌｄｌｓｓａｌｅ．ｓｓｄｎｈｇ —ｅｐｒｔｒｆｏｉｈｔｍｅａｕｅｌｗｃａｇｃｎｔｕｉｅａｈｎｅｏｓｉｔｌｗａｄｔｅａｃｎａｔｏｄｃａｃｃｍｐｔｔｏｔｖｎｈｒｌｏｔｃｃｎｕｔｎｅｏｕａｉｎｍｍｏｅ，ＦｒｒｎｌｎｕｇｓｕｅｏｄｖｌｐｏＳＭａｃＣｏｓｄｒｎｈｏｔｉｕｉｎｏｅｔｄｌｏｔａａｇａｅｉｓｄｔｅｅｏｎＭＣｒ．ｎｉｅｉｇｔｅｃｎｒｔｆｈａｂｏｇｎｒｔｄｂｌｓｉ — ｌｓｉｅｏｍａｉｎｆｔｅｒｌｎｔｉｎａｔｇｓｒｐｈｈｎｅｆｅｅａｅｙｅａｔｃｐａｔｄｆｒｔｏｈｏｌｇｓｒｐａｄｃｓｉｔｉ，ｔｅｃａｇｏｃｏｉｎｔｍｐｒｔｒｓａａｙｅｕｉｇｔｅｗｈｌｒｃｓｆｃｓ— ｏｌｇｏａａｙｅｔｅｔｕｒｃｓｉｇｅｅａｕｅｉｎｌｚｄｄｒｎｈｏｅｐｏｅｓｏａｔｒｌｎ；Ｔｎｌｚｈｒｅｐｏｅｓｎｉｒｌｓｔｅｉｉａｏｄｔｎｏａｔｎｔｐｉｈｎｅ．ｅｉｆｅｃｆｉｉａｅｅａｕｅｔｈｕｅ，ｈｎｔｌｃｎｉｏｆｃｓｉｇｓｒｓｃａｇｄＴｈｎｕｎｅｏｔｌｔｍｐｒｔｒｏｔｅｉｉｉｌｎｉｒｓｌｔｍｐｒｔｒｆａｔｇｓｒｎｅｆｒａｉｎｏｏｔｉｓａａｙｅ．ｉａｌ，ｈｉｌｔｏｅｕｔｅｅａｕｅｏｓｉｔｉａｄｔｏｃｎｐｈｍｔｆｈｔｓｒｉｎｌｚｄＦｎｌｔｅｓｍｕａｉｎｏｐｙｒｓｌｉｖｌａｅｒｕｈｅｐｒｍｅｔｅｕｔｓａｉｔｄｔｏｇｘｅｉｎ．ｄｈＫｅｒｓｏｔｎｏｓｒｌｃｓｉｇｔｒｅｄｍｅｓｏｏｐｅｎｌｓｓＭＳａｃｆｎｔｌｍｅｔｙｗｏｄ：ｃｎｉｕｕｏｌａｔ；ｈｅ — ｉｎｉｎｃｕｌｄａａｙｉ；ＣＭｒｉｉｅｅｎｎｅａａｙｉ；ｎｔｌｅｐｒｔｒ；ｔｂｅｔｍｐｒｔｒ；ｈｔｔｉｎｌｓｓｉｉａｍｅａｕｅｓａｌｉｔｅｅａｕｅｏｒｐｓ

轧机振动及其耦合效应研究

II
重庆大学硕士学位论文
英文摘要
4. On the basis of Chapter 2, 3,4, the Uermxo Equation and the elastic-plastic theory were involved to deeply study the deformation process of rolled products. The stress compatibility equations in the direction of thickness and length were established to fulfill the coupling of three sub-systems. The rolling mill coupling model with 17 degrees of freedom was set up and different rolling mill parameters, rolling parameters and response situations of the rolling mill systems under different interference signals were calculated through using MATLAB and C#. 5. Taking 1780 four-roller hot rolling mill as example, the article conducted the simulation analysis of the coupling model. The variation situation of rolled products’ output thickness under different interference signals was obtained. The study achievement of the article is of great guiding meaning and has important practical value to the rolling mill design. Keywords: Rolling Mill Vibration, Coupled Vibration, Natural Frequency

特钢φ85mm圆钢轧制工艺及孔型分析

特钢φ85mm圆钢轧制工艺及孔型分析摘要： 40Cr 合金钢在机械制造业中应用广泛，其轧制圆钢的质量对最终机械零件的质量和使用寿命有很大影响。

通过分析40Cr 钢的热塑性特征，建立了40Cr 钢的 Hensel-Spittel 流动应力模型。

针对φ85mm 40Cr 钢205*205轧制坯可能的连轧规程，采用 LARSTRAN/SHAPE 粘塑性有限元技术，建立了8道次热连轧过程的三维热力耦合模型。

通过对轧制过程的模拟，得到了轧制过程中的应力、应变、温度分布和轧制力变化情况。

模拟结果包括了圆孔型与曲边孔型、圆孔型与直边孔型的塑性变形比较，以及产生轧制缺陷(如裂纹)的原因。

在此基础上，构建了可靠的轧辊孔型数值分析，并通过实际试验进行了验证。

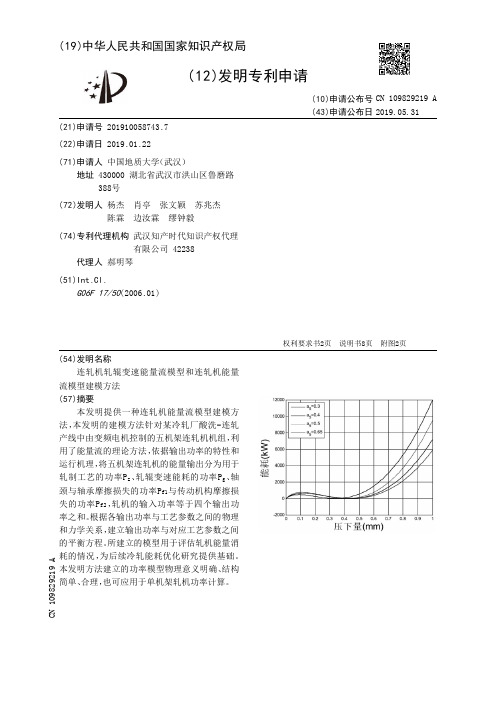
关键词：特钢φ85mm 圆钢轧制工艺孔型1.引言40Cr 调质合金钢广泛用于制造轴类、套圈类重要机械零件。

目前对40Cr 圆钢的研究主要集中在冶金过程中的裂纹和质量控制方面。

已有学者研究了40Cr 钢的奥氏体动态重结晶和晶粒细化规律。

但是，从40Cr 圆钢的质量来看，文献中没有论述孔型顺序对40Cr 钢轧制力学参数的影响以及轧制规程的合理性。

本文建立了φ85mm 40Cr 钢圆钢八道次热连轧轧制孔型序列，并利用基于LARSTRAN/SHAPE 的热力耦合有限元模拟对其进行了验证。

通过分析连轧过程中应力、应变、温度和轧制力的变化特点，指出了产生轧制缺陷(如裂纹)的原因。

为了轧制更精确的合金钢圆钢，对两种不同的精轧圆钢道次进行了比较。

1.孔型设计及有限元模型2.1 轧制孔型设计根据合金钢水平(H)立(V)轧机连续轧制工艺，设计了φ85mm 40Cr 钢205*205轧制坯最终圆钢轧制孔型连铸。

连铸坯截面尺寸为200mm × 200mm，角部圆角半径为8mm。

考虑到轧制圆钢的变形要求，轧制孔型顺序为八道次: 第一道次(H1)和第三道次(H3)采用扁平箱形孔型，第二道次(V2)和第四道次(V4)采用方箱形孔型，第五道次(H5)和第七道次(H7)采用椭圆孔型，第六道次(V6)和第八道次(V8)采用圆孔型。

基于粒子群算法的双辊铸轧工艺优化_曹光明

收稿日期:2010-08-05基金项目:国家自然科学基金资助项目(50734001);中央高校基本科研业务费青年教师科研启动基金资助项目(N100307006) 作者简介:曹光明(1982-),男,四川绵阳人,东北大学讲师,博士;刘振宇(1967-),男,内蒙古赤峰人,东北大学教授,博士生导师第32卷第5期2011年5月东北大学学报(自然科学版)Journal of Northeastern U niversity(Natural Science)Vol 32,No.5M ay 2011基于粒子群算法的双辊铸轧工艺优化曹光明1,李成刚1,刘振宇1,高柏宏2(1.东北大学轧制技术及连轧自动化国家重点实验室,辽宁沈阳 110819; 2.沈阳机床有限公司,辽宁沈阳 110819)摘要:针对双辊铸轧过程中凝固终点位置这一关键参数,基于贝叶斯方法的神经网络和理论模型,根据经验模型及熔池断面几何关系建立凝固终点位置数学模型在化学成分和工艺约束已知的条件下,采用粒子群优化算法针对凝固终点位置这一铸轧过程中的关键因素进行相应的工艺参数的优化计算铸轧实验结果验证了优化结果的可行性,从而为提高双辊铸轧板形和板厚的控制精度,改善铸带表面质量提供可能关键词:凝固终点;贝叶斯方法;粒子群优化算法;过程工艺优化中图分类号:T P 183 文献标志码:A 文章编号:1005-3026(2011)05-0667-04Optimizing Processing Parameters for Twin -Roll Strip Casting Using Particle Swarm OptimizationCA O Guang -ming 1,L I Cheng -gang 1,LI U Zhen -yu 1,GA O Bo -hong2(1.T he State K ey Laboratory of Rolling and Auto mation,N ortheastern U niversity,Shenyang 110819,China; 2.Shenyang M achine T ool Co.L td.,Shenyang 110819,China.Corresponding author :CAO G uang -ming ,E -mail:caogm @r )Abstract:In order to improve the flat,gaug e control precision and surface quality of casting strips,processing parameters w ere optimized based on a kiss point position calculation model (combining a Bayesian neural netw ork and a theoretical model)and using a particle sw arm optimization method under given chemical composition and process constraint conditions.Optim ized and experimental results show ed good agreement.Key words:kiss po int;Bayesian method;particle sw arm optimization method;processing parameters optimization双辊铸轧是不经过中间冷却和再加热工序,从液态金属直接加工成金属成品或半成品的一种新型加工工艺它是连续浇注和压力加工联合的工艺过程[1-2]凝固终点位置是铸轧过程中的一个重要的动态因素[3],准确预测和控制凝固终点位置不仅直接影响到铸带板形和板厚的控制精度,同时是保证铸轧过程正常进行和获得良好的表面和内部质量薄带钢的前提考虑到凝固终点位置的不可检测性,本文通过铸轧区横断面几何形状及凝壳生成速率推导出凝壳厚度与各工艺参数之间的关系,同时根据实测铸轧力数据,采用反算法计算凝固终点位置,引入基于贝叶斯方法的前向训练算法的神经网络[4-5],采用综合网络和数学模型的组合形式进行凝固终点位置的建模[6]优化的概念已经在钢铁行业广泛应用,例如Saito 应用最速下降法优化连续冷却过程[7] Malas 采用控制理论优化AISI 1030钢热挤压的组织演变过程从而获得预设的晶粒尺寸[8] 本文针对凝固终点位置这一关键参数,基于上述预测模型,在化学成分和工艺约束已知的条件下,采用粒子群优化算法优化铸轧工艺参数,获得理想的铸带1 凝固终点位置预测模型1.1 神经网络与数学模型的组合考虑到双辊铸轧过程具有多变量、强耦合、非线性、时变性的特点,面对这样复杂过程的建模问题,传统数学模型、经验公式具有较大的局限性,因此引入神经网络作为增强数学模型,提高预测精度的手段采用综合网络和数学模型的组合形式,如图1所示图1 模型结构示意图Fig.1 Schem atic view of m odels structure1.2 数学模型双辊铸轧过程中凝壳厚度关系式[9]:k =k (T k - ),(1)式中:模型参数k , 主要取决于金属成分、轧辊冷却能力、过热度;T k 为金属运动到凝固终点所用时间:T k =R arcsin -1L R -arcsin -1pk Rv(2)根据熔池断面的几何关系,凝固终点位置p k和 k 具有如下关系式:( k +R ) R 2-p 2k =R R +d2,(3)其中d 为出口厚度考虑到arcsin -1p kRp k R ,将式(1),式(2)代入式(3)得:k arcsin -1L R -p k Rn-+R R 2-p 2k =R 2+R d 2(4)采用牛顿-拉斐逊方法求解方程(4),即可计算出凝固终点位置p k1.3 神经网络建立1.3.1 网络原理在贝叶斯框架下对神经网络进行改进,引入融入了奥克姆因子的网络显著度作为评价神经网络结构好坏的一个参数,是判断网络训练是否充分的依据将权、阈值进行分组并在目标函数中引入了表示网络复杂程度的惩罚项f (w )= E D +12Gg=1g E W g =12Ok=1Nj=1(t jk -y jk )2+12Gg =1gWgi=1W 2i (5)式中:E D 为常规误差项;E W g 为网络复杂程度的惩罚项;t jk ,y jk 分别为期望和实际输出;O,N 分别为输出变量数和训练样本数;G ,W g 分别为网络权、阈值划分的组数和第g 组中权、阈值的个数; g , 为参数 1.3.2 超参数、最大显著度的计算超参数 g , 的计算见式(6),式(7),具体的推导过程见文献[10]g = g2 E W g ,(6)=N -Ggg2 E D(7)1.3.3 网络的训练流程1)初始化超参数和网络连接权、阈值;2)采用Levenberg -Marquardt[11]算法训练网络;3)计算参数 g ,预测误差和显著度;4)根据式(6),式(7)调整参数;5)重复步骤2)~4)直到收敛1.4 综合网络和数学模型组合的建立和测试1.4.1 综合网络输入的确定综上所述,网络的输入参数包括浇铸温度,预设辊缝,铸轧速度,熔池液位高度,铸辊内冷却水温度以及数学模型计算的凝固终点位置网络的输入和输出参数归一化处理至[0,1]区间隐层和输出层单元激励函数为Sig mo id 函数采用1Cr17铸轧实验实测铸轧力通过反向计算凝固终点位置用于网络训练、测试本文采用的样本数据共1000组,其中700组用于网络的训练,300组用于网络验证1.4.2 综合网络结构选取选择不同隐层节点进行训练测试,由图2所示,当隐层节点为3时,开始出现冗余连接权随着隐层节点的增加,网络的训练速度会越来越慢图3为显著度最大区域,预测误差和显著度之间图2 有效参数个数与隐层单元数的关系Fig.2 The relationshi p between wel-l determinedparam eter and hidden units关系当隐层节点数为3时,其预测误差分布集中且较其他结点数的预测误差小,因此,通过显著度668东北大学学报(自然科学版) 第32卷和预测误差双重标准确定隐层节点数为3图3 预测误差与显著度的关系Fig.3 Relationshi p between SEP and log evidence1.4.3 综合网络和数学模型组合计算精度采用综合网络和数学模型组合计算的凝固终点位置与实测铸轧力反算凝固终点位置的对比如图4所示,90 7%的验证数据计算精度在 7 0%范围内,说明采用所建立的模型具有很高的计算精度图4 模型计算与实测反算的凝固终点位置对比Fig.4 C om pari son between kiss point positi oncalculated by m odel and inversel y calcu -lated by m easured rolling force2 粒子群优化算法2.1 基本原理粒子群优化方法最初是由Kenned 和Eberhart 在1995年提出的[12],是通过微粒个体间的相互作用在复杂的多维空间中寻找最小化目标函数的最优解粒子群优化算法利用个体在解空间中的随机速度来改变个体,其解群相对进化代数而言,表现出更强的随机性同时粒子具有记忆的特性,它们通过自我学习和向他人学习,使其下一代解有针对性的从先辈那里继承更多的信息,从而能在较短的时间内找到最优解另外粒子群优化算法的信息共享机制是单向的,这使得整个搜索更新过程跟随当前最优解在一个N 维目标搜索空间中,粒子表示为x i =(x i 1,x i 2, ,x iN )T,i =1,2, ,M ,飞行速度v i =(v i 1,v i 2, ,v iN )T ,M 为粒子个数在每一次迭代过程中,粒子通过以下公式改变位置:v i (t )=w v i (t -1)+ r 1(p i -x i (t -1))+r 2(p g -x i (t -1)),(8)x i (t)=v i (t)+x i (t -1)(9)式中:r 1,r 2是[0,1]间的随机数;p i 是第i 个粒子之前经历过的最好位置;p g 是所有粒子经历过的最好位置;w 为惯性系数起着平衡全局和局部搜索的作用,惯性系数增大,全局搜索的能力增强,相反,则局部搜索能力加强加速因子和惯性系数作如下调整:= 0+tN t,t =1,2, ,N t ,(10)w =w 0+(1-w 0)r 3(11)其中:w 0 [0,1];r 3是[0,1]的随机数 2.2 算法流程1)初始化粒子群设群体规模,在允许的范围内随机设置粒子的初始位置和速度;2)评价个体粒子,设置个体最优和全局最优;3)根据式(8),式(9)调整每一个粒子的速度和位置;4)检查终止条件如果达到最大迭代次数genmax 或最好解停滞不再变化,终止迭代,输出全局最优,否则返回2)3 铸轧工艺的优化设计3.1 优化设计流程综合上述凝固终点位置预测模型和粒子群优化算法,进行了铸轧过程工艺优化设定 K P 为凝固终点模型计算值,K P,obj 通过基本的物理冶金学规律及大量实验和模拟研究得出的最优凝固终点位置则设置优化目标函数为m in f =K P,obj -K P(12)优化搜索的工艺参数为浇铸温度、熔池液位高度及铸轧速度优化搜索的工艺参数约束条件如表1所示表1 约束条件Table 1 Constraint condition参数浇铸温度液位高度mm 铸轧速度m min -1上限159010014下限1520140303.2 优化结果以1Cr17铁素体不锈钢(化学成分见表2)作669第5期曹光明等:基于粒子群算法的双辊铸轧工艺优化为铸轧实验钢种,通过物理冶金学规律及大量实验表明其凝固终点最优位置为10mm,设定粒子群优化算法中粒子数为100,最大迭代次数为20,实验结果与优化结果对比如表3所示,铸带如图5所示表2 1Cr17铁素体不锈钢的化学成分(质量分数)Table 2 Component of 1C r17%C Si M nS P Cr 0.12 0.75 0.800.0300.03516~18表3 实验结果与优化结果Table 3 Experi m ent results and optimization results序号浇铸温度液位高度mm 铸轧速度m min -1凝固终点位置mm 实际值156********.15优化值1562.32108.8914.7510.13图5 铸轧1Cr17薄带钢实物图Fi g.5 Picture of casting 1C r17s trip4 结语根据经验模型及熔池断面几何关系建立凝固终点位置数学模型引入基于贝叶斯理论的神经网络作为增强数学模型,提高预测精度的手段采用综合网络和数学模型的组合形式建立凝固终点计算模型在此基础上,采用粒子群优化算法针对凝固终点位置这一铸轧过程中的关键因素进行相应工艺参数的优化计算,实验结果验证优化结果可行性,从而为提高双辊铸轧板形和板厚的控制精度,改善铸带表面质量提供可能参考文献:[1]S hin Y K,Kang T,Reynolds T ,et al .Devel opment of tw i n roll strip cas ter for sheet steels [J ].I ron M aking a nd Ste elmaking ,1995,22(1):35-44.[2]邸洪双,鲍培伟,苗雨川,等双辊铸轧薄带钢实验研究及工艺稳定性分析[J] 东北大学学报:自然科学版,2000,21(3):274-277 (Di Hong -shuang,Bao Pe -i w ei,M iao Yu -chuan,et al .Experimental study on th e tw in roll strip casting and analysis of processing stability [J ].JournalofN ortheaster nUniv ersity:Natural S cience ,2000,21(3):274-277.)[3]金珠梅,赫冀成,徐广携双辊连续铸轧工艺中流场、温度场和热应力场的数值计算[J] 金属学报,2000,36(4):391-394 (Jin Zhu -mei,He J -i cheng,Xu Guang -jun.Numericalsimulation of flow ,temperature and therm al stress fi leds during tw in -roll casting process [J ].A CTA M etallu rgica S inica ,2000,36(4):391-394.)[4]Foresee F D,Hagan M T.Gauss -New ton approximation to bayesian learning [C ] Proceedings of the International Conference on Neural Networks.Houston,1997:1930-1935.[5]M ackay D J C.A practical bayesian framew ork for back -propagation networks [J ].Neural Comp utation ,1992,4(3):448-472.[6]王国栋,刘相华金属轧制过程人工智能优化[M ] 北京:冶金工业出版社,2000:102-107(W ang Guo -dong,Liu Xiang -hua.Intelli gent optimizati on in metalrolling [M ].Beijing:M etallurgical Industry Press,2000:102-107.)[7]S aito Y.M odelling of microstructural evolution in thermo -m echanical processi ng of structural steel s [J ].M ater ialsScie nc e and Engineering A ,1997,223(1/2):134-145.[8]M alas J C .Optimizati on of m i crostructure development during hot w orking usi ng control theory [J ].M etallurgical and M aterials T ransactions A ,1997,28(9):1921-1930.[9]Hong K S ,Kim J G,Tomizuka M.Control of strip casting process :decentralization and optimal rol l force control[J ].Control E ngineering Practice ,2001(9):933-945.[10]T hodberg H H.A review of bayesian neural networks w ith an application to near infrared spectroscopy [J ].I EEE Transactions on Neural Netw orks ,1996,7(1):56-72.[11]Hagan M T,M ohammad B.Training feedforward netw orks w ith the marquardt algorithm [J ].IEEE T ransactions on Neur al Netw orks ,1994,5(6):989-993.[12]Kennedy J,Eberhart R.Particle sw arm optimization[C] IEEEInternationalCon ference onNeuralNetw orks.Piseataw ay:IEEE S ervice,1995:1942-1948.670东北大学学报(自然科学版)第32卷。

宽厚复合板热轧成形轧制力模型

文章编号: 0254 - 0037(2014)12 - 1905 - 06
Wide-thick Clad Plate Hot Rolling Force Model During Forming Process
(1. Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education of China, 3. Center of Technology, China First Heavy Industries, Qiqihar 161042, Heilongjiang, China) 2. College of Mechanical Engineering,Yanshan University,Qinhuangdao 066004, China; Yanshan University,Qinhuangdao 066004, China;
确定各界面上摩擦切应力 τ 的方向,进而推导出热轧不锈钢复合板成形轧制力计算公式. 研究结果表明:该轧制力模型可准确预测轧制力的大小,有效提高轧制力的计算精度. 经轧制成形制造的不锈钢复合板满足设计技术要求,制定工关键词: 宽厚复合板; 热轧制造; 成形工艺; 热力耦合; 复合轧制力文献标志码: A
宽厚不锈钢复合板的轧制示意
第 12 期
金贺荣, 等: 宽厚复合板热轧成形轧制力模型
1907
意图,c 层为低合金钢 Q345R( 软金属层 ) ,m 层为不锈钢 316 L( 硬金属层) . k c ,软硬金属层接触面的剪切应力为 τ m = k m . Ⅱ 区轧辊与软金属层接触面的剪切应力 τ c = - k c , 软硬金属层接触面上剪切应力为 τ m = - k m . 图 3 所示为宽厚不锈钢复合板截面应力. Ⅰ区轧辊与软金属层接触面的剪切应力 τ c =

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

关键词：铸轧辊；合；型耦模
中图分类号：０２
文献标识码：Ａ
文章编号：０５９９（０２ｏ１ —３１０ —７２２０）４２０
快速超薄铸轧机铸轧辊与一般的热、轧辊不冷同，主要表现在辊芯与辊套为２种不同材质配合而成的复合体，在不连续的结合面，辊芯内有几何存结构复杂的内冷水槽而非单一实心体；向温差较周
４３ｌ
｛∑ ；为元数；为点；表的步骤为：ｎ单节点节温度为
面吸收率；ｑ为边界热流密度；，ｑ为单位面积射流率；为材料的热力系数矩阵；Ｐ］，，［］［＝［ …，
ａＮｒ
，
耦合求解方程（）现已化为方程（）和（）Ｉ（３）２式ａ令｛｝＝｛｝，｝＝｛｝一｝．．口一｛口＝｛。
比容；］ ∑ ［］＝ … ［热矩阵［＝ ∑Ｉ］
收稿日期：０１１５２０ —１ —１基金项目：国家计委计划项目（高技［９８１８）计１９］９５
系数；为Ｂｔ￣常数；表面热辐射率；＝呀ｏｎｍ为
何结构复杂的内冷水槽而非单一实心体，向温差较大，温度场为非对称三维温度场，周其工作在多种物理场（、热
力），下作者运用热弹性力学理论，建立热弹耦合方程并求解，并结合接触压力（轧制力分布）型，定了铸轧辊温模确度场边界条件，得到了超薄铸轧机铸轧辊变形的计算模型．
（）１
积分面积；＝ｓ＋ｓ＋ｓ＋ｓ，积分边线；ｌｓ，ｌ２３４为ｓ，２
式中：］ ∑［］＝∑ Ｉｐ［］ Ⅳ ｄ，［＝ｃ一ＪｃⅣ ］ｎ为ｃ［
ｓ，别为第１２３类及辐射边界条件的边界线ｓ分，，长度；，物体的密度和比热容；ｐｃ为ｂ为边界热交换
维普资讯
第３卷第４期３２００２年８月
中南工业大学学报
ＪＥＴ．ＳＴＵＮＶ．１Ｃ珈．ＣＮＯＵＨＩＥＯＬ．
Ｖ０．３Ｎ４１３ｏ．Ａｕｇ．２００２
度场｛｝的有限元方程为』：
节点至规定温度的热载荷向量；Ｒ］［＝∑ ［量ｊｐＮｄ为热成载向；Ｔ，
［足＝∑ ［］］足ｑⅣ ｄ，表热＝∑Ｉｓ］Ｔ面流［为载向；＝［＝∑Ｉ６［］Ｔ荷量［］ ∑ Ｒ］Ｒ Ⅳ ，，ｄ
由于铸轧辊内部几何结构复杂且材质相异，因此，必须建立铸轧辊三维热力耦合模型，对各种复杂边并
界条件进行处理ｕ』。．
∑［ｒ＝∑４。［］Ⅳｄ，热射ｇ］Ｉ Ⅳ ］为辐．［Ｔ
矩；＝［ ∑ １Ⅳ ［］］阵［ ∑ ＝Ｊ［］Ⅳ［］］
为表面热交换载荷向量；Ｒ］＝∑ ［，［，Ｒ］
＝
［｛｝［］］］］｛｝Ｃ］＋［＋［＋［＋［］＿
｛｝尺｝足６＋｛｝足｝尺ｒ＋｛。＋｛｝足，＋｛．
ｎ（）ｃ
∑ｌ匈［］Ｔ受射热荷量ｎ。，，辐的载向；为． Ⅳｄ为
［Ｐ］・｛｝一｛一｝ｄ，热耦合矩阵；Ｒ，（。）Ｔ为［］
＝
∑ ［，＝。口，［］ｔ维表足］ ∑Ｉ（・），持面．１Ⅳ ｄ为
１热弹耦合方程及其求解
在热弹性力学中，传导方程和热弹性力学方热程是相互耦合的．传导耦合项的存在，明热弹性热表体上的温度场与热弹性应变有关．合热弹性问题耦的控制方程由热传导方程和热弹性力学方程构成．对于平面问题，由具耦合项的热传导方程导出的温
［ｒ・Ｂｄ，ｉ］［］ｎ为热传导矩阵；］ｃ［＝∑ ［］
＝
∑ ＩｂⅣ］ Ⅳ］Ｔ为热交换矩阵；］［ｄ，［［＝
大。其温度场为非对称三维温度场．因此，必须考虑热弹性应变与温度场的相互影响，考虑非稳态过程．
作者简介：勇刚（９６，，熊１一）男湖南安化人，６株洲工学院副教授，中南大学在读博士研究生，事ＣＤ机电一体化、限元应用研究从Ａ有
维普资讯
第４期
熊勇刚，：速超薄铸轧机铸轧辊变形热力耦合模型等快
快速超薄铸轧机铸轧辊变形热力耦合模型
熊勇刚，军辉王桥医ｈ，建平李，谭（．洲工学院机械系，南株洲１株湖２．中南大学机电工程学院，南长沙湖４２０；１０８４０８）１０３
摘要：快速超薄铸轧机铸轧辊的辊芯与辊套为２种不同材质配合而成的复合体，存在不连续的结合面，辊芯内有几