四跨连续梁的内力计算
结构力学公式大全e
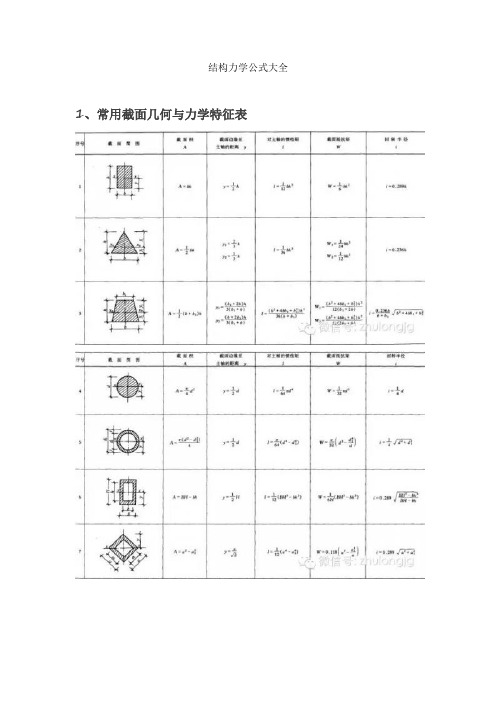
结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴〔形心轴〕的截面惯性矩〔mm4〕。
根本计算公式如下:2.W称为截面抵抗矩〔mm3〕,它表示截面抵抗弯曲变形能力的大小,根本计算公式如下:3.i称截面回转半径〔mm〕,其根本计算公式如下:4.上列各式中,A为截面面积〔mm2〕,y为截面边缘到主轴〔形心轴〕的距离〔mm〕,I为对主轴〔形心轴〕的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=〔-0.125×11.76×52〕+〔-0.188×29.4×5〕=〔-36.75〕+〔-27.64〕=-64.39kN·mVB左=〔-0.625×11.76×5〕+〔-0.688×29.4〕[例2] 三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
连续梁的内力包络图

连续梁的内力包络图
计算各截面在活载作用下的最大、最小弯矩时,需要事 先利用影响线来确定最不利荷载位置。但如果连续梁受均布 活载时,则各个截面的最大、最小弯矩的计算将可以简化。 图16-15中给出了五跨连续梁某些截面的弯矩影响线和引起最 大、最小弯矩的最不利荷载位置。从图中可以看出,连续梁 受均布活载作用时,各截面弯矩的最不利荷载位置并不是活 载布满各跨的情况,而是在若干跨内布满活载。例如,支座 截面最小弯矩:支座两个邻跨有活载,然后隔一跨有活载, 如图16-15(d)所示。又如,跨中截面最大弯矩:本跨有活载, 然后每隔一跨有活载,如图16-15(f)所示。
连续梁的内力包络图
将各截面的最大(小)弯矩值以曲线相连,即得连续梁的 弯矩包络图。
用类似的方法可绘制剪力包络图。由于设计连续梁时, 通常只需要用到各跨支座两侧截面上的剪力最大、最小值, 而其最不利荷载位置也是在若干跨内布满活载,所以可先分 别绘出连续梁在恒载和各跨单独布满均布活载时的剪力最大、 最小值,即
连续梁的内力包络图
式中,FSik表示ik跨i端的剪力;FgSik表示恒载单 独作用下ik跨i端的剪力值;∑FPSik(+)、∑FPSik(-)表示 当各跨分别单独承受均布活载时,在ik跨i端所产生 的所有正剪力值或负剪力值的总和。
将各跨两侧截面上的最大(小)剪力值以直线相连, 即得近似的剪力包络图。按此设计比实际的剪力包 络图偏于安全。
连续梁的内力包络图
这样,各截面的最大、最小弯矩均可由某几跨单独布 满活载时的弯矩叠加得到。据此,绘制连续梁的弯矩包络 图时,可采用如下的办法:先分别绘出连续梁在恒载及各 跨单独布满活载时的弯矩图(可用力矩分配法求解或查建筑 结构静力计算手册),并将每一跨分为若干等份,在弯矩图 中标明各等分点处截面的弯矩值,然后按下式计算任一等 分点处截面K的最大、最小弯矩值为
多跨连续梁计算程序

多跨连续梁计算程序V2.0用户使用手册上海易工工程技术服务有限公司目 次一、功能简介 (3)1.1 基本功能 (3)1.2 运行环境 (3)1.3 计算依据 (3)1.4 参数输入约定 (3)1.4.1 坐标系约定 (3)1.4.2 作用效应值的正负号约定 (3)1.4.3 参数采用的量纲 (3)1.5 计算原理 (3)1.5.1 内力计算 (3)1.5.2 效应组合 (4)1.5.3 配筋计算 (4)二、程序说明 (5)2.1 程序功能 (5)2.2 程序界面 (5)三、参数输入 (6)3.1基本参数输入 (6)3.2 地基系数 (6)3.3 截面参数 (6)3.4 连续梁参数 (8)3.5 节点支撑、连接方式 (9)3.6 荷载定义 (10)3.7 荷载输入 (11)3.8 组合参数输入 (13)四、结果查询、显示和输出 (15)4.1 计算结果查询 (15)4.2 计算结果图形显示 (15)4.3 计算结果报告书输出 (15)五、计算算例 (17)5.1、算例1刚性支座 (17)5.2 算例2弹性支座 (21)5.3 算例3弹性地基梁 (23)六、附录 (27)6.1 分项系数设置 (27)6.2 材料设置 (27)6.3 支撑方式设置 (27)6.4 背景颜色设置 (28)一、功能简介1.1 基本功能多跨连续梁计算系统是依据港口工程最新技术规范开发的工程辅助设计软件,该系统考虑多种支撑方式(弹性支撑、刚性支撑、自定义支撑)、多种单元模式(普通梁单元、弹性地基梁单元)、多种连接方式(节点铰接、节点固结)、多种荷载(集中力、均布力、滚动力),并且考虑叠合构件问题,此外该系统提供直观的3D视图方式显示连续梁实体模型、荷载、作用效应等,并且为用户提供完整的WORD格式报告书。
1.2 运行环境项 目最 低推 荐处理器Pentium II 350Pentium III450内 存128MB256MB可用硬盘50MB100MB显示分辨率800*6001024*768打印机Windows支持的图形打印机激光打印机操作系统Windows 98Windows 2000/xp1.3 计算依据使用规范《港口工程荷载规范》 (JTS 144-1-2010)《港口工程混凝土结构设计规范》(JTJ 267)1.4 参数输入约定1.4.1 坐标系约定X方向为沿连续梁方向,X零点为连续梁左侧。
结构力学公式大全

结构力学公式大全结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
梁 弯矩图 梁 内力图 (剪力图与弯矩图)
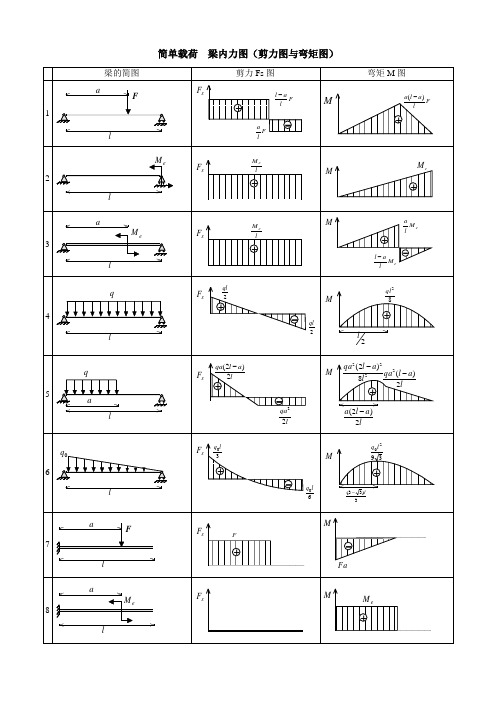
简单载荷 梁内力图(剪力图与弯矩图)梁的简图剪力Fs 图弯矩M 图1laFsF F l a F l al -+-F la l a )(-+M2l eMsF lM e +MeM +3laeMsF lM e +Me M lal -e M la +-4lqsF +-2ql 2qlM82ql +2l5lq asF +-la l qa 2)2(-lqa 22M2228)2(l a l qa -+la l qa 2)(2-la l a 2)2(-6lqsF +-30l q 60l qM3920l q +3)33(l-7aFlsF F+Fa-M8aleMsF+eM M9lqs F ql+M22ql -10lqsF 2l q +M620l q -注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征某一段梁上的外力情况 剪力图的特征弯矩图的特征无载荷水平直线斜直线或集中力 F突变 F 转折或或集中力偶eM 无变化 突变e M均布载荷q斜直线抛物线 或零点极值表3 各种约束类型对应的边界条件约束类型 位移边界条件力边界条件(约束端无集中载荷)固定端0=w ,0=θ —简支端0=w0=M 自由端—0=M ,0=S F注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
结构力学公式大全
精品文档结构力学公式大全1、常用截面几何与力学特征表.精品文档.精品文档.精品文档)。
基本计算公式如mm4.I称为截面对主轴(形心轴)的截面惯性矩(1注:下:),它表示截面抵抗弯曲变形能力的大小,基本mm3W称为截面抵抗矩(2.计算公式如下:mm),其基本计算公式如下:3.i称截面回转半径(为截面边缘到主轴(形心轴)的距y为截面面积(mm2),.上列各式中,4A I为对主轴(形心轴)的惯性矩。
mm离(),.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
52、单跨梁的内力及变形表简支梁的反力、剪力、弯矩、挠度2.1 .精品文档.精品文档.精品文档2.2 悬臂梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.4 两端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.5 外伸梁的反力、剪力、弯矩和挠度.精品文档.精品文档.精品文档.等截面连续梁的内力及变形表3 3.1 二跨等跨梁的内力和挠度系数.精品文档;。
qlql2;V=表中系数×注:1.在均布荷载作用下:M=表中系数×;。
;V =表中系数×F 2.在集中荷载作用下:M=表中系数×Fl,每跨各有一集11.76kN/m,均布荷载q=例1] 已知二跨等跨梁l=5m [ =29.4kN,求中间支座的最大弯矩和剪力。
中荷载F 5))+(-0.188×29.4××解[] MB 支=(-0.125×11.7652m64.39kN·36.75)+(-27.64)=-=(-29.40.688×)0.625 VB左=(-×11.76×5)+(-56.98kN)+(-20.23)=-=(-36.75,求边跨最大跨中11.76kN/m6m,均布荷载q==2] [例已知三跨等跨梁l 弯矩。
连续梁桥(T构)计算

计算方法
结果分析
采用有限元法进行计算,将主梁离散化为 多个单元,建立整体有限元模型。
通过计算和分析,得出主梁在各种工况下 的应力、应变和挠度等结果,验证主梁的 受力性能是否满足设计要求。
某高速公路的T构优化设计
工程概况
某高速公路连续梁桥(T构)需 要进行优化设计,以提高结构 的承载能力和稳定性。
优化内容
和意外事故。
提高施工质量
施工控制有助于提高桥梁的施工 质量,通过控制施工过程中的各 项参数,确保桥梁的线形、内力
和变形等指标符合设计要求。
节约成本
合理的施工控制可以避免施工过 程中的浪费和不必要的返工,从
而节约施工成本。
施工控制的主要内容
施工监控
对桥梁施工过程中的线形、内力和变形进行实时 监测,确保施工状态符合设计要求。
对主梁的截面尺寸、配筋和桥墩 的布置进行优化设计,降低结构 的自重和提高结构的刚度。
优化方法
采用有限元法进行计算和分析, 通过调整结构参数和材料属性, 对结构进行多方案比较和优化。
结果分析
经过优化设计,结构的承载能力 和稳定性得到了显著提高,同时
降低了结构的自重和造价。
某铁路桥的T构施工控制与监测
03
需要保证桥面平度的桥梁
连续梁桥(T构)的桥面平度较高,能够满足高速铁路、高速公路等对桥
面平度的要求。
02
T构的力学分析
静力学分析
1
计算T构在静力作用下的内力和变形,包括恒载 和活载。
2
分析T构在不同工况下的应力分布和最大、最小 应力值。
3
评估T构的承载能力和稳定性,确保满足设计要 求和使用安全。
在满足安全性和功能性 的前提下,降低T构的造
基于ANSYS的多跨连续梁的内力分析

基于ANSYS的多跨连续梁的内力分析王伟(长沙理工大学土木与建筑学院,湖南长沙 410004)【摘要】多跨连续梁的内力分析是结构力学中平面弯曲内力的重点和难点之一。
文章利用ANSYS软件的结构静力分析功能来实现多跨连续梁的内力分析,基于此方法可用来解决其他梁桥的内力分析。
【关键词】ANSYS;有限元;多跨连续梁;内力分析Internal Force Analysis of Multi-span Continuous Beam Based on ANSYSWANG Wei(School of Civil Engineering & Architecture, Changsha University of Science andTechnology. Changsha 410004, China)【Abstract】Internal force analysis of multi-span continuous beam is one of the structural mechanics plane bending problem emphases and difficulties. The article utilizes the structure static analysis capabilities of ANSYS software to achieve multi-span continuous beam of the internal force,basing on this method, we can solve other internal force analysis of bridges.【Key words】ANSYS;finite element;multi-span continuous beam;internal force analysis0引言多跨连续梁是由若干根梁用铰相联,并用若干支座与基础相联而组成的结构,在实际工程中应用广泛,故了解其内力特点,对分析其他结构的受力有着重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四跨连续梁的内力计算
四跨连续梁模型图如下所示,各个杆件抗弯刚度EI相同,利用平面梁单元分析它的变形和内力
1.结构力学分析
利用结构力学方法可以求出这个连续梁的剪力图和弯矩图如下
这里只给出了梁的弯曲刚度相同条件,没有指定梁截面的几何参数和材料的力学性质。
从结构力学分析的条件上看,这些条件对于确定梁的内力已经足够,但是对于梁的变形分析和应力计算,还需要补充材料的力学参数和截面几何参数。
所以以下分析中,假定梁的截面面积位0.3m2,抗弯惯性矩为0.003m4,截面高度为0.1m;材料的弹性模量为1000kN/m2,泊松比为0.3。
补充这些参数对于梁的内力没有影响,但是对于梁的变形和应力是有影响的。
2.用节点和单元的直接建模求解
按照前面模型示意图布置节点和单元,在图示坐标系里定位节点的坐标和单元连接信息,以及荷载作用情况和位移约束。
由于第二跨中间有两个集中力,所以在集中力位置设置两个节点。
这样,就可以将这两个集中力直接处理成节点荷载。
对于平面梁单元的节点只需输入平面上的两个坐标值,所以这里只输入节点的x坐标和y坐标。
(1)指定为结构分析
运行主菜单中preference偏好设定命令,然后在对话框中,指定分析模块为structural结构分析,然后单击ok按钮
(2)新建单元类型
运行主菜单preprocessor—element type—add/edit/delete命令,接着在对话框中单击add按钮
新建单元类型
(3)定义单元类型
先选择单元为beam,接着选2d elastic 3,然后单击ok按钮确定,完成单元类型的选择
(4)关闭单元类型的对话框
回到单元类型对话框,已经新建了beam3的单元,单击对话框close按钮关闭对话框
(5)定义实力常量
运行主菜单preprocessor—real constants—add/edit/delete命令,接着在对话框中单击add按钮新建实力常量
接着选择定义单元beam3的实力常量,选择后单击ok按钮,然后输入该单元的截面积为0.3,抗弯惯性矩为0.003m4,截面高度为0.1m,输入后单击ok按钮
(6)设置材料属性
运行主菜单preprocessor—material props—material models材料属性命令,选择材料属性命令后,系统会显示材料属性设置对话框
(7)设置杨氏弹性模量与泊松比
在材料属性设置对话框右侧依序选择两次structural—linear—elastic—isotropic
完成选择命令后,接着在对话框中EX杨氏弹性模量输入1e6,PRXY泊松比输入0.3,在数值输入后,单击ok按钮完成设置
(8)关闭材料属性设置对话框
完成材料属性的设置后,可在对话框右侧上方单击按钮,关闭材料属性设置
(9)生成节点
运行主菜单preprocessor—modeling—create—nodes—in active cs生成节点于目前坐标系统命令。
1(0,0)、2(4,0)、3(6,0)、4(8,0)、5(10,0)、6(16,0)、7(20,0)和8(22,0)的定义
(10)生成单元
运行主菜单preprocessor—modeling—create—elements—auto numbered—thru nodes穿越节点命令,依次选择节点1、节点2,完成输入后单击apply按钮
依照上述步骤完成单元的生成,其完成图如下
(11)显示节点与单元编号
运行下拉菜单中plotctrls—numbering编号显示命令,接着在编号控制对话框中将选择打开node numbers,并选择element numbers显示单元编号,完成后单击ok按钮,此时系统将会以颜色区分单元编号
(12)施加负载
运行主菜单solution—difine loads—apply—structural—displacement—on nodes施加位移在节点上命令,1号节点是固定铰链支座,有两个线位移被约束,其余2、5、6、7号节点只约束y方向位移
依次设定2、5、6、7号节点,如下图所示
(13)施加作用力
运行主菜单solution—define loads—apply—structural—force/moment—on nodes施加力在节点上命令,3号和4号节点上大小为30kN的集中力,8号节点上20kN的集中力,5号单元上均不荷载20kN/m
(14)运行分析
运行主菜单solution—solve—current ls分析当前的负载步骤命令,接着单击ok按钮开始运行分析,分析完毕后,再信息窗口中提示计算完成,单击close按钮将其关闭
统计窗口可单击右上方按钮将其关闭
(15)显示变形图
运行主菜单general—postproc—plot results—deformed变形图命令接着选择显示def—undeformed变形与未变形图,然后单击ok按钮
此时系统将会显示梁未受力和受力后的变形显示
(16)列表节点解
运行下拉菜单中general postproc—list results—nodal sulation节点解命令,接着选择列表形式为dof solution的all dofs dof所有位移解,然后单击ok按钮完成设置
完成设置后,系统将列出各节点的x、y方向位移,并显示最大位移量的节点
(17)绘制剪力图和弯矩图
在菜单中依次选取general postproc—element table—define table选项,弹出单元表数据对话框,单击add按钮,弹出定义单元数据对话框,选中下图所示选项后输入数据6,并单击apply 按钮,使用同样的方法选中该选项并分别输入数据12;2,8,每输入一次单击apply一次,最后单击对话框中的ok按钮
完成后,在菜单中依次选取general postproc—plot results—contour plot—line element results 菜单,弹出单元结果对话框,依次在labi和labj下拉列表框中选取smis2和smis8选项,单击apply按钮查看结果,得到剪力图如下
结果,得到弯矩图如下
(18)结果比较
比较结构分析和ansys分析的剪力图和弯矩图,可以发现剪力图符合很好,但是弯矩图在均布荷载作用段趋势不对,本来应该是曲线变化的弯矩图变成了直线,说明用单元表绘制内力
的命令只是将单元两端的内力按照直线连接的方式得到内力图。
