控制图计算公式
SPC控制图的系数和公式表

11
0.285
3.173 0.256 1.744 0.927 0.9754 0.321 1.679
12
0.266
3.258 0.283 1.717 0.886 0.9776 0.354 1.646
13
0.249
3.336 0.307 1.693
0.85 0.9794 0.382 1.618
14
0.235
18
0.194
3.64
0.391 1.608 0.718 0.9854 0.482 1.518
19
0.187
3.689 0.403 1.597 0.698 0.9862 0.497 1.503
20
0.18
3.735 0.415 1.585
0.68 0.9869 0.51
1.49
21
0.173
3.778 0.425 1.575 0.663 0.9876 0.523 1.477
8
0.433
2.847 0.136 1.864 1.054 2.847 0.136 1.864
9
0.412
2.97
0.184 1.816
1.01
2.97
0.184 1.816
10
0.362
3.078 0.223 1.777 0.975 3.078 0.223 1.777
UCLX/LCLX
=
控制限计
UCLR
E2 2.66 1.772 1.457 1.29
单值图*
极差R图
标准差估 计值的除
计算控制限用的系数
d2
D3
D4
1.128
—
3.267
监理工程师常用公式

监理工程师常用公式在监理工程中,监理工程师需要运用各种公式和计算方法来对工程进展、质量等进行评估和监控。
这些公式不仅可以帮助监理工程师更好地了解和管理工程项目的各项指标,还可以提供科学依据来做出合理的决策。
本文将介绍监理工程师常用的一些公式。
一、施工图纸中的常用公式1. 总包施工图中的面积计算公式在施工图中,常常需要计算某一区域的面积,可以通过以下公式进行计算:面积 = 宽度 ×长度2. 建筑工程用钢材的重量计算公式如果需要计算建筑工程用钢材的重量,可以使用以下公式:重量 = 钢材长度 ×钢材截面面积 ×钢材密度其中,钢材密度需要根据具体的材料进行调整。
二、测量中的常用公式1. 距离测量公式在工程测量中,计算两点之间的距离是非常常见的需求,可以通过距离公式进行计算:距离= √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)其中,(x1, y1, z1)和(x2, y2, z2)分别为两点的坐标。
2. 斜距公式当需要测量两点之间的水平距离时,可以使用斜距公式:斜距= √((x2 - x1)^2 + (y2 - y1)^2)其中,(x1, y1)和(x2, y2)分别为两点的水平坐标。
三、质量控制中的常用公式1. 控制图中的计算公式在质量控制中,控制图是常用的方法之一。
通过以下公式可以计算控制图的各项指标:均值= ΣX / n其中,ΣX表示所有数据的总和,n表示数据的数量。
通过计算均值来监控质量的变化情况。
2. 过程能力指数公式过程能力指数可以用来评估生产过程中的稳定性和一致性。
以下是常用的过程能力指数公式:过程能力指数 = (USL - LSL) / (6σ)其中,USL为上限规格限制,LSL为下限规格限制,σ为标准差。
四、安全监控中的常用公式1. 极限负荷计算公式在安全监控中,经常需要计算工程结构的极限负荷。
以下为一般情况下的负荷计算公式:F = P × A其中,P为可承受的荷载,A为受力面积。
计数值数据控制图过程能力分析

计数值数据控制图过程能力分析引言计数值数据控制图是一种用于监控过程稳定性和能力的有效工具。
通过收集样本数据并绘制控制图,可以帮助我们判断过程是否处于统计性控制,并评估过程的能力。
本文将介绍计数值数据控制图的基本原理和常用的过程能力分析方法。
计数值数据控制图介绍计数值数据控制图是一种用于监控离散型数据的过程控制工具。
它通过收集数据并绘制控制界限来判断过程的稳定性和能力。
计数值数据通常指的是在一定时间或空间范围内,某个特定事件的发生次数。
常见的计数值数据控制图包括:P图、NP图、C图和U图。
P图和NP图适用于二项分布的离散型数据,C图适用于计数型数据,U图适用于事件发生的时间间隔。
过程能力分析方法过程能力分析是指通过统计量和控制界限来评估过程的能力。
常用的过程能力指标有过程潜在能力指数(Cp)、过程实际能力指数(Cpk)和过程盒子能力指数(Cpm)。
过程潜在能力指数(Cp)过程潜在能力指数是用来评估过程在规格范围内的可变性的指标。
它是根据过程的规格上下限与控制限之间的距离来计算的。
Cp的计算公式为:Cp = (USL - LSL) / (6 * sigma)其中,USL表示过程的规格上限,LSL表示过程的规格下限,sigma 表示过程的标准差。
Cp的值越接近1,表示过程的能力越高。
过程实际能力指数(Cpk)过程实际能力指数是用来评估过程在规格范围内的偏移和可变性的指标。
它考虑了过程的中心位置。
Cpk的计算公式为:Cpk = min((USL - μ) / (3 * sigma), (μ - LSL) / (3 * sigma))其中,USL表示过程的规格上限,LSL表示过程的规格下限,mu 表示过程的均值,sigma表示过程的标准差。
Cpk的值越接近1,表示过程的能力越高。
过程盒子能力指数(Cpm)过程盒子能力指数是用来评估过程在规格范围内的偏移、可变性和非正常情况比例的指标。
它考虑了过程的中心位置和不符合规格的比例。
ucl和lcl计算公式

ucl和lcl计算公式UCL与LCL是统计控制图中最常用的两个量度,分别代表上限控制限(Upper Control Limit,简称UCL)和下限控制限(Lower Control Limit,简称LCL),是运用质量工程技术对程序的制约,是统计控制的基石,是质量控制技术的核心。
二、UCL与LCL的计算公式UCL与LCL的计算是基于特定的数据样本,根据这些样本的属性和分布,将质量检测的结果转换为统计控制图中的点。
通常情况下,UCL和LCL使用下面的公式来计算:UCL = X-bar + A2*RLCL = X-bar - A2*R其中,X-bar代表样本均值,R代表样本极差,A2为一个质量控制参数,值可以在质量控制表中查询到。
三、UCL和LCL的应用UCL和LCL的计算是基于统计控制的原理,它被广泛应用于各种行业中,如质量控制、过程控制、设备维护、工艺装备等领域,主要用于对特定过程中数据进行统计检验,进而采取有效控制措施,改进工艺,以达到提高工艺效率,提升产品质量的目的。
四、UCL与LCL的优缺点UCL和LCL是统计控制图最重要的两个参数,它与样本数据的变动关系密切,可以动态调节,从而更加灵活地提高效率,让检测数据更加准确。
此外,由于UCL和LCL的概念简单易懂,使用及其简单,因此比较受欢迎。
缺点是,UCL和LCL计算大多依赖于概率,且公式繁杂,有一定的难度,不容易理解,计算过程比较复杂,且实际应用中,UCL和LCL 参数的调节仍需要一定的经验,因此,UCL和LCL的使用还有很多方面需要加强。
五、结论UCL和LCL是统计控制图中最常用的两个量度,它可以有效地提高检测的准确性和效率,同时让控制图变得更加灵活。
然而,其计算过程比较复杂,实际应用中,UCL和LCL参数的调节仍需要一定的经验,因此,UCL和LCL使用方面需要更多的努力,才能更好地改善质量管理系统。
均值-极差控制图(x-R)
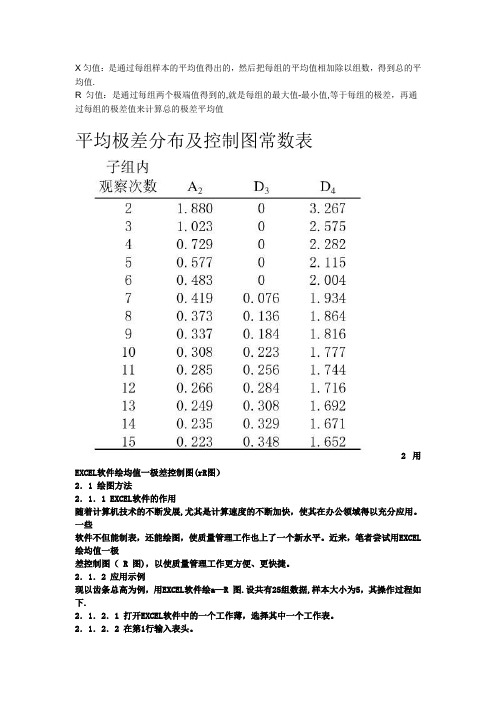
X匀值:是通过每组样本的平均值得出的,然后把每组的平均值相加除以组数,得到总的平均值.R 匀值:是通过每组两个极端值得到的,就是每组的最大值-最小值,等于每组的极差,再通过每组的极差值来计算总的极差平均值平均极差分布及控制图常数表2 用EXCEL软件绘均值一极差控制图(rR图)2.1 绘图方法2.1.1 EXCEL软件的作用随着计算机技术的不断发展,尤其是计算速度的不断加快,使其在办公领域得以充分应用。
一些软件不但能制表,还能绘图,使质量管理工作也上了一个新水平。
近来,笔者尝试用EXCEL 绘均值一极差控制图( R 图),以使质量管理工作更方便、更快捷。
2.1.2 应用示例现以齿条总高为例,用EXCEL软件绘a—R 图.设共有25组数据,样本大小为5,其操作过程如下.2.1.2.1 打开EXCEL软件中的一个工作薄,选择其中一个工作表。
2.1.2.2 在第1行输入表头。
2.1_2.3 在第l列单元格输入样本编号:选定要填充的第1个单元格A2,输入1,A3格输入2,选择A2、A3格将鼠标移到A3格右下角的填充柄上,当鼠标指针变成小黑十字时,按鼠标左键在要填充的区域上拖动(即从A4到A26),松开鼠标左键,填充自动完成。
2.1.2.4 在第2列单元格输入标准值:选定单元格B2,输入2.8,将鼠标移到B2格右下角的填充柄上,当鼠标指针变成小黑十字时,按鼠标左键在B3到B26格上拖动,松开鼠标左键填充自动完成。
2.1.2.5 将收集到的数据输入表中。
2.1.2.6 计算均值:选定H2,选“常用"工具栏中的“粘贴函数”(即厂),出现“粘贴函数”对话框,在函数分类栏中选“常用函数",在函数名栏中选“AV—ERAGE”,点“确定”,在“Number1"栏中输入“C2:G2”,点“确定”,即求得一个均值,选定H2格,点常用工具栏中的“复制”,再选定H3到H26,选“常用”工具栏中的“粘贴”,即求出其余24个均值。
控制图的系数和公式表
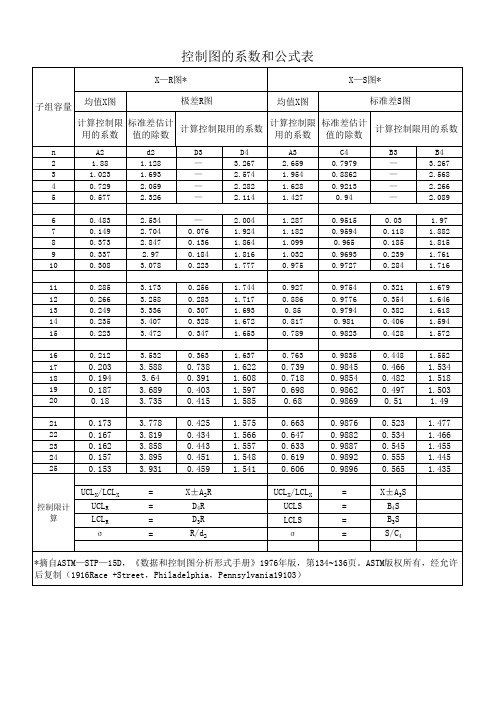
控制限计 算
*摘自ASTM—STP—15D,《数据和控制图分析形式手册》1976年版,第134~136页。ASTM版权所有,经允许 后复制(1916Race +Street,Philadelphia,Pennsylvania19103)
控制图的系数和公式表
中位数图** 中位数X图 子组容量 计算控制限 标准差估计 计算控制限 标准差估计 计算控制限用的系数 计算控制限用的系数 用的系数 值的除数 用的系数 值的除数
0.738 0.391 0.403 0.415 0.425 0.434 0.443 0.451 0.459 X±A2R D4 R D3 R R/d2
1.622 1.608 1.597 1.585 1.575 1.566 1.557 1.548 1.541
0.747 0.633 0.619 0.606 UCLX/LCLX UCLS LCLS σ
控制图的系数和公式表
X—R图* 均值X图 子组容量 计算控制限 标准差估计 计算控制限 标准差估计 计算控制限用的系数 计算控制限用的系数 用的系数 值的除数 用的系数 值的除数
n 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 A2 1.88 1.023 0.729 0.577 0.483 0.149 0.373 0.337 0.308 0.285 0.266 0.249 0.235 0.223 0.212 d2 1.128 1.693 2.059 2.326 2.534 2.704 2.847 2.97 3.078 3.173 3.258 3.336 3.407 3.472 3.532 D3 — — — — — 0.076 0.136 0.184 0.223 0.256 0.283 0.307 0.328 0.347 0.363 D4 3.267 2.574 2.282 2.114 2.004 1.924 1.864 1.816 1.777 1.744 1.717 1.693 1.672 1.653 1.637 A3 2.659 1.954 1.628 1.427 1.287 1.182 1.099 1.032 0.975 0.927 0.886 0.85 0.817 0.789 0.763 C4 0.7979 0.8862 0.9213 0.94 0.9515 0.9594 0.965 0.9693 0.9727 0.9754 0.9776 0.9794 0.981 0.9823 0.9835 B3 — — — — 0.03 0.118 0.185 0.239 0.284 0.321 0.354 0.382 0.406 0.428 0.448 B4 3.267 2.568 2.266 2.089 1.97 1.882 1.815 1.761 1.716 1.679 1.646 1.618 1.594 1.572 1.552
控制图
品管部
控制图
准则五:连续3点有2点落在中心线一侧B区以外 准则六:连续5点有4点落在中心线一侧C区以外
品管部
控制图
准则七:连续15点落在C区中心线上下 准则八:连续8点在中心线两侧但无一点落在C区
注:避免出现规律型图形
品管部
控制图
现场控制图:1、如果没有出现异常点,控制线是固定的。 2、数据采集是每班一组五个数据,连续采集。 3、如有异常点,排查原因并解决,重新计算控制线。
控制图基础知识
制作部署: 品管部
控制图
控制图
1.内容
品管部
控制图
Байду номын сангаас1.内容
平均值作为控 制图描点数据
品管部
控制图
2.作用:
预知不合格,为解决问题提供方向
3.作图: (1) 确认子组容量 确认子组数 确认子组频率 (2) 数据采集:连续采集
(3) 计算
(4)确定控制线:Xbar图控制线确定:中心线:CL= X 上控制线:UCL= X + A2 R
品管部
品管部
公式常数(n为子组容量)
下控制线:LCL= X - A2 R
R图控制线确定:中心线:CL= R 上控制线:UCL=D4 R
品管部
下控制线:LCL= D3 R
控制图 4.描点 5.判异 准则一:出现超限的点
准则二:连续7点上升,连续7点下降
品管部
控制图
准则三:连续7点位于中心线一侧
准则四:连续14点一升一降
控制图作图方法
统 以上,计算试样的平均值x和标准偏差S
计 过
:
程
控
制
x x1 xn n
S x1 x2 xn x2
n 1
单值控制图(x控制图)
x 第 这时μ 和σ 值可由 和S近似得出,则:
五
章
统 计
CL= x UCL= x +3S
过 程
LCL= x -3S
控 制
求出CL、UCL、LCL后,就可以相应作出
统 UCL = np + 3√np(1- p) =2.6 +
计 过
3√2.6 (1 - 0.026) =7.4
程 控
LCL = np - 3√np(1- p) =2.6-
制
3√2.6(1- 0.026) = ( - ),无意义。
•
第 五 章
统 计 过 程 控 制
(二)不合格品率控制图(P控制图)
制
LCLX= X -A2R =3.861-0.729×1.028
=3.112
第
5)计算R图的参数
五 章
本例中n=4,查表,得D4=2.282,因n小于6,D3=0
统 ,所以下控制限可以不考虑,根据表5-4计算结
计 果如下:
过
程 控
CLR = R =1.028
制
UCLR = D4 R =2.282×1.028=2.346
3.861
程 控
样本平均极差 R 的计算公式为
制
R R1 R2 Ri Rk
R 25.7
K
25
1 K
K i1 Ri
1.028
4)计算 X 图的参数
第 五 章
本例中n=4,查表5-5得A2=0.729,根据表5-4计算 结果如下:
Control-Chart(控制图)
控制图的类型
按质量特性值的类型及其统计量划分
计量值控制图 计数值控制图
类别
计 量 值 控 制 图
计 数 值 控 制 图
名称
均值—极差 控制图
中位数—极 差控制图 两极控制图
单值—移动 极差控制图
不合格品数 控制图
不合格品率 控制图
缺陷数控制 图
单位缺陷数 控制图
控制图种类及适用场合
管理图
Control Chart
图a
图c
Control Chart
生产过程的几种状态
公差上限 公差下限
公差上限 公差下限
图b 时间 图d
公差上限 公差下限
公差上限 公差下限
统计过程控制的概念
在生产过程中,判别工序是否在受着异常因素的影响可以采 取下面的方法 :每隔一定的时间间隔,在生产的产品中进 行随机抽样,并根据样本数据观察质量特性值的分布状态 。 若工序分布状态不随时间的推移而变化(即如图a),说明工 序处于稳定状态,只受着偶然因素的影响;若工序分布状态 随着时间的推移发生变化(如图b,c,d),说明工序处于非稳 定状态,正在有异常因素影响着它,必须立即采取措施消除 异常因素的影响 。
1找出或计算出各样本的中位数2计算各样本极差rn为奇数时第i样本中按大小顺序排列起的数据列中间位置的数据n为偶数时第i样本中按大小顺序排列起的数据列中中间位置的两个数据的平均值最小值平均值3计算平均极差4计算范围中值m计算移动极差rsi第i样本的不合格品数各样本样本容量皆为n第i样本的样本容量各样本样本容量可以不等第i样本的缺陷数各样本样本容量相等ijijminmaxijijminmax为偶数为奇数minmax在坐标图上画出三条控制线控制中线一般以细实线表示控制上下线以虚线表示
SPC计算公式范文
SPC计算公式范文SPC(Statistical Process Control)是一种统计过程控制方法,用于监控和控制工业过程的质量。
它通过收集数据、分析数据并提供即时反馈,帮助确定过程是否正常运行,并识别异常情况。
SPC计算公式是用来计算过程的控制图中的上限、下限、中心线以及其他统计参数的公式。
在SPC中,常用的计算公式包括平均值(mean)、标准差(standard deviation)、上限(upper control limit)、下限(lower control limit)和中心线(center line)等。
1. 平均值(mean):计算数据的平均值用于确定中心线。
平均值的计算公式为:Mean = ΣX / n其中,X是样本数据的总和,n是样本个数。
2. 标准差(standard deviation):衡量数据的离散程度。
标准差的计算公式为:Standard Deviation = sqrt(Σ(X - Mean)^2 / n)其中,Σ(X - Mean)^2表示每个数据与平均值的差的平方和,n是样本个数,sqrt表示开方。
3. 上限(upper control limit)和下限(lower control limit):用于识别过程异常情况。
上限和下限的计算公式为:Upper Control Limit = Mean + k * Standard DeviationLower Control Limit = Mean - k * Standard Deviation其中,k是控制图的参数,可以根据过程的要求进行设定,通常为2或34. 中心线(center line):表示过程的目标值。
中心线的位置通常与平均值相等。
除了上述基本参数外,SPC还可以计算其他统计参数,如极差(range)、方差(variance)、过程能力指数(process capability index)等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
__________________________________________________
__________________________________________________
控制图计算公式
控制图
控制限 计算公式
均值
极差图
X
图
控制上限UCL
UCL=X+A2R
中心线CL
CL=X
控制下限LCL
LCL= X-A2R
R图 控制上限UCL UCL=D4R 中心线CL
CL=R
控制下限LCL
LCL=D3R
均值
标准差图
X
图
控制上限UCL
UCL=X+A3S
中心线CL
CL=X
控制下限LCL
LCL= X-A3S
S图 控制上限UCL UCL=B4S 中心线CL
CL=S
控制下限LCL
LCL=B3S
单值-移动
极差图
I图 控制上限UCL UCL=MREX2 中心线CL
CL=X
控制下限LCL
LCL=MREX2
MR图 控制上限UCL UCL=D4MR 中心线CL
CL=MR
控制下限LCL
LCL=D3MR
不良率
控制图
P图
控制上限UCL
UCL=PPPn31()
中心线CL
CL=P
控制下限LCL
LCL=nPPP)1(3
不合格品
数 控制图 np图 控制上限UCL UCL=)1(3Pnpnp 中心线CL
CL=np
控制下限LCL
UCL=)1(3Pnpnp
缺陷数
控制图
C图 控制上限UCL UCL=C+3C 中心线CL
CL=C
控制下限LCL
LCL=CC3
缺陷率
控制图
U图
控制上限UCL
UCL=U+3Un
中心线CL
CL=U
__________________________________________________
__________________________________________________
控制下限LCL
LCL=U-3Un
