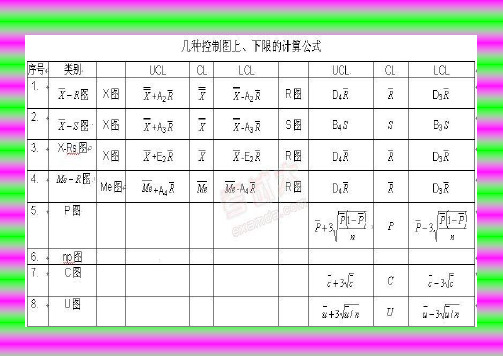
质量工程师--八种控制图上、下限的计算公式
cpk规格上限与下限的计算

cpk规格上限与下限的计算摘要:1.引言2.CPK 规格上限与下限的定义3.CPK 规格上限的计算方法4.CPK 规格下限的计算方法5.计算实例6.总结正文:1.引言在制造业中,过程能力指数(CPK)是用于衡量一个过程生产稳定性和加工精度的重要指标。
CPK 指标包括规格上限和下限,它们可以判断过程是否处于受控状态,以及产品的质量是否达到要求。
本文将介绍如何计算CPK 规格上限与下限。
2.CPK 规格上限与下限的定义CPK 规格上限是指过程能够生产的最大值,即过程的最大容忍值;CPK 规格下限是指过程能够生产的最小值,即过程的最小容忍值。
3.CPK 规格上限的计算方法CPK 规格上限的计算公式为:上限= 公差上限- 过程标准差其中,公差上限是指产品尺寸允许的最大偏差,过程标准差是指过程的波动程度。
通过这个公式,我们可以计算出CPK 规格上限,从而判断过程是否能够满足产品的尺寸要求。
4.CPK 规格下限的计算方法CPK 规格下限的计算公式为:下限= 公差下限- 过程标准差其中,公差下限是指产品尺寸允许的最小偏差,过程标准差同样是指过程的波动程度。
通过这个公式,我们可以计算出CPK 规格下限,从而判断过程是否能够满足产品的尺寸要求。
5.计算实例假设某个产品的尺寸公差为±0.05mm,过程标准差为0.03mm,那么:CPK 规格上限= 0.05 - 0.03 = 0.02mmCPK 规格下限= -0.05 - 0.03 = -0.08mm可见,该过程的规格上限为0.02mm,规格下限为-0.08mm。
这意味着该过程的尺寸稳定性较好,产品尺寸基本能满足要求。
6.总结通过计算CPK 规格上限与下限,我们可以了解过程的尺寸稳定性和加工精度,从而判断产品是否达到质量要求。
控制图计算公式
2.判断异常的准则在讨论控制图原理时,已经知道点子出界就判断异常,这是判断异常的最基本的一条准则。
为了增加控制图使用者的信心,即使对于在控制界限内的点子也要观察其排列是否随机。
若界内点排列非随机,则判断异常。
判断异常的准则:符合下列各点之一就认为过程存在异常因素:(1)点子在控制界限外或恰在控制界限上控制界限内的点子排列;(2)链:连续链,连续7个点以上排列在一侧;间断链,大多数点在一侧(3)多数点靠近控制界限(在2一3倍的标准差区域内出现)(4)倾向性与周期性。
控制图是用于确定生产或工作过程是否处于稳定状态的图形,通过它可以发现并及时消除生产和工作过程中的失控情况。
控制图是通过对过程中各特性值进行测定、记录、评估和监察过程是否处于控制状态的一种用统计方法设计的图。
在控制图中有两条平行的上下控制界限和中心线,并有按时间序列排列的样本统计量数值的描点序列。
如果控制图中描点落在控制界限之内,则表明过程正常;若控制图中描点落在控制界限之外或描点序列在界限之间有某一种或几种不正常的趋势,则表明过程异常。
(一)控制图的分类控制图可以分为两类,即计量值控制图和计数值控制图。
计量值控制图所依据的数据均属于由测量工具实际测量出来的数据,如长度、重量等控制特性,具有连续性,它包括:①单值控制图;②平均值与极差控制图;③平均值与标准差控制图;④中位值与极差控制图;⑤个别值与移动极差控制图。
计数值控制图所依据的数据均属于以单位个数或次数计算,如不合格品数、不合格品率等。
它包括:①不合格品数控制图;②不合格品率控制图;③缺陷数控制图;④单位缺陷数控制图。
(二)控制图的应用控制图可用于以下几方面:①预测,通过现有图形的分析和研究可大致预测下一步可能的位置。
②评价与诊断,可以评价过程的变化情况,评估过程的稳定性,并能与其他方法结合,可以找到产生状况的原因。
③控制,可对品质状况及时掌控,决定何时需要调整,何时需要保持原有状态。
SPC公式汇总范文

SPC公式汇总范文SPC,也就是统计过程控制,是一种用来监控和控制过程稳定性和一致性的统计方法。
它通过收集、分析和解释过程中产生的数据,帮助组织了解过程的特性并进行持续改进。
SPC的使用可以有效地降低过程变异性,并减少缺陷和不一致性的发生。
SPC方法的基础是SPC公式,下面将对常用的SPC公式进行汇总和解释。
1.均值和范围控制图公式:-均值控制图公式:控制界限的计算通常是通过计算样本均值的上下界限,即控制上界限=过程平均值+3σ/样本大小的平方根;控制下界限=过程平均值-3σ/样本大小的平方根;其中,σ表示样本中的标准差。
-范围控制图公式:控制界限的计算通常是通过计算样本范围的上下界限,即控制上界限=过程范围平均值+3*A2/样本大小的平方根;控制下界限=过程范围平均值-3*A2/样本大小的平方根;其中,A2是与样本大小相关的常数。
2.方差和标准差控制图公式:-方差控制图公式:控制界限的计算通常是通过计算样本方差的上下界限,即控制上界限=过程方差*F/(样本大小-1);控制下界限=过程方差*F/(样本大小-1);其中,F是与样本大小和置信水平相关的常数。
-标准差控制图公式:控制界限的计算是通过计算样本标准差的上下界限,即控制上界限=过程标准差+3σ/样本大小的平方根;控制下界限=过程标准差-3σ/样本大小的平方根;3.质量比率控制图公式:-质量比率控制图公式:控制界限的计算通常是通过计算样本中缺陷项目的数量比率的上下界限,即控制上界限=过程中缺陷比率的上界限;控制下界限=过程中缺陷比率的下界限;4.不良品数控制图公式:-不良品数控制图公式:控制界限的计算通常是通过计算样本缺陷数量的上下界限控制上界限=过程中缺陷数的平均值+3σ/样本大小的平方根;控制下界限=过程中缺陷数的平均值-3σ/样本大小的平方根;需要注意的是,以上是一些常见的SPC公式,具体使用时可能会根据实际情况进行调整和计算。
此外,还有其他一些SPC公式,例如强度控制图公式、极差控制图公式等,但由于篇幅限制无法一一列举。
质量工程师考试资料

X-R控制图将X图与R图组合使用,同时分析和监控过程的均值和离散度变化 选用X-R控制图的条件: 特性连续可计量,服从或近似服从正态分布 样本容量n为定数,且n < 10 按时序可采集20个以上的样本(即k ≥ 20) 应采集同一过程的特性值,且测量值之间相互独立
~
~
~
又称为长期过程能力指数
C系列过程能力指数- Cp、Cpu 、Cpl 、 Cpk
P系列过程性能指数- Pp、Ppu 、Ppl 、 Ppk
03
01
02
过程性能指数
各类常规控制图的使用场合
X—R图
X—s图
X—Rs图
c图
Me—R图
p图
u图
第五节 常规控制图的作法及其应用
各类常规控制图的使用场合
常规计量值控制图
X—s图
X-S控制图将X图与S图组合使用,同时分析和监控过程的均值和离散度变化 选用X-S控制图的条件: 特性连续可计量,服从或近似服从正态分布 样本容量n为定数,且n > 1 按时序可采集20个以上的样本(即k ≥ 20) 应采集同一过程的质量特性值,且测量值之间相互独立 计算工具应方便在现场计算S值
X-Rs控制图适用场合:
小批量生产,无法获得较多数据 只能获得一个观测值(如,生产效率、消耗定额) 过程质量均匀,无需多次观测(流程型材料生产) 因费用或时间关系,只能取得一个观测值(破坏性试验)
选用X-Rs控制图的条件:
质量特性连续可计量 样本服从或近似服从正态分布 样本容量n=1
X—Rs图
Rsi
UCL=3.267 Rs, LCL=0
CL= Rs
Rs图
n=1
Xi
UCL=X+2.660R, LCL=X-2.660R
质量管理常用的18个公式

质量管理常用的18个公式质量管理是一个涵盖各种工具和技术的综合领域,旨在帮助组织提高产品和服务的质量。
在质量管理过程中使用的许多公式是为了帮助组织量化和评估各种质量指标。
以下是18个常用的质量管理公式:1. 产品可靠性公式(Reliability Formula): 评估产品在一定时间内无故障运行的概率。
可靠性 = 故障免费时间 /(故障免费时间+故障时间)2. 故障率公式(Failure Rate Formula): 表示单位时间内产品发生故障的频率。
故障率 = 发生故障的次数 / 监测时间3. 不良品率公式(Defect Rate Formula): 表示在生产过程中出现问题的产品数量与总产量之间的比率。
不良品率 = 不良品的数量 / 总产量4. 成本质量平衡点公式(Cost of Quality Break-even Formula): 帮助确定当质量费用超过潜在嵌入成本时,质量活动的回报率。
质量成本= 内部和外部劣质 + 预防质量费用5. 流程能力指数公式(Process Capability Index Formula): 用于衡量流程是否能够在规定的公差范围内生产产品。
Cp = (公差上限 - 公差下限)/(6*S)6. 制程稳定性指数公式(Process Stability Index Formula): 衡量制程的稳定性和可预测性。
Cpk = min(Cpu,Cpl)7. 效能公式(Efficiency Formula): 用于衡量资源使用效率的指标。
效能 = 实际产出 / 标准产出8. 效益公式(Effectiveness Formula): 衡量达到预期结果的能力。
效益 = 实际产出 / 预期产出9. 成本效益比公式(Cost-effectiveness Ratio Formula): 表示单位成本所能达到的预期成果量。
成本效益比 = 花费 / 预期成果10. 缺陷定位率公式(Defect Localization Rate Formula): 用于评估在测试过程中发现的缺陷的准确性。
【SPC控制图 计算公式 】 SPC控制图的计算公式有哪些?

SPC控制图的计算公式有哪些?导语:SPC控制图是对过程质量加以测定、记录从而进行控制管理的一种用科学方法设计的图。
问世数十年来,SPC控制图在众多现代化工厂中得到了普遍应用,通过其计算公式,凭借其强大的分析功能,为工厂带来丰厚的实时收益。
控制图对生产过程的关键质量特性值进行测定、记录、评估并监测过程是否处于控制状态的一种图形方法。
根据假设检验的原理构造一种图,用于监测生产过程是否处于控制状态。
它是统计质量管理的一种重要手段和工具。
那么,SPC控制图的计算公式有哪些?下面我们就详细介绍:图示:SPC控制图的计算公式有哪些?常规休哈特控制图包括计量控制图四种和计数控制图四种计量SPC控制图四种:均值—极差控制图(Xbar—R)、均值—标准差控制图(Xbar—Rs)、中位数—极差控制图(Xmed—R,也有写成X-MR的)、单值—移动极差控制图(x—Rs);计数SPC控制图四种:不合格品率控制图(P)、不合格品数控制图(Pn)、缺陷数控制图(C)、单位缺陷数控制图(U)。
1.Xbar-R控制图是最常用的基本SPC控制图。
它适用于各种计量值(适用样品数小于10以下的抽样分析)。
Xbar控制图主要用于观察分布的均值变化;R控制图用于观察分布的分散情况或变异度的变化,而Xbar—R控制图则将两者联合运用,以观察分布的变化。
2.Xbar—S控制图(适用样品数大于10以下的抽样分析)。
与Xbar—R控制图相似,只是用标准差图(s图)代替极差图(R图)。
极差计算简便,故R图得到广泛应用,但当样本容量较大时,应用极差估计总体标准差的效率降低,需要用s图来代替R图。
3.Xmed—R控制图与Xbar—R控制图相比,只是用中位数代替均值图。
由于中位数的计算比均值简单,所以多用于需在现场把测定数据直接记入控制图的场合。
4.x—Rs控制图多用于:对每一个产品都进行检验,采用自动化检查和测量的场合;取样费时、检验昂贵的场合;样品均匀,多抽样也无太大意义的场合。
质量管理用到的公式

质量管理用到的公式在质量管理中,有许多公式可以用于计算和评估质量的各个方面。
下面将介绍几个常用的质量管理公式。
1. 制程能力指数(Cp)和加工能力指数(Cpk):制程能力指数和加工能力指数是用来评估制程或加工过程的能力,以确定是否满足质量要求。
计算公式如下:Cp=(USL-LSL)/(6*标准差)Cpk = Min(Cpu,Cpl)其中,USL是上限规格限,LSL是下限规格限,标准差是统计数据的标准差,Cpu是过程能力指数的上限,Cpl是过程能力指数的下限。
2.不良品率(DPPM):不良品率是描述单位产品或过程中的不良品数量的指标,通常以每百万单位产品(DPPM)的方式表示。
计算公式如下:3.检出率(DR):检出率是指在进行质量检验时,能够正确判定产品是否合格的能力。
计算公式如下:DR=(合格品数量/总样本数量)*1004. 合格品率(Yield):合格品率是指生产过程中生产出的合格产品占总产品数量的百分比。
计算公式如下:Yield = (合格产品数量 / 总产品数量) * 1005. 效能(Efficiency):效能是指生产过程中实际生产的产品数量与理论最大产能之间的比率。
计算公式如下:Efficiency = (实际生产数量 / 理论最大产能) * 1006. 效益(Effectiveness):效益是指实际生产的产品数量与计划生产的产品数量之间的比率。
计算公式如下:Effectiveness = (实际生产数量 / 计划生产数量) * 1007. 效率(Productivity):效率是指单位时间内实现的产量与所需资源之间的比率。
计算公式如下:Productivity = (产量 / 资源消耗) * 1008.成本绩效指数(CPI)和进度绩效指数(SPI):成本绩效指数和进度绩效指数是用于评估项目的成本和进度表现的指标。
计算公式如下:CPI=挣值(EV)/实际成本(AC)SPI=挣值(EV)/计划值(PV)其中,挣值(EV)是实际完成工作的预算成本,实际成本(AC)是实际花费的成本,计划值(PV)是计划的预算成本。
质量工程师考试中级公式

E(aX+b)=aE(X)+b Var(aX+b)= a2Var(X) 对任意两个随机变量X1与X2,有 E(X1+X2)= E(X1)+E(X2) 设随机变量X1与X2独立,有 Var(X1±X2)= Var(X1)+Var(X2)
*二项分布b(n,p)
P( X x)
n x
Px (1 P) nx , x 0,1, n
b Lxy / Lxx
a y bx
总计T ST Lyy , 回归 SR bLxy , 残差 SE ST SR
自由度 fT n 1 , fR 自变量个数 , fE fT fR
均方 VR SR / fR
VE SE / fE
F VR /VE ,当F F1 ( fR , fE )时,表明在水平上方程是有意义的 预测 ( yˆ0 , yˆ0 )
性质2 设 X ~ N ( ,2 ) ,则对任意实数a,b有:
(1)PX b b
(2) P( X a ) 1 ( a )
(3)Pa X b b a
*均匀分布U(a,b)
P(x)
b
1
a
,a
x
b
0,其它
E(X
)
a
2
b
,Var
(X
)
(b
a)2 12
*单因子方差分析(正态分布、数据独立、方差相等)
水平
试验数据
和
均值
A1
y11 , y12 , … , y1m
T1=
y1=
A2
y21 , y22 , … , y2m
T2
y2
…
…
…
…
Ar
