武汉大学刘觉平群论第二次作业
华工离散数学第二次作业

B.F={<1,c>,<2,a>,<3,b>,<4,e>,<5,d>}
C.F ={<1,b>,<2,a>,<3,d>,<4,a>}
D.F={<1,e>,<2,a>,<3,b>,<4,c>,<5,e>}
答题: A. B. C. D.
参考答案:B
13.运算“+”是整数集I上的普通加法,则群<I,+>的么元是( )
A.1 B.0 C.2 D.3
答题: A. B. C. D.
参考答案:B
14.下列说法不对的是()
A.简单图不含平行边和环
B.每个图中,度数为奇数的节点数为偶数
C.有向图中节点的入度等于出度
D.完全图的边数为
答题: A. B. C. D.
C.f ={<1,7>,<2,6>,<3,5>,<4,6>}
D.f ={<1,10>,<2,6>,<3,7>,<4,8>,<5,10>}
答题: A. B. C. D.
参考答案:B
9.设A={1,2,3,4,5, 6},B={a,b,c,d,e},以下哪个函数是从A到B的满射函数( )
A.F ={<1,b>,<2,a>,<3,c>,<1,d>,<5,e>, <6,e>}
第二次数学建模作业
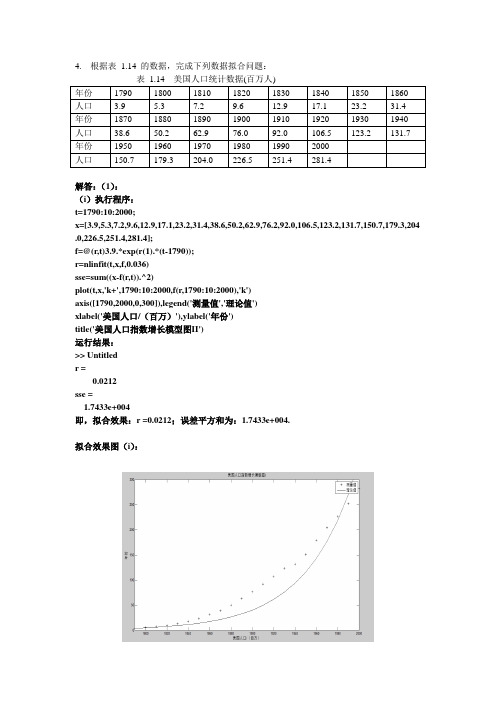
4. 根据表1.14 的数据,完成下列数据拟合问题:年份1790 1800 1810 1820 1830 1840 1850 1860 人口 3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4年份1870 1880 1890 1900 1910 1920 1930 1940 人口38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 年份1950 1960 1970 1980 1990 2000人口150.7 179.3 204.0 226.5 251.4 281.4解答:(1):(i)执行程序:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204 .0,226.5,251.4,281.4];f=@(r,t)3.9.*exp(r(1).*(t-1790));r=nlinfit(t,x,f,0.036)sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:10:2000,f(r,1790:10:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值')xlabel('美国人口/(百万)'),ylabel('年份')title('美国人口指数增长模型图II')运行结果:>> Untitledr =0.0212sse =1.7433e+004即,拟合效果:r =0.0212;误差平方和为:1.7433e+004.拟合效果图(i):(ii)由表1.14我们知道,当t=1800时,有5)101(0≈+r x ,所以我们可以猜测,r=0.1,x =2.5.对待定参数0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-1790)); r0=[2.5,0.1]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图II')命令窗口显示的计算的结果如下: >> Untitled r =15.0005 0.0142 sse =2.2657e+003即我们知道,拟合结果为:r=r(2)= 0.0142, 0x =r(1)= 15.0005;误差平方和为:2.2657e+003. 拟合效果图(ii ):(iii)由表1.14我们知道,当t=1900时,有()76)-t 1900101(00≈+r x ,所以我们可以猜测,r=0.03,x =19, 0t =1800.对待定参数0t ,0x ,r 进行数据拟合同时进行绘图,其程序如下:t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.2,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];f=@(r,t)r(1).*exp(r(2).*(t-r(3))); r0=[19,0.03,1800]; r=nlinfit(t,x,f,r0) sse=sum((x-f(r,t)).^2)plot(t,x,'k+',1790:1:2000,f(r,1790:1:2000),'k')axis([1790,2000,0,300]),legend('测量值','理论值',2) xlabel('美国人口/(百万)'),ylabel('年份') title('美国人口指数增长模型图III')命令窗口显示的计算的结果如下:>> UntitledWarning: The Jacobian at the solution is ill-conditioned, and some model parameters may not be estimated well (they are not identifiable). Use caution in making predictions. > In nlinfit at 224 In Untitled at 5 r =1.0e+003 *0.0159 0.0000 1.7939 sse =2.2657e+003即,拟合效果:r =0,0x =7.9,0t =1742.5;误差平方和为:2.2657e+003我们由MATLAB9给出的警告信息,知道这个拟合存在病态条件,所以数据可能拟合的不太好。
工程数学作业(第二次)hao

工程数学作业(第二次)(满分100分)第3章 线性方程组 第4章 矩阵的特征值及二次型(一)单项选择题(每小题2分,共16分)⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪的解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为(C ).A. [,,]102-'B. [,,]--'722C. [,,]--'1122D. [,,]---'1122⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪(B ).A. 有无穷多解B. 有唯一解C. 无解D. 只有零解 解:将增广矩阵进行初等行变换123212321232101602440244033403340⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-→--→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--***⎣⎦⎣⎦⎣⎦增广矩阵的秩=系数矩阵的秩=3=未知量的个数,线性方程组有唯一解; 故B 正确。
⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,的秩为(A ). A. 3 B. 2 C. 4 D. 5⒋设向量组为αααα12341100001110101111=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,则(B )是极大无关组.A. αα12,B. ααα123,,C. ααα124,,D. α1解:[]123410111011101110010*******,,,01110111011101010*******αααα⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥=→→→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ 1011101100100111011100100000000⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥→⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦所以极大无关组是ααα123,,.故B 正确。
第二次算法作业

第二次算法作业
交作业时间12:00 p.m., December 13, 2007
证明以下 6 个问题的 NP-完全性
1.Set Packing
实例: 有限集 S 上的某些子集的集合 C, 正整数 K<=|C|.
问题: C 中是否有 K个互不相教的子集?
2.Minimum Sum of Squares
实例:有限个正整数的几何 A, 两个正整数 K, J。
问题: $A$中正整数是否可被划分为 K 个互不相交的子集 A_1,A_2,… ,A_K 满足
Sum{1<=i<=K}(Sum{a in A_i}a)2 <=J ?
3.Hamiltonian Path Between Two Points
实例: 图 G=(V,E), 及其两个特定顶点 a 和 b.
问题: G 中是否有 a 和 b 之间的 Hamiltonian 通路?
4.Steiner Tree in Graphs
实例:图 G=(V,E), V 的子集 R, 正整数 K<=|V|.
问题:G 中是否存在包括 R 所有点但总数又不多于个 K 个点的子树?
5.Set Splitting
实例:有限集 S 上的某些子集的集合 C.
问题:可否划分 S 成两个子集 S_1 和 S_2 使得 C 中每一个子集都既不被 S_1 也不被 S_2 包含?
6.Graph 3-Colorability
实例:图 G=(V,E).
问题:图 G可 3 着色吗?即, 是否有函数 f:V {1,2,3}满足若{u,v} 是 G 中边则 f(u)不等于 f(v)?。
北邮离散数学第二次阶段作业

得分:
[10]
试题分值:
10.0
提示:
二、单项选择题(共5道小题,共50.0分)
1.设 是有理数集,在 定义运算 为 ,则 的单位元为
A.
B.
C.1
D.0
知识点:
代数系统的基本概念
学生答案:
[D;]
得分:
[10]
试题分值:
10.0
提示:
2.在整数集 上,下列哪种运算是可结合的
A.
B.
C.
D.
知识点:
代数系统的基本概念
学生答案:
[B;]
得分:
[10]
试题分值:
10.0
提示:
3.循环群 的所有子群为
A.
B.
C. 和
D.
知识点:
群、环和域
学生答案:
[C;]
得分:
[10]
试题分值:
10.0
提示:
4.循环群 的生成元为1和2,它们的周期为
A.5
B.6
C.3
D.9
知识点:
群、环和域
学生答案:
[C;]
得分:
[10]
试题分值:
10.0
提示:
5.在下面偏序集的哈斯图中,哪一个是格
A.
B.
C.
D.
知识点:
格和布尔代数
学生答案:
[A;]
得分:
[10]
试题分值:
10.0
提示:
10.0
提示:
3.(错误)
⊙11〉是群.
A.正确
B.错误
知识点:
群、环和域
学生答案:
[B;]
得分:
《离散数学》第二次在线作业

《离散数学》第⼆次在线作业第⼆次第1题代数系统是指由集合及其上的⼀元或⼆元运算符组成的系统您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查代数系统的基本概念第2题设< L,*1,*2> 是代数系统,其中是*1,*2⼆元运算符,如果*1,*2都满⾜交换律、结合律,并且*1和*2满⾜吸收律,则称< L,*1,*2> 是格您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查格的基本概念第3题对实数的普通加法和乘法,0是加法的幂等元,1是乘法的幂等元您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查幂等元的基本概念第4题零元是不可逆的您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查零元的不可逆性第5题群中每个元素的逆元都是惟⼀的您的答案:正确批注:本题考查逆元的惟⼀性第6题设a,b,c是阿贝尔群< G,+> 的元素,则-(a+b+c)=(-a)+( -b)+( -c)您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查阿贝尔群的基本概念第7题< {0,1,2,3,4},MAX,MIN> 是格您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查格的基本概念第8题⼀个图的哈密尔顿路是⼀条通过图中所有结点⼀次且恰好⼀次的路您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查哈密尔顿路的基本概念第9题在有向图中,结点v的出度deg+(v)表⽰以v为起点的边的条数,⼊度deg-(v)表⽰以v为终点的边的条数您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查结点的出⼊度的基本概念第10题⼀个图的欧拉回路是⼀条通过图中所有边⼀次且恰好⼀次的回路您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查欧拉回路的基本概念第11题不含回路的连通图是树题⽬分数:0.5此题得分:0.5批注:本题考查树的基本概念第12题简单图邻接矩阵主对⾓线上的元素全为0您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查简单图邻接矩阵的基本概念第13题树⼀定是连通图您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查树和连通图的基本概念第14题⽆向图的邻接矩阵是对称阵您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查⽆向图的邻接矩阵的基本性质第15题不与任何结点相邻接的结点称为孤⽴结点您的答案:正确题⽬分数:0.5此题得分:0.5批注:本题考查孤⽴结点的基本概念第16题⼀个⽆向图是⼀个有序的⼆元组< V,E> ,记作G,其中(1)V不为空集,称为顶点集,其元素称为顶点或结点。
离散数学形成性考核作业(三)
离散数学形成性考核作业(三)本次活动是本学期的第二次活动(2020.11.18),主要是针对第二单元图论的重点学习内容停止辅导,方式是经过解说一些典型的综合练习标题,协助大家进一步了解和掌握图论的基本概念和方法。
图论作为团圆数学的一局部,主要引见图论的基本概念、实际与方法。
教学内容主要有图的基本概念与结论、图的连通性与连通度、图的矩阵表示、最短路效果、欧拉图与汉密尔顿图、平面图、对偶图与着色、树与生成树、根树及其运用等。
本次综合练习主要是温习这一局部的主要概念与计算方法,与集合论一样,也布置了五种类型,有单项选择题、填空题,判别说明题、计算题、证明题。
这样的布置也是为了让同窗们熟习期末考试的题型,可以较好地完成这一局部主要内容的学习。
下面区分解说。
一、单项选择题1.设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡010*******000011100000100 那么G 的边数为( ).A .5B .6C .3D .4正确答案:D上学期的作业中,有的同窗选择答案B 。
主要是对邻接矩阵的概念了解不到位。
我们温习定义:定义3.3.1 设G =<V ,E >是一个复杂图,其中V ={v 1,v 2,…, v n },那么 n 阶方阵A 〔G 〕=〔a ij 〕称为G 的邻接矩阵.其中各元素⎪⎩⎪⎨⎧==ji v v v v a j i j i ij 不相邻或与相邻与01 而当给定的复杂图是无向图时,邻接矩阵为对称的.即当结点v i 与v j 相邻时,结点v j 与v i 也相邻,所以衔接结点v i 与v j 的一条边在邻接矩阵的第i 行第j 列处和第j 行第i 列处各有一个1,题中给出的邻接矩阵中共有8个1,故有8÷2=4条边。
2.设图G =<V , E >,那么以下结论成立的是 ( ).A .deg(V )=2∣E ∣B .deg(V )=∣E ∣C .E v V v 2)deg(=∑∈D .E v Vv =∑∈)deg(正确答案:C该题主要是反省大家对握手定理掌握的状况。
数学第二次作业
实验设计与数据处理第二次作业2.2、证明配对比较试验中ANOVA的F检验统计量与(2.1)中的配对t统计量的平方的等价性。
配对比较设计是随机化区组设计中区组大小为2的特殊情况。
如果是自然发生的,则配对是有效的,那么配对设计要优于非配对设计。
对于配对比较试验,随机化区组设计的线性模型为:证明:对于配对比较试验,模型可以设为:对于配对比较试验,k=2, b=N。
由课本公式可知,且则代入b=2, F统计量可以表示为:当b=2时,配对比较试验的t统计量为:那么t2可以表示为:同时:可得,证毕。
所以,配对比较试验中ANOVA的F检验统计量与(2.1)中的配对t统计量的平方是等价的。
2.7、表2.32中的元素是按照三个区组的随机化区组设计所收集的数据确定的,5组数的处理均值分别是45,56,46,45和56。
(a)完成表2.31中的ANOVA(是否能用所给的信息来确定表中任意的元素?解释之).(b)用Tukey方法在水平0.01下同时比较五种处理方法均值,并报告那些认为是显著不同的处理对.(c)不经过实际计算,由(b)中的结果,试解释为什么F检验在水平0.01下会拒绝处理效应是相同的零假设?表2.32 随机化区组设计的ANOVA表来源自由度平方和均方区组520处理498残差40总计14(a)由于区组效应和总自由度在表格中都已列出,所以表中的自由度是确定的,通过自由度和平方和的数据可以求出表格中ANOVA中的其它元素。
计算方法如下:区组自由度以及处理自由度可通过区组和处理个数减1确定来确定。
残差自由度等于总的自由度减去区组自由度和处理自由度,其均方是平方和除以自由度,总平方和是区组、处理、残差平方和之和:SS=SS b+SS t+SS r,其中SS b为区组平方和,SS t为处理平方和,SS r为残差平方和,把表格填充完整如下:来源自由度平方和均方区组 2 520 260处理 4 498 124.5残差8 40 5总计14 105875.57(b)用Tukey方法判断的判据如下:计算方法为:错误!未找到引用源。
数值分析第二次作业答案answer2
S4 = 0.11157238253891,S8 = 0.11157181325263。 同学们根据自己理解计算 S4 ,S8 都可。 复合梯形公式和复合 Simpson 公式的代码已重复多次,同学们自己整 理。 3. 用 Simpson 公式计算积分 误 差 为 |R(f )| = | − η ∈ (0, 1)。 4. 推导下列三种矩形求积公式: ∫b f (x)dx ∫a b f (x)dx ∫a b a f (x)dx = (b − a)f (a) + = (b − = (b −
14.7 53.63 从而 a = −7.855048,b = 22.25376。 2. 已知实验数据如下: 。 xi 19 25 31 38
44
yi 19.0 32.3 49.0 73.3 97.8 用最小二乘法求形如 y = a + bx2 的经验公式。 答案:两个待定常数,只能两个 φ。 φ0 ,φ1 也必须形如 y = a + bx2 。 可设 φ0 = 1,φ1 = x2 。法方程为: ( 5 5327 )( a b ) = ( 271.4 369321.5 )
第三章 函数逼近 1. 观测物体的直线运动,得出以下数据: 时间 t(s) 0 0.9 1.9 3.0 3.9 5.0 距离 s(m) 0 求运动方程。 ( 10 φ0 = 1,φ1 = t。法方程为: 6 14.7 )( a b ) = ( 280 1078 )
6
1. 用 LU 分解及列主元高斯消去法解线性方程组 8 10 −7 0 1 x1 −3 2.099999 6 2 x 5.900001 2 = 5 5 − 1 5 − 1 x 3 x4 1 2 1 0 2 输出 Ax = b 中系数 A = LU 分解的矩阵 L 及 U ,解向量 x 及 det A;列 主元法的行交换次序,解向量 x 及 det A;比较两种方法所得的结果。 代码: A=[10,-7,0,1;-3,2.099999,6,2;5,-1,5,-1;2,1,0,2]; b=[8,5.900001,5,1]'; x=A\b;x(1) 结果:1.7764e-016 LU分解代码: A=[10,-7,0,1;-3,2.099999,6,2;5,-1,5,-1;2,1,0,2]; b=[8,5.900001,5,1]'; [m,n] = size(A); if m~=n, error('A matrix needs to be square'); end for i=1:n-1 pivot = A(i,i); if abs(pivot)<50*eps, error('zero pivot encountered'); end for k = i+1:n A(k,i) = A(k,i)/pivot; A(k,i+1:n) = A(k,i+1:n) - A(k,i)*A(i,i+1:n); end end 7
电子科大图论-第二次作业(4、5章)-答案
习题四
3.(1)画一个有 Euler 闭迹和 Hamilton 圈的图;
(2)画一个有 Euler 闭迹但没有 Hamilton 圈的图; (3)画一个有 Hamilton 圈但没有 Euler 闭迹的图; (4)画一个即没有 Hamilton 圈也没有 Euler 闭迹的图; 解:找到的图如下: (1) 一个有 Euler 闭迹和 Hamilton 圈的图;
(2) 一个有 Euler 闭迹但没有 Hamilton 圈的图;
(3) 一个有 Hamilton 圈但没有 Euler 闭迹的图;
(4)一个即没有 Hamilton 圈也没有 Euler 闭迹的图.
7. 将 G 中的孤立点去掉后的图为 G1,则 G1 也是没有奇度点的,且 G1 的最小
度大于等于 2.则 G1 存在一个圈 S1,在 G1 –S1 中去除孤立的点,得到一个新的 图 G2,显然 G2 也没有奇度的点,且 G2 的最小度大于等于 2.这样 G2 中也存在 的点。这 样 E(G) = E(G1)并 E(G2)…并 E(Gm).命题得证。
则 是非 Hamilton 图
(2)因为 是具有二分类 的偶图,又因为
,在这里假设
,则有
,也就是说:对于
的非空顶点集 ,有:
成
立,则可以得出则 是非 Hamilton 图。
习题五
1. (1)证明:每个 k 方体都有完美匹配(k 大于等于 2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Problem 1.
Show that a group must be an Abelian group if the order of any element in the group, except for
the identity , is 2.
Solution:
在恒元之外,任取两个元素R和S,设他们的乘积为RST
由群的定义ERRE ,ESSE
由题意知:2RE,2SE
RTRRSS,TSRSSR
由恒元和逆元的唯一性,T不等于E且不等于R,S
因此:2TE
RSRTTSSR
因此该群中的任意元素乘积可以对易,该群是Abelian group
Problem 2.(Lorentz group)
Prove that in Minkowski space-time where the four coordinates of an event is expressed as
(,,,)ctxyz
, all the Lorentz tansformations along with the X-axis (namely all boosts along with
X-axis) of the form
()()ctctxxxctyyzz
where vc,211, form a group.
Solution:
将沿着X轴的Lorentz变换用矩阵 表示
000000100001
(1) 封闭性:对于任意两个的变换矩阵12,
111222
111222
12
12121212
12121212
000000000010001000010001(1)()00()(1)0000100001
仍然是该群中的元素
(2) 结合性:矩阵乘法满足结合律,因此该群元素也满足结合律
(3) 存在单位元素: 1000010000100001
(4) 反元素:det0,因此存在逆矩阵,1即为其反元素
综上,所有沿X方向的Lorenz变换构成一个群
Problem 3.
Let G be a finite cyclic group, and let n be a positive integer which divides the order of G , ()oG.
Prove that G has a cyclic subgroup of G of order n, |1ngGg.
Solution:
设G的阶数为m,由n是m的因子,因此,存在正整数p使得:npm
设循环群|1mGaGa
那么令子群H的生成因子pgaG,且npnmgaae
因此H子群的阶数为n,且n可以为m任意一个正整数因子
H为一个循环群,|g1nHgH
因此G有一个循环子群 |g1nHgH
Problem 4.
Let 42118,:1,GDababbaba. Let x,y be the permutations in 4S which are
given by (12)x,(34)y,and let K be the subgroup ,xy of 4S. Show that the function
:GK
, defined by
:rsrsabxy
(03,01rs),
is a homomorphism.
(Notation:,xy means the subgroup generated by the group elements x and y.)
Solution:
由11baba ,得到113babaabab
2112baabaab,3
baab
我们得到8个元素,如下表,他们两两之间乘积仍然在该群中,并且由乘法,我们可以得到
任意a,b的元素组合
因此:我们得到G中有且只有8个元素2323,,,,,,,Gaaababababe
a 2a 3a b ab 2ab 3ab e
a 2a 3a e ab 2ab 3ab b a
2a 3a e a 2ab 3ab b ab 2
a
3a e a 2a 3ab b ab 2ab 3
a
b 3ab 2ab ab e 3a 2a a b
ab b 3ab 2ab a e 3a 2a ab
2ab ab b 3ab 2a a e 3a 2
ab
3ab 2ab ab b 3a 2a a e 3
ab
e a 2a 3a b ab 2ab 3ab e
对于K群
X Y XY
E
X E XY Y X
Y XY E X Y
XY Y X E XY
E X Y XY E
令:
3
()()aaX
2
(b)(b)aY
3
()(b)abaXY
2
()(e)aE
因此存在一个映射 ,可以满足G与K同态
