数值分析第一次作业及参考答案
数值分析

数值分析第一次作业信计2 20121314044 王峥虹一、实验内容:1、已知函数在下列各点的值为:38.064.081.092.098.0|0.18.06.04.02.0|y x -------------------试用4次牛顿插值多项式)(4x P 及三次样条函数)(x S (自然边界条件)对数据进行插值,用图给出(){}10,11,1,008.02.0,=+=i i x y x i i i ,,,)(4x P 及)(x S 。
分析:先求4次插值多项式:根据差分形式的牛顿差值公式:))...(](,...,,[...))(](,,[)](,[)()(1010102100100---++--+-+=n n n x x x x x x x f x x x x x x x f x x x x f x f x Px=[0.2,0.4,0.6,0.8,1.0];y=[0.98,0.92,0.81,0.64,0.38];n=length(y);z=zeros(n,n);for i=1:nz(i,1)=y(i);endfor k=2:nfor l=k:nz(l,k)=(z(l,k-1)-z(l-1,k-1))/(x(l)-x(l-k+1));endendz结果:4次牛顿插值多项式为:)6.0)(4.0)(2.0(2083.0)4.0)(2.0(625.0)2.0(3.098.04---------=x x x x x x P )8.0)(6.0)(4.0)(2.0(5208.0-----x x x x再求三次样条插值函数:由上面及已知的:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡075.65.475.30200005.025.00005.025.00005.025.00000243210M M M M M 程序如下:A=[2,0,0,0,0;0.5,2,0.5,0,0;0,0.5,2,0.5,0;0,0,0.5,2,0.5;0,0,0,0,2];B=[0,-3.75,-4.5,-6.75,0]';M=inv(A)*B结果:则由表达式:j j j j j j j j j j j j j j j j h x x h M y h x x h M y h x x M h x x M x S -⎪⎪⎭⎫ ⎝⎛-+-⎪⎪⎭⎫ ⎝⎛-+-+-=+++++666)(6)()(2111231311,...,1,0-=n j得,三次样条插值多项式为:⎪⎪⎩⎪⎪⎨⎧∈-+-+----∈-+-+----∈-+-+----∈-+-+---=]0.1,8.0[),8.0(9.1)0.1(3036.3)8.0(0)0.1(5893.2]8.0,6.0[),6.0(3036.3)8.0(0857.4)6.0(5893.2)8.0(8929.0]6.0,4.0[),4.0(0857.4)6.0(6536.4)4.0(8929.0)6.0(3393.1]4.0,2.0[),2.0(6536.4)4.0(9.4)2.0(3393.1)4.0(0)(3333333x x x x x x x x x x x x x x x x x x x x x S 绘制4次插值多项式及三次样条插值多项式的图像:代码:x=[0.2,0.4,0.6,0.8,1.0];y=[0.98,0.92,0.81,0.64,0.38];plot(x,y)hold onfor i=1:1:5y(i)=0.98-0.3*(x(i)-0.2)-0.625*(x(i)-0.2)*(x(i)-0.4)-0.20833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0.5 2083*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)*(x(i)-0.8)endk=[0 1 10 11];x0=0.2+0.08*k;y0=zeros(4);for i=1:1:4y0(i)=0.98-0.3*(x(i)-0.2)-0.625*(x(i)-0.2)*(x(i)-0.4)-0.20833*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0. 52083*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)*(x(i)-0.8)endplot(x0,y0,'o',x0,y0)hold ony1=spline(x,y,x0)plot(x0,y1,'o')hold ons=csape(x,y,'variational')fnplt(x,'r')hold ongtext('原图像')gtext('三次样条自然边界')gtext('4次牛顿插值')一、实验内容:2、在区间[]11,-上分别取20,10=n 用两组等距节点对龙格函数22511)(x x f +=作多项式插值及三次样条插值,对每个n 值,分别画出插值函数及)(x f 的图形。
《数值分析》第一章答案

《数值分析》第⼀章答案习题11.以下各表⽰的近似数,问具有⼏位有效数字?并将它舍⼊成有效数。
(1)*1x =451.023, 1x =451.01;(2)*2x =-0.045 113, 2x =-0.045 18;(3)*3x =23.421 3, 3x =23.460 4;(4)*4x =31, 4x =0.333 3;(5)*5x =23.496, 5x =23.494;(6)*6x =96×510, 6x =96.1×510;(7)*7x =0.000 96, 7x =0.96×310-;(8)*8x =-8 700, 8x =-8 700.3。
解:(1) =*1x 451.023 =1x 451.01=-1*1x x 0.01311021-?≤,1x 具有4位有效数字。
→1x 451.0(2) -=*2x 0.045 113 -=2x 0.045 18=-241021x x 0.045 18045113.0-=0.000 06731021-?<2x 具有2位有效数字,045.02-→x(3)=*3x x =-4604.234213.23=-4213.234604.231 10210391.0-?≤3x 具有3位有效数字,4.233→x (不能写为23.5) (4) =*4x 31 ,=4x 0.3333=-4*4x x 41021000033.0-?<,4x 具有4位有效数字,=4x 0.3333(5) =*5x 23.496,=5x 23.494=-5*5x x =-494.23496.2321021002.0-?<5x具有4位有效数字,→5x 23.50 (不能写为23.49)(6) =*6x 51096?710961.0?==-6*6x x 710001.0-?72101021--??≤6x 具有2位有效数字,57610961096.0?=?=x(7) =*7x 0.00096 371096.0-?=x3*71096.0-?=x =-7*7x x 0 7x 精确(8) 8700*8-=x 8x 3.8700-=8*8x x -010213.0?≤=8x 具有4位有效数字,8x 8700-=精确2.以下各数均为有效数字: (1) 0.1062 + 0.947; (3)2.747?6.83; (2)23.46―12.753; (4)1.473 / 0.064 。
数值分析课第一次作业答案answer1

计算机习题: 1. 作多项式 p,以 −1,0,1 为零点,首项系数为 2,并计算 p(3)。 4
答案:p = poly ([−1, 0, 1]),s = polyval(p, 3)。 2. 已知函数在下列各点的值为 xi 0.2 0.4 0.6 0.8 1.0
2
a 6 6e+154 0 1 1
b 10 10e+154 1 -1e+5 -4
c -4 -4e+154 1 1 3.999999
-1e+155 -7e+155 1e+155 答案:第二种方法更准确,因为第一种方法是一个累加的过程。 matlab 的 x = a : h : b 和 x = a + (0 : n) ∗ h 是第二种方法实现的。 代码: format long e a = 0; b = 8; n = 9; h = (b-a)/n; x(1) = a; y(1) = a; for j = 1:n, x(j+1) = x(j) + h; y(j+1) = y(1) + j*h; end [x',y',(a:h:b)',a+(0:n)’*h] 第二章 插值法 1. 当 x = 1, −1, 2 时,f (x) = 0, −3, 4,求 f (x) 的二次插值多项式。 (计算两遍,分别用拉格朗日插值和牛顿插值)
5
f (xi ) 0.98 0.92 0.81 0.64 0.38 求 4 次牛顿插值多项式 P4 (x) 并画图。 答案: 代码: x=0.2:0.2:1.0; y=[0.98,0.92,0.81,0.64,0.38]; n = length(y); if length(x)~=n, error('x and y are not compatible'); end D = zeros(n,n); D(:,1)=y(:); for j=2:n for i=j:n D(i,j) = (D(i,j-1)-D(i-1,j-1))/(x(i)-x(i-j+1)); end end p=D(1,1)*[zeros(1,n-1),1]; for k=2:n p=p+D(k,k)*[zeros(1,n-k),poly(x(1:k-1))]; end x=0.2:0.01:1.0; z=polyval(p,x); plot(x,z) 比较:p = polyf it(x, y, 4)。
(完整版)数值分析第一次作业

问题1:20.给定数据如下表:试求三次样条插值S(x),并满足条件 (1)S`(0.25)=1.0000,S`(0.53)=0.6868; (2)S ’’(0.25)=S ’’(0.53)=0。
分析:本问题是已知五个点,由这五个点求一三次样条插值函数。
边界条件有两种,(1)是已知一阶倒数,(2)是已知自然边界条件。
对于第一种边界(已知边界的一阶倒数值),可写出下面的矩阵方程。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡432104321034322110d M M M M M 200020000020022d d d d λμμλμλμλ其中μj =j1-j 1-j h h h +,λi=j1-j j h h h +,dj=6f[x j-1,x j ,x j+1], μn =1,λ0=1对于第一种边界条件d 0=0h 6(f[x 0,x 1]-f 0`),d n =1-n h 6(f`n-f `[x n-1,x n ]) 解:由matlab 计算得:由此得矩阵形式的线性方程组为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡ 2.1150-2.4286-3.2667-4.3143-5.5200-M M M M M 25714.00001204286.000004000.026000.0006429.023571.0001243210解得 M 0=-2.0286;M 1=-1.4627;M 2= -1.0333; M 3= -0.8058; M 4=-0.6546S(x)=⎪⎪⎩⎪⎪⎨⎧∈-+-+-∈-+-+-∈-+-+-∈-+-+-]53.0,45.0[x 5.40x 9.1087x 35.03956.8.450-x 1.3637-x .5301.67881- ]45.0,39.0[x 9.30x 11.188x 54.010.418793.0-x 2.2384-x .450(2.87040-]39.0,30.0[x 03.0x 6.9544x 9.30 6.107503.0-x 1.9136-x .3902.708779-]30.0,25.0[x 5.20x 10.9662x 0.3010.01695.20-x 4.8758-x .3006.76209-33333333),()()()(),()()()),()()()(),()()()(Matlab 程序代码如下:function tgsanci(n,s,t) %n代表元素数,s,t代表端点的一阶导。
JZX高等数值分析第一次实验作业
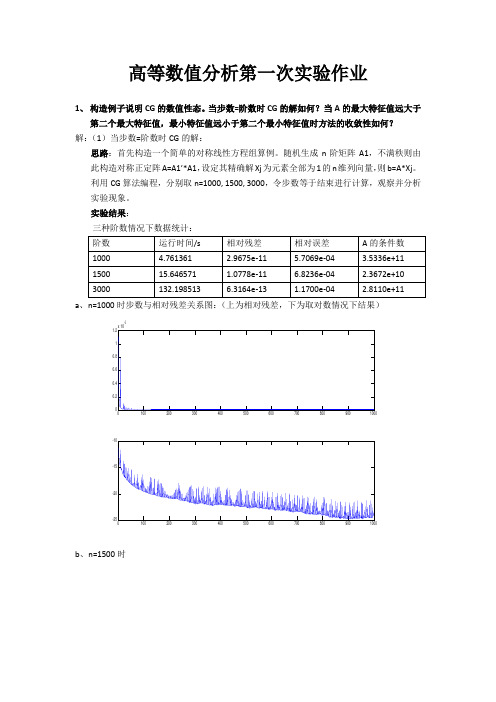
相对残差 6.1302e-16 8.7797e-09 8.0295e-09 8.5677e-09 9.1433e-09
a、 m=1 (左为相对残差,右为取对数情况)
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 1
1.5
0
-5
-10
-15
-20
-25
-30
-35
-40
1000
4.761361
2.9675e-11
5.7069e-04
3.5336e+11
1500
15.646571
1.0778e-11
6.8236e-04
2.3672e+10
3000
132.198513
6.3164e-13
1.1700e-04
2.8110e+11
a、n=1000 时步数与相对残差关系图:(上为相对残差,下为取对数情况下结果)
(2)当 A 最大特征值远大于第二个特征值,最小特征值远小于第二个最小特征值时收敛
性情况。
思路:构造题目要求的矩阵 A。首先随机生成 n 阶矩阵 B,B 不满秩,构造对角阵 A1(最
大特征值远大于第二个最大特征值,最小特征值远小于第二个最小特征值),则由此构
造出对称正定矩阵 A: b1=B’*B; A=b1’*A1*b1。同样设定精确解 Xj 为元素全部为 1 的 n
5、 构造对称不定的矩阵,验证 Lanczos 方法的近似中断,观察收敛曲线中的峰点个数和特
征值的分布关系;观察当出现峰点时,MINRES 方法的收敛性态怎样。
解:思路:类似前两题,首先构造出一个 n 阶对角阵 D,其对角线上有 m 个负值,再对随
西南交大数值分析第一次大作业答案

数值分析大作业1、证明:1-x-sinx=0在[0,1]内有一个根,使用二分法求误差不大于0.5*10^-4的根要迭代多少次,并输出每一步的迭代解和迭代误差证明:令f(x)= 1-x-sinx;f(0)=1,f(1)=-sin1f(0)*f(1)<0f’(x)=1-cosx<0在[0,1]内恒成立所以1-x-sinx=0在[0,1]内恒有一个根程序:function chap2bisecta = 0;b = 1;fprintf('n || a || b || c || r \n')for k=1:15c = (a+b)/2;r=(b-a)/2;fa =1-a-sin(a);fb =1-b-sin(b);fc =1-c-sin(c);fprintf('%d || %f || %f || %f \n',k,a,b,c,r);if abs(fc)<0.5*10^(-4) r=c; sprintf('the root is: %d' , r);elseif fa*fc<0 b=c;elseif fb*fc<0 a=c;endendroot = (a+b)/2结果:n || a || b || c || r1 || 0.000000 || 1.000000 || 0.500000 ||5.000000e-001 ||2 || 0.500000 || 1.000000 || 0.750000 ||2.500000e-001 ||3 || 0.500000 || 0.750000 || 0.625000 ||1.250000e-001 ||4 || 0.500000 || 0.625000 || 0.562500 ||6.250000e-002 ||125 || 0.500000 || 0.562500 || 0.531250 ||3.125000e-002 ||6 || 0.500000 || 0.531250 || 0.515625 ||1.562500e-002 ||7 || 0.500000 || 0.515625 || 0.507813 ||7.812500e-003 ||8 || 0.507813 || 0.515625 || 0.511719 ||3.906250e-003 || 9 || 0.507813 || 0.511719 || 0.509766 ||1.953125e-003 || 10 || 0.509766 || 0.511719 || 0.510742 ||9.765625e-004 || 11 || 0.510742 || 0.511719 || 0.511230 ||4.882813e-004 || 12 || 0.510742 || 0.511230 || 0.510986 ||2.441406e-004 || 13 || 0.510742 || 0.511230 || 0.510986 ||2.441406e-004 || 14 || 0.510742 || 0.511230 || 0.510986 ||2.441406e-004 || 15 || 0.510742 || 0.511230 || 0.510986 ||2.441406e-004 || root =0.510986328125000。
数值分析练习题加答案(一)

数值分析期末考试一、 设80~=x ,若要确保其近似数的相对误差限为0.1%,则它的近似数x 至少取几位有效数字?(4分)解:设x 有n 位有效数字。
因为98180648=<<=,所以可得x 的第一位有效数字为8(1分) 又因为21101011000110821--⨯=<⨯⨯≤n ε,令321=⇒-=-n n ,可知x 至少具有3位有效数字(3分)。
二、求矩阵A 的条件数1)(A Cond (4分)。
其中⎥⎦⎤⎢⎣⎡=4231A 解:⎥⎦⎤⎢⎣⎡--=-5.05.1121A (1分) 1A =7(1分) 2711=-A (1分)249)(1=A Cond (1分)三、用列主元Gauss 消元法法求解以下方程组(6分)942822032321321321=++-=++--=+-x x x x x x x x x解:→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----5.245.2405.35.230914220321821191429142821120321 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---8175835005,245.24091425.33.2305.245.2409142(4分) 等价三角方程组为:⎪⎪⎩⎪⎪⎨⎧-=-=+-=++,8175835,5.245.24,942332321x x x x x x (1分)回代得1,3,5123==-=x x x (1分)四、设.0,2,3,1,103)(3210234=-===-+-=x x x x x x x x f 1)求以3210,,,x x x x 为节3次Lagrange 多项式;(6分) 2)求以3210,,,x x x x 为节3次Newton 多项式;(6分)3)给出以上插值多项式的插值余项的表达式(3分)解:由0,2,3,13210=-===x x x x 可得10)(,34)(,1)(,11)(3210-==-=-=x f x f x f x f即得: +------+------=))()(())()(()())()(())()(()()(312101320130201032103x x x x x x x x x x x x x f x x x x x x x x x x x x x f x L=------+------))()(())()(()())()(())()(()(23130321033212023102x x x x x x x x x x x x x f x x x x x x x x x x x x x f+-+--+-⨯-+-+--+-⨯-)03)(23)(13()0)(2)(1()1()01)(21)(31()0)(2)(3(11x x x x x x326610.)20)(30)(10()2)(3)(1()10()02)(32)(12()0)(3)(1(34x x x x x x x x x -+--=+--+--⨯-+---------⨯2)计算差商表如下:i x )(i x f 一阶差商 二阶差商 三阶差商1 -11 3 -1 5 -2 34 -7 4 0-10-225-1则=+-----+-+-=)2)(3)(1()3)(1(4)1(511)(3x x x x x x x N326610x x x -+--3))2)(3)(1())()()((!4)()(3210)4(3+--=----=x x x x x x x x x x x x f x R ξ五、给定方程组b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100131w w w w A 。
清华大学高等数值分析 第一次实验作业

10
-10
0
100
200
300
400
500
600
700
800
900
迭代次数
图9
m=100时,Lanczos法求解Ax=b的收敛曲线
高等数值分析实验作业一
10
4
Lanzcos 算法的收敛曲线 (阶数 n=1002)
10
2
10
0
||rk||/||b||
10
-2
10
-4
10
-6
10
-8
10
-10
0
200
迭代次数
图12 m=10时,Minres法求解Ax=b的收敛曲线
10
2
Minres 算法的收敛曲线 (阶数 n=1002)
10
0
10
-2
||rk||/||b||
10
-4
10
-6
10
-8
10
-10
0
100
200
300
400
500
600
700
迭代次数
图13
10
2
m=50时,Minres法求解Ax=b的收敛曲线
10
0
Lanzcos 算法的收敛曲线 (阶数 n=1002)
m=10 m=50 m=100 m=400 m=800
10
-2
10
-4
||rk||/||b||
10
-6
10
-8
10
-10
10
-12
0
2
4
6
8
10
12
14
16
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值计算方法第一次作业及参考答案1. 已测得函数()y f x =的三对数据:(0,1),(-1,5),(2,-1),(1)用Lagrange 插值求二次插值多项式。
(2)构造差商表。
(3)用Newton 插值求二次插值多项式。
解:(1)Lagrange 插值基函数为0(1)(2)1()(1)(2)(01)(02)2x x l x x x +-==-+-+-同理 1211()(2),()(1)36l x x x l x x x =-=+ 故 2202151()()(1)(2)(2)(1)23631i i i p x y l x x x x x x x x x =-==-+-+-++=-+∑ (2)令0120,1,2x x x ==-=,则一阶差商、二阶差商为0112155(1)[,]4,[,]20(1)12f x x f x x ---==-==-----0124(2)[,,]102f x x x ---==-实际演算中可列一张差商表:(3)用对角线上的数据写出插值多项式22()1(4)(0)1*(0)(1)31P x x x x x x =+--+-+=-+2. 在44x -≤≤上给出()xf x e =的等距节点函数表,若用二次插值求xe 的近似值,要使截断误差不超过610-,问使用函数表的步长h 应取多少解:()40000(),(),[4,4],,,, 1.x k x f x e f x e e x x h x x h x x th t ==≤∈--+=+≤考察点及(3)200044343()()[(()]()[()]3!(1)(1)(1)(1)3!3!.(4,4).6fR x x x h x x x x ht t tet h th t h e heξξ=----+-+≤+⋅⋅-=≤∈-则436((1)(1)100.006.t t th--+±<<Q在点得3.求2()f x x=在[a,b]上的分段线性插值函数()hI x,并估计误差。
解:22221111112211111()()k k k kh k kk k k k k kk k k kk k k kk kx x x x x xI x x x xx x x x x xx x x xx x x x xx x+++++++++++---=+=---⋅-⋅-=+--[]2112211()()()[()]11()()44h h k k k kk k k kR x f x I x x x x x x xx x x x x x h++++=-=-+-=--≤-=4.已知单调连续函数()y f x=的如下数据用插值法计算x约为多少时() 1.f x=(小数点后至少保留4位)解:作辅助函数()()1,g x f x=-则问题转化为x为多少时,()0.g x=此时可作新的关于()ig x的函数表。
由()f x单调连续知()g x也单调连续,因此可对()g x的数值进行反插。
的牛顿型插值多项式为1()0.110.097345( 2.23)0.451565( 2.23)( 1.10)0.255894( 2.23)( 1.10)(0.17)x g y y y yy y y-==-+++++-++-故 1(0) 1.321497.x g -==5. 设函数()f x 在区间[0,3]上具有四阶连续导数,试用埃尔米特插值法,求一个次数不高于3的多项式3()P x ,使其满足3(0)0P =,3(1)1P =,3'(1)3P =,3(2)1P = 。
并写出误差估计式。
解:由所给条件可用埃尔米特插值法确定多项式3()P x , 32357()722p x x x x =-+-2112(1)()(2);()(1)(2);();2x x x x x x x x x x αβα-=--=---=由题意可设23()()()()(1)(2)R x f x p x k x x x x =-=--为确定待定函数()k x ,作辅助函数: 23()()()()(1)(2)g t f t p t k t t t t =---- 则()g t 在[0,3]上存在四阶导数且在[0,3]上至少有5个零点,0,1,2(1t x t ==为二重零点),反复应用罗尔定理,知至少有一个零点(0,3)ξ∈使4()0g ξ=,从而得(4)1()()4!k x f ξ=。
故误差估计式为(4)21()()(1)(2)(0,3)4!R x f x x x ξξ=--∈6. 设函数()y f x =在节点0,1,2,3x =的函数值均为零,试分别求满足下列边界条件下的三次样条插值函数()S x :(1)''(0)1,(3)0f f == (2)''''(0)1,(3)0f f ==解:(1)取i x 处的一阶导数i m 作为参数,1,2i =。
由于11111,1,3([,][,])022i i i i i i i i i i i i i h g f x x f x x h h λμλλμ-+-===-==+=+以及由三转角方程 112,1,2i i i i i i m m m g i λμ-+++==得 012123112022112022m m m m m m ⎧++=⎪⎪⎨⎪++=⎪⎩ 由于031,0,m m ==从而 12124140m m m m +=-⎧⎨+=⎩解之可得124/15,1/15m m =-=故 2(1)(1511)/15,[0,1]()(1)(2)(73)/15,[1,2](3)(2)/15,[2,3]x x x x S x x x x x x x x --∈⎧⎪=---∈⎨⎪--∈⎩(2)取i x 处的二阶导数i M 作为参数,1,2i =。
由于111111,1,6[,,]022i i i i i i i i i i h d f x x x h h μλμ--+-===-===+以及由三弯矩方程0121112311202221,2112022i i i i i iM M M M M M d i M M M μλ-+⎧++=⎪⎪++==⇒⎨⎪++=⎪⎩ 由于031,0,M M ==代入方程可得 134/15,1/15,M M =-=故 (1)(1926)/90,[0,1]()(1)(2)(512)/90,[1,2](3)(2)(4)/90,[2,3]x x x x S x x x x x x x x x --∈⎧⎪=---∈⎨⎪---∈⎩7.编程实现题:略。
8、试求 ()sin ,[0,]2f x x x π=∈最佳一次一致逼近多项式。
解:因为''()sin f x x =-在[0,/2]π内不变号,故最佳一次一致逼近多项式为*1111()[(0)()]/2(/2)P x f f x a x x =++-式中 '11111(/2)(0)20.63661977()cos 0.88068924/20f f a a f x x x πππ-=====⇒=-从而 *1111()(sin )/2(/2)0.105256830.63661977P x x a x x x =+-=+9、给定43()1f x x x =+-,试利用最小零偏差定理,即切比雪夫多项式的最小零偏差性质,在[0,1]上求()f x 的三次最佳一致逼近多项式。
2342234(()21,()43,()881)T x x T x x x T x x x =-=-=-+解:令4311121()()()3() 1.222t t t t x f x f +++=-⇒==+- 设*3()P x 为()f x 在[0,1]上的三次最佳一致逼近多项式,由于1()2t f +的首项系数为412,故 *3441*43423*434233211116[()()]()2221111()()()1(881)2221681()(31)[8(21)8(21)1]168511293.[0,1]44128t t f P T t t t t P t t P x x x x x x x x x -++-=+++⇒=+---+⨯⇒=+-----+⨯=-+-∈10、设{}{}100101121,,,span x span x x ϕϕ==,分别在12ϕϕ、上求一函数,使其为2[0,1]x C ∈的最佳平方逼近,并比较其结果。
解:**01112000100121110011220100***010*1***101221221 (,)11,(,),211(,),(,),3211(,)1,(,),34111123()611161234a a xdx xdx x dx f x dx f x xdx a a a x xa a a fϕϕϕϕϕϕϕϕϕϕϕϕδ=+========⋅==⋅=⎧+=⎧⎪=-⎪⎪⇒⇒⇒=-+⎨⎨⎪⎪=+=⎩⎪⎩=-⎰⎰⎰⎰⎰*1(1)设因1*(,)0.00556k k k a f ϕ=≈∑**100*1012011110021001010001100011110121021031101000**01**01(2)()11(,)(),(,)(,),201202111(,)(),(,),(,).203103104111201202103111202203104x b x b x x dx x x dx x dx f x dx f x dx b b b b ϕϕϕϕϕϕϕϕϕϕϕ=+====⋅=======⎧+=⇒+=⎰⎰⎰⎰⎰设*0*1*10010121122*4222375.24253375.14825()375.24253375.14825.11(,)[375.24253375.14825]0.16406103104k k k b b x x x fb f x dx ϕδϕ=⎪⎧≈⎪⇒⎨⎨≈-⎩⎪⎪⎩⇒=-=-=-⨯-⨯≈∑⎰ 由结果知(1)比(2)好。
11、用最小二乘法求一个形如2y a bx =+的经验公式,使它与下列数据拟合,并计算均方误差。
44222010000442011001044411110044000042110()1,().(,)()15,(,)(,)()()5327,(,)()()7277699,(,)()271.4,(,)()i i i i i i i i i i i i i i i i i i i i i i x x x x x x x x x x y x y y y x y x ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ==========================∑∑∑∑∑∑∑∑∑因有422201222369321.5,55327271.40.972604553277277699369321.50.05003510.97260450.0500351.(,)(,)0.016954.0.130207526.i i y a b a a b b y x y a y b y δϕϕδ==+==⎧⎧⇒⇒⎨⎨+==⎩⎩⇒=+=--==∑12、用格拉姆-施密特方法构造正交多项式求()sin f x x π=在[0,1]上的二次最佳平方逼近多项式。
