第八章 常见回转体
高考复习指导讲义第八章多面体和旋转体
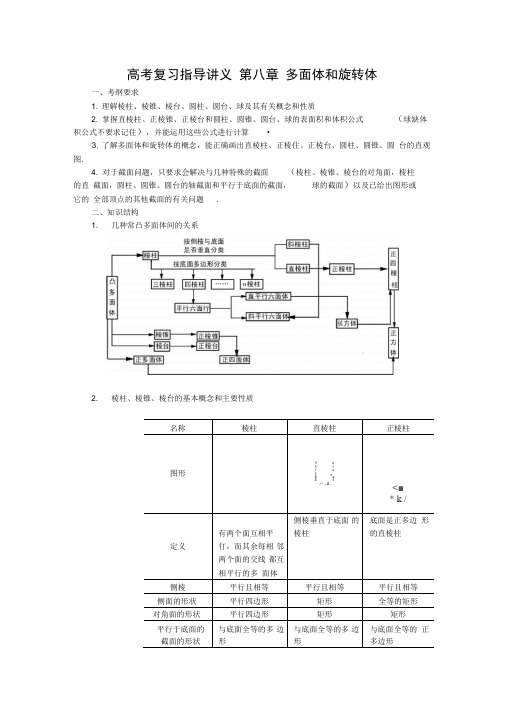
高考复习指导讲义第八章多面体和旋转体一、考纲要求1. 理解棱柱、棱锥、棱台、圆柱、圆台、球及其有关概念和性质2. 掌握直棱柱、正棱锥、正棱台和圆柱、圆锥、圆台、球的表面积和体积公式(球缺体积公式不要求记住),并能运用这些公式进行计算•3. 了解多面体和旋转体的概念,能正确画出直棱柱、正棱住、正棱台、圆柱、圆锥、圆台的直观图.4. 对于截面问题,只要求会解决与几种特殊的截面(棱柱、棱锥、棱台的对角面,棱柱的直截面,圆柱、圆锥、圆台的轴截面和平行于底面的截面,球的截面)以及已给出图形或它的全部顶点的其他截面的有关问题.二、知识结构1. 几种常凸多面体间的关系2. 棱柱、棱锥、棱台的基本概念和主要性质名称棱柱直棱柱正棱柱图形1 a1 1i ■1 ;4 ■4 ¥.-1- —A.<■* k /定义有两个面互相平仃,而其余每相邻两个面的交线都互相平行的多面体侧棱垂直于底面的棱柱底面是正多边形的直棱柱侧棱平行且相等平行且相等平行且相等侧面的形状平行四边形矩形全等的矩形对角面的形状平行四边形矩形矩形平行于底面的截面的形状与底面全等的多边形与底面全等的多边形与底面全等的正多边形4.面积和体积公式下表中S表示面积,c'、c分别表示上、下底面周长,h表斜高,h'表示斜高,I表示侧棱长.(7)正四面体内任意一点到四个面的距离之和为定值(等于正直角四面体的性质 有一个三面角的各个面角都是直角的四面体叫做直角四面体四面体有下列性质:如图,在直角四面体 AOCB 中/ AOB=Z BOC M COA=90 , OA=a,OB=b,OC=c >则① 不含直角的底面 ABC 是锐角三角形;② 直角顶点O 在底面上的射影H 是厶ABC 的垂心;1③ 体积 V= abc ;6④ 底面△ ABC =— ,a2b 2b 2c 2c 2a 2 ;2⑤ S △ABC F S X BHC • S ^ABC ; ⑥ S 2 △ BO(=S △ AO +S △AO C=S △ ABC11 1+ +2 、c⑧外切球半径 R= 1 . a 2 b 2 c 2 ;2名称 侧面积(S 侧) 全面积(S 全) 体积(V) 棱 棱柱 直截面周长x lS 侧+2S 底S 底• h=S 直截面• h柱直棱柱 ch S底,h棱锥棱锥 各侧面积之和■— S 底• h3正棱锥 1『 —ch 2S 侧+S 底棱台:各侧面面积之和1—h(S 上底+S 下底棱 台正棱台1 -(c+c ' )h '2S 侧+S 上底+S 下底3+JS 下底S 下底)设正四面体的棱长为 a ,则这个正四面体的(1)全面积S全=3 a 2;⑵体积v=2123a ;(3)对棱中点连线段的长d=a ;2(4)相邻两面所成的一二面角 .6 a ; 4 1a =arccos -3(5)外接球半径R=(6)内切球半径r=.6a.12⑦OH 2b 25.正四面体的性质⑨内切球半径r= S A OB £ 吟七碎a +b + c6.旋转体 圆柱、圆锥、圆台、球的公式 (1)面积和体积公式圆柱圆锥 圆台 球S 侧 2 n rl n rl n (r 1+r 2)lS 全2 n r(l+r)n r(l+r) n (r 计r 2)1+ n2 2(r 1+r 2)24 n RVn r 2h(即 n r 2l)1 2 -n r h 31 — n32 2h(r 1+nr 2+r 2)4 3 —n R 3表中I 、h 分别表示母线、咼,r 表示圆柱、圆锥与球冠的底半径, r i 、「2分别表示圆台上、下底面半径,R 表示半径.(2)圆锥、圆台某些数量关系②圆锥 圆锥轴截面两腰的夹角叫圆锥的顶角如图,圆锥的顶角为3,母线与下底面所成角为 a ,母线为I ,高为h ,底面半径为r , 则pa =COS —=2a +E=90° 二彳2h=ls in a r-r ' =lcos a .③球的截面用一个平面去截一个球,截面是圆面.⑴ 过球心的截面截得的圆叫做球的大圆;不经过球心的截面截得的圆叫做球的小圆 (2) 球心与截面圆圆心的连线垂直于截面(3) 球心和截面距离d,球半径R,截面半径r 有关系:r= . R 2-d 2 .(3)球冠、球带和球缺① 球缺 球面被平面所截得的一部分叫做球冠, 截得的圆(圆周)叫做球冠的底,垂直于截面 的直径被截得的一段叫做相应球冠的高.球冠也可以看作一段圆弧绕经过它的一个端点的直径旋转一周所成的曲面 球冠的面积公式 若球的半径为 R,球冠的高为h ,则S 球冠=2 n Rh其中h 表示球冠的高,R 是球冠所在的球的半径. ② 球带 球面在两个平行截面之间的部分叫做球带 .球带也可以看作一段圆弧绕它所在的半圆的直径旋转一周所成的曲面 球带的面积公式 若球的半径为 R,球带的高为h ,则sin②圆台 别为r '、Pa =sin — 2r I *如图,圆台母线与下底面所成角为a ,母线为I ,高为h , 上、下底面半径分r ,则cosS球带=2 n Rh③球缺用一个平面截球体所得的部分叫做球缺,截面叫做球缺的底面,直径被截得的线段长叫做球缺的高•垂直于截面的球缺的体积公式若球的半径为R,球缺的高h,底面半径为r,则1 2V球缺=n h (3R-h)=3 1 2 2 n h(3r +h ) 6、知识点、能力点提示(一)多面体例1 如图,三棱柱ABC-ABC中,若E、F分别为AB AC的中点,平I 柱分成体积为V i、7的两部分,那么V i : w= ________________ .解:设三棱柱的高为h,上下底的面积为S,体积为V,则V=V+V a= Sh. ••• E、F分别为AB AC的中点,EBG将三棱S A AEF=—S,11 17M= —h(s+—S+ S )= Sh3 4 . ^12V2=Sh-V1 = —Sh,12••• W: Va=7 : 5.例2 一个长方体全面积是20cm2,所有棱长的和是24cm,求长方体的对角线长EG • tg / EFG= =1,/ EFG=45 . GF应选C.例4设正六棱锥的底面边长为 1,侧棱长为,5,那么它的体 积为()设正六棱锥的高为 h ,则h= ( . 5)2 -12 =2.V =1 X 口 X 2-3.34应选C.例5如果三棱锥S- ABC 的底面是不等边三角形,侧面与底面所成的二面角都相等, 且顶点S 在底面的射影 O 在厶ABC 内,那么O 是厶ABC 的()A.垂心B.重心C.外心D .内心解:作 OEL AB OF 丄 BC, OM 丄 CA •••/ SEO 2 SFO 玄 SMO, •••△ SEO^A SFO^^ SMO. • OE=OF=OM.• 0为厶ABC 的内心,应选 D.解:设长方体的长、宽、高、对角线长分别为2(xy+yz+zx)=20 依题意得:: 4(x+y+Z)=24 由② 2得:x 2+y 2+z 2+2xy+2yz+2xz=36 由③-①得x 2+y 2+z 2=16 即 I =16 •/ l=4(cm). 例3如图,正三棱锥 S — ABC 的侧棱和底面 点,那么异面直线 EF 与SA 所成的角等于() A.90 ° B.60 ° 解:取AC 的中点G,连结FG EG •/ FG// SA •••/ GFE 为异面直线EF 与SA 所成的角.1正三棱锥的棱长为 1,则GF=GE 二.2•••顶点到A 、B C 等距,△ ABC 等边 •顶点在底面 ABC 的射影0是厶ABC 的中心, 即"正三棱锥中两相对棱垂直”•••/ FGE=90 . xcm 、ycm zcm> lcm①边长相等,如果E 、F 分别为AB SC 的中C .450D.30从而SA 在底面上的射影丄 Bfc SA 丄 BC,A.6、3B.2、3D.2解:由已知可得正六棱锥的底面积例6 在棱长为1的正方体 ABC —A i BCD 中,M 和N 分别为AB 和BB 的中点,那么直 线AM 和CN 所成角的余弦值是()B.卫10C .35D.-5解:如图,设 P 为AA 的中点,Q 为AiM 的中点,贝U DP// CN PQ 〃 AM •••/ DPQ 是异面直线 AM 和CN 的成角. 在厶DPC 中, DP=. DA 2 AP 2PQ=! AM=! X 5 =丄,2 2 2 4DQ= DA 12 A 1Q 2 = DD 12 D 1A 12 A 1Q 2.33 4由余弦定理得cos / DPQ=兰PQ -DQ2 DP PQ(空)2 •(二)2-I-33)22 442逅西=25.又异面直线所成的角的范围是(0, •••直线AM 和CN 所成角的余弦值是90°).25.应选D.例7 已知三棱锥A — BCD 勺体积是S 和S.设面ABC 和面DBC 所成的二面角是V,棱BC 的长是a ,面ABC 和面DBC 的面积分别是 a ,那么 sin a = ________解:如图,作 AQL 面BCD 于 0,作0E ! BC 于E ,连结 AE.1由 V=—AO ・ S,3得 AO=g2S又 S 1=AE- BC,得 AE= 1 a由三垂线定理知,AE± BC•••/ AEC 是二面角 A — BC- D 的平面角. 即/ AEC a ,例8若正棱锥的底面边长与侧棱长相等,则该棱锥 一定不是() A.三棱锥B.四棱锥C.五棱锥D.六棱锥解:该棱锥一定不是正六棱锥 •否则设正棱锥 S- ABCDE 符合题设,则在△ SAB 和△ CAB 中(C 为顶点S 在底面的射影),•/ SA=SB=AB=CA=CB,• △ SAB^A CAB但厶CAB>^A SAB 在底面的射影,不可能••应选D.例9 如图,AB i C i — ABC 是直三棱柱,/ BCA= 90°,点 D 、F i 分别是 点,若BC=CA=CC 则BD 与AF i 所成的角的余 弦值是()• sin a =sin / AEC=ACAE 3 2S-|S 10C.旦10易知 FE=DB= B^2B 1D 1212 (J 2由/ BCA=90,得 AE=J AC 2 +CE 2AFjAA +AF 1 =十 +(》2 =乎 由余弦定理有cos / EFA=EF 2 FA 2 - AE 2 2 EF FA62.52'5 2p(I 5) rJ 6 <52 ----- -----2 2■ 30 10即BD 和AF 1成角的余弦值是 30 10解:设BC=CA=CC1.取BC中点E,连结EF、DF,贝U EF// BD/ EFA为BD和AF所成的角•应选A.例10 一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面()A.必然都是非直角三角形B.至多只能有一个是直角三角形C.至多只能有二个直角三角形D.可能都是直角三角形解:如图,三棱锥P—ABC中,/ ABC=9C° , PA!面ABC.则PAL AC, PAL AB,△ PAC^D^ PAB都是直角三角形.又/ ACB=90,即ACL BC••• PC丄CB 即/ PCB=90 ,•••△ PCB也是直角三角形.应选D.例11侧棱长为3cm,底面边长为4cm的正四棱锥的体积为______________ cm3.解:由已知有底面对角线长为 4 2 cm.h= .,32 -(2.2)2=1(cm)1 12 16 3V=_ • h • S=—X1X4 = — (cm)3 3 3例12 已知长方体ABCD-A B' C' D'中,棱AA' =5, AB=12,那么直线B' C'和平面A BCD的距离是解:如图•/ B' C'// BC, B' C'二面A C, BC二面AC,• B' C'//面A C.•••点B到平面A BCD的距离即直线 B ' C'到平面A' BCD的距离.作B ' H丄A ' B 于H,又CBL面A ' ABB' , B ' H 二面A ' ABB' , B' H 商A ' B,所以B ' H± CB,从而B ' H丄平面A ' BCD .•/ B ' H- A ' B=B' A' • B' B,° BABB 12^5 60A'B 13 13即直线B ' C'到平面A' BCD的距离是一.13(二)旋转体例13如果圆台的上底面半径为5,下底面半径为R 中截面把圆台分为上、下两个圆台,它们的侧面积的比为 1 : 2,那么R=()A.10B.15C.20D.25解D.例14长方体一个顶点上三条棱的长度分别为面上,这个球的表面积是3, 4, 5,且它的8个顶点都在同一球A.20 .2 7tB.25 2 nC.50 nD.200 n解:设长方体的对角线长为 I ,球半径为R ,由已知及对称性知l=2R,l= . 32 42 52 =5 2,得 R=— . 2 . 2••• S 球=4 n R=50 n 应选C.例15 若母线长为4的圆锥的轴截面的面积为 8,则圆锥的侧面积为 ______ (结果中保1解:设轴截面SAB 贝U SA=SB=4,S SAE =8= SA- SB- sin / SBA 得 sin /ASB=1,2• / ASB=90 , AB=V 2 SA=4/2 , AB — —• - S 侧=n rl= n () - SA=n - 2打2 - 4=8 . 2 n .2例16如果等边圆柱(即底面直径与母线相等的圆柱)的体 积是16 n cm 3,那么它的底半径等于()D.2cm解: 16 n = n r - (2r )=2 n r ,得 r=2(cm ) 应选D.例17圆柱轴截面的周长1为定值,那么圆柱体积的最大值是()应选A.AB 和圆锥的轴的距离为 1,则该圆锥的体积为 ____________解:如图0为底面圆心,OCL AB 于C. 由OA=OE 得C 为AB 中点,A.4 勺 2 cmB.4cmC.2 -牛2 cm1 \ 3A.( )n61 1 ()3 n 4 4解:设r 为底半径,I 为母线.1 - 4r由 4r+2l=1,得 l=2B.( 1)3 n3C.( 1)3nD.V=n r 2l= - n8 1= n8(2r)(2r)(2l) 2r 2r 2l )3等号仅当2r=2l1丁)=81即r=l= 时成立.6(4r 2l7t3 1 3 1 3-()=()n . 36例18设圆锥底面圆周上两点 A 、B 间的距离为2,圆锥顶点到直线AB 的距离为.3 ,由SA=SB C为AB中点得SC± AB于C. • 0C=1,SC=. 3 ,AC=CB=1,so= .SO 2-OC 2 = . ( 3)2 -12 -.2 , 0B= ,0C 2 BC 2 = ,2 .二 V=1 n • OB • SO=1 n ( . 2 ) 2=红 n .3 3 3例19在一个实心圆锥体的零部件, 它的轴截面是边 长为10厘米的等边三角形,现要在它的整个表面镀上一层防腐材料,已知每平方厘米的工料价为0.1元,则需要费用_____ 元(n 取 3.2).解:设圆锥的底半径为 r,由已知有r=5cm,母线长为10cm.2 2S 全=n • 5 + n • 5 • 10=75 n = 240(cm )元•侧面展开圆心角为 240 °,该圆锥的体积是()n解:设圆锥底半径为r , 240° =4 n =N ,得3 I• h= . |2 - r222,2' 5 一(—)=一33• V=[ n r 2h=i n3 3(2)2•邑倍n3 3 81应选C.(三)综合题赏析 例21如图,平面 在直线 MN 上,/ ACM N BCN =45°, A-MN-B 是 60 求:(1)点A 到平面3的距离;(2) 二面角A — BC- M 的大小. 解:⑴作AH L 平面3于H HD£ MN 于 D, A — MN-B 的平面角,所以/ ADH=60 . 在 Rt △ ACD 中,/ ACD=45,/ ADC=90 , a 和3相交于直线MN 点 A 在平面a 上,点B 在平面3上, 的二面角,AC=1. • AD 』AC 』• 1 =)2 2 2在 Rt △ ADH 中,AH=AD sin Z ADH 「• sin60 °2•••工料价为 240X 0.仁24 例20圆锥母线长为I4 n81B.-8 n81 C. — n81D.1081由已知有2 r=3即点A 到平面3的距离是一6 ,4⑵设二面角A — BC- M 为0度,在等腰Rt △ ADC 中,由斜边 AC=1,得DC=ADW?2在 Rt △ ADH 中, DH=AD 2 - AH 2作HE!直线BC 于 E ,则/ AEH •••/ HCB =180° -( / HCD # BCN)=180 ° - / HCD-45,• sin / HCE=sin(45••• HE=HC sin / HCE=34tg / AEH=A H ^-6HE 3即0 =arctg —6 为所求.3例22 如图,ABCD 是边长为, ABCD GC=2. 求点B 到平面EFG 的距离. 解:连 GB GE GF FE 、FB , _1 o-V B —EFG = — dS A GFE3 _ 1 _ 2V B —EF(=Vs -BEF =— X GCS BEF = — S △ BEF 3 34的正方形,E 、F 分别是AB AD 的中点, 设点B 到面EFG 的距离为d.GC 垂直平面... d=GC SB EF =2J S^EF S.E FG在 Rt △ DHC 中, HC= CD 2 DH 2.10 4旦一面角A - BC- M 的平面角.+ /HCD) =几2/HCD+c,2(DH _ DC) = 32HC 4HCS A BEF=- S △AB F=-( -AF- AB)=2,2 2 2在△ EFG 中,GF=GE= GC2 CF? =2 、. 6 ,EF=2 .2 ,故它的周长之半1P=_(EF+FG+GE)=2. 6 +22•••S A EFG= P(P - EF)(P - EF)(P- GE) P(P-EF)(P-EF)(P-GE)=2 . 11••• d=2 2=U2,11 11即点B到平面EFG的距离是2.. 11例23 如图,在直三棱柱ABC-ABC1 中,/ ACB=90,/ BAC=30 , BC=1,AA=J6 ,M 是CG的中点.求证:AB丄AM证明:由题设知BC丄AC, BC丄CC• BC丄侧面AACC.连C1A,贝U C1A是B1A在面AACG上的射影•设AC 1与A 1M交于点D.在Rt △ A1B1G 中,BQ=1, / B1AC=Z BAC=30,得•电=6 = (2)A1C1:,3在Rt△ A1G M中,△^=二3= _2MC1yf66AA 1 A1C1A C二 1 1,又/ AAG=/ACM=90°,•••△AAC s^ ACM,得/ 3=Z 4由AA1 // CC,得/ 仁/2,•/ CDM M CAA= 90°,•AG 丄AM.由三垂线定理,得AB丄AM.例24如图,圆锥的轴截面为等腰Rt△ SAB Q为底面圆周上一点(1) 若QB的中点为C, OH L SC,求证OH丄平面SBQ⑵如果/ AOQ=60 , QB=2 3,求此圆锥的体积;晁⑶如果二面角A—SB— Q的大小为arctg ,求/ AOQ的大小.3q2 解:⑴连0C.•/ SQ=SB OQ=OB,QC=CB•••Q BL SC, QB 丄OC 得 OBL 面 SOC. •/ OH 面 SOC 得 QB1 OH 又 OHL SC, • OHL 面 SQB. ⑵连AQ.T Q 为底面圆周上的一点, AB 为直径,• AQL QB在 Rt △ AQB 中,/ QBA=30 , QB=2〕3cos30•••△ SAB 是等腰直角三角形.1• SO — AB=2,2 1 o8 • V 圆锥=n • OA • SO — n33⑶过Q 作QM L AB 于M.由于面SAB 丄面ABQ 得QM L 面SAB.作MPL SB 于P,连PQ 则由三垂线定理知 QPL SB. • / MPQ 是二面角 A — SB- Q 的平面角. -■.: 6/ MPQ=arctg 为已知,3设圆锥底半径为r, / AOQ a ,在 Rt △ MPB 中 , / PBM=45 , MB=r(1+cos a ),2• MP= r(1+cos a )2Rsin : _ . 6 sin :3----------------- ,即---231 cos :3r(1 cos :)• AB=2.3=4,故/ AOQ=60 2例25 如图,ABC — ABC 是正三棱柱,D 是AC 中点. (1)证明AB //平面DBC ;⑵假设AB L BC ,求以BC 为棱、以DBC 与CBC 为面的二面角a 的度数. 证明:⑴ 由于ABG — ABC 是正三棱柱,故四边形 BBCC 是矩形 连BQ 交BC 于E ,则B&EC,连DE. 在^ ABC 中,AD=DC 得 DE// AB . 又 AB 二面 DBC , DE 二面 DBC , • AB //平面 DBC.⑵作DF L BC 于F ,贝U DF 丄面BBCC ;连EF ,贝U EF 是ED 在面BBCC 上的射影. •/ AB 丄 BG ,又由(1)知,AB // DE • DEI BC ,从而 BC 丄 EF • ••/ DEF 是二面角a 的平面角.1设 AC=1,贝U DC=_.2•/△ ABC 是正三角形.•••在 Rt △ DCF 中,DF=DC sinC=二,41CF=DC■ cosC=—.4取BC 中点G,因BE=EC 故EG! BC. 在 Rt △ BEF 中, EF 2=BF - GF3 1 又 BF=BC-FC — ,GF=.44• EF=3 - - , 得 EF=—34 2 4即二面角a 为45□ 5例 26 如图,梯形 ABCD 中, AD// BC, / ABC —,AB=a,AD=3a, / ADC=arcsin ,PA 丄面2ABCD,PA=^:(1) 二面角P — CD-A 的大小(用反三角函数表示): (2) 点A 到平面PBC 的距离. 解:⑴作AE 丄直线CD 于 E 连PE.••• tg / DEF=D-EF也4^4=1. / DEF=45由PAL面ABCD据三垂线定理知PEI CD. •••/ PEA是二面角P—CD- A的平面角.在 Rt △ AED 中,AD=3a, / ADE=arcsin5••• AE=A D sin / ADE 旦卫5 PA 在 Rt △ PAE,中 tg / PEA=一AE:丄 PEA=arctg -3⑵作AF U PB 于H 由 PAL 面 ABCD 得 PB 丄 BC. 又AB 丄BC,得BC 丄面PAB 得BC 丄AH • AH!面PBC AH 的长为点 A 到面PBC 的距离 在等腰 Rt △ PAB 中,AH=)a.2•••点A 到平面PBC 的距离是a2例27 如图,已知 Rt △ ABC 的两直角边 AC=2 BC=3, P 为 斜边AB 上一点,现沿 C P 将此直三角形析成直二面角 A — PC- B , AB=. 7,求二面角P — AC-B 的大小.解:由已知 A — CP-B 是直二面角,作 BDL CP 于D,贝U BD 丄平面 ACP 作 DEI AC 于E , 则BE L AC / BED 是二面角 P — AG- B 的平面角•作AF 丄DC 于F ,连BF ,则/ AFB 丄.2设/ ACP a ,则/ BCP —- a ,2在Rt △ AFB 中A B'=AF 2+F B'=A F'+D ^+D F'=7■/ AF=2sin a ,CF=2cos a BD=3sin(90 ° - a )-3cos a CD=3sin(90 ° - a )-3cos a DF=CD-CF=3sin a -2cos a2 2 2• (2sin a ) +(3cos a ) +(3sin a -2cos a ) =7JT 解得a =—.4在 Rt △ BED 中即二面角 P — CD- A 的大小为arctg>5323 DE=CD sin a =3sin a =— 2tg Z BED=BD = . 2 .DE/•Z BED=arctg .一 2即二面角P — AC — B 的大小是arctg 2例28设三棱锥S — ABC 的底面为等腰直角三角形,已知该直角三角形的斜边 10, 三棱锥的侧棱 SA=SB=SC=1,求:(1) 顶点S 到底面的距离;(2) 侧棱SB 与底面所有角的大小(用反三角函数表示); (3) 二面角A — SB-C 的大小(用反三角函数表示); 解:如图(1 )作SO L 底面 ABC 由已知 SA=SB=S (知,O 为底面△ ABC 的外心, 又厶ABC 为直角三角形,故 O 为斜边AC 的中点. ••• SO=、SA 2 -AO 2 = ,132 -52 =12. 即顶点S 到底面的距离是12.⑵Z SOB 是 SB 与底面ABC 所成的角.SO 12 Z COB=arcsin=arcsin -SB13⑶作AD 丄SB 于D,连结CD. •/ SB 丄 AD,SB 丄 AC. • SB 丄平面ADC• CD! SB, Z ADC 是二面角 A — SB-C 的平面角• 易得 AB=BC=5 :2AD =DC 31325 • Z ADC=arccos(- )31325即二面角 A — SB — C 的大小是arccos(-).313例29 如图,在平行六面体 ABC —A1B1GD 中,AB=5. AD=4,AA=3,AB 丄 AD, Z AAB=/ AAD=—.3(1) 求证:顶点 A 在底面ABCD 的射影O 在Z BAD 的平分线上; (2) 求这个平行六面体的体积 V.解:(1)连AO,则AO 丄底面,作 OM L AB 于M , ON 丄AD 于N,连AM , AN , A O ,由三垂 线定理得 AM 丄AB, AN 丄AD又Z AAM Z AAN.AC 长为A• Rt △ ANA^ Rt △ A1MA••• AM=AN,得OM=ON.•••点O在/ BAD的平分线上⑵V=302四、能力训练(一)选择题1.长方体一个顶点上的三条棱的长分别是3, 4, 5,且它的八个顶点都球的表面积是A.20 2 nB.25 2 nC.50 nD.200 n 2. 两球体积和是 A.33. 地球表面北纬 距离与地球表面AA.3 : 24. 已知圆锥内有12 n ,且两球大圆周长的和是B.26n ,则这两个球半径的差是C.1() D.0.5 60°圈上有A 、B 两点,它们的经度差为 180°, A 、B 两点沿纬度圈的B 两点最短距离的比是()B.2 : 3C.3 : 4D.4: 3(球冠部分)之比为18: 5,则圆锥母线间最大夹角为 ()55A.2arccosB.2arcs in66C.2arcsin -6D. n1 -arcs in65.球O 的半径R A B 、C 为球面上三点,A 与B 、A 与C 的球面距离为2球面距离为二R ,则球O 在二面角B-OA-C 内的部分的体积是()31 A.-9B. 1 n R 33D.A n R 3276.三棱锥A-BCD 的高AH=3.3 a ,且H 是底面△ BCD 的垂心,若 AB=AC 二面角 A-B C-D为60°,ABC 的重心,贝U HG 的长为()A. ■. 10 a C. ,6a7.底面半径为R 高为H 的圆锥的内接正方体的棱长为H 2R、2RHB.H R-A /'2RHC. ---------------H 2RD.、2RHH • 3R8. 棱锥P-ABCD.90ABCD 且PB=2PA 那么侧面 ABP 与10. 三棱锥一条棱长为x,其余各条棱长都等于1,则体积F (x )最大时,x 的取值是() C.V2(二)填空题11. 已知球面上A 、B C 三点所在的截面与球心距离是球半径的一半, 则球面面积是 ____________ .12. 已知球的两个平行截面的面积分别为 5 n 和8 n,它们位 于球心的同一侧,且相距为1,则这个球的半径是13. 一个正方体的所有顶点都在球面上,若这个球的体积是 V,则这个正方体的体积是14. 把一个木制的棱长为 1的正方体镟成一个尽可能大的球,则镟去部分的体积是15. 把一个大金属球 表面涂漆,需油漆 2.4kg ,若把这个金属球熔化,制成 6 4个半径相等的小金属球(设损耗为零),将这些小金属球表面涂漆,需用油漆 __________ .16. 在长方体 ABCD-ABQD 中,已知 AB=2, AA=AD=1则截面 ABC 和ABQ 所成的二面 角等于 ________ .17. 棱锥的底面是斜边为 C,锐角为30°的直角三角形,各侧棱与底面都成 45°角,则它的体积是 _________ .18. 如果一个球的外切圆锥的高是这个球半径的 3倍,那么圆锥侧面积和球面积的比为19. _____________________________________________正四棱台ABCD-ABQD ,上底AB=1,下底AB 1=2,侧棱AA 与底面成60。
项目二 简单形体2- 回转体、相贯体

4.能对形体的三视图尺寸标注。
图2-20回转体立体图
项目二 简单形体
学习案例 绘制圆柱被平面切割以后的三视图(图2-21)。
(1)分析 图2-21是一个圆柱体左端开槽 ( 中间被两个正 平面和一个侧平面切割 ), 右端切肩 ( 上、 下 被水平面和侧平面对称地切去两块 ) 而形成。 所产生的截交线为直线和平行于侧面的圆。 (2)作图 作出槽口的侧面投影 ( 两条竖线 ), 再按投影 关系作出槽口的正面投影 2) 作出切肩的侧面投影 ( 两条虚线 ), 再按投 影关系作出切肩的水平投影 图2-21圆柱被平面切割立体图 3) 擦去多余的图线 , 描深。图2-22d 为完整的 切割体的三视图。 作图步骤如图2-22所示。
5.平面与组合回转体相交
当平面与组合回转体相交时,截交线是由截平面与各回转 表面所得交线组成的复合平面曲线。截交线的连接点应在相 邻两回转体的分界圆处。作组合回转体的截交线时,首先要 分析各组成部分曲面的性质,确定各段截交线的形状,再分 别作出其投影。
例
如图所示,求作组合回转体截交线的水平投影。
实实相贯
实虚相贯
虚虚相贯
项目二 简单形体
1、相贯线的性质
表面性 位于两基本体的表面上。 封闭性 一般是封闭的空间曲线(或空间折线) 共有性 相贯线是两立体表面的共有线。
作相贯线实质是找出两基本体表 面的若干共有点的投影。
项目二 简单形体
▲平面体与回转体相贯
实质是:求各棱面与回转面的截交线
项目二 简单形体
3、 圆环表面上点的投影
圆环表面上点的投影作法如图 所示
圆环的三视图
项目二 简单形体
2.2.5 平面与回转体相交
回转体的截交线形状,取决于——回转体表面形状及截平面与 回转体的相对位置。 截交线的性质: 截交线是截平面与回转体表面的共有线。 截交线都是封闭的平面图形。
杨可桢《机械设计基础》(第5版)笔记和课后习题(回转件的平衡)

第8章 回转件的平衡8.1 复习笔记一、回转件平衡的目的机械中有许多构件是绕固定轴线回转的,这类作回转运动的构件称为回转件(或称转子)。
1.不平衡的原因由于回转件的结构不对称、材质不均匀或是制造不准确等因素,使回转件在转动时产生离心力系的不平衡,使离心力系的合力和合力偶矩不等于零。
2.不平衡的危害(1)在运动副中产生附加的动压力,从而增大构件中的内应力和运动副中的摩擦,加剧运动副的磨损,降低机械效率和使用寿命;(2)使机械产生周期性振动,降低工作可靠性和精度、零件材料的疲劳损坏以及令人厌倦的噪声。
3.回转件平衡的目的调整回转件的质量分布,使转子工作时的离心力达到平衡,以消除附加动压力,尽可能减轻有害振动,改善机构工作性能。
二、回转件的平衡计算根据组成回转件各质量的不同分布,可分两种情况。
1.质量分布在同一回转面内轴向尺寸很小的回转件(B/D <0.2),将其质量看作是分布在同一平面内,如风扇叶轮、飞轮、砂轮等。
对于这类转子,利用在刚性转子上重心的另一侧加上一定的质量,或在重心同侧去掉一些质量,使质心位置落在回转轴线上,从而使离心惯性力达到平衡,即平衡条件为:b 0=+∑=i F F F式中,F 、b F 、i F ∑分别表示总离心力、平衡质量的离心力、原有质量的离心力。
写成质径积的形式为:b b 0=+∑=i i me m r m r特点:若重心不在回转轴线上,则在静止状态下,无论其重心初始在何位置,最终都会落在轴线的铅垂线的下方,这种不平衡现象在静止状态下就能表现出来,故称为静平衡。
静平衡的条件:分布于回转件上各个质量的质径积的向量和为零,即:b b 0+∑=i i m r m r2.质量分布不在同一回转面内 对于轴向尺寸较大(B/D ≥0.2)的回转件,如内燃机中的曲轴和凸轮轴、电机转子、机床主轴等,其质量的分布不能再近似地认为是位于同一回转面内,而应看作分布在垂直于轴线的许多互相平行的回转平面内,离心惯性力将形成一个不汇交空间力系,因此必须使各质量产生的离心力的合力和合力偶都等于零,才能达到平衡,即平衡条件为:0F ∑= 0M ∑=平衡方法:对于动不平衡的转子,无论其具有多少个偏心质量以及分布在多少个回转平面内,只要将各不平衡质量产生的惯性力分别分解到两个选定的平衡基面内,则动平衡即转化为在两平衡基面内的静平衡计算问题。
回转体与回转体相交

回转体与回转体相交相贯线的概述表面取点法辅助平面法相贯线的特殊情况相贯线的概述1.相贯线的概念两立体表面的交线称为相贯线。
相贯线相贯线不仅出现在两立体外表面,有时还见到两立体内表面,以及立体被穿孔的情况相贯线相贯线的概述2.影响相贯线形状的因素相交的两立体的形状。
相交的两立体的相对尺寸大小。
相交的两立体的相对位置。
相贯线的概述2.影响相贯线形状的因素相交的两立体的形状。
相交的两立体的相对尺寸大小。
相交的两立体的相对位置。
相贯线的概述3.求相贯线的方法相贯线是两立体表面的共有线。
相贯线是两立体表面的分界线。
工程中常见的曲面立体是回转体,常用的求两回转体表面相贯线的方法有:表面取点法辅助平面法表面取点法1.什么是表面取点法当相交的两回转体中有一个是圆柱且轴线垂直于投影面时,圆柱面在该投影面上的投影积聚为圆,因此,相贯线在该投影面上的投影就积聚在圆柱面有积聚性的投影(圆)上。
这时,可以将相贯线看成是另一回转面上的曲线,利用回转面上取点的方法作出相贯线的其它投影。
表面取点法注意:表面取点法只适用于相交两回转体中至少有一个是圆柱,并且其轴线与投影面垂直的情况下。
表面取点法2.作图举例已知两圆柱轴线垂直相交,求它们的相贯线投影。
表面取点法3.两圆柱轴线垂直相交情况分析工程上经常见到两圆柱轴线垂直相交的情况,它们的相贯线一般有三种情况。
辅助平面法1.什么是辅助平面法假想的用一个平面截切相贯的两回转体,分别求出该平面与两回转体的截交线,则两组截交线的交点,即为相贯线上的点。
这种求作相贯线的方法,称为辅助平面法。
辅助平面法假想的用一个平面截切相贯的两回转体,分别求出该平面与两回转体的截交线,则两组截交线的交点,即为相贯线上的点。
这种求作相贯线的方法,称为辅助平面法。
1.什么是辅助平面法辅助平面法2.作图举例作圆柱与圆锥的相贯线。
分析:由于圆柱面侧面投影积聚为圆,因而相贯线的侧面投影重合在此圆上,水平和正面投映待求。
第八章 零件图的识读与绘制

零件图的识读与绘制
本章教学目标:
1.了解零件图的作用与内容; 2.掌握典型零件的表达方案和尺寸标注方法; 3.了解常见工艺结构; 4.掌握零件图上常见技术要求的含义及标注方法; 5.能看懂中等难度的零件图、画简单零件图。
本章重点难点:
重点: 零件图的识读。
难点: 零件图的视图选择及尺寸标注。
内
4
(b) 不 合 理
15
20
15
35
31 35
加工顺序:
(1)车4×φ15退刀槽 (2)车φ20外圆及倒角
20
不容易测量
容易测量
不容易测量
容易测量
A L
B A L
B B L
C B
C L
五、毛面与加工面的尺寸标注
对铸、锻件,同一个方向的加工面和非加 工面应各选一个基准分别标注有关尺寸,且两 基准之间只允许有一个联系尺寸。 A:加工面 B、C、D:非加工面
C
8 34 48
C D
B A
8
A
合理 不合理
8
34 42 48
D
B
例:如图所示标注传动轴的尺寸。
轴承 挡套 32 +0.05 0 齿轮 弹簧挡圈 轴承
按 设 计 主要基准 基 准 (设计基准) 标 (工艺基准) 注 的 辅助基准 尺 寸 (工艺基准)
2 1 2 1 30 主要基准 (设计基准) 106 2 1 1.3 1 0 32 -0.05 67 17 30
设计基准
例:
零件图
设计基准
22 15 10
F
18 26 52 70
F
18 26 52 70
工艺基准
二、主要尺寸应直接注出
回转面及回转体多面正投影

导点、导线、导面: 控制母线运动而本身 不动的点、线、面
回转面:由母线旋转而形成的曲面,如圆柱 曲面
非回转面:如双曲抛物面等
按是否由 母线绕轴 旋转而成
直纹面:由直线作为母线旋转而形成的曲面 回转面
(又称直线面) ,如柱面、锥面等
曲线面:由曲线作为母线旋转而形成的曲面, 如球面、圆环面等 母线类型
圆柱投影特性
最后素线 最右素线
最左素线 最右素线 最前素线 最后素线 最左素线 最前素线
圆柱轴线垂直于H面,上下 端面的H面投影反映实形,V面和 W面的投影积聚为直线。圆柱面 的H投影积聚为圆周,V面和W面 投影为矩形。
注意圆柱面上最左、最右、 最前、最后素线在V面和W面投 影中的位置。 后半圆柱面的V面投影不可见; 右半圆柱面的W面投影不可见。
f" d"
c
e f
圆柱面上取点,可利用H面投影的积聚性来求其余投 影。注意后半圆柱面的V面投影不可见;右半圆柱面的W 面投影不可见。
A
O1
A1
a0′
′ c0′ b0′ (d0)
) d0″ a0″(c0″
b0″
d(d0) a(a0) b(b0) c(c0)
在图示位置时,圆柱轴线 3 )布图 由“长对正” ( 画出反映立体 4 利用“宽相等” 1 : 选回转轴 (2 2 BB 、DDO为 1) ) AA 轮廓线素线的 O 为铅垂线,圆柱的顶面和底 O、CCO 开始画三视图! 和立体的高度画出主 对W面的转向轮廓线, 主要形状特征的俯视 和 "高平齐”画出左 和底面棱线为画图参 对V面的转向轮廓线, 投影分析与曲面的可 面是水平面,水平投影为反 它左边的点可见。 视图。 它前边的点可见。 图。 视图(二求三)。 考基准。 见性的判断 映实形的圆。圆柱面的俯视 图积聚成一个圆;在另两个 视图上分别以两个方向的转 向轮廓线的投影表示。
2-4基本(常见)回转体的轴测图
1-6 常见回转体的轴测图一、常见回转体的正等轴测图1.平行于坐标面的圆的投影特性和画法2.圆柱、圆锥、圆台、圆球的正等轴测图3.半圆柱的正等轴测图二、圆柱的斜二轴测图侧平面椭圆正平面椭圆水平面椭圆(1)圆的正等轴测图投影特性(2)圆的斜二轴测图投影特性1.平行于坐标面的圆的投影特性和画法(2)画法(3)分别在两根轴上圆心两侧量取半径标记4个点画图步骤:(1)确定圆心(2)过圆心绘制两根轴测轴(4)过4个点连成椭圆注意事项:四心扁圆法菱形法(1)轴测轴角度准确(2)轴测轴上4个点标记准确(3)利用圆的轴测图投影特性校正绘图ɸ302.常见回转体的正等轴测图(2)圆台(Φ30,Φ20,35)Z(1)圆柱(Φ30,20)Z(3)圆(Φ30,32)Z(4)圆球(Φ30)正平侧平水平分析:3.圆柱的斜二轴测图正平圆的斜二轴测图水平圆的斜二轴测图侧平圆的斜二轴测图(1)轴线Y方向的圆柱(3)过圆心绘制端面圆画图步骤:(1)确定圆心(2)过圆心绘制轴测轴(4)在Y轴上量取高度的一半确定另一端面的圆心(5)绘制另一个端面圆(6)作两个圆的公切线(7)轮廓线加粗(3)轴线X方向的圆柱(2)轴线Z方向的圆柱根据长短轴画椭圆1.06d0.33d沿Z轴方向画轮廓线椭圆顺时针旋转7º10’画椭圆中心线沿X轴方向画轮廓线轴线逆时针旋转7º10’根据长短轴画椭圆小结:1.平行于坐标面的3种圆的正等轴测图和斜二轴测图的投影特性侧平椭圆正平椭圆水平椭圆3.绘制圆柱、圆锥、圆台、圆球的正等轴测图4.绘制轴线为Y方向的圆柱的斜二轴测图作业注意事项:(1)轴测轴角度准确(2)严格按尺寸画图(3)图线粗细分明,轴测轴用细实线绘制,轴测图可见轮廓线要加粗,不可见轮廓不必画出。
2.平行于坐标面的3种圆的正等轴测图的画法现代工程制图(上)。
08第二章回转体
圆柱
圆锥
圆球
圆环
2013年7月5日星期五
上一页
下一页
青海油田培训中心培训二部
§2-5 回转体
二、常见回转体
1. 圆锥体
(1) 圆锥体的形成
2013年7月5日星期五
上一页
下一页
青海油田培训中心培训二部
§2-5 回转体
二、常见回转体
1. 圆锥体
(2) 圆锥体的投影分析
2013年7月5日星期五
上一页
下一页
上一页
下一页
青海油田培训中心培训二部
§2-5 回转体
二、常见回转体
4. 圆环
(3) 圆弧回转体
一段圆弧绕与它在同一平面内但不通过圆心 的轴线回转一周而形成的曲面称为圆弧回转面。 圆弧回转面是圆环内环面的一部分。
圆弧回转体由圆弧回转面和上、下底面围成。
2013年7月5日星期五
上一页
下一页
青海油田培训中心培训二部
2013年7月5日星期五
上一页
下一页
二、常见回转体
3. 圆球
(1) 圆球的形成
球是由球面围成的。 球面可以看成由半圆绕其直径回转一周而成。
2013年7月5日星期五
上一页
下一页
青海油田培训中心培训二部
§2-5 回转体
二、常见回转体
3. 圆球
(2) 圆球的投影分析
2013年7月5日星期五
上一页
下一页
青海油田培训中心培训二部
§2-5 回转体
青海油田培训中心培训二部
§2-5 回转体
二、常见回转体
1. 圆锥体
(3) 圆锥面上取点
2013年7月5日星期五
上一页
画法几何与工程制图_8基本立体_83同轴回转体和拉伸体_
画法几何与工程制图A
王彦峰
高丽华、张贤、乔忠云、芦新春、孙启新
淮海工学院
第8章 基本立体
8.3 同轴回转体和拉伸体
拉伸体的形成
拉伸体的投影
8.3同轴回转体和拉伸体
拉伸体的形成
8.3同轴回转体和拉伸体
拉伸体的投影
作图步骤: 画出动平面的投影 画出棱线 判别可见性、连线
初终始止位置
淮海工学院
参照立体图,画出水 平投影和侧面投影。
淮海工学院
Байду номын сангаас
王彦峰
谢谢观看
高丽华、张贤、乔忠云、芦新春、孙启新
王彦峰
谢谢观看
高丽华、张贤、乔忠云、芦新春、孙启新
淮海工学院
画法几何与工程制图A
王彦峰
高丽华、张贤、乔忠云、芦新春、孙启新
淮海工学院
第8章 基本立体
8.3同轴回转体和拉伸体
一、同轴回转体的形成 二、同轴回转体的投影 例13 例14 三、同轴回转体上的点
8.3同轴回转体和拉伸体
同轴回转体的形成
表 7-2 同轴回转体的形成
以动平面的一条边为回转轴
回转轴与动平面相离
8.3同轴回转体和拉伸体
同轴回转体的投影
两个投影图形相同,另外一 个投影为若干个同心圆。
排气阀门
8.3同轴回转体和拉伸体
同轴回转体表面上的点
本章结束
8.3同轴回转体和拉伸体
画全正面投影,并画出水平投影。
8.3同轴回转体和拉伸体
5.1回转体及平面立体其表面上的点和线1
2. 圆锥体
2. 圆锥体
s'
对正面转向轮廓线的投影
s''
S
D a'
c' (d') b' d s d'' a''(b'') c''
对侧面转向轮廓线的投影
B C
A
a
c
b
圆锥体的尺寸
40
圆锥体的尺寸
圆锥底圆的直径 圆锥的高度
60
注意:
尺寸应集中标注在非圆视图上。 不要漏写直径尺寸的符号“ ” 。
(2)
(2)
k
1
(m) 1
★(纬圆法)辅助圆法
7. 圆弧回转体表面取点、线
a' b' a'' (b'')
A
B
分析
a b
空间分析 投影分析
作图——利用纬圆法作图
小结:
回转体的投影特点:
在与轴线垂直的投影面上,其投影是 圆或同心圆。 在与轴线平行的投影面上,其投影反 映母线形状特征,且为对称于轴线的 图形。
形体特征
圆柱体由圆柱面和上、下底面围成 圆柱面的素线与轴线平行
a`
A
a``
a1` a1``
A1
a(a1)
投影特性
在与圆柱轴线垂直的投影面内,圆柱面的投影具 有积聚性,其投影是一个圆。 其余两投影是大小相同的矩形。
回转体三视图及其投影特性
1. 圆柱体
回转体三视图及其投影特性
1. 圆柱体
1. 圆反映了上、下底面的实形 2. 圆的圆周为圆柱面的积聚投影
