大学物理-稳恒磁场习题思考题及答案
大学物理-磁学习题课和答案解析
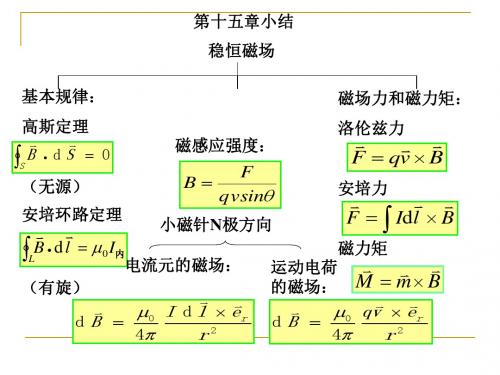
2. 均匀磁场的磁感应强度 B 垂直于半径为r的圆面.今
4. 如图,在面电流线密度为 j 的均匀载流无限大平板附近, 有一载流为 I 半径为 R的半圆形刚性线圈,其线圈平面与载流 大平板垂直.线圈所受磁力矩为 ,受力 0 0 为 .
μ
5、(本题3分) 长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体 中有等值反向均匀电流I通过,其间充满磁导率为μ的均匀磁介 质.介质中离中心轴距离为r的某点处的磁场强度的大小H I =________________ ,磁感强度的大小B =__________ . I 2 r 2 r
B (A) B (B) √ R B x (D) O 圆筒 电流 O x
B
0 I (r R) 2r
(r R)
O B
R
x O (C) x O
B
(E)
B0
O
R
R
x
R
x
2、(本题3分)一匀强磁场,其磁感强度方向垂直于纸面(指 向如图),两带电粒子在该磁场中的运动轨迹如图所示,则 (A) 两粒子的电荷必然同号. (B) 粒子的电荷可以同号也可以异号. (C) 两粒子的动量大小必然不同. (D) 两粒子的运动周期必然不同.
(C) B dl B dl , BP BP 1 2
(D) B dl B dl , BP1 BP2
L1 L2
L1
L2
L1
L2
[ ]
5.有一矩形线圈 AOCD ,通以如图示方向的电流 I,将它置 于均匀磁场 B 中,B 的方向与X轴正方向一致,线圈平面与X 轴之间的夹角为 , 90 .若AO边在OY轴上,且线圈可 绕OY轴自由转动,则线圈 (A)作使 角减小的转动. (B)作使 角增大的转动. (C)不会发生转动. (D)如何转动尚不能判定.
大学物理习题稳恒磁场

稳恒磁场一、选择题1. 一圆电流在其环绕的平面内各点的磁感应强度B 【 】 (A) 方向相同, 大小相等; (B) 方向不同,大小不等; (C) 方向相同, 大小不等; (D) 方向不同,大小相等。
2. 电流由长直导线流入一电阻均匀分布的金属矩形框架,再从长直导线流出,设图中321O ,O ,O 处的磁感应强度为B B B 123,,,则 【 】(A)B B B 123==; (B) 0B 0B B 321≠== ;(C) 0B ,0B ,0B 321=≠= ; (D) 0B ,0B ,0B 321≠≠=3. 所讨论的空间处在稳恒磁场中,对于安培环路定律的理解,正确的是 【 】(A) 若⎰=⋅L0l d B ,则必定L 上B 处处为零(B) 若⎰=⋅L0l d B, 则必定L 不包围电流(C) 若⎰=⋅L0l d B, 则L 所包围电流的代数和为零(D) 回路L 上各点的B 仅与所包围的电流有关。
4. 在匀强磁场中,有两个平面线圈,其面积21A 2A =, 通有电流21I 2I =, 它们所受的最大磁力矩之比M M 12/等于 【 】 (A) 1 (B) 2(C) 4(D) 1/45. 由N 匝细导线绕成的平面正三角形线圈,边长为a , 通有电流I , 置于均匀外磁场B中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩M m 值为: 【 】(2)选择题(A) 2/IB Na 32,(B)4/IB Na 32, (C) 60sin IB Na 32,(D) 06. 一带电粒子以速度v 垂直射入匀强磁场 B 中,它的运动轨迹是半径为R 的圆, 若要半径变为2R ,磁场B 应变为: 【 】 B 22)D (B 21)C (B 2)B (B 2)A ( 7. 图中所示是从云室中拍摄的正电子和负电子的轨迹照片,均匀磁场垂直纸面向里,由两条轨迹可以判断【 】(A) a 是正电子,动能大; (B) a 是正电子, 动能小; (C) a 是负电子,动能大; (D) a 是负电子,动能小。
4大学物理习题_稳恒磁场

稳恒磁场一、选择题1.一个半径为r 的半球面如右图放在均匀磁场中,通过半球面的磁通量为 (A )22r B π; (B )2r B π;(C )22cos r B πα; (D )2cos r B πα。
2.下列说法正确的是:(A )闭合回路上各点磁感应强度都为零时,回路内一定没有电流穿过; (B )闭合回路上各点磁感应强度都为零时,回路内穿过电流的代数和必为零; (C )磁感应强度沿闭合回路的积分为零时,回路上各点的磁感应强度必为零;(D )磁感应强度沿闭合回路的积分不为零时,回路上任意一点的磁感应强度都不可能为零。
3.如图,在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理可知(A )0=⋅⎰Ll d B,且环路上任意一点0=B 。
(B )0=⋅⎰Ll d B,且环路上任意一点0≠B 。
(C )0≠⋅⎰Ll d B ,且环路上任意一点0≠B 。
(D )0≠⋅⎰Ll d B,且环路上任意一点=B 常量。
4.图中有两根“无限长” 载流均为I 的直导线,有一回路L ,则正确的是(A )0=⋅⎰Ll d B,且环路上任意一点0=B ;(B )0=⋅⎰Ll d B,且环路上任意一点0≠B ;(C )0≠⋅⎰Ll d B,且环路上任意一点0≠B ;(D )0≠⋅⎰Ll d B,且环路上任意一点0=B 。
5.取一闭合积分回路L ,使三根载流导线穿过它所围成的面,现改变三根导线之间的相互间隔,但不越出积分回路,则:·LOI图(A )回路L 内的I ∑不变,L 上各点的B不变;(B )回路L 内的I ∑不变,L 上各点的B改变;(C )回路L 内的I ∑改变,L 上各点的B不变; (D )回路L 内的I ∑改变,L 上各点的B改变。
6.在球面上竖直和水平的两个载流圆线圈中,通有相等的电流I ,方向如图所示,则圆心处磁感应强度B的大小为(A )R I 0μ(B )R I20μ (C )RI 220μ(D )R I40μ7.一长直载流I 的导线,中部折成图示一个半径为R 的圆,则圆心的磁感应强度大小为 (A )R I 20μ;(B )RIπ20μ; (C )RIRIπ2200μμ+;(D )0。
第7章 稳恒磁场习题解答

40 第7章 稳恒磁场7-1 如图,一个处在真空中的弓形平面载流线圈acba ,acb 为半径cm 2=R 的圆弧,ab 为圆弧对应的弦,圆心角090aob ∠=, A 40=I ,试求圆心O 点的磁感应强度的大小和方向。
解 由例7-1 线段ba 的磁感应强度 o o 40140(cos45-cos135) =410T4π0.02cos45B μ-=⨯⨯︒方向垂直纸面向外。
由例7-2 圆弧 acb的磁感应强度 4002π1402 3.1410T 2π2420.02I μB R μ-==⨯=⨯方向垂直纸面向内。
4120.8610TB B B -=-=⨯方向垂直纸面向外。
7-2 将载流长直导线弯成如图所示的形状,求圆心O 点处磁感应强度。
解 如图,将导线分成1(左侧导线)、2(半圆导线)、3(右侧导线)三部分,设各部分在O 点处产生的磁感应强度分别为1B 、2B 、3B。
根据叠加原理可知,O 点处磁感应强度321B B B B ++=。
01=B024I B Rμ=,方向垂直于纸面向里034πI B Rμ=,方向垂直于纸面向里O 点处磁感应强度大小为0O 23(1π)4πIB B B Rμ=+=+ ,方向垂直于纸面向里。
7-3 一圆形载流导线圆心处的磁感应强度为1B ,若保持导线中的电流强度不变,而将导线变成正方形,此时回路中心处的磁感应强度为2B ,试求21:B B解 设导线长度为l ,为圆环时, 2πl R = 001π2I I B R l μμ==为正方形时,边长为4l,由例7-100024(cos 45cos135)4π8IBlμ=⨯-=⨯习题7-1图41212 :πB B =7-4 如图所示,一宽为a 的薄长金属板,均匀地分布电流I ,试求在薄板所在平面、距板的一边为a 的点P 处的磁感应强度。
解 取解用图示电流元,其宽度为d r ,距板下边缘距离为r ,其在P 点处激发的磁感应强度大小为00d d d 2π22π(2)II r B (a r)a r aμμ==--,方向垂直于纸面向外。
大连理工大学大学物理作业10(稳恒磁场四)及答案详解

作业 10 稳恒磁场四1.载流长直螺线管内充满相对磁导率为r μ的均匀抗磁质,则螺线管内中部的磁感应强度B 和磁场强度H 的关系是[ ]。
A. 0B H μ>B. r B H μ=C. 0B H μ=D. 0B H μ< 答案:【D 】解:对于非铁磁质,电磁感应强度与磁场强度成正比关系H B r μμ0=抗磁质:1≤r μ,所以,0B H μ<2.在稳恒磁场中,关于磁场强度H →的下列几种说法中正确的是[ ]。
A. H →仅与传导电流有关。
B.若闭合曲线内没有包围传导电流,则曲线上各点的H →必为零。
C.若闭合曲线上各点H →均为零,则该曲线所包围传导电流的代数和为零。
D.以闭合曲线L 为边界的任意曲面的H →通量相等。
答案:【C 】解:安培环路定理∑⎰=⋅0I l d H L ρρ,是说:磁场强度H ρ的闭合回路的线积分只与传导电流有关,并不是说:磁场强度H ρ本身只与传导电流有关。
A 错。
闭合曲线内没有包围传导电流,只能得到:磁场强度H ρ的闭合回路的线积分为零。
并不能说:磁场强度H ρ本身在曲线上各点必为零。
B 错。
高斯定理0=⋅⎰⎰SS d B ρρ,是说:穿过闭合曲面,场感应强度B ρ的通量为零,或者说,.以闭合曲线L 为边界的任意曲面的B ρ通量相等。
对于磁场强度H ρ,没有这样的高斯定理。
不能说,穿过闭合曲面,场感应强度H ρ的通量为零。
D 错。
安培环路定理∑⎰=⋅0I l d H L ρρ,是说:磁场强度H ρ的闭合回路的线积分等于闭合回路包围的电流的代数和。
C 正确。
3.图11-1种三条曲线分别为顺磁质、抗磁质和铁磁质的B H -曲线,则Oa 表示 ;Ob 表示 ;Oc 表示 。
答案:铁磁质;顺磁质; 抗磁质。
图中Ob (或4.某铁磁质的磁滞回线如图11-2 所示,则'Ob )表示 ;Oc (或'Oc )表示 。
答案:剩磁;矫顽力。
5.螺线环中心周长10l cm =,环上线圈匝数300N =,线圈中通有电流100I mA =。
大学物理A2稳恒磁场习题解答PPT课件
7、D
B
0 Ir , 2R 2 0I ,r 2r
rR R
8、B
3
2
1
45 6
6
9、C 10、C 11、B
12、D
Rm ,T2m ,m 4,Q 2
qB qB m H Q H
R m P
eB eB
Sin D eBD
RP
R BO•
-e
D
MP mB0
7
13、C
123 F3
F1
F2
1A 2A 3A
L3、L4在O点产生的磁感应强度的大小相 等,方向相反,总值为0。即
B3B4 0
ቤተ መጻሕፍቲ ባይዱ19
O点的磁感应强度:
B0
B1B2 B3 B4
0I 4R
方向垂直图面向外。
20
3、带电粒子在均匀磁场中由静止开始下降,磁场方 向与与重力方向( X轴方向)垂直,求粒子下落 距离为 X 时的速率 V, 并叙述求解方法的理论依据。
16
2、用两根彼此平行的半无限长的直导线 L、1 L 2
把半径为 R的均匀导体圆环连到电源上,如图所
示,已知直导线上的电流为 I,求圆环中心 O
点的磁感应强度。
O
a
L1
R
b
L2
17
解:L1在O点产生的磁感应强度: 由于L1与O点在一条直线,由毕奥—萨伐定律可求出
B1=0
L2在O点产生的磁感应强度: L2为半无限长直电流,它在O处产生的场是无限长直 电流的一半,由安培环路定律和叠加原理有
0
I1
3
4、D I
a1 O1
I
O2
a2
B12a01I;B222a20I(见2题)
大学物理稳恒磁场习题及答案之欧阳治创编

衡水学院理工科专业《大学物理B 》稳恒磁场习题解答时间2021.03.10创作:欧阳治一、填空题(每空1分)1、电流密度矢量的定义式为:dIj n dS ⊥=,单位是:安培每平方米(A/m2)。
2、真空中有一载有稳恒电流I 的细线圈,则通过包围该线圈的封闭曲面S 的磁通量=0 .若通过S 面上某面元d S 的元磁通为d,而线圈中的电流增加为2I 时,通过同一面元的元磁通为d ',则d∶d'=1:2 。
3、一弯曲的载流导线在同一平面内,形状如图1(O 点是半径为R1和R2的两个半圆弧的共同圆心,电流自无穷远来到无穷远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=。
4、一磁场的磁感强度为k c j b i a B++= (SI),则通过一半径为R ,开口向z 轴正方向的半球壳表面的磁通量的大小为πR2cWb。
5、如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情况下,等于:对环路a :d B l ⋅⎰=____μ0I__; 对环路b :d B l ⎰=___0____; 对环路c :d B l ⋅⎰=__2μ0I__。
6、两个带电粒子,以相同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,运动轨迹半径之比是_____1∶2_____。
二、单项选择题(每小题2分)( B )1、均匀磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为O I R 1 R 2图1 b ⊗⊙ c I I c a图2A. 2r2BB.r2BC. 0D.无法确定的量( C )2、有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中心产生的磁感强度的大小之比B1 / B2为A. 0.90B. 1.00C. 1.11D.1.22(D )3、如图3所示,电流从a 点分两路通过对称的圆环形分路,汇合于b 点.若ca 、bd 都沿环的径向,则在环形分路的环心处的磁感强度 A. 方向垂直环形分路所在平面且指向纸内B. 方向垂直环形分路所在平面且指向纸外C .方向在环形分路所在平面内,且指向aD .为零( D )4、在真空中有一根半径为R 的半圆形细导线,流过的电流为I ,则圆心处的磁感强度为A.R 140πμ B. R 120πμ C .0D .R140μ ( C )5、如图4,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B1;此正方形同样以角速度绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感强度的大小为B2,则B1与B2间的关系为A. B1= B2B. B1= 2B2C .B1=21B2D .B1= B2 /4 (B )6、有一半径为R 的单匝圆线圈,通以电流I ,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中心的磁感强度和线圈的磁矩分别是原来的(A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4.(D) 2倍和1/2.三、判断题(每小题1分,请在括号里打上√或×)c Id b a 图3A CqqqqO图4( × )1、电源的电动势是将负电荷从电源的负极通过电源内部移到电源正极时,非静电力作的功。
大学物理稳恒磁场理论及习题解读

250 0 方向垂直A面
B
BC
0 N C I C
2 RC
0 20 5
2 0.10
O BA
5000 方向垂直C面
B
2 BA
2 BC
7.02 10 T 方向 : tan
4
1
BC 63.4 BA
NIZQ
第14页
大学物理学
恒定磁场
NIZQ
问题: 磁现象产生的原因是什么?
第 2页
大学物理学
恒定磁场
• 电流的磁效应 1820年奥斯特实验表明: 电流对磁极有 力的作用. 1820年 9月 11日在法国科学院演示的奥 斯特的实验 ,引起了安培的兴趣 .一周之后 安培发现了电流间也存在着相互作用力.
此后安培又提出了著名的安 培定律 : 磁体附近的载流导线 会受到力的作用而发生运动.
NIZQ
第 3页
大学物理学
恒定磁场
结论: 磁现象与电荷的运动有着密切的关系 . 运动电荷既能产 生磁效应,也受到磁力的作用. 安培把磁性归结为电流之间的相互作用 . 1822年安培提 出了分子电流假说:
• 一切磁现象起源于电荷的运动.
• 磁性物质的分子中存在分子电流, 每个分子电流相当于一基元磁体。
写成矢量表示:
0 Idl sin
2 4π r 0 Idl r dB 4π r 3
真空中的磁导率: 0= 410-7亨利· 米-1 (H· m-1)
NIZQ
第 8页
大学物理学
恒定磁场
• 毕奥—萨伐尔定律的应用 恒定磁场的计算: 1.选取电流元或某些典型电流分布为积分元. 2.由毕-萨定律写出积分元的磁场dB .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题14-1. 如图所示的弓形线框中通有电流I ,求圆心O 处的磁感应强度B . 解:圆弧在O 点的磁感应强度 R6IR 4I B 001μπθμ==方向垂直纸面向外直导线在O 点的磁感应强度 R 2I 3)]60sin(60[sin 60cos R 4I B 000002πμπμ=--=方向垂直纸面向里 总场强 )313(R 2I B 0-=πμ 方向垂直纸面向里14-2. 两根长直导线沿半径方向引到铁环上A 、B 两点,并与很远处的电源相连,如图所示.求环中心O 点的磁感应强度B .解:设两段圆弧电流对O 的磁感应强度大小分别为1B 、 2B ,导线长度分别为1L 和2L ,横截面积为S ,电阻 率为ρ,电流1I 和2I 的关系12121221L L SL S L R R I I ===ρρ即 2211L I L I = r L I 4r dl 4I B 110L 21011⋅==⎰πμπμ r L I 4r dl 4I B 220L 22022⋅==⎰πμπμ由于两段圆弧电流对O 的磁感应强度方向相反,所以 0B =14-3. 无限长细导线弯成如图所示的形状,其中c 部分是在xoy 平面内半径为R 的半圆,试求通以电流I 时o 点的磁感应强度。
解: a 段 R4IB 01πμ=b 段 0B 2=c 段 R4IB 03μ=O 点的总场强 0044I IB R Rμμπ=-j +k 方向如图 14-4. 无限长直圆柱形导体内有一无限长直圆柱形空腔(如图所示),空腔与导体的两轴线平行,间距为a ,若导体内的电流密度均匀为j ,j 的方向平行于轴线。
求腔内任意点的磁感应强度B 。
解:采用补偿法,以导体的轴线为圆心,过空腔中任一点作闭合回路20r j d πμ=∙⎰L B 1 2rj B 01μ= 同理还是过这一点以空腔导体的轴线为圆心作闭合回路20)r a (j d -=∙⎰πμL B 2 2)r a (j B 02-=μ 1201B B B μ=+=⨯j a 14-5.在半径cm 1=R 的无限长半圆柱形金属片中,有电流A 5=I 自下而上通过,如图所示。
试求圆柱轴线上一点P 处的磁感应强度的大小。
解:将半圆柱形无限长载流薄板细分成宽为θRd dl =的长直电流 πθπd R dl dI ==在P 点处的磁感应强度 R2Id R 2dI dB 200πθμπμ==θθπμθd sin R2Isin dB dB 20x ==005220sin 6.3710T x x I IB dB d πμμθθππ-====⨯⎰⎰14-6. 如图所示的空心柱形导体,柱的半径分别为a 和b ,导体内载有电流I ,设电流I 均匀分布在导体横截面上。
证明导体内部各点(a <r <b )的磁感应强度B 由下式给出:r a r a b IB 22220)(2--=πμ 试以0=a 的极限情形来检验这个公式, b r ≥时又如何?解:可根据安培环路定理 )()(2222a r a b II -⨯-='ππr a r a b IB 22220)(2-⋅-=πμ 0=a 202b IrB πμ=实心圆柱载流导线内部的磁感应强度 b r ≥ rIB πμ20=相当于带电直导线 14-7. 一橡皮传输带以速度v 匀速向右运动,如图所示,橡皮带上均匀带有电荷,电荷面密度为σ。
(1)求像皮带中部上方靠近表面一点处的磁感应强度B 的大小;(2)证明对非相对论情形,运动电荷的速度v 及它所产生的磁场B 和电场E 之间满足下述关系:E v B ⨯=21c (式中001με=c ) 解:(1)垂直于电荷运动方向作一个闭合回路abcda ,根据安培环路定理有i L d d d d d 0μ=∙+∙+∙+∙=∙⎰⎰⎰⎰⎰dacdbcababcdL B L B L B L B L B其中 v i σ= 20vB σμ=(2)匀速运动的点电荷产生的磁场和电场分别为232222220)s i n 1(4s i n )1(c v r c v qv B θπθμ--= 323222220)s i n 1(14rc v c v q r E ⋅--⋅=θπε θθπεμεθsin 1)sin 1(14sin 12232222200022⋅⋅--⋅==⨯r c v c v q v c vE c E v B cv r c v qv =--=232222220)sin 1(4sin )1(θπθμ 所以 E v B ⨯=21c14-8. 一均匀带电长直圆柱体,电荷体密度为ρ,半径为R 。
若圆柱绕其轴线匀速旋转,角速度为ω,求:(1)圆柱体内距轴线r 处的磁感应强度的大小; (2)两端面中心的磁感应强度的大小。
解:(1)过r 点作一个闭合回路,此回路的电流)(2122r R l dr r l I Rr-==⎰ωρωρ根据安培环路定理I d 0μ=∙⎰L B)(2220r R B -=ωρμ(2)带电长直圆柱体旋转相当于螺线管,端面的磁感应强度是中间磁感应强度的一半,所以端面的磁感应强度 204R B μωρ=14-9. 如图所示,两无限长平行放置的柱形导体内通过等值、反向电流I ,电流在两个阴影所示的横截面的面积皆为S ,两圆柱轴线间的距离d O O =21.试求两导体中部真空部分的磁感应强度.解:利用补偿法,在真空部分任取一点,真空部分在那一点产生的磁感应强度为0B ,其中一个阴影在那一点产生的磁场为1B ,另一个为2B02012B rπr πS I μB -=)()(2)(0202B r d πr d πS IμB ----=SIdμB B B 2021=+= 14-10. 无限长直线电流1I 与直线电流2I 共面,几何位置如图所示.试求直线电流2I 受到电流1I 磁场的作用力.解:在直线电流2I 上任意取一个小电流元dl I 2,此电流元到长直线 的距离为x ,无限长直线电流1I 在小电流元处产生的磁感应强度 xI B πμ210=21021060cos 22dxx I I dl x I I dF ⋅==πμπμ ab I I dxx I I F ba ln 60cos 22100210πμπμ=⋅=⎰14-11. 在电视显象管的电子束中,电子能量为eV 12000,这个显像管的取向使电子沿水平方向由南向北运动。
该处地球磁场的垂直分量向下,大小为55.510T B -=⨯,问:(1)电子束将偏向什么方向?(2)电子的加速度是多少?(3)电子束在显象管内在南北方向上通过cm 20时将偏转多远?解:(1)根据B v f ⨯=q 可判断出电子束将偏向东 (2)221mv E =m E v 2=ma qvB f ==1141028.62-⋅⨯===s m m EmqB m qvB a(3)2211()322Ly at a mm v===14-12.一半径为R 的无限长半圆柱面导体,载有与轴线上的长直导线的电流I 等值反向的电流,如图14-52所示。
试求轴线上长直导线单位长度所受的磁力。
解:B l F ⨯=Id d 而 RI B πμ210=故 dl R I I dl BI dF 2221022πμ==θc o s dF dF x = 0cos 2022210==⎰πθθπμRd R I I F xθsin dF dF y = RI I Rd R I I F y 2210022210sin 2πμθθπμπ==⎰21I I = 所以 RI F y 220πμ=14-13.截面积为S 、密度为ρ的铜导线被弯成正方形的三边,可以绕水平轴O O '转动,如图14-53所示。
导线放在方向竖直向上的匀强磁场中,当导线中的电流为I 时,导线离开原来的竖直位置偏转一个角度θ而平衡。
求磁感应强度。
解:设正方形的边长为a ,质量为m ,aS m ρ=。
平衡时重力矩等于磁力矩 B p M m ⨯= 磁力矩的大小θθc o s )90sin(202BIa BIa M =-=重力矩为 θθθs i n 2s i n 22s i nm g a a mg mga M =⋅+= 平衡时 22s i n c o sm g a B I a θθ= θρθt a n 2t a n 2ISgIa mg B ==14-14.有一个U 形导线,质量为m ,两端浸没在水银槽中,导线水平部分的长度为l ,处在磁感应强度大小为B 的均匀磁场中,如图14-54所示。
当接通电源时,U 导线就会从水银槽中跳起来。
假定电流脉冲的时间与导线上升时间相比可忽略。
试由导线跳起所达到的高度h 计算电流脉冲的电荷量q 。
解:跳起来达到最大高度这个过程机械能守恒mgh mv =221 gh v 2= 接通电流时有 dt dv m BIl = 而 dtdqI =⎰⎰=v q mdv Bldq 00 gh BlmBl mv q 2==14-15.半径为R 的半圆形闭合线圈,载有电流I ,放在均匀磁场中,磁场方向与线圈平面平行,如图14-55所示。
求(1)线圈所受力矩的大小和方向(以直径为转轴);(2)若线圈受上述磁场作用转到线圈平面与磁场垂直的位置 ,则力矩做功为多少? 解:(1) n p m IS = B p M m ⨯=IB R B p M m 2212sinππ== 方向为垂直于B 的方向向上 (2) 2221)021(R IB R B I I W ππφ=-⋅=∆=思考题14-1.在图(a )和(b )中各有一半径相同的圆形回路1L 、2L ,圆周内有电流1I 、2I ,其分布相同,且均在真空中,但在(b )图中2L 回路外有电流3I ,1P 、2P 为两圆形回路上的对应点,则:2121,d d )(P P L L A B B l B l B =⋅=⋅⎰⎰;2121,d d )(P P L L B B B l B l B =⋅≠⋅⎰⎰; 2121,d d )(P P L L C B B l B l B ≠⋅=⋅⎰⎰;2121,d d )(P P L L D B B l B l B ≠⋅≠⋅⎰⎰.答:B 的环流只与回路中所包围的电流有关,与外面的电流无关,但是回路上的磁感应强度却是所有电流在那一点产生磁场的叠加。
所以C 对。
14-2. 哪一幅图线能确切描述载流圆线圈在其轴线上任意点所产生的B 随x 的变化关系?(x 坐标轴垂直于圆线圈平面,原点在圆线圈中心O )答:载流圆线圈在其轴线上任意点所产生的磁感应强度232220)(2x R IR B +=μ0=x RIB 20μ=R x 3202x IR B μ≈根据上述两式可判断C 图对14-3. 取一闭合积分回路L ,使三根载流导线穿过它所围成的面.现改变三根导线之间的相互间隔,但不越出积分回路,则: (A)回路L 内的∑I 不变,L 上各点的B 不变; (B)回路L 内的∑I 不变,L 上各点的B 改变; (C)回路L 内的∑I 改变,L 上各点的B 不变; (D)回路L 内的∑I 改变,L 上各点的B 改变.答:B 对14-4. 一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管 (r R 2=),两螺线管单位长度上的匝数相等.两螺线管中的磁感应强度大小R B 和r B 应满足:r R B B A 2)(=;r R B B B =)( ;r R B B C =2)(;r R B B D 4)(=.答:对于长直螺线管 nI B 0μ=,由于两螺线管单位长度上的匝数相等,所以两螺线管磁感应强度相等。
