《管理运筹学》第2版习题答案_韩伯棠
管理运筹学试题二(含答案)

运筹学试题二
一、用单纯形法求解下述线性规划问题(20分)
⎧⎨⎪⎪⎩
⎪⎪0
,824424m ax 2121212121≥≤-≤-≤+-+=x x x x x x x x x x z
二、设一线性规划问题为(25分)
234
700件,且在第二、三周能加班生产。
加班后,每周可增产200件产品,但成本每件增加5元。
产品如不能在本周交货,则每件每周存贮费是3元。
问如何安排生产计划,使总成本最小,要求建立运输问题数学模型求解。
(25分)
四、某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知,每周星期一至星期五不能出席某一讲座的学生数如下表:(20分)
座的学生总数。
试题二答案
()0
1310232>=⎪⎪⎭⎫
⎝⎛-=r
6
*=Z
(3) 最优解不满足新增加的约束条件2231≥+-x x ∴最优解要发生改变 将约束条件改写为 22631-=+-x x x
加入最优表中继续迭代。
管理运筹学答案.docx
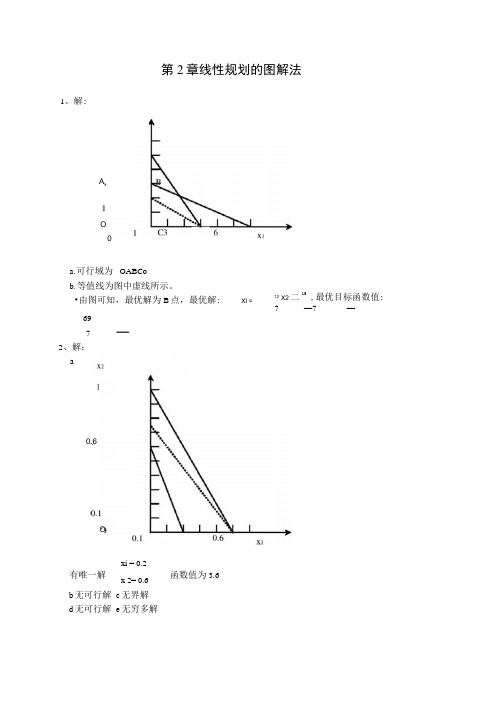
第2章线性规划的图解法1、解:12X2二15,最优目标函数值:7 —7—b 无可行解c 无界解d 无可行解e 无穷多解AO 0a. 可行域为b. 等值线为图中虚线所示。
OABCo69 0.6O72、解:axi = 0.2有唯一解x 2= 0.6函数值为3.6•由图可知,最优解为B 点,最优解:Xl =3、解:a 标准形式: max f = 3xi + 2 x 2 + Osi + 0 s 2 + Os 39 xi + 2 x 2 + si = 30 3xi + 2 x 2+ s 2= 13 2 xi+ 2x2 +S3 =9 X1 , X 2, Si , S 2, S3> 0max f = - xr+ 2 X2- 2 X2- Osi 一 0s2—3xi + 5 x 2— 5 x 2•+ si = 70 2 xr- 5 x‘2+ 5 x'2'= 50 3xr+ 2 x 2— 2 x T — S 2= 30 xr, X*2, X 21, Si , S 2> 03xi + 4 x 2 + si = 9 5 xi + 2 x 2+ s 2= 8 xi, x 2, si, s 2> 0f 有唯一解X2 =3函数值为—834、解:标准形式: max z = 10X 】 + 5X 2+0SI + 0S 2SI = 2, S2 = 0b 标准形式:max f = -4 xi - 6 X3- Osi - 0s23xi - x 2 - si = 6 XI + 2 X 2+ S 2= 10 7 xi - 6 x 2= 4 X1 , X 2, Si , S 2> 0c 标准形式:min f = 1 lxi + 8 x 2 + Osi + Os 2+ Os310 xi + 2 x 2- si = 20 3xi + 3x 2— s 2= 18 4XI + 9X 2-S3=36Xl,X2,Sl,S2,S3>0Si = 0, S2= 0, S3= 13 6、解:b 1 < ci< 3c 2 < C2 < 6xi = 6X2= 4e xi 丘[4,8] x 2= 16 - 2 xif 变化。
卫生管理运筹学第二版答案

习题参考答案习题一1.设选用第1种、第2种、第3种、第4种、第5种饲料的量分别为12345,,,,x x x x x 。
Min 543218.03.07.04.02.0x x x x x Z ++++=12345123451234512345326187000.50.220.530..0.50.220.8100,,,,0x x x x x x x x x x s t x x x x x x x x x x ++++≥⎧⎪++++≥⎪⎨++++≥⎪⎪≥⎩2.设x ij 为生产第i 种食品所使用的第j 种原料数,i =1,2,3分别代表甲、乙、丙,j =1,2,3分别代表A 、B 、C 。
其数学模型为:Max Z =)(0.1)(5.1)(2)(95.1)(45.2)(9.2332313322212312111333231232221131211x x x x x x x x x x x x x x x x x x ++⨯-++⨯-++⨯-++⨯+++⨯+++⨯s.t.)3,2,1,3,2,1(,05.06.015.02.06.01200250020003332313323222123232221211312111313121111332313322212312111==≥≤++≤++≥++≤++≥++≤++≤++≤++j i x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ij3.将下列线性规划问题化为标准形式(1)引入剩余变量1s ,松弛变量2sMax 32142x x x Z ++=123112321231231225623215..327,,0,,0x x x s x x x s s t x x x x x x s s +--=⎧⎪+++=⎪⎨--+=⎪⎪≥≥⎩ (2)令'22x x =-,'''333x x x =-,引入松弛变量1s Max 33217785x x x x Z ''-'+'--= ⎪⎩⎪⎨⎧≥''''=''-'+'+=+''+'-'-0,,,,152245106..13321332113321s x x x x x x x x s x x x x t s4.(1)唯一最优解 1x =1.7143,2x =2.1429,Max Z =9.8571;(2)无可行解; (3)无界解;(4)无可行解;(5)多重最优解,Max Z=66,其中一个解为1x =4,2x =6; (6)唯一最优解,为1x =6.6667,2x =2.6667,Max Z =30.6667。
运筹学课后答案2

运筹学(第2版)习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297-298 第12章 博弈论 P325~326 全书360页由于大小限制,此文档只显示第6章到第12章,第1章至第5章见《运筹学课后答案1》习题六6.1如图6-42所示,建立求最小部分树的0-1整数规划数学模型。
【解】边[i ,j ]的长度记为c ij ,设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为:,12132323243434364635365612132434343546562324463612132446362335244656121324354656m in 52,22,233344,510ij ijij i j ij Z c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6-43所示,建立求v 1到v 6的最短路问题的0-1整数规划数学模型。
图6-42【解】弧(i ,j )的长度记为c ij ,设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij数学模型为:,1213122324251323343524344546253545564656m in 100,00110,(,)ijiji jij Z cx x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6-43所示,建立求v 1到v 6的最大流问题的线性规划数学模型。
管理运筹学第二章课后答案

管理运筹学(谢家平)第二章课后答案1 解maxZ=200x1+240x260x1+50x2≤420030x1+40x2≤300060x1+50x2≤4500化成标准型为:maxZ=200x1+240x2+0x3+0x4+0x560x1+50x2+x3=420030x1+40x2+x4=300060x1+50x2+x5=4500**********************最优解如下*************************目标函数最优值为: 18400变量最优解相差值------- -------- --------x1 20 0x2 60 0约束松弛/剩余变量对偶价格------- ------------- --------1 0 .8892 0 4.8893 300 0目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 180 200 288x2 166.667 240266.667常数项数范围:约束下限当前值上限------- -------- -------- --------1 3750 4200 45002 2100 3000 33603 4200 4500 无上限最优生产方案是生产甲产品20,生产乙产品60。
x3=0,x4=0,x5=300说明:生产甲乙产品的材料为瓶颈材料增加材料会增加甲乙二设备D为富余设备。
因为甲产品上升100大于88所以甲需要调整,而乙产品下降的60小于73.33所以不需要调整。
由表可知非紧缺资源最多可以减少300,紧缺资源分别可以增加300,360。
2 设项目第一二三年年初投资为x1,x5x6;项目I第一年年初投资x2项目III第二年年初投资为x3项目IV第三年年初投资为x4MaxZ=0.2x1+0.5x2+0.6x3+0.4x4+0.2x5+0.2x6+30X1+X2≤30X2≤20X5+x3≤30—(x1+x2)+1.2x1X3≤15X6+x4≤30-(x1+x2)+1.2x1-x5-x3+1.5x2X4≤10X1,x2,x3,x4,x5,x6≥0**********************最优解如下*************************目标函数最优值为: 27.5变量最优解相差值------- -------- --------x1 12.5 0x2 17.5 0x3 15 0x4 10 0x5 0 .3x6 16.25 0约束松弛/剩余变量对偶价格------- ------------- --------1 0 .32 2.5 03 0 .34 0 .15 0 .26 0 .2目标函数系数范围:变量下限当前值上限------- -------- -------- --------x1 .08 .2 .56x2 .14 .5 .62x3 .5 .6 无上限x4 .2 .4 无上限x5 无下限.2 .5x6 0 .2 .28常数项数范围:约束下限当前值上限------- -------- -------- --------1 15 30 452 17.5 20 无上限3 9 30 334 12 15 285 13.75 30 无上限6 0 10 26.25项目一一二三年年初投资为12.5, 0,16.25项目二第一年初投资为17.5项目三第二年年初投资为15项目四年初投资为10 万元3设五种家具分别为x1,x2,x3,x4,x5。
管理运筹学试卷和答案2

《管理运筹学》考试试卷(B)一、(10分)某咨询公司,受厂商委托,对新上市的一种新产品进行消费者反映的调查。
该公司采用了挨户调查的方法,委托他们调查的厂商以及该公司的市场研究专家对该调查提出下列几点要求:(1)必须调查2000户人家;(2)在晚上调查的户数和白天调查的户数相等;(3)至少应调查700户有孩子的家庭;(4)至少应调查450户无孩子的家庭。
每会见一户家庭,进行调查所需费用为家庭白天会见晚上会见有孩子25元30元无孩子20元24元问为使总调查费用最少,应调查各类家庭的户数是多少?(只建立模型)二、(10分)某公司受委托,准备把120万元投资两种基金A和B,其中A基金的每单位投资额为50元,年回报率为10%,B基金的每单位投资额为100元,年回报率为4%。
委托人要求在每年的年回报金额至少达到6万元的基础上要求投资风险最小。
据测定每单位A基金的投资风险指数为8,每单位B基金的投资风险指数为3,投资风险指数越大表明投资风险越大。
委托人要求在B基金中的投资额不少于30万元。
为了使总的投资风险最小,该公司应该在基金A和基金B中各投资多少单位?这时每年的回报金额是多少?为求该解问题,设可以建立下面的线性规划模型使用《管理运筹学》软件,求得计算机解如下图所示,最优解目标函数值 = 62000.000变量值相差值x1 4000.000 0.000x2 10000.000 0.0003约束松驰/剩余变量对偶价格1 0.000 0.0572 0.000 -2.1673 7000.000 0.000目标系数范围变量下限当前值上限x1 3.750 8.000 无上限x2 无下限 3.000 6.400常数项范围变量下限当前值上限1 780000.000 1200000.000 1500000.0002 48000.000 60000.000 102000.0003 无下限 3000.000 10000.000根据图回答问题:a.最优解是什么,最小风险是多少?b.投资的年收入是多少?c.每个约束条件的对偶价格是多少?d.当每单位基金A的风险指数从8降为6,而每单位基金B的风险指数从3上升为5时,用百分之一百法则能否断定,其最优解变或不变?为什么?e.对图中的右边值范围的上、下限给予具体解释,并阐述如何使用这些信息。
大学期间各科目的课后习题答案与模拟卷及往年原题

《新视野大学英语读写教程(第二版)第三册》课后答案新视野大学英语读写教程(第二版)第一册》课后答案《马·克思主·义大体原理概论》新版完整答案《毛·泽东思想和中国特色社会主·义理论体系概论》习题答案(2020年修订版的)21世纪大学实用英语综合教程(第一册)课后答案及课文翻译西方经济学(高鸿业版)教材详细答案《新视野大学英语读写教程(第二版)第二册》课后答案思想道德修养与法律基础课后习题答案《中国近代史纲要》完整课后答案(高教版)《全新版大学英语综合教程》(第三册)练习答案及课文译文《全新版大学英语综合教程》(第一册)练习答案及课文译文《会计学原理》同步练习题答案《微观经济学》课后答案(高鸿业版)《统计学》课后答案(第二版,贾俊平版)《西方经济学》习题答案(第三版,高鸿业)可直接打印毛邓三全部课后思考题答案(高教版)/毛邓三课后答案新视野大学英语听说教程1听力原文及答案下载西方宏观经济高鸿业第四版课后答案《管理学》经典笔记(周三多,第二版)《中国近代史纲要》课后习题答案《理论力学》课后习题答案《线性代数》(同济第四版)课后习题答案(完整版)高等数学(同济第五版)课后答案(PDF格式,共527页)中国近现代史纲要课后题答案曼昆《经济学原理》课后习题解答21世纪大学英语读写教程(第三册)参考答案谢希仁《计算机网络教程》(第五版)习题参考答案(共48页)《概率论与数理统计》习题答案《模拟电子技术基础》详细习题答案(童诗白,华成英版,高教版)《机械设计》课后习题答案(高教版,第八版,西北工业大学)《大学物理》完整习题答案《管理学》课后答案(周三多)机械设计基础(第五版)习题答案[杨可桢等主编]程守洙、江之永主编《普通物理学》(第五版)详细解答及辅导新视野大学英语课本详解(四册全)21世纪大学英语读写教程(第四册)课后答案新视野大学英语读写教程3册的课后习题答案新视野大学英语第四册答案(第二版)《中国近现代史》选择题全集(共含250道题目和答案)《电工学》课后习题答案(第六版,上册,秦曾煌主编)完整的英文原版曼昆宏观、微观经济学答案《数字电子技术基础》习题答案(阎石,第五版)《电路》习题答案上(邱关源,第五版)《电工学》习题答案(第六版,秦曾煌)21世纪大学英语读写教程(第三册)课文翻译《生物化学》复习资料大全(3套试卷及答案+各章习题集)《模拟电子技术基础》课后习题答案(共10章)《概率论与数理统计及其应用》课后答案(浙江大学盛骤谢式千编著)《理论力学》课后习题答案(赫桐生,高教版)《全新版大学英语综合教程》(第四册)练习答案及课文译文《化工原理答案》课后习题答案(高教出版社,王志魁主编,第三版)《国际贸易》课后习题答案(海闻P.林德特王新奎)大学英语综合教程1-4册练习答案《流体力学》习题答案《传热学》课后习题答案(第四版)高等数学习题答案及提示《高分子化学》课后习题答案(第四版,潘祖仁主编)马·克思主·义大体原理概论答案《计算机网络》课后习题解答(谢希仁,第五版)《概率论与数理统计》优秀学习资料《离散数学》习题答案(高等教育出版社)《模拟电子技术基础简明教程》课后习题答案(杨素行第三版)《信号与线性系统分析》习题答案及辅导参考(吴大正版)《教育心理学》课后习题答案(皮连生版)《理论力学》习题答案(动力学和静力学)选修课《中国现当代文学》资料包机械设计课程设计——二级斜齿圆柱齿轮减速器(WORD+原图)《成本会计》配套习题集参考答案《概率论与数理统计》8套习题及习题答案(自学推荐)《现代西方经济学(微观经济学)》笔记与课后习题详解(第3版,宋承先)《计算机操作系统》习题答案(汤子瀛版,完整版)《毛·泽东思想和中国特色社会主·义理论体系概论》有史以来最全面的温习资料!!!《线性代数》9套习题+9套相应答案(自学,复习推荐)《管理理论与实务》课后题答案(手写版,中央财经大学,赵丽芬)统计学原理作业及参考答案机械设计课程设计——带式运输机的传动装置的设计《物理学》习题分析与解答(马文蔚主编,清·华大学,第五版)《新编大学英语》课后答案(第三册)《通信原理》课后习题答案及每章总结(樊昌信,国防工业出版社,第五版)《c语言程序与设计》习题答案(谭浩强,第三版)《微生物学》课后习题答案(周德庆版)新视野第二版全四册听说教程答案《宏观经济学》课后答案(曼昆,中文版)《电力电子技术》习题答案(第四版,王兆安,王俊主编)《土力学》习题解答/课后答案《公司法》课后练习及参考答案《全新版大学英语综合教程》(第二册)练习答案及课文译文新视野大学英语视听说第三册答案《工程力学》课后习题答案(梅凤翔主编)《理论力学》详细习题答案(第六版,哈工大出版社)《成本会计》习题及答案(自学推荐,23页)《自动控制原理》课后题答案(胡寿松,第四版)《复变函数》习题答案(第四版)《信号与系统》习题答案(第四版,吴大正)《有机化学》课后答案(第二版,高教版,徐寿昌主编)《电工学——电子技术》习题答案(下册)《财务管理学》章后练习参考答案(人大出版,第四版)现代汉语题库(语法部分)及答案《概率论与数理统计》习题详解(浙大二、三版通用)《有机化学》习题答案(汪小兰主编)《微机原理及应用》习题答案《管理运筹学》第二版习题答案(韩伯棠教授)《古代汉语》习题集(附习题答案)福建人民出版社《金融市场学》课后习题答案(张亦春,郑振龙,第二版)《公共关系学》习题及参考答案(复习必备)现代汉语通论(邵敬敏版)词汇语法课后练习答案《国际经济学》教师手册及课后习题答案(克鲁格曼,第六版)《教育技术》课后习题答案参考(北师大)《金融市场学》课后答案(郑振龙版)《组织行为学》习题集答案(参考下,还是蛮好的)《分析化学》课后习题答案(第五版,高教版)大学英语精读第3册答案(外教社)《国际经济学》习题答案(萨尔瓦多,英文版)《复变函数与积分变换》习题答案《信息论与编码》辅导PPT及部分习题答案(曹雪虹,张宗橙,北京邮电大学出版社)《宏观经济学》习题答案(第七版,多恩布什)《物理化学》习题解答(天津大学, 第四版,106张)新视野大学英语视听说教程第一册《机械制造技术》习题集与答案解析新视野大学英语听说教程2册听力原文及答案下载管理学试题(附答案)《材料力学》详细辅导及课后答案(PDF格式,共642页)六级词汇注解《大学基础物理学》课后答案(共16个单元)《管理学——原理与方式》课后习题答案新视野2版第三册(大2上学期用)曼昆《经济学原理》中文第四版.课后习题答案-清晰图片版《数据库系统概论》课后习题(第四版)大学数学基础教程课后答案(微积分)《投资学》课后习题答案(博迪,第四版)流体力学课后答案(高教版,张也影,第二版)《语言学概论》习题答案(自考,新版教材)《统计学》各章练习题答案《数字电子技术基础》课后习题答案(完整答案版)《积分变换》习题答案(配套东南大学张元林编的)《中级财务会计》习题答案(第二版,刘永泽)《计算机网络》课后习题答案(第5版和第4版)《单片机原理及应用》课后习题答案(张毅刚主编,高教版)《金融工程》课后题答案(郑振龙版)《液压传动》第2版思考题和习题解答(共36页)《动物学》习题集与答案(资料相当丰富)《高频电子线路》习题参考答案(第四版)《国际经济法》课后参考答案大学英语四级十年真题+听力《信号与系统》习题详解(奥本海姆版)《电路分析》课后答案及学习指导(第二版,胡翔骏,高教版)《C语言设计》(谭浩强,第三版)227页新视野大学英语课后习题答案1-4册全集《数字电路与逻辑设计》课后习题答案,讲解详细《电路》第五版课后答案《材料力学》详细习题答案及辅导(第四版,刘鸿文)《传播学教程》课后答案(郭庆光主编,完整版)《物理化学》习题答案与课件集合(南大)《金融市场学》电子书(张亦春,郑振龙,第二版)毛邓三95%考点高等教育出版社《毛·泽东思想和中国特色社会主·义道路》(09版,原毛邓三)课后题答案《线性代数》课后习题答案(陈维新,科学出版社)自动控制原理习题集(自学辅导推荐)《现代通信原理》习题答案(曹志刚版)高等数学上下《习题PPT》《数据结构习题集》答案(C版,清·华大学,严蔚敏)《大学物理学》习题解答《物理化学》习题答案(南大,第五版)《机械原理》复习精要与习题精解(第7版,西北大学)《宏观经济学》答案(曼昆,第五版,英文版)pdf格式《化工热力学》习题与习题答案(含各种版本)《材料力学》习题答案教育统计与测量管理心理学(自考必备资料,牛逼打印版)离散数学习题解答(第四版)清·华大学出版社货币银行学《技术经济学概论》(第二版)习题答案《毛·泽东思想和社会主·义建设理论题概论》精炼考试题目,耐心整理《数字信号处理》课后答案及详细辅导(丁美玉,第二版)《语言学概论练习题》答案《会计电算化》教材习题答案(09年)《数据库系统概论》习题答案(第四版)《微观经济学》课后答案(平狄克版)《控制工程基础》课后习题解答(清·华版)《高分子化学》习题答案(第四版)《电机与拖动基础》课后习题答案(第四版,机械工业出版社,顾绳谷主编)《机械工程测试技术基础》(第三版,熊诗波等主编)课后答案《宏观经济学》课后答案(布兰查德版)《机械原理》习题答案和超多例题(西北工业大学,第六版)《大学物理基础教程》课后习题答案(第二版,等教育出版社)简明乐谱基础知识《语言学教程》课后答案《公司理财》课后答案(英文版,第六版)《信息论与编码》学习辅导及习题详解(傅祖芸版)《遗传学》课后习题答案(朱军主编,完整版)现代人心理实战700题处世韬略《自动控制原理》习题答案《普通动物学》完整课后答案(刘凌云,郑光美版)《微机原理》作业答案(李继灿版)尼尔·波兹曼《娱乐至死》《电力电子技术》习题答案(第4版,西安交通大学)大学英语四级(CET-4)历年真题大全[89-07年39套](精品级)753页word 《通信原理》习题答案《普通化学(第五版)》习题详解(配套浙大编的)经济法课后复习及思考答案《结构化学基础》习题答案(周公度,北大版)财务管理学课后答案荆新王化成《C++程序设计》课后习题答案(第2版,吴乃陵,高教版)药用植物的两份习题(自己感觉比较有用)《数学物理方法》习题解答案详细版(梁昆淼,第二版)《机械制图》习题册答案(近机类、非机类,清·华大学出版社)《控制工程基础》习题答案(第二版,燕山大学)《画法几何》资料包(含习题答案,自学辅导课件)《畜禽解剖学与组织胚胎学》习题答案参考《统计学》课后习题答案(周恒彤编)《西方经济学简明教程》课后习题全解(尹伯成,上海人民出版社)《汽车理论》课后答案详细解答(余志生,机械工业出版社)《数学物理方法》(第三版)习题答案新视野听力原文及课后答案新编大学英语4(外研版)课后练习答案《材料力学》习题答案(单辉祖,北京航空航天大学)大学英语精读第3册课文及课后答案《自动控制原理》课后习题答案———胡寿松,第五版《数据库系统原理与设计》课后答案(第四版,王珊,萨师煊)《数字电子技术基础》详细习题答案(阎石第四版)财经应用文笔记《管理学》课后习题答案(罗宾斯,人大版,第7版)《概率论与数理统计》习题答案(复旦大学出版社)《数字信号处理——基于运算机的方式》习题答案(第二版)《传热学》课后答案(杨世铭,陶文铨主编,高教版)C语言资料大全(有课后答案,自学资料,C程序等)毛邓三重点归纳《电力拖动自动控制系统》习题答案逄锦聚《政治经济学》(第3版)笔记和课后习题详解《概率论与数理统计》课后习题解答(东南大学出版社)《有机化学》课后习题答案(胡宏纹,第三版)《常微分方程》习题解答(王高雄版)▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆▆【因为太多了,没方法再粘贴到那个地址了,更多答案,直接进入下面那个搜索就好】源地址:||。
《管理运筹学》习题6解答
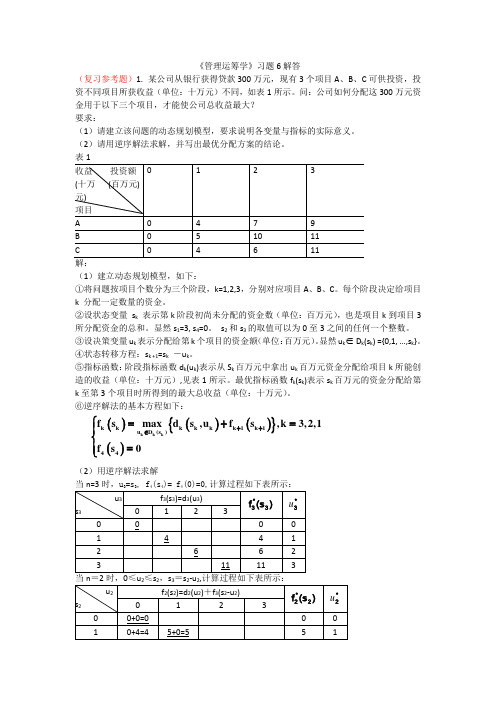
《管理运筹学》习题6解答(复习参考题)1. 某公司从银行获得贷款300万元,现有3个项目A 、B 、C 可供投资,投资不同项目所获收益(单位:十万元)不同,如表1所示。
问:公司如何分配这300万元资金用于以下三个项目,才能使公司总收益最大? 要求:(1)请建立该问题的动态规划模型,要求说明各变量与指标的实际意义。
(2)请用逆序解法求解,并写出最优分配方案的结论。
(1)建立动态规划模型,如下:①将问题按项目个数分为三个阶段,k=1,2,3,分别对应项目A 、B 、C 。
每个阶段决定给项目k 分配一定数量的资金。
②设状态变量 s k 表示第k 阶段初尚未分配的资金数(单位:百万元),也是项目k 到项目3所分配资金的总和。
显然s 1=3, s 4=0。
s 2和s 3的取值可以为0至3之间的任何一个整数。
③设决策变量u k 表示分配给第k 个项目的资金额(单位:百万元)。
显然u k ∈ D k (s k ) ={0,1, …,s k }。
④状态转移方程:s k +1=s k -u k 。
⑤指标函数:阶段指标函数d k (u k )表示从S k 百万元中拿出u k 百万元资金分配给项目k 所能创造的收益(单位:十万元),见表1所示。
最优指标函数f k (s k )表示s k 百万元的资金分配给第k 至第3个项目时所得到的最大总收益(单位:十万元)。
⑥逆序解法的基本方程如下:(2)用逆序解法求解33444()()(){}()k k k k k k k k k 1k 1u D (s )44f s max d s ,u f s ,k 3,2,1f s 0 ++∈⎧=+=⎪⎨⎪=⎩当n=1时,0≤u≤3,s =3-u 本题有两个最优方案:方案一:*1u =0, *2u =2 *1u =1 ***211s =s -u =3-0=3 ***322s =s -u =3-2=1即项目A 、项目B 、项目C 分别分配0、2、1百万元,最大总收益为*1f (3)=14百万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章是没有的第 2 章 线性规划的图解法11a.可行域为 OABC 。
b.等值线为图中虚线所示。
12c.由图可知,最优解为 B 点,最优解: x 1 = 769 。
7 2、解:15 x 2 =7, 最优目标函数值:a x 210.60.1O1有唯一解 x 1 = 0.2 函数值为 3.6 x 2 = 0.6 b 无可行解 c 无界解 d 无可行解 e 无穷多解1 2 2 1 2f 有唯一解20 x 1 =3 8函数值为 92 33、解:a 标准形式:b 标准形式:c 标准形式:x 2 =3max fmax f= 3x 1 + 2 x 2 + 0s 1 + 0s 2 + 0s 3 9 x 1 + 2x 2 + s 1 = 30 3x 1 + 2 x 2 + s 2 = 13 2 x 1 + 2x 2 + s 3 = 9x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0 = −4 x 1 − 6x 3 − 0s 1 − 0s 2 3x 1 − x 2 − s 1 =6x 1 + 2x 2 + s 2 = 10 7 x 1 − 6 x 2 = 4 x 1 , x 2 , s 1 , s 2 ≥max f = −x ' + 2x '− 2 x '' − 0s − 0s' ''− 3x 1 + 5x 2− 5x 2 + s 1 = 702 x ' − 5x ' + 5x '' = 50122 ' ' '' 3x 1 + 2 x 2 − 2x 2− s 2 = 30' ' ''4 、解:x 1, x 2, x 2, s 1 , s 2 ≥ 0标准形式: max z = 10 x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4 x 2 + s 1 = 9 5x 1 + 2 x 2 + s 2 = 8 x 1 , x 2 , s 1 , s 2 ≥ 0s 1 = 2, s 2 = 0标准形式: min f = 11x 1 + 8x 2 + 0s 1 + 0s 2 + 0s 310 x 1 + 2x 2 − s 1 = 20 3x 1 + 3x 2 − s 2 = 18 4 x 1 + 9x 2 − s 3 = 36x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0s 1 = 0, s 2 = 0, s 3 = 136 、解:b 1 ≤c 1 ≤ 3c 2 ≤ c 2 ≤ 6d x 1 = 6x 2 = 4e x 1 ∈ [4,8]x 2 = 16 − 2x 1f 变化。
原斜率从 − 2变为 − 137、解: 模型:max z = 500 x 1 + 400 x 22 x 1 ≤ 300 3x 2 ≤ 540 2 x 1 + 2x 2 ≤ 440 1.2 x 1 +1.5x 2 ≤ 300x 1 , x 2 ≥ 0a x 1 = 150x 2 = 70 即目标函数最优值是 103000b 2,4 有剩余,分别是 330,15。
均为松弛变量c 50, 0 ,200, 0 额外利润 250d 在 [0,500]变化,最优解不变。
e 在 400 到正无穷变化,最优解不变。
f 不变a 模型:min f=8xa +3xb50xa +100 xb≤12000005xa +4xb≥60000100 xb≥300000x a , xb≥0基金a,b 分别为4000,10000。
回报率:60000b 模型变为:max z = 5xa +4 xb50xa +100 xb≤1200000100 xb≥300000x a , xb≥0推导出:x1 =18000x2=3000故基金a 投资90 万,基金b 投资30 万。
第4 章线性规划在工商管理中的应用1、解:为了用最少的原材料得到10 台锅炉,需要混合使用14 种下料方案设按14 种方案下料的原材料的根数分别为x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,则可列出下面的数学模型:min f=x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14s.t.2x1+x2+x3+x4 ≥80x2+3x5+2x6+2x7+x8+x9+x10 ≥350x3+x6+2x8+x9+3x11+x12+x13 ≥420x4+x7+x9+2x10+x12+2x13+3x14 ≥10x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥0用管理运筹学软件我们可以求得此问题的解为:x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0,x9=0,x10=0,x11=140,x12=0,x13=0,x14=3.333最优值为300。
2、解:从上午11 时到下午10 时分成11 个班次,设x i 表示第i 班次安排的临时工的人数,则可列出下面的数学模型:min f=16(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11)s.t.x1+1 ≥9x1+x2+1 ≥9x1+x2+x3+2 ≥9x1+x2+x3+x4+2 ≥ 3x2+x3+x4+x5+1≥ 3x3+x4+x5+x6+2≥3x4+x5+x6+x7+1≥6x5+x6+x7+x8+2≥12x6+x7+x8+x9+2≥12x7+x8+x9+x10+1 ≥7x8+x9+x10+x11+1 ≥7x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥0用管理运筹学软件我们可以求得此问题的解为:x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0,x10=0,x11=0最优值为320。
a、在满足对职工需求的条件下,在10 时安排8 个临时工,12 时新安排1个临时工,13 时新安排1 个临时工,15 时新安排4 个临时工,17 时新安排6 个临时工可使临时工的总成本最小。
b、这时付给临时工的工资总额为80 元,一共需要安排20 个临时工的班次。
约束松弛/剩余变量对偶价格------- ------------------ -------------1 0 -42 0 03 2 04 9 05 0 -46 5 07 0 08 0 09 0 -410 0 011 0 0根据剩余变量的数字分析可知,可以让11 时安排的8 个人工作3 小时,13 时安排的1 个人工作3 小时,可使得总成本更小。
C、设在11:00-12:00 这段时间内有x1 个班是4 小时,y1个班是3 小时;设在12:00-13:00 这段时间内有x2 个班是4 小时,y2个班是3 小时;其他时段也类似。
则:由题意可得如下式子:11 11min z =16∑x1 +12∑y1i =1i =1S.Tx 1 + y1+1≥9x 1 + y1+x2+ y2+1≥9x 1 + y1+x2+ y2+x3+ y3+1+1≥9x 1 +x2+ y2+x3+ y3+x4+ y4+1+1≥3x 2 +x3+ y3+x4+ y4+x5+ y5+1≥3x 3 +x4+ y4+x5+ y5+x6+ y6+1+1≥3x 4 +x5+ y5+x6+ y6+x7+ y7+1≥6x 5 +x6+ y6+x7+ y7+x8+ y8+1+1≥12x 6 +x7+ y7+x8+ y8+x9+ y9+1+1≥12x 7 +x8+ y8+x9+ y9+x10+ y10+1≥7x 8 +x9+ y9+x10+ y10+x11+ y11+1≥7x i ≥0, yi≥i=1,2,…,11稍微变形后,用管理运筹学软件求解可得:总成本最小为264 元。
安排如下:y1=8(即在此时间段安排8 个3 小时的班),y3=1,y5=1,y7=4,x8=6 这样能比第一问节省:320-264=56 元。
3、解:设生产A、B、C 三种产品的数量分别为x1,x2,x3,则可列出下面的数学模型:max z=10 x1+12 x2+14 x2s.t.x1+1.5x2+4x3 ≤20002x1+1.2x2+x3 ≤1000x1 ≤200x2 ≤250x3 ≤100x1,x2,x3≥0用管理运筹学软件我们可以求得此问题的解为:x1=200,x2=250,x3=100最优值为6400。
a、在资源数量及市场容量允许的条件下,生产A 200 件,B 250 件,C 100件,可使生产获利最多。
b、A、B、C 的市场容量的对偶价格分别为10 元,12 元,14 元。
材料、台时的对偶价格均为0。
说明A 的市场容量增加一件就可使总利润增加10元,B 的市场容量增加一件就可使总利润增加12 元,C 的市场容量增加一件就可使总利润增加14 元。
但增加一千克的材料或增加一个台时数都不能使总利润增加。
如果要开拓市场应当首先开拓C 产品的市场,如果要增加资源,则应在975 到正无穷上增加材料数量,在800 到正无穷上增加机器台时数。
4、解:设白天调查的有孩子的家庭的户数为x11,白天调查的无孩子的家庭的户数为x12,晚上调查的有孩子的家庭的户数为x21,晚上调查的无孩子的家庭的户数为x22,则可建立下面的数学模型:min f=25x11+20x12+30x21+24x22s.t.x11+x12+x21+x22 ≥2000x11+x12 =x21+x22x11+x21 ≥700x12+x22 ≥450x11, x12, x21, x22 ≥0用管理运筹学软件我们可以求得此问题的解为:x11=700,x12=300,x21=0,x22=1000最优值为47500。
a、白天调查的有孩子的家庭的户数为700 户,白天调查的无孩子的家庭的户数为300 户,晚上调查的有孩子的家庭的户数为0,晚上调查的无孩子的家庭的户数为1000 户,可使总调查费用最小。
b、白天调查的有孩子的家庭的费用在20-26 元之间,总调查费用不会变化;白天调查的无孩子的家庭的费用在19-25 元之间,总调查费用不会变化;晚上调查的有孩子的家庭的费用在29-无穷之间,总调查费用不会变化;晚上调查的无孩子的家庭的费用在-20-25 元之间,总调查费用不会变化。
c、调查的总户数在1400-无穷之间,总调查费用不会变化;有孩子家庭的最少调查数在0-1000 之间,总调查费用不会变化;无孩子家庭的最少调查数在负无穷-1300 之间,总调查费用不会变化。
5、解:设第i 个月签订的合同打算租用j 个月的面积为x ij,则需要建立下面的数学模型:min f=2800(x11+x21+x31+x41)+4500(x12+x22+x32)+6000(x13+x23)+7300 x14s.t.x11+x12+x13+x14 ≥15x12+x13+x14+x21+x22+x23 ≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12x ij ≥0,i,j=1,2,3,4用管理运筹学软件我们可以求得此问题的解为:x11=5,x12=0,x13=10,x14=0,x21=0,x22=0,x23=0,x31=10,x32=0,x41=0最优值为102000。
