电容的串联与并联
电容器并联与串联分析

电容器并联与串联分析电容器是电子电路中常见的元件之一,它具有储存电荷的功能。
在实际应用中,常常需要将多个电容器进行并联或者串联以达到特定的电路要求。
本文将对电容器的并联和串联进行分析,并探讨其特点和应用。
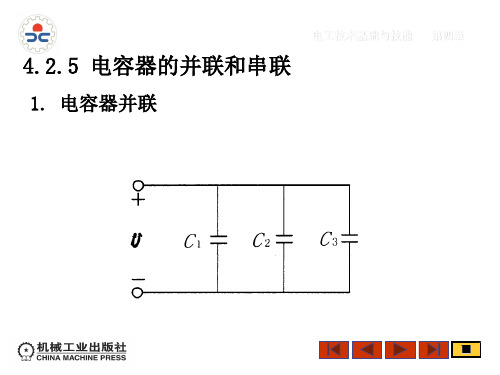
一、电容器的并联电容器的并联是指将多个电容器的正极连接在一起,负极连接在一起,形成一个集合电容器。
并联的电容器的总电容值等于各个电容器的电容值之和。
并联的电容器示意图如下所示:[插入图片]并联的电容器具有以下特点:1. 总电容值之和:并联的电容器的总电容值等于各个电容器的电容值之和,即Ct = C1 + C2 + ... + Cn。
2. 充电时间:并联的电容器在充电过程中,其总充电时间等于其中电容值最小的电容器的充电时间。
3. 放电时间:并联的电容器在放电过程中,其总放电时间等于其中电容值最大的电容器的放电时间。
并联的电容器可以用于增大电容值以匹配电路的要求。
在电子设备中,通常会使用并联电容器来过滤高频噪音,提供稳定的电源供应。
二、电容器的串联电容器的串联是指将多个电容器的正极和负极相连,形成一个串联电容器。
串联的电容器的总电容值等于各个电容器电容值的倒数之和的倒数。
串联的电容器示意图如下所示:[插入图片]串联的电容器具有以下特点:1. 电容值的倒数和:串联的电容器的总电容值等于各个电容器电容值的倒数之和的倒数,即1/Ct = 1/C1 + 1/C2 + ... + 1/Cn。
2. 充电时间:串联的电容器在充电过程中,其总充电时间等于其中电容值最大的电容器的充电时间。
3. 放电时间:串联的电容器在放电过程中,其总放电时间等于其中电容值最小的电容器的放电时间。
串联的电容器可以用于减小电容值,调节电路的频率特性。
在振荡电路中,常常会使用串联电容器来控制振荡频率。
三、并联与串联的应用1. 滤波电路:并联电容器可以用于滤波电路,对输入的电源信号进行滤波,去除高频噪音,提供稳定的直流电压输出。
2. 振荡电路:串联电容器可以用于振荡电路,通过调节串联电容器的电容值,可以改变振荡频率。
电容器的串并联与电容比值

电容器的串并联与电容比值在电路中,电容器是常见的电子元件之一,用于储存电荷。
电容器的串并联连接是电路设计中常见的组合方式,能够影响电容值,并对电路的性能产生重要影响。
本文将介绍电容器的串并联连接方式以及求解电容比值的方法。
一、电容器的串联连接电容器的串联连接是指将两个或多个电容器的正极与负极依次相连。
串联连接会使电容器的电容值减小,即总电容值相对于单个电容器来说更小。
假设有两个电容器C1和C2,其电容值分别为C1和C2。
当两个电容器串联连接时,它们的正极相连,负极也相连:--------C1-------C2--------在串联连接中,电荷在电容器C1与C2之间流动,最终使得总电荷量相等。
根据电容器的电荷公式Q=CV,其中Q为电荷量,C为电容值,V为电压,可得到:Q1 = C1 * VQ2 = C2 * V由于电荷量相等,可得到:Q1 = Q2C1 * V = C2 * VC1/C2 = V2/V1其中,V1和V2分别为两个电容器所连接处的电压。
二、电容器的并联连接电容器的并联连接是指将两个或多个电容器的正极与负极相连。
并联连接会使电容值增加,即总电容值相对于单个电容器来说更大。
假设有两个电容器C1和C2,其电容值分别为C1和C2。
当两个电容器并联连接时,它们的正极与负极都相连:---C1---|---C2---在并联连接中,电荷可以从总电路中的某一点流入两个电容器,最终使得两个电容器的电压相等。
根据电容器的电荷公式Q=CV,可得到:Q1 = C1 * V1Q2 = C2 * V2由于电压相等,即V1=V2,可得到:Q1 = Q2C1 * V1 = C2 * V2C1/C2 = V1/V2三、求解电容比值的应用电容器的串并联连接中,求解电容比值的应用非常广泛。
例如,在电路设计中,当需要特定数值的电容值时,可以通过串并联连接不同数值的电容器来得到所需的电容值。
另外,电容比值的求解也可以应用在滤波电路设计中。
电容器的串并联组合

电容器的串并联组合电容器是电子领域中常见的电子元件,广泛应用于电路中。
在电路中,电容器的串并联组合对电路的性能有着重要影响。
本文将探讨电容器串并联组合的原理及其在电路设计中的应用。
一、电容器的基本原理电容器是一种可以存储电荷的电子元件。
它由两个金属板和介质组成,金属板上的电荷被阻隔在介质中,形成电场。
电容器的容量取决于金属板的面积、金属板之间的距离以及介质的介电常数。
二、电容器的串联组合电容器的串联组合是指多个电容器按照一定方式相连接。
在串联组合中,多个电容器的正极连接在一起,负极也连接在一起。
串联组合能够增加总的电容量,即串联电容器的容量等于各个电容器容量的总和。
例如,将两个容量分别为C1和C2的电容器串联,其总电容量为C = C1 + C2。
当串联电容器接入电路时,电流将依次通过各个电容器,电压分割在各个电容器之间。
三、电容器的并联组合电容器的并联组合是指多个电容器并排连接。
在并联组合中,多个电容器的正极和负极相连。
并联组合能够增加总的电压承受能力,即并联电容器的电压等于各个电容器电压的最大值。
例如,将两个容量分别为C1和C2的电容器并联,其总电容量为C = C1 + C2。
并联电容器接入电路时,电流将分流通过各个电容器,电压在各个电容器之间相等。
四、电容器串并联组合在电路设计中的应用1. 波形整形在电子设备中,常需要对信号波形进行整形处理。
串联电容器可以起到平滑电压波形的作用。
当信号经过串联电容器时,电容器会对高频信号产生较大的阻抗,从而过滤掉高频噪声,使信号更加平滑。
2. 滤波电路滤波电路用于去除电路中的噪声或杂波。
在滤波电路中,常用并联电容器来消除高频成分。
高频信号在电容器上的阻抗较低,可以通过电容器直接排除。
3. 多级放大器的耦合在多级放大器中,为了实现信号的传递和放大,各个级联放大器之间需要耦合。
串联电容器可以作为耦合电容器,连接各级放大器之间,实现信号的传递,并避免不同级放大器之间的互相影响。
电学电容器的串并联及等效电容计算

电学电容器的串并联及等效电容计算电学电容器是电路中常用的元件之一,它具有存储电荷的能力。
在电路中,电容器可以通过串联和并联的方式连接,以达到不同的电路特性和应用需求。
本文将详细介绍电学电容器串并联的原理及等效电容的计算方法。
一、电学电容器的串联电学电容器的串联指的是将两个或多个电容器按照一定的方式连接在一起,形成一个串联的电容器组合。
在串联连接时,各个电容器的正极和负极按照一定的规则连接起来。
假设有两个电容器C1和C2,它们的电容分别为C1和C2。
当它们串联连接时,形成一个整体的电容器组合,电容为C。
根据串联连接的规则,在电学电容器串联中,各个电容器的正极与负极依次相连。
具体连接方式如下图所示:```----------C1-----------C2----------| |------------------------------------```器组合的电压等于各个电容器电压之和。
根据该特性,可以确定电学电容器串联的等效电容计算公式如下:```1/C = 1/C1 + 1/C2```其中,C为电学电容器串联的等效电容。
二、电学电容器的并联电学电容器的并联指的是将两个或多个电容器按照一定的方式连接在一起,形成一个并联的电容器组合。
在并联连接时,各个电容器的正极和负极按照一定的规则连接起来。
假设有两个电容器C1和C2,它们的电容分别为C1和C2。
当它们并联连接时,形成一个整体的电容器组合,电容为C。
根据并联连接的规则,在电学电容器并联中,各个电容器的正极与正极相连,负极与负极相连。
具体连接方式如下图所示:```---------C1------- ---------C2--------| |-----------------------------------------------------------------```器组合的电荷量等于各个电容器电荷量之和。
根据该特性,可以确定电学电容器并联的等效电容计算公式如下:```C = C1 + C2```其中,C为电学电容器并联的等效电容。
电容的串联并联
Q Q1 Q2 Qn
电容器并联使用时应注意:并联电容器的额定电压和总电 容量要符合使用要求。
【例】
电工技术基础与技能
第四章
有一电容电路,其工作电压为120 V,需要电容量﹥80 µ F。 现有几种规格的电容器为:100 µ F/50 V;47 µ F/160 V; 22 µ F/250 V;10 µ F/400 V。请选择合适规格的电容器 接入电路中。
U2
C 1.8 U 100 82 V C2 2.2
电工技术基础与技能
第四章
由以上计算可知,2.2 µ F的电容器额定电压值(63 V) 低于使用电压值(82 V),电容器将因耐压不足而损坏。 一旦此电容器击穿短路,100V电压将加在10µ F的电容 器上,还会造成10µ F的电容器击穿损坏。 所以在电容器串联电路中,各电容器的耐压一定要符合 电路要求。串联电路中各电容器的质量要好,因为质量 差的电容器工作一段时间后可能电容量会下降,造成电 容器两端电压上升而使电容器击穿。
电工技术基础与技能
第四章
•
2. 电容器串联
串联电路如上图所示,电路具有以下特点: (1)电容器串联时,各电容极板上所带电荷量相等,即
Q Q1 Q2 Qn
电工技术基础与技能
第四章
(2)电容器串联电路的总电容量C的倒数等于各电容器电容 量的倒数之和,即
1 1 1 1 C C1 C 2 Cn
练习: 有三个电容器串联起来后,接到60V的电压上,其中, C1=2µ F,C2=3µ F,C3=6µ F,求每只电容器所承受的 电压U1,U2,U3各是多少?
练习:
1、当单独一个电容器的( 耐压 )不能满足电路要求, 而它的( )足够大时,可将电容器串联起来使 容量 用。 2、当单独一个电容器的( 电容量 )不能满足电路要 求,而其( 耐压 )能够满足电路要求时,可将电 容器并联起来使用。 3、串联电容器的总电容比每个电容器的电容( 小 ) 每个电容器两端的电压和自身的电容成( 反比 )。
电容器串联并联详解

电容器串联并联详解在电路中,电容器是一种常见且重要的电子元件。
电容器的串联和并联连接方式会对电路的性能产生显著影响。
接下来,让我们详细了解一下电容器的串联和并联。
首先,我们来看看电容器的并联。
当两个或多个电容器并联连接时,它们的两端分别连接在一起。
这就相当于增加了电容的容量。
打个比方,如果我们有两个电容器,电容分别为C1 和C2,它们并联在一起,那么总电容 C 总等于 C1 + C2。
为什么会这样呢?这是因为在并联电路中,每个电容器两端的电压是相同的。
电荷可以在各个电容器之间自由流动,所以总的存储电荷能力就增加了。
这就好比有多个水桶并行摆放,每个水桶都能独立地装水,而总装水量就是各个水桶装水量之和。
电容器并联在实际电路中有很多应用。
比如说,在电源滤波电路中,常常会并联多个电容器,以增加滤波效果,提供更稳定的直流电压。
因为并联后的电容能够存储更多的电荷,从而平滑掉电源中的交流成分,使得输出的电压更加平稳。
接下来,我们再讲讲电容器的串联。
当电容器串联时,情况就有所不同了。
在串联电路中,每个电容器所存储的电荷量是相同的。
而总电容的计算则要稍微复杂一些,总电容的倒数等于各个电容器电容倒数之和。
还是用一个比喻来帮助理解,想象把几个电容器串联起来就像是把几个不同粗细的水管连接在一起,水(电荷)在通过这些串联的水管时,受到的阻力(电容)会增加。
电容器串联的一个重要应用是在分压电路中。
通过串联不同电容值的电容器,可以实现对输入电压的分压,从而得到我们需要的特定电压值。
那么,在实际应用中,我们如何选择是串联还是并联电容器呢?这取决于我们的具体需求。
如果我们需要增加电容的容量,以存储更多的电荷或者提供更大的电流滤波能力,那么并联电容器是一个不错的选择。
比如在一些大型电子设备中,为了满足对电源稳定性的高要求,会并联多个大容量的电容器。
而当我们需要改变电压分配或者增加电容的耐压值时,串联电容器可能更合适。
例如,在高压电路中,单个电容器的耐压值可能不够,这时通过串联多个电容器,可以分担电压,从而满足电路的要求。
电容器的串并联(共10张PPT)

第8页,共10页。
( 海南卷)如图,一平行板电容器的两极板与一 电压恒定的电源相连,极板水平放置,极板间距为 d;在下极板上叠放一厚度为l的金属板,其上部空 间有一带电粒子P静止在电容器中。当把金属板从 电容器中快速抽出后,粒子P开始运动。重力加速 度为g。粒子运动的加速度为()
第9页,共10页。
分析:
第10页,共10页。
D.换一块形状大小相同、介电常数更大的电介质
第5页,共10页。
分析:这两个电容是串联还是并联呢?说是串联或并联都有道 理,根本原因是是缺少电压源。它两端都接地,相当于构成如 下回路。我们想用的结论是两端,原图中间两板上带电总量不为零
第4页,共10页。
(08宁夏)21.如图所示,C为中间插有电介质的电容器,a和b为 其两极板,a板接地;P和Q为两竖直放置的平行金属板,在 两板间用绝缘线悬挂一带电小球;P板与b板用导线相连,Q 板接地。开始时悬线静止在竖直方向,在b板带电后,悬线偏转 了角度α。在以下方法中,能使悬线的偏角α变大的是() A.缩小a、b间的距离 B.加大a、b间的距离 C.取出a、b两极板间的电介质
(但和一定),所以还是不能看成串联,电压相等,所以带电量和 电容成正比,要使得场强变大,也就是使得电压变大,,也就是要 使得右边电容器分得电量减小,所以,只改变左边的话,那就是要 使得左边电容要减小即可。
第6页,共10页。
二、往电容器中冲入介质:
第7页,共10页。
三、往电容器中间插入导体(金属板):
电容器的串并联
电容的串并联计算方法
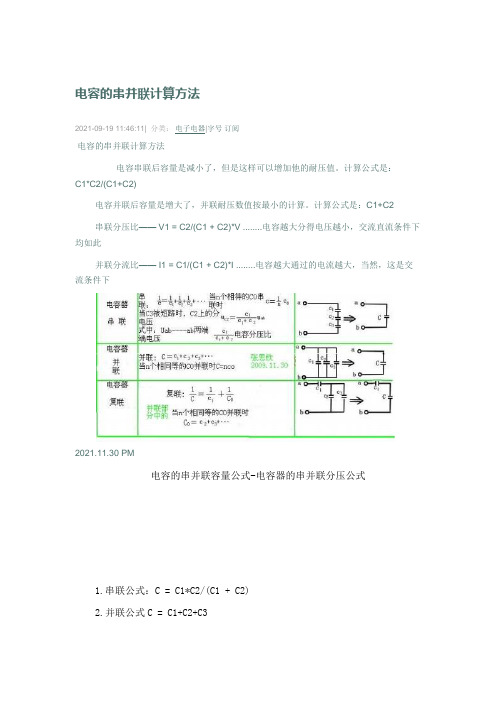
电容的串并联计算方法2021-09-19 11:46:11| 分类:电子电器|字号订阅电容的串并联计算方法电容串联后容量是减小了,但是这样可以增加他的耐压值。
计算公式是:C1*C2/(C1+C2)电容并联后容量是增大了,并联耐压数值按最小的计算。
计算公式是:C1+C2串联分压比—— V1 = C2/(C1 + C2)*V ........电容越大分得电压越小,交流直流条件下均如此并联分流比—— I1 = C1/(C1 + C2)*I ........电容越大通过的电流越大,当然,这是交流条件下2021.11.30 PM电容的串并联容量公式-电容器的串并联分压公式1.串联公式:C = C1*C2/(C1 + C2)2.并联公式C = C1+C2+C3补充部分:串联分压比—— V1 = C2/(C1 + C2)*V ........电容越大分得电压越小,交流直流条件下均如此并联分流比—— I1 = C1/(C1 + C2)*I ........电容越大通过的电流越大,当然,这是交流条件下一个大的电容上并联一个小电容大电容由于容量大,所以体积一般也比较大,且通常使用多层卷绕的方式制作,这就导致了大电容的分布电感比较大〔也叫等效串联电感,英文简称ESL〕。
电感对高频信号的阻抗是很大的,所以,大电容的高频性能不好。
而一些小容量电容那么刚刚相反,由于容量小,因此体积可以做得很小〔缩短了引线,就减小了ESL,因为一段导线也可以看成是一个电感的〕,而且常使用平板电容的构造,这样小容量电容就有很小ESL这样它就具有了很好的高频性能,但由于容量小的缘故,对低频信号的阻抗大。
所以,假设我们为了让低频、高频信号都可以很好的通过,就采用一个大电容再并上一个小电容的方式。
常使用的小电容为的CBB电容较好(瓷片电容也行),当频率更高时,还可并联更小的电容,例如几pF,几百pF的。
而在数字电路中,一般要给每个芯片的电源引脚上并联一个的电容到地〔这个电容叫做退耦电容,当然也可以理解为电源滤波电容,越靠近芯片越好〕,因为在这些地方的信号主要是高频信号,使用较小的电容滤波就可以了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电容的串联与并联
电容器是电路中常用的元器件之一,它可以存储电荷并在电路中起到储能的作用。
在实际应用中,我们常常需要将多个电容器连接在一起,以满足电路的特定要求。
电容的串联与并联是电路中常见的连接方式,它们具有不同的特点和应用场景。
本文将详细介绍电容的串联和并联原理以及其在电路中的应用。
一、串联电容的原理及应用
串联电容是指将多个电容按照一定的方式连接在一起,其电容值等效为串联电容的总和。
电容器的串联连接方式如下:
[图示:三个电容依次串联连接]
在串联连接中,电容器之间通过正极与负极相连,且电荷量在各个电容器中是相等的。
根据串联电容器的电荷守恒原理及欧姆定律,我们可以推导出串联电容的等效电容公式为:
C_eq = 1 / (1/C1 + 1/C2 + ... + 1/Cn)
其中,C_eq为串联电容的等效电容,C1、C2、...、Cn为串联电容的各个电容值。
串联电容在电路中的应用非常广泛。
它可以用于提高电压稳定性,并且能够实现电容值的增加。
例如,在电源滤波电路中,串联电容可以起到平滑电压波动、抑制噪声的作用。
此外,串联电容还可以用于模拟电路中的交流耦合、直流隔离等应用。
二、并联电容的原理及应用
并联电容是指将多个电容同时连接在一起,其电容值等效为并联电
容的总和。
电容器的并联连接方式如下:
[图示:三个电容同时并联连接]
在并联连接中,电容器的正极与正极相连,负极与负极相连,且电
压在各个电容器中是相等的。
根据并联电容器的电压守恒原理及欧姆
定律,我们可以推导出并联电容的等效电容公式为:
C_eq = C1 + C2 + ... + Cn
其中,C_eq为并联电容的等效电容,C1、C2、...、Cn为并联电容
的各个电容值。
并联电容器在电路中的应用十分常见。
它可以用于提高电容储存能
量的能力,并且能够实现电容值的增加。
例如,在音频放大器的输入端,通过并联电容可以阻隔直流信号,只传递交流信号,从而起到耦
合作用。
此外,并联电容还可以用于电源开关稳压电路、电子滤波器
等领域。
三、串联与并联电容的对比及应用场景选择
串联电容与并联电容相比,其特点和应用场景略有不同。
总结如下:
1. 串联电容的等效电容值小于各个串联电容的电容值之和,而并联
电容的等效电容值等于各个并联电容的电容值之和。
2. 串联电容可以用于增加电压稳定性和信号的隔离,适合用于电源滤波、信号传输等场景。
而并联电容可以用于增加电容储存能量和阻隔直流信号,适合用于能量存储、耦合等场景。
3. 选择串联电容或并联电容应根据具体的电路要求和应用需求来决定。
如果需要增加电容值、提高电压稳定性或阻隔直流信号,可以选择串联电容。
如果需要增加能量存储能力或传递交流信号,可以选择并联电容。
总之,电容的串联与并联是电路中常见的连接方式,具有不同的特点和应用场景。
了解并掌握串联电容和并联电容的原理及其在电路中的应用,可以帮助我们更好地设计和优化电路,满足特定的需求。
