水力计算基本公式
排洪系统水力计算

⑵排洪系统水力计算截洪沟采用矩形断面,按以下公式进行水力计算:流量公式:Q=ω·V流速公式:V=I R C ⋅曼宁公式:C= 式中:Q —流量(m 3/S );ω—过水断面面积(m 2);V —流速(m/s );R —水力半径(过水断面面积与湿周的比值)(m ); I —水力坡度;C —流速系数(谢才系数);n —沟壁粗糙系数(据材料而定),毛石混凝土截水沟内壁n 取0.015、浆砌片石取0.025。
ω=bhR=ω/(b+2h)b —沟宽(m );h —水深(m );一号截洪沟根据其沿程的地形地质情况,其纵向坡度Ⅰ值取为0.03,采用M7.5水泥砂浆砌MU30块石结构,若沟净断面宽取1.5m 、高取1.4 m (充水高度按1.0m 考虑),则其流速和流量的计算如下:ω=1.5×1.0=1.50(m 2)R=1.50/(1.0×2+1.5)=0.429(m)611R n ⋅V=34.738×(0.429×0.03)1/2=3.941(m/s)Q=ω·V=1.50×3.941=5.912(m3/s)截水沟过水流量已大于了该沟汇流区域的洪峰流量5.188m3/s,最大设计流速为3.941m/s,略小于于浆砌片石水渠允许的最大不冲流速(4m/s),考虑到流速计算未考虑水沟转弯对流速的影响,故该断面可行,可最大限度地排除该区域汇集的洪水。
2#截水沟根据其沿程的地形地质情况,其纵向坡度Ⅰ值取为0.03,采用C20毛石混凝土结构,若沟净断面宽取1.8m、高取1.6m (充水高度按1.2m考虑),则其流速和流量的计算如下:ω=1.8×1.2=2.16(m2)R=2.16/(1.2×2+1.8)=0.514(m)C=(1/0.015)×0.5141/6=59.667V=59.667×(0.514×0.03)1/2=7.409(m/s)Q=ω·V=2.16×7.409=16.003(m3/s)截水沟过水流量已大于了该沟汇流区域的洪峰流量14.206m3/s,最大设计流速为7.409m/s,小于毛石混凝土水渠允许最大不冲流速(8m/s),故该断面可行,可最大限度地排除该区域汇集的洪水。
钢管水力计算

钢管和铸铁管水力计算1 计算公式钢管和铸铁管水力计算沿用甫·阿·舍维列夫著水力计算表。
表中所采用的两种计算水头公式如下:(1)按水力坡降计算水头损失:水管的水力计算,一般采用公式(1-1):(1-1)式中i ――水力坡降;λ ――摩阻系数;d j ――管子的计算内径(m);υ――平均水流速度(m/s);g ――重力加速度,为9.81(m/s2)应用公式(1-1)时,必须先确定求取系数λ值的依据。
对于旧的钢管和铸铁管:当ν/v≥9.2×105/m时,ν――液体的运动粘滞度,(m2/s),则(1-2)当ν/v<9.2×105/m时,则(1-3)或采用ν=1.3×10-6m2/s(水温为10℃)时,则(1-4)管壁如发生锈蚀或沉垢,管壁的粗糙度就增加,从而使系数λ值增大。
公式(1-2)和公式(1-3)适合于旧钢将公式(1-2)和公式(1-4)中求得的λ值,代入(1-1)中,得出的旧钢管和铸铁管的计算公式为:当v≥1.2m/s 时,(1-5)当v<1.2m/s 时,(1-6)钢管和铸铁管水力计算表即按公式(1-5)和公式(1-6)制成。
(2)按比阻计算水头损失:由公式(1-5)求得比阻公式(1-7)为:(1-7)钢管和铸铁管的A 值,按公式(1-7),列表于1-4、5。
由于钢管和铸铁管的计算内径d j 不同,如公称直径DN=50mm 时,钢管的计算内径dj=52mm;铸铁管的计算内径dj=49mm。
因此同一公称直径,钢管2 水力计算表制表和使用说明(1)钢管及铸铁管水力计算表采用管子计算内径内的尺寸,见表2-1。
在确定计算内径d j 时,直径小于300m公称直径外径内径计算内径公称直径外径计算内径公称直径外径DN D d dj DN D dj DN D 813.598125146125400426101712.511.51501681474504781521.2515.7514.751751941735005292026.7521.2420.252002191986006302533.527262252452247007203242.2535.7534.752502732528008204048414027529927990092050605352300325305100010207075.56867325351331120012208088.580.579.5350377357130013201001141061051400142012514013113015001520150165156155160016201800182020002020220022202400242026002620①为壁厚10mm 的管子。
水力学计算公式

能量方程图示
掌握总头线、测压管水头线、水力坡 度的概念及水头线的绘制。
0v02
1
2g
H
v0
v2 2g
v
总水头线
v2
H0 hw 2g
2
1
o
v
2
❖恒定总流动量方程
Q (2 v 2 x1 v 1 x)F x
Q (2 v2y1v1y)
F y
Q (2 v 2 z1v 1 z)F z
〔2〕共轭水深公式:h 2
h 21
q2 1பைடு நூலகம்gh13 1
水力学重点及难点
❖ 水跃函数曲线
❖ 水面线变化规律 2条水深线把5种底坡上的流动空间划分为12
个流区,每个流区有一条水面曲线。
❖
壅水曲线 〔水深沿流程增加〕;
❖
降水曲线〔水深沿流程减小〕
五种底坡十二条水面曲线
N1
1
b1
N1
h01
N2
N2
QK J
长管水力计算方法 ❖复杂管道水力计算 〔并联〕 ❖ 水击现象和水击分类
水力学重点及难点
Chapter 6、7
❖ 明渠均匀流特征: 〔1〕水深,底坡沿程不变及过水断面
形状尺寸不变 〔2〕断面平均流速沿程不变 〔3〕三线平行J = Jz= i
❖ 均匀流形成条件: 恒定流,长直棱柱体渠 道,正坡渠道,糙率沿程不变
水力学重点及难点
静水压强: 掌握静水压强特性,等压面,水头的概念,
以及静水压强的计算和不同表示方法。 重力作用下静水压强的根本公式
p=p0+ h
p
z C
其中 : z—位置水头, p /γ—压强水头
〔z + p /γ—测压管水头 “水头〞:表示单位重量液体含有的能量。
水力计算教材

燃气工程庭院户内水力计算重庆市川东燃气工程设计研究院齐海鸥2010.01= 6.26 ⨯10λ 5ρ dv 0.25 Q 2) Q d 1一、水力计算基础知识水力计算的目的:树立“成本意识”,合理的确定管网的管径、流量、压力 (压力降)。
由于项目公司所做设计多为小区内的燃气管道,因此这里主要介绍小区庭 院燃气管道水力计算、户内燃气管道水力计算、商业用户燃气管道水力计算。
1、水力计算步骤(1)选择一条最不利管路(离已知压力点最远的一条管路),标好节点及 管道长度;(2)确定节点流量;(3)初选管径,再进行校核并修改;(4)完善水力计算图(标管径,压力降,节点压力)。
2 、水力计算的基本公式(1)总压力降=局部压力降+沿程压力降(简化计算:总压力降=1.05~1.1 倍沿程压力降) (2)压力降计算公式: A 、低压管道计算公式∆P l 7 Q 2d TT 0B 、中压管道计算公式P 2 - P 22L = 1.4 ⨯109 ( Kd + 192.2 5ρ T T 0C 、速度控制低压管道流速控制在 5m-8m (经济流速为 6m ),中压管道流速控制在 10- 16m 。
3、燃气小时计算流量的确定燃气管道及设备的通过能力都应按燃气计算月的小时最大流量进行计算。
小时计算流量的确定,关系着燃气输配系统的经济性和可靠性。
确定燃气小时 计算流量的方法有两种:不均匀系数法和同时工作系数法。
(1)不均匀系数法适用于城镇燃气分配管道计算流量,对于整个城市管网的水力计算一般用此方法。
计算公式如下:Q h=(1/n)·Q a式中:Q h—燃气小时计算流量(m3/h);Q a—年燃气用量(m3/a);n—燃气最大负荷利用小时数(h);其值n=(365×24)/K m K d K hK m—月高峰系数。
计算月的日平均用气量和年的日平均用气量之比;K d—日高峰系数。
计算月中的日最大用气量和该月日平均用气量之比;K h—小时高峰系数。
供热系统水力计算

p -压强水头,(压力能水头)表明流体在断面压强作用 g
下,测压管上升的高度。
Z -位置水头,相对于基准面的高度。
2 -流速水头,(动能水头)以初速度铅直上升射流时的
2g
理论高度
总水头:
H p Z 2
g
2g
即压力能水头、位置水头之和动能水
头三者之和
总水头线(A-B线)
测压管水头线——水压线(C-D线)
管道直径(如何计算?) 管段压力损失(实际值) 管道流量(管径、管段允许压降已知)
◆水力计算有什么用处?
一、热水网路水力计算基本公式
2、管段的压力 (能量) 损失包括 哪两部分?
沿程阻力损失 p y 局部阻力损失 p j
○总阻力损失 p p y p j
一、热水网路水力计算基本公式
3、管段的沿程损失计算公式?
问题思考
请问:教材P36例2-4中各供暖热用户与 外网可采取何种连接方式?
用户1: 用户2:? 用户3:? 用户4:
To be continued
§4.4热网水泵的选择
一、热网循环水泵的选择方法 1、选择参数的确定 1)流量的确定
流速与质量流量的关系?
3.实际中往往不修正的原因是什么? (P23例子)
§4.2水力计算的方法与步骤
简述水力计算步骤?
0
+2
Q2=1.05×106 W
F2
P3=2.0×104 Pa
+4
+2 60m
0
h3=33m -2 -3
-5
-8
A 150m
B
160m
C
200m D 3
100m
Q3=0.69×106 W P3=1.45×104 Pa
水力计算公式选用

长距离输水管道水力计算公式的选用1. 常用的水力计算公式:供水工程中的管道水力计算一般均按照均匀流计算,目前工程设计中普遍采用的管道水力计算公式有:达西(DARCY )公式:gd v l h f 22**=λ(1)谢才(chezy )公式:i R C v **= (2)海澄-威廉(HAZEN-WILIAMS )公式:87.4852.1852.167.10dC lQ h h f ***= (3) 式中h f ------------沿程损失,mλ―――沿程阻力系数 l ――管段长度,md-----管道计算内径,mg----重力加速度,m/s 2C----谢才系数 i----水力坡降; R ―――水力半径,mQ ―――管道流量m/s 2v----流速 m/sC n ----海澄――威廉系数其中大西公式,谢才公式对于管道和明渠的水力计算都适用。
海澄-威廉公式影响参数较小,作为一个传统公式,在国内外被广泛用于管网系统计算。
三种水力计算公式中 ,与管道内壁粗糙程度相关的系数均是影响计算结果的重要参数。
2. 规范中水力计算公式的规定3. 查阅室外给水设计规范及其他各管道设计规范,针对不同的设计条件,推荐采用的水力计算公式也有所差异,见表1:表1 各规范推荐采用的水力计算公式4. 公式的适用范围: 3.1达西公式达西公式是基于圆管层流运动推导出来的均匀流沿程损失普遍计算公式,该式适用于任何截面形状的光滑或粗糙管内的层流和紊流。
公式中沿程阻力系数λ值的确定是水头损失计算的关键,一般采用经验公式计算得出。
舍维列夫公式,布拉修斯公式及柯列勃洛克(C.F.COLEBROOK )公式均是针对工业管道条件计算λ值的著名经验公式。
舍维列夫公式的导出条件是水温10℃,运动粘度1.3*10-6 m 2/s,适用于旧钢管和旧铸铁管,紊流过渡区及粗糙度区.该公式在国内运用教广. 柯列勃洛可公式)Re 51.27.3lg(21λλ+∆*-=d (Δ为当量粗糙度,Re 为雷诺数)是根据大量工业管道试验资料提出的工业管道过渡区λ值计算公式,该式实际上是泥古拉兹光滑区公式和粗糙区公式的结合,适用范围为4000<Re<108.大量的试验结果表明柯列勃洛克公式与实际商用圆管的阻力试验结果吻合良好,不仅包含了光滑管区和完全粗糙管区,而且覆盖了整个过渡粗糙区,该公式在国外得到及为广泛的应用.布拉修斯公式25.0Re 316.0=λ是1912年布拉修斯总结光滑管的试验资料提出的,适用条件为4000<Re<105,一般用于紊流光滑管区的计算. 3.2 谢才公式该式于1775年由CHEZY 提出,实际是达西公式的一个变形,式中谢才系数C 一般由经验公式y e R n C *=1计算得出,其中61=y 时称为曼宁公式,y 值采用)1.0(75.013.05.2---=n R n y (n 为粗糙系数)公式计算时称为巴浦洛夫斯基,这两个公式应用范围均较广.就谢才公式本身而言,它适用于有压或无压均匀流动的各阻力区,但由于计算谢才系数C 的经验公式只包括反映管壁粗糙状况的粗糙系数n 和水力半径R,而没有包括流速及运动年度,也就是与雷诺数Re 无关,因此该式一般仅适用于粗糙区.曼宁公式的适用条件为n<0.02,R<0.5m;巴浦洛夫斯基公式的适用条件为0.1m ≤R ≤3m;0.011≤n ≤0.04.3.3 海澄-威廉公式是在直径≤3.66m 工业管道的大量测试数据基础上建立的著名经验公式,适用于常温的清水输送管道,式中海澄-威廉系数Ch 与不同管材的管壁表面粗糙程度有关.因为该式参数取值简单,易用,也是得到广泛应用的公式之一.此公式适用范围为光滑区至部分粗糙度区,对应雷诺数Re 范围介于104-2*106.通过对各相关规范所推荐计算公式的比较,除混凝土管仍然推荐采用谢才公式外,其它管材大多推荐采用达西公式.在新版《室外给水设计规范》中取消舍维列夫公式的相关条文,笼统采用达西公式,但未明确要求计算λ值采用的经验公式.由于舍维列夫公式是建立在对旧钢管及旧铸铁管研究的基础上,然而现在一般采用的钢或铸铁材质管道,内壁通常需进行防腐内衬,经过涂装的管道内壁表面均比旧钢管,旧铸铁管内壁光滑得多,也就是Δ值小得多,采用舍维列夫公式显然也就会产生较大得计算误差,该公式得适用范围相应较窄.经过内衬得金属管道采用柯列勃洛克公式或谢才公式计算更为合理.PVC-U,PE 等塑料管道,或者内衬塑料得金属管道,因为其内壁Δ值很低,一般处于0.0015-0.015,管道流态大多位于紊流光滑区,采用适用光滑区得布拉修斯公式以及柯列勃洛克公式一般均能够得到与实际接近得计算结果.因此, 《埋地硬聚氯乙稀给水管道工程技术规程》及《埋地聚乙稀给水管道工程技术规程》中对塑料管道水力计算公式均是合理得且与《室外给水设计规范》并不矛盾. 海澄-威廉公式可以适用于各种不同材质管道得水力计算,其中海澄-威廉系数Ch 得取值应根据管材确定.对于内衬水泥砂浆或者涂装有比较光滑得内防腐涂层得管道,其海澄-威廉系数应该参考类似工程经验参数或者实测数据,合理取用.因此,无论采用达西公式,谢才公式或者海澄-威廉公式计算,不同管材得差异均表现在 管内壁表面当量粗糙程度得不同上,各公式中与粗糙度相关系数得取值是影响计算结果得重要因素.值得一提得是,同种材质管道由于采用不同得加工工艺,其内表面得粗糙度也可能有所差异,这一因素在设计过程种也应重视(常用管材得粗糙度系数参考值见表2) 表2 常见管材粗糙度相关系数参考值5.管径对选择计算公式得影响 根据雷诺数计算公式vVdRe ,雷诺数与流速v,管径d 成正比,与运动粘度成反比,因此对应管道得不同设计条件应对所使用计算公式得适用范围进行复核.保证计算得准确性.大多说供水工程得设计按照水温10℃,运动粘度1.3*10-5 m 2/s 得条件考虑,因此雷诺数实际受流速及管道口径得影响.以塑料管道为例,在正常设计流速范围条件下,管道内径大于100mm 时,虽然管道仍然处于紊流光滑区,但其雷诺数Re>105,也就是说已经超出了布拉修斯公式得适用范围,而且误差大小与雷诺数成正比.对PVC-U 管,采用布拉修斯公式与柯列勃洛克公式对比计算,当管内径为500mm ,流速1.5 m/s 时,采用布拉修斯公式得出得水力坡降比柯列波列克得结果低11%以上.采用《埋地硬聚氯乙稀给水管道工程技术规程》推荐得修正公式与柯式对比计算,修正公式计算结果,小口径管偏安全,中等口径与柯式符合较好,大口径管得负误差达5%以上.因此笔者认为,大口径塑料管或采用塑料内衬管不宜采用布拉修斯公式计算,而更宜于采用如柯列波洛克公式等适用条件更宽得其它经验公式,或应通过试验等对其进行修正.与上述情况类似,采用谢才公式计算时,如果管道内径大于2m 时则不采用曼宁公式计算谢才系数.如果采用巴甫洛夫斯基公式,其适用管径可以达到12m,对一般输水工程管道已完全足够了.海澄-威廉公式的数据基础是WILLIAMS 和HAZEN 在大量工业管道现场或试验测量或得的.该公式因为简单易用,被广泛运用在管网水力计算中,国内外不少管道水力计算软件均采用该公式编制.由此可见,对于口径大于2m 得管道应尽量避免采用海澄-威廉公式计算以策安全.6.值得提出得是,上述所有水力计算公式中采用得管径均为计算内径,各种管道均应采用管道净内空直径计算,对于采用水泥砂浆内衬得金属管道应考虑内衬层厚度得影响.大口径管道计算应尽量避免采用海澄-威廉公式,建议采用柯列勃洛克公式计算,大量试验结果证明该公式计算结果与实际工业管道符合性好,水力条件适用范围广,虽然运用该式需要进行多次迭代计算才能得到λ值,较为麻烦,不过运用计算机简单编程既能方便地得到较为准确地结果,手工计算时也可以通过查表或者查询蓦迪图辅助计算.。
3.3非满流管渠水力计算
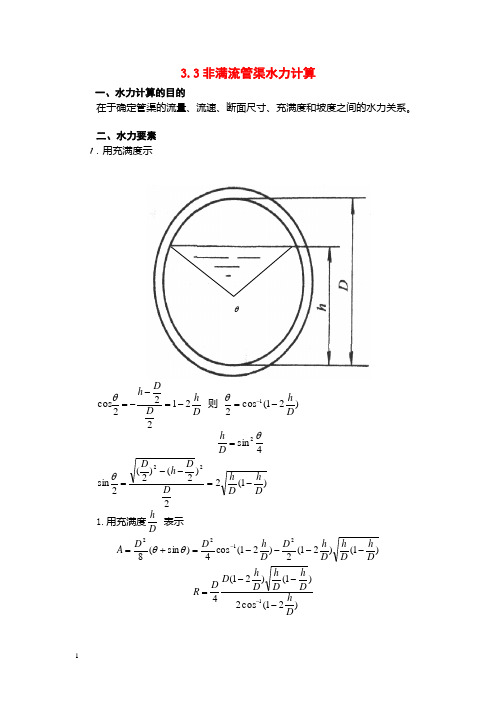
3.3非满流管渠水力计算一、水力计算的目的在于确定管渠的流量、流速、断面尺寸、充满度和坡度之间的水力关系。
二、水力要素 1.用充满度示D h D Dh 21222cos -=--=θ 则 )21(cos 21D h -=-θ 4sin 2θ=D h)1(22)2()2(2sin 22D h D h D D h D -=--=θ 1.用充满度D h表示)1()21(2)21(cos 4)sin (82122Dh D h D h D D h D D A ----=+=-θθ)21(cos 2)1()21(41DhDh D h D h D DR ---=-θ2.用充盈角θ表示过水断面面积)sin (8)2sin(42142222θθθπππθ-=-•+•=D D D A 湿周2Dx •=θ水力半径)sin 1(4θθ-==D x A R三、水力计算公式2132)/,(1I D h D R n v m=2132)/,()/,(1I D h D R D h D A n q m=这就是非满流管渠水力计算的基本公式,该两式中有q 、D 、h 、I 和v 共五个变量,任意已知其中三个,就可以求出另两个。
由于上式的形式很复杂,所以非满流管渠水力计算比满流管渠水力计算要复杂得多,特别是在已知流量、流速等参数求其充满度时,需要解非线性方程,除非使用计算机计算,手工计算是非常困难的。
为此,必须找到手工计算的简化手段。
四、水力特性<1> 当D 、I 、n 一定时,Q 何时最大?令0)(323521=•=R A n I d d d dq θθ,当D 、I 、n 一定时,则有0)sin (3235=⎥⎥⎦⎤⎢⎢⎣⎡-θθθθd d 整理后得0sin 32cos 351=+-θθθ 解得0308=θ(95.04308sin 4sin 022===θD h ) <2> 当D 、I 、n 一定时,v 何时最大?32212132)sin 1(41⎥⎦⎤⎢⎣⎡-==θθd n I I R n v 令0=θd dv 得/030257=θ(81.0430257sin 4sin/022===θD h )四、计算方法 1、解析计算法232138356.20)sin (⎥⎦⎤⎢⎣⎡•-=nq I D θθθ2383532)sin (6.20⎥⎦⎤⎢⎣⎡-•=D nq I θθθ 2比例变换法首先假设有一条满流管渠与待计算的非满流管渠具有相同的管径D 和水力坡度,并记其过水断面面积为A 。
涵管过水能力计算计算过程

A d 2 sin
8
(1-1)
湿周: d 2
水力半径:
(1-2)
R
d 4
1
sin
(1-3)
所以
2
v
1 n
d 4
1
sin
3
11 i 2=
n
21
R3i2
(1-4)
2
Q
d2 8
sin 1
n
d 4
1
sin
3
1
i2
1 n
21
AR 3i 2
(1-5)
为便于计算,表 1-2 列出不同充满度时圆形管道过水断面面积 A 和水力半 径 R 的值。
不同充满度时圆形管道过水断面积 A 和水力半径 R 的值(表中 d 以 m 计) 表 1-2
充满度
过水断面积 A(m2)
水力半径 充满度
(R)
过水断面积 A(m2)
水力半径 (R)
0.05
0.0147 d2
0.0326d 0.55
0.4426 d2
0.0635 d 0.60
0.1982 d2
0.1709 d 0.80
0.6736 d2
0.3042 d
0.35
0.2450 d2
0.1935 d 0.85
0.7115 d2
0.3033 d
0.40
0.2934 d2
0.2142 d 0.90
0.7445 d2
0.2980 d
0.45
0.3428 d2
0.2331 d 0.95
P0 水gh
当管径为 d=1m 时,P0=8.1KN; 当管径为 d=1.5m 时,P0=7.35KN。 4.竖向土压力 G4,取土覆盖厚度 H=50cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水力计算基本公式
水力计算是涉及水流和流体力学的计算过程。
其基本公式包括渠道流量公式、摩擦阻力公式和水力损失公式等。
下面将详细介绍这些基本公式及其应用。
1.渠道流量公式
渠道流量公式是用来计算水流通过给定横截面的流量的公式。
根据不同的渠道形状和流量条件,可以使用相应的公式。
以下是几种常见的渠道流量公式:
1.1矩形渠道流量公式:
Q=b*h*v
式中,Q为流量,b为矩形渠道的宽度,h为水深,v为流速。
1.2圆形渠道流量公式:
Q=π*r^2*v
式中,Q为流量,r为圆形渠道的半径,v为流速。
1.3梯形渠道流量公式:
Q=(a+b)*h*v/2
式中,Q为流量,a和b为梯形渠道上下底的长度,h为水深,v为流速。
2.摩擦阻力公式
摩擦阻力公式用于计算水流通过渠道时所受到的阻力。
常用的摩擦阻力公式有曼宁公式和切比雪夫公式。
2.1曼宁公式:
h=(1/n)*(Q/A)^2*l/(2*g)
式中,h为渠道水深(摩擦阻力损失),n为曼宁摩擦系数,Q为流量,A为横截面面积,l为渠道长度,g为重力加速度。
2.2切比雪夫公式:
h=α*(Q^2/A^2)*l/(2*g)
式中,h为渠道水深(摩擦阻力损失),α为切比雪夫系数,Q为流量,A为横截面面积,l为渠道长度,g为重力加速度。
3.水力损失公式
水力损失公式用于计算水流通过管道或渠道时所产生的能量损失。
常见的水力损失公式有弗朗西斯公式和达西-魏本巴赫公式。
3.1弗朗西斯公式:
h=(f*l*v^2)/(2*g*d)
式中,h为水力损失,f为摩擦阻力系数,l为管道或渠道长度,v为流速,g为重力加速度,d为管道或渠道的直径或水深。
3.2达西-魏本巴赫公式:
h=(f*l*v^2)/(2*g*d)
式中,h为水力损失,f为达西-魏本巴赫摩擦系数,l为管道或渠道长度,v为流速,g为重力加速度,d为管道或渠道的直径或水深。
这些基本公式在水力学相关领域中都有广泛的应用,通过对水流的流速、渠道形状和摩擦阻力等因素的计算,可以帮助工程师设计和优化水利工程。
