7.2直棱柱的侧面展开图(1)
北师大版数学七年级上册第一章2展开与折叠第2课时柱体、锥体的展开与折叠课件

可以得到的几何体是( A )
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥
3.如图,将圆柱的表面展开后得到的平面图形是( B )
4.【教材 P10 想一想·变式】下列选项经过折叠能围 成一个棱柱的是( D )
A
B
C
D
5.【2019·连云港】一个几何体的侧面展开图如 图所示,则该几何体的底面是( B )
半径为 或1 cm.
(1)如图②给出三种纸样甲、乙、丙,在甲、乙、丙 中,正确的有 甲、丙 ;
(2)从已知正确的纸样中选出一种,在原图上标注出尺
寸; (2)如图,标注尺寸只需在甲图或丙图中标出一种即
可
(3)利用你所选的一种纸样,求出包装盒的侧面积和 表面积(侧面积与两个底面积的和).
(3)S侧=(3+5+3+5)×13=208(cm2);S表=S侧+2S底= 208+2×3×5=238(cm2).
第一章 丰富的图形世界
2 展开与折叠 第2课时 柱体、锥体的展开与折
课前导读
课中导学
课后导练
1.圆柱的侧面展开图是 长方形 ,底面是 圆 ;直棱柱的侧面展开图是 长方形 ,底面是
多边形 . 2.圆锥的侧面展开图是 扇形 ,底面是
圆 ;棱锥的侧面展开图是 三角形组成的图 形,底面是 多边形 .
柱体的展开与折叠 例 1 如图,在第一行中找出与第二行对应的几何体的 表面展开图,并用线把它们连起来.
解:有4种粘贴法,如图:
谢谢观看
Thank you for watching
8.如图,请你在横线上写出哪种立体图形的表面能展 开成下面的图形.
三棱柱
ቤተ መጻሕፍቲ ባይዱ
六棱柱
棱柱的侧面展开图
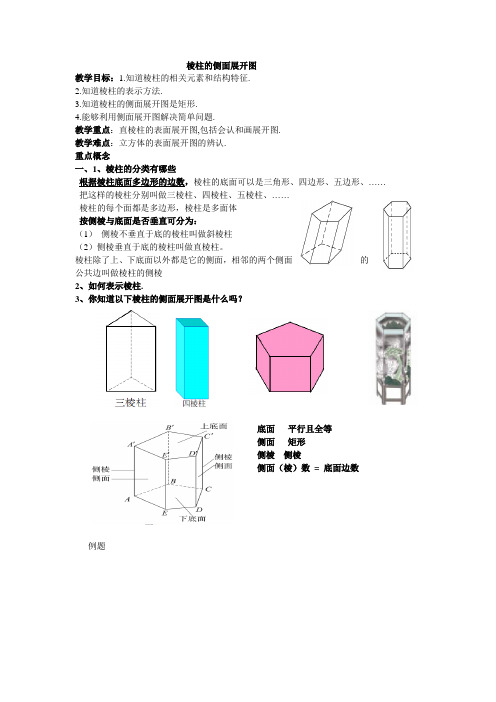
棱柱的侧面展开图
教学目标:1.知道棱柱的相关元素和结构特征.
2.知道棱柱的表示方法.
3.知道棱柱的侧面展开图是矩形.
4.能够利用侧面展开图解决简单问题.
教学重点:直棱柱的表面展开图,包括会认和画展开图.
教学难点:立方体的表面展开图的辨认.
重点概念
一、1、棱柱的分类有哪些
根据棱柱底面多边形的边数,棱柱的底面可以是三角形、四边形、五边形、……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……
棱柱的每个面都是多边形,棱柱是多面体
按侧棱与底面是否垂直可分为:
(1)侧棱不垂直于底的棱柱叫做斜棱柱
(2)侧棱垂直于底的棱柱叫做直棱柱。
棱柱除了上、下底面以外都是它的侧面,相邻的两个侧面的
公共边叫做棱柱的侧棱
2、如何表示棱柱.
3、你知道以下棱柱的侧面展开图是什么吗?
底面平行且全等
侧面矩形
侧棱侧棱
侧面(棱)数= 底面边数例题
二、课堂练习:1、
2、如图,长方体的长为15cm ,宽为10cm ,高为20cm ,点B 到点C 的距离为5cm ,一只蚂蚁如果要沿着长方体的表面从A 点爬到B 点,需要爬行的最短距离是多少?。
最新青岛版九年级数学下册第7章空间图形的初步认识PPT

12
棱数b
9
12
15
18
面数c
5
6
7
8
观察上表中的结果,你能发现a、b、c之间有什么关系吗?
请写出关系式. a+c-b=2
思考3:你学习过哪些几何体的表面积公式 和体积公式?你能用字母表示他们吗?
四种常见几何体表面积与体积公式 1.长方体 表面积=2(ab+bc+ca) 体积=abc(a、b、c分别长、宽、高) 2.正方体
1.一个圆柱形水池的底面半径为4米,池深1.2米.在池 的内壁与底面抹上水泥,抹水泥部分的面积是___2_5_.6平π 方 米.
2、已知一个圆柱的底面半径为3米,高都为4米.
则S柱侧=__2_4_π __平方米。
3.一个圆柱侧面展开图是正方形,这个图形的高 是底面半径的( C )
圆柱的特征: ①圆柱的轴通过上、下底面的圆心,且垂直于 上、下底;②圆柱的母线平行于轴且长都相等,等于圆柱的
高;③ 圆柱的底面圆平行且相等.
将圆柱的侧面沿母线剪开,得到什么图形?你能想象出圆柱 的展开图吗?
圆柱的侧面展开图与圆柱元素之间的关系?
①圆柱的侧面展开图为矩形; ②一边是圆柱的母线(高),一边是圆柱底面圆的周长; ③ S圆柱侧=底面圆周长×圆柱母线(S圆柱侧=底面周长×高 ).
πh 3.14 2.5
S侧 2πrh 2 3.141.13 2.5 17.75(m2 ) S底 πr 2 3.141.132 4.01(m2 ).
S表 S侧 S底 17.75 4.01 21.8(m2 ).
所以,供需钢板约21.8 m2
例题 解
棱柱
(2)侧棱垂直于底的棱柱叫做直棱柱。
青岛版 九年级数学下册 第7章 空间图形的初步认识 单元课时同步练习 习题合集(含答案解析)

7.1 几种常见的几何体1.半圆面绕它的直径旋转一周形成.2.一个正方体有个面.3.“枪挑一条线,棍扫一大片”这个现象说明: .4.根据几何体的特征,填写它们的名称.(1) :上下两个底面是大小相同的圆,侧面是由长方形围成的.(2) :6个面都是长方形.(3) :6个面都是正方形.(4) :上下底面是形状大小相同的多边形,侧面是长方形.(5) :下底面是圆,上方有一个顶点,侧面是由扇形围成的.(6) :下底面是多边形,上方有一个顶点.5.在小学里,我们曾学过圆柱的体积计算公式:V=πR2h(R是圆柱底面半径,h为圆柱的高).现有一个长方形,长为2cm,宽为1cm,分别以它的两边所在的直线为轴旋转一周,得到的几何体的体积分别是多少?它们之间有何关系?6.18世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察如图所示的几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是. (2)一个多面体的面数与顶点数相等,有12条棱,这个多面体是面体参考答案1.【解析】半圆面绕它的直径旋转360度形成球.答案:球2.【解析】正方体有6个面.答案:63.【解析】“枪挑一条线,棍扫一大片”这个现象说明:点动成线,线动成面.答案:点动成线,线动成面4.【解析】由几何体的特征可知,几何体的名称依次为:(1)圆柱.(2)长方体.(3)正方体.(4)棱柱.(5)圆锥.(6)棱锥.5.【解析】(1)当以长方形的宽所在的直线为轴旋转时,如图①,得到的圆柱的底面半径为2cm,高为1cm.所以其体积V1=π×22×1=4π(cm3).(2)当以长方形的长所在的直线为轴旋转时,如图②,得到的圆柱的底面半径为1cm,高为2cm,所以其体积V2=π×12×2=2π(cm3).因此,得到的两个几何体的体积之间的关系为V1=2V2.6.【解析】(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:V+F-E=2.(2)由题意得:V=F,所以F+F-12=2,解得F=7.7.2.1 直棱柱的侧面展开图1.下列几何体中,直棱柱的是。
浙教版数学九年级下册_直棱柱的表面展开图
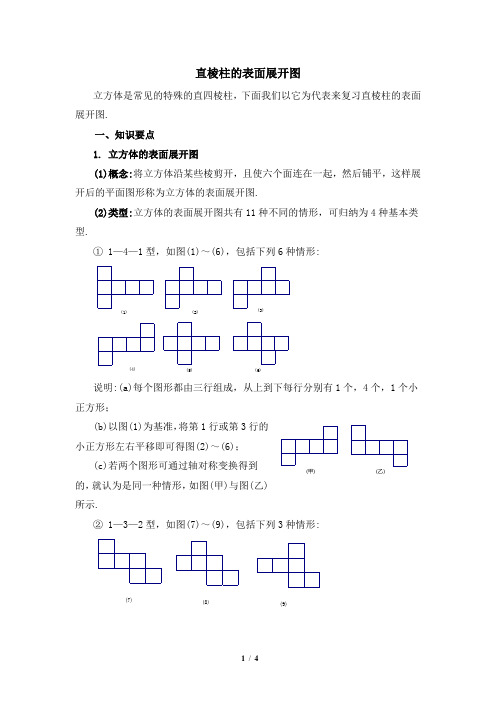
直棱柱的表面展开图立方体是常见的特殊的直四棱柱,下面我们以它为代表来复习直棱柱的表面展开图.一、知识要点1. 立方体的表面展开图(1)概念:将立方体沿某些棱剪开,且使六个面连在一起,然后铺平,这样展开后的平面图形称为立方体的表面展开图.(2)类型:立方体的表面展开图共有11种不同的情形,可归纳为4种基本类型.① 1—4—1型,如图(1)~(6),包括下列6种情形:(6)(5)(4)(3)(2)(1)说明:(a)每个图形都由三行组成,从上到下每行分别有1个,4个,1个小正方形;(b)以图(1)为基准,将第1行或第3行的小正方形左右平移即可得图(2)~(6);(c)若两个图形可通过轴对称变换得到的,就认为是同一种情形,如图(甲)与图(乙)所示.② 1—3—2型,如图(7)~(9),包括下列3种情形: (9)(8)(7)(乙)(甲)说明:每个图形都由三行组成,从上到下每行分别有1个,3个,2个小正方形;③2—2—2型,如图(10),只有1种情形.说明:这个图形由三行组成,从上到下每行都有2个小正方形;④3—0—3型,如图(11),只有1种情形.说明:这个图形可看作由三行组成,从上到下每行分别有3个,0个,3个小正方形,这样便于统一编写、记忆它们的型号.(3)注意点:①展开图的面与面之间必须以棱相连接,不能以顶点相连接;②行与行之间,不能同时有两对或两对以上的小正方形具有公共边;③有下列情形之一者,肯定不是立方体的表面展开图:(a)小正方形的个数不足6个或超过6 个; (b)行数是1行或超过3行(经旋转变换的图形除外);(c)图中包含“田”字型部份;(d)整个图形呈“L ”字型.2.直棱柱的侧面展开图直棱柱的侧面展开图是由若干个长方形或正方形组合而成的,整个图形是一个长方形或正方形.3.直棱柱的表面积与侧面积计算直棱柱的表面积与侧面积,实质上就是利用长方形或正方形的面积公式进行面积计算.二、典例赏析例1 如图是某些多面体的平面展开图,说出这些多面体的名称.解:因为图(1)是由6个正方形组成的多面体的平面展开图,所以它是立方体;图(2)是由2个直角三角形,3个长方形组成的多面体的平面展开图,所以它是直三棱柱. (10)(11)析解:(1)根据平面展开图中所给图形的形状,先判断几何体的底面是什么图形,从而确定是哪一种多面体.(2) 如图,图(1)可看作由上述“1—3—2型”的基本图形(8)旋转变换而得.例2 如图是一个几何体的三视图,主视图与左视图是大小相同的长方形,俯视图是等边三角形.(1)任意画出它的一种表面展开图;(2)若长方形的长为10cm,等边三角形的边长为4cm,求这个几何体的表面积.解:(1) 如图是该几何体的一种表面展开图.(2)这个几何体的表面积为3×(10×4)+)24421(222-⨯⨯⨯ =120+83(cm 2).析解:整个图形是一个不规则的图形,不能直接利用公式来计算,可用分割法把它转化为规则图形的面积来计算.例3 如图甲,有一个棱长为10cm 的立方体盒子,在盒子底部A 处有一只蚂蚁,欲吃顶点C 1处的一粒熟米.问蚂蚁应沿什么路径爬行,才能在最短的间内吃到这粒熟米?求出蚂蚁爬行的最短路径长.解:如图乙,它是立方体盒子沿侧棱展开的平面图形之一. 观察图形,根据“两点之间,线段最短”,可知蚂蚁沿线段AC 1爬行的路径最短,所用时间最短.在Rt △AB 1C 1中,AB 1=20cm ,B 1C 1=10cm.由勾股定理得AC 12=AB 12+B 1C 12=202+102=400+100=500,∴AC 1=105(cm).因此,蚂蚁沿着路径AC爬行,才能在最短的时间内吃到熟米,最短路径长1为105cm.析解:因为蚂蚁必须沿着立方体盒子的侧面爬行,所以要想在最短时间内吃两点不在同一个面内,须将它展开转到熟米,必须选择最短的路径.此时A、C1化为平面图形来解决.图乙是立方体盒子沿侧棱展开的平面图形之一.观察图形爬行的路径最短,所用时间最短.可知,蚂蚁沿线段AC1。
湘教版九年级数学下册:直棱柱圆锥的侧面展开图PPT教学课件

情景引入
湘教版九年级数学下册课件:3.2 直棱柱、圆锥的侧面展开图
例题讲解
例1 一个食品包装盒的侧面展开图如图所示,它的底面是边长为2的正 六边形,这个包装盒是什么形状的几何体?试根据已知数据求出它
的侧面积.
获取新知
棱柱的性质:
1、棱柱的各个侧面都是平行四边形,所有的侧棱都平行且相等;直棱柱的各个侧面都 是矩形;正棱柱的各个侧面都是全等的矩形。
2、棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形。
3、过棱柱不相邻的两条侧棱的截面都是平行四边形。
4、直棱柱的侧棱长与高相等;直棱柱的侧面及经过不相邻的两条侧棱的截面都是矩形。
湘教版九年级数学下册课件:3.2 直棱柱、圆锥的侧面展开图
湘教版九年级数学下册课件:3.2 直棱柱、圆锥的侧面展开图
获取新知 将圆锥沿一条母线剪开,观察圆锥的侧面展开图.
a h
Or
扇形半径R
高h
母线a
a
h
底面周长c
湘教版九年级数学下册课件:3.2 直棱柱、圆锥的侧面展开图
Or
扇形弧长l 侧面积s
l=c=2πr
h1 r
圆锥的母线长为:√3.342+22 ≈3.85 (m)
侧面展开积扇形的弧长为: 2π×3.34≈20.98 (m)
圆锥侧面为:
1 2
×3.85×20.98≈40.81
(m2)
h2 r
因此,搭建20个这样的蒙古包至少需要毛毡: 20× (31.45+40.81)≈1445(m2)
湘教版九年级数学下册课件:3.2 直棱柱、圆锥的侧面展开图
【精编】北师大版高中数学必修二课件7.1柱、锥、台的侧面展开与面积-精心整理
答:圆台的侧面积为600cm2.
互动探究
圆台的上、下底面半径分别为2和4,高为,2 3 求其侧面展开图扇环所对的圆心角. 分析:抓住相似三角形中的相似比是解题的关键. 答:180°
【提升总结】圆柱、圆台、圆锥表面积公式 圆柱的表面积为:
几何体 圆台
直棱柱
侧面展开图
侧面积公式 S圆台侧=_π__(_r_1+_r_2_)_l_ r1为上底面半径 r2为下底面半径 l为_侧__面__母__线__长__ S直棱柱侧=_c_h_ c为底面_周__长__
h为_高___
正棱锥 正棱台
S正棱锥侧=__12__c_h′___ c为底面__周__长__ h′为__斜__高__,即侧 面等腰三角形的高
x
o′r1 A
r2
即 x r1l ,
r2 r1
所以 S扇环
1 2
2 r2 l
2p r1 扇 环
l 2pr2
r2l r2l
r2l r1l
B
(r1 r2 )l.
x1 2
r2 x r2
2 r1 x
r1 x r1 x
思考4:将圆柱、圆锥、圆台的侧面积公式进行比 较,你能发现它们的联系和区别吗?
S圆锥侧 = p rl
r1 = 0
S圆台侧 = p (r1 + r2 )l
r1 = r2 = r
S圆柱侧 = 2p rl
例1.一个圆柱形的锅炉,底面直径,d高= 1m
h,=求2.锅3 m炉的表面积(保留2个有效数字).
解: S =
S侧面积 +
2S底面积
=
1直棱柱和圆锥的侧面展开图
棱柱的侧面展开图
诸冯学校数学备课组—卜振强
学习目标:
1.知道棱柱的相关元素和结构特征. 2.知道棱柱的表示方法. 3.知道棱柱的侧面展开图是矩形. 4.能够利用侧面展开图解决简单问题.
棱柱的分类
根据棱柱底面多边形的边数,棱柱的底面可 以是三角形、四边形、五边形、…… 把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……
三棱柱
四棱柱
五棱柱
棱柱的每个面都是多边形,棱柱是多面体
棱柱的分类
按侧棱与底面是否垂直可分为:
(1) 侧棱不垂直于底的棱柱叫做斜棱柱。 我
们
斜 棱 柱
直 棱 柱
只 研 究 直
棱
(2)侧棱垂直于底的棱柱叫做直棱柱。 柱
a _-_2_,b _-_7_,c __1__
2 c 7 -1 b
a
2. “坚”在下,“就”在后,胜利在哪 里?
坚
持就是
胜
利
3. 下列的三幅平面图是三棱柱的表面展开图的有 ()
甲
乙
丙
4. 5.
6. 如图,长方体的长为15cm,宽为10cm,高为 20cm,点B到点C的距离为5cm,一只蚂蚁如果要 沿着长方体的表面从A点爬到B点,需要爬行的最 短距离是多少?
B C
20
15 A 10
通常用表示底面各顶点的字母来表示棱柱. 棱1
C1
B1 A
1
C1 A1 B1 B1
E1 D1 C1
D
C
A
BA
C A
BB
E
D C
底面 平行且全等 侧面 矩形 侧棱 平行且相等 侧面(棱)数 = 底面边数
