计量经济学试验报告书三 2
计量经济学实验报告

计量经济学实验报告实验报告:《计量经济学》一、数据以下是中国部分省市城镇居民家庭人均年可支配收入(X)与消费性支出(Y)的统计数据:地区可支配收入(X)消费性支出(Y)北京 .69 8493.49天津 8140.50 6121.04河北 5661.16 4348.47山西 4724.11 3941.87内蒙古 5129.05 3927.75辽宁 5357.79 4356.06吉林 4810.00 4020.87黑龙江 4912.88 3824.44上海 .01 8868.19江苏 6800.23 5323.18浙江 9279.16 7020.22山东 6489.97 5022.00河南 4766.26 3830.71湖北 5524.54 4644.5湖南 6218.73 5218.79广东 9761.57 8016.91陕西 5124.24 4276.67甘肃 4916.25 4126.47青海 5169.96 4185.73新疆 5644.86 4422.93二、理论模型的设计解释变量:可支配收入X 被解释变量:消费性支出Y 软件操作:1.X与Y散点图从散点图可以看出,随着可支配收入的增加,消费性支出也在增加,大致呈线性关系。
因此,建立一元线性回归模型:Yi = β + β1Xi + μi2.对模型做OLS估计OLS估计结果为:Y = 272.3635 + 0.7551Xt1 = 1.7057t2 = 32.3869R2 = 0.9831DW。
= 1.3017F = 1048.912三、模型检验从回归估计结果看,模型拟合较好,可决系数为0.98,表明家庭人均年可消费性支出变化的98.31%可由支配性收入的变化来解释。
t检验:在5%的显著性水平下,β1不显著。
表明可支配收入增加1个单位,消费性支出平均增加0.7551单位。
1.预测现已知2018年人均年可支配收入为元,预测消费支出预测值为:Y = 272.3635 + 0.7551× = .3635E(X) = 6222.209,Var(X) = 1994.033则在95%的置信度下,E(Y)的预测区间为(874.28,.68)。
计量经济学 实验报告 2
《计量经济学》实验报告二开课实验室:财经科学实验室2014年 5 月12 日班级:_财政1112班__ 学号:2011410060_ 姓名:蓝锦达_实验项目名称:_______OLS参数估计与检验_________ 成绩:_____________ 实验性质:□验证性□综合性□设计性指导教师签字:__________【实验目的】掌握用Eviews软件进行参数估计、检验的方法,并进行预测。
【实验要求】熟悉基本操作步骤,读懂各项上机输出结果的含义并能进行分析、预测.【实验软件】Eviews, Excel软件【实验方案与进度】1.学习软件操作,运用EViews软件建立新文件2.收集数据、资料并在EViews软件上进行输入和编辑3.建立线性回归模型4.检验修正模型5.进行图形分析、回归分析6.对回归分析所得结果进行检验,并对结果进行预测【实验过程】经研究发现,家庭书刊消费受家庭收入几户主受教育年数的影响,表中为对某地区部分家庭抽样调查得到样本数据:1222.1 1981.2 18 1253 3624。
6 20123i i i i Y X T u βββ=+++其中:Y 为家庭书刊年消费支出、X 为家庭月平均收入、T 为户主受教育年数 (2)利用样本数据估计模型的参数; 估计模型参数,结果为:即 ˆ50.01620.0864552.3703i i iY X T =-++ (49.46026)(0。
02936) (5.20217)t= (-1。
011244) (2。
944186) (10。
06702) R2=0.951235 20.944732R = F=146。
2974(3)检验户主受教育年数对家庭书刊消费是否有显著影响;由估计检验结果, 户主受教育年数参数对应的t 统计量为10.06702, 明显大于t 的临界值0.025(183) 2.131t -=,同时户主受教育年数参数所对应的P 值为0.0000,明显小于0.05α=,均可判断户主受教育年数对家庭书刊消费支出确实有显著影响。
【免费下载】计量经济学实验报告三
Coefficient Std. Error t-Statistic
46.35435 6.393929 7.249745
88.12667 8.691372 3.957333 4.050746 734.6830 0.000000
Prob. 0.0000
X AR(1)
R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat
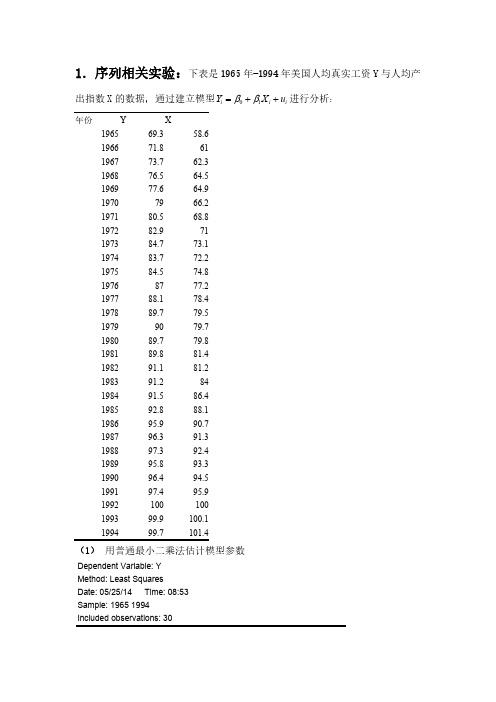
1.序列相关实验:下表是 1965 年-1994 年美国人均真实工资 Y 与人均产
出指数 X 的数据,通过建立模型Yi 0 1Xi ui 进行分析:
年份
1965
1966
1967
1968
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
1980
1981
销售额 X
114862 123968 121454 131917 129911 140976 137828 145645 136989 145126 141536 151776 148826 158913 155727 168409 162781 176057 172419 183327 170415 181313 176712 180370
扰动项不存在一阶自相关。
Dependent Variable: Y Method: Least Squares Date: 05/25/14 Time: 09:04 Sample(adjusted): 1966 1994 Included observations: 29 after adjusting endpoints Convergence achieved after 4 iterations
计量经济 实验报告三
计量经济实验报告实验三异方差的识别与补救一、实验目的:1.掌握异方差的识别方法2.能针对具体问题提出解决异方差问题的措施二、实验内容:下表是储蓄与收入得样本观测值,试建立储蓄Y关于收入X的线性模型并进行异方差的检验与修正。
个人储蓄与收入数据(百万英镑)序号Y X 序号Y X1 264 8777 17 1578 241272 105 9210 18 1654 256043 90 9954 19 1400 265004 131 10508 20 1829 276705 122 10979 21 2200 283006 107 11912 22 2017 274307 406 12747 23 2105 295608 503 13499 24 1600 281509 431 14269 25 2250 3210010 588 15522 26 2420 3250011 898 16730 27 2570 3250012 950 17663 28 1720 3350013 779 18575 29 1900 3600014 819 19635 30 2100 3620015 1222 21163 31 2300 3820016 1702 228801.用以上数据对储蓄-收入模型进行估计2.检验模型是否存在异方差3.假设随机项的异方差形式为22var()i ixμσ=,消除模型的异方差并重新对模型进行估计。
三、实验结果:1、模型估计:Dependent Variable: YMethod: Least SquaresDate: 12/06/13 Time: 16:58Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob.C -655.9600 124.2692 -5.278540 0.0000X 0.085352 0.005161 16.53779 0.0000R-squared 0.904132 Mean dependent var 1250.323 Adjusted R-squared 0.900826 S.D. dependent var 820.9407 S.E. of regression 258.5299 Akaike info criterion 14.01024 Sum squared resid 1938294. Schwarz criterion 14.10276 Log likelihood -215.1587 F-statistic 273.4984 Durbin-Watson stat 1.039802 Prob(F-statistic) 0.0000002、white检验:White Heteroskedasticity Test:F-statistic 11.18080 Probability 0.000270 Obs*R-squared 13.76465 Probability 0.001026Test Equation:Dependent Variable: RESID^2Method: Least SquaresDate: 12/06/13 Time: 17:00Sample: 1 31Included observations: 31Variable Coefficient Std. Error t-Statistic Prob.C 38802.30 71391.21 0.543516 0.5911X -4.563188 7.025231 -0.649543 0.5213X^2 0.000217 0.000154 1.411320 0.1692R-squared 0.444021 Mean dependent var 62525.62 Adjusted R-squared 0.404308 S.D. dependent var 75015.93S.E. of regression 57898.10 Akaike info criterion 24.86252 Sum squared resid 9.39E+10 Schwarz criterion 25.00130 Log likelihood -382.3691 F-statistic 11.18080 Durbin-Watson stat 1.491234 Prob(F-statistic) 0.0002703、消除模型的异方差并重新对模型进行估计。
计量经济学实验报告

计量经济学实验报告:马艺菡学号:4班级:9141070302任课教师:静文实验题目简单线性回归模型分析一实验目的与要求目的:影响财政收入的因素可能有很多,比如国生产总值,经济增长,零售物价指数,居民收入,消费等。
为研究国生产总值对财政收入是否有影响,二者有何关系。
要求:为研究国生产总值变动与财政收入关系,需要做具体分析。
二实验容根据1978-1997年中国国生产总值X和财政收入Y数据,运用EV软件,做简单线性回归分析,包括模型设定,模型检验,模型检验,得出回归结果。
三实验过程:(实践过程,实践所有参数与指标,理论依据说明等)简单线性回归分析,包括模型设定,估计参数,模型检验,模型应用。
(一)模型设定为研究中国国生产总值对财政收入是否有影响,根据1978-1997年中国国生产总值X和财政收入Y,如图11978-1997年中国国生产总值和财政收入(单位:亿元)1996 66850.5 7407.991997 73452.5 8651.14根据以上数据作财政收入Y 和国生产总值X的散点图,如图2从散点图可以看出,财政收入Y和国生产总值X大体呈现为线性关系,所以建立的计量经济模型为以下线性模型:(二)估计参数1、双击“Eviews”,进入主页。
输入数据:点击主菜单中的File/Open/EV Workfile—Excel—GDP.xls;2、在EV主页界面点击“Quick”菜单,点击“Estimate Equation”,出现“Equation Specification”对话框,选择OLS估计,输入““y c x”,点击“OK”。
即出现回归结果图3;参数估计结果为:Y=857.8375+0.100036iX(67.12578)(0.002172)t=(12.77955)(46.04910)2r=0.991583F=2120.520S.E.=208.5553DW=0.864 0323、在“Equation”框中,点击“Resids”,出现回归结果的图形(图4):剩余值(Residual)、实际值(actual),拟合值(fitted)4、.(三)模型检验1.经济意义检验回归模型为:Y=857.8375+0.100036*X(其中Y为财政收入,iX为国生产总值;)所估计的参数=0.100036,说明国生产总值每增加1亿元,财政收入平均增加0.100036亿元。
计量经济学实训报告范文

一、实训背景随着我国经济的快速发展,经济学研究越来越注重实证分析。
计量经济学作为经济学的重要分支,已经成为经济学研究的重要手段。
为了提高学生对计量经济学理论的理解和应用能力,我们学院组织了本次计量经济学实训。
二、实训目的1. 帮助学生理解计量经济学的基本原理和方法;2. 培养学生运用计量经济学方法进行实证分析的能力;3. 提高学生运用统计软件进行数据处理和分析的能力;4. 增强学生团队合作意识和沟通能力。
三、实训内容本次实训主要分为以下几个部分:1. 计量经济学基本原理讲解:包括回归分析、多元线性回归、非线性回归、时间序列分析等基本概念和方法。
2. 实证案例分析:选取实际经济问题,运用计量经济学方法进行分析,包括数据收集、模型设定、参数估计、模型检验等。
3. 统计软件操作:学习并熟练运用计量经济学常用软件,如EViews、Stata等,进行数据处理和分析。
4. 团队合作与沟通:学生分成小组,共同完成实训任务,培养团队合作意识和沟通能力。
四、实训过程1. 第一阶段:讲解计量经济学基本原理和方法,学生进行自学和笔记。
2. 第二阶段:教师选取实际经济问题,学生分组进行讨论,确定研究问题、数据来源和模型设定。
3. 第三阶段:学生运用统计软件进行数据处理和分析,完成实证研究。
4. 第四阶段:各小组进行成果展示,其他小组成员进行提问和评价。
五、实训结果1. 学生对计量经济学基本原理和方法有了更深入的理解;2. 学生的实证分析能力得到提高,能够运用计量经济学方法进行实际问题的分析;3. 学生的统计软件操作能力得到提高,能够熟练运用EViews、Stata等软件进行数据处理和分析;4. 学生的团队合作意识和沟通能力得到提升。
六、实训总结1. 计量经济学实训对于提高学生的实证分析能力具有重要意义;2. 在实训过程中,学生需要充分发挥自己的主观能动性,积极学习理论知识,并注重实际操作;3. 教师应注重引导学生进行团队合作,培养学生的沟通能力;4. 学校应加强计量经济学软件资源的建设,为学生提供更好的学习环境。
计量经济学课程实验报告

计量经济学课程实验报告实验序号2实验名称Eviews的异方差检验与校正实验组别12模拟角色实验地点2教602指导老师刘冬萍实验日期11月29日实验时间16:05——17:45一、实验目的及要求学会使用计量学分析^p 软件Eviews的异方差检验与校正功能。
二、实验环境2教602,经管学院电脑实验室三、实验内容与步骤 ?DATA Y _SORT _1.生成相关图SCAT _ Y根据相关图随着_的增大Y的取值范围不断增大,所以方程存在异方差.2.方程的异方差检验(1)WHITE 检验建立回归模型 LS Y C _ Dependent Variable: Y Method: Least SquaresDate: 11/22/12 Time: 17:06 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.8594690.7090571.2121300.2411_0.0363400.0096333.7723930.0014R-squared0.441531Mean dependent var3.100000Adjusted R-squared0.410504S.D.dependent var2.255986S.E.of regression1.732115Akaike info criterion4.031203Sum squared resid54.09Schwarz criterion4.130776Log likelihood-38.31203F-statistic14.23095Durbin-Watson stat2.111232Prob(F-statistic)0.001395进行WHITE 检验White Heteroskedasticity Test: F-statistic6.172459Probability0.009656Obs_R-squared8.413667Probability0.014893Test Equation:Dependent Variable: RESID^2 Method: Least SquaresDate: 11/22/12 Time: 17:07 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-0.8401623.268547-0.2570450.8002_0.0346910.0966160.3590620.7240_^20.0002590.4703750.6441R-squared0.420683Mean dependent var 2.70020__Adjusted R-squared 0.352528S.D.dependent var5.061699S.E.of regression4.072927Akaike info criterion 5.784082Sum squared resid 282.0085Schwarz criterion5.933442Log likelihood-54.84082F-statistic6.172459Durbin-Watson stat 2.196613Prob(F-statistic)Nr^2=8.413677 因为检验的P=0.014893小于0.05,所以存在异方差.(2) PARK检验LS Y C _Dependent Variable: YMethod: Least SquaresDate: 11/22/12 Time: 17:13Sle: 1 20Included observations: 20VariableCoefficientStd.Errort-StatisticProb.C0.8594690.7090571.2121300.2411_0.0363400.0096333.7723930.0014R-squared0.441531Mean dependent varAdjusted R-squared0.410504S.D.dependent var2.255986S.E.of regression1.732115Akaike info criterion 4.031203Sum squared resid54.09Schwarz criterion4.130776Log likelihood-38.31203F-statistic14.23095Durbin-Watson stat2.111232Prob(F-statistic)0.001395GENR E2=LOG(RESID2) GENR LN_=LOG(_)LS LNE2 C LN_ Dependent Variable: LNE2 Method: Least SquaresDate: 11/22/12 Time: 17:16 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-7.6927982.272023-3.3858810.0033LN_1.8393580.5713163.2195140.0048R-squared0.365421Mean dependent var-0.465580Adjusted R-squared0.330167S.D.dependent var1.915506S.E.of regression1.567714Akaike info criterion3.831754Sum squared resid44.23911Schwarz criterion3.931327Log likelihood-36.31754F-statistic10.36527Durbin-Watson stat1.937606Prob(F-statistic)0.004754由上图可看出P分别为0.0033 ,0.0048,0.004754都是小概率事件,所以方程是显著的,表明随机误差项的方差随着解释变量的取值不同而不断变化,即存在异方差性.(3)GLEISER检验LS Y C _GENR E=ABS(RESID)eq \o\ac(○,1)GENR _1=_^0.5LS E C _1Dependent Variable: E1Method: Least SquaresDate: 11/28/12 Time: 13:14Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-1.2504440.637839-1.9604370.0656_10.3265340.0812324.0197750.0008R-squared0.473046Mean dependent var1.192860Adjusted R-squared0.443771S.D.dependent var1.159531S.E.of regression0.864787Akaike info criterion2.641972Sum squared resid13.46141Schwarz criterion2.741545Log likelihood-24.41972F-statistic16.15859Durbin-Watson stat2.047999Prob(F-statistic)0.000804|e1|=-1.250444+0.326534_1^0.5 R^2=0.473046 F=16.15859 P= eq \o\ac(○,2)GENR _2=_^-2LS E C _2Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:27 Sle: 1 20Included observations: 20 VariableCoefficientStd.t-StatisticProb.C1.6651230.3427744.8577860.0001_2-657.9505338.0359-1.9463920.0674R-squared0.173874Mean dependent var 1.192860Adjusted R-squared 0.127978S.D.dependent var1.159531S.E.of regression1.082794Akaike info criterion 3.091607Sum squared residSchwarz criterion3.191180Log likelihood-28.91607F-statistic3.788442Durbin-Watson stat1.454864Prob(F-statistic)0.067388|e2|=1.665123-657.9505_^-2R^2=0.173874 F=3.788442 P= eq \o\ac(○,3)GENR _3=_^2LS E C _3Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:32 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.5805350.2376322.4430010.0251_30.0001132.67E-054.2339310.0005R-squared0.498972Mean dependent var 1.192860Adjusted R-squared 0.471138S.D.dependent var1.159531S.E.of regression0.843245Akaike info criterion 2.591520Sum squared resid 12.79911Schwarz criterion2.691093Log likelihood-23.91520F-statistic17.92617Durbin-Watson stat2.064289Prob(F-statistic)0.000499|e3|=0.580535+0.000113_4^2R^2=0.498972 F=17.92617 P=0.000499 eq \o\ac(○,4)GENR _4=_^-0,5LS E C _4Dependent Variable: EMethod: Least SquaresDate: 11/28/12 Time: 13:36Sle: 1 20Included observations: 20VariableCoefficientStd.Errort-StatisticProb.C3.4730600.7618054.5589870.0002_4-15.53960-3.1195030.0059R-squared0.350914Mean dependent var 1.192860Adjusted R-squared 0.314854S.D.dependent var1.159531S.E.of regression0.959785Akaike info criterion 2.850424Sum squared resid 16.58137Schwarz criterion2.949998Log likelihood-26.50424F-statistic9.731299Durbin-Watson stat 1.759756Prob(F-statistic)|e4|=3.473060-15.53960 _^-0.5 R^2=0.350914 F=9.731299 P= eq \o\ac(○,5)GENR _5=_^-1LS E C _5Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:45 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C2.2657780.4628754.8950140.0001_5-45.8762517.27699-2.6553390.0161R-squared0.281461Mean dependent var1.192860Adjusted R-squared0.241542S.D.dependent var1.159531S.E.of regression1.009829Akaike info criterion2.952079Sum squared resid18.35560Schwarz criterion3.051653Log likelihood-27.52079F-statistic7.050824Durbin-Watson stat1.627325Prob(F-statistic)0.016106|e5|=2.265778-45.87625_^-1R^2=0.281461 F=7.050824 P=0.016106由以上的五个方程表明,利润函数存在异方差性(只要取显著水平a大于0.067388)3.WLS方法估计利润函数(1)利用最小二乘法估计模型LS Y C _Dependent Variable: Y Method: Least SquaresDate: 11/28/12 Time: 12:40 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.8594690.7090571.2121300.2411_0.0363400.0096333.7723930.0014R-squared0.441531Mean dependent var3.100000Adjusted R-squared0.410504S.D.dependent var2.255986S.E.of regression1.732115Akaike info criterion4.031203Sum squared resid54.09Schwarz criterion4.130776Log likelihood-38.31203F-statistic14.23095Durbin-Watson stat2.111232Prob(F-statistic)0.001395得到:y^=0.859469+0.036340_ R^2=0.441531 (0.0014)T=(1.212130) (3.772393 )(2)生成权数变量:根据帕克检验得到:Ls y c _Genr lne2=log(resid^2)Genr ln_=log(_)Ls lne2 c ln_Dependent Variable: LNE2 Method: Least SquaresDate: 11/28/12 Time: 12:56 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-7.6927982.272023-3.3858810.0033LN_1.8393580.5713163.2195140.0048R-squared0.365421Mean dependent var-0.465580Adjusted R-squared0.330167S.D.dependent var1.915506S.E.of regression1.567714Akaike info criterion3.831754Sum squared resid44.23911Schwarz criterion3.931327Log likelihood-36.31754F-statistic10.36527Durbin-Watson stat1.937606Prob(F-statistic)0.004754LNEi^2=--7.692798+1.839358LN_ R^2=0.365421 进行戈里瑟检验LS Y C _GENR E=ABS(RESID)eq \o\ac(○,1)GENR _1=_^0.5LS E C _1Dependent Variable: E1 Method: Least SquaresDate: 11/28/12 Time: 13:14 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C-1.2504440.637839-1.9604370.0656_10.3265340.0812324.0197750.0008R-squared0.473046Mean dependent var1.192860Adjusted R-squared0.443771S.D.dependent var1.159531S.E.of regression0.864787Akaike info criterion2.641972Sum squared resid13.46141Schwarz criterion2.741545Log likelihood-24.41972F-statistic16.15859Durbin-Watson stat2.047999Prob(F-statistic)0.000804|e1|=-1.250444+0.326534_1^0.5 R^2=0.473046 F=16.15859 P= eq \o\ac(○,2)GENR _2=_^-2LS E C _2Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:27 Sle: 1 20Included observations: 20Variable CoefficientStd.Errort-StatisticProb.C1.6651230.3427744.8577860.0001_2-657.9505338.0359-1.9463920.0674R-squared0.173874Mean dependent var 1.192860Adjusted R-squared 0.127978S.D.dependent var1.159531S.E.of regression1.082794Akaike info criterion3.091607Sum squared resid21.18Schwarz criterion3.191180Log likelihood-28.91607F-statistic3.788442Durbin-Watson stat1.454864Prob(F-statistic)0.067388|e2|=1.665123-657.9505_^-2R^2=0.173874 F=3.788442 P= eq \o\ac(○,3)GENR _3=_^2LS E C _3Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:32 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.5805350.2376322.4430010.0251_30.0001132.67E-054.2339310.0005R-squared0.498972Mean dependent var 1.192860Adjusted R-squared 0.471138S.D.dependent var1.159531S.E.of regression0.843245Akaike info criterion 2.591520Sum squared resid 12.79911Schwarz criterionLog likelihood-23.91520F-statistic17.92617Durbin-Watson stat2.064289Prob(F-statistic)0.000499|e3|=0.580535+0.000113_4^2R^2=0.498972 F=17.92617 P=0.000499 eq \o\ac(○,4)GENR _4=_^-0,5LS E C _4Dependent Variable: EMethod: Least SquaresDate: 11/28/12 Time: 13:36Sle: 1 20Included observations: 20VariableCoefficientStd.Errort-StatisticProb.C3.4730600.7618054.558987_4-15.539604.981434-3.1195030.0059R-squared0.350914Mean dependent var 1.192860Adjusted R-squared 0.314854S.D.dependent var1.159531S.E.of regression0.959785Akaike info criterion 2.850424Sum squared resid 16.58137Schwarz criterion2.949998Log likelihood-26.50424F-statistic9.731299Durbin-Watson stat1.759756Prob(F-statistic)0.005921|e4|=3.473060-15.53960 _^-0.5 R^2=0.350914 F=9.731299 P= eq \o\ac(○,5)GENR _5=_^-1LS E C _5Dependent Variable: E Method: Least SquaresDate: 11/28/12 Time: 13:45 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C2.2657780.4628754.8950140.0001_5-45.8762517.27699-2.6553390.0161R-squared0.281461Mean dependent var1.192860Adjusted R-squared0.241542S.D.dependent var1.159531S.E.of regression1.009829Akaike info criterion2.952079Sum squared resid18.35560Schwarz criterion3.051653Log likelihood-27.52079F-statistic7.050824Durbin-Watson stat1.627325Prob(F-statistic)0.016106|e5|=2.265778-45.87625_^-1R^2=0.281461 F=7.050824 P=由上可得在戈里瑟检验里最显著的是:|e3|=0.580535+0.000113_4^2 R^2=0.498972 F=17.92617 P=所以取权数变量为 : GENR W1=1/_^1.839358GENR W2=_^2另外取:GENR W3=1/ABS(RESID)GENR W4=1/RESID^2(3)利用最小二乘法估计模型:模型一LS(W=W1) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:00Sle: 1 20Included observations: 20Weighting series: W1VariableCoefficientStd.Errort-StatisticProb.C-0.6259810.318225-1.9671030.0648_0.0116496.1001610.0000Weighted Statistics R-squared0.573253Mean dependent var 1.734420Adjusted R-squared 0.549545S.D.dependent var0.940124S.E.of regression0.630973Akaike info criterion 2.011533Sum squared resid7.166292Schwarz criterion2.06Log likelihood-18.11533F-statistic24.17958Durbin-Watson statProb(F-statistic)0.000111Unweighted StatisticsR-squared-0.050320Mean dependent var3.100000Adjusted R-squared-0.108671S.D.dependent var2.255986S.E.of regression2.375406Sum squared resid.5659Durbin-Watson stat1.104724怀特检验的结果是White Heteroskedasticity Test: F-statistic0.986667Probability0.393Obs_R-squared2.080114Probability0.353435Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:36 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.8994860.4380022.0536110.0557_-0.0146130.012947-1.1286980.2747_^26.64E-057.37E-050.9011740.3801R-squared0.104006Mean dependent var0.358315Adjusted R-squared-0.001405S.D.dependent var0.545410S.E.of regression0.545793Akaike info criterion1.764328Sum squared resid5.064137Schwarz criterion1.913688Log likelihood-14.64328F-statistic0.986667Durbin-Watson stat2.743143Prob(F-statistic)0.393得到估计结果Y^=-0.625981+0.071060_(0.318225) (6.100161)R^2=0.573253 NR^2=2.080114 P=0.393 模型二LS(W=W2) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:12Sle: 1 20Included observations: 20Weighting series: W2VariableCoefficientStd.Errort-StatisticProb.C4.3789433.2559741.3448950.1954_0.0060140.0227010.2649070.7941Weighted StatisticsR-squared0.702288Mean dependent var 4.737844Adjusted R-squared 0.685748S.D.dependent var8.767922S.E.of regression4.915135Akaike info criterion 6.117155Sum squared resid 434.8540Schwarz criterion6.216728Log likelihood-59.17155F-statistic42.46109Durbin-Watson stat 2.705915Prob(F-statistic)0.000004Unweighted Statistics R-squared-0.428848Mean dependent var3.100000Adjusted R-squared-0.508229S.D.dependent var2.255986S.E.of regression2.770576Sum squared resid138.1696Durbin-Watson stat0.87进行怀特检验的结果是White Heteroskedasticity Test: F-statistic46.95441Probability0.000000Obs_R-squared16.93442Probability0.000210Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:39 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C36.1706519.848121.8223720.0860_-1.6942460.586696-2.8877740.0102_^20.0166170.0033394.9760240.0001R-squared0.846721Mean dependent var21.74270Adjusted R-squared0.828688S.D.dependent var59.75546S.E.of regression24.73269Akaike info criterion9.391610Sum squared resid19.00Schwarz criterion9.540970Log likelihood-90.91610F-statistic46.95441Durbin-Watson stat2.837461Prob(F-statistic)0.000000得到结果是:Y^=4.378943+0.006014_(3.255974) (0.022701)R^2=0.702288 NR^2=16.93442 P=0.00000 模型三LS(W=W3) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:19Sle: 1 20Included observations: 20 Weighting series: W3 VariableCoefficientStd.Errort-StatisticProb.C0.7076590.2082663.3978670.0032_0.0387920.0053887.20__1690.0000Weighted StatisticsR-squared0.945796Mean dependent var2.344549Adjusted R-squared0.942785S.D.dependent var2.209824S.E.of regression0.528582Akaike info criterion 1.657402Sum squared resid5.029181Schwarz criterion1.756975Log likelihood-14.57402F-statistic314.0812Durbin-Watson stat 1.849162Prob(F-statistic)0.000000Unweighted Statistics R-squared0.439521Mean dependent var 3.100000Adjusted R-squared 0.408383S.D.dependent var2.255986S.E.of regression1.735229Sum squared resid54.19836Durbin-Watson stat2.097049进行怀特检验得White Heteroskedasticity Test: F-statistic0.494755Probability0.618232Obs_R-squared1.100097Probability0.576922Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:40 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.1819650.0821532.2149610.0407_0.0050.0024280.7558340.4601_^2-8.06E-061.38E-05-0.5831500.5674R-squared0.055005Mean dependent var 0.251459Adjusted R-squared-0.056171S.D.dependent var0.099611S.E.of regression0.102370Akaike info criterion-1.582959Sum squared resid0.178155Schwarz criterion-1.433599Log likelihood18.82959F-statistic0.494755Durbin-Watson stat2.096222Prob(F-statistic)0.618232Y^=0.707659+0.038792_(0.208266) (0.005388)R^2=0.945796 NR^2=1.100097 P=0.618232 模型四 LS(W=W4) Y C _Dependent Variable: YMethod: Least SquaresDate: 11/28/12 Time: 14:24Sle: 1 20Included observations: 20Weighting series: W4VariableCoefficientStd.Errort-StatisticProb.C0.5918930.1283534.6114400.0002_0.0429390.00409310.490560.0000Weighted Statistics R-squared0.994979Mean dependent var 2.087552Adjusted R-squared 0.994700S.D.dependent var4.277070S.E.of regression0.311364Akaike info criterion 0.598931Sum squared resid1.745056Schwarz criterion0.698505Log likelihood-3.989313F-statistic3567.168Durbin-Watson stat 2.173306Prob(F-statistic)0.000000Unweighted Statistics R-squared0.422958Mean dependent var 3.100000Adjusted R-squared 0.390900S.D.dependent var2.255986S.E.of regression1.760681Sum squared resid 55.79997Durbin-Watson stat 2.027424进行怀特检验的结果是White Heteroskedasticity Test: F-statistic0.851707Probability0.444108Obs_R-squared1.821500Probability0.402222Test Equation:Dependent Variable: STD_RESID^2 Method: Least SquaresDate: 11/28/12 Time: 14:42 Sle: 1 20Included observations: 20 VariableCoefficientStd.Errort-StatisticProb.C0.2750730.1762821.5604170.1371_-0.0048390.005211-0.9285840.3661_^22.04E-052.97E-050.6876810.5009R-squared0.091075Mean dependent var 0.087253Adjusted R-squared-0.015857S.D.dependent var0.217943S.E.of regression0.219664Akaike info criterion -0.055951Sum squared resid0.820291Schwarz criterion0.093409Log likelihood3.559512。
计量经济学实验报告(完成)

实验报告课程名称:计量经济学实验项目:我国国内资金利用研究学生姓名:曾健超学号:200973250131班级:0901班专业:国际经济与贸易指导教师:刘潭秋2011 年 06 月计量经济学实验报告实验时间:2011年6月24日实验地点:一教10楼实验目的:使用Eviews软件,将多元线性回归模型的理论和方法应用于我国的资金来源的研究分析。
实验原理:改革开放以来,我们国家经济持续显著的增长,经济发展一片大好。
经济的持续快速增长需要资本的不断注入,所以我对我们国家的近15年的资金利用做了一个研究。
随着资金的源源不断的涌入,我们国家的资金构成大致分成五个部分,国家预算内资金,国内贷款,利用外资,自筹资金和其他资金。
这五个部分基本上构成了我国资金来源的全部,我选取了改革开放30年来中的15个年份,具有一定的代表性。
资金是经济发展的血液,对我国的资金来源的构成做一个研究十分必要。
在这个实验中,选取国家预算内资金为被解释变量Y,解释变量为国内贷款X1利用外资X2,自筹资金X3,其他资金X4,对我国的资金利用的各部分之间的关系做一个细致的研究。
一、计量经济学模型:根据变量之间的关系,我们假定回归模型为:Y=β0+β1X1+β2X2+β3X3+β4X4+U其中Y表示我国的国家内预算资金,X1、X2、X3、X4分别代表国内贷款,利用外资,自筹资金,其他资金, 0表示在不变的情况下,资金利用的固定部分,β1β2、β3、β4、分别代表我国资金利用的各部分的权数,U 代表随机误差项。
由式子可知,我国资金利用的后面四个部分每增长1个百分点,国家预算内资金会如何变化。
二、验证方法选择:多元线性计量经济学模型的初步估计与分析、异方差检验、序列相关检验、多重共线性检验三、实验步骤:1、基本假设:设国家预算内资金为被解释变量Y,解释变量为国内贷款X1,国外资金X2,自筹资金X3,其他资金X4,U是随机干扰项,代表所有的影响因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R有所下降,且在X2、X1基础上,加入X3后的回归模型y=f( x2, x1, x3),2
检验不显著;加入X4或X5后回归模型y =f(x2, x1 ,x4)或y =f( x2, x1, x5)
回归系数T检验不显著,甚至X4的回归系数也不符合经济理论分析和经验判断;加入y =f( x2, x1, x5)与加入X4后的回归模型相同,X5回归系数经济意义不合理且
相较而言加入X3后的回归模型y=f( x2, x1, x3)其回归系数经济合理,
果,以此为基础,建立四元回归模型:
在X2、X1、X3基础上引入X4后,2
R虽有所上升,但X1的回归系数T检验不通过且
的回归系数为负值,与经济理论分析和经验判断不符;引入X5后也与引入X4相同,
升,但X3与X5的回归系数T检验不通过且经济意义不合理,故引入所有的变量建立回归模型,结果如下:
Ls y c x2 x1 x3 x4 x5
经检验X4和X5的回归系数符号为负值,且X1与X5的T检验不显著。
逐步回归估计结果表:
R
X2 X1 X3 X4 X5 2
0.9952
Y=f(x2) 0.8841
(62.4859)
Y=f(x2,x1) 0.4872 0.4159 0.997047
例5.服装需求函数。
根据理论和经验分析,影响居民服装需求Y的主要因素有:可支配收入X、流动资产拥有量K、服装类价格指数P1和总物价指数P0 ,统计资料如下。
设服装需求函数为:Y=a+b1x+b2P1+b3P0+b4K+ε
(1)多重共线性检验
运用①相关系数、②辅助回归模型以及③方差膨胀因子检验服装需求回归模型的多重共线性的可能类型;
(2)逐步回归法
①根据相关分析,建立服装需求一元基本回归模型
②根据逐步回归原理,建立服装需求模型
答案:
(1)多重共线性检验
①相关系数检验
键入:COR Y X K P1 P0 输出的相关系数矩阵为:
由上表可以看出,解释变量之间相关系数至少为0.969477,表明模型存在严重的多重共线性,且解释变量都与服装需求高度相关。
②辅助回归模型检验③方差膨胀因子检验:
操作命令:建立可支配收入X对其他解释变量的辅助回归模型
Ls x c K P1 P0
X = -221.5036 + 1.5264K - 1.0540P1 + 3.9467P0
R2= 0.992164,F= 253.2420,prob(F)= 0.000001
F统计量其伴随概率为0.000001小于 =0.05,表明模型存在严重多重共线性
方差膨胀因子检验Genr VIF1=1/(1-0.992164)
VIF1=1/(1- R2)=1/(1-0. 0.992164)= 127.6161, TOL1=1/VIF1
方差膨胀因子(VIF)大于10, 表明模型存在严重多重共线性
操作命令:建立流动资产拥有量K对其他解释变量的辅助回归模型
Ls K c x P1 P0
K = 52.5175+ 0.4434X + 0.7331P1 - 1.4518P0
R2= 0.981982,F= 108.9972,prob(F)= 0.000013
F统计量其伴随概率小于α=0.05,表明模型存在严重多重共线性
方差膨胀因子检验Genr VIF2=1/(1- 0.981982)
VIF2=1/(1- R2)=1/(1- 0.981982)= 55.5000555001, TOL2=1/VIF2
方差膨胀因子(VIF)大于10,表明模型存在严重多重共线性
操作命令:建立服装类价格指数P1对其他解释变量的辅助回归模型
Ls P1 c x K P0
P1 = -31.2521 - 0.0917X + 0.2196K + 1.3415P0
R2= 0.986309,F= 144.0798,prob(F)= 0.000006
F统计量其伴随概率小于α=0.05,表明模型存在严重多重共线性
方差膨胀因子检验Genr VIF3=1/(1-0.986309)
VIF3=1/(1- R2)=1/(1-0.986309)= 73.0406836608, TOL3=1/VIF3
方差膨胀因子(VIF)大于10,表明模型存在严重多重共线性
操作命令:建立总物价指数P0对其他解释变量的辅助回归模型
Ls P0 c x K P1
P0 = 42.7011 + 0.1234X - 0.1563K + 0.4820*P1
R2= 0.992102,F= 251.2234,prob(F)= 0.000001
F统计量其伴随概率小于α=0.05,表明模型存在严重多重共线性
方差膨胀因子检验Genr VIF4=1/(1- 0.992102)
VIF4=1/(1- R2)=1/(1- 0.992102)= 126.614332742, TOL4=1/VIF4
方差膨胀因子(VIF)大于10,表明模型存在严重多重共线性
上述辅助回归模型的F统计量,其伴随概率均接近于零,表明模型存在严重多重共线性,这一结论也可通过各方差膨胀因子(VIF)均大于10中得到。
(2)逐步回归法
①建立服装需求一元基本回归模型
由相关系数图表可知,收入与服装需求的相关性最强,所以,以Y=a+bX +ε即Y与X的一元线性回归模型,作为服装需求基本回归模型,Ls y c x
估计结果如下:
服装需求一元基本回归模型为
yˆ= -1.2489 + 0.1179X
T (42.4860)
R=0.995036 F= 1805.063 prob(F)= 0.000000
R2= 0.995588 2
②根据逐步回归原理,建立服装需求模型
以上述一元线性回归模型为基本模型,顺次引入其他变量估计二元回归模型,结果如下:
Ls y c x K
Ls y c x P1
Ls y c x P0
经比较可知,新加入K的回归模型Y=f(x,K),K的回归系数为负,不符合实际的经济意义且T检验不通过;新加入P1的回归模型Y=f(x,P1)及新加入P0的回归模型Y=f(x,P0)虽P1和P0回归系数的T检验均不通过,但经济意义合理,
R值略高于Y=f(x,P1),因此,Y=f(x,P0)估计的由于Y=f(x,P0) 的调整判定系数2
结果为最优的二元回归模型,以此为基础,建立三元回归模型:
Ls y c x P0 K
Ls y c x P0 P1
在X 、P0基础上,加入K 后的回归模型y=f(X, P0, K ),2R 有所下降, K 的回归系数为负数,与经济意义不符合,T 检验也不显著;加入P1后回归模型y=f(X,
P0, P1)
,2R 有所上升,回归系数T 检验显著,且回归系数符合经济理论分析和
经验判断,经济合理,故选择y=f(X, P0, P1)估计结果,以此为基础,建立四元回归模型:
Ls y c X P0 P1 K
R有所下降K,K的回归系数T检验不在X、P0 、P1基础上引入K后,2
通过且K的回归系数为负值,与经济理论分析和经验判断不符。
逐步回归估计结果表:
注:表中数字为估计的回归系数及其T统计量值
经过反复的引入-检验-剔除,比较检验都通过的回归模型y=f(X, P0, K)与Y=f(x,P0),由于回归模型y=f(X, P0, K)的2
R高于Y=f(x,P0),故服装需求最终确定理想模型为
Yˆ= -12.4457 + 0.1042X + 0.3132P0 - 0.1866P1
(0.0138) (0.1208) (0.0754)
t= (7.5469) (2.5919) (-2.4739)
R2=0.9980,2
R=0.9970,F=638.3684,prob(F)= 0.000000DW=3.4957此模型经济意义合理,可决系数为0.997358,接近于1,表明模型对样本拟合优度高;F统计量为3208.727,其伴随概率为0.000000,接近于零,表明模型整体线性关系显著;回归系数显著。
模型估计结果说明,服装需求Y主要取决于可支配收入X、服装类价格指数P1和总物价指数P0;在其他因素不变的情况下,可支配收入X每增加1元,服装需求Y增加0.1042元;在其他因素不变的情况下,总物价指数P0每增长1%,服装需求Y将增长0.3132元;在其他因素不变的情况下,服装类价格指数P1每增长1%,服装需求Y减少0.1866元。
