大学物理(刘克哲版)第六章习题答案
第6章大学物理(I-1)教材课后习题答案

与一边平行。(1)线圈平面与地磁场 B 的夹角为什么值时,线圈中产生的感应电动势最大;
(2)设地磁场的 B 0.55G ,这时要在线圈中最大产生 10mV 的感应电动势,求线圈的匝
数N。
解(1)由题意知: S 0.01m2, n 30 revs-1,
平面法线
B
2n 60 rads-1
l
x
2
l
6.5 解图
因为
v dl , dt
所以
i
dm dt
0 I tan [v ln(1 a ) av ]
2
l la
若 l d 时,因为 tan b a ,
所以
i
0 Ivb [ln(1 2a
a) d
d
a
] ,其方向为顺时针方向。 a
6.6 一正方形线圈每边长 100mm,在地磁场中转动,每秒转 30 圈,转轴通过中心并
2.958103 sin(120t) ,
所以
imax 2.958 V, Iimax 2.958103 A
6.2 半 径为 a 10cm , 匝数 为 N 100 的圆 形线 圈以 o1o2 为 转轴 ,在均 匀磁 场
B 0.5T 中以转速 n 600 转/分转动。开始时,线圈平面垂直于磁场,如题 6.2 图所示, 当线圈转过π/2 时,求:(1)线圈中的感应电流,已知线圈的电阻 R 100 ;(2)感应电
2
a
6.4 如题 6.4 图所示,导体棒 ab 与金属轨道 ca 和 db 接触,
整个线框放在 B 0.50 T 的均匀磁场中,磁场方向与图面垂直。 (1)若导体棒以 4.0 m s-1 的速度向右运动,求棒内感应电动
大学物理下答案第六章

(2)
6-25声波是流体或固体中的压缩波,在讨论声波时,讨论声波中的压强(即压力)变化要比讨论声波中质元的位移更方便些,可以证明,当声波的位移波函数为 时,对应于压力变化的波函数为
是相对于为扰动时压力 的压强变化值, 是介质的体密度。
(1)人耳能够忍受的强声波中的最大压强变化pm约为28N/m2(正常的大气压强约为1.0×105N/m2)若这一强度波的频率为1000Hz,试求这声波所对应的最大位移。
此时系统做振幅为A,圆频率为w的简振动。
6-7有一鸟类学家,他在野外观察到一种少见的大鸟落在一棵大树的细枝上,他想测得这只鸟的质量,但不能捉住来称量,于是灵机一动,测得这鸟在数枝上在4s内来回摆动了6次,等鸟飞走以后,他又用1kg的砝码系在大鸟原来落得位置上,测出树枝弯下了12cm,于是很快算出了这只鸟的质量。你认为这位鸟类学家是怎样算的?你想到了这种方法了吗?这只鸟的质量是多少?
6-44试解释弦乐器的以下现象:
(1)较松的弦发生的音调较低,而较紧的弦则音调较高;
(2)较细的弦发生的音调较高,而较粗的弦则音调较低(古人称之为“小弦大声,大弦小声”);
(3)正在振动的两端固定的弦,若用手指轻按弦的中点时,音调变高到两倍,若改按弦的三分之一处时,音调增至三倍;
(4)用力弹拨琴弦(而非用手指按弦)时,能同时听到若干音调各异的声音。(提示:音调高低与弦振动的频率成正比。此外,在(4)情形中弦以基频振动的同时还以若干泛频振动。)
试据此推导(6.11)、(6.12)及(6.40)式。
6-42海啸是一种波长约为几十至几百千米、在海水中传播的波动现象。它在深海区域并不易被察觉,但一旦海啸接近岸边往往会造成巨大的灾害。试从能量角度分析其中的原因。
大学物理第6章真空中的静电场课后习题与答案

第6章真空中的静电场习题及答案1.电荷为q 和2q 的两个点电荷分别置于x1m 和x1m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷 q 位于点电荷 0q 的右侧,它受到的合力才可能为0,所以2qqqq00224(x 1)4(x1) ππ 00故x3222.电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放 一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都 为零)?(2)这种平衡与三角形的边长有无关系?解:(1)以A 处点电荷为研究对象,由力平衡知,q 为负电荷,所以2 4 1 π 0 q a 22 cos304 1 π 0 ( q 33qa 2 )3故qq3(2)与三角形边长无关。
3.如图所示,半径为R 、电荷线密度为1的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dqdl 1,dq 在带电圆环轴 线上x 处产生的场强大小为 dE 4 dq20(xRy2 )根据电荷分布的对称性知,yE0E zdEdEcos x41xdq 1R 3 22 2O(xR) 02xl式中:为dq 到场点的连线与x 轴负向的夹角。
E x4x 220(xR) 3 2dqzx21R R 1 x4x 2R2()3 2 2xR 2( 02 )3 2下面求直线段受到的电场力。
在直线段上取dqdx2,dq受到的电场力大小为Rx12dFxdxEdq32222(xR)0方向沿x轴正方向。
直线段受到的电场力大小为Rlx12FdxdF3202220xR)(11R1121/22R22lR方向沿x轴正方向。
4.一个半径为R的均匀带电半圆环,电荷线密度为。
求:(1)圆心处O点的场强;(2)将此带电半圆环弯成一个整圆后,圆心处O点场强。
(完整版)《大学物理》习题册题目及答案第6单元 气体动理论

第6单元 气体动理论 序号 学号 姓名 专业、班级一 选择题[ C ]1.在标准状态下, 若氧气(视为刚性双原子分子的理想气体)和氦气的体积比2121=V V ,则其内能之比21/E E 为: (A) 1/2 (B) 5/3 (C) 5/6 (D) 3/10[ B ]2.若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻耳兹曼常量,R 为摩尔气体常量,则该理想气体的分子数为(A) pV/m (B) pV/(kT)(C) pV/(RT) (D) pV/(mT)[ D ]3.若)(v f 为气体分子速率分布函数,N 为分子总数,m 为分子质量,则 )(21221v Nf mv v v ⎰ d v 的物理意义是 (A) 速率为v 2的各分子的总平均动能与速率为v 1的各分子的总平均动能之差。
(B) 速率为v 2的各分子的总平动动能与速率为v 1的各分子的总平动动能之和。
(C) 速率处在速率间隔v 1~ v 2之内的分子的平均平动动能。
(D) 速率处在速率间隔v 1~ v 2之内的分子平动动能之和。
[ D ]4.在一密闭容器中,储有A 、B 、C 三种理想气体,处于平衡状态,A 种气体的分子数密度为 1n ,它产生的压强为 1p ,B 种气体的分子数密度为 12n ,C 种气体的分子数密度为3n 1,则混合气体的压强p 为(A)31p (B)41p(C)51p (D)61p二 填空题1.在定压下加热一定量的理想气体,若使其温度升高1K 时,它的体积增加了0.005倍,则气体原来的温度是_________200k__________。
2.用总分子数N 、气体分子速率v 和速率分布函数f(v),表示下列各量:(1)速率大于0v 的分子数= ⎰∞0)(v dv v Nf ;(2)速率大于0v 的那些分子的平均速率=⎰⎰∞∞00)()(v v dv v f dv v vf ;(3)多次观察某一分子的速率,发现其速率大于0v 的概率=⎰∞0)(v dv v f 。
大学物理第6节练习答案

第六章 热力学基础练 习 一一. 选择题1. 一绝热容器被隔板分成两半,一半是真空,另一半是理想气体,若把隔板抽出,气体将进行自由膨胀,达到平衡后( A ) (A) 温度不变,熵增加; (B) 温度升高,熵增加;(C) 温度降低,熵增加; (D) 温度不变,熵不变。
2. 对于理想气体系统来说,在下列过程中,哪个过程系统所吸收的热量、内能的增量和对外作做的功三者均为负值。
( C ) (A) 等容降压过程; (B) 等温膨胀过程; (C) 等压压缩过程; (D) 绝热膨胀过程。
3. 一定量的理想气体,分别经历如图1(1)所示的abc 过程(图中虚线ac 为等温线)和图1(2)所示的def 过程(图中虚线df 为绝热线) 。
判断这两过程是吸热还是放热:( A ) (A) abc 过程吸热,def 过程放热; (B) abc 过程放热,def 过程吸热; (C) abc 过程def 过程都吸热; (D) abc 过程def 过程都放热。
4. 如图2,一定量的理想气体,由平衡状态A 变到平衡状态B(A p =B p ),则无论经过的是什么过程,系统必然( B ) (A) 对外做正功; (B) 内能增加; (C) 从外界吸热; (D) 向外界放热。
二.填空题1. 一定量的理想气体处于热动平衡状态时,此热力学系统不随时间变化的三个宏观量是P V T ,而随时间变化的微观量是每个分子的状态量。
2. 一定量的单原子分子理想气体在等温过程中,外界对它做功为200J ,则该过程中需吸热__-200__ ___J 。
3. 一定量的某种理想气体在某个热力学过程中,外界对系统做功240J ,气体向外界放热620J ,则气体的内能 减少,(填增加或减少),21E E = -380 J 。
4. 处于平衡态A 的热力学系统,若经准静态等容过程变到平衡态B ,将从外界吸热416 J ,若经准静态等压过程变到与平衡态B 有相同温度的平衡态C ,将从外界吸热582 J ,所以,从平衡态A 变到平衡态C 的准静态等压过程中系统对外界所做的功为 582-416=166J 。
(完整版)大学物理学(课后答案)第5-6章
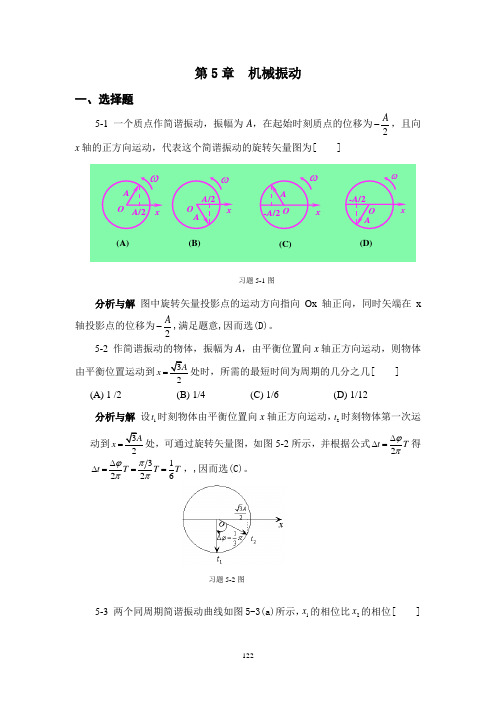
第5章 机械振动一、选择题5-1 一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2A-,且向x 轴的正方向运动,代表这个简谐振动的旋转矢量图为[ ]分析与解 图中旋转矢量投影点的运动方向指向Ox 轴正向,同时矢端在x 轴投影点的位移为2A-,满足题意,因而选(D)。
5-2 作简谐振动的物体,振幅为A ,由平衡位置向x 轴正方向运动,则物体由平衡位置运动到32Ax =处时,所需的最短时间为周期的几分之几[ ] (A) 1 /2 (B) 1/4 (C) 1/6 (D) 1/12分析与解 设1t 时刻物体由平衡位置向x 轴正方向运动,2t 时刻物体第一次运动到32A x =处,可通过旋转矢量图,如图5-2所示,并根据公式2t T ϕπ∆∆=得31226t T T T ϕπππ∆∆===,,因而选(C)。
5-3 两个同周期简谐振动曲线如图5-3(a)所示,1x 的相位比2x 的相位[ ] O O OO A Axxx(A) (B)(D)(C)A /2-A /2 A /2 -A /2A Aωωωωx习题5-1图习题5-2图(A) 落后2π (B) 超前2π(C) 落后π (D) 超前π分析与解 可通过振动曲线作出相应的旋转矢量图(b ),正确答案为(B )。
5-4 一弹簧振子作简谐振动,总能量为E ,若振幅增加为原来的2倍,振子的质量增加为原来的4倍,则它的总能量为[ ](A) 2E (B) 4E (C) E (D) 16E 分析与解 因为简谐振动的总能量2p k 12E E E kA =+=,因而当振幅增加为原来的2倍时,能量变为原来的4倍,因而答案选(B)。
5-5 两个同振动方向、同频率、振幅均为A 的简谐振动合成后,振幅仍为A ,则这两个简谐振动的相位差为[ ](A) 60 (B) 90 (C) 120 (D) 180分析与解 答案(C )。
由旋转矢量图可知两个简谐振动的相位差为120时,合成后的简谐运动的振幅仍为A 。
大学物理习题册答案 第六单元 气体动理论
率分布曲线。其中曲线(a),是____氦____气分子的速率分布曲线;曲线(c)是____氩_____气分子的
பைடு நூலகம்
速率分布曲线;
三 计算题
1. 一超声波源发射声波的功率为 10 W。假设它工作 10 s,并且全部波动能量都被 1 mol 氧气吸收
1
而用于增加其内能,问氧气的温度升高了多少?
(氧气分子视为刚性分子,摩尔气体常量 R = 8.31 (J·mol 1 ·K 1 ))
用转变为内能的增加量 N i kT 2
1 (Nm) 2 N i kT N 5 kT
2
2
2
T m 2 2 32 103 1002 7.7(K )
5k 5R
5 8.31
2
解: E Pt M i RT ,式中 P 为功率,则 2
T Pt 10 10 4.81(K)
M
5 2
R
1 5 8.31 2
2.储有氧气的容器以 100m·s 1 的速度运动。假设该容器突然停止,全部定向运动的动能都变为 气体分子热运动的动能,问容器中氧气的温度将会上升多少?
解:
容器停止,分子集合的定向机械运动动能 1 (Nm) 2 ,经过分子与分子,分子与器壁之间的相互作 2
质量 M mol = 27.8×10-3 kgmol-1
。 [摩尔气体常量 R = 8.31 (J·mol 1 ·K 1 )]
4.一能量为 10 12 eV 的宇宙射线粒子,射入一氖管中,氖管内充有 0.1mol 的氖气,若宇宙射线粒
子的能量全部被氖分子所吸收,则氖气温度升高了
1.28×10-7
K。
[1eV = 1.6×10 19 J,摩尔气体常数 R = 8.31 (J·mol 1 ·K 1 )]
大学物理第6章静电场中的导体和电介质解答(精)
第六章静电场中的导体和电介质解答一、选择题1.D 2.C 3.B 4.D 5.D 6.B 7.D 8.B 二、填空题1.-q; -q 2.3.r1r22322U04. 45. 6.7.Qd2ε0S;Qdε0SλQ04πε0εrr12λ2πr;;2πε0εrrQ04πr12Q04πr22;;Q04πεr202Q1+Q22s2s8.εr; 1;εr;εr;Q1-Q2; -Q1-Q22s;Q1+Q22s三、计算题1.解:电荷重新分布后,设c板左侧面带电荷为-q1,右侧面带电荷+q2,但电荷总和不变,即 q=-q1+q2 (1)此时(可用髙斯定理证明),a板上带电荷为+q1,b板上带电荷为-q2 设c板电势为Uc,则a、c板之间电势差为U-Uc=E1d2a、c板之间电场强度大小为E1=q1ε0S⎛q1所以 U-Uc= εS⎝0⎫d⎪⎪2⎭由此得 q1=同理可得c、b板之间电势差为2ε0Sd(U-Uc) (2)Uc⎛q2= εS⎝0⎫d⎪⎪2⎭由此得 q2=2ε0Sd将(2)、(3)代入(1)化简得c板之电势为Uc=Uc (3)⎫1⎛dU+⎪ q⎪2 2εS0⎝⎭2.解:设两平行长直导线A、B,单位长度上分别带电量+λ 和 - λ ,如图所示,离Ox轴原点为x 处一点P的电场强度为λλE= +2πε0x2πε0(d-x)则两导线之间电势差为UA-UB=⎰d-aaE⋅dl=⎰d-aa[λ2πε0xa+λ2πε0(d-x)=]dxA≈=λ2πε[lnx-ln(d-x)]d-aλπεlnd-aaλπεlnda(d >>a)所以两导线单位长度的电容为 C=λUA-UB=πεlnda3. 解:(1)点电荷+q使导体球产生感应电荷±q'在球表面上。
球心O处的电场强度为±q'的电场强度E'以及点电荷+q的场强E得叠加。
即EO=E+E'由静电平衡,EO=0,若取球心O为坐标原点,则E'=-E=q4πε0rˆrˆ是从O指(r向电荷+q的单位矢量)。
大学物理第五章和第六章习题答案
( B) 刚体受力越大,此力对刚体转轴的力矩也越大; (C)刚体绕定轴转动,则一定受到力矩的作用; (D)刚体绕定轴的转动定律表述了作用于刚体上的外力对转轴的合外力矩与角加速度两者之间的瞬 时关系。 解答 转动定律 M Ja 表述了作用于给定刚体上的外力对定轴的合外力矩与角加速度之间的瞬 时关系,即某时刻对定轴的合外力矩将引起该时刻刚体转动状态的改变,使刚体获得角加速度,可类比 于牛顿第二定律 F ma 表示的合外力与加速度之间的瞬时关系。 刚体受外力 F 作用,如果力的作用线通过刚体的转轴 0,力臂为零,这时力矩 M 为零,因此虽然刚体受 力作用,但对刚体不一定有力矩作用。即使刚体受力大,若此力对定轴的力臂甚小,则力矩仍也可能很
——————1——————
大学物理习题集(上)
解答
如图 5-4(a)所示,设滑轮半径为 R,转动惯量为 J。当绳下滑挂一质量为 m 的物体时,受
绳的张力 FT 和重力 W=mg 作用,加速度 a 铅直向下。由牛顿第二定律知, mg FT ma ,又按滑轮的 转动定律知 FT R J ,已知 a aR ,解之得
1 2 ml ,则棒在竖直位置时的角加速度大小 3
;若将棒拉到水平位置,然后由静止释放,此时棒的角加速 。 棒在竖直位置时,受重力 mg 和轴的支承力 FN 作用,此两
力的作用线通过棒轴 O ,力臂为零,所以力矩为零,所以力矩为零,按转动定律,角加速度 a 为零。 棒被拉到水平位置,自静止释放,重力的力矩 M mg 律,可求得角加速度为
1 mL2 。开始时细杆静止,有一个质量为 m 的小球沿桌面正对着杆的 的竖直轴自由转动,其转动惯量为 3
2L
; (B)
2 3 4 ; (C) ; (D) 。 3L 4L 5L
大学物理第五章和第六章习题答案
大学物理习题集(上)专业班级 姓名_ 学号_第五章 刚体的定轴转动一.选择题1.关于刚体对轴的转动惯量,下列说法中正确的是[ C ](A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B )取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D )只取决于转轴的位置,与刚体的质量和质量的空间分布无关。
2. 均匀细棒 OA 可绕通过某一端 O 而与棒垂直的水平固定光滑轴转动,今使棒从水平位置由静止开始自 由下降,在棒摆到竖直位置的过程中,下述说法哪一种是正确的?[ A ](A )角速度从小到大,角加速度从大到小。
A(B )角速度从小到大,角加速度从小到大。
(C )角速度从大到小,角加速度从大到小。
(D )角速度从大到小,角加速度从小到大。
3. 如图所示,一圆盘绕水平轴 0 做匀速转动,如果同时相向地射来两个质量相同、速度大小相同,且沿同一直线运动的子弹。
子弹射入圆盘均留在盘内,则 子弹射入后的瞬间,圆盘的角速度将 [ B ](A )增大; (B )减小; (C )不变; (D )无法确定。
解答 以圆盘和两子弹为系统,外力矩为零,系统的角动量守恒。
按题意, 两个子弹的初始角动量(对 0 轴之和为零。
两子弹留在圆盘内,增大了圆盘的 转动惯量。
设圆盘的转动惯为 J ,转动的角速度为 ω0 ,则有J ω0 = ( J + ∆J )ωω0 > ω有速度减小,所以应选(B )4. 一轻绳绕在具有水平转轴的定滑轮上,绳下端挂物体,物体的质量为 m ,此时滑轮的角加速度为 a 。
若将物体卸掉,而用大小等于 mg 、方向向下的力拉绳子,则滑轮的角加速度将[ A ](A)变大; (B )不变; (C )变小; (D )无法判断。
解答如图 5-4(a)所示,设滑轮半径为 R,转动惯量为 J。
当绳下滑挂一质量为m 的物体时,受绳的张力F T 和重力W=mg 作用,加速度a 铅直向下。
