勾股定理9种证明(有图)
勾股定理16种证明方法

勾股定理16种证明方法(总页)-CAL-FENGHAL-(YICAI)-Company One 1■CAL■本页仅作为文档封面,使用请直接删除整理得则每个直它的面积勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b,斜边长为c,再做 三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b,所以而积相等.即 (T +b 2 +4x —ab = c 2 +4x —ab 2 2 【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形, 丄,积等于㊁".把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上, B 、F 、C 三点在一条直线上,C 、G 、 •・• Rt AHAE 今 RtAEBF,・•・ ZAHE = ZBEF.•••乙 AEH+ ZAHE = 90o,AAEH+ ABEF = 90o.••• A HEF = 180o—90o= 90o.四边形EFGH 是一个边长为正方形•它的面积等于c2.••• RtAGDH w RtAHAE,ZHGD=乙 EHA ・ZHGD+ 乙 GHD = 90o,ZEHA+ AGHD = 90o.乙 GHE = 90o,ADHA = 90o+ 90o= 180o.••- ABCD 是一个边长为a + b 的正方形, (»)—4冷如匚 宀宀几【证法3】(赵爽证明)以a 、b 为直角边(b>a ),以c 为斜 边作四个全等的直角三角形,则每个直角_ 丄三角形的面积等于2 •把这四个直角三 角形拼成如图所示形状.••• RtADAH w RtAABE,•■- ZHDA= A EAB.•••乙 HAD+ AHAD = 90o, D 三点在 C•• A EAB + ZHAD = 90o,•• ABCD是一个边长为c的正方形,它的面积等于c2.••• EF = FG =GH =HE = b—a , Z HEF = 90o.EFGH是一个边长为b—a的正方形,它的面积等于(b-a)\a2 +h2 =".【证法4] (1876年美国总统Garfield证明)以a、b为直角边.以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于2 •把这两个直角三角形拼成如图所示形状,使A、% B三点在一条直线上.•RtAEAD w RtACBE,•AADE= ABEC ・•乙AED + A ADE = 90o,•ZAED+ ZBEC = 90o.・乙DEC = 180o一90o= 90o.• ZXDEC是一个等腰直角三角形,J_ .2它的面积等于・又 *.* 乙DAE = 90o, Z_EBC = 90o,・•・AD〃BC・••- ABCD是一个直角梯形,它的面积等于2('/ + /?)...如+疔=2冷¥••・ a2 +b2 =c2.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c・把它们拼成如图那样的一个多边形,使D、E、F在一条直线上•过C作AC的延长线交DF 于点P・T D、E、F 在一条直线上,且RUGEF w RtAEBD,AEGF=乙BED,•••乙EGF+ 乙GEF = 90°,••• ZBED+ 乙GEF = 90°,Z_ BEG =180o一90o= 90o.又T AB = BE = EG = GA = c,••• ABEG是一个边长为c的正方形.••• ZABC+ ACBE = 90o.T RtAABC w RtAEBD,A ABC = AEBD・••・ ZEBD+ ZCBE = 90o.即ACBD= 90Oe 又•••ZBDE = 90o, ZBCP = 90o, BC = BD = a.BDPC是一个边长为a的正方形. 同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,贝IJc2 = S + 2x—ab2a2 +b2 =c2.【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a、b (b>a),斜边长为c ・再做一个边长为c的正方形•把它们拼成如图所示的多边形,使E、A、C三点在一条直线上. E过点Q作QP〃BC,交AC于点P・过点B作BM丄PQ,垂足为M;再过点尸F作FN丄PQ,垂足为N・••• ZBCA = 90o, QP〃BC,••• ZMPC = 90o, c••• BM 丄PQ,••• ZBMP = 90o,BCPM是一个矩形,即乙MBC = 9£••• ZQBM + AMBA = ZQBA = 90o,乙ABC + 乙MBA = ZMBC = 90o,ZQBM=乙ABC,又ZBMP = 90o, ZBCA = 90o, BQ = BA = c,••• RtABMQ w RtABCA.同理可证RtAQNF w RtAAEF・从而将问题转化为【证法4】(梅文鼎证明).【证法7】(欧几里得证明)做三个边长分别为a、b、c的正方形,把它们拼成如图所示形状使H、C、B三点在一条直线上,连结BF、CD•过C作CL IDE, 交AB于点M,交DE于点L.•/ AF = AC, AB = AD, FZFAB= A GAD,••• AFAB AGAD,£ 2••• AFAB的面积等于㊁",AGAD的面积等于矩形ADLM 的面积的一半,•••矩形ADLM的面积=/・同理可证,矩形MLEB的面积=心又•••ADG Z.DH F = 90o,•••正方形ADEB的面积=矩形ADLM的面积+矩形MLEB的面积c2 =a2 +b2 .即cr +b2 =c2.【证法8](利用相似三角形性质证明)如图,在RtAABC中,设直角边AC、BC的长度分别为a、b,斜边AB的长为c,过点C作CD丄AB,垂足是D・在Z\ADC 和Z\ACB 中,••• AADC=乙ACB = 90o, ACAD=ABAC,••• AADC s AACB・AD :AC = AC : AB, 即AC2=AD^AB.同理可证,ZXCDB S AACB,从而有BC~BD・AB・AC2 + BC2 =(AD + DByAB = AB2即a2+h2 =c2.【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a、b (b>a),斜边长为c・再做一个边长为c的正方形•把它们拼成如图所示的多边形•过A作AF丄AC, AF交GT 于F, AF交DT于R・过B作BP丄AF,垂足为P・过D作DE与CB的延长线垂直,垂足为E, DE交AF于H・••• ZBAD = 90o, ZPAC = 90o,••• ZDAH= ZB AC.又•••ADHA = 90o, ZBCA = 90o,AD = AB = c,••• RtADHA w RtABCA・DH = BC = a, AH = AC = b・由作法可知,PBCA是一个矩形, 所以RtAAPB w RtABCA・艮[J PB = CA = b,AP= a,从而PH = b一a・••• RtADGT w RtABCA ,RtADHA W RtABCA.・•・ RtADGT W RtADHA .DH = DG = a?AGDT = Z.HDA •AGDH = AGDT + ATDH = ZHDA+ Z.TDH = 90o? DGFH是一个边长为a的正方形.••・GF = FH = a • TF丄AF, TF = GT—GF = b—a •••• TFPB是一个直角梯形,上底TF=b—a,下底BP=b,高FP=a + (b—a)・用数字表示面积的编号(如图),则以c为边长的正方形的面积为c~ = S] + S2+S3+S4+S5ZDBC+ 乙 BHT= ZTBH+ ZBHT = 90o u•乙GHF= ZDBC ・■ DB = EB 一ED = b 一a,ZHGF= ZBDC = 90o,• RtAHGF w RtABDC ・即 S 产 S 】.过Q 作QM 丄AG,垂足是M ・由ABAQ= ZBEA = 90o,可知 乙ABE =A QAM,而 AB = AQ = c,所以 RtAABE w RtAQAM ・又 RtAHBT w RtAABE.所以 RtAHBT w RtAQAM •即凡=比.由 RtAABE w RtAQAM,又得 QM 二 AE = a, A AQM =乙 BAE. / ZAQM+ ZFQM = 90o,乙BAE + 乙CAR = 90o, AAQM= ABAE, ••乙 FQM= A CAR ・.• ZQMF = ZARC = 90o, QM = AR = a,•• RtAQMF w RtAARC ・即 S 产 .• c~ = S] + S 》+ + S4 + S 气 = S] + S 6 b~ = S* + S? +• ■ t 9, -S 1 = S 2 = S 5 S 4 = S 6 • J I 1 + S. + S 4 = — [/? + (/?-«)]•[« + (/?-6/)] b 2 - — ab *.* 2 = 2 t S5 =S& +S9 ... S3+S4"—抄-S j-sr •② 把②代入①,得 =+ S 2+S 9 - i, +a 2. a 2 +b 2 =c 2. 【证法10](李锐证明) 设直角三角形两直角边的长分别为a 、b (b>a),斜边的长为c ・做三个边长分别为 a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上•用数字 表示面积的编号(如图).• ZTBE= ZABH = 90o, • ATBH = A ABE ・ • ZBTH= ZBEA = 90o, BT = BE = b,• RtAHBT w RtAABE ・ • HT = AE = a. • GH = GT —HT = b —a ・ •乙 GHF+ ZBHT = 90o, 又・ 又・ 8 D Xc . K A R H 4 5•= S] + 比 + S3 +S7 + 比—S | + S4 + S3 + S«> + S5【证法【证法11](利用切割线定理证明)在RtAABC 中,设直角边BC = a, AC = b,斜边AB = c.如图,以B 为圆心a 为半 径作圆,交AB 及AB 的延长线分别于D 、E,则BD = BE = BC = a.因为ZBCA = 90o, 点C 在OB 上,所以AC 是OB 的切线•由切割线定理得=(AB + BE\AB - BD)= (c + dXc_d)2 °=即 b 2=c 2-a 2,a 2 +b 2= c 2.在RtAABC 中,设直角边BC = a, AC 乖 斜边AB = c (如图)•过点A 作AD 〃 CB,过点B 作BD 〃CA,则ACBD 为矩形,矩形ACBD 内接于一个圆•根据多列米定 理,圆内接四边形对角线的乘积等于两对边乘积之和,有AB^ DC = AD> BC + AC< BD fT AB = DC = c, AD = BC = a,AC = BD = b, AB 2 = BC 2 +AC 2 即 c 2 =a 2 +b 2:.a 2 +b 2 =c 2. 【证法13】(作直角三角形的内切圆证盼) b在RtAABC 中,设直角边BC = a, AC = b,斜边AB = c.作RtZXABC 的内切圆0 O,切点分别为D 、E 、F (如图),设OO 的半径为匚V AE = AF, BF = BD, CD = CE,AC + BC-AB =(AE + CE )+(BD + CD )_(AF + BF )=CE+CD = r + r = 2r,a+b-c = 2r t a+ b = 2r + c.(a+ b )2=(2r + c )2cr +b 2 + lab = 4(r 2 +rc )+c 2 D AE a B ab B又•••1—cr +=2眈=S MOB + S、B0C + S\\oc =—(2r + c + c)r-ar +—br Swc =㊁"12ab = 4Swc・40,+ rc)= 2aba2 +b2 +2ab = 2ab + c2f a2 +b2 =c2.或者 BD : a 、 ,斜边的长为c •做两个边长分别为使E 、 B H 、三【证法14](利用反证法证明)如图,在RtAABC 中,设直角边AC 、BC 的长度分别为a 、b,斜边AB 的长为c, 过点C 作CD 丄AB,垂足是D ・假设/+宀[即假设AC 2+BC 2^AB\则由AB 2 =AB^AB = AB (AD + BD )=AB^AD+AB^BD可知 AC 2^AB^AD t 或者 BCJAB ・BD.即 AD : ACMAC : AB,AB ・在Z\ADC 和Z\ACB 中,T AA = ZA,•••若 AD : ACHAC : AB, 乙ADCH 乙ACB ・ 在Z\CDB和ZXACB 中, ••• ZB = ZB.若 BD : BCMBC : AB.乙CDBH 乙ACB ・又••• ZACB = 90o.•••乙 ADCH90O,乙 CDBH90O.这与作法CD 丄AB 矛盾•所以,AC 2 + BC? h 佔2的假设不能成立.a 2 +b 2 =c 2.【证法15](辛卜松证明)设直角三角形两直角边的长分别为a 、b,斜边的长为c ・作边长是a+b 的正方形 ABCD.把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为 (a+ b)2=^+lr +2ab ;把正方形ABCD 划分成上方右图所示的几个部分,则正方形… , (a + bY =4x — ab + c 2.ABCD 的面积为 2 =2ah + c-./. a 2 +b 2 +2ab = 2ab + c 2a 2 +b 2 = c‘.【证法16](陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a) b 的正方形(b>a),把它们拼成如图所示形状, 数字表示面积的编号(如图). 在EH = b 上截取ED = a,连结DA 、DC, 贝lj AD= c. •/ EM = EH + HM = b + a , ED = a,••• DM = EM—ED = (+)—a = b ・ 又 T ZCMD = 90o, CM = a, /_ AED = 90o, AE = b, 则b A C b aH M 4 F・•・ RtAAED W RtADMC> •••乙EAD= ZMDC, DC = AD = c. •••乙ADE+ Z.ADC+ ZMDC=180o,AADE+ AMDC= ZLADE+ AEAD = 90o,乙ADC = 90o..•.作AB〃DC, CB〃DA,则ABCD是一个边长为c的正方形. T ZBAF + 乙FAD = A DAE + 乙FAD = 90o,•■- ZBAF=ZDAE・连结FB,在ZXABF和Z\ADE中,AB =AD = c, AE = AF = b, Z_ BAF= /_ DAE,••• AABF w AADE・A AFB = A AED = 90o, BF = DE = a・点B、F、G、H在一条直线上.在RtAABF 和RtABCG 中,AB = BC = c, BF = CG = a,••• RtAABF w RtABCG・• • = S, + S; + S4 + S、b~ = Sj + S, + S & Q ~ = S? + S?S] = S5 = S4 = S& + S79.・.Cl" + b" = + 5^7 +-S*! + 5*2 +=S2 + S3 + S] + (s6 + S7)=S2 + S3 + S4 + S5=c2a2 +b2 =c2.。
关于“勾股定理”的60种证法
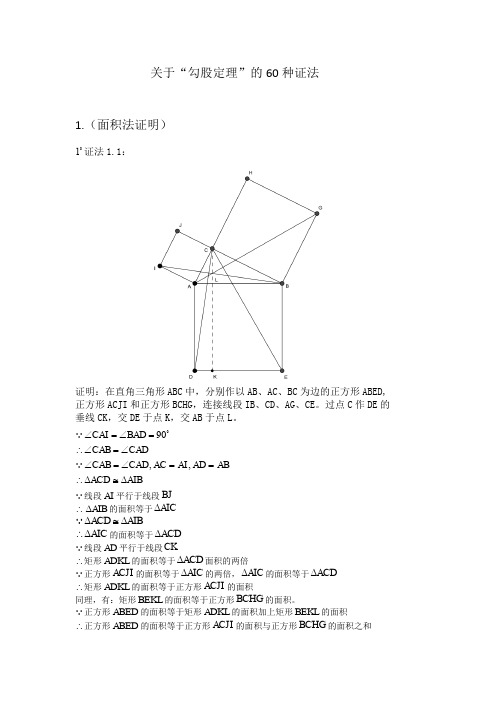
关于“勾股定理”的60种证法1.(面积法证明)1 证法1.1:证明:在直角三角形ABC 中,分别作以AB 、AC 、BC 为边的正方形ABED,正方形ACJI 和正方形BCHG ,连接线段IB 、CD 、AG 、CE 。
过点C 作DE 的垂线CK ,交DE 于点K ,交AB 于点L 。
90,,CAI BAD CAB CADCAB CAD AC AI AD AB ACD AIB∠=∠=∴∠=∠∠=∠==∴∆≅∆线段AI 平行于线段BJ ∴AIB ∆的面积等于AIC ∆ACD AIB ∆≅∆AIC ∴∆的面积等于ACD ∆ 线段AD 平行于线段CK∴矩形ADKL 的面积等于ACD ∆面积的两倍正方形ACJI 的面积等于AIC ∆的两倍,AIC ∆的面积等于ACD ∆ ∴矩形ADKL 的面积等于正方形ACJI 的面积同理,有:矩形BEKL 的面积等于正方形BCHG 的面积。
正方形ABED 的面积等于矩形ADKL 的面积加上矩形BEKL 的面积∴正方形ABED 的面积等于正方形ACJI 的面积与正方形BCHG 的面积之和即222AC BC AB +=.Remark :此为欧几里得(Euclid,约公元前330年-公元前275年)在几何原本中的证明方法。
2 证法1.2:证明:在上图中,整个正方形的面积为2()a b +,又等于四个直角三角形的面积加上里面的小正方形的面积,等于22ab c +。
因此,22()2a b ab c +=+,此即:222a b c +=。
Remark :此证法据Bretschneider 和Hankel 的推测,为毕达哥拉斯(Pythagoras ,约公元前580~约前500)的证法。
3 证法1.3(总统证明法)如图,三角形ABC 与三角形BDE 完全相等,易证三角形ABE 为等腰直角三角形。
整个直角梯形ACDE 的面积为21()2a b +,又等于两个直角三角形的面积加上等腰直角三角形ABE 的面积,等于212ab c +,故2211()22a b ab c +=+。
勾股定理的几种证明方法

勾股定理的证明方法勾股定理是初等几何中的一个基本定理。
这个定理有十分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活实际,以至于古往今来,下至平民百姓,上至帝王总统都愿意探讨和研究它的证明.下面结合几种图形来进行证明。
一、传说中毕达哥拉斯的证法(图1)左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、,斜边为的直角三角形拼成的。
右边的正方形是由1个边长为的正方形和4个直角边分别为、,斜边为的直角三角形拼成的。
因为这两个正方形的面积相等(边长都是),所以可以列出等式,化简得。
在西方,人们认为是毕达哥拉斯最早发现并证明这一定理的,但遗憾的是,他的证明方法已经失传,这是传说中的证明方法,这种证明方法简单、直观、易懂。
二、赵爽弦图的证法(图2)第一种方法:外围正方形可以看作是边长为的正方形和由4个直角边分别为、,斜边为的直角三角形围在外面形成的。
因为边长为的正方形面积加上4个直角三角形的面积等于外围正方形的面积,所以可以列出等式,化简得:。
第二种方法:内部边长为的正方形可以看作是由4个直角边分别为、,斜边为的三角形拼接形成的(虚线表示),不过中间缺出一个边长为的正方形“小洞”。
因为边长为的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积,所以化简得。
可以列出等式,这种证明方法很简明,很直观,它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神,是我们中华民族的骄傲。
三、美国第20任总统茄菲尔德的证法(图3)这个直角梯形是由2个直角边分别为、,斜边为的直角三角形和1个直角边为的等腰直角三角形拼成的。
因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。
这种证明方法由于用了梯形面积公式和三角形面积公式,从而使证明更加简洁,它在数学史上被传为佳话。
勾股定理16种证明方法

勾股定理的证明【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º, ∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状.∵ Rt ΔDAH ≌ Rt ΔABE,∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º, ∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2.∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯.∴ 222c b a =+. 【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC .∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º. ∴ ΔDEC 是一个等腰直角三角形,它的面积等于221c.又∵ ∠DAE = 90º, ∠EBC = 90º, ∴ AD ∥BC .∴ ABCD 是一个直角梯形,它的面积等于()221b a +. ∴ ()222121221c ab b a +⨯=+. ∴ 222c b a =+.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c . 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF 于点P .∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ Rt ΔEBD, ∴ ∠EGF = ∠BED ,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c , ∴ ABEG 是一个边长为c 的正方形∴ ∠ABC + ∠CBE = 90º. ∵ Rt ΔABC ≌ Rt ΔEBD, ∴ ∠ABC = ∠EBD .∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a .∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则abS c 2122⨯+=,∴ 222c b a =+. 【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P . 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N . ∵ ∠BCA = 90º,QP ∥BC , ∴ ∠MPC = 90º, ∵ BM ⊥PQ , ∴ ∠BMP = 90º, ∴ BCPM 是一个矩形,即∠MBC = 90∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA .同理可证Rt ΔQNF ≌ Rt ΔAEF . 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD . 过C 作CL ⊥DE , 交AB 于点M ,交DE 于点L . ∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+. 【证法8】(利用相似三角形性质证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .在ΔADC 和ΔACB 中,∵ ∠ADC = ∠ACB = 90º,∠CAD = ∠BAC , ∴ ΔADC ∽ ΔACB .AD ∶AC = AC ∶AB , 即 AB AD AC •=2.同理可证,ΔCDB ∽ ΔACB ,从而有 AB BD BC •=2. ∴ ()222AB AB DB AD BC AC =•+=+,即 222c b a =+. 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c . 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R . 过B 作BP ⊥AF ,垂足为P . 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H .∵ ∠BAD = 90º,∠PAC = 90º, ∴ ∠DAH = ∠BAC .又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c ,∴ Rt ΔDHA ≌ Rt ΔBCA . ∴ DH = BC = a ,AH = AC = b .由作法可知, PBCA 是一个矩形,所以 Rt ΔAPB ≌ Rt ΔBCA . 即PB = CA = b ,AP= a ,从而PH = b ―a . ∵ Rt ΔDGT ≌ Rt ΔBCA , Rt ΔDHA ≌ Rt ΔBCA . ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++= ①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得= 922S S b ++ = 22a b +.∴ 222c b a =+.【证法10】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE . 又∵ ∠BTH = ∠BEA = 90º,BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE . ∴ HT = AE = a . ∴ GH = GT ―HT = b ―a .又∵ ∠GHF + ∠BHT = 90º,∠DBC + ∠BHT = ∠TBH + ∠∴ ∠GHF = ∠DBC .∵ DB = EB ―ED = b ―a , ∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC . 即 27S S =.过Q 作QM ⊥AG ,垂足是M . 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE . 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE .∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE , ∴ ∠FQM = ∠CAR .又∵ ∠QMF = ∠ARC = 90º,QM = AR = a ,∴ Rt ΔQMF ≌ Rt ΔARC . 即64S S =.∵ 543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴8736122S S S S S b a ++++=+ =52341S S S S S ++++=2c , 即 222c b a =+. 【证法11】(利用切割线定理证明)在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c . 如图,以B 为圆心a 为半径作圆,交AB 及AB 的延长线分别于D 、E ,则BD = BE = BC = a . 因为∠BCA = 90º,点C 在⊙B 上,所以AC 是⊙B 的切线. 由切割线定理,得=()()BD AB BE AB -+ =()()a c a c -+= 22a c -,即222a cb -=, ∴ 222c b a =+. 【证法12】在Rt ΔABC 中,设直角边BC . 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=, ∴ 222c b a =+.【证法13】在Rt ΔABC 中,设直角边BC = a ,作Rt ΔABC 的内切圆⊙O ,切点分别为D 、E 、F (如图),设⊙O 的半径为r .∵ AE = AF ,BF = BD ,CD = CE ,∴ ()()()BF AF CD BD CE AE AB BC AC +-+++=-+= CD CE += r + r = 2r,即 r c b a 2=-+, ∴ c r b a +=+2.∴ ()()222c r b a +=+,即 ()222242c rc r ab b a ++=++,∵ab S ABC 21=∆,∴ ABC S ab ∆=42, 又∵ AOC BOCAOB ABC S S S S ∆∆∆∆++= = br ar cr 212121++ = ()r c b a ++21= ()r c c r ++221= rc r +2,∴()ABC S rc r ∆=+442, ∴ ()ab rc r242=+,∴ 22222c ab ab b a +=++, ∴ 222c b a =+.【证法14】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB .在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB . 在ΔCDB 和ΔACB 中, ∵ ∠B = ∠B , ∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB . 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法15】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+. 【证法16】(陈杰证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c . 做两个边长分别为a 、b 的正方形(b>a ),把它们拼成如图所示形状,使E 、H 、M 三点在一条直线上. 用数字表示面积的编号(如图).在EH = b 上截取ED = a ,连结DA 、DC , 则 AD = c .∵ EM = EH + HM = b + a , ED = a , ∴ DM = EM ―ED = ()a b +―a = b . 又∵ ∠CMD = 90º,CM = a ,∠AED = 90º, AE = b , ∴ Rt ΔAED ≌ Rt ΔDMC .∴ ∠EAD = ∠MDC ,DC = AD = c . ∵ ∠ADE + ∠ADC+ ∠MDC =180º,∠ADE + ∠MDC = ∠ADE + ∠EAD = 90º, ∴ ∠ADC = 90º.∴ 作AB ∥DC ,CB ∥DA ,则ABCD 是一个边长为c 的正方形. ∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90º, ∴ ∠BAF=∠DAE .连结FB ,在ΔABF 和ΔADE 中,∵ AB =AD = c ,AE = AF = b ,∠BAF=∠DAE , ∴ ΔABF ≌ ΔADE .∴ ∠AFB = ∠AED = 90º,BF = DE = a . ∴ 点B 、F 、G 、H 在一条直线上. 在Rt ΔABF 和Rt ΔBCG 中,∵ AB = BC = c ,BF = CG = a , ∴ Rt ΔABF ≌ Rt ΔBCG .∵ 54322S S S S c +++=, 6212S S S b ++=, 732S S a +=,76451S S S S S +===,∴6217322S S S S S b a ++++=+ =()76132S S S S S ++++=5432S S S S +++=2c ∴ 222c b a =+.。
勾股定理16种证明方法

【证法1】(课本的证明)勾股定理的证明做8个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c ,再做 三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是 a + b ,所以面积相等.即2 21 2 1a 2b 2 4 ab 二c 2 4 ab22, 整理得【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积ab等于2 .把这四个直角三角形拼成如图所示形状, 使A E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C G D 三点在一条直线上.v Rt △ HAE 坐 Rt △ EBF, ••• / AHE = / BEFv / AEH + / AHE = 90o,• / AEH + / BEF = 90o.• / HEF = 180o — 90o= 90o. •四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2. v Rt △ GDH 坐 Rt △ HAE,D b G a C bF a Bv / HGD + / GHD = 98,• / EHA + / GHD = 98. 又v /GHE = 90o,• / DHA = 90o+ 90o= 180o.2• ABCD 是一个边长为a + b 的正方形,它的面积等于(a +a b 2 =4 -ab c 22【证法3】(赵爽证明)以a 、b 为直角边(b>a ), a 2 =c 2ac\ca 2b 2以c 为斜边作四个全等的直角三角形,则每个直角1ab三角形的面积等于2 .把这四个直角三角形拼成如图所示形状•v Rt △ DAH 坐 Rt △ ABE,••• / HDA = / EABv / HAD + / HAD = 90o , • / EAB + / HAD = 900,• ABCD 是一个边长为c 的正方形,它的面积等于c 2. v EF = FG =GH =HE = b — a , / HEF = 900.2• EFGH 是一个边长为b —a 的正方形,它的面积等于(b -a ).1 2 2 4 疋一ab + (b —a f = c 2• 2【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面1 c 它的面积等于2又 v / DAE = 90o, / EBC = 90o, • AD // BC• ABCD 是 一个直角梯形,它的面积等于1 1 12(a +b 32^ab *c 2• a 2 +b 2 = c 2.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c.把它 们拼成如图那样的一个多边形,使 D E 、F 在一条直线上.过C 作AC 的延长线交DF 于 点P 八、、■・a 2b 2二 c 2积等于2ab把这两个直角三角形拼成如图所示形状,使B 三点在一条直线上v Rt △ EAD 坐 Rt △ CBE,• / ADE = / BECv / AED + / ADE = 90o,• / AED + / BEC = 90o.• / DEC = 180o — 90o= 90o. • △ DEC 是 一个等腰直角三A Ecav D、E、F在一条直线上,且Rt △ GEF幻Rt △ EBD,v / EGF + / GEF = 90°, •• / BED + / GEF = 90°, •• / BEG =18(0—90o= 90o./ AB = BE = EG = GA = c , •• ABEG 是•• / ABC + / CBE = 900.•• Rt △ ABC 刍 Rt △ EBD, •• / ABC = / EBD•• / EBD + / CBE = 900.即 / CBD= 9(0.又 v / BDE = 900,/ BCP = 900,BC = BD = a .••• BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCB 的面积为S ,则2 21a b = S 2 ab,2c 2二 S 21ab2【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a )c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使 E 、A 、 直线上.过点Q 作QP// BC 交AC 于点P. 过点B 作BM L PQ 垂足为M ;再过点 F 作FNL PQ 垂足为Nv / BCA = 900 , QP// BC• / MPC = 900 , v BM 丄 PQ• / BMP = 900 ,• BCPM 是一个矩形,即/ MBC = 9 v / QBM + / MBA = / QBA = 900 ,/ ABC + / MBA = / MBC = 900 , • / QBM = / ABC又 v / BMP = 900 , / BCA = 900 , BQ = BA = c ,a 2b 2 =c 2G 个边长为c 的正方形. a bHa,斜边长为 C 三点在一条ccacP bba、• Rt △ BMQ坐Rt △ BCA 同理可证Rt △ QNF坐Rt △ AEF从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、 在一条直线上,连结 BF CD 过 C 作 CL ± DE 交AB 于点M 交DE 于点 L.v AF = AC , AB = AD ,/FAB = / GAD••• △ FAB 坐 △ GAD1av △ FAB 的面积等于2△ GAD 勺面积等于矩形ADLM 的面积的一半,•矩形ADLM 勺面积二a同理可证,矩形MLEE 的面积v 正方形ADEB 勺面积=矩形ADLM 勺面积+矩形MLEB 勺面积 • c 2=a 2+b 2,即 a 2+b 2=c 2. 【证法8】(利用相似三角形性质证明) 如图,在Rt △ABC 中,设直角边 点C 作CDL AB 垂足是D 在△ ADC 和△ ACB 中, v / ADC = / ACB = 90o , / CAD = / BAC •△ ADC s A ACBAD : AC = AC : AB,即 AC 2 = AD • AB .同理可证,△ CDB s △ ACBAC BC 的长度分别为 a 、b ,斜边AB 的长为c ,过 从而有 BC — BD *AB2 = c 2• AC 2 BC 2 二 AD DB ・ AB 二 AB 2 ,即 a 2 b 【证法9](杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为 再做一个边长为c 的正方形.把它们拼成如图所示的多边形 于F , AF 交DT 于R.过B 作BP! AF, E , DE 交 AF 于 H v / BAD = 90o ,Z PAC = 90o ,• / DAH = / BAC又 v / DHA = 90o ,Z BCA =AD = AB = c ,a 、b (b>a ),斜边长为c. .过A 作AF 丄AC AF 交GT 垂足为P.过D 作DE 与CB 的延长线垂直,垂足为 的正方形,把它们拼成如图所示形状,使 H C B 三点 c••• Rt △ DHA 坐 Rt △ BCA ••• DH = BC = a , AH = AC = b. 由作法可知,PBCA 是一个矩形,所以 Rt △ APB 坐 Rt △ BCA 即 PB = CA = b , AP= a ,从而 PH = b — a.v Rt △ DGT 坐 Rt △ BCA ,Rt △ DHA 坐 Rt △ BCA• Rt △ DGT 坐 Rt △ DHA.• DH = DG = a ,/ GDT = / HDA. 又 v / DGT = 90o ,Z DHF = 90o ,/ GDH = / GDT + / TDH = / HDA+ / TDH = 90o , • DGFH 是一个边长为a 的正方形.• GF = FH = a . TF 丄AF, TF = GT — GF = b — a .• T FPB 是一个直角梯形,上底 TF=b-a ,下底BP= b ,高FP=a + (b — a ) 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为2CS 1S 2S 3S 4S5①把②代入①,得c 2 二 S S 2 b 2 - 3 - S8 & S 9 =b 2 +S 2 0 = b 2 +a 2【证法10】(李锐证明)设直角三角形两直角边的长分别为 a 、b (b>a ),斜边的长为c.做三个边长分别为a 、 b 、c 的正方形,把它们拼成如图所示形状,使 A 、E 、G 三点在一条直线上.用数字表示 • HT = AE = a . • GH = GT — HT = b — a. 又v / GHF + / BHT = 90o ,/ DBC + / BHT = / TBH + S 8 S 3 S 4A2 b 亠[b - aa 亠[b -a 1b 2 - 1 ab2,S 3 S 4 =b 2 —fab —S 8b 2 - S i - S ga 2b 2二 c 2面积的编号(如图).v / TBE = / ABH = =90o , • / TBH = / ABE 又v / BTH = / BEA = =90o , BT = BE =b ,• Rt △ HBT 坐 Rt △ ABE B b28 D61 3M F E45 c/ BHT = 90O ,QS 7 =S S 2 S 3 S 4 S 5 =S 2= S5S4a 2 = S 1 S 6b 2 = S 3 S 7 S 82 2a b ^S 1 S 6 S 3 S 7 S 8=S i S 4 S 3 S 2 S 52=c即 a 2 +b 2 =c 2.【证法11】(利用切割线定理证明)在Rt △ ABC 中,设直角边 BC = a ,AC = b ,斜边AB = c.如图,以B 为圆心a 为半 径作圆,交AB 及AB 的延长线分别于 D E ,贝S BD = BE = BC = a .因为/ BCA = 90o , 点C 在。
勾股定理的证明(比较全的证明方法)
∴S矩形ADNM+S矩形MNEB=S正方形ACHK+S正方形CBFG. 即S正方形ADEB=S正方形ACHK+S正方形CBAFG ,
DN
也就是 a2+b2=c2.
F B
E
12
返回
刘徽的证法
刘徽在《九章算术》中对勾股定理的证明:
勾自乘为朱方,股自乘为青方,令出入相补,各
从其类,因就其余不移动也.合成弦方之幂,开 方除之,即弦也.
里德(Euclid,是公元前三百年左右的人)在编著《几何原本》
时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个
定理称为“毕达哥拉斯定理”,以后就流传开了。(为了庆祝这一定理
的发现,毕达哥拉斯学派杀了一百头牛酬谢供奉神灵,因此这个定理又有人叫做
“百牛定理”.)
A
3
走
进
数
学
史
A
4
勾股定理的证明
美妙的勾股定理
——数形结合之美
32
42
52
A
1
勾 股
勾股弦的定义
在中国古代,人们把弯曲成直角的手臂的上半部分称为
"勾",下半部分称为"股"。我国古代学者把直角三角形
较短的直角边称为“勾”,较长的直角边称为“股”,
斜边称为“弦”.
A
2
勾股定理的由来
走 进 数 学 史
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉
勾 看 关 砖 一
你系 铺 次
股 能 , 成 毕
发同 的 达
A
现学 地 哥 什们 面 拉
定 么 , 反 斯
?我 映 去
理 们 直 朋 9
数学家毕达哥拉斯的发现:
勾股定理16种证明方法

ABCD 是一个边长为 a + b 的正方形,它的面积等于 14 ab 2c 2【证法3】(赵爽证明)以a 、b 为直角边(b>a ),以c 为斜 边作四个全等的直角三角形,则每个直角【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c ,再做 三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形 .从图上可以看到,这两个正方形的边长都是1 2 14 ab c 4 ab222 2, 整理得 a b 【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形, 则每个直角三角形的面积1ab等于2 .把这四个直角三角形拼成如图所示形状, 使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C G 、D 三点在一条直线上.Rt A HAE 坐 Rt A EBF, / AHE = / BEF/ AEH + / AHE = 90o, / AEH + / BEF = 90o / HEF = 180—90o= 90o.四边形EFGH 是一个边长为 正方形.它的面积等于c 2. Rt A GDH 坐 Rt A HAE, / HGD = / EHA/ HGD + / GHD = 90o, / EHA + / GHD = 900 又 T / GHE = 90o,/ DHA = 90o+ 90o= 180o勾股定理的证明aa/ba + b,所以面积相等.即a 2b 2aabbaaccbabba2a ba 2b 2Cab三角形的面积等于2 .把这四个直角三角形拼成如图所示形状•v Rt A DAH 坐 Rt A ABE, ••• / HDA = / EABv / HAD + / HAD = 90o, • / EAB + / HAD = 90o• ABCD 是一个边长为c 的正方形,它的面积等于c 2.v EF : =FG =GH =HE =—a ,/ HEF = 90oEFGH 是一个边长为b —a 的正方形,它的面积等于b a4 i ab b a 2 c 2 '• 2 . \ a 2 b 2 c 2.【证法4】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面ab积等于2.把这两个直角三角形拼成如图所示形状,使 A 、E 、v Rt A EAD 坐 Rt A CBE, • / ADE = / BEC v / AED + / ADE = 90o, • / AED + / BEC = 90o • / DEC = 180—90o= 90o. • A DEC 是一个等腰直角三角形,1 2 c 它的面积等于2 .又 v / DAE = 90o, / EBC = 90o,• AD// BCABCD 是一个直角梯形,它的面积等于 1 「2 c 1「 1 2a b 2 ab c • 2 2 2 .• a 2 b 2 c 2.【证法5】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c.把它 们拼成如图那样的一个多边形,使 D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于 点P 八、、■・v D 、E 、F 在一条直线上,且Rt A GEF 幻 Rt A EBD,/ EGF = / BED,B 三点在一条直线上A b E a B/ EGF + / GEF = 90 , / BED + / GEF = 90 ,••• / BEG =180— 90o= 90o. 又T AB = BE = EG = GA = c• ABEG 是一个边长为c 的正方形. • / ABC + / CBE = 90o T Rt A ABC 刍 Rt A EBD, • / ABC = / EBD• / EBD + / CBE = 90o 即 / CBD= 900又 T / BDE = 90o / BCP = 90oBC = BD = a• BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S,则2a b 2 S 2】ab, 2 2c S2 lab 2J.a 2 b 2 c 2【证法6】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c.再做一个边长为c 的正方形.把它们拼成如图所示的多边形,使 直线上. E过点Q 作QP// BC,交AC 于点P. b 过点B 作BM 丄PQ,垂足为M ;再过点F 作FN 丄PQ ,垂足为N. T / BCA = 90o QP / BC, • / MPC = 90o T BM 丄 PQ,• / BMP = 90o,• BCPM 是 T / QBM + / MBA = / QBA = 90o,/ ABC + / MBA = / MBC = 90o, • / QBM = / ABC,又 T / BMP = 90o, / BCA = 90o BQ = BA = c• Rt A BMQ 坐 Rt A BCA 同理可证Rt A QNF 幻Rt A AEF 从而将问题转化为【证法4】(梅文鼎证明). 【证法7】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使 H 、C B 三点 在一条直线上,连结 G BF CD 过 C 作 CL ± DE, 口 / X.E 、A 、C 三点在一条 [A\Pb个矩形,即/ MBC = 90o交AB 于点M ,交DE 于点 L.v AF = AC AB = AD, / FAB = / GAD,••• △ FAB 刍 △ GAD,1 2 a v △ FAB 的面积等于2 ,△ GAD 的面积等于矩形 ADLM 的面积的一半,•矩形ADLM 的面积二. 同理可证,矩形MLEB 的面积=. v 正方形ADEB 的面积=矩形ADLM 的面积+矩形MLEB 的面积 • c 2 a 2 b 2,即 a 2 b 2 c 2.【证法8】(利用相似三角形性质证明)如图,在Rt A ABC 中,设直角边 点C 作CD 丄AB ,垂足是D.在厶ADC 禾口 △ ACB 中, v / ADC = / ACB = 90o / CAD = / BAG • △ ADC s △ ACBAD : AC = AC : AB , 即 AC 2 AD? AB .同理可证,△ CDB s △ ACB, 2 2AF 交DT 于R.过B 作BP 丄AF ,垂足为 交AF 于H./ BAD = 90o / PAC = 900 / DAH = / BAC又 v / DHA = 90q / BCA = 900 AD =AB = c• Rt A DHA 坐 Rt A BCA • DH = BC = a AH = AC = b由作法可知,PBCA 是一个矩形, 所以 Rt △ APB 坐 Rt A BCA 即 PB = CA = b AP= a,从而 PH = b-a.v Rt A DGT 坐 Rt A BCA , Rt ADHA 坐 Rt A BCAAC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过 从而有2,即 • AC BC AD DB ? AB AB 【证法9】(杨作玫证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c.再 做一个边长为c 的正方形.把它们拼成如图所示的多边形.过A 作AF 丄AC,AF 交GT 于F , P.过D 作DE 与CB 的延长线垂直,垂足为E, DEBC 2 BD?ABa 2b 2c 2AbRt A DGT 坐 Rt A DHA . ••• DH = DG = a 广 GDT = / HDA . 又••• / DGT = 90q / DHF = 90Q/ GDH = / GDT + / TDH = / HDA+ / TDH = 90(,• DGFH 是一个边长为a 的正方形. GF = FH = a TF 丄AF , TF = GT-GF = b —a . TF=b-a ,下底 BP=b 高 FP=a +(b —a ) ,则以c 为边长的正方形的面积为c 2 S iS 2 S 3 S 4 S 5①..S 8S 3S 4 1b b a ? a b ab 2 iab2二2S 5 S 8S 9• S 3S 4b 2丄ab 2S8= b 2 S iS 8②把②代入①, 得c 2 S i S 2 b 2 S i S 8 S 8S 9• TFPB是 一个直角梯形,上底 用数字表示面积的编号(如图) 2=b S 2S 9 = b 2 a 2a 2b 2c 2【证法10】(李锐证明)设直角三角形两直角边的长分别为 b 、c 的正方形,把它们拼成如图所示形状,使 面积的编号(如图).v / TBE = / ABH = 90o, • / TBH = / ABE 又 v / BTH = / BEA = 90( BT = BE = b • Rt A HBT 坐 Rt A ABE • HT = AE = a • GH = GT- HT = b- a. 又 v / GHF + / BHT = 90oa 、b (b>a ),斜边的长为c.做三个边长分别为a 、A 、E 、G 三点在一条直线上.用数字表示/ DBC + / BHT = / TBH + / BHT = 90( Qv DB = EB- ED = b- a ,/ HGF = / BDC = 90o • Rt A HGF 坐 Rt A BDC 即卩 S7 辺过Q 作QM 丄AG ,垂足是 M.由/ BAQ = / BEA = 90(可知 / ABE =/QAM ,而 AB = AQ = c 所以 Rt A ABE 幻 Rt A QAM .又 Rt A HBT 幻 Rt A ABE 所以 Rt A HBT 幻 Rt A QAM .即 S8 S5.由 Rt A ABE 坐 Rt A QAM ,又得 QM = AE = a / AQM = / BAEv / AQM + / FQM = 90o,/ BAE + / CAR = 90q / AQM = / BAE ••• / FQM = / CAR 又 v / QMF = / ARC = 90o QM = AR = a【证法11】(利用切割线定理证明)在Rt A ABC 中,设直角边 BC = a AC = b,斜边AB = c 如图,以B 为圆心a 为半径 作圆,交AB 及AB 的延长线分别于D 、E,贝S BD = BE = BC 三a 因为/ BCA = 90q 点C 在 O B 上,所以AC 是。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理)勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果三角形的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴ ∴.【证法2】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理的9种证明(有图)【证法1】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF.∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º. ∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA.∵ ∠HGD + ∠GHD = 90º, ∴ ∠EHA + ∠GHD = 90º. 又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.【证法2】(梅文鼎证明)做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上. 过C 作AC 的延长线交DF于点P.∵ D 、E 、F 在一条直线上, 且Rt ΔGEF ≌ ∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180º―90º= 90º.又∵ AB = BE = EG = GA = c ,∴ ABEG 是一个边长为c 的正方形. ∴ ∠ABC + ∠CBE = 90º.∵ Rt ΔABC ≌ Rt ΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90º. 即 ∠CBD= 90º.又∵ ∠BDE = 90º,∠BCP = 90º,BC = BD = a.∴ BDPC 是一个边长为a 的正方形. 同理,HPFG 是一个边长为b 的正方形. 设多边形GHCBE 的面积为S ,则,21222ab S b a ⨯+=+ abS c 2122⨯+=,∴ 222c b a =+.【证法3】(项明达证明)做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ) ,斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形,使E 、A 、C 三点在一条直线上.过点Q 作QP ∥BC ,交AC 于点P. 过点B 作BM ⊥PQ ,垂足为M ;再过点 F 作FN ⊥PQ ,垂足为N. ∵ ∠BCA = 90º,QP ∥BC ,∴ ∠MPC = 90º,∵ BM ⊥PQ ,∴ ∠BMP = 90º,∴ BCPM 是一个矩形,即∠MBC = 90º. ∵ ∠QBM + ∠MBA = ∠QBA = 90º,∠ABC + ∠MBA = ∠MBC = 90º, ∴ ∠QBM = ∠ABC ,又∵ ∠BMP = 90º,∠BCA = 90º,BQ = BA = c , ∴ Rt ΔBMQ ≌ Rt ΔBCA.同理可证Rt ΔQNF ≌ Rt ΔAEF. 从而将问题转化为【证法4】(梅文鼎证明). 【证法4】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结BF 、CD. 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点 L.∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a ,ΔGAD 的面积等于矩形ADLM的面积的一半,∴ 矩形ADLM 的面积 =2a .同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积∴ 222b ac += ,即 222c b a =+. 【证法5】(杨作玫证明) 做两个全等的直角三角形,设它们的两条直角边长分别为a 、b (b>a ),斜边长为c. 再做一个边长为c 的正方形. 把它们拼成如图所示的多边形. 过A 作AF ⊥AC ,AF 交GT 于F ,AF 交DT 于R. 过B 作BP ⊥AF ,垂足为P. 过D 作DE 与CB 的延长线垂直,垂足为E ,DE 交AF 于H.∵ ∠BAD = 90º,∠PAC = 90º,∴ ∠DAH = ∠BAC.又∵ ∠DHA = 90º,∠BCA = 90º, AD = AB = c , ∴ Rt ΔDHA ≌ Rt ΔBCA. ∴ DH = BC = a ,AH = AC = b.由作法可知, PBCA 是一个矩形, 所以 Rt ΔAPB ≌ Rt ΔBCA. 即PB =CA = b ,AP= a ,从而PH = b ―a. ∵ Rt ΔDGT ≌ Rt ΔBCA ,Rt ΔDHA ≌ Rt ΔBCA. ∴ Rt ΔDGT ≌ Rt ΔDHA .∴ DH = DG = a ,∠GDT = ∠HDA . 又∵ ∠DGT = 90º,∠DHF = 90º,∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º, ∴ DGFH 是一个边长为a 的正方形.∴ GF = FH = a . TF ⊥AF ,TF = GT ―GF = b ―a .∴ TFPB 是一个直角梯形,上底TF=b ―a ,下底BP= b ,高FP=a +(b ―a ). 用数字表示面积的编号(如图),则以c 为边长的正方形的面积为543212S S S S S c ++++=①∵()[]()[]a b a a b b S S S -+•-+=++21438 =ab b 212-, 985S S S +=,∴ 824321S ab b S S --=+= 812S S b -- . ②把②代入①,得98812212S S S S b S S c ++--++==922S S b ++= 22a b +.∴ 222c b a =+.【证法6】(李锐证明)设直角三角形两直角边的长分别为a 、b (b>a ),斜边的长为c. 做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使A 、E 、G 三点在一条直线上. 用数字表示面积的编号(如图).∵ ∠TBE = ∠ABH = 90º, ∴ ∠TBH = ∠ABE. 又∵ ∠BTH = ∠BEA = 90º, BT = BE = b , ∴ Rt ΔHBT ≌ Rt ΔABE. ∴ HT = AE = a. ∴ GH = GT ―HT = b ―a. 又∵ ∠GHF + ∠BHT = 90º, ∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º, ∴ ∠GHF = ∠DBC.∵ DB = EB ―ED = b ―a ,∠HGF = ∠BDC = 90º, ∴ Rt ΔHGF ≌ Rt ΔBDC. 即 27S S =.过Q 作QM ⊥AG ,垂足是M. 由∠BAQ = ∠BEA = 90º,可知 ∠ABE = ∠QAM ,而AB = AQ = c ,所以Rt ΔABE ≌ Rt ΔQAM . 又Rt ΔHBT ≌ Rt ΔABE. 所以Rt ΔHBT ≌ Rt ΔQAM . 即 58S S =.由Rt ΔABE ≌ Rt ΔQAM ,又得QM = AE = a ,∠AQM = ∠BAE.∵ ∠AQM + ∠FQM = 90º,∠BAE + ∠CAR = 90º,∠AQM = ∠BAE ,∴ ∠FQM = ∠CAR.又∵ ∠QMF = ∠ARC = 90º,QM = AR = a , ∴ Rt ΔQMF ≌ Rt ΔARC. 即64S S =. ∵543212S S S S S c ++++=,612S S a +=,8732S S S b ++=,又∵ 27S S =,58S S =,64S S =,∴ 8736122S S S S S b a ++++=+=52341S S S S S ++++ =2c ,即 222c b a =+.【证法7】(利用多列米定理证明) 在Rt ΔABC 中,设直角边BC = a ,AC = b ,斜边AB = c (如图). 过点A 作AD ∥CB ,过点B 作BD ∥CA ,则ACBD 为矩形,矩形ACBD 内接于一个圆. 根据多列米定理,圆内接四边形对角线的乘积等于两对边乘积之和,有BD AC BC AD DC AB •+•=•,∵ AB = DC = c ,AD = BC = a , AC = BD = b ,∴ 222AC BC AB +=,即 222b a c +=,∴ 222c b a =+.【证法8】(利用反证法证明)如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D.假设222c b a ≠+,即假设 222AB BC AC ≠+,则由AB AB AB •=2=()BD AD AB +=BD AB AD AB •+•可知 AD AB AC •≠2,或者 BD AB BC •≠2. 即 AD :AC ≠AC :AB ,或者 BD :BC ≠BC :AB.在ΔADC 和ΔACB 中,∵ ∠A = ∠A ,∴ 若 AD :AC ≠AC :AB ,则∠ADC ≠∠ACB.在ΔCDB 和ΔACB 中,∵ ∠B = ∠B ,∴ 若BD :BC ≠BC :AB ,则 ∠CDB ≠∠ACB. 又∵ ∠ACB = 90º,∴ ∠ADC ≠90º,∠CDB ≠90º.这与作法CD ⊥AB 矛盾. 所以,222AB BC AC ≠+的假设不能成立.∴ 222c b a =+. 【证法9】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c. 作边长是a+b 的正方形ABCD. 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD 的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD的面积为()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.。
