习题参考解答
电气控制与PLC应用-第5、8章习题与思考题参考解答

第5章S7-200 PLC的指令系统习题与思考题1.S7-200指令参数所用的基本数据类型有哪些?答:S7-200 PLC的指令参数所用的基本数据类型有1位布尔型(BOOL)、8位无符号字节型(BYTE)、8位有符号字节型(SIMATIC模式仅限用于SHRB指令)、16位无符号整数(WORD)、16位有符号整数(INT)、32位无符号双字整数(DWORD)、32位有符号双字整数(DINT)、32位实数型(REAL)。
实数型(REAL)是按照ANSI/IEEE 754-1985标准(单精度)的表示格式规定。
2~255字节的字符串型(STRING)2.立即I/O指令有何特点?它应用于什么场合?答:立即指令允许对输入和输出点进行快速和直接存取。
当用立即指令读取输入点的状态时,相应的输入映像寄存器中的值并未发生更新;用立即指令访问输出点时,访问的同时,相应的输出映像寄存器的内容也被刷新。
由于立即操作指令针对的是I/O端口的数字输入和数字输出信号,所以它们的位操作数地址只能是物理输入端口地址Ix.x和物理输出端口地址Qx.x。
3.逻辑堆栈指令有哪些?各用于什么场合?答:复杂逻辑指令,西门子称为逻辑堆栈指令。
主要用来描述对触点进行的复杂连接,并可以实现对逻辑堆栈复杂的操作。
复杂逻辑指令包括:ALD、OLD、LPS、LRD、LPP和LDS。
这些指令中除LDS外,其余指令都无操作数。
这些指令都是位逻辑指令。
栈装载与指令ALD用于将并联子网络串联起来。
栈装载或指令OLD用于将串联子网络并联起来。
逻辑推入栈指令LPS,在梯形图中的分支结构中,用于生成一条新的母线,左侧为主控逻辑块时,第一个完整的从逻辑行从此处开始。
逻辑读栈指令LRD,在梯形图中的分支结构中,当左侧为主控逻辑块时,该指令用于开始第二个和后边更多的从逻辑块。
逻辑栈弹出指令LPP,在梯形图中的分支结构中,用于恢复LPS指令生成的新母线。
装入堆栈指令LDS,复制堆栈中的第n级值,并将该值置于栈顶。
结构化学练习之原子结构习题附参考解答

原子结构习题一、填空题(在划线处填上正确答案)2101、在直角坐标系下,Li 2+ 的Schr ödinger 方程为________________ 。
2102、已知类氢离子 He +的某一状态波函数为:()022-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π 则此状态的能量为 )(a ,此状态的角动量的平方值为 )(b ,此状态角动量在 z 方向的分量为 )(c ,此状态的 n , l , m 值分别为 )(d ,此状态角度分布的节面数为 )(e 。
2103、写出 Be 原子的 Schr ödinger 方程 。
2104、已知类氢离子 He +的某一状态波函数为ψ= ()022-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π 则此状态最大概率密度处的 r 值为 )(a ,此状态最大概率密度处的径向分布函数值为 )(b ,此状态径向分布函数最大处的 r 值为 )(c 。
2105、原子轨道是原子中的单电子波函数, 每个原子轨道只能容纳 ______个电子。
2106、H 原子的()φr,θψ,可以写作()()()φθr R ΦΘ,,三个函数的乘积,这三个函数分别由量子数 (a) ,(b), (c) 来规定。
2107、给出类 H 原子波函数()θa r Z a Zr a Z a Zr cos e6812032022023021-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π=ψ 的量子数 n ,l 和 m 。
2108、H 原子 3d 电子轨道角动量沿磁场方向分量的可能值 。
2109、氢原子的波函数131321122101-++=ψψψψc c c 其中 131211210-ψψψψ和,,都是归一化的。
那么波函数所描述状态的能量平均值为(a ),角动量出现在 π22h 的概率是(b ),角动量 z 分量的平均值为(c )。
2110、氢原子中,归一化波函数131321122101-++=ψψψψc c c ( 131211210-ψψψψ和,,都是归一化的 )所描述的状态, 其能量平均值是 (a )R , 能量 -R /4 出现的概率是(b ),角动量平均值是(c )π2h , 角动量π22h 出现的概率是(d ),角动量 z π2h ,角动量 z 分量π22h 出现的概率是(f )。
庞皓第三版计量经济学练习题及参考解答(完整版)
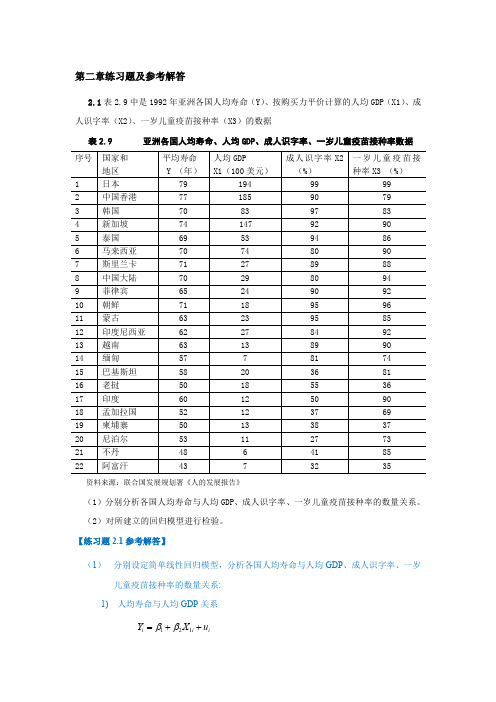
百户拥有 家用汽车量(辆) Y 37.71 20.62 23.32 18.60 19.62 11.15 11.24
北 京 天 津 河 北 山 西 内蒙古 辽 宁 吉 林
黑龙江 上 海 江 苏 浙 江 安 徽 福 建 江 西 山 东 河 南 湖 北 湖 南 广 东 广 西 海 南 重 庆 四 川 贵 州 云 南 西 藏 陕 西 甘 肃 青 海 宁 夏 新 疆
5 6 7 8 9 10 11 12 根据上表资料:
2.56 3.54 3.89 4.37 4.82 5.66 6.11 6.23
1678 1640 1620 1576 1566 1498 1425 1419
(1)建立建筑面积与建造单位成本的回归方程; (2)解释回归系数的经济意义; (3)估计当建筑面积为 4.5 万平方米时,对建造的平均单位成本作区间预测。
650 m 2.23 5.4772 1 5.0833 650 m 30.1250
2.4 假设某地区住宅建筑面积与建造单位成本的有关资料如表 2.11: 表 2.11 建筑地编号 1 2 3 4 某地区住宅建筑面积与建造单位成本数据 建筑面积(万平方米)X 0.6 0.95 1.45 2.1 建造单位成本(元/平方米)Y 1860 1750 1710 1690
(1)消费支出 C 的点预测值;
(2)在 95%的置信概率下消费支出 C 平均值的预测区间。 (3)在 95%的置信概率下消费支出 C 个别值的预测区间。
【练习题 2.3 参考解答】 (1)当 X f 1000 时,消费支出 C 的点预测值;
ˆ 50 0.6 X =50+0.6*1000=650 C i i
e2 ˆ2 i n 1 ˆ
2
电工与电子技术习题参考答案第9章

第9章时序逻辑电路习题解答9.1 d R端和d S端的输入信号如题9.1图所示,设基本RS触发器的初始状态分别为1和0两种情况,试画出Q端的输出波形。
题9.1图解:9.2 同步RS触发器的CP、R、S端的状态波形如题9.2图所示。
设初始状态为0和1两种情况,试画出Q端的状态波形。
题9.2图解:9.3 设主从型JK触发器的初始状态为0,J、K、CP端的输入波形如题9.3图所示。
试画出Q端的输出波形(下降沿触发翻转)。
解:如题9.3图所示红色为其输出波形。
第9章时序逻辑电路225题9.3图9.4 设主从型JK触发器的初始状态为0,J、K、CP端输入波形如题9.4图所示。
试画出Q端的输出波形(下降沿触发翻转)。
如初始状态为1态,Q端的波形又如何?解:如题9.4图所示红色为其输出波形。
题9.4图9.5 设维持阻塞型D触发器的初始状态为0,D端和CP端的输入波形如题9.5图所示,试画出Q端的输出波形(上升沿触发翻转)。
如初始状态为1态,Q端的波形又如何?解:如题9.5图所示红色为其输出波形。
第9章时序逻辑电路226题9.5图9.6 根据CP时钟脉冲,画出题9.6图所示各触发器Q端的波形。
(1)设初始状态为0;(2)设初始状态为1。
(各输入端悬空时相当于“1”)题9.6图解:第9章时序逻辑电路2279.7 题9.7图所示的逻辑电路中,有J和K两个输入端,试分析其逻辑功能,并说明它是何种触发器。
题9.7图=⋅⋅⋅=⋅+⋅解:由图得D Q F J Q Q F J QJ K Q n D Q n+10 0 0 0 00 0 1 1 10 1 0 0 00 1 1 0 01 0 0 1 11 0 1 1 11 1 0 1 11 1 1 0 0此电路为D触发器和与非门组成的上升沿触发的JK触发器。
9.8 根据题9.8图所示的逻辑图和相应的CP、d R、D的波形,试画出Q1和Q2端的输出波形。
设初始状态Q1=Q2=0。
题9.8图解:第9章时序逻辑电路2289.9 试用4个D触发器组成一个四位右移移位寄存器。
机械工程材料习题及参考解答

♦ 变质处理
机械工程材料 第三章 金属的结晶
♦ (二) 填空题
– 1. 结晶过程是依靠两个密切联系的基本过程来实现的,这两个 过程是 形核和 长大 。 – 2. 在金属学中,通常把金属从液态过渡为固体晶态的转变称 为 结 晶 ;而把金属从一种固态过渡为另一种固体晶态的转变 称为 同素异构转变 。 – 3. 当对金属液体进行变质处理时,变质剂的作用是 促进形核,细化晶粒 。 – 4. 液态金属结晶时,结晶过程的推动力是 自由能差降低(△F) , 阻力是 自由能增加 。 – 5. 能起非自发生核作用的杂质,必须符合 结构相似,尺寸相当 的原则。 – 6. 过冷度是指 理论结晶温度与实际结晶温度之差 ,其表示符 号为 △T 。 – 7. 过冷是结晶的 必要 条件。 – 8. 细化晶粒可以通过 增加过冷度 和 加变质剂 两种途径实现。 – 9. 典型铸锭结构的三个晶区分别为: 细晶区、柱状晶区和等轴晶区。
中 南 大 学 机 电 工 程 学 院
机械工程材料 第二章 金属的结构
♦ (二) 填空题
中 南 大 学 机 电 工 程 学 院
– 1. 同非金属相比,金属的主要特征是良好的导电性、导热性, 良好的塑性,不透明,有光泽,正的电阻温度系数。 – 2. 晶体与非金属最根本的区别是 晶体内部的原子(或离子) 是按一定几何形状规则排列的,而非晶体则不是 。 – 3. 金属晶体中最主要的面缺陷是 晶界 和 亚晶界 。 – 4. 错位分两种,它们是刃型位错 和 螺旋位错,多余半原子面 是 刃型 位错所特有的。 0 1 2 – 5. 在立方晶系中,{120}晶面族包括 ( 20)、(1 0)、(12 )、 等 (1 2 0)、(1 2 0)、(1 2 0 )、(1 20 )、(120) – 6. 点缺陷 有 空位和 间隙原子 两种;面缺陷中存在大量 的 位错 。 4 2 – 7. γ-Fe、α-Fe的一个晶胞内的原子数分别为 和 。 – 8. 当原子在金属晶体中扩散时,它们在内、外表面上的扩散 速度较在体内的扩散速度 快得多。
有机化学习题参考答案

O
CH3
O
CH2
C H
C
O
CH3
O
CH2
C H
C
O
CH3
(2)
CH2
C H
O
CH3
(3)
CH2
C H
Br
O
(4)
CH2
C H
C
CH3
H CH2 C O CH3
H CH2 C Br
HO CH2 C C CH3
O
CH2
C H
C
CH3
CH2
C H
O
CH3
CH2
C H
Br
O
CH2
C H
C
CH3
(5)
H2C
Answers:
2-6 下列共轭体系的共振结构式:
O
(1)
CH2
C H
C
O
CH3
(2)
CH2
C H
O
CH3
O
(4)
CH2
C H
C
CH3
Answers:
(5)
CH2
C H
C
NO(1) NhomakorabeaCH2
C H
C
O
CH3
HO CH2 C C O CH3
(3)
CH2
C H
Br
(6) CH3 C N O
O
CH2
C H
C
(6)
2-4 将下列化合物的结构式改写出为纽缦投影式,并用纽缦投影式表示每个化合物的优势构象。
H
H
H
Br
(1) H3C H3C
Br H
(2) H
(完整版)电气控制与PLC应用_第1章习题与思考题参考解答
第1章 常用低压控制电器习题与思考题1. 何谓电磁式电器的吸力特性与反力特性?吸力特性与反力特性之间应满足怎样的配合关系?答:不同的电磁机构,有不同的吸力特性。
电磁机构动作时,其气隙δ是变化的,22F B Φ∝∝。
对于直流电磁机构:其励磁电流的大小与气隙无关,衔铁动作过程中为恒磁动势工作,根据磁路定律/1/m m IN R R Φ=∝,式中R m 为气隙磁阻,则222m 1/1/F R Φδ∝∝∝,电磁吸力随气隙的减少而增加,所以吸力特性比较陡峭。
对于交流电磁机构:设线圈外加电压U 不变,交流电磁线圈的阻抗主要决定于线圈的电抗,若电阻忽略不计,则 4.44U E f N Φ≈=,/(4.44)U fN Φ=,当电压频率f 、线圈匝数N 、外加电压U 为常数时,气隙磁通Φ也为常数,即励磁电流与气隙成正比,衔铁动作过程中为恒磁通工作,但考虑到漏磁通的影响,其电磁吸力随气隙的减少略有增加,所以吸力特性比较平坦。
为了保证衔铁能牢固吸合,反作用力特性必须与吸力特性配合好。
在整个吸合过程中,吸力都必须大于反作用力,即吸力特性高于反力特性,但不能过大或过小,吸力过大时,动、静触头接触时以及衔铁与铁心接触时的冲击力也大,会使触头和衔铁发生弹跳,导致触头的熔焊或烧毁,影响电器的机械寿命;吸力过小时,会使衔铁运动速度降低,难以满足高操作频率的1-直流电磁铁吸力特性;2-交流电磁铁吸力特性;3-反力特性 答案图1F/Iδ0 123要求。
因此,吸力特性与反力特性必须配合得当,才有助于电器性能的改善。
在实际应用中,可调整反力弹簧或触头初压力以改变反力特性,使之与吸力特性有良好配合,参见答案图1所示。
2.单相交流电磁机构为什么要设置短路环?它的作用是什么?三相交流电磁铁要否装设短路环?答:由于单相交流接触器铁心的磁通是交变的,故当磁通过零时,电磁吸力也为零,吸合后的衔铁在反力弹簧的作用下将被拉开,磁通过零后电磁吸力又增大,当吸力大于反力时,衔铁又被吸合。
质点力学习题与参考解答
【郑重说明】《理论力学》课程的习题及解答方面的参考书很多,学习者可以通过各种形式阅读与学习,按照学院对教学工作的要求,为了满足学习者使用不同媒体学习的实际需要,通过各种渠道收集、整理了部分习题及参考解答,仅供学习者学习时参考。
由于理论力学的题目解答比较灵活,技巧性也比较强,下面这些解答不一定是最好的方法,也可能会存在不够完善的地方,希望阅读时注意之。
学习理论力学课程更重要的是对物理概念的掌握与理解,学习处理问题的思想与方法,仅盲目的做题目或者阅读现成的答案,很难达到理想的结果。
质点动力学思考题与习题及参考解答思考题(1) 有一质量为m 的珠子, 沿一根置于水平面内的铁丝滑动, 采用自然坐标法描述. 珠子受重力g m W=, 铁丝施与的约束力b Nb n Nn t Nt Ne F e F e F F ++=.t Nt e F 即为滑动摩擦力f F, 设动摩擦因数为μ. 试判断下列各式正误: (1) mg F f μ=; (2) Nb f F F μ= (3)Nn f F F μ=;(4) 22Nb Nnf F F F +=μ(2) 用极坐标系描述单摆的运动. 某甲如思考题(2图(a)规定θ角正向, 得到动力学方程θθsin mg ml -= ; 某乙如思考题(2图(b)规定θ角正向, 则得到θθsin mg ml += . 你认为谁的做法正确?(a) (b)思考题(2图(3) 质量为m 的质点, 由静止开始自高处自由落下. 设空气阻力f F与速度成正比, 比例系数为k . 某甲建立竖直向上的坐标如思考题(3图(a), 得到方程为y k mg y m+-=. 某乙建立竖直向下的坐标如思考题(3图(b), 得到方程为y k mg y m-=.他们列出的方程对吗?(a) (b)思考题(3(4)有人认为: 用极坐标系讨论质点的平面运动时, 如果0≡r F , 则沿径向动量守恒,==rm p r 常量;若0≡θF , 则沿横向动量守恒. 这种看法对吗? (5) 试判断以下二论断是否正确:(1) 若质点对固定点O 的角动量守恒, 则对过O 点的任意固定轴的角动量守恒. (2) 若质点对固定轴的角动量守恒, 则对该轴上任一固定点的角动量守恒.(6) 一质点动量守恒, 它对空间任一固定点的角动量是否守恒? 如质点对空间某一固定点角动量守恒, 该质点动量是否守恒?(7) 当质点做匀速直线运动时, 其动量是否守恒? 角动量是否守恒?(8) 在固定的直角坐标系Oxyz 中, 质量为m 的质点的速度k v j v i v v z y x++=, 所受合力为k F j F i F F z y x ++=. 能否将质点的动能定理r F mv d )21(d 2⋅=向x 轴方向投影而得出分量方程x F mv x x d )21(d 2= 该方程是否正确?思考题解答(1) 仅(4)式正确.(2) 甲正确. 乙错在角度不可以定义为从动线指向定线.(3) 乙的方程正确. 甲错在空气阻力亦应为yk -,y 取负值,y k -取正值. (4) 仅对固定方向才有动量守恒的分量形式. 径向和横向均不是空间固定方向. (5) (1)对;(2)错. (6) 一质点动量守恒,则对空间任一固定点角动量守恒. 质点对空间某一固定点角动量守恒,其动量不一定守恒.(7) 质点作匀速直线运动时,其动量和角动量均守恒.(8) 动能定理是标量方程,不可能投影而得出分量方程. 但xF mv x d )21(d 2=是正确的. 仿照动能定理的导出,用x t v x d d =乘牛顿第二定律的x 分量方程x xF t v m=d d 即可证明.质点动力学习题及参考解答【1】研究自由电子在沿x 轴的振荡电场中的运动. 已知电场强度i t E E)cos(0ϕω+=,ϕω,,0E 为常量. 电子电量为e -, 质量为m . 初始时, 即当0=t 时i x r00=, i v v 00=. 忽略重力及阻力, 求电子的运动学方程.【解】力为时间的函数,积分两次可得)cos(200ϕωω+++=t m eE t V X x ,其中ϕωcos 2000m eE x X -=,ϕωsin 00m eE v V +=.【2】 以很大的初速度0v自地球表面竖直上抛一质点, 设地球无自转并忽略空气阻力, 求质点能达到的最大高度. 已知地球半径为R , 地球表面处重力加速度为g .【解】以地心O 为原点,建立x 轴经抛出点竖直向上. 质点受万有引力沿x 轴负方向. 所以2x GMm xm -= . 因为2R GMmmg =,故g R GM 2=. 故有22x g R x -= . 做变换)2(d d d d d d d d 2x x x x x t x x x x ===,则x x g R x d )2(d 222-= . 积分并用0=t 时R x =,0v x = 定积分常数,得到 )11()(212202R x g R v x -=- . 质点达最大高度时H R x +=,0=x,可求出 1220)21(2--=Rg v g v H .三点讨论:(1)令∞=H ,对应Rg v 20=为第二宇宙速度.(2)若Rg v 220<<,则回到重力场模型所得结果. (3)题中不考虑地球自转及空气阻力,均不大合理,试进一步讨论之.【3】 将质量为m 的质点竖直上抛, 设空气阻力与速度平方成正比, 其大小22gv mk F R =.如上抛初速度为0v , 试证该质点落回抛出点时的速率2201v k v v +=.【解】质点运动微分方程为(Oy 轴竖直向上);上升阶段22y g mk mg y m--=,下降阶段22y g mk mg ym +-=. 【4】向电场强度为E 、磁感应强度为B 的均匀稳定电磁场中入射一电子. 已知B E⊥, 电子初速0v 与E 和B 均垂直, 如题4图所示. 试求电子的运动规律. 设电子电量为e -.题4图【解】令m eB=ω,电子运动微分方程为y xω-=, (1) m eEx y-= ω, (2)0=z . (3)对(2)式求导,利用(1)式得02=+y yω,解出)sin(αω+=t A y . 0=t 时0=y 故0=α,由t A y ωωcos = ,且0=t 时m eBv Ee y0+-= ,故B Bv E A 0+-=,则t B Bv E y ωsin 0+-= . 积分得)cos 1()(20t m eB eB Bv E m y -+-=. 代入(1)式积分可得t m eB eB Bv E m t B E x sin )(20--=.【5】 旋轮线如题5图所示, 可理解为一半径为a 的圆轮在直线上做无滑滚动时轮缘上一点P 的轨迹, 其参数方程为)sin (ϕϕ+=a x , )cos 1(ϕ-=a y . 在重力场中, 设y 轴竖直向上, 一质点沿光滑旋轮线滑动, 试证质点运动具有等时性(绕O 点运动周期与振幅无关).题5图【解】(旋轮线是如图圆轮在直线AB 上作无滑滚动时P 点的轨迹,曲线上P 点切线方向即为轮上P 点速度方向. 因无滑,0P 为瞬心,故P 点切线与P P 0垂直,因此可知P 点切线与x 轴夹角为2ϕ. )以曲线最低点(0=ϕ)为自然坐标原点,弧长正方向与t e 一致. 质点运动微分方程为2sinϕmg s m -= .对曲线参数方程求微分,得ϕϕd )cos 1(d +=a x 和ϕϕd sin d a y =,所以ϕϕd 2cos 2d d d 22a y x s =+=,积分并用0=ϕ时0=s 定积分常数,得2sin 4ϕa s =. 代入质点运动微分方程消去ϕ,得到4=+s a gs ,s 作简谐振动而具有等时性. 其解为)cos(0αω+=t A s ,a g40=ω与振幅无关.【6】 一小球质量为m , 系在不可伸长的轻绳之一端, 可在光滑水平桌面上滑动. 绳的另一端穿过桌面上的小孔, 握在一个人的手中使它向下做匀速运动, 速率为a , 如题【6图所示. 设初始时绳是拉直的, 小球与小孔的距离为R , 其初速度在垂直绳方向上的投影为0v . 试求小球的运动规律及绳的张力.题6图【解】小球运动微分方程为T F r r m -=-)(2θ , (1) 0)2(=+θθr r m , (2)a r-= . (3) 由(3)式求出at R r -=,代入(2)式求出)/(0at R t v -=θ,再由(1)式求出3220)(at R R mv F T -=.【7】 一质量为m 的珠子串在一半径为R 的铁丝做成的圆环上, 圆环水平放置. 设珠子的初始速率为0v , 珠子与圆环间动摩擦因数为μ, 求珠子经过多少弧长后停止运动 (根据牛顿第二定律求解).【解】珠子的运动微分方程为2b 2n d d N N F F t v m+-=μ, (1)n 2/N F mv =ρ, (2)mg F N -=b 0, (3)R =ρ(约束方程). (4)把(2)、(3)、(4)式代入(1)式,作变换sv t v d /)21(d d d 2=,可求出]/)ln[()2/(224020Rg g R v v R s ++=μ.【8】 质量为m 的小球沿光滑的、半长轴为a 、半短轴为b 的椭圆弧滑下, 此椭圆弧在竖直平面内且短轴沿竖直方向. 设小球自长轴端点开始运动时其初速度为零. 求小球达到椭圆弧最低点时对椭圆弧的压力 (根据牛顿第二定律求解). 【解】以椭圆最低点为自然坐标原点O ,弧长正方向指向小球初始位置,θ为切向与水平方向的夹角,小球的运动微分方程为θsin mg vm -= , (1) θρcos /2mg F mv N -=. (2)Oy 竖直向上,将s y d /d sin =θ代入(1)式得s y g s v v d /d d /d -=,积分可求出小球达最低点时gb v 22=. 由轨道方程22x a a by --=求出当0=x 时0='y ,2/a b y ='',由公式可求出22/32)1(1a b y y ='+''=ρ. 再由(2)式求出0=θ时)/21(/cos 22a b mg mv mg F N +=+=ρθ.【9】 力1F 和2F分别作用在长方体的顶角A 和B 上, 长方体的尺寸和坐标系如题【9图所示. 试计算1F 和2F对原点O 及3个坐标轴的力矩.题9图【解】11bF M x =,11aF M y -=,01=z M ,2222/b a bcF M x +=,2222/b a acF M y +-=,02=z M .【10】 已知质量为0m 的质点做螺旋运动, 其运动学方程为t r x ωcos 0=, t r y ωsin 0=,kt z =,k r ,,0ω为常量. 试求: (1)t 时刻质点对坐标原点的角动量;(2) t 时刻质点对过),,(c b a P 点, 方向余弦为),,(n m l 的轴的角动量.【解】由运动学方程求出→v ,根据定义即可求出→→→→→→++--=⨯=k r m j t t t r km i t t t r km v r m L ωωωωωωω200000000)sin (cos )cos (sin ,)]cos ()sin )([(]cos )()sin ([000000),,(a t r k t r c kt m m t r c kt b t r k l m L n m l -+-----=ωωωωωω)sin cos (00200t br t ar r n m ωωωωω--+.【11】 如题【11图所示, 质量为m 的小球安装在长为l 的细轻杆的A 端, 杆的B 端与轴21O O 垂直地固连. 小球在液体中可绕21O O 轴做定轴转动, 轴承1O 和2O 是光滑的. 转动中小球所受液体阻力与角速度成正比, ωαm F R =,α为常量. 设初始角速度为0ω,试求经多少时间后, 角速度减小为初始值的一半,以及在这段时间内小球所转圈数.(忽略杆的质量及所受阻力.)题 11图【解】由对21O O 轴的角动量定理ωαωm l ml t -=)(d d2,积分可得lt /0e αωω-=,求出α/)2ln (l t =. 将角动量定理化为l /d d θαω-=,积分可以求得αωαωθπ4/)r a d (2/00l l ==(圈)【12】 质量为m 的质点沿椭圆轨道运动, 其运动学方程为kt a x cos =, kt b y sin = (k b a ,,为常量). 用两种方法计算质点所受合力在0=t 到k t 4π=时间内所做的功.【解】(1)由动能定理)(4121212222122b a mk mv mv W -=-=.(2)用曲线积分算⎰⎰+=⋅=→→2121)d d (y ym x x m r d F W ,把轨道参数方程kt b y kt a x sin ,cos ==代入,则曲线积分化为对t 的积分,可得同样结果.【13】 试用动能定理求解7题.【解】珠子的动能定理为sF F mv N N d )21(d 2b 2n 2--=μ,参见3.7提示【14】 有一小球质量为m , 沿如题【14图所示的光滑的水平的对数螺旋线轨道滑动. 螺旋线轨道方程为θa e r r -=0, a 为常数. 已知当极角0=θ时,小球初速为0v . 求轨道对小球的水平约束力N F 的大小. (用角动量及动能定理求解, 图中δ为θe 与v 方向间夹角,a =δtg.)题14图【解】因机械能守恒,小球动能不变,因此0v v =.过O 点作z 轴竖直向上(垂直纸面向外),质点对z 轴的角动量δcos rmv L z =. 质点所受对z 轴力矩δsin N z rF M -=. 由对z 轴的角动量定理得δδsin )cos (d d0N rF rmv t -=.由于θθθθθ ar ar t r r v a r -=-===-e d d d d 0,θθ r v =. 故a v v r =-=θδtan . 将它代入角动量定理方程,得到N N arF rF rmv -=-=δtan 0 . 而δδsin sin 0v v v r r -=-== ,所以θδδδa N a r mv a r mv ar mv ar mv F e 11tan 1tan sin 2020220222020+=+=+==.【15】 已知质点所受力F 的3个分量为z a y a x a F x 131211++=,z a y a x a F y232221++=, z a y a x a F z 333231++=,系数)3,2,1,(=j i a ij 都是常量. 这些ij a 满足什么条件时与力F相关的势能存在? 在这些条件被满足的条件下, 计算其势能.【解】当0=⨯∇→F 时势能存在,要求311332232112,,a a a a a a ===. 以原点为势能零点,则)222(21132312233222211xz a zy a xy a z a y a x a V +++++-=.【16】 一带有电荷q 的质点在电偶极子的场中所受的力为3c o s 2r pq F r θ=,3sin r pq F θθ=,p 为偶极距, r 为质点到偶极子中心的距离.试证此力场为有势场.【解】)/cos (d d d )d d (d 2r pq r F r F e r e r F r F r r θθθθθ-=+=+⋅=⋅→→→→→,故为有势场 【17】 如题17图所示, 自由质点在Oxy 平面内运动, 静止中心A 和B 均以与距离成正比的力吸引质点M , 比例系数为k . 试证明势能存在并求出质点的势能.v题【17图【解】y ky x kx y ky ky x b x k b x k r F d 2d 2d )(d )]()([d --=--+--+-=⋅→→)](d [22y x k +-=.故势能存在. 以O 为势能零点,则)(22y x k V +=.【18】 试用机械能守恒定律求解8题.【解】根据机械能守恒定律,以椭圆弧最低点为势能零点,mgbmv =221,可知gb v 2=,参见3.8提示.【20】 将质量为m 的质点竖直抛上于有阻力的媒质中。
科学出版社 江文杰编著《光电技术》习题答案
4-7 说明 PIN 管、雪崩光电二极管的工作原理和各自特点。PIN 管的频率特性为什么比普通 光电二极管好? 答:(一)PIN 光电二极管
工作原理:PIN 光电二极管是一种快速光电二极管,PIN 光电二极管在掺杂浓度很高的 P 型半导体和 N 型半导体之间夹着一层较厚的高阻本征半导体 I,其基本原理与光电二极管 相同。但由于其结构特点,PIN 光电二极管具有其独特的特性。如下图所示。
=
SΦ m
R1 RL
=
SΦ m
Rb Rb + RL
=
0.6 × 5 × 125 125 + 125
= 1.5μA
交流输出电压 UL 的有效值
UL = ILmRL / 2 = 1.5μA ×125kΩ/ 2 = 132.6mV
(3)上限截止频率
f HC
=
1 2πR1C1
=
1 2 × 3.14 × 125 ×103 × 6 ×10−12
科学出版社《光电技术》第 1 版习题与思考题及参考解答
第 4 章 光伏探测器
4-1 (1)证明:光电二极管输出的光电流 Ip = eηΦ0 / (hν ) ,式中:Ф0 为入射辐射功率,e
为电子电量,η为量子效率,hv 为入射光子能量;(2)通常光电二极管的内增益 M=1,不会 出现 M>1。试从光伏效应的机理上加以解释。
压,负载电阻 50Ω 自身的噪声电压):
U
2 in
=
2eiΔf
⋅
R2
+
4kT Δf
⋅
R
=
第3章 习题及参考解答
第3章习题及参考解答1.指出下列各指令中源操作数和目的操作数的寻址方式。
(1)MOV DI,100(2)MOV CX.100[SI](3)MOV [SI],AX(4)ADD AX,[BX+DI](5)AND AX,BX(6)MOV DX,[1000](7)MOV BX,[BP+DI+100](8)PUSHF(9)SUB [1050],CX(10)AND DH,[BP+4]解源操作数目的操作数(1)立即寻址寄存器寻址(2)变址寻址寄存器寻址(3)寄存器寻址寄存器间接寻址(4)基址加变址寻址寄存器寻址(5)寄存器寻址寄存器寻址(6)直接寻址寄存器寻址(7)基址加变址寻址寄存器寻址(8)寄存器寻址寄存器间接寻址(9)寄存器寻址直接寻址(10)变址寻址寄存器寻址2.试述指令MOV AX,2000H和MOV AX,DS:[2000H]的区别?解区别有三条:(1)MOV AX,2000H对源操作数是立即寻址,而MOV AX.[2000H]对源操作数是直接寻址;(2)前者功能是把立即数2000H送入AX中,而后者是把内存2000H单元与2001H单元的内容取出送入AX 中;(3)两者的机器代码不同,执行速度也不同,前者执行时间快,后者执行时间慢。
4.若DS=4000H,BX=0800H,[40800H]=05AOH,[40802H]=2000H,求执行指令LDS SI,[BX]后,DS与SI中的内容。
若上题中的DS换成ES,其他条件不变,求执行指令LES DI,[BX]后,ES与DI 中的内容。
解SI=05AOH,DS=2000HDI=05AOH,ES=2000H5.若AX=98ABH,BX=A8BCH。
求执行指令ADD AX,BX后,AX与BX中的内容,并指出SF,ZF,AF,PF,CF和OF的状态。
解AX=4167H,BX=A8BCH,SFZFAFPFCFOF=001011B。
6.若CX=6700H,DX=78FFH,CF=1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章进程及进程管理
4-3什么是进程进程与程序的主要区别是什么
答:进程,即是一个具有一定独立功能的程序关于某个数据集合的一次活动。
进程与程序的主要区别是:
(1)程序是指令的有序集合,是一个静态概念,其本身没有任何运行的含义,进程是程序
在处理机上的一次执行过程,是一个动态概念。
(2)程序作为软件资料可长期保存,而进程是有生命期的,因创建而产生、因调度而执行、因得不到资源而暂停、因撤消而消亡。
(3)程序是记录在介质上指令的有序集合,而进程则由程序、数据和进程控制块3部分组成。
(4)进程与程序之间无一一对应关系。
不同的进程可以包含同一程序,同一程序在执行中也可以产生多个进程。
(5)进程是一个独立的运行单位,也是系统进行资源分配和调度的独立单位。
而程序无此概念。
4-6进程有哪几个基本状态在一个系统中为什么必须区分出这几种状态
答:进程有三个基本状态:运行状态、就绪状态和等待状态(又称阻塞、挂起、睡眠)
对进程区分出这几种状态主要是为了便于系统对进程的管理和控制。
4-7试用图画出批处理系统的进程状态变迁图。
4-8试用图画出分时系统的进程状态变迁图。
4
(1) 什么原因导致变迁2、变迁3、变迁4 变迁2:某进程的时间片满
变迁3:某进程请求服务,或等待事件
变迁4:某进程请求服务完成,或等待事件发生
(2) 当观察系统中进程时,可能看到某一进程产生的一次状态变迁将导致另一进程做一次状
态变迁,这两个变迁称为因果变迁。
在什么情况下,一个进程的变迁3能立即引起另一个进程发生变迁1
当有一个进程发生变迁3时,将会让出处理器,这时调度必然在就绪队列中选中一个进程使之由就绪状态变为运行状态。
(3) 下述因素变迁是否可能发生如果可能,是在什么情况下发生
1可能发生。
有一个进程由运行状态变就绪状态,它让出处理器,则这时必有一个进程由就
绪状态转运行状态。
2不可能发生。
有一个进程由运行状态变等待状态,它让出处理器,这种变迁不会导致另一
个进程由运行状态转就绪状态。
1不可能发生。
一个进程由等待状态变就绪状态,只是自身进程的状态变迁,不涉及处理器, 故不会引起其它进程由就绪状态变运行状态。
4-11什么是进程控制块它有什么作用
为了描述一个进程和其它进程,以及系统资源的关系,为了刻画一个进程在各个不同时期所
处的状态,人们采用了一个与进程相联系的数据块,称为进程控制块(PCB)。
其作用:标识一个进程的存在。
4-12 n个并发进程共用一个公共变量Q,写出用信号量实现n个进程互斥时的程序描述,给出信号量取值的范围,并说明每个取值的物理意义。
main ()
{
int mutQ=1;
V(mutQ);
}
mutQ的取值范围:1-n〜1
1-n :表示一个进程正在使用公共变量Q,另有n-1个进程在等待使用公共变量Q
0 :表示一个进程正在使用公共变量Q,没有进程等待使用公共变量Q
1:表示初始情况下没有进程使用该变量
P、V操作实现下图(a)、(b)中所示进程之间的同
⑻解:
main ()
{
int s12=0,s13=0,s14=0; cobegi n
p1();
p2();
p3();
P4();
coe nd } p1()
{ (b)
V(s12);
V(s13);
V(s14);
}
p2()
{
P(s12);
p2 execute;
}
p3()
{
P(s13);
p3 execute;
}
p4()
{
P(s14);
p4 execute;
P(s2);
解:
mai n()
}
pb()
{
}
4-15如下图所示,get、copy、put三进程共用两个缓冲区s、t (其大小为每次存放一个记录)。
get 进程负责不断地把输入记录送入缓冲区s中,copy进程负责从缓冲区s
取出记录复制到缓冲区t中,而put进程负责从缓冲区t中取出记录打印。
试用P、V 作实现这三个进程之间的同步,并写出程序描述。
V(s2);
V(s1);
}
(1)设a、b两并发进程,它们共享一临界资源。
其执行临界区的算法框图如下图,
进程A和进程B为互斥进程,则需一个互斥信号量s,初值为1,表示临界资源初始情况下
无进程使用。
main ()
{
int s=1;
cobegi n
pa();
pb();
coe nd
}
pa()
{
P(s);
进入csa…
V(s);
}
pb()
{
P(s);
进入csb…
V(s);
}
4-21什么是线程线程和进程有什么区别
答:线程有时也称为轻量级进程,它是比进程更小的活动单位,它是进程中的一个执行路径。
一个进程可以有多个执行路径即线程。
线程和进程的主要区别如下:
(1)线程是进程的一个组成部分。
一个进程可以有多个线程,而且至少有一个可执行的线
程。
(2)进程是资源分配的基本单位,它拥有自己的地址空间和各种资源。
线程是处理机调度的基本单位,它只能和其他线程共享进程的资源,而本身并不具有任何资源。
(3)进
程的多个线程都在进程的地址空间内活动。
这样,在以线程为单位进行处理机调度和切换时,由于不发生资源变化特别是地址空间的变化,因此切换时间较短。
而以进程为单位进行处理
机调度和切换时,由于涉及到资源转移及现场保护等问题,将导致切换时间变长和资源利
用率降低。
(4)线程和进程一样,都有自己的状态和相应的同步机制。
但是,由于线程没
有自己单独的程序和数据空间,因而不能像进程的程序和数据那样交换到外存去。
(5)进程的调度和控制大多由操作系统的内核完成,而线程的控制既可以由操作系统内核
完成,也可以由用户控制完成。
4-22说明Linux系统进程状态
TASK_RUNNING 就绪/运行状态
TASK_INTERRUPTIBLE 尝试睡眠状态
TASK_UNINTERRUPTIBLE 浅度睡眠状态
TASK_STOPPED 暂停状态
TASK_ZOMBIE 僵死状态
4-23说明Linux系统进程状态变迁,及变迁的可能原因。
