七年级下学期第七章三角形期末复习
考点及题型总结七下第七章(三角形)
人教版初中数学七年级下册考点及题型总结(七)创作者:付红刚创作时间:20XX年5月9日星期四第七章三角形一.知识框架第一节与三角形有关的线段一、知识要点:(一)三角形的概念1、三角形定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2、三角形的边:组成三角形的线段叫做三角形的边;3、三角形的顶点:相邻两边的公共端点叫做三角形的顶点;4、三角形的角:相邻两边所组成的角叫做三角形的内角,简称三角形的角。
(二)三角形中的主要线段1、三角形的高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
2、三角形的中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
3、三角形的角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
(三)三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫做三角形的稳定性。
(四)三角形的分类1、三角形按边的关系分类如下:不等边三角形三角形底和腰不相等的等腰三角形等腰三角形等边三角形2、三角形按角的关系分类如下:直角三角形(有一个角为直角的三角形)三角形锐角三角形(三个角都是锐角的三角形)斜三角形钝角三角形(有一个角为钝角的三角形)3、把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。
它是两条直角边相等的直角三角形。
4、在等腰三角形中,相等的两边都叫腰,另一边叫底,两腰的夹角叫做顶角,腰和底边的夹角叫做底角(五)三角形的三边关系定理及推论1、三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
2、三角形三边关系定理及推论的作用:①判断三条已知线段能否组成三角形②当已知两边时,可确定第三边的范围。
③证明线段不等关系。
二、题型分析:题型一:根据三角形三边关系求距离范围例题:如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A、20米B、15米C、10米D、5米解析:因为三角形的三边满足任意两边之和大于第三边,任意两边之差小于第三边,所以第三边AB的取值范围是:15-10<AB<15+10,即5<AB<25.答案:D.题型二:根据三角形三边关系判断线段组合例1:长为11,8,6,4的四根木条,选其中三根组成三角形有种选法,它们分别是答案:三种; 11、8、6 ;11、8、4; 8、6、4;例2:已知线段a>b>c,它能组成三角形需满足的条件是()A、a=b+c B.a+c>b C.b+c<a D.a-b<c答案:D习题:以长为3cm,5cm,7cm,10cm的四根木棍中的三根木棍为边,可以构成三角形的个数是()A、1个B、2个C、3个D、4个答案:B题型三:根据三角形三边关系求等腰三角形周长例1:等腰三角形的两边长分别为12和6,则此三角形的周长为()。
七年级(下)(第七章~第九章)期末复习指导:第七章 三角形

点 评 也 可 以 由 多边 形 的 内 角和 公 式 , 出边 数 , 设 多边 推 如
例 4 ( 0 5年 济 南 市 中考 题 ) 们 常 用 各 种 多边 形地 砖 拼 20 我
1 0・ 一 3 0 化简 , L4 2 2 6, 得 z - y一 6 因为 L, 都是 正整 数 , 以只有 当 . z 所
பைடு நூலகம்
D AE 一 B+ A DC得 C DA 一 B一 B AC, 其中某个 可设
角为未知数 , 用它把 △AB 的三个角表示出来 , D 列方程求解即可.
绥 解 设 D — 度) c D一2( . 为A A c ( , A 则 z度)因 D平
分 E C, 以 CAD 一 DAE 一 2 .因 为 EA 一 B+ A 所 x D ADC. 以 B = z, 为 AC — B 所 以 B 所 因 C. AC — z, AABD 在
中, B+ A Dc+ B AD = 10 度)即 z 8 ( , +z +z x一 10度 ) +2 8( , 所以 3一 3 ( , 以 AB 一 3 ( ) 5 6度)所 " c 6度 .
点评 本例 考 查 了三 角形 的外 角 、 角平 分 线 、 等腰 三 角形 的
AD — Z CA D,则 AB C 等 于 c
度.
图1
分析
要求 A c的度数 , B 就是要找到 AB c与其他角问
的关 系 , 借助 于三 角形 内 角和等 于 10 而解 得. AC — BC, 8。 由 知 B一 /B AC, AD 平 分 CAE 得 C 而 AD 一 DAE 一 2 lADC, 由
圈
例 1 有 四根 长 度 分 别 为 4c 6c 1 m,5C I m, m, 0c 1 1 的钢 条 , T
七年级数学下册第七章三角形小结与复习学案

课题:三角形小结与复习【学习目标】1、通过学生对本章所学知识的回顾与思考,进一步掌握知识点;2、经历考点例题解析,使学生进一步提高运用所学知识解决问题的能力。
【学习重点】本章知识点的回顾与思考。
【学习难点】运用所学知识解决问题。
【复习流程】 活动一:本章知识结构图1、三角形的边(1)两边之和 第三边,两边之差 第三边。
(2)两边之差 < 第三边 < 两边之和2、三角形的高、中线、角平分线(1)△的高、△的中线、△的角平分线都是 (选填‘线段、射线和直线’)(2)交点情况a.三条高所在的直线交于一点:△是锐角三角形时交点位于△的内部;△是直角三角形时,交点位于直角三角形的直角顶点;△是钝角三角形时,交点位于三角形的外部。
b.△的三条中线交于一点,交点位于△的内部。
第条中线都把三角形分成面积相等的两个三角形。
c.△的三条角平分线交于一点,交点位于△的内部。
3、△的高、中线、角平分线几何符号语言表示(1)∵AD 是△ABC 的边BC 上的高,∴AD ⊥BC ,∴∠ADB=∠ADC=90°(2)∵AE 是△ABC 的边BC 上的中线,∴2,△ABE 的面积 = △AEC 的面积 (3)∵AF 是△ABC 的角平分线, ∴∠1=∠2 =21∠ 4、三角形的角(1)∠A + ∠B + ∠C = 180°△内角和定理: 任何三角形的内角和都等于 度三角形 与三角 形有关 的线段 三角形的内角和 三角形的外角和 边 高 中线 角平分线 多边形的内角和多边形的外角和(2)∠1 = ∠ A + ∠B.∠1 > ∠ A ,∠1 > ∠ B ,△的外角性质: 。
5、三角形的分类a.按边分: △ ()()⎪⎩⎪⎨⎧⎩⎨⎧=角形腰和底不相等的等腰三底腰等边三角形等腰三角形三角形三条边都不相等不等边三角形)()(21 B.按角分:(1)锐角三角形(三个角都是锐角);(2)直角三角形(有一个角为直角);(3)钝角三角形(有一个角为钝角)。
新人教版七年级下学期数学第七章三角形复习专练
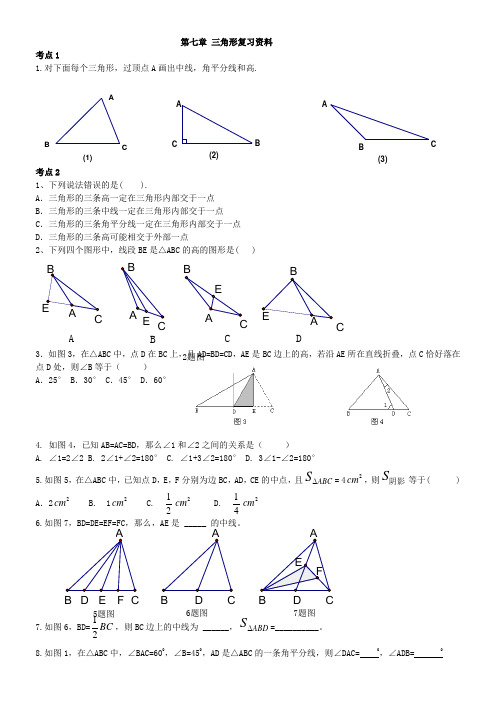
2题图D C B A E E A C B A C B A B C A B CE E 6题图7题图5题图F EDD F DE B C A A C B BCA 第七章 三角形复习资料 考点11.对下面每个三角形,过顶点A 画出中线,角平分线和高.考点21、下列说法错误的是( ).A .三角形的三条高一定在三角形内部交于一点B .三角形的三条中线一定在三角形内部交于一点C .三角形的三条角平分线一定在三角形内部交于一点D .三角形的三条高可能相交于外部一点2、下列四个图形中,线段BE 是△ABC 的高的图形是( )3.如图3,在△ABC 中,点D 在BC 上,且AD=BD=CD ,AE 是BC 边上的高,若沿AE 所在直线折叠,点C 恰好落在点D 处,则∠B 等于( )A .25° B.30° C.45° D.60°4. 如图4,已知AB=AC=BD ,那么∠1和∠2之间的关系是( )A. ∠1=2∠2B. 2∠1+∠2=180°C. ∠1+3∠2=180°D. 3∠1-∠2=180°5.如图5,在△ABC 中,已知点D ,E ,F 分别为边BC ,AD ,CE 的中点,且ABC S ∆= 42cm ,则S 阴影等于( )A .22cm B. 12cm C.122cm D. 142cm 6.如图7,BD=DE=EF=FC ,那么,AE 是 _____ 的中线。
7.如图6,BD=12BC ,则BC 边上的中线为 ______,ABD S ∆=__________。
8.如图1,在△ABC 中,∠BAC=600,∠B=450,AD 是△ABC 的一条角平分线,则∠DAC= 0,∠ADB= 0(1)C B AC B A (2)C BA (3)9.如图2,在△ABC 中,AE 是中线,AD 是角平分线,AF 是高,则根据图形填空: ⑴BE= =21 ;⑵∠BAD= =21 ⑶∠AFB= =900;10.如图在△ABC 中,∠ACB=900,CD 是边AB 上的高。
新人教版七年级下册第七章三角形知识点归纳总结及配套练习

第七章《三角形》知识归纳及配套练习题➢ 与三角形有关的线段 (1)三角形的概念(2) ①⎪⎩⎪⎨⎩⎨⎧等边三角形底和腰不相等的三角形等腰三角形三角形按边)( ②⎪⎩⎪⎨⎧⎩⎨⎧钝角三角形锐角三角形斜三角形直角三角形三角形按角 (3)三角形的主要线段①三角形的中线:极点与对边中点的连线,三中线交点叫重心②三角形的角平分线:内角平分线与对边相交,极点和交点间的线段,三角角平分线的交点叫心里③三角形的高:极点向对边作垂线,极点和垂足间的线段.三条高的交点叫垂心(分锐角三角形,钝角三角形和直角三角形的交点的位置不同)(4)三角形三边间的关系.①两边之和大于第三边 b a c a c b c b a >+>+>+,, ②两边之差小于第三边 a c b c b a b a c <-<-<-,, (5)三角形的稳固性:三角形的三条边肯定后,三角形的形状和大小不变了,那个性质叫做三角形 的稳固性.三角形的稳固性在生产和生活中有普遍的应用.➢ 本章知识结构图例1:已知BD,CE 是ABC ∆的高,直线BD,CE 相交,所成的角中有一个角为50°, 则等于BAC ∠分析:本题中由于没有图形, ABC ∆的形状不肯定,应分两种情形:①ABC ∆是锐角三角形 ②ABC ∆是钝角三角形 解:50或130(进程略)例2:如图,已知ABC ∆中,ACB ABC ∠∠和的角平分线BD,CE 相交于点O,且60=∠A ,求BOC ∠的度数例3:三角形的最长边为10,另两边的长别离为x 和4,周长为c,求x 和c 的取值范围.解:已知三角形的两边为10和4.那么第三边x 的范围应知足: 410410+<<-x 即6<x <14.2420,41010641010610≤<++≤<++∴≤<∴c c c x 即的范围满足周长是最长边➢ 与三角形有关的角(1)三角形的内角和定理及性质定理:三角形的内角和等于180°。
新人教版七年级下册第七章《三角形》知识点归纳总结及配套练习

第七章《三角形》➢ 与三角形有关的线段(1)三角形的定义(2) ①⎪⎩⎪⎨⎩⎨⎧等边三角形底和腰不相等的三角形等腰三角形三角形按边)( ②⎪⎩⎪⎨⎧⎩⎨⎧钝角三角形锐角三角形斜三角形直角三角形三角形按角 (3)三角形的主要线段①三角形的中线:顶点与对边中点的连线,三中线交点叫重心②三角形的角平分线:三角形一个角的平分线与对边相交,顶点和交点间的线段,三角角平分线的交点叫心③三角形的高:过三角形的一个顶点向对边作垂线,顶点和垂足间的线段.三条高的交点叫垂心注意:①三角形的角平分线、中线和高都是线段;②任意一个三角形都有三条角平分线,三条中线和三条高;③任意一个三角形的三条角平分线、三条中线都在三角形的部。
但三角形的高却有不同的位置:锐角三角形的三条高都在三角形的部;直角三角形有一条高在三角形的部,另两条高恰好是它两条直角边;钝角三角形一条高在三角形的部,另两条高在三角形的外部(图形讲解)。
(4)三角形三边间的关系.①三角形任意两边之和大于第三边 b a c a c b c b a >+>+>+,,②任意两边之差小于第三边 a c b c b a b a c <-<-<-,,(5)三角形的稳定性:三角形的三条边确定后,三角形的形状和大小不变了,这个性质叫做三角形 的稳定性.三角形的稳定性在生产和生活中有广泛的应用.考点一:三角形的分类例1:具备下列条件的三角形中,不是直角三角形的是( )。
A.∠A+∠B=∠CB.∠A=∠B= ∠CC.∠A=90°-∠B例2:等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( ).A .60°B .120°C .60°或150°D .60°或120°考点二:三角形三边的关系例3:现有两根木棒,它们的长分别是40cm 和50cm ,若要钉成一个三角形木架,则在下列四根木棒中应选取长为( C )A.100cm 的木棒B.90cm 的木棒C.40cm 的木棒D.10cm 的木棒例4:三角形的最长边为10,另两边的长分别为x 和4,周长为c,求x 和c 的取值围.解:已知三角形的两边为10和4.那么第三边x 的围应满足:410410+<<-x 即6<x <14.2420,41010641010610≤<++≤<++∴≤<∴c c c x 即的范围满足周长是最长边练习下列长度的三条线段能组成三角形的是 ( )A 、 3,4,8B 、 5,6,11C 、 1,2,3D 、 5,6,10➢ 与三角形有关的角(1)三角形的角和定理及性质定理:三角形的角和等于180°。
人教版七年级下第七章三角形复习课
人教版七年级下第七章“三角形”复习课()——“与角有关的三角形复习课”教学设计方案一、教学目标:通过复习“与角有关的三角形”知识点,进一步领会建模、有序思维、数形结合、分类、化归、从特殊——一般——特殊等数学思想,体会事物之间相互联系和运动变化、量变引起质变等辩证唯物主义观点:同时培养学生分析问题、解决问题能力,培养学生学习数学的乐趣;体现“探究有尺度,归纳有顺序,习题有难易,精彩有延续”.二、教学重点、难点:教学重点:有序思维、数形结合教学难点:动点问题教学手段:多媒体课件教学方法:探究式互动性教学三、教学过程一.温顾新知,巩固认知.三角形内角和三角形内角和等于度直角三角形的两个锐角互余。
.三角形外角和三角形的三个外角的和是°.三角形的外角与内角的关系三角形的一个外角等于与它不相邻的两个内角的和.三角形的一个外角大于与它不相邻的任何一个内角.. 三角形的分类() 按角分三角形 直角三角形 斜三角形 锐角三角形钝角三角形 () 按边分三角形 不等边三角形 等腰三角形 底和腰不等的等腰三角形 等边三角形 二、应用新知,深化认知.根据下图已知角的度数,求的值.⎧⎨⎩⎧⎨⎩⎧⎨⎩⎧⎨⎩() () (). 在△中,∠∠∠,则∠°,∠ ° 。
.在△中 若∠:∠:∠ ::,则∠°,∠ ° 。
小结:求三角形角的一般方法。
由形定数,由数思形,数形结合,方程思想。
三、应用新知,活化认知.已知等腰三角形的一个内角为°,则其顶角为( ).° .° .° .°或°. 等腰三角形的一个外角为°,则它的底角为( )° ° °或° .以上都不对小结:等腰三角形的角的求法,体现分类思想.四、应用新知,升华认知.有一块直角三角尺,放在△上,如图所示,△的两条直角边、分别经过、两点,在△中,∠ 求∠∠的度数;问题:若∠(锐角),其它条件不变, 求∠∠的度数;问题:若∠(钝角)呢?问题:探究∠、∠、∠与∠ 之间的数量关系.变式二:若点在△的外部,两条边、仍过、两点,∠∠∠∠是否还成立?请画出图形,探究∠、∠、∠与∠ 之间的数量关系?特例:若点是△中∠ 、∠ 的角平分线交点,试探究∠与∠ 之间1902D ∠=︒+∠A的数量关系.答案:特例: 若点是∠的角平分线与∠ 的外角平分线的交点,试探究∠与∠ 与之间的数量关系.答案: 特例: 若点是∠的外角平分线与∠的外角平分线的交点,试探究∠与∠ 与之间的数量关系.答案: 变式三: 若将△的两条边、分别经过、两点,改为△的两条边、分别与△两条边、相交,以上探究的结论是否还成立?小结:数学的解题方法:从特殊——一般——特殊.五:归纳总结,反思提炼 本节课,你有什么收获?还有什么困惑? 学习数学常用有序思维、数形结合、分类、从特殊——一般——特殊等数学思想,解题时学会多思、多想、多动,学起数学感觉趣味无穷.教学反思本节课为复习课,为了区分复习课和习题课,整节课贯穿了由形定数,由数思形,数形结合,方程思想、有序思维、分类讨论、从特殊——一般——特殊等重要数学思想,从学生最熟悉的简单习题入手,再层层提升问题难度,培养学生思考的逻辑性。
新版北师大版七年级下册三角形期末复习
【知识点总结】一、认识三角形1、三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形。
2、三角形三边的关系:两边之和大于第三边;两边之差小于第三边。
(已知三条线段确定能否组成三角形,已知两边求第三边的取值范围)3、三角形的内角和是180°;直角三角形的两锐角互余。
锐角三角形(三个角都是锐角)4、三角形按角分类直角三角形(有一个角是直角)钝角三角形(有一个角是钝角)5、三角形的特殊线段:a)三角形的中线:连结顶点与对边中点的线段。
(分成的两个三角形面积相等)b)三角形的角平分线:内角平分线与对边的交点到内角所在的顶点的线段。
c)三角形的高:顶点到对边的垂线段。
二、全等三角形:1、全等三角形:能够重合的两个三角形。
2、全等三角形的性质:全等三角形的对应边、对应角相等。
3、全等三角形的判定:判定方法内容简称边边边三边对应相等的两个三角形全等SSS边角边两边与这两边的夹角对应相等的两个三角形全等SAS角边角两角与这两角的夹边对应相等的两个三角形全等ASA角角边两角与其中一个角的对边对应相等的两个三角形全等AAS注意:三个角对应相等的两个三角形不能判定两个三角形形全等(AAA)两条边与其中一条边的对角对应相等的两个三角形不能判定两个三角三角形全等(SSA) 4、全等三角形的证明思路:条件下一步的思路运用的判定方法已经两边对应相等找它们的夹角SAS 找第三边SSS已经两角对应相等找它们的夹边ASA 找其中一个角的对边AAS已经一角一边找另一个角ASA或AAS找另一边SAS5、三角形具有稳定性,例1、如图,已知在△AB C 中,ABC ACB ∠∠与的平分线交于点O ,试说明: (1)01180()2BOC ABC ACB ∠=-∠+∠ (2)01902BOC A ∠=+∠例2、如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
1、如果等腰三角形的有一个角是40°,它的顶角是( )。
新疆乌鲁木齐县第一中学人教版七年级数学下册第七章《三角形》整章复习小结
第七章 三角形复习小结一、知识结构二、回顾与思考1、什么是三角形?什么是多边形?什么是正多边形?三角形是不是多边形?2、什么是三角形的高、中线、角平分线?什么是对角线?三角形有对角线吗?n 边形的的对角线有多少条?3、三角形的三条高,三条中线,三条角平分线各有什么特点?4、三角形的内角和是多少?n 边形的内角和是多少?你能用三角形的内角和说明n 边形的内角和吗?5、三角形的外角和是多少?n 边形的外角和是多少?你能说明为什么多边形的外角和与边数无关吗?6、怎样才算是平面镶嵌?平面镶嵌的条件是什么?能单独进行平面镶嵌的多边形有哪些?你能举一个几个多边形进行平面镶嵌的例子吗?三、例题导引例1 如图,在△ABC 中,∠A ︰∠B ︰∠C=3︰4︰5,BD 、CE 分别是边AC 、AB 上的高,BD 、CE 相交于点H ,求∠BHC 的度数。
例2 如图,把△ABC 沿DE 折叠,当点A 落在四边形BCDE 内部时, 探索∠A 与∠1+∠2有什么数量关系?并说明理由。
ABC D EH例3、如图,一个任意五角星的五个角的和是多少?例4、一个多边形的每一个内角都比相邻的外角的3倍还多20°,求这个多边形对角线的条数。
例5、如图所示,有一块三角形ABC 空地,要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价230元,AC =12m,BD =15m ,(1)购买这种草皮至少需要多少元?(2)现在学校想到这块空地上种红、黄、白、紫色四种花,而且要保证这四种花的面积相等,画出你的分法。
例6、如图,按规定,一块横板中AB 、CD 的延长线相交成85角,因交点不在板上,不便测量,工人师傅连结AC ,测得∠BAC=320,∠DCA=650,此时AB 、CD 的延长线相交所成的角是不是符合规定?为什么?F EDCB A四、巩固练习课本90页复习题7(第3题可不做).αA AB C BC D O 91 2A BC D ED A C 15m 12m。
