周练 高考模拟 仁寿一中 南校区 廖根华
仁寿第一中学校南校区2020届高三数学仿真模拟考试试题理含解析

由题意可得4=2|b|,解得|b|=2,c2=a2+b2,
所以双曲线的离心率e ,
故选:D。
【点睛】本题主要考查了双曲线的简单几何性质,考查了基本运算求解能力,属于基础题.
7。 等差数列 的公差不为零,其前 项和为 ,若 ,则 的值为( )。
A. 15B. 20C。 25D. 40
【详解】 ,故 .即 。
故选:B
【点睛】本题主要考查了交集的基本运算,属于基础题。
2. 在复平面内,复数 对应的点位于( )
A. 第一象限B. 第二象限C。 第三象限D. 第四象限
【答案】B
【解析】
【分析】
先利用复数的乘法运算进行化简,再利用复数的几何意义选出答案。
【详解】由 ,
在复平面内对应的点的坐标为 ,
【答案】B
【解析】
【分析】
利用奇偶性可排除A、C;再由 的正负可排除D。
【详解】 ,
,故 为奇函数,排除选项A、C;又 ,排除D,选B.
故选:B。
【点睛】本题考查根据解析式选择图象问题,在做这类题时,一般要结合函数的奇偶性、单调性、对称性以及特殊点函数值来判断,是一道基础题。
9。 函数 是定义在 上的奇函数,当 时, ,则 的值为( ).
故选:C.
【点睛】本题主要考查二项式定理的应用、二项展开式的通项公式,属于基础题.
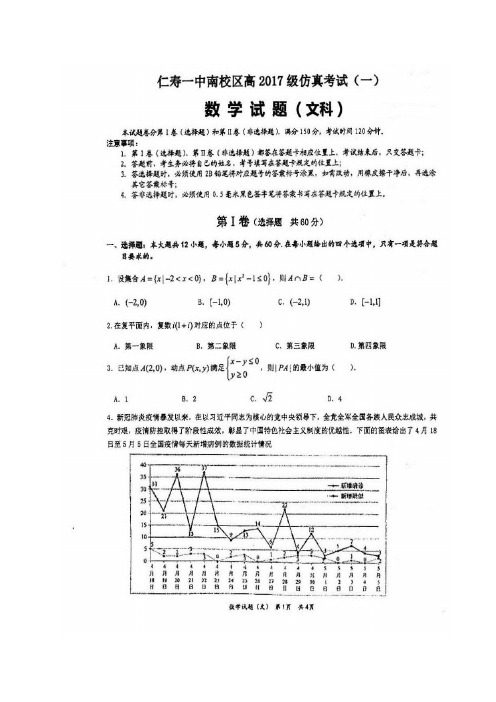
4。 新冠肺炎疫情暴发以来,在以习近平同志为核心的党中央领导下,全党全军全国各族人民众志成城,共克时艰,疫情防控取得了阶段性成效,彰显了中国特色社会主义制度的优越性。下面的图表给出了 月 日至 月 日全国疫情每天新增病例的数据统计情况
【详解】对于A选项,每天新增疑似病例数由小到大依次为 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 、 ,中位数为 ,A选项正确;
2020年6月四川省仁寿一中南校区2020届高三高考仿真模拟考试理科综合试题及答案

仿真模拟考试一生物答案
1.B 2. C 3.B 4. D 5.D 6.A
29.(10分,出标注外每空2分)
(1)生产者(1分)化能合成细菌、光合细菌、蓝藻(1分,答对一个给分)
(2)反应式11)显微镜;(2分)
(2)制作菠菜叶在清水中的临时装片——显微镜观察记录气孔状态——再换为浓盐水的——再在显微镜下观察记录气孔状态(3分)
(3)在清水中气孔应开启,原因是植物细胞液浓度大于外界清水的浓度,保卫细胞吸水后,会膨胀变形,气孔开启;
在浓盐水中气孔应关闭,原因是植物细胞液浓度小于外界浓盐水的浓度,保卫细胞失水后,会收缩拉直,气孔关闭。(3分)
31.(共9分,出标注外每空2分)
(1)种群(1分)自身生长发育繁殖(储存)
(2)同化能量的百分比
对鸡饲料进行精细加工促进消化吸收,减少鸡粪便中的能量,提高鸡同化能量
(3)实现能量多级利用,提高能量利用率(物质循环再生)
32.(共12分)
(1)(5分)
如果等位基因在X染色体上如果致病基因在XY染色体的同源区段上
由上可知,不论等位基因在X染色体上,还是在XY染色体的同源区段上均可出现同样的遗传图解,故不能确定。
(2)抗病(♀):不抗病(♀):抗病(♂):不抗病(♂)=5:3:2:6(2分)
(3)能(2分)根据子代表现型可以推理得出母本基因型为XbXb,父本基因型为XbYB,进而确定子代雄性抗病个体基因型为XbYB,因此可以确定Y染色体上的抗病基因(B)一定来自于父本(3分)
37.(共15分)
(1).无机盐、碳源、氮源(3分)(2).熔化(2分)(3). a(2分)(4).不能合成蛋白酶(或合成的蛋白酶量不足或合成的蛋白酶不分泌或分泌量不足或分泌的蛋白酶活性低)(2分)(5).大幅度降低发酵液中其他酶的活性(2分)(6).粗分离(2分)(7).凝胶色谱柱(2分)
四川省眉山市仁寿第一中学校南校区2025届高三数学第一学期期末质量跟踪监视模拟试题含解析

四川省眉山市仁寿第一中学校南校区2025届高三数学第一学期期末质量跟踪监视模拟试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若()()()20192019012019111x a a x a x -=+++++,x ∈R ,则22019122019333a a a ⋅+⋅++⋅的值为( )A .201912--B .201912-+C .201912-D .201912+2.已知,a b ∈R ,函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩,若函数()y f x ax b =--恰有三个零点,则( ) A .1,0a b <-< B .1,0a b <-> C .1,0a b >-<D .1,0a b >->3.设复数z 满足()117i z i +=-,则z 在复平面内的对应点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限4.在区间[]1,1-上随机取一个实数k ,使直线()3y k x =+与圆221x y +=相交的概率为( )A .12B .14C.2D5. “2a =”是“直线210ax y +-=与(1)20x a y +-+=互相平行”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件6.已知四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是边长为2的正方形,PA =E 为PC 的中点,则异面直线BE 与PD 所成角的余弦值为( ) A. BC.D.57.函数1()ln ||1xf x x+=-的图象大致为A .B .C .D .8.设 2.71828...e ≈为自然对数的底数,函数()1xxf x e e-=--,若()1f a =,则()f a -=( )A .1-B .1C .3D .3-9.已知,,,m n l αβαβαβ⊥⊂⊂=,则“m ⊥n”是“m ⊥l ”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件10.设a 、b R +∈,数列{}n a 满足12a =,21n n a a a b +=⋅+,n *∈N ,则( )A .对于任意a ,都存在实数M ,使得n a M <恒成立B .对于任意b ,都存在实数M ,使得n a M <恒成立C .对于任意()24,b a ∈-+∞,都存在实数M ,使得n a M <恒成立D .对于任意()0,24b a ∈-,都存在实数M ,使得n a M <恒成立11. “纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷200个点,己知恰有80个点落在阴影部分据此可估计阴影部分的面积是( )A .165B .325C .10D .18512.历史上有不少数学家都对圆周率作过研究,第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,开创了圆周率计算的几何方法,而中国数学家刘徽只用圆内接正多边形就求得π的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种π值的表达式纷纷出现,使得π值的计算精度也迅速增加.华理斯在1655年求出一个公式:π2244662133557⨯⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯,根据该公式绘制出了估计圆周率π的近似值的程序框图,如下图所示,执行该程序框图,已知输出的 2.8T >,若判断框内填入的条件为?k m ≥,则正整数m 的最小值是A .2B .3C .4D .5二、填空题:本题共4小题,每小题5分,共20分。
2024学年四川省眉山市仁寿第一中学校南校区高三数学第一学期期末质量跟踪监视模拟试题含解析

2024学年四川省眉山市仁寿第一中学校南校区高三数学第一学期期末质量跟踪监视模拟试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )A .203π B .6πC .103π D .163π 2.已知函数()sin(2)f x x ϕ=+,其中(0,)2πϕ∈,若,()6x R f x f π⎛⎫∀∈≤ ⎪⎝⎭恒成立,则函数()f x 的单调递增区间为( ) A .,()36k k k z ππππ⎡⎤-+∈⎢⎥⎣⎦B .2,()33k k k z ππππ⎡⎤-+∈⎢⎥⎣⎦C .2,()33k k k z ππππ⎡⎤++∈⎢⎥⎣⎦D .2,()3k k k Z πππ⎡⎤+⎢⎥⎣∈⎦3.已知复数为纯虚数(为虚数单位),则实数( )A .-1B .1C .0D .24.若函数()ln f x x x h =-++,在区间1,e e ⎡⎤⎢⎥⎣⎦上任取三个实数a ,b ,c 均存在以()f a ,f b ,()f c 为边长的三角形,则实数h 的取值范围是( )A .11,1e ⎛⎫-- ⎪⎝⎭B .11,3e e ⎛⎫--⎪⎝⎭C .11,e ⎛⎫-+∞⎪⎝⎭D .()3,e -+∞5.圆柱被一平面截去一部分所得几何体的三视图如图所示,则该几何体的体积为( )A .12πB .32π C .2π D .3π6.已知()21,+=-∈a i bi a b R ,其中i 是虚数单位,则z a bi =-对应的点的坐标为( ) A .()12,-B .()21,-C .()1,2D .()2,17.已知m 为一条直线,,αβ为两个不同的平面,则下列说法正确的是( ) A .若,m ααβ∥∥,则m β∥ B .若,m αβα⊥⊥,则m β⊥ C .若,m ααβ⊥∥,则m β⊥ D .若,m ααβ⊥∥,则m β⊥8.已知,,,m n l αβαβαβ⊥⊂⊂=,则“m ⊥n”是“m ⊥l ”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件9.设集合{}2A x x a =-<<,{}0,2,4B =,若集合A B 中有且仅有2个元素,则实数a 的取值范围为A .()0,2B .(]2,4C .[)4,+∞D .(),0-∞10. “tan 2θ=”是“4tan 23θ=-”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件11.函数f(x)=sin(wx +φ)(w >0,φ<2π)的最小正周期是π,若将该函数的图象向右平移6π个单位后得到的函数图象关于直线x =2π对称,则函数f(x)的解析式为( ) A .f(x)=sin(2x +3π) B .f(x)=sin(2x -3π) C .f(x)=sin(2x +6π) D .f(x)=sin(2x -6π)12.已知非零向量a 、b ,若2b a =且23a b b -=,则向量b 在向量a 方向上的投影为( ) A .32b B .12b C .32b -D .12b -二、填空题:本题共4小题,每小题5分,共20分。
四川省仁寿第一中学校南校区2020届高三仿真模拟数学(文)含答案
即四边形 EFDC 是平行四边形, 所以 EC∥FD , ........... 4 分
又因为 EC 平面 SAD , FD 平面 SAD ,
所以 CE∥平面 SAD ;
................................................. 5 分
(Ⅱ)取 AD 中点 G ,连接 SG ,
直线
PA
:
y
2 3
x
8 3
,直线
PB
:
y
2x
8
,所以,
M
2,
4 3
,
N
2, 12
,
所以,圆心坐标为
2,
16 3
,半径
r
20 3
,焦点到圆心的距离
d
16 256 20 r , 93
数学参考答案(文) 第 2页 共 4页
此时,以 MN 为直径的圆过焦点 F .当直线 l 与 x 轴不垂直时,
................................... 7 分
....................................... 12 分
18.解:(1)
x
1113 12
8
11,
y
25
29
26
16
24
4
4
n
i 1
xi
x
yi
y
0
1
2
5
1
2
38
36
n
i 1
xi
x
2
高 2017 级仿真考试(一)文科数学 参考答案
一、1-5 BBCDC 6-10 DBBCC 11-12 BD
2021届四川省仁寿第一中学校南校区高三第五次模拟考试数学(理)试题

2019届四川省仁寿第一中学校南校区高三第五次模拟考试数学(理)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.集合{}2|30A x x x =-≤,(){}|lg 2B x y x ==-,则A B ⋂=( ) A .{}|02x x ≤< B .{}|13x x ≤< C .{}|23x x <≤ D .{}|02x x <≤ 2.若(1+2ai)i =1-bi ,其中a ,b ∈R ,则|a +bi|=( ).A .12BCD .53.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.A .互联网行业从业人员中90后占一半以上B .互联网行业中从事技术岗位的人数超过总人数的20%C .互联网行业中从事运营岗位的人数90后比80前多D .互联网行业中从事技术岗位的人数90后比80后多4.使得()3nx n N+⎛+∈ ⎝的展开式中含有常数项的最小的n 为( ) A .4 B .5 C .6 D .7 5.中心在原点,对称轴为坐标轴的双曲线C 的两条渐近线与圆22(2)1x y -+=都相切,则双曲线C 的离心率是( )A .2B .2C 2D 或26.设12,x x 为()()cos 0f x x x ωωω=->的两个零点,且12x x -的最小值为1,则ω=( )A .πB .2πC .3πD .4π 7.执行如图所示的程序框图,若输出的,则输入的整数的最大值为( )A .7B .15C .31D .638.如图所示,直三棱柱的高为4,底面边长分别是5,12,13,当球与上底面三条棱都相切时球心到下底面距离为8,则球的体积为 ( )A .160√5π3B .64√2π3C .96√3π3D .256√2π39.已知{}n a 为正项等比数列,n S 是它的前n 项和,若116a =,且4a 与7a 的等差中项为98,则5S 的值是( ) A .29B .30C .31D .32 10.设双曲线22221y x a b-=(0a >,0b >)的一条渐近线与抛物线213y x =+有且只有一个公共点,且椭圆22221x y a b+=的焦距为2,则双曲线的标准方程为( ) A .22143x y -= B .22143y x -= C .22123x y -= D .22132y x -= 11.如图,在平面四边形ABCD 中,,,120,1,AB BC AD CD BAD AB AD ⊥⊥∠=== 若点E 为边CD 上的动点,则AE BE ⋅的最小值为 ( )A .2116B .32C .2516D .3 12.已知函数()ln 1f x x =+,()122x g x e -=,若()()f m g n =成立,则m n -的最小值是( )A .1ln 22+B .2e -C .1ln 22- D12二、填空题13.若变量x ,y 满足约束条件1,,3215,x y x x y ≥⎧⎪≥⎨⎪+≤⎩则2z x y =+的最大值是______.14.已知数列{}n a 递增的等比数列,若2312a a +=,1427a a =,则n a =______. 15.已知()||f x x x =,则满足(21)()0f x f x -+≥的x 的取值范围为_______. 16.如图所示,平面BCC 1B 1⊥平面ABC ,∠ABC =120︒,四边形BCC 1B 1为正方形,且AB =BC =2,则异面直线BC 1与AC 所成角的余弦值为_____.三、解答题17.在ABC ∆中,内角,,A B C 的边长分别为,,a b c ,且2c =.(1)若πA 3=,3b =,求sin C 的值; (2)若22sin cos sin cos 3sin 22B A A B C +=,且ABC ∆的面积25sin 2S C =,求a 和b 的值.18.某百货商店今年春节期间举行促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店经理对春节前7天参加抽奖活动的人数进行统计,y 表示第x 天参加抽奖活动的人数,得到统计表格如下:(1)经过进一步统计分析,发现y 与x 具有线性相关关系.请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆybx a =+; (2)该商店规定:若抽中“一等奖”,可领取600元购物券;抽中“二等奖”可领取300元购物券;抽中“谢谢惠顾”,则没有购物券.已知一次抽奖活动获得“一等奖”的概率为16,获得“二等奖”的概率为13.现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额X 的分布列及数学期望. 参考公式:1221ˆn ii i ni i x y nx y b x nx ==-=-∑∑,ˆˆa y bx =-,71364i i i x y ==∑,721140i i x ==∑. 19.如图,四棱锥P ABCD -,侧面PAD 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ABC ∠=的菱形, M 为棱PC 上的动点,且([01])PM PCλλ=∈,. (I)求证:PBC ∆为直角三角形; (II)试确定λ的值,使得二面角P AD M --.20.已知顶点是坐标原点的抛物线Γ的焦点F 在y 轴正半轴上,圆心在直线12y x =上的圆E 与x 轴相切,且E F ,关于点()10M -,对称. (1)求E 和Γ的标准方程;(2)过点M 的直线l 与E 交于A B ,,与Γ交于C D ,,求证:CD >. 21.已知函数()ln 2ln 35f x x x x x =-+-,22()ln x a a g x x x x-=++. (1)求证:()f x 在区间(1,)+∞上有且仅有一个零点0x ,且037,24x ⎛⎫∈⎪⎝⎭; (2)若当1x ≥时,不等式()0g x ≥恒成立,求证:494a <. 22.在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin x t y t αα=+⎧⎨=+⎩(t 为参数,0απ≤<).在以O 为极点,x 轴正半轴为极轴的极坐标中,曲线C :4cos ρθ=.(1)当4πα=时,求C 与l 的交点的极坐标; (2)直线l 与曲线C 交于A ,B 两点,线段AB 中点为(1,1)M ,求||AB 的值.23.已知函数()|2|f x x =-,()||1g x a x =-.(1)若不等式(3)3g x -≥-的解集为[]2,4,求a 的值.(2)若当x ∈R 时,()()f x g x ≥,求a 的取值范围.参考答案1.A【分析】解一元二次不等式化简集合A ,再根据对数的真数大于零化简集合B ,求交集运算即可.【详解】由230x x -≤可得03x ≤≤,所以{|03}A x x =≤≤,由20x ->可得2x <,所以{|2}B x x =<,所以{|02}A B x x ⋂=≤<,故选A .【点睛】本题主要考查了集合的交集运算,涉及一元二次不等式解法及对数的概念,属于中档题. 2.C【解析】试题分析:由已知,-2a +i =1-bi ,根据复数相等的充要条件,有a =-12,b =-1所以|a +bi|=,选C 考点:复数的代数运算,复数相等的充要条件,复数的模3.D【分析】根据饼图中的数据结合岗位分布图中的数据,对选项进行一一分析,即可得答案;【详解】对A ,可知90后占了56%,故A 正确;对B ,技术所占比例为39.65%,故B 正确;对C ,可知90后明显比80前多,故C 正确;对D ,因为技术所占比例,90后和80后不清楚,所以不一定多,故D 错误.故选:D.【点睛】本题考查统计图的信息提取,考查数据处理能力,属于基础题.4.B【解析】二项式展开式的通项公式为r -n 3x n r r C (),若展开式中有常数项,则3--=02n r r ,解得5=2n r ,当r 取2时,n 的最小值为5,故选B 【考点定位】本题考查二项式定理的应用.5.A【解析】【分析】根据题意,由圆的切线求得双曲线的渐近线的方程,再分焦点在x 、y 轴上两种情况讨论,进而求得双曲线的离心率.【详解】设双曲线C 的渐近线方程为y=kx1k ∴=, , 得双曲线的一条渐近线的方程为3y =∴焦点在x 、y 轴上两种情况讨论: ①当焦点在x轴上时有: b c e a a == ②当焦点在y 轴上时有: 2a c e b a ====; ∴求得双曲线的离心率 2. 故选:A .【点睛】本小题主要考查直线与圆的位置关系、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想.解题的关键是:由圆的切线求得直线 的方程,再由双曲线中渐近线的方程的关系建立等式,从而解出双曲线的离心率的值.此题易忽视两解得出错误答案. 6.A【分析】 先化简已知得()2sin()6f x wx π=-,再根据题意得出f (x )的最小值正周期T 为1×2,再求出ω的值.【详解】 由题得()2sin()6f x wx π=-,设x 1,x 2为f (x )=2sin (ωx ﹣6π)(ω>0)的两个零点,且12x x -的最小值为1, ∴2T =1,解得T=2; ∴2πω=2,解得ω=π.故选A .【点睛】本题考查了三角恒等变换和三角函数的图象与性质的应用问题,是基础题.7.B【解析】试题分析:由程序框图可知:①,;②,;③,;④,;⑤,. 第⑤步后输出,此时,则的最大值为15,故选B. 考点:程序框图.8.A【解析】【分析】设球心为O ,三棱柱的上底面ΔA 1B 1C 1的内切圆的圆心为O 1,该圆与边B 1C 1切于点M ,根据球的几何性质可得ΔOO 1M 为直角三角形,然后根据题中数据求出圆O 1半径,进而求得球的半径,最后可求出球的体积.【详解】如图,设三棱柱为ABC −A 1B 1C 1,且AB =12,BC =5,AC =13,高AA 1=4. 所以底面ΔA 1B 1C 1为斜边是A 1C 1的直角三角形,设该三角形的内切圆为圆O 1,圆O 1与边B 1C 1切于点M ,则圆O 1的半径为O 1M =12+5−132=2.设球心为O,则由球的几何知识得ΔOO1M为直角三角形,且OO1=8−4=4,所以OM=√22+42=2√5,即球O的半径为2√5,所以球O的体积为43×π×(2√5)3=160√5π3.故选A.【点睛】本题考查与球有关的组合体的问题,解答本题的关键有两个:(1)构造以球半径R、球心到小圆圆心的距离d和小圆半径r为三边的直角三角形,并在此三角形内求出球的半径,这是解决与球有关的问题时常用的方法.(2)若直角三角形的两直角边为a,b,斜边为c,则该直角三角形内切圆的半径r=a+b−c2,合理利用中间结论可提高解题的效率.9.C【分析】设正项等比数列的公比为q,运用等比数列的通项公式和等差数列的性质,求出公比,再由等比数列的求和公式,计算即可得到所求.【详解】设正项等比数列的公比为q,则a4=16q3,a7=16q6,a4与a7的等差中项为98,即有a 4+a 7=94, 即16q 3+16q 6,=94,解得q=12(负值舍去), 则有S 5=()5111a q q--=511612112⎛⎫⨯- ⎪⎝⎭-=31. 故选:C . 【点睛】本题考查等比数列的通项和求和公式的运用,同时考查等差数列的性质,考查运算能力,属于中档题. 10.B 【分析】设双曲线的渐近线方程为y kx =,与抛物线方程联立,利用0∆=,求出k 的值,得到a b的值,求出,a b 关系,进而判断,a b 大小,结合椭圆22221x y a b+=的焦距为2,即可求出结论.【详解】设双曲线的渐近线方程为y kx =, 代入抛物线方程得2103x kx -+=,依题意240,3k k ∆=-==a ab b ∴==>, ∴椭圆22221x y a b+=的焦距2=, 22222411,3,433b b b b a -====,双曲线的标准方程为22143y x -=.故选:B. 【点睛】本题考查椭圆和双曲线的标准方程、双曲线的简单几何性质,要注意双曲线焦点位置,属于中档题. 11.A 【详解】分析:由题意可得ABD △为等腰三角形,BCD 为等边三角形,把数量积AE BE ⋅分拆,设(01)DE tDC t =≤≤,数量积转化为关于t 的函数,用函数可求得最小值。
四川省仁寿第一中学校南校区2019届高三下学期第三次模拟考试数学(理)试题(扫描版)
A. -4C. 3D. -3仁寿一中南校区2016级高考第三次模拟测试数学(理)试卷"、选择题:(毎小删只冇•个正从选项:毎小题5分.共60分)!,.4 = j (x.J«)I = 7I ^X 2|,H = {(x,J ;)I V = 2^} . M/(n 中元素的个聂为(〉 A. 3B. 2Cw 1D 、U2.若复数z 满足(1“)二足戌数畝位人 刚z 的炼部为()3. 如图足果地区2000年至2016年环境基础设施投资絶)•(俶位:亿元)的折线民.则下 列结论中茨述不正幽的定<)A 、 从2000年至2016年.该地区环境慕础设确投空紳谜年增加B 、 2011年该地区环境球础设施的投资额比2000年至2004年的枪资总験还多C 、 2012年谆地区茯础设施的投资無比2004年的投資额朋了两希» 为了横测该地区2019 :]的坏境基跆设施投资轨 WIW2010年至2016年的啟据(时闾 变胶/的值依次为I ・2•…・7)建*.「投资额丿,与时间变菸/的纨性回归樓盘/ = 99 + 17.5/, 根据选模型移测该地X 2019的川境菇砒设施投资離为256.5亿元. 4、 (卄以2”-刃‘的展开式中的系敷为《 ) A.・30B. -40C. 40I 人 505. 28C 中.| AB + AC 冃 AB - JC L ・4B = 4./C = 3 ■则 BC (LCA 方向上的投影败 )rm 、刑 22R 性A. 战坐标仰长到廉来的2借《纵坐标不变' •再问左平移f 个紙位长度6 B.橘坐标伸长利原来的2怡(纽I 生标不变人再向右平移中个单位长度1JIC. 橫坐标缩切刘廉米的〒(纵生扮不变、・冉向A :T^-个虹位长度D.坐标缩純到廉來的丄(纵坐林不变)•洱向右个单位长度2 <>7. n.r>Oo >0. '/W ・• 丫 4 2丿=2返亍”的•个充分不必競条件斥C ) A% xs y11. x*2yC. .v»2Rj>«=l人已知第臺数刊S.}的公#为-2,湘〃琐和为丫・升6"•代为某二角形的三边长・ 目•该三角形帝一•个内巾为12『•则S.的跋大値为()A M 5 IK !l C!・ 20D. 259. 己间(1・Zr)"廉开弋今第三加的二血式系和9第舛项的二序式豕敷梱徐,(I 4 Zv)* =% 4件〒 4 吋'4 -•» a.x ,■若q +u 2 + ・-a M = 242 ■划q _吗十偽 _・•-+(-l) <i fc 的惟为()A. I以 TC 、816 -8110. 已fepfi?k/(x) = ~x4-cos( j,jre -彳•冷 « 则f(x)的機大伍点为()XJtn_ srAi -------B ・ ------C 、丁D% —3 6 6 311. 阿疣罗尼Br (古希匚淮于筑 公元的262 -叽*:)的携作4岡惟曲线论、是古代IU 界 比澤的科学成采.它将恢1權曲线的性质网罗翁尽,几乎他后人没有栩足的余地.他证聖过这 样•个命XS ;平面内与两址点距凤的比为席数.上Hl)的点的轨进是岡,后人将 试牛阀瑶为阿波第尼靳碉.現右祈岡 斗“「=H 。
仁寿第一中学校南校区2020届高三数学仿真模拟考试试题文含解析
【详解】(1)若函数 满足条件③,
则 。
这与 , 矛盾,故 不能满足条件③,
所以函数 只能满足条件①,②,④。
由条件①,得 ,
又因为 ,所以 。
由条件②,得 .
由条件④,得 ,
又因为 ,所以 。
所以 。
(2)由 , ,
又 ,
所以 ,
故选:B.
【点睛】本题考查了等差数列的前n项和公式与等差数列性质的综合应用,是高考重点考查的内容,属于基础题。
8.函数 图象的大致形状是( )
A。 B. C. D。
【答案】B
【解析】
【分析】
利用奇偶性可排除A、C;再由 的正负可排除D。
【详解】 ,
,故 为奇函数,排除选项A、C;又 ,排除D,选B.
四川省仁寿第一中学校南校区2020届高三数学仿真模拟考试试题 文(含解析)
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分150分,考试时间120分钟.
注意事项:
1.第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)都答在答题卡相应位置上,考试结束后,只交答题卡;
2.答题前,考生务必将自己的姓名、考号填写在答题卡规定的位置上;
4.新冠肺炎疫情暴发以来,在以习近平同志为核心的党中央领导下,全党全军全国各族人民众志成城,共克时艰,疫情防控取得了阶段性成效,彰显了中国特色社会主义制度的优越性.下面的图表给出了 月 日至 月 日全国疫情每天新增病例的数据统计情况
下列说法中不正确的是( )
A. 每天新增疑似病例的中位数为
B. 在对新增确诊病例的统计中,样本容量为
12。已知点 为抛物线 的焦点,过点 的直线 交 于 , 两点,与 的准线交于点 ,若 ,则 的值等于( )
2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科数学试卷-学生用卷
2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科数学试卷-学生用卷一、选择题(本大题共12小题,每小题5分,共60分)1、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第1题5分 已知集合A ={x|(x +1)(x −4)⩽0},B ={x |log 2x ⩽2},则A ∩B =( ).A. [−1,4]B. [1,+∞)C. (0,4]D. [−2,+∞)2、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第2题5分 2019年河南郑州高三三模理科第2题5分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第2题5分已知z =(1+i)(2−i),则|z |2=( ).A. 2+iB. 3+iC. 5D. 103、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第3题5分 在(√x −x 2)n 的二项展开式中,若仅第四项的二项式系数最大,则n =( ).A. 9B. 8C. 7D. 64、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第4题5分 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第4题5分已知向量a →=(12,−√32),|b →|=2√3,若a →⋅(b →−a →)=2,则向量a →与b →的夹角为( ). A. π6B. π4C. π3D. π25、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第5题5分 2019~2020学年浙江高一下学期期中(A9协作体联考)第5题4分在△ABC 中,若sinB =2sinAcosC ,那么△ABC 一定是( ).A. 等腰直角三角形B. 等腰三角形C. 直角三角形D. 等边三角形6、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第6题5分 已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为( ).(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ−σ<X ⩽μ+σ)=0.6826,P(μ−2σ<X ⩽μ+2σ)=0.9544,P(μ−3σ<X ⩽μ+3σ)=0.9974.)A. 4.56%B. 13.59%C. 27.18%D. 31.74%7、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第7题5分 2020年四川攀枝花高三一模文科第8题5分2020年四川攀枝花高三一模理科第8题5分2020~2021学年10月四川绵阳涪城区南山中学实验学校高三上学期月考理科第7题5分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第7题5分已知a =312,b =log 2√3,c =log 92,则a ,b ,c 的大小关系为( ).A. a >b >cB. a >c >bC. b >a >cD. c >b >a8、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第8题5分 2020~2021学年10月四川成都锦江区成都市盐道街中学高三上学期月考文科第8题5分2020~2021学年12月西藏拉萨城关区西藏自治区拉萨中学高三上学期月考文科第9题5分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第8题5分宋元时期,中国数学鼎盛时期中杰出的数学家有“秦(九韶)、李(冶)、杨(辉)、朱(世杰)四大家”,朱世杰就是其中之一.朱世杰是一位平民数学家和数学教育家.朱世杰平生勤力研习《九章算术》,旁通其它各种算法,成为元代著名数学家.他全面继承了前人数学成果,既吸收了北方的天元术,又吸收了南方的正负开方术、各种日用算法及通俗歌诀,在此基础上进行了创造性的研究,写成以总结和普及当时各种数学知识为宗旨的《算学启蒙》,其中有关于“松竹并生”的问题:松长四尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图,是源于其思想的一个程序框图.若输入的a,b分别为3,1,则输出的n=().A. 2B. 3C. 4D. 59、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第9题5分的大致图象是().若函数y=a−x(a>0且a≠1)为增函数,则函数f(x)=log a1x+1A.B.C.D.10、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第10题5分2020年四川绵阳高三三模理科第10题5分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第11题5分已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π2)的最小正周期为π,且关于(−π8,0)中心对称,则下列结论正确的是().A. f(1)<f(0)<f(2)B. f(0)<f(2)<f(1)C. f(2)<f(0)<f(1)D. f(2)<f(1)<f(0)11、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第11题5分2020~2021学年黑龙江齐齐哈尔高二上学期期末文科第9题5分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第12题5分已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0,2√2)(x0>p2)是抛物线C上一点,以点M为圆心的圆与直线x=p2交于E,G两点,若sin∠MFG=13,则抛物线C的方程是().A. y2=xB. y2=2xC. y2=4xD. y2=8x12、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第12题5分已知函数f (x )={1m,x =0e−|x|,x ≠0,若方程3mf 2(x )−(2m +3)f (x )+2=0有5个解,则m 的取值范围是( ).A. (1,+∞)B. (0,1)∪(1,+∞)C. (1,32)D. (1,32)∪(32,+∞)二、填空题(本大题共4小题,每小题5分,共20分)13、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第13题5分 2020~2021学年10月江西南昌西湖区南昌市外国语学校高一上学期月考第13题5分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第13题5分函数f (x )={2x −1,−1⩽x <3f (x −4),x ⩾3,则f (9)= .14、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第14题5分已知实数x ,y 满足{x −y +1⩽0x +y −2⩽0x ⩾0,则z =x −2y 的最大值为 .15、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第15题5分 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第15题5分在三角形ABC 中,AB =8,AC =4,∠BAC =60°,双曲线以A 、B 为焦点,且经过点C ,则该双曲线的离心率为 .16、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第16题5分 2018年河南濮阳高三二模理科第15题5分2017~2018学年江西赣州寻乌县寻乌县第二中学高三上学期期中文科第16题5分2018~2019学年3月四川成都金牛区成都七中万达学校高二下学期月考理科第15题5分2019~2020学年江苏南京秦淮区南京市第一中学高二下学期期中第15题5分已知正三棱锥P−ABC,点P,A,B,C都在半径为√3的球面上,若PA,PB,PC,两两相互垂直,则球心到截面ABC的距离为.三、解答题(本大题共5小题,共58分)17、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第17题10分已知等差数列{a n}满足a6=6+a3,且a3−1是a2−1,a4的等比中项.(1) 求数列{a n}的通项公式.(n∈N∗),求数列{b n}的前n项和T n.(2) 设b n=1a n a n+118、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第18题12分足球是当今世界传播最广,参与人数最多的体育运动,具有广泛的社会影响,深受世界各国民众喜爱.(1) 为调查大学生喜欢足球是否与性别有关,随机选取50名大学生进行问卷调查,若问卷评分不低于80分.则认为喜欢足球,若评分低于80分,则认为不喜欢足球,这50名大学生问卷评分的茎叶图如图所示.依据上述数据制成如下列联表:请问是否有90%的把握认为喜欢足球与性别有关?(2) 小明和小华是足球爱好者,他们假期相约到体育馆训练足球.小明每天早上在6:00到7:00之间的任意时刻来到场地,小华每天早上在6:30到7:30分之间的任意时刻来到场地,求连续3天内,小明比小华早到场地的天数的数学期望.附:临界值表参考公式:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),n=a+b+c+d.19、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第19题12分2020~2021学年江西景德镇昌江区江西省景德镇市第一中学高二上学期期中(1班)第18题12分2017年湖南郴州高三三模文科第19题12分2018~2019学年5月广东广州越秀区广州市培正中学高二下学期月考理科第20题12分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第19题12分如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.(1) 求证:直线l⊥平面PAC;(2) 直线l上是否存在点Q,使直线PQ分别与平面AEF,直线EF所成的角互余?若存在,求出|AQ|的值;若不存在,请说明理由.20、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第20题12分2018~2019学年12月广东深圳南山区深圳市第二高级中学高二上学期月考理科第18题12分2019~2020学年11月天津河东区天津市第四十五中学高二上学期月考第17题2016~2017学年北京高二上学期单元测试《圆锥曲线》第13题2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第20题12分设椭圆M:x 2a2+y2b2=1(a>b>0)的离心率与双曲线x2−y2=1的离心率互为倒数,且椭圆的长轴长为4.(1) 求椭圆M的方程.(2) 若直线y=√2x+m交椭圆M于A,B两点,P(1,√2)为椭圆M上一点,求△PAB面积的最大值.21、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第21题12分2020~2021学年12月山东青岛市北区青岛第九中学高三上学期月考第22题12分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第21题12分已知函数f(x)=12x2−ax+lnx(a∈R).(1) 若f(x)在定义域单调递增,求a的取值范围.(2) 设a<e+1e,m,n分别是f(x)的极大值和极小值,且S=m−n,求S的取值范围.四、选做题(本大题共2小题,选做1题,共10分)选修4-4:坐标系与参数方程22、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第22题10分2019~2020学年5月重庆沙坪坝区重庆市第一中学高三下学期月考理科第22题10分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第22题10分在平面直角坐标系xOy中,曲线C1的参数方程为{x=1+cosϕy=1+sinϕ(ϕ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ2(1+sin2θ)=2.(1) 求曲线C1的极坐标方程.(2) 射线OA:θ=α(0<α<π2)与曲线C1交于两点A,B,并与曲线C2交于点C,求|OA|⋅|OB||OC|的取值范围.选修4-5:不等式选讲23、【来源】 2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模理科第23题10分2020年四川眉山仁寿县仁寿县第一中学(南校区)高三二模文科第23题10分已知函数f(x)=|x−1|+|x+k|(k>0).(1) 当k=2时,求不等式f(x)⩾5的解集.(2) 若函数f(x)的最小值为3,且a,b,c∈R+,a+b+c=k,证明:a2+b2+c2⩾43.1 、【答案】 C;2 、【答案】 D;3 、【答案】 D;4 、【答案】 A;5 、【答案】 B;6 、【答案】 B;7 、【答案】 A;8 、【答案】 C;9 、【答案】 D;10 、【答案】 D;11 、【答案】 C;12 、【答案】 D;13 、【答案】1;14 、【答案】−2;15 、【答案】√3+1;16 、【答案】√33;17 、【答案】 (1) a n=2n+1(n∈N∗).;(2) T n=12(13−12n+3).;18 、【答案】 (1) 有90%的把握认为喜欢足球与性别有关.;(2) 78.;19 、【答案】 (1) 证明见解析.;(2) 存在,|AQ|=1.;20 、【答案】 (1) x24+y22=1.;(2) √2.;21 、【答案】 (1) a⩽2.;(2) S∈(0,e4−4e2−12e2).;22 、【答案】 (1) ρ2−2(cosθ+sinθ)ρ+1=0.;(2) √1+sin2α√2∈(√22,1).;23 、【答案】 (1) {x|x⩽−3或x⩾2}.;(2) 证明见解析.;。
四川省仁寿一中南校区2020学年高一数学下学期第五周周练试题理
四川省仁寿一中南校区 2021学年高一数学下学期第五周周练试题理一、选择题1.向量a(3,1),b(x, 2),c(0,2),假设a b c ,那么实数x 的值为A .4B.3C. 3D.4 3443答案:A2.e 1,e 2 是不共线向量,a2e 1e 2,be 1e 2 ,当a ∥b 时,实数 等于A.1C.1D.22答案:Duuur uurb, 那么a b=(3.正△ABC 的边长为1,且BC a,CA)A.3 B3C. 2D.1答案:A4.平面向量a(x 1,y 1),b(x 2,y 2),假设|a| 2,|b| 3,ab6,那么x1y 1 的值为()x 2y 2A.2B.222C.D.3 3答案:C 设a,b 的夹角为,那么ab abcos6 cos 1,∴180.即a,b 共线且反向,∴222x 1 y 12a=3b,x 1 3x 2,y13y 2,∴x2y 23.5、假设-2π<α<- 3π1-cosα-π )2 ,那么 2的值是(ααααA .sin 2B .cos 2C .-sin 2D .-cos 2答案:D66.设a =sin14°+cos14°,b =sin16°+cos16°,c = 2,那么a ,b ,c 的大小关系是( )A .a <b <cB .b <a <cC .c <b <aD .a <c <b解析:a = 2sin59°,b =2sin61°,c =2sin60°,∴a<c <b. 答案:Dπtan 4+α·cos2α)7、计算 2 π的值为(-α2cos 4A .-2B .2C .-1D .1答案:D8.如果函数ysin2xacos2x 的图象关于直线 x8 对称,那么a 等于〔 〕A.2B.-2D.-1答案:D9.锐角A ,B 满足2tanA =tan(A +B),那么tanB 的最大值为A .22B.22 2C.2D.4tanA +B -tanAtanA=1,解析tanB =tan[(A +B)-A]==11+tanA +BtanA1+2tan 2AtanA +2tanA112又tanA >0,那么tanA +2tanA ≥2 2,那么tanB ≤2 2 = 4.[注]直接按和角公式展开也可.答案Da 1 a 2=a 1a 4-a 2a 3.将函数f(x)=sin2x 3的图象向左平移 π 10.定义行列式运算a 4 cos2x1 个单位,以下是a 36 所得函数图象的一个对称中心是( ).πππD.π,0B.,0C.,0,0A.42312f(x)=sin2x -3cos2x =2sinπ解析根据行列式的定义可知2x -3 ,向左平移π2x + π - π π 2× π =2sin =π0,所以 π是 个单位得到g(x)=2sin6 =2sin2x ,所以g 2 =2sin 2 ,0 63 2函数的一个对称中心,答案 B二.填空题(每题5分,共25分)r4,2 rr r11.a ,b6,y,且a 与b 共线,那么y=答案:312.向量a cos ,sin,b1,2,假设是 .答案:5π5,那么tan2α=________.13.α∈(,π),sin α=52rr2sin cos 的值 a ∥b ,那么代数式sin cos[答案]- 433π3 π 12 π14.4<β<α<π,sin(α+β)=-5,sin β-4=13,那么cos α+4=________.56答案-65如图, ,且 OA OB,C 点在以 O 为圆心OA 为半径的B15. OAOB圆弧AB 上,假设OC xOA yOB,那么xy 的范围是:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仁寿一中南校区2013届数学试卷(理)高三周练命题人 廖根华 第I 卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数i a a a z )3()32(2++-+=为纯虚数(i 为虚数单位),则实数a 的值是( ) A .3- B .3-或1 C .3 或1- D .1 2.已知集合2{|2,},{|,},x M y y x R N y y x x R M N ==∈==∈⋂则 A .{2,4} B .{(2,4),(4,16)} C .(0,∞) D .[0,+∞)3.下列说法中,正确的是( )A . 命题“若a b <,则22am bm <”的否命题是假命题.B .设,αβ为两个不同的平面,直线l α⊂,则“l β⊥”是 “αβ⊥” 成立的充分不必要条件.C .命题“存在2,0x R x x ∈->”的否定是“对任意2,0x R x x ∈-<”.D .已知x R ∈,则“1x >”是“2x >”的充分不必要条件.4.在△ABC 中,tanA 是第3项为-4,第7项为4的等差数列的公差,tanB 是第3项为13,第6项为9的等比数列的公比,则△ABC 是 ( ) A .锐角三角形B .等腰三角形C .直角三角形D .钝角三角形5.计算机是将信息转换成二进制数进行处理的。
二进制即“逢二进一”,如)1101(2表示二进制的数,将它转化成十进制的形式是32112120212⨯+⨯+⨯+⨯,那么将二进制1...11(共16位)转换成十进制数的形式是( ) A .2217- B.1217- C1216- D215-6.若A 为抛物线214y x =的顶点,过抛物线焦点的直线交抛物线于B C 、两点,则AB AC⋅等于 ( )A .-3B .3C .5D .-57设函数()321563f x x ax x =+++在区间[,1,]3是单调函数,则实数a 的取值范围是( )A. ),5[+∞-B. ]3,(--∞C., ),5[]3,(+∞---∞D. ]5,5[-8.如图,有一条长度为1的线段M N ,其端点,M N 在边长为3的正方形A B C D 的四边上滑动,当点N 绕着正方形的四边滑动一周时,M N 的中点P 所形成的轨迹长度最接近于( )A.8B.11C.12D.109.经过正方体ABCD-A 1B 1C 1D 1任意两个顶点的直线中,与AC 成异面直线且所成角为60°的直 线的概率为A .114B .17C .314D .2710. 关于函数)0(||1lg )(2≠+=x x x x f ,有下列命题:①其图象关于y 轴对称;②当0>x 时,)(x f 是增函数;当0<x 时,)(x f 是减函数; ③)(x f 的最小值是2lg ;④)(x f 在区间)、(+∞-,2)0,1(上是增函数; 其中所有正确结论的序号是( )A .①③④B .②③④C .③④D .①②④第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上11.命题“若22,12x x x -<-<<则”的否定是 。
12. 若函数)11lg(--=x m y 的图像关于原点成中心对称,则非零实数m = .13. 双曲线1322=-yx的两个焦点为P F F ,,21是双曲线上的点,当△21PF F 的面积为2时,21PF PF ⋅的值为14.已知是)(x g 定义在R 上的奇函数,2)21()(+-=x g x f ,则=+++)2()2()2(89sin2sin1sinf f f 。
15.已知)(x f 是定义在[-1,1]上的奇函数且1)1(=f ,对1x 、∈2x [-1,1],且021≠+x x 时,有0)()(2121>++x x x f x f ,若12)(2+-≤am m x f 对所有]1,1[-∈x 、]1,1[-∈a 恒成立,则实数m 的取值范围是 。
AABD M (第5题图)三、解答题:本大题共6小题,共75分. 16.设函数()sin cos )cos ().f x x x x x x R π=-+∈(1)求()f x 的最小正周期;(II )若函数()y f x =的图象按,42b π⎛⎫=⎪⎪⎝⎭平移后得到函数()y g x =的图象,求()y g x =在(0,]4π上的最大值。
17.设函数323()(1)132a f x x x a x =-+++,其中a 为实数.(1)已知函数()f x 在1x =处取得极值,求a 的值;(2)已知不等式'2()1f x x x a >--+对任意(0,)a ∈+∞都成立,求实数x 的取值范围.18. (本小题满分12分)某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:(1)从该小学任选两名教职工,用η表示这两人请假次数之和,记“函数2()1f x x x η=--在区间(4,6)上有且只有一个零点”为事件A ,求事件A 发生的概率P ;(2)从该小学任选两名职工,用ξ表示这两人请假次数之差的绝对值,求随机变量ξ的分布列及数学期望E ξ.19.设等比数列{}a n 的前项和为s n ,已知)*(,212N s a n n n ∈+=+(1).求数列{}a n 的通项公式;(2).在a n 与a n 1+之间插入n 个数,使这个2+n 数组成公 差为dn的等差数列,求数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧d n 1的前n项和T n20.(本小题满分12分)如图,四棱锥P ABC D-的底面ABC D 为菱形,PA ⊥平面ABC D ,2PA AB ==,E F 、分别为C D PB、的中点,AE=.(Ⅰ)求证:平面AEF ⊥平面PAB . (Ⅱ)求平面PAB 与平面P C D 所成的锐二面 角的余弦值.21.已知椭圆中心在原点,焦点在x 轴上,离心率2e =,过椭圆的右焦点且垂直于长轴的弦长为 2.(Ⅰ)求椭圆的标准方程;(Ⅱ)已知直线l 与椭圆相交于,P Q 两点,O 为原点,且O P O Q ⊥.试探究点O 到直线l 的距离是否为定值?若是,求出这个定值;若不是,说明理由.18. (本小题满分12分)【解】(1) 函数()21f x x x η=--过(0,1)-点,在区间(4,6)上有且只有一个零点,则必有(4)0(6)0f f <⎧⎨>⎩即:1641036610ηη--<⎧⎨-->⎩,解得:153546η<<,所以,4η=或5η=…………3分当4η=时,211201015125068245C C C P C+==,当5η=时,11201522501249C C P C==…………5分4η=与5η=为互斥事件,由互斥事件有一个发生的概率公式,所以681212824549245P =+=6分 (2) 从该小学任选两名教职工,用ξ表示这两人请假次数之差的绝对值,则ξ的可能取值分别是0,1,2,3,于是()22225102015250207C C C C P C ξ+++===,1111115101020152025022(1)49C C C C C C P C ξ++===,1111520101525010(2)49C C C C P C ξ+===,115152503(3)49C C P Cξ===…………10分从而ξ的分布列:ξ的数学期望:222103*********494949E ξ=⨯+⨯+⨯+⨯=. …………12分19.证明:(Ⅰ)∵四边形ABC D 是菱形,∴2AD C D AB ===. 在AD E ∆中,AE =,1D E =,∴222AD D E AE =+.∴90AED ∠=︒,即AE C D ⊥.又AB C D //, ∴AE AB ⊥.…………2分 ∵PA ⊥平面ABC D ,AE ⊂平面ABC D ,由(Ⅰ)知AE ⊥平面PAB ,故平面PAB 的一个法向1(0,1,0)n =.………8分设平面P C D 的一个法向量为2(,,)n x y z = ,则2200n PE n CE ⎧=⎪⎨=⎪⎩ ,即200z x -=-=⎪⎩,令2y =,则2(0,n = . (10)分∴121212cos ,n n n n n n ===.所以,平面PAB 与平面P C D.……12分20. 解 (Ⅰ)设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),因为e =22,所以c a =22,据题意⎝ ⎛⎭⎪⎫c ,22在椭圆上,则c 2a 2+12b 2=1,于是12+12b 2=1,解得b =1,因为a =2c ,a 2-c 2=b 2=1,则c =1,a =2,故椭圆的方程为x 22+y 2=1.(Ⅱ)当直线l 的斜率存在时,设直线l 的方程为y =kx +m ,点P (x 1,y 1),Q (x 2,y 2),由⎩⎪⎨⎪⎧x 22+y 2=1,y =kx +m ,得(2k 2+1)x 2+4kmx +2m 2-2=0,所以x 1+x 2=-4km 2k 2+1,x 1x 2=2m 2-22k 2+1于是y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2=k 2·2m 2-22k 2+1+km ·-4km 2k 2+1+m 2=m 2-2k 22k 2+1. 因为O P O Q ⊥ ,所以x 1x 2+y 1y 2=2m 2-22k 2+1+m 2-2k 22k 2+1=3m 2-2k 2-22k 2+1=0,即3m 2-2k 2-2=0,所以m 2=2k 2+23.设原点O 到直线l 的距离为d ,则d =|m |k 2+1=m2k 2+1=63.当直线l 的斜率不存在时,因为⊥,根据椭圆的对称性,不妨设直线OP ,OQ 的方程分别为y =x ,y =-x 可得P ⎝ ⎛⎭⎪⎫63,63,Q ⎝ ⎛⎭⎪⎫63,-63或者P ⎝ ⎛⎭⎪⎫-63,-63,Q ⎝ ⎛⎭⎪⎫-63,63.此时,原点O 到直线l 的距离仍为63. 综上所述,点O 到直线l 的距离为定值63.。
